1. Introduction
During the recent financial crisis, a strong nexus between the financial sector and the sovereign credit risk has emerged worldwide. This potentially dangerous linkage is particularly pronounced in Europe, where banks—compared to the US or UK—are more important for providing liquidity to the economy and hold a much higher share of local government debt. The home bias is extreme for countries in the periphery, where in 2011 the holdings of sovereign bonds amounted to more than 15% of GDP (
Merler and Pisan-Ferry 2011). While the vicious spiral in Ireland started with problems in the financial sector and the bailouts triggered the sovereign default risk, the country’s high debt-to-GDP ratio seems to be the starting point of the problems for Italian banks (
Acharya et al. 2012).
The distinct and peculiar Italian circumstances require an accurate analysis of the linkage between the sovereign risk and the banking sector. First, in the past, Italian banks were much more focused on classical business and were less exposed to risky financial products. Therefore, before 2008 they had lower Credit default swap (shortly, CDS) spreads than banks from other European countries (
Acharya et al. 2012). Second, the amount of wealth invested by Italian banks in government bonds of their own country (the so-called
home bias) is historically higher than in any other troubled country (
Merler and Pisan-Ferry 2011). Moreover, Italian banks used part of the cheap liquidity offered by the European Central Bank (ECB) via the two long-term refinancing operations (LTROs) to further increase their exposure in government bonds to more than 40% until May 2012 (
Bank of Italy 2012). Therefore, their fate is particularly linked to the creditworthiness of the state. In fact, rising credit spreads cause direct losses in the treasury of the banks
Angeloni and Wolff 2012;
De Bruyckere et al. 2013, and they have an impact (although less evidently) on the net interest income (
Albertazzi et al. 2014). Furthermore, an increase in the government yield induces higher interest rates on loans and a consequent decline in the lending volume of banks. In addition and more generally, higher sovereign credit spreads might be a signal that potential future bailouts become less affordable.
Since the beginning of the European government crisis in the years from 2011 to 2013, the main issue has been how to mitigate the systemic risk and how to ensure that the future probability of such a crisis reoccurring is reduced. In particular, the relationship between sovereigns and the banking industry is still at the center of academic attention, and various papers have investigated different aspects of this issue (e.g.,
Baglioni and Cherubini (
2013);
Delis and Mylonidis (
2011);
Kalbaska and Gatkowski (
2012);
Kohonen (
2014);
Reboredo and Ugolinia (
2015a,
2015b);
Xu et al. (
2017)). The current paper addresses the following three research questions: (1) Is there a statistically significant dependence between the sovereign default risk and the stock returns of Italian banks, especially in the period 2011–2013? (2) Do large and small capitalized banks differ with respect to this relationship? (3) Is an increasing sovereign risk transferred through contagion to the equity returns of Italian banks? Compared to the literature, as a methodological contribution our investigation is mainly based on a two-step approach. First, we remove possible heteroscedasticity in the estimation of the time-varying dependence by using a parametric filtering procedure. Second, the research questions are answered by referring to the framework of (rank-invariant) association measures and tail dependence (
Patton 2012).
The remainder of the paper is organized as follows:
Section 2 provides a discussion on the meaning of the idiom
financial contagion and an overview of the tools for investigating the interdependence between the government yield spread and stock returns of the banking sector in Italy during the years 2003–2015.
Section 3 provides a detailed description of our empirical analysis.
Section 4 concludes and provides a discussion on the financial and policy implications of the empirical findings.
2. What Financial Contagion Is, and How to Detect It
Financial contagion refers to the diffusion of financial distress from one market/economy to another. In a recent survey by
Pericoli and Sbracia (
2003), for instance, various definitions of contagion are discussed that reflect the wide variety of meanings ascribed to this term. A contagious episode typically results in an unprecedented high correlation level among the affected systems: If a financial crisis arises, stock returns may start behaving more similarly than they did in the pre-crisis period. A common approach to detecting the occurrence of contagion therefore consists of identifying breaks in the transmission of shocks and inferring from them a significant rise in the correlation of asset returns. In practice, analysts compare cross-market correlations in tranquil and crisis periods, under the assumption that a significant rise in the correlation is caused by a break in the data-generating process. Such a method is consistent with the “very restrictive” definition of contagion provided by the World Bank (
World Bank 2016).
Although increased correlation may provide one way of measurement, simultaneous jumps in correlation are hardly contagion per se. For instance,
Pericoli and Sbracia (
2003) define contagion as an episode with excessive comovements in prices and quantities, conditional upon a crisis occurring in one market or a group of markets, which cannot be explained by simple interdependence. A similar definition is provided by
Kaminsky et al. (
2003), who make an explicit condition, writing “Only if there is
excess comovement in financial and economic variables [...] in response to a common shock do we consider it contagion”.
This paper contributes to the discussion in the following way. First, our technique avoids a potential sample selection bias (and consequently, spurious results) in the identification of specific shocks or tranquil/crisis periods. As
Pericoli and Sbracia (
2003) point out, the correct identification of the origin of the crisis matters—in particular for those tools based on correlation breakdown (i.e., structural breaks in correlation): Empirical analysis may be affected by a sample selection bias problem, which occurs whenever tests are conducted on ad hoc subsamples. Second, we refer to the “No Contagion, Only Interdependence” principle (see
Forbes and Rigobon (
2002)), since during turmoils some increase in comovements is merely an implication of interdependence. To be consistent with the previously mentioned definitions of contagion, we focus on the observed joint distribution function of the asset returns over the whole period, and we distinguish between comovements merely implied by interdependence, mainly related to the central region of the joint distribution, and comovements implied by contagious episodes, associated with the Left tail of the distribution (where extreme losses are located). We thus ground our analysis on the following general definition of financial contagion.
Definition 1. Financial contagion stands for a significant increase in excessive comovements of prices above typical comovements.
Definition 1 first recalls the use of excessive comovements, and second, it implicitly requires a comparison between comovements associated with different regions of the whole joint distribution function. This definition is consistent with that provided in
Bradley and Taqqu (
2004,
2005), who locally analyze the dependence structure of the involved financial time series by using a linear measure of association. Definition 1 is also consistent with the group of empirical works on the international transmission of shocks, where contagion is defined in terms of discontinuities in the data-generating process, and its presence is tested by checking for structural breaks in correlation (see the classification in
Pericoli and Sbracia (
2003) and the references therein).
According to Definition 1, the key point is the specification of an appropriate measure of contagion, able to distinguish contagious episodes from simple interdependence. To illustrate our methodology, we exploit some results from early works (see
Durante and Jaworski (
2010);
Durante and Foscolo (
2013);
Durante et al. (
2013)), in which contagion in European markets during the Great Recession and the European sovereign debt crisis has been investigated.
Generally speaking, we say that there is contagion between market/asset
X and market/asset
Y if there is more dependence between
X and
Y when they perform (very) badly than when they exhibit a typical performance. Thus, contagion is related to the strength of the dependence between
X and
Y at different regions of the domain of the joint distribution of
.
Durante and Jaworski (
2010) propose a contagion test grounded on the concept of copula (i.e., a function able to capture the rank-invariant dependency among random variables). Such an approach is based on the determination of a suitable threshold (i.e., quantile level)
that draws a distinction between normal comovements due to simple interdependence and excessive comovements.
Let X and Y be the random variables representing the returns of two financial markets/assets. In order to analyze contagion according to our definition, we are interested in the conditional distribution function of , which is supposed to be well defined in the following, where the conditioning set is one of the following types:
B is a tail set (usually denoted by T) that includes the realizations of that are judged to represent a risky scenario;
B is a central set, or mediocre set (usually denoted by M) that includes the realizations of that are judged to represent an “untroubled scenario”.
In particular, we assume here that the tail and the central set can be defined as suitable rectangles of whose boundaries are determined by quantile levels of X and/or Y. For instance, given two financial markets X and Y, if the contagion from X to Y is of main interest, then the following sets can be considered:
, representing possible extreme negative returns of X;
, representing returns of X that are judged to be usual fluctuations in the markets.
Here, and is the quantile function associated with X.
As shown in
Durante and Jaworski (
2010), contagion can be introduced in terms of a suitable comparison between copulas associated with the joint conditional distribution of a tail and a central set (see
Cherubini et al. (
2011);
Durante and Sempi (
2016);
Mai and Scherer (
2012)). To this end, we recall here the definition of concordance ordering in the bivariate case; see
Durante and Sempi (
2016). Given two continuous random pairs
and
with marginal distribution functions
and copulas
and
, respectively,
is said to be more concordant than
, written
, if
for all
,
and
,
. In order to indicate the case when
but
for at least one
, the symbol ≺ is used.
Definition 2. Let X and Y be the random variables representing the returns of two financial markets/assets. Let and be a tail and a central set, respectively, for which are determined by a suitable level α. Contagion between X and Y at the level exists if , where (respectively, ) is the copula of the conditional distribution function of (respectively, ).
Definition 2 has the following interesting features. It is a distribution-based notion, since it is grounded on the comparison between the dependence in a tail region (the copula related to the tail set) and the dependence in a central region (the copula of the central set) of the joint distribution function of . It is more informative than other methods based on linear Pearson’s correlation coefficient or tail dependence coefficients, since it is able to catch nonlinear dynamics and it is not restricted to the extreme tail. It depends on a suitable definition of tail (and central) set, according to the threshold . Finally, it appears when there is a strict order between the copulas. For instance, two markets that are perfectly comonotone (i.e., one market is an increasing function of the other) exhibit no (symmetric) contagion, since their dependence does not change at any time—these markets are simply interdependent.
Checking contagion as in Definition 2 could be difficult to implement in practice because the identification of the copula of the conditional distribution function of
may be complicated. In order to avoid such troubles, a non-parametric procedure has been suggested by
Durante and Jaworski (
2010). Given two copulas
C and
D, if
, then
, where
is the Spearman’s rank correlation coefficient (see
Schmid et al. (
2010), which for any pair of continuous random variables
X and
Y with copula
C is given by
Then, we check the absence of contagion by comparing the values of the associated Spearman’s rank-correlation coefficient. The following test can be thus performed:
where
and
are the copulas associated with the conditional distribution function of
X and
Y with respect to the tail and the central set, respectively. We define
, and
its empirical counterpart. Under some mild assumptions on the involved threshold copulas (
Durante and Jaworski 2010), the asymptotic behavior of
is given by
where
N stands for the sample size and the subscript of the variance term reflects the fact that the variance depends on the way the tail and the central sets are defined. By using the Gaussian approximation in Equation (
1), a contagion test could be easily implemented. The one-sided hypothesis test procedure reads as follows (
Dobric et al. 2013;
Durante and Jaworski 2010):
Compute and from the observations in and , for a given .
Compute bootstrap replications from the entire sample.
1 For each replication, calculate
and
, as well as the corresponding difference
.
On the basis of the vector of the bootstrap estimated difference between Spearman correlation coefficients , estimate the asymptotic variance of and calculate the test statistic , where is the bootstrap estimate of .
Reject the null hypothesis if , where denotes the standard normal distribution function and the chosen significance level.
An approach connected with our methodology has been recently proposed by
Li and Zhu (
2014), who use Kendall’s tau instead of Spearman’s coefficient. There are two main differences between our procedure and that introduced in
Li and Zhu (
2014): First, our test statistic does not require the identification of the trigger events that discriminate tranquil and crisis periods, since it is implicitly determined by choosing a suitable threshold
. Second, our methodology directly works on the dependence structure—it is grounded on the comparison between typical comovements, implied by interdependence and mainly related to the central region of the joint distribution, and excessive comovements implied by contagious episodes and associated with the tail of the joint distribution.
As shown by
Durante et al. (
2013), the occurrence of contagion strongly depends on the choice of the threshold
—a fact that could represent a key point when one wants to draw conclusions from the empirical analysis.
A formal test of contagion may have the drawback that it cannot quantify the size of the “jump” in the comovement—information that could be useful for classifying different markets according to their “extreme” linkages. In order to provide this feature, an empirical measure of contagion has been proposed in
Durante and Foscolo (
2013), called
Spearman’s Contagion Index (briefly,
). The
at level
is defined as
The domain of the
is by construction
: the higher the dependence in the tail of the distribution compared to its center, the larger the values of the
(in absolute terms) as evidence of contagion. The
assumes that during crisis times the correlation in the tail increases compared to the center. Under mild assumptions, the estimator of
is asymptotically Gaussian distributed. Moreover, its variance—which depends on
—can be estimated with bootstrapping, as explained in
Durante and Jaworski (
2010) and
Dobric et al. (
2013).
The value of
may be interpreted as follows. If
, then
, which could indicate the presence of contagion. Analogously, if
, then
, and contagion does not occur. If there is no difference in the conditional correlation between tail and central set, then
, meaning that no shift of the dependence structure has been realized. As for the test statistic, in order to prevent the arbitrary choice of
,
Durante et al. (
2014) suggest an average measure of contagion, where the index
is evaluated on an interval of threshold values.
The contagion index thus goes beyond the use of linear correlation: it can be calculated via non-parametric methods, and it does not require the specification of crisis/tranquil periods a priori. As such, it avoids possible problems of mis-specifying the dependence structure.
3. Data, Empirical Investigation, and Results
Our empirical analysis is based on first differences (i.e., changes) in the 10-year bond yield spread between Italy (
TRYDE10Y-FDS) and Germany (
TRYDE10Y-FDS), and log-returns of the FTSE Italy All Share Bank Index (
T8300-FTX) over the period 01/2003–07/2015 (
Datastream mnemonics in parenthesis). We use first differences, as
changes in the yield spread influence the market price of government bonds. To measure the impact of changes in the yield spread on Italian banks, we rely on equity returns because they seem to lead other market indicators (e.g., CDS rates) (
Fung et al. 2008;
Norden and Weber 2009). In order to alleviate non-synchronous trading hours in the past, we stick to a weekly frequency
Cappiello et al. 2006). Furthermore, we also use all time series of those constituents of the banking index (date July 2015) listed since January 2003, which corresponds to the start of the index and the start of our investigation period.
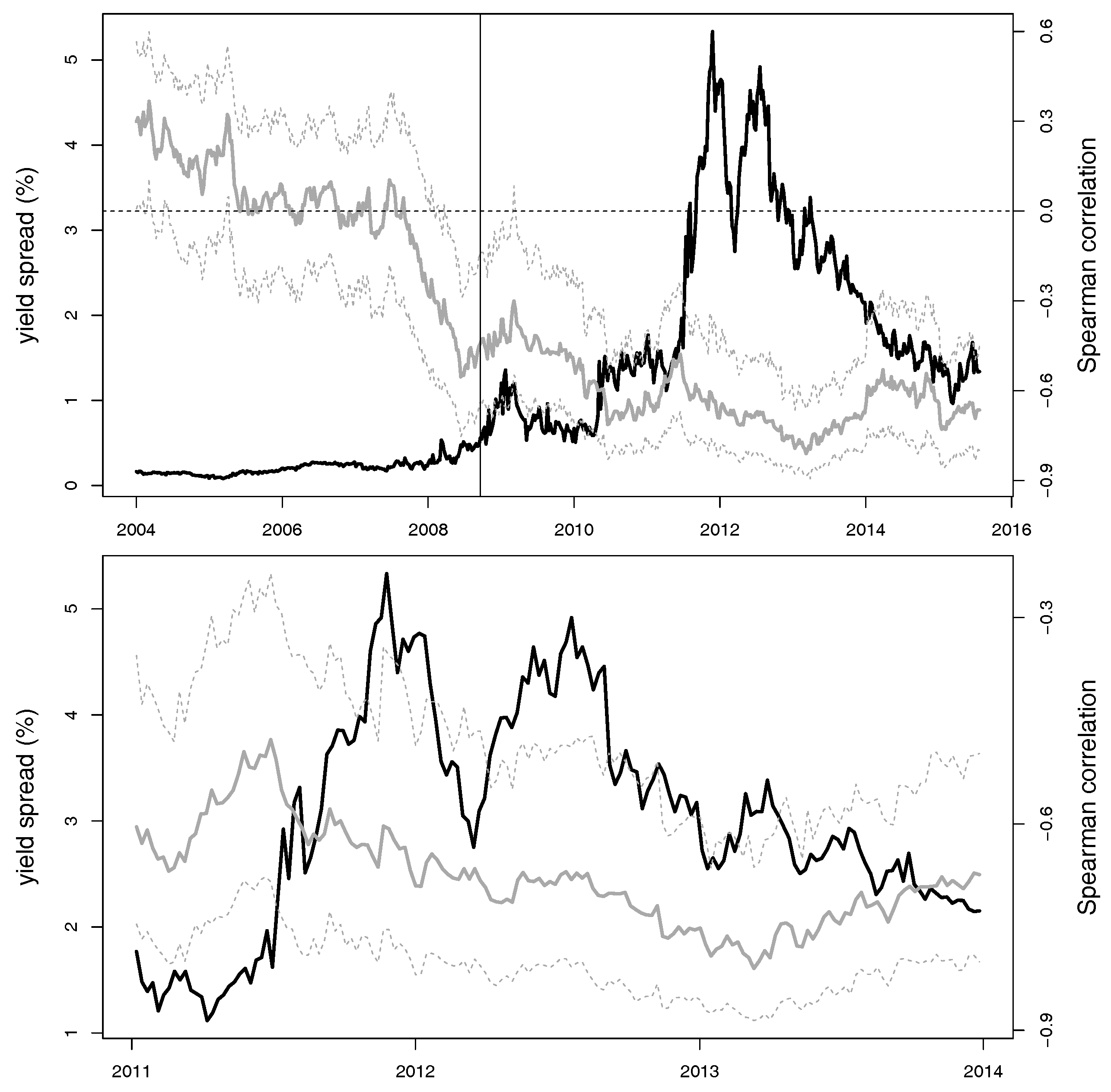
Figure 1 shows the evolution of the Italian yield spread (as solid black line) and the 1-year rolling window Spearman’s rank correlation between differences in yields and log-returns of the banking index (solid gray line) with 95% confidence intervals (dotted gray lines).
2 While before 2008 the independence assumption between changes in yield spread and stock returns of the bank index cannot be rejected (at 5% level) according to a nonparametric test of independence for multivariate time series proposed by
Genest and Rémillard (
2004), afterwards it turned out that the Spearman’s rank correlation was significant. Given that
Figure 1 suggests two different regimes for the correlation over time, we conduct the nonparametric test for change-point detection based on the (multivariate) empirical distribution function proposed by
Holmes et al. (
2013) and implemented in
R by
Kojadinovic (
2015). We find a change-point to be located approximately at the end of September 2008,
3 the time when the investment bank Lehman Brothers filed for Chapter 11 bankruptcy protection. Indeed, the Spearman’s correlation in the two highlighted periods is statistically different: While until September 2008 the correlation between the two time series is
with a 95% block bootstrap confidence interval of
(indicating that the independence assumption cannot be rejected at the 5% significance level), afterwards the correlation declines to
with the corresponding confidence interval
, with a peak of
and a corresponding confidence interval
in the period 2011–2013. We observe that the negative dependence is statistically significant after 2008. In the following, for simplicity we refer to these two time intervals as first and second period, respectively. For each period, we carry out a dependence analysis by estimating several measures of association between changes in the yield spread and stock returns of the banking system.
In order to focus on the contagion effect, following
Forbes and Rigobon (
2002) it should be considered that heteroscedasticity in the univariate financial time series might induce a bias in the estimation of the dependence. Moreover, the calculation of copula-based measures (like Spearman’s correlation) usually benefits from considering data that are not serially dependent. For all these reasons, it is convenient to filter each time series in each sub-period with a univariate time series model for the conditional mean and the conditional variance, and hence apply our methodology to the residuals of the fitted models. As shown in
Rémillard (
2017), the limiting distribution of rank-based dependence measures computed with the residuals are the same as if the dependence measures were computed with the innovation (i.e., they are able to detect the (marginal-free) dependence among the time series). Specifically, in order to capture stylized facts in financial markets, we assume that each time series follows an ARMA-GJR-GARCH model
Glosten et al. 1993), whose standardized residuals have a constant conditional
t-distribution. The Bayesian information criterion (BIC) is used to select the model order. The estimated standardized residuals are given by
where
stands the observation of the time series
j at time
t,
is the vector of estimated parameters for the ARMA models,
is the vector of estimated parameters for the GJR-GARCH models, and
stands for past information of the time series. The goodness-of-fit of this model choice is checked by different diagnostic tests. The Box–Ljung and the ARCH test (at one and four lags) assess the absence of residual autocorrelation and heteroscedasticity at a significance level of 1%. Moreover, the Kolmogorov–Smirnov test confirms the
t-distribution assumption for the residuals, and the Augmented Dickey–Fuller test does not show the presence of unit roots at a significance level of 1%.
4In order to focus on rank-invariant dependence, we further compute the so-called pseudo-observations
: Therefore, for each time series and sub-period, the estimated standardized residuals
have been sorted and scaled by
,
5 where
n stands for the sample size (
Patton 2012).
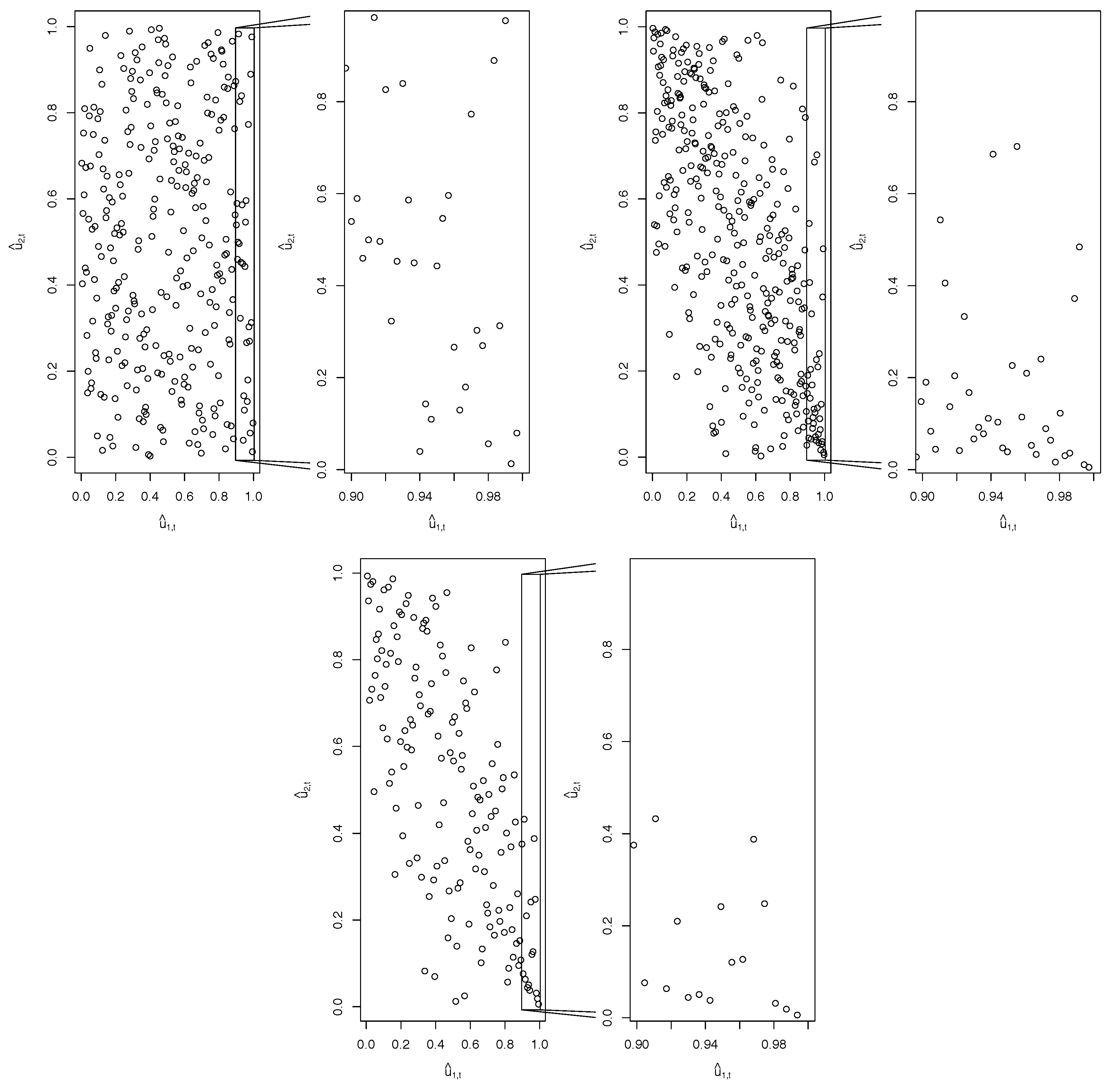
Figure 2 shows the scatter plot of pseudo-observations for the yield spread
against the returns of the banking index
, separately for the first (Upper Left Panel) and second period (Upper Right Panel), respectively, with a focus on the period 2011–2013 in the Bottom Panel of
Figure 2. By focusing on the enlarged Right Rectangles of the bivariate distributions (which focus on the upper tail sets of the time series), for the second period we notice an increased (negative) dependence between high changes in the yield spread and low returns of the banking index, as previously quantified and shown in
Figure 1; i.e., the Italian banking industry seems to suffer more under a severe increase in the sovereign default risk during the second period than during the first one.
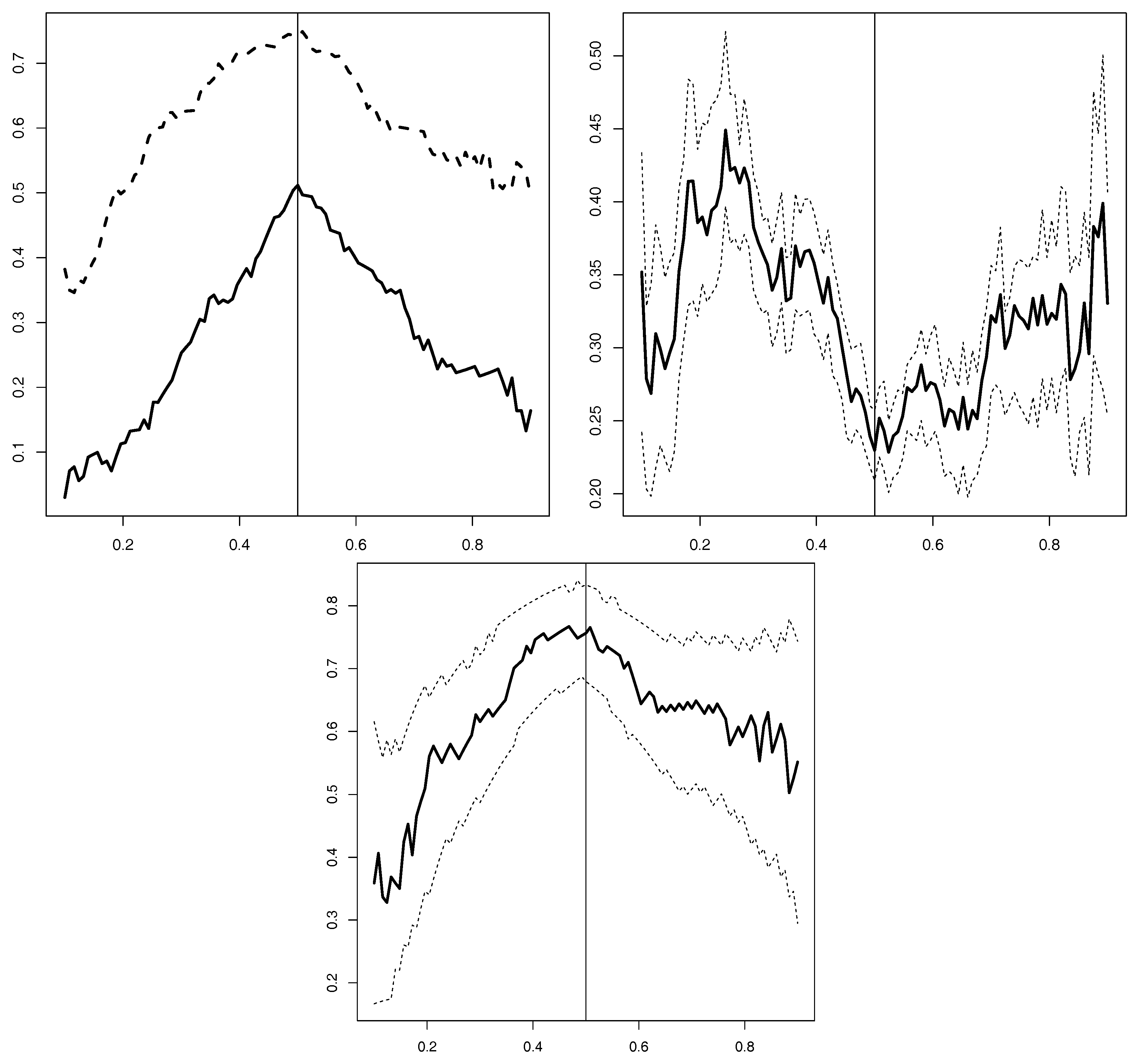
In order to analyze the behavior in the tails and to better understand the change observed in the second period, the Upper Left Panel of
Figure 3 shows the estimated quantile dependence (also called tail concentration function, see
Patton (
2012) and
Durante et al. (
2015)) for the first period (solid line) and the second period (dashed line), respectively, by conditioning on the the yield spread. Once again, a focus on the period 2011–2013 is provided in the Bottom Panel of
Figure 3. The upper quantile dependence is defined by
i.e., gives the probability to observe
low pseudo-observations in stock returns conditional on
high pseudo-observations in changes of the yield spread with
; analogously, the lower quantile dependence is defined by
with
. Two findings are noteworthy. First, the right-tail quantile dependence is higher than the left-tail one in both periods. Therefore, the probability that large increases in the yield spread induce low stock returns is higher than for the contrary case of large declines in the yield spread. Second, the dependence in the second period (dashed line) is generally higher than in the first period (solid line). In the Upper Right Panel of
Figure 3, we calculate the difference between the tail dependence in both periods together with 95% bootstrap confidence intervals. The figure confirms that for all quantile values the difference between the dependence in the two periods is statistically significant.
Finally, we use the Spearman’s contagion index proposed by
Durante and Foscolo (
2013) to quantify potential contagion effects from changes of the yield spread to returns of the banking index. The
from
to
is defined by
where
indicates the operator to calculate the Spearman correlation and
the chosen quantile value.
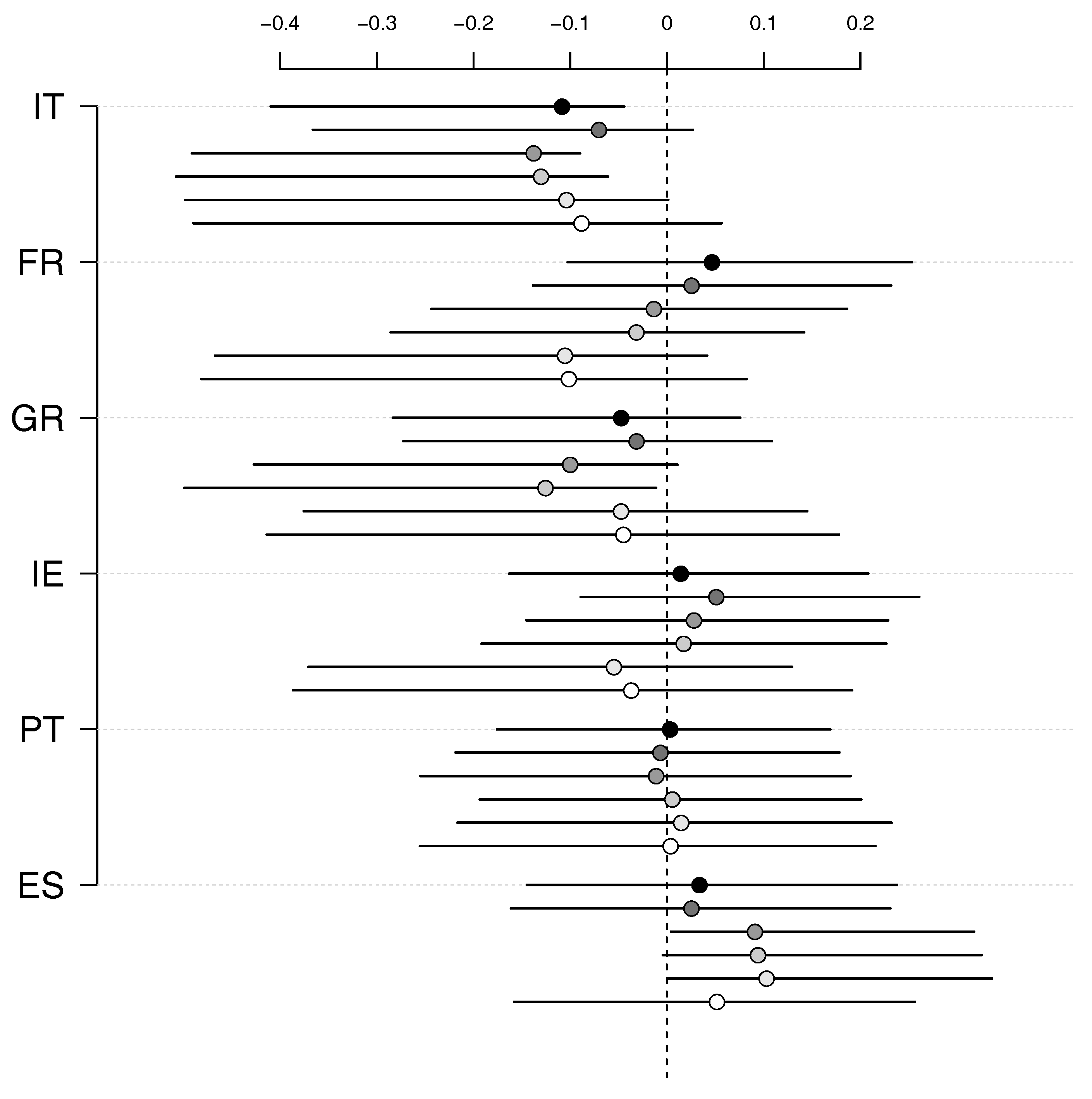
Figure 4 shows the
for extreme pseudo-observations of changes in the yield spread by choosing
with the 95% bootstrap confidence interval in the second period. Although the
is negative, which indicates that the dependence in the tails is smaller than in the center, we cannot claim that our findings are statistically significant in the second period (as also confirmed by the formal test of contagion shown in
Figure 7). Therefore, in line with other papers (
Caporin et al. 2013;
Forbes and Rigobon 2002;
Serwa and Bohl 2005), we cannot claim that contagion effects caused the increased dependence in the recent past (compared to
Broto and Perez-Quiros (
2015);
De Bruyckere et al. (
2013)). We repeated the same exercise for other EU countries. Interestingly, the same conclusion—an unclear picture of contagion effects—applies to France (one core European country) and other peripheral countries (i.e., Greece, Ireland, Portugal, and Spain, respectively); see
Figure 4.
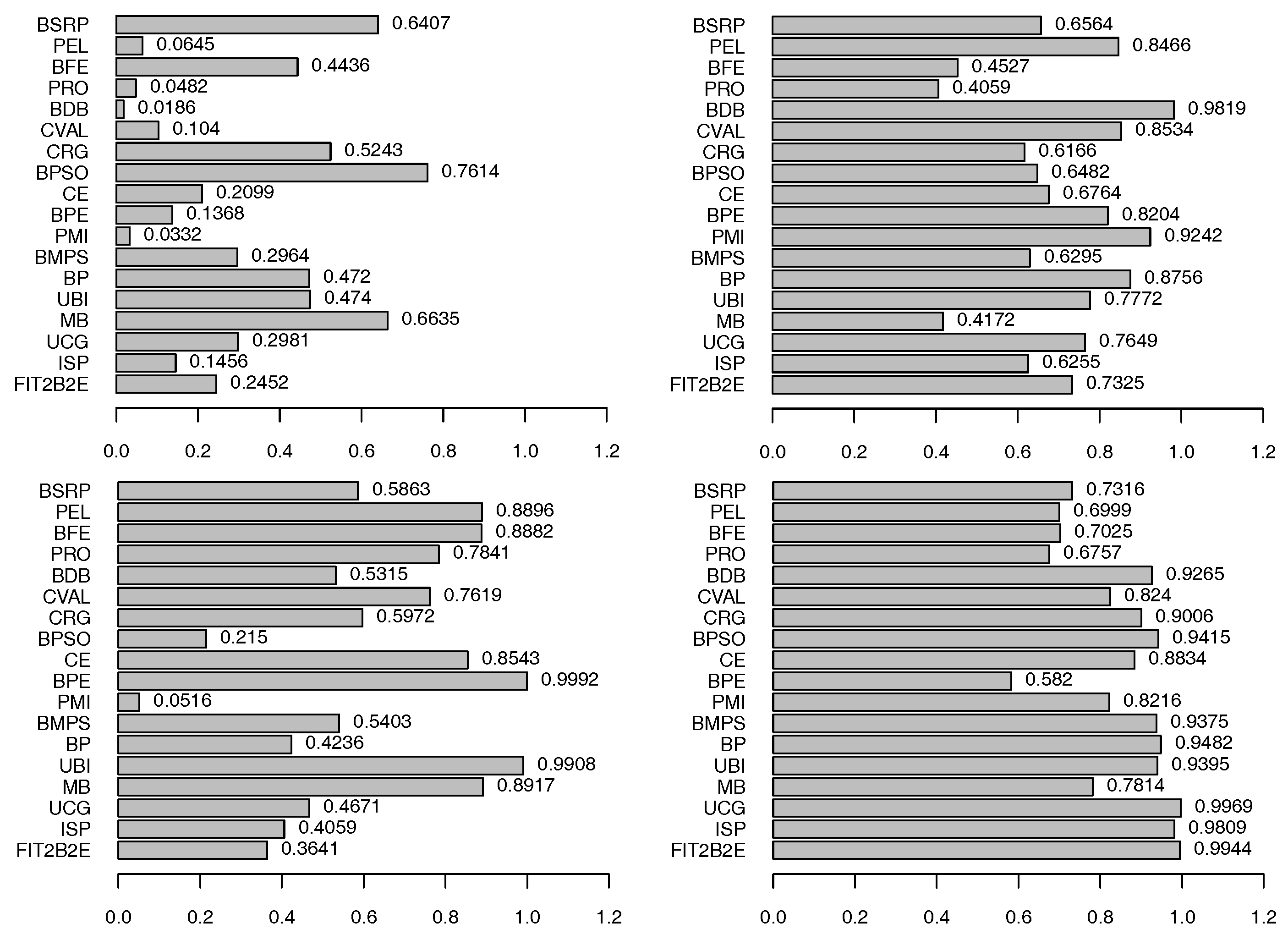
3.1. Large vs. Small Banks
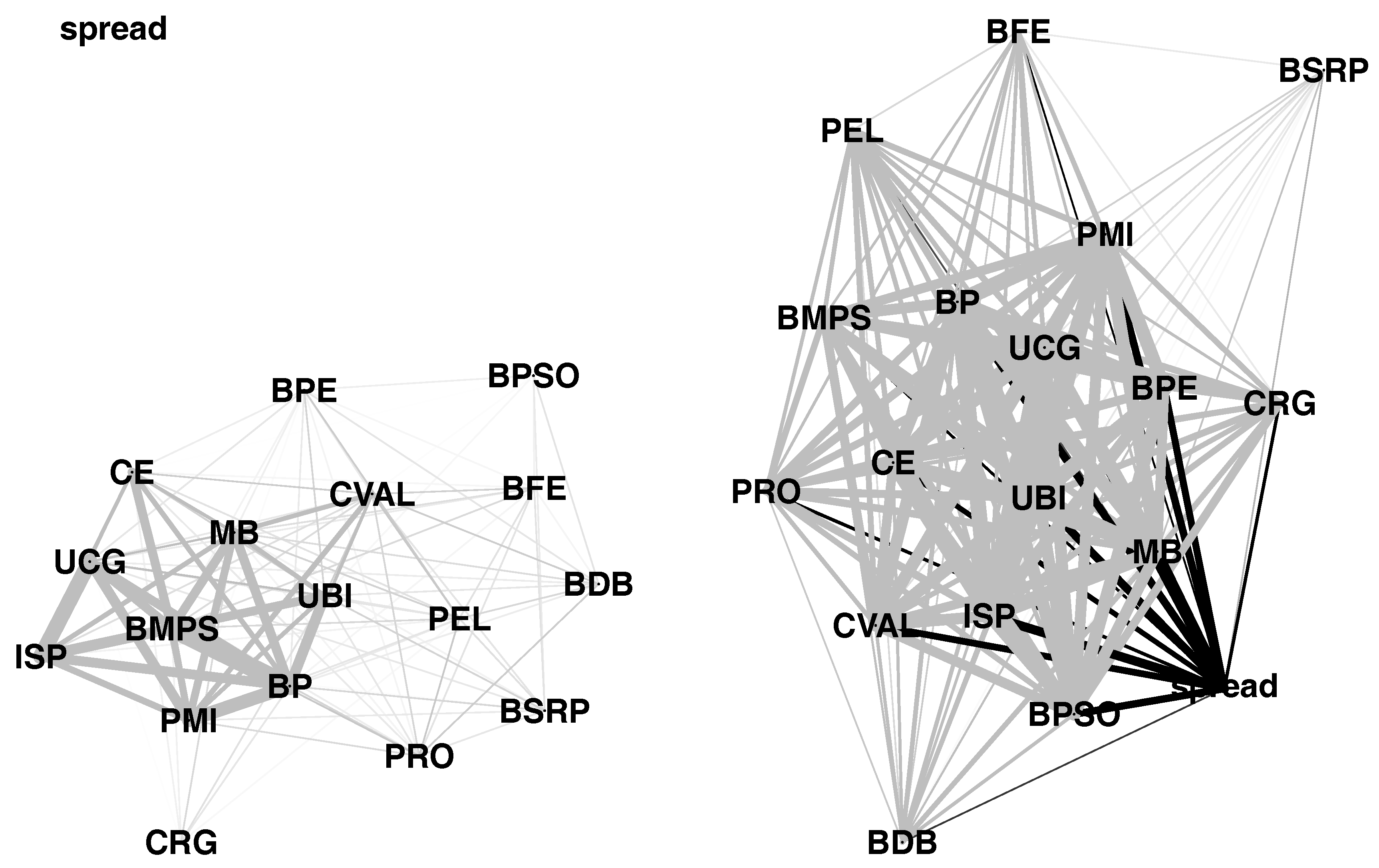
In
Figure 5, we use a network representation to compare the dependence of pseudo-observations between changes in the yield spread and the returns of the single constituent Italian banks.
6 The width of the lines shows the extent of the dependence, and the gray (respectively, black) color indicates a positive (respectively, negative) correlation.
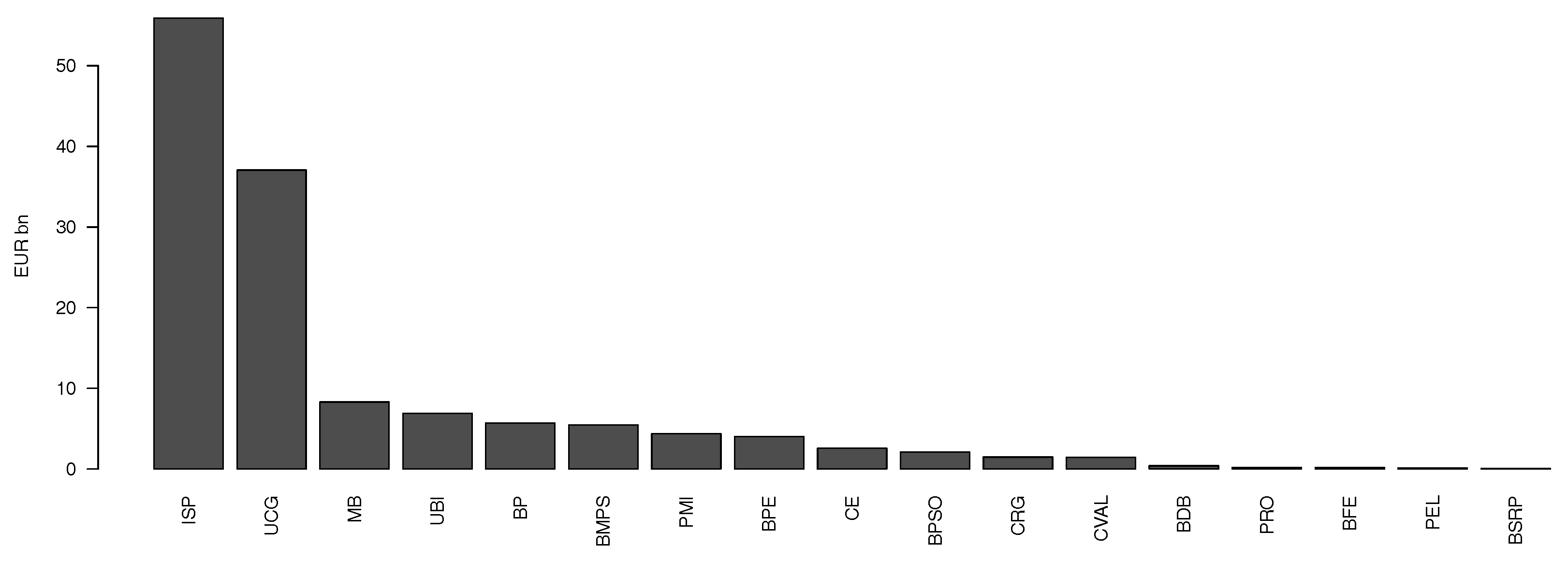
It can be easily seen that during the first period there is basically no relationship between changes in the yield spread and the single banks. During the second period, a high negative correlation (shown by thick black lines) between changes in the yield spread and the single banks can be observed. Furthermore, compared to the first period, the correlation among the banks seems to increase considerably. In order to investigate the relationship between the dependence and the size of the banks, in
Figure 6 we indicate the corresponding market capitalization (in billions). By ranking the Italian banks according to their market capitalization, it can be seen that especially during the crisis period, large capitalized banks are highly and negatively correlated to changes in the yield spread (see the Right Panel of
Figure 5). This might also explain the high correlation
among the large capitalized banks at the center of the network, while small capitalized banks in the outer regions seem to be less affected.
Despite the observed increased correlation in the second period, we are not able to detect a significant evidence of contagion from spread to banks in both periods (
Figure 7, Upper Panels). Reverse causality has also been tested, since impaired interbank markets raised funding costs of all banks, and increased the expectations that governments have to bailout their indigenous banks. The contagion test procedure rejects this conjecture (
Figure 7, Bottom Panels). Therefore, potential bi-directional contagious effects seem to be unlikely according to our methodology.
Figure 7.
p-values associated with the contagion test statistic at the level . In the (Upper Panels), the null hypothesis of absence of contagion from spread to banks is tested in the first (Left Panel) and second period (Right Panel), respectively. In the Bottom Panels, the null hypothesis of absence of contagion from banks to spread is tested in the first (Left Panel) and second period (Right Panel), respectively.
Figure 7.
p-values associated with the contagion test statistic at the level . In the (Upper Panels), the null hypothesis of absence of contagion from spread to banks is tested in the first (Left Panel) and second period (Right Panel), respectively. In the Bottom Panels, the null hypothesis of absence of contagion from banks to spread is tested in the first (Left Panel) and second period (Right Panel), respectively.