Bayesian Calibration of Generalized Pools of Predictive Distributions
Abstract
:1. Introduction
2. Combination and Calibration
2.1. A General Combination Model
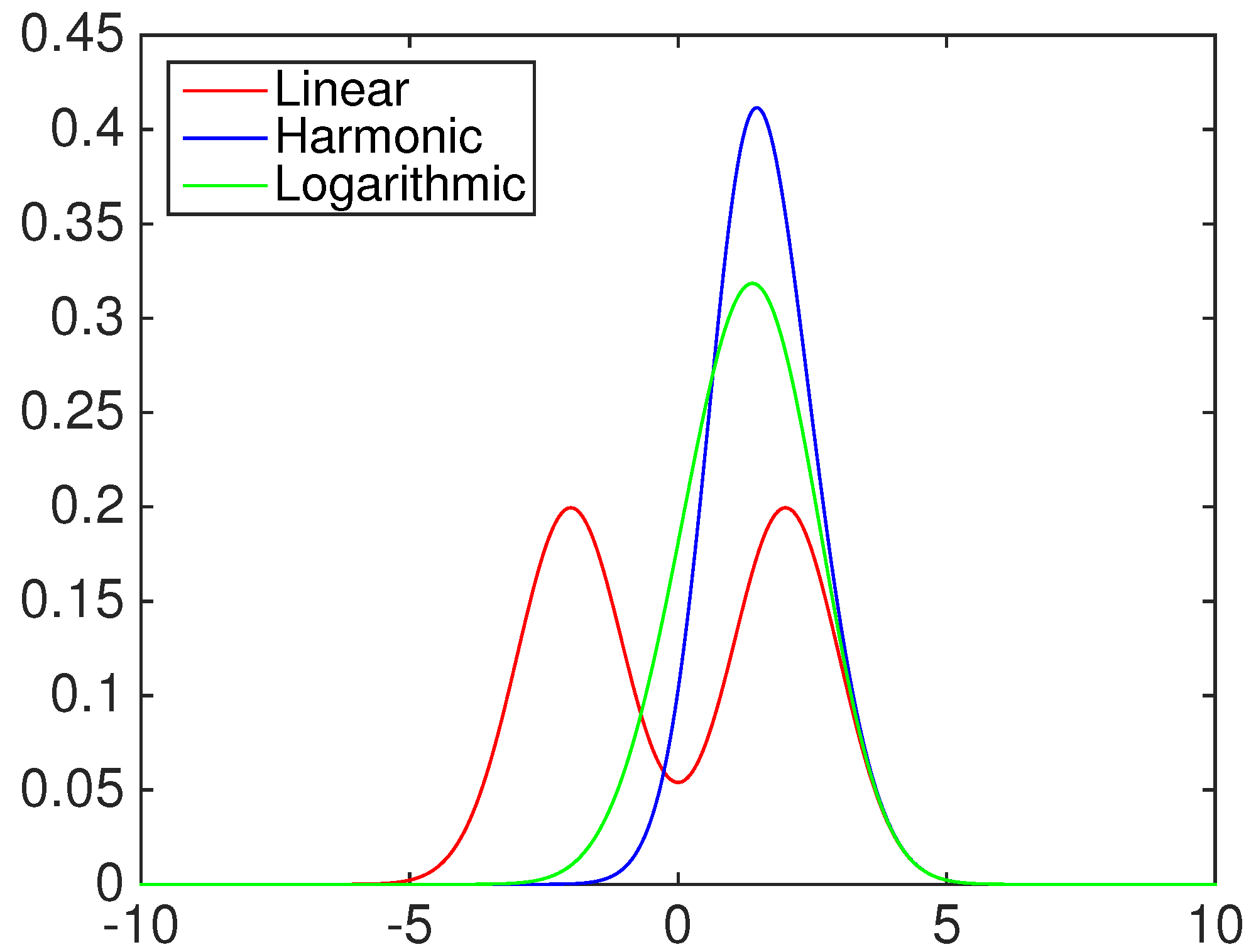
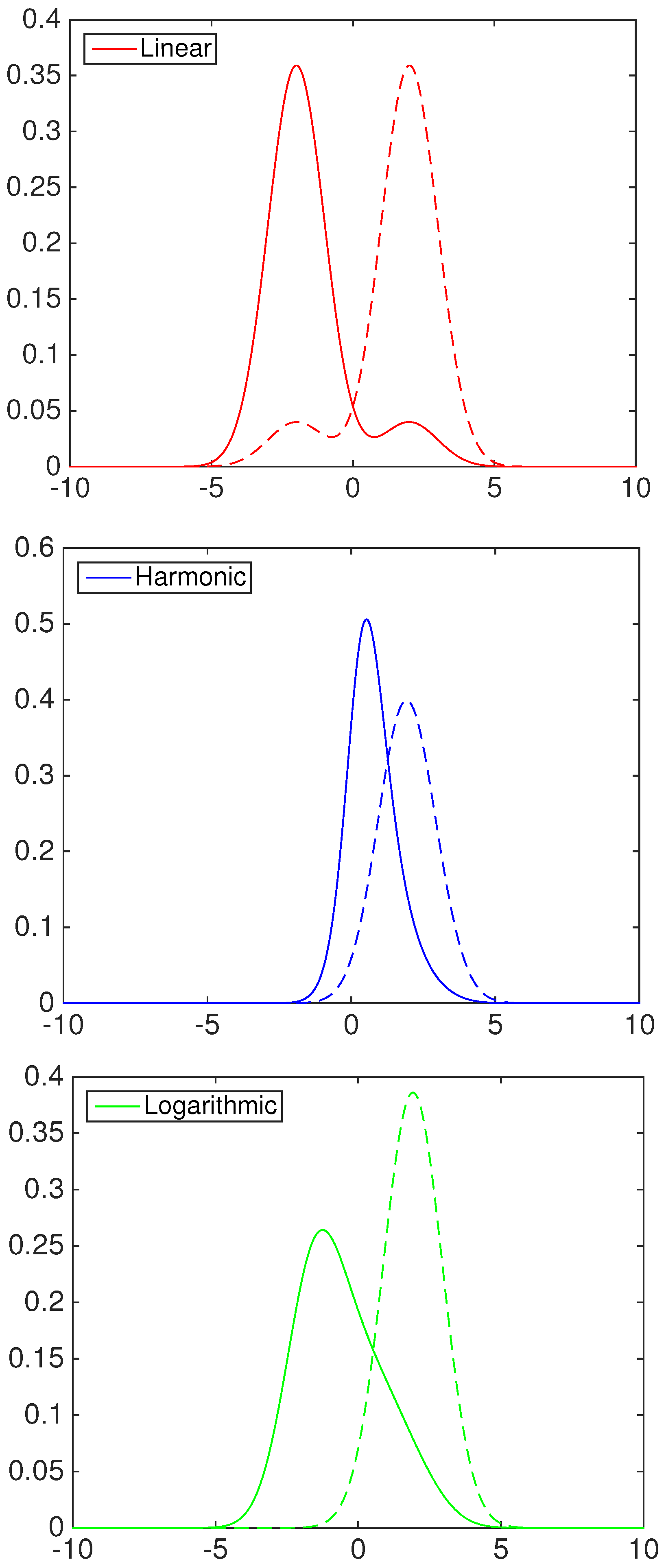
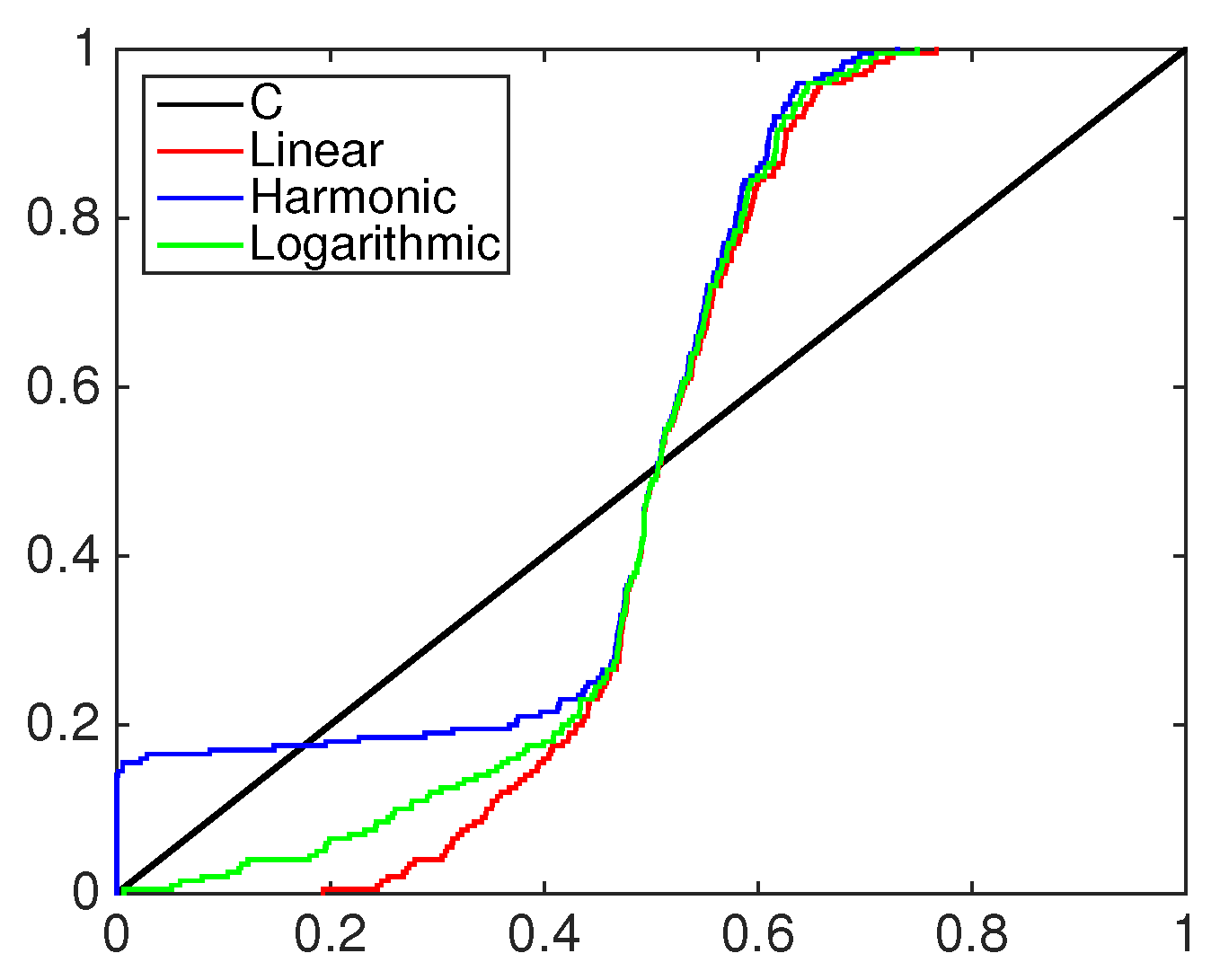
- Linear opinion pool (), i.e., :
- Harmonic opinion pool (), i.e., :
- Logarithmic opinion pool (), i.e., :
- Linear opinion pool ():
- Harmonic opinion pool ():
- Logarithmic opinion pool ():
2.2. A Calibration Model
- The combination formula is flexibly dispersive if for the class of fixed, non-random cdfs, for all and , , then is a neutrally-dispersed forecast (i.e., ).
- The combination formula is exchangeably flexible dispersive if for the class of fixed, non-random cdfs, for all and , , then H is anonymous, i.e., , and a neutrally-dispersed forecast.
2.3. A Beta Mixture Calibration and Combination Model
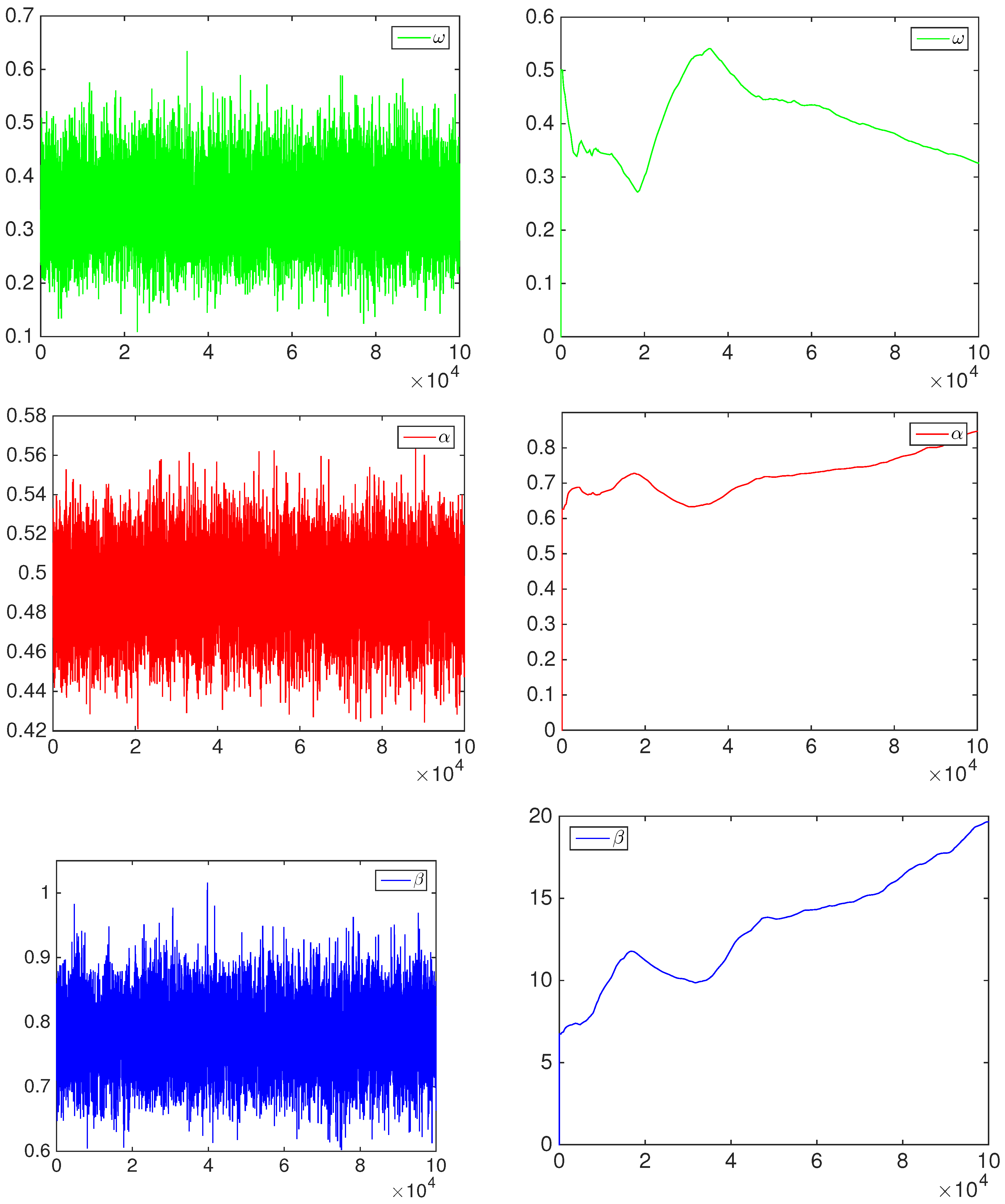
3. Bayesian Inference
4. Empirical Results
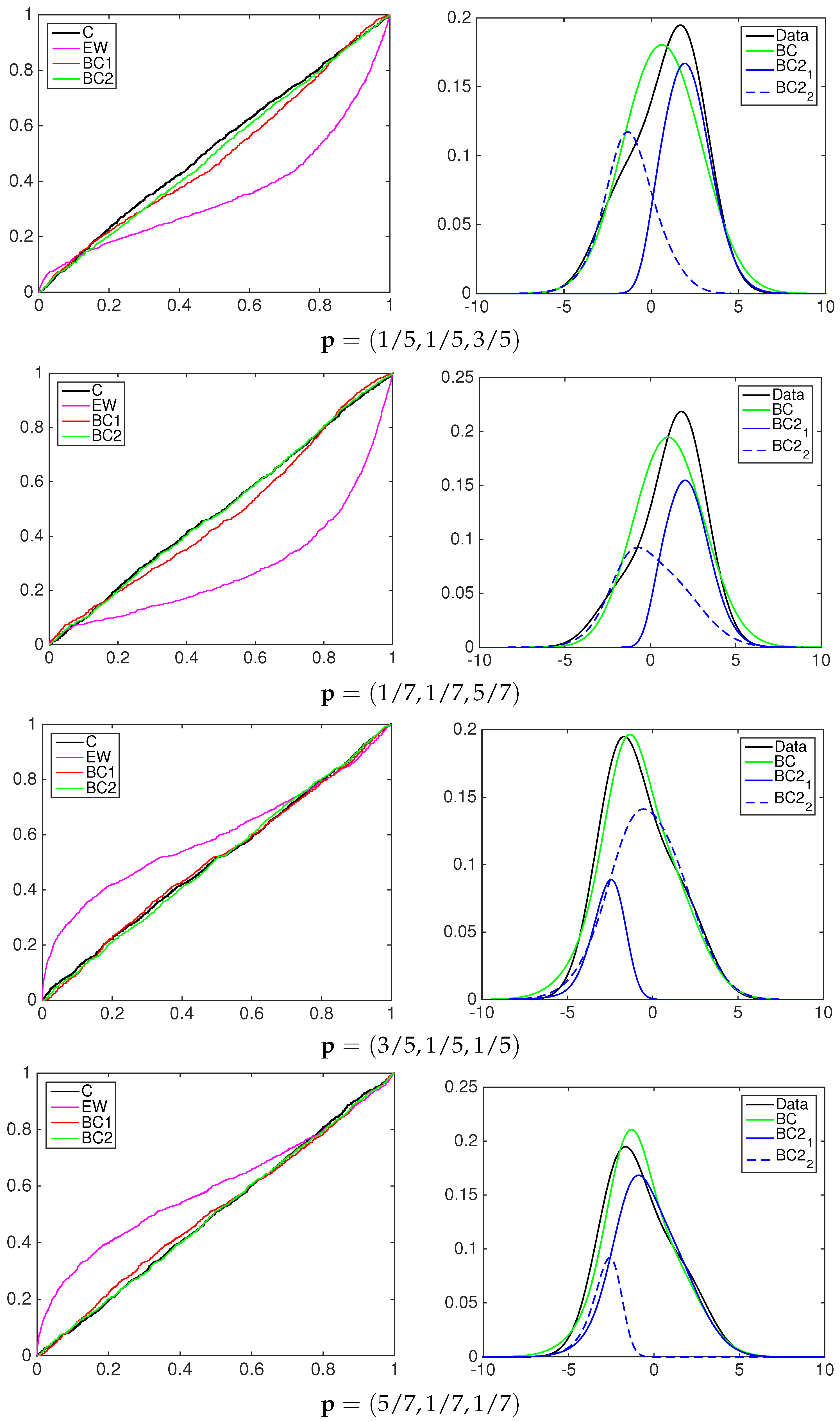
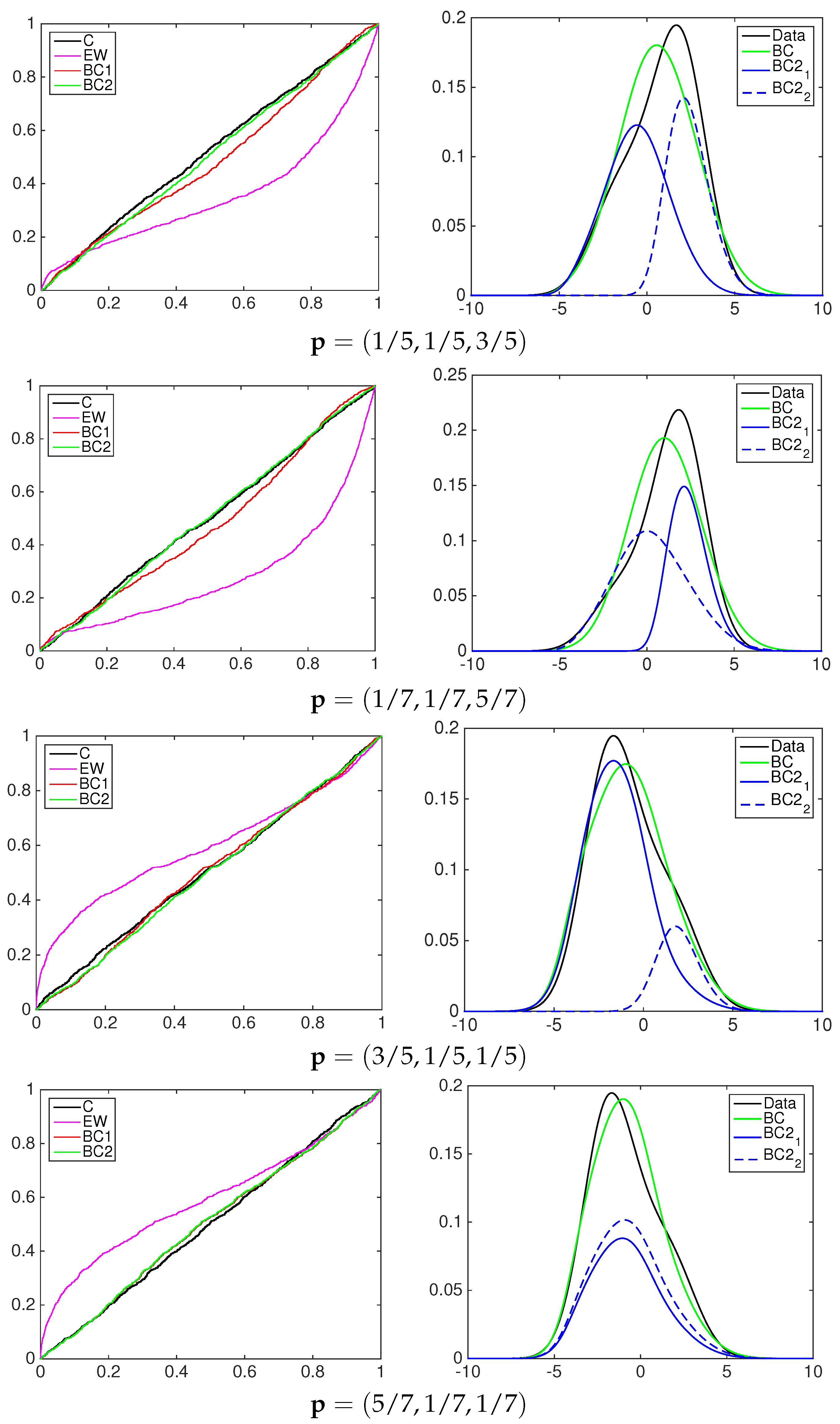
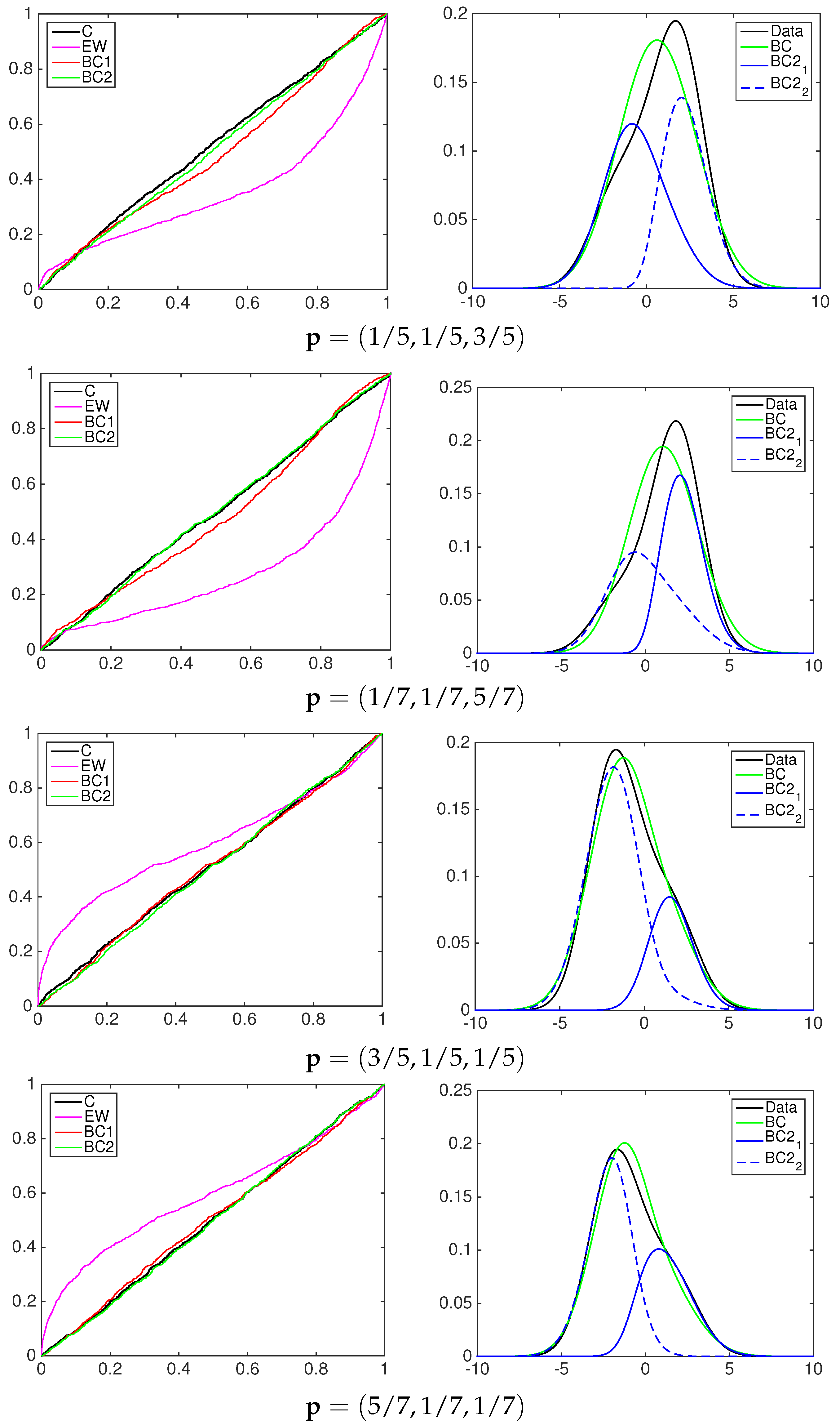
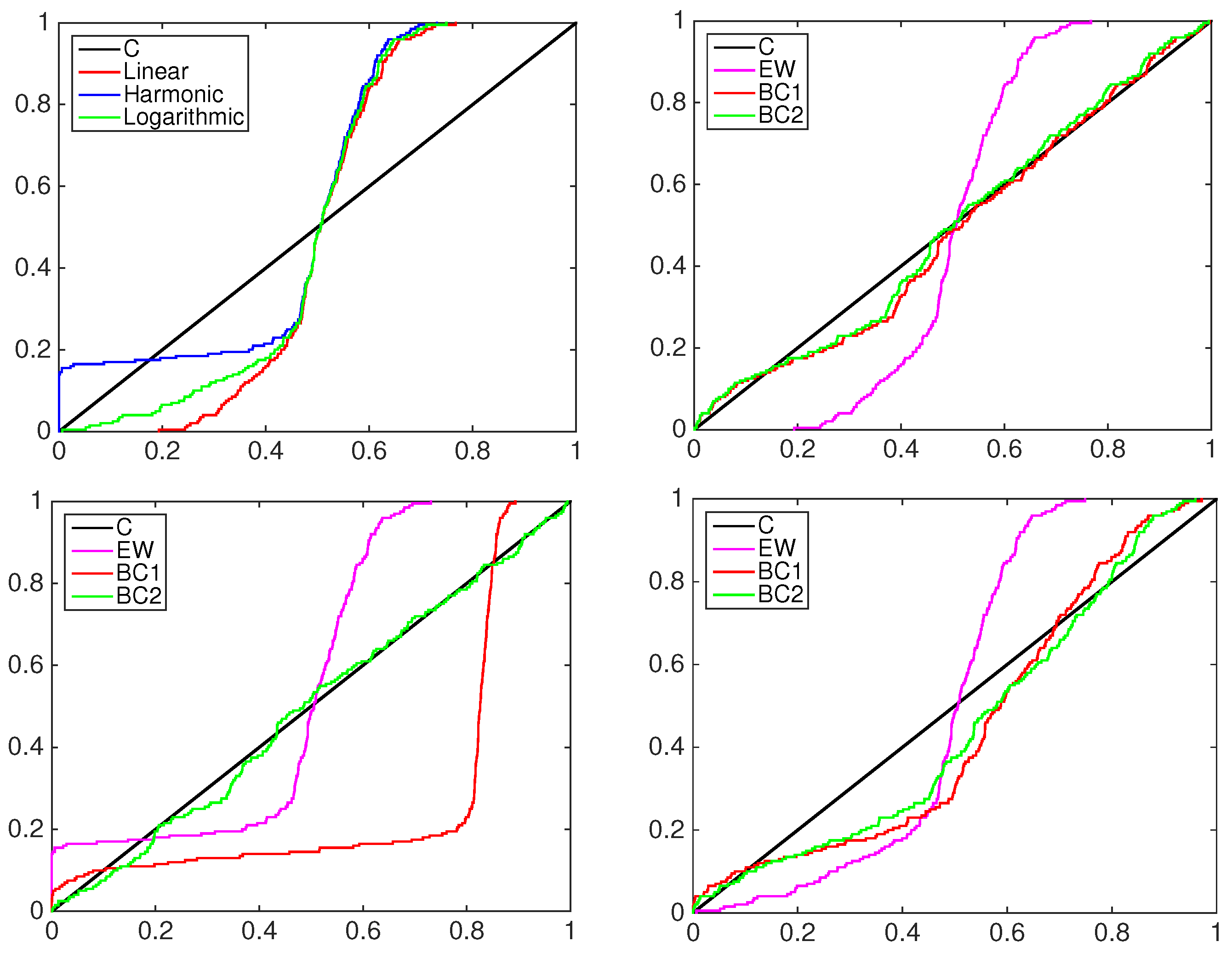
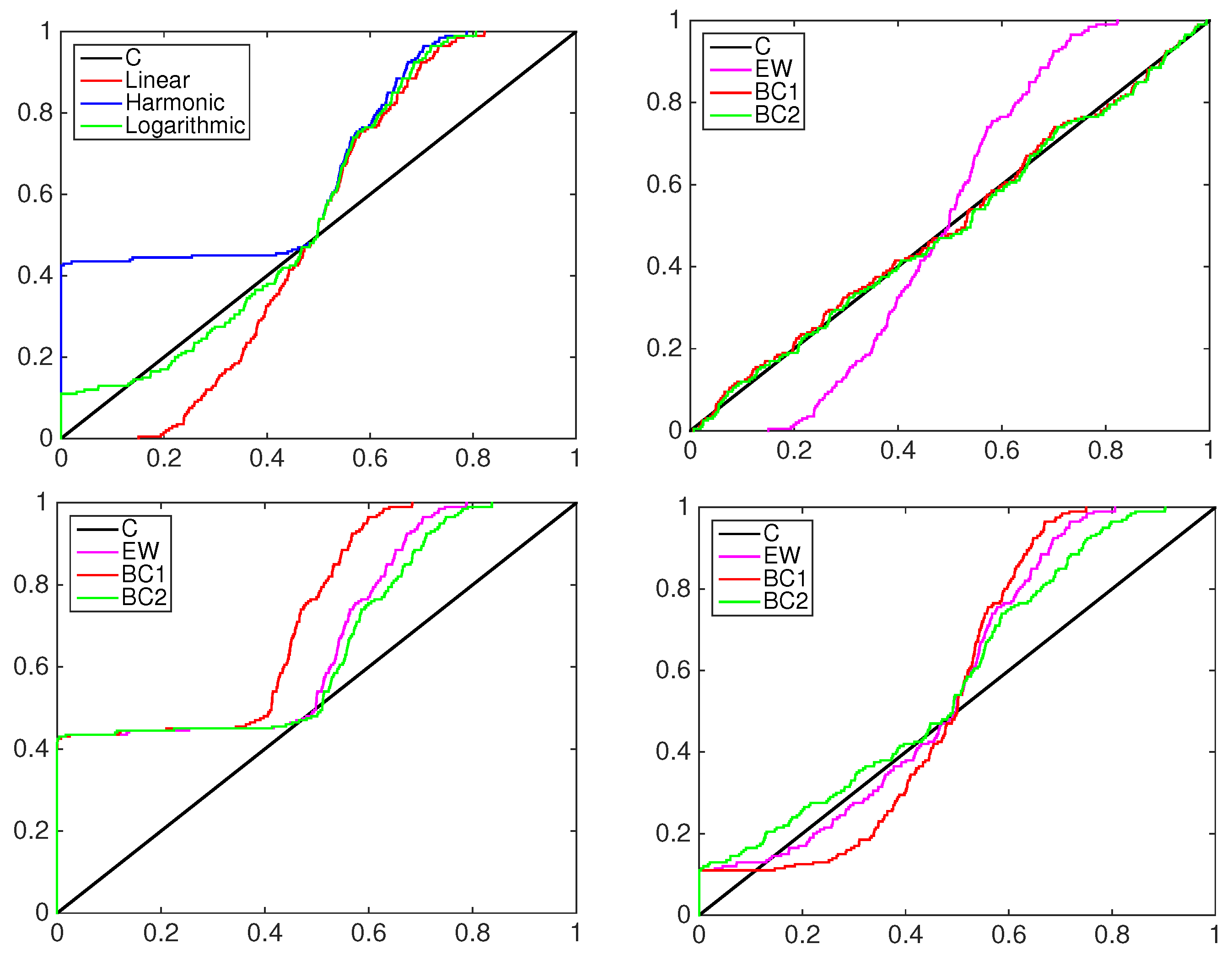
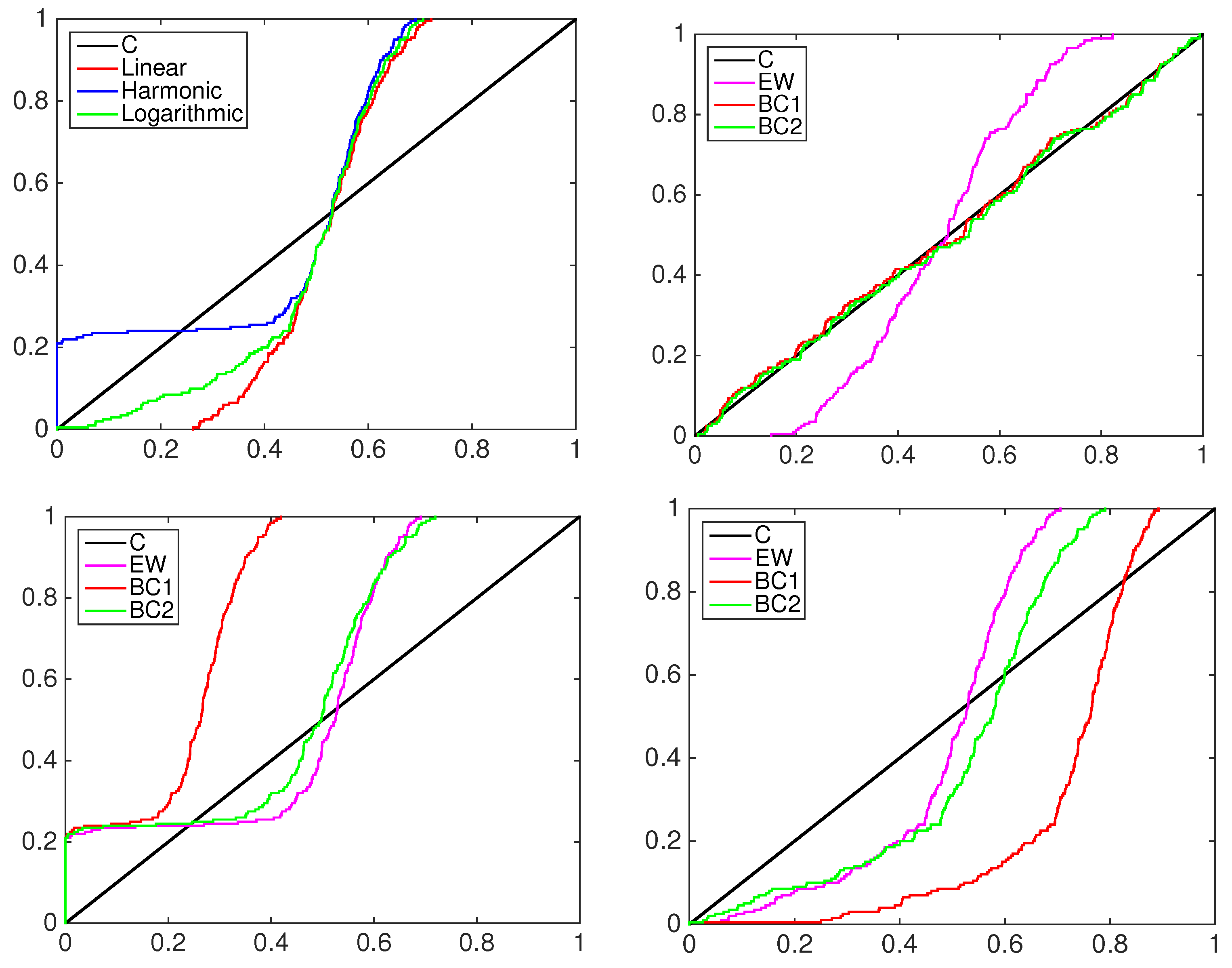
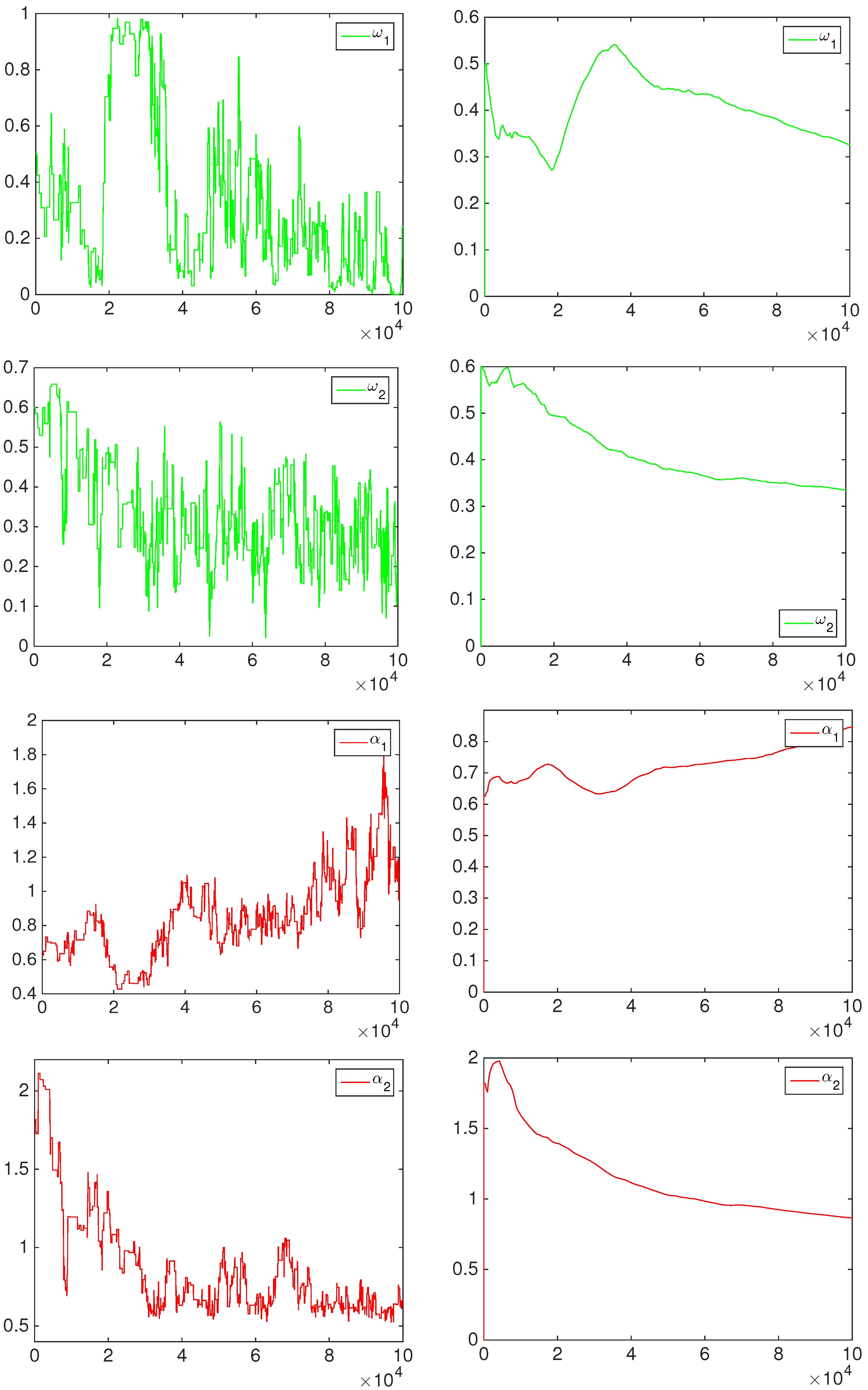
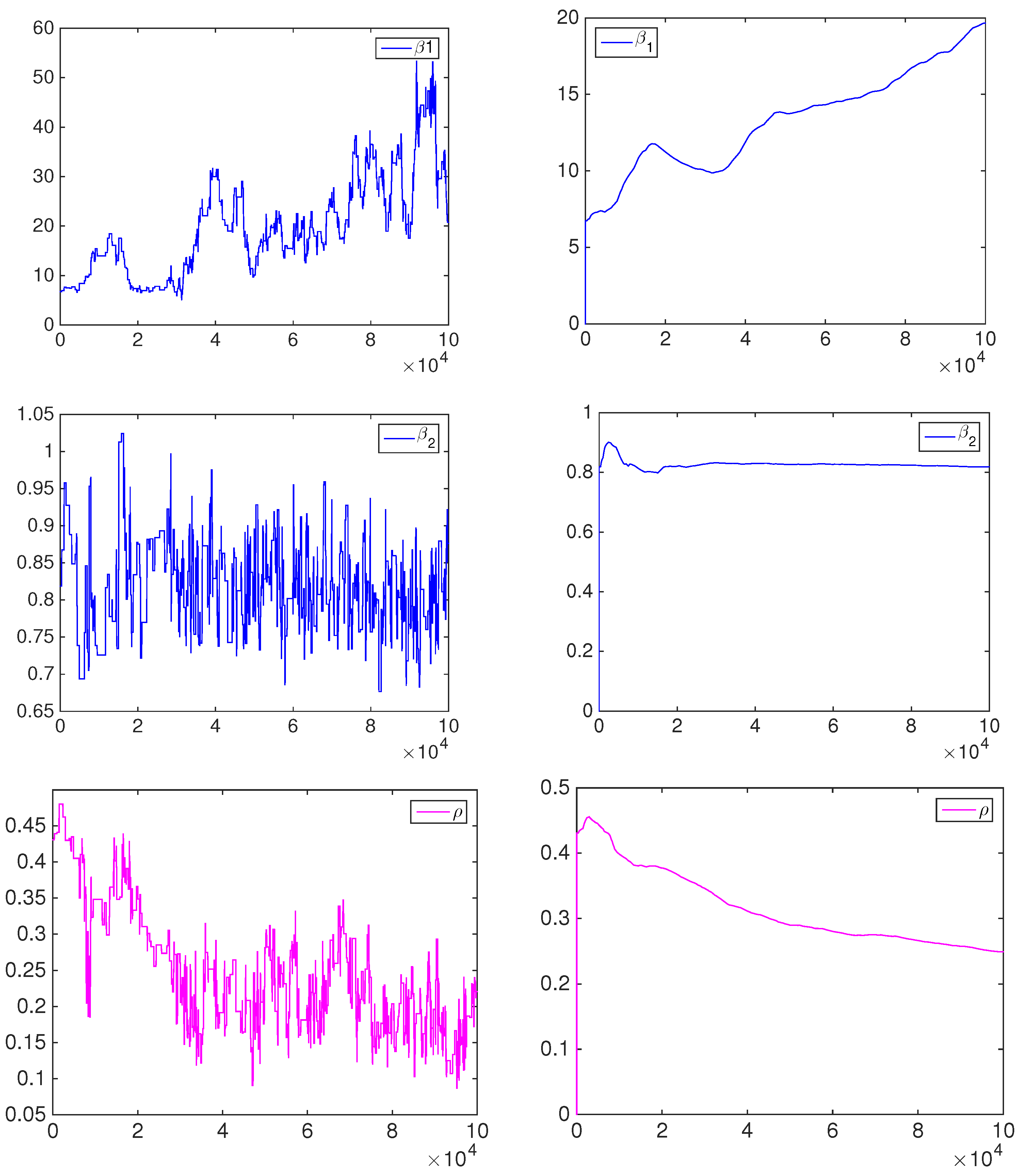
4.1. Simulation Study
- the equally-weighted model (EW):where ω is the combination weight equal to . correspond to Equations (3)–(5), for linear, harmonic and logarithmic pool, respectively, when ;
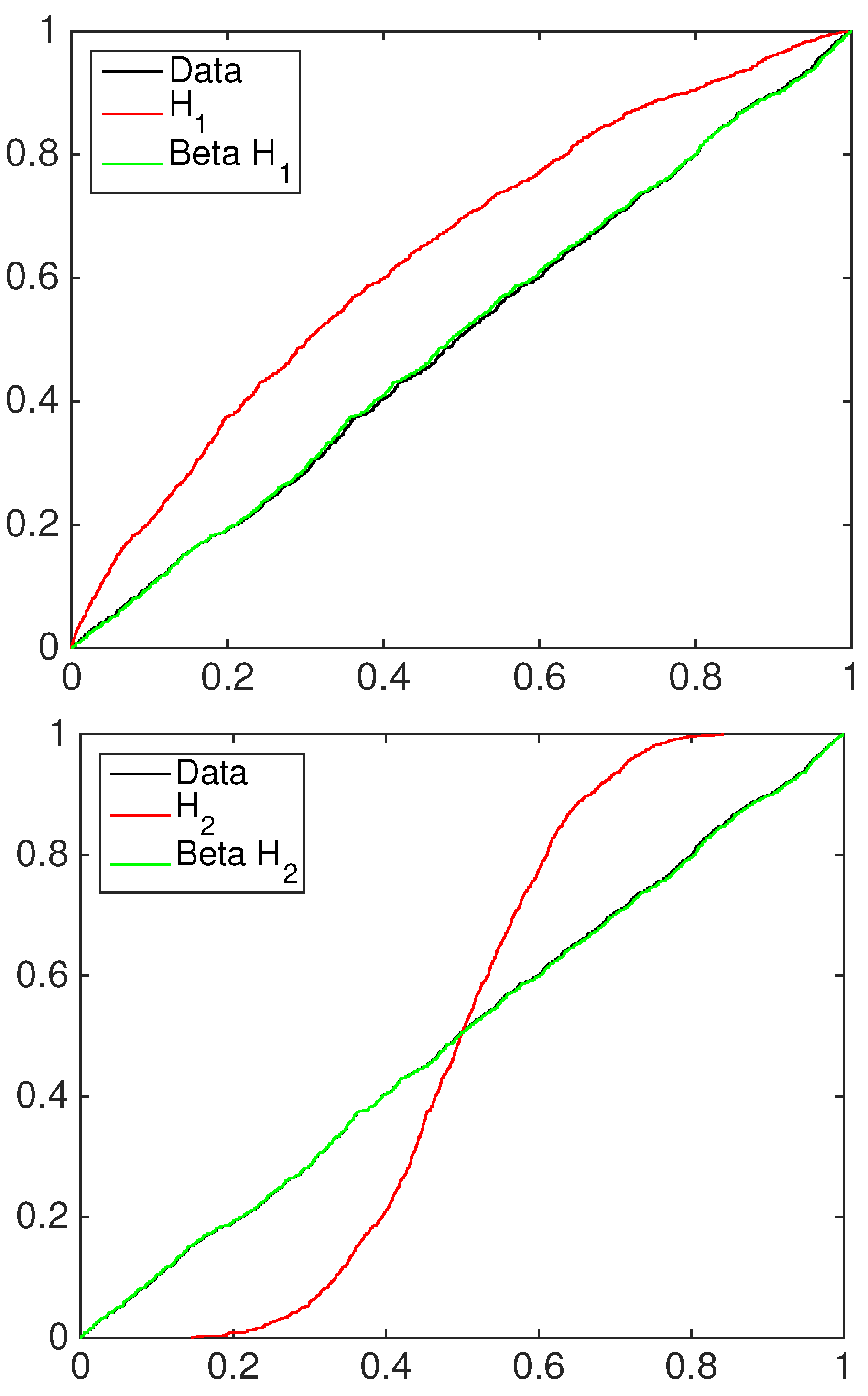
- the beta calibration model (BC1):where , and , with , is defined by Equations (3)–(5);
- the two-component beta mixture calibration model (BC2):where and is the same as in the BC1 model.
4.2. Financial Application: Standard&Poors500 Index
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix. Computational Details
References
- G.A. Barnard. “New methods of quality control.” J. R. Stat. Soc. Ser. A 126 (1963): 255–259. [Google Scholar] [CrossRef]
- H.V. Roberts. “Probabilistic prediction.” J. Am. Stat. Assoc. 60 (1965): 50–62. [Google Scholar] [CrossRef]
- J.A. Hoeting, D. Madigan, A.E. Raftery, and C.T. Volinsky. “Bayesian model averaging: A tutorial.” Stat. Sci. 14 (1999): 382–417. [Google Scholar]
- J.M. Bates, and C.W.J. Granger. “Combination of forecasts.” Oper. Res. Q. 20 (1969): 451–468. [Google Scholar] [CrossRef]
- A. Timmermann. “Forecast combinations.” In Handbook of Economic Forecasting. Edited by G. Elliot, C. Granger and A. Timmermann. North-Holland, The Netherlands: Elsevier, 2006, Chapter 4; Volume 1, pp. 135–196. [Google Scholar]
- V. Corradi, and N.R. Swanson. “Predictive density and conditional confidence interval accuracy tests.” J. Econom. 135 (2006): 187–228. [Google Scholar] [CrossRef]
- S.G. Hall, and J. Mitchell. “Combining density forecasts.” Int. J. Forecast. 23 (2007): 1–13. [Google Scholar] [CrossRef]
- J. Mitchell, and S.G. Hall. “Evaluating, comparing and combining density forecasts using the KLIC with an application to the Bank of England and NIESER “fan” charts of inflation.” Oxf. Bull. Econ. Stat. 67 (2005): 995–1033. [Google Scholar] [CrossRef]
- K.F. Wallis. “Combining density and interval forecasts: A modest proposal.” Oxf. Bull. Econ. Stat. 67 (2005): 983–994. [Google Scholar] [CrossRef]
- C. Genest, and J. Zidek. “Combining probability distributions: A critique and an annotated bibliography.” Stat. Sci. 1 (1986): 114–148. [Google Scholar] [CrossRef]
- M. Stone. “The opinion pool.” Ann. Math. Stat. 32 (1961): 1339–1342. [Google Scholar] [CrossRef]
- M.H. DeGroot, A.P. Dawid, and J. Mortera. “Coherent combination of experts’ opinions.” Test 4 (1995): 263–313. [Google Scholar]
- M.H. DeGroot, and J. Mortera. “Optimal linear opinion pools.” Manag. Sci. 37 (1991): 546–558. [Google Scholar] [CrossRef]
- J. Geweke, and G. Amisano. “Optimal prediction pools.” J. Econom. 164 (2011): 130–141. [Google Scholar] [CrossRef]
- R. Ranjan, and T. Gneiting. “Combining probability forecasts.” J. R. Stat. Soc. Ser. B 72 (2010): 71–91. [Google Scholar] [CrossRef]
- M. Billio, R. Casarin, F. Ravazzolo, and H. van Dijk. “Time-varying combinations of predictive densities using nonlinear filtering.” J. Econom. 177 (2013): 213–232. [Google Scholar] [CrossRef]
- R. Casarin, S. Grassi, F. Ravazzolo, and H. van Dijk. “Parallel sequential Monte Carlo for efficient density combination: The DeCo MATLAB toolbox.” J. Stat. Softw. 68 (2015): 1–30. [Google Scholar] [CrossRef]
- N. Fawcett, G. Kapetanios, J. Mitchell, and S. Price. “Generalised density forecast combinations.” J. Econom. 188 (2015): 150–165. [Google Scholar] [CrossRef]
- F. Bassetti, R. Casarin, and F. Ravazzolo. Bayesian Nonparametric Calibration and Combination of Predictive Distributions. Paper Series No. 04/WP/2015; Venice, Italy: University Ca’ Foscari of Venice, Department of Economics, 2015. [Google Scholar]
- T. Gneiting, and R. Ranjan. “Combining predictive distributions.” Electron. J. Stat. 7 (2013): 1747–1782. [Google Scholar] [CrossRef]
- R. Casarin, S. Grassi, F. Ravazzolo, and H.K. van Dijk. Dynamic Predictive Density Combinations for Large Datasets. Tinbergen Institute Discussion Paper 15-084/III; Amsterdam, The Netherlands: Tinbergen Institute, 2015. [Google Scholar]
- K.J. McConway. “Marginalization and linear opinion pools.” J. Am. Stat. Assoc. 76 (1981): 410–415. [Google Scholar] [CrossRef]
- M. Bacharach. “Group decisions in the face of differences of opinion.” Manag. Sci. 22 (1975): 182–191. [Google Scholar] [CrossRef]
- R. Laddaga. “Lehrer and the consensus proposal.” Synthese 36 (1977): 473–477. [Google Scholar] [CrossRef]
- S.C. Hora. “An analytic method for evaluating the performance of aggregation rules for probability densities.” Oper. Res. 58 (2010): 1440–1449. [Google Scholar] [CrossRef]
- A.P. Dawid. “Intersubjective statistical models.” In Exchangeability in Probability and Statistics. Edited by G. Koch and F. Spizichino. North Holland, Amsterdam, The Netherlands, 1982, pp. 217–232. [Google Scholar]
- M. Rosenblatt. “Remarks on multivariate transformation.” Ann. Math. Stat. 23 (1952): 1052–1057. [Google Scholar] [CrossRef]
- A.P. Dawid. “Statistical theory: The prequential approach.” J. R. Stat. Soc. Ser. A 147 (1984): 278–290. [Google Scholar] [CrossRef]
- T. Gneiting, and R. Ranjan. “Comparing density forecasts using threshold and quantile weighted proper scoring rules.” J. Bus. Econ. Stat. 29 (2011): 411–422. [Google Scholar] [CrossRef]
- R. Casarin, F. Leisen, G. Molina, and E. Ter-Horst. “Beta markov random field calibration of the term structure of implied risk neutral densities.” Bayesian Anal. 10 (2015): 791–819. [Google Scholar] [CrossRef]
- C.P. Robert, and J. Rousseau. A Mixture Approach to Bayesian Goodness of Fit. Technical Report 02009; Paris, France: CEREMADE, Université Paris-Dauphine, 2002. [Google Scholar]
- M. Billio, and R. Casarin. “Beta autoregressive transition Markov-switching models for business cycle analysis.” Stud. Nonlinear Dyn. Econom. 15 (2011): 1–32. [Google Scholar] [CrossRef]
- N. Bouguila, D. Ziou, and E. Monga. “Practical Bayesian estimation of a finite beta mixture through Gibbs sampling and its applications.” Stat. Comput. 16 (2006): 215–225. [Google Scholar] [CrossRef]
- R. Casarin, L. Dalla Valle, and F. Leisen. “Bayesian model selection for beta autoregressive processes.” Bayesian Anal. 7 (2012): 1–26. [Google Scholar] [CrossRef]
- J. Geweke, and G. Amisano. “Comparing and evaluating Bayesian predictive distributions of asset returns.” Int. J. Forecast. 26 (2010): 216–230. [Google Scholar] [CrossRef]
- The MathWorks, Inc. MATLAB—The Language of Technical Computing. version R2011b; Natick, MA, USA: The MathWorks, Inc., 2011. [Google Scholar]
| p | (1/5, 1/5, 3/5) | (1/7, 1/7, 5/7) | (3/5, 1/5, 1/5) | (5/7, 1/7, 1/7) | ||||
|---|---|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 0.755 | 3.293 | 0.921 | 6.970 | 0.461 | 0.452 | 0.496 | 0.650 | |
| 0.642 | 0.953 | 0.639 | 0.937 | 0.816 | 3.744 | 0.812 | 0.876 | |
| 0.015 | 0.191 | 0.000 | 0.500 | 0.256 | 0.925 | 0.342 | 0.230 | |
| 0.692 | 0.665 | 0.550 | 0.707 | |||||
| 3.093 | 0.713 | 0.827 | 13.033 | |||||
| 0.150 | 0.233 | 0.063 | 0.315 | |||||
| ρ | 0.697 | 0.512 | 0.215 | 0.806 | ||||
| p | (1/5, 1/5, 3/5) | (1/7, 1/7, 5/7) | (3/5, 1/5, 1/5) | (5/7, 1/7, 1/7) | ||||
|---|---|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 0.744 | 7.026 | 0.906 | 7.775 | 0.416 | 0.383 | 0.457 | 0.457 | |
| 0.634 | 0.878 | 0.632 | 1.013 | 0.755 | 0.827 | 0.747 | 0.778 | |
| 0.042 | 0.529 | 0.024 | 0.456 | 0.363 | 0.734 | 0.507 | 0.511 | |
| 0.615 | 0.665 | 3.720 | 0.462 | |||||
| 0.929 | 0.651 | 1.133 | 0.734 | |||||
| 0.380 | 0.302 | 0.093 | 0.474 | |||||
| ρ | 0.453 | 0.415 | 0.824 | 0.456 | ||||
| p | (1/5, 1/5, 3/5) | (1/7, 1/7, 5/7) | (3/5, 1/5, 1/5) | (5/7, 1/7, 1/7) | ||||
|---|---|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 0.751 | 7.062 | 0.917 | 6.514 | 0.441 | 2.587 | 0.469 | 2.180 | |
| 0.639 | 0.950 | 0.640 | 0.966 | 0.764 | 1.109 | 0.753 | 0.869 | |
| 0.018 | 0.517 | 0.000 | 0.431 | 0.370 | 0.031 | 0.465 | 0.411 | |
| 0.578 | 0.645 | 0.367 | 0.515 | |||||
| 0.823 | 0.680 | 0.875 | 2.770 | |||||
| 0.426 | 0.379 | 0.843 | 0.423 | |||||
| ρ | 0.484 | 0.510 | 0.274 | 0.389 | ||||
| P | Linear | Harmonic | Logarithmic | |||
|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 5.840 | 0.000 | 0.084 | 17.573 | 2.468 | 34.692 | |
| 5.807 | 0.000 | 0.371 | 15.114 | 2.867 | 34.462 | |
| 1.000 | 0.000 | 1.000 | 0.863 | 1.000 | 0.706 | |
| 5.812 | 0.020 | 1.781 | ||||
| 5.651 | 0.466 | 2.166 | ||||
| 1.000 | 0.199 | 0.93 | ||||
| ρ | 0.000 | 0.7926 | 0.269 | |||
| P | Linear | Harmonic | Logarithmic | |||
|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 7.025 | 278.600 | 0.977 | 0.944 | 0.974 | 1.010 | |
| 6.646 | 803.260 | 0.865 | 1.014 | 1.292 | 1.018 | |
| 1.000 | 1.000 | 0.740 | 0.263 | 0.821 | 0.031 | |
| 6.760 | 0.975 | 1.131 | ||||
| 6.334 | 1.010 | 0.972 | ||||
| 1.000 | 0.247 | 0.298 | ||||
| ρ | 0.000 | 0.000 | 0.000 | |||
| P | Linear | Harmonic | Logarithmic | |||
|---|---|---|---|---|---|---|
| BC1 | BC2 | BC1 | BC2 | BC1 | BC2 | |
| 6.542 | 47110.000 | 1.031 | 0.972 | 1.127 | 1.007 | |
| 6.071 | 0.000 | 0.419 | 0.942 | 2.275 | 1.066 | |
| 1.000 | 1.000 | 0.823 | 0.967 | 0.186 | 0.406 | |
| 6.710 | 1.039 | 0.891 | ||||
| 6.307 | 0.938 | 1.015 | ||||
| 1.000 | 0.920 | 0.921 | ||||
| ρ | 0.000 | 0.000 | 0.000 | |||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casarin, R.; Mantoan, G.; Ravazzolo, F. Bayesian Calibration of Generalized Pools of Predictive Distributions. Econometrics 2016, 4, 17. https://doi.org/10.3390/econometrics4010017
Casarin R, Mantoan G, Ravazzolo F. Bayesian Calibration of Generalized Pools of Predictive Distributions. Econometrics. 2016; 4(1):17. https://doi.org/10.3390/econometrics4010017
Chicago/Turabian StyleCasarin, Roberto, Giulia Mantoan, and Francesco Ravazzolo. 2016. "Bayesian Calibration of Generalized Pools of Predictive Distributions" Econometrics 4, no. 1: 17. https://doi.org/10.3390/econometrics4010017
APA StyleCasarin, R., Mantoan, G., & Ravazzolo, F. (2016). Bayesian Calibration of Generalized Pools of Predictive Distributions. Econometrics, 4(1), 17. https://doi.org/10.3390/econometrics4010017








