Forecasting Interest Rates Using Geostatistical Techniques
Abstract
:1. Introduction
2. Background on Estimating and Forecasting Models of Interest Rates
3. Geostatistical Methods: A Brief Overview
4. An empirical Application: Forecasting Euro Zero Rates
4.1. Data Description
| Common Features | ||||
| Maturities m (years) | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, 25, 30, 40 and 50 | |||
| Period | From 1 January 2003 to 30 June 2014 | |||
| Reference curve | Euro (ID: S45) | |||
| Data source | Bloomberg | |||
| Specific Features | ||||
| Type of rate | Swap | Zero | Forward (Zero) | |
| Name | EUR Swap Annual | EUR Zero Rate | EUR Forward (Zero) Rate | |
| Bloomberg ticker | EUSAm Curncy | S0045Z mY BLC2 Curncy | - | |
| Symbol | ESR | EZR | EFR | |
| Time horizon h (months) | - | - | 3, 6 and 12 | |
| Day count | Fixed | 30U/360 | Determined by bootstrapping the EUR Swap Annual curve for m ≥ 2, while for m = 1 it was considered the Euribor 12 months ACT/360 (ticker: EUR012M Index). | Determined on the basis of the EUR Swap Annual bootstrapped curve (rate type “Zc”, side “Mid”) using the “BCurveFwd” Bloomberg function. |
| Floating | ACT/360 | |||
| Payment frequency | Fixed | Annual | ||
| Floating | Semi-annual | |||
| Floating | Index | Euribor 6 months | ||
| Index ticker | EUR006M Index | |||
| Reset frequency | Semi-annual | |||
| Maturity m (Years) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 15 | 20 | 25 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2003 | 2.33 | 2.64 | 2.96 | 3.26 | 3.51 | 3.73 | 3.92 | 4.09 | 4.23 | 4.35 | 4.46 | 4.56 | 4.79 | 5.04 | 5.14 | 5.15 | 5.09 | 5.00 |
| 2004 | 2.27 | 2.64 | 2.97 | 3.25 | 3.49 | 3.70 | 3.88 | 4.04 | 4.18 | 4.29 | 4.39 | 4.48 | 4.70 | 4.94 | 5.04 | 5.07 | 5.07 | 5.03 |
| 2005 | 2.33 | 2.54 | 2.71 | 2.85 | 2.99 | 3.12 | 3.24 | 3.35 | 3.45 | 3.54 | 3.62 | 3.69 | 3.86 | 4.03 | 4.11 | 4.13 | 4.14 | 4.12 |
| 2006 | 3.44 | 3.62 | 3.69 | 3.75 | 3.80 | 3.84 | 3.89 | 3.93 | 3.98 | 4.02 | 4.06 | 4.10 | 4.19 | 4.28 | 4.31 | 4.30 | 4.25 | 4.19 |
| 2007 | 4.45 | 4.44 | 4.43 | 4.43 | 4.45 | 4.46 | 4.48 | 4.51 | 4.54 | 4.57 | 4.60 | 4.63 | 4.70 | 4.75 | 4.74 | 4.70 | 4.60 | 4.49 |
| 2008 | 4.83 | 4.32 | 4.29 | 4.30 | 4.32 | 4.35 | 4.40 | 4.45 | 4.50 | 4.55 | 4.60 | 4.65 | 4.74 | 4.75 | 4.64 | 4.54 | 4.37 | 4.23 |
| 2009 | 1.61 | 1.88 | 2.28 | 2.59 | 2.85 | 3.07 | 3.25 | 3.40 | 3.53 | 3.65 | 3.75 | 3.85 | 4.07 | 4.19 | 4.05 | 3.89 | 3.57 | 3.43 |
| 2010 | 1.35 | 1.47 | 1.75 | 2.02 | 2.27 | 2.50 | 2.69 | 2.86 | 3.00 | 3.12 | 3.23 | 3.32 | 3.53 | 3.62 | 3.54 | 3.37 | 3.14 | 3.06 |
| 2011 | 2.01 | 1.85 | 2.06 | 2.28 | 2.50 | 2.67 | 2.83 | 2.95 | 3.06 | 3.16 | 3.25 | 3.34 | 3.52 | 3.57 | 3.47 | 3.34 | 3.20 | 3.18 |
| 2012 | 1.11 | 0.78 | 0.88 | 1.04 | 1.24 | 1.43 | 1.61 | 1.76 | 1.89 | 2.01 | 2.12 | 2.21 | 2.40 | 2.47 | 2.44 | 2.41 | 2.46 | 2.53 |
| 2013 | 0.54 | 0.52 | 0.68 | 0.89 | 1.10 | 1.30 | 1.49 | 1.66 | 1.82 | 1.96 | 2.09 | 2.20 | 2.44 | 2.59 | 2.62 | 2.61 | 2.66 | 2.73 |
| 2014 | 0.57 | 0.44 | 0.57 | 0.75 | 0.95 | 1.15 | 1.34 | 1.52 | 1.69 | 1.83 | 1.96 | 2.08 | 2.33 | 2.52 | 2.56 | 2.56 | 2.57 | 2.57 |
| Observations | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 | 2944 |
| Mean | 2.31 | 2.34 | 2.52 | 2.70 | 2.87 | 3.02 | 3.16 | 3.29 | 3.40 | 3.49 | 3.58 | 3.66 | 3.84 | 3.96 | 3.95 | 3.90 | 3.81 | 3.76 |
| St. deviation | 1.34 | 1.32 | 1.26 | 1.21 | 1.15 | 1.10 | 1.06 | 1.02 | 1.00 | 0.97 | 0.95 | 0.93 | 0.91 | 0.92 | 0.94 | 0.96 | 0.94 | 0.90 |
| Minimum | 0.47 | 0.31 | 0.39 | 0.50 | 0.65 | 0.82 | 1.00 | 1.17 | 1.33 | 1.47 | 1.60 | 1.71 | 1.89 | 1.88 | 1.85 | 1.81 | 1.83 | 1.85 |
| Maximum | 5.53 | 5.48 | 5.40 | 5.27 | 5.19 | 5.14 | 5.10 | 5.08 | 5.07 | 5.09 | 5.10 | 5.12 | 5.15 | 5.28 | 5.38 | 5.40 | 5.43 | 5.37 |
| Date t | Year | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Day/Month | 29/12 | 28/12 | 31/12 | 31/12 | 31/12 | 30/12 | 29/12 | 31/12 | 31/12 | 31/12 | 31/12 | |
| Time horizon h | Maturity m = 10 (years) | |||||||||||
| 3 month | 4.54 | 3.90 | 3.51 | 4.22 | 4.75 | 3.83 | 3.77 | 3.46 | 2.46 | 1.66 | 2.29 | |
| 6 months | 4.62 | 3.97 | 3.54 | 4.23 | 4.76 | 3.89 | 3.87 | 3.55 | 2.51 | 1.73 | 2.37 | |
| 12 months | 4.78 | 4.08 | 3.59 | 4.24 | 4.80 | 4.01 | 4.04 | 3.70 | 2.63 | 1.86 | 2.53 | |
| Time horizon h | Maturity m = 20 (years) | |||||||||||
| 3 month | 5.07 | 4.45 | 3.83 | 4.35 | 4.98 | 3.92 | 4.25 | 3.85 | 2.75 | 2.28 | 2.86 | |
| 6 months | 5.12 | 4.48 | 3.84 | 4.36 | 4.98 | 3.92 | 4.28 | 3.88 | 2.76 | 2.31 | 2.90 | |
| 12 months | 5.19 | 4.54 | 3.87 | 4.36 | 4.99 | 3.94 | 4.35 | 3.93 | 2.80 | 2.36 | 2.96 | |
| Time horizon h | Maturity m = 30 (years) | |||||||||||
| 3 month | 5.18 | 4.56 | 3.86 | 4.29 | 4.90 | 3.45 | 3.98 | 3.49 | 2.56 | 2.33 | 2.83 | |
| 6 months | 5.21 | 4.58 | 3.86 | 4.29 | 4.90 | 3.44 | 4.00 | 3.50 | 2.56 | 2.35 | 2.85 | |
| 12 months | 5.25 | 4.62 | 3.88 | 4.29 | 4.90 | 3.44 | 4.03 | 3.51 | 2.58 | 2.39 | 2.88 | |
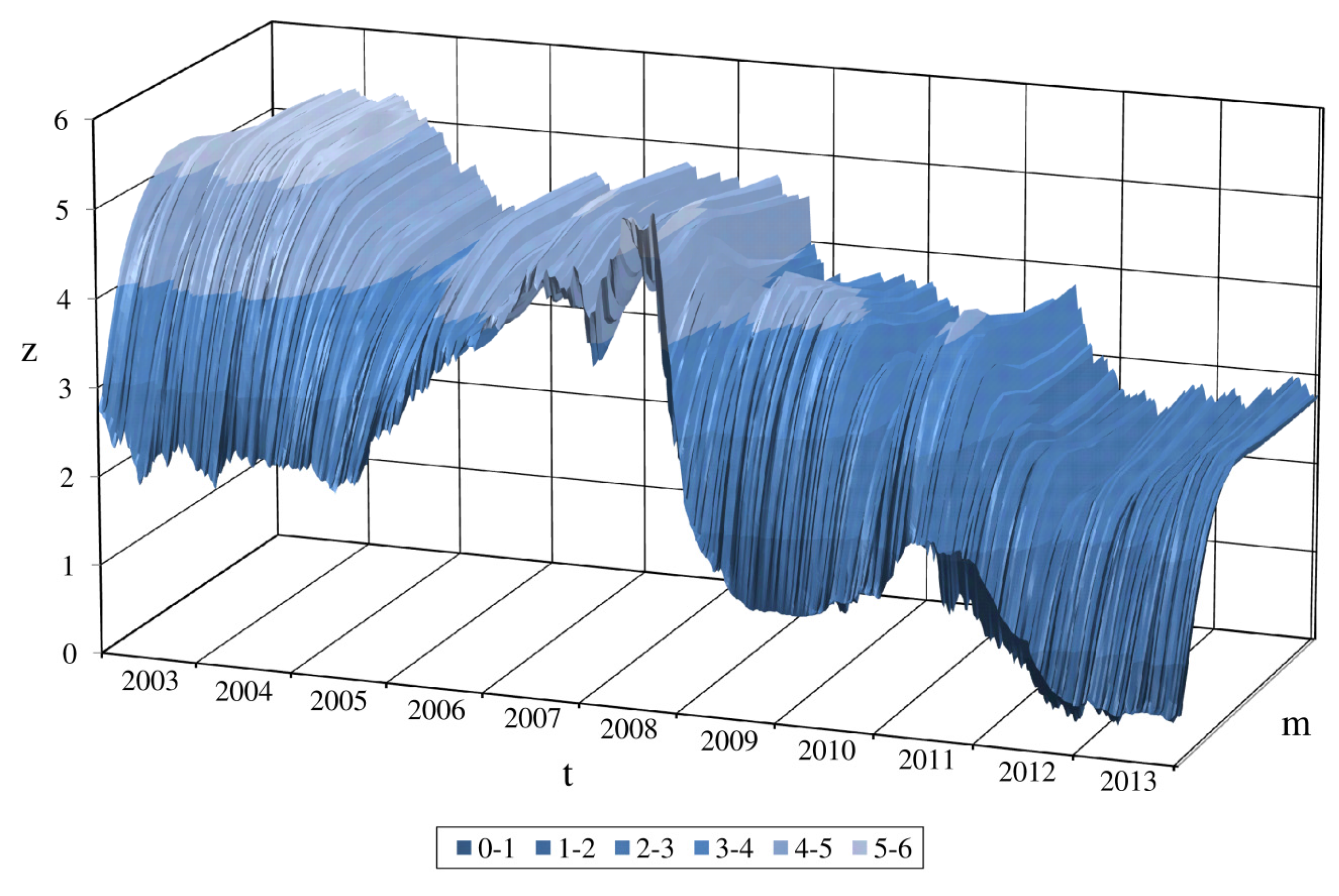
4.2. The Ordinary Kriging Model
4.3. The Extended Dynamic Nelson-Siegel Model
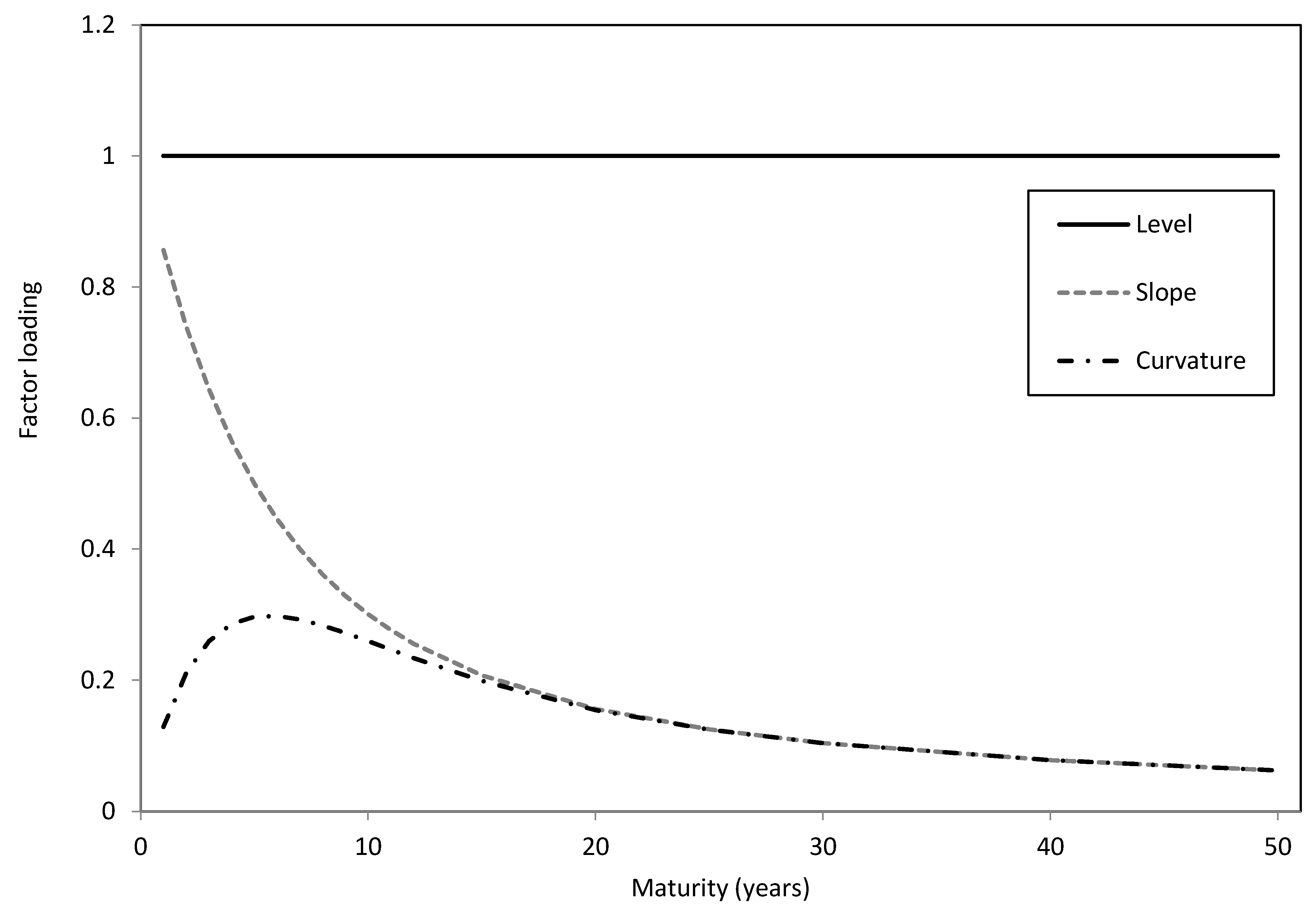
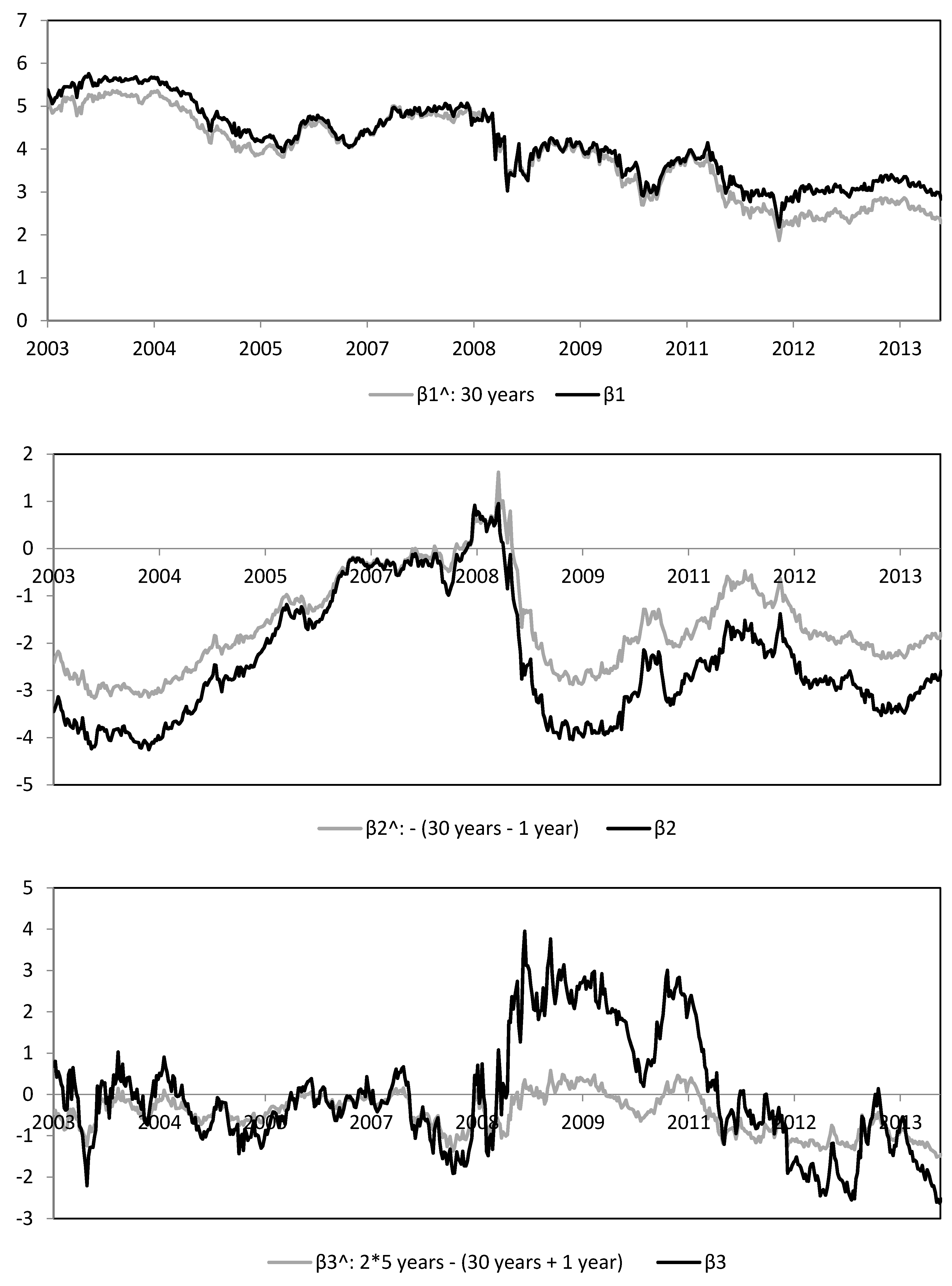
4.4. Measures of Prediction Accuracy
5. Empirical Results
5.1. The Ordinary Kriging Model
| Dataset Length d | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 year | Exp | Bes | Exp | Gau | Bes | Bes | Pow | Bes | Bes | Bes | Bes |
| 3 years | - | - | Exp | Pow | Pow | Bes | Bes | Bes | Pow | Pow | Pow |
| Max | mod (1 year) | Bes | mod (3 year) | Pow | Pow | Bes | Pow | Pow | Pow | Pow | Pow |
| Statistics of | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | - | |||||||||
| Time horizon h | Maturity m (years) | 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 |
| 3 months | Max | 0.57 | 0.59 | 0.60 | 0.44 | 0.42 | 0.43 | 0.44 | 0.42 | 0.45 | 0.51 | 0.46 | 0.46 |
| Q3 | 0.35 | 0.34 | 0.36 | 0.36 | 0.27 | 0.27 | 0.34 | 0.31 | 0.34 | 0.35 | 0.26 | 0.24 | |
| Median | 0.27 | 0.23 | 0.21 | 0.26 | 0.20 | 0.18 | 0.26 | 0.20 | 0.21 | 0.30 | 0.18 | 0.19 | |
| Q1 | 0.11 | 0.14 | 0.18 | 0.14 | 0.12 | 0.16 | 0.10 | 0.08 | 0.12 | 0.11 | 0.08 | 0.12 | |
| Min | 0.05 | 0.10 | 0.02 | 0.03 | 0.00 | 0.03 | 0.01 | 0.05 | 0.05 | 0.04 | 0.02 | 0.01 | |
| 6 months | Max | 0.87 | 0.97 | 0.99 | 0.70 | 0.75 | 0.76 | 0.70 | 0.76 | 0.83 | 0.90 | 0.79 | 0.77 |
| Q3 | 0.60 | 0.64 | 0.67 | 0.59 | 0.63 | 0.63 | 0.61 | 0.67 | 0.68 | 0.72 | 0.68 | 0.66 | |
| Median | 0.38 | 0.44 | 0.58 | 0.44 | 0.38 | 0.54 | 0.40 | 0.31 | 0.54 | 0.48 | 0.40 | 0.57 | |
| Q1 | 0.21 | 0.29 | 0.25 | 0.25 | 0.32 | 0.23 | 0.23 | 0.25 | 0.16 | 0.23 | 0.23 | 0.24 | |
| Min | 0.07 | 0.00 | 0.00 | 0.14 | 0.14 | 0.01 | 0.12 | 0.18 | 0.02 | 0.04 | 0.03 | 0.02 | |
| 12 months | Max | 1.02 | 0.94 | 1.37 | 0.93 | 0.95 | 1.37 | 0.89 | 0.98 | 1.32 | 1.27 | 1.18 | 1.45 |
| Q3 | 0.79 | 0.70 | 0.64 | 0.75 | 0.72 | 0.71 | 0.59 | 0.54 | 0.53 | 0.97 | 0.73 | 0.72 | |
| Median | 0.35 | 0.34 | 0.42 | 0.50 | 0.54 | 0.45 | 0.46 | 0.37 | 0.37 | 0.62 | 0.58 | 0.58 | |
| Q1 | 0.23 | 0.23 | 0.35 | 0.29 | 0.38 | 0.34 | 0.32 | 0.25 | 0.34 | 0.53 | 0.48 | 0.45 | |
| Min | 0.12 | 0.06 | 0.24 | 0.15 | 0.17 | 0.18 | 0.08 | 0.20 | 0.06 | 0.32 | 0.29 | 0.26 | |
| No. underlined—All (1) | 12 | 14 | 21 | - | |||||||||
| No. underlined—Median (2) | 3 | 2 | 4 | - | |||||||||
| No. bold—All (3) | 10 | 11 | 19 | 7 | |||||||||
| No. bold—Median (4) | 3 | 1 | 4 | 1 | |||||||||
| (1) Number of underlined statistics (total = 45, plus eventual repetitions for d = max); (2) Number of underlined median values (total = 9, plus eventual repetitions for d = max); (3) Number of statistics in bold (total = 45, plus eventual repetitions for d = max); (4) Number of median values in bold (total = 9, plus eventual repetitions for d = max). | |||||||||||||
| Statistics of | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | - | |||||
| Time horizon h | Sub-period | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 |
| 3 months | Max | 0.60 | 0.49 | 0.42 | 0.43 | 0.45 | 0.41 | 0.46 | 0.39 |
| Q3 | 0.45 | 0.25 | 0.35 | 0.20 | 0.42 | 0.24 | 0.20 | 0.26 | |
| Median | 0.19 | 0.23 | 0.27 | 0.16 | 0.21 | 0.20 | 0.19 | 0.18 | |
| Q1 | 0.18 | 0.19 | 0.23 | 0.11 | 0.17 | 0.10 | 0.13 | 0.12 | |
| Min | 0.02 | 0.10 | 0.18 | 0.03 | 0.06 | 0.05 | 0.02 | 0.01 | |
| 6 months | Max | 0.99 | 0.69 | 0.76 | 0.62 | 0.83 | 0.70 | 0.77 | 0.76 |
| Q3 | 0.83 | 0.61 | 0.72 | 0.58 | 0.76 | 0.59 | 0.67 | 0.64 | |
| Median | 0.55 | 0.60 | 0.68 | 0.49 | 0.61 | 0.48 | 0.65 | 0.50 | |
| Q1 | 0.25 | 0.26 | 0.48 | 0.23 | 0.20 | 0.15 | 0.04 | 0.30 | |
| Min | 0.00 | 0.12 | 0.01 | 0.21 | 0.02 | 0.14 | 0.02 | 0.23 | |
| 12 months | Max | 1.37 | 0.66 | 1.37 | 0.81 | 1.32 | 0.83 | 1.45 | 0.96 |
| Q3 | 0.68 | 0.60 | 1.07 | 0.52 | 0.57 | 0.42 | 0.74 | 0.54 | |
| Median | 0.44 | 0.39 | 0.67 | 0.35 | 0.37 | 0.37 | 0.65 | 0.50 | |
| Q1 | 0.34 | 0.39 | 0.54 | 0.30 | 0.34 | 0.34 | 0.62 | 0.43 | |
| Min | 0.24 | 0.26 | 0.37 | 0.18 | 0.22 | 0.06 | 0.42 | 0.26 | |
| No. underlined—All (1) | 5 | 2 | 4 | 7 | 7 | 6 | - | - | |
| No. underlined—Median (2) | 2 | 0 | 0 | 2 | 1 | 1 | - | - | |
| No. bold—All (3) | 5 | 2 | 2 | 6 | 5 | 5 | 4 | 2 | |
| No. bold—Median (4) | 2 | 0 | 0 | 2 | 1 | 1 | 0 | 0 | |
| (1) Number of underlined statistics (total = 15, plus eventual repetitions for d = max); (2) Number of underlined median values (total = 3, plus eventual repetitions for d = max); (3) Number of statistics in bold (total = 15, plus eventual repetitions for d = max); (4) Number of median values in bold (total = 3, plus eventual repetitions for d =max). | |||||||||
5.2. The Extended Dynamic Nelson-Siegel Model
| Statistics of | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | - | |||||||||
| Time horizon h | Maturity m (years) | 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 |
| 3 months | Max | 1.57 | 1.61 | 1.64 | 0.46 | 0.40 | 0.36 | 0.59 | 0.60 | 0.61 | 0.51 | 0.46 | 0.46 |
| Q3 | 0.60 | 0.54 | 0.48 | 0.29 | 0.28 | 0.33 | 0.38 | 0.40 | 0.40 | 0.35 | 0.26 | 0.24 | |
| Median | 0.32 | 0.34 | 0.37 | 0.26 | 0.25 | 0.21 | 0.17 | 0.12 | 0.17 | 0.30 | 0.18 | 0.19 | |
| Q1 | 0.27 | 0.28 | 0.29 | 0.20 | 0.20 | 0.15 | 0.07 | 0.08 | 0.10 | 0.11 | 0.08 | 0.12 | |
| Min | 0.05 | 0.00 | 0.05 | 0.07 | 0.08 | 0.10 | 0.03 | 0.03 | 0.01 | 0.04 | 0.02 | 0.01 | |
| 6 months | Max | 1.24 | 1.24 | 1.24 | 1.53 | 1.46 | 1.40 | 1.32 | 1.34 | 1.37 | 0.90 | 0.79 | 0.77 |
| Q3 | 1.09 | 1.10 | 1.11 | 0.96 | 0.95 | 0.93 | 0.72 | 0.75 | 0.78 | 0.72 | 0.68 | 0.66 | |
| Median | 0.90 | 0.85 | 0.80 | 0.96 | 0.51 | 0.53 | 0.48 | 0.51 | 0.52 | 0.48 | 0.40 | 0.57 | |
| Q1 | 0.51 | 0.52 | 0.53 | 0.52 | 0.34 | 0.26 | 0.16 | 0.12 | 0.07 | 0.23 | 0.23 | 0.24 | |
| Min | 0.16 | 0.12 | 0.07 | 0.40 | 0.21 | 0.14 | 0.10 | 0.01 | 0.05 | 0.04 | 0.03 | 0.02 | |
| 12 months | Max | 2.12 | 1.99 | 1.88 | 2.30 | 2.14 | 2.00 | 1.35 | 1.27 | 1.20 | 1.27 | 1.18 | 1.45 |
| Q3 | 1.10 | 1.15 | 1.20 | 1.51 | 1.42 | 1.35 | 1.10 | 1.10 | 1.05 | 0.97 | 0.73 | 0.72 | |
| Median | 0.73 | 0.74 | 0.71 | 0.59 | 0.49 | 0.46 | 0.88 | 0.77 | 0.70 | 0.62 | 0.58 | 0.58 | |
| Q1 | 0.28 | 0.33 | 0.37 | 0.34 | 0.36 | 0.35 | 0.35 | 0.27 | 0.23 | 0.53 | 0.48 | 0.45 | |
| Min | 0.08 | 0.03 | 0.02 | 0.09 | 0.01 | 0.04 | 0.09 | 0.01 | 0.04 | 0.32 | 0.29 | 0.26 | |
| No. underlined—All (1) | 8 | 11 | 29 | - | |||||||||
| No. underlined—Median (2) | 0 | 4 | 6 | - | |||||||||
| No. bold—All (3) | 4 | 8 | 16 | 18 | |||||||||
| No. bold—Median (4) | 0 | 3 | 5 | 1 | |||||||||
| (1) Number of underlined statistics (total = 45, plus eventual repetitions for d=max); (2) Number of underlined median values (total = 9, plus eventual repetitions for d=max); (3) Number of statistics in bold (total = 45, plus eventual repetitions for d=max); (4) Number of median values in bold (total = 9, plus eventual repetitions for d=max). | |||||||||||||
| Statistics of | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | - | |||||
| Time horizon h | Sub-period | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 |
| 3 months | Max | 0.40 | 1.64 | 0.11 | 0.36 | 0.61 | 0.47 | 0.46 | 0.39 |
| Q3 | 0.35 | 1.12 | 0.11 | 0.34 | 0.52 | 0.21 | 0.20 | 0.26 | |
| Median | 0.29 | 0.43 | 0.11 | 0.27 | 0.40 | 0.14 | 0.19 | 0.18 | |
| Q1 | 0.26 | 0.36 | 0.11 | 0.19 | 0.30 | 0.09 | 0.13 | 0.12 | |
| Min | 0.22 | 0.05 | 0.11 | 0.10 | 0.11 | 0.01 | 0.02 | 0.01 | |
| 6 months | Max | 1.11 | 1.24 | 0.53 | 1.40 | 1.37 | 1.00 | 0.77 | 0.76 |
| Q3 | 1.10 | 1.06 | 0.53 | 0.96 | 1.04 | 0.72 | 0.67 | 0.64 | |
| Median | 1.09 | 0.71 | 0.53 | 0.65 | 0.53 | 0.39 | 0.65 | 0.50 | |
| Q1 | 0.78 | 0.55 | 0.53 | 0.22 | 0.38 | 0.11 | 0.04 | 0.30 | |
| Min | 0.07 | 0.52 | 0.53 | 0.14 | 0.07 | 0.05 | 0.02 | 0.23 | |
| 12 months | Max | 1.20 | 1.88 | 0.04 | 2.00 | 1.20 | 1.19 | 1.45 | 0.96 |
| Q3 | 1.00 | 1.35 | 0.04 | 1.53 | 0.88 | 1.00 | 0.74 | 0.54 | |
| Median | 0.76 | 0.62 | 0.04 | 0.68 | 0.37 | 0.77 | 0.65 | 0.50 | |
| Q1 | 0.54 | 0.41 | 0.04 | 0.42 | 0.26 | 0.40 | 0.62 | 0.43 | |
| Min | 0.02 | 0.08 | 0.04 | 0.28 | 0.04 | 0.21 | 0.42 | 0.26 | |
| No. underlined—All (1) | 2 | 2 | 12 | 1 | 4 | 12 | - | - | |
| No. underlined—Median (2) | 0 | 1 | 3 | 0 | 1 | 2 | - | - | |
| No. bold—All (3) | 1 | 1 | 11 | 1 | 1 | 7 | 3 | 6 | |
| No. bold—Median (4) | 0 | 0 | 3 | 0 | 1 | 2 | 0 | 1 | |
| (1) Number of underlined statistics (total = 15, plus eventual repetitions for d = max); (2) Number of underlined median values (total = 3, plus eventual repetitions for d = max); (3) Number of statistics in bold (total = 15, plus eventual repetitions for d = max); (4) Number of median values in bold (total = 3, plus eventual repetitions for d = max). | |||||||||
5.3. The Comparison between the OK Model and the DNS Model
| Model | Model with the Lowest Statistic of | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | |||||||
| Time horizon h | Maturity m (years) | 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 |
| 3 months | Max | OK | OK | OK | OK | DNS | DNS | OK | OK | OK |
| Q3 | OK | OK | OK | DNS | OK | OK | OK | OK | OK | |
| Median | OK | OK | OK | DNS | OK | OK | DNS | DNS | DNS | |
| Q1 | OK | OK | OK | OK | OK | DNS | DNS | OK | DNS | |
| Min | DNS | DNS | OK | OK | OK | OK | OK | DNS | DNS | |
| 6 months | Max | OK | OK | OK | OK | OK | OK | OK | OK | OK |
| Q3 | OK | OK | OK | OK | OK | OK | OK | OK | OK | |
| Median | OK | OK | OK | OK | OK | DNS | OK | OK | DNS | |
| Q1 | OK | OK | OK | OK | OK | OK | DNS | DNS | DNS | |
| Min | OK | OK | OK | OK | OK | OK | DNS | DNS | OK | |
| 12 months | Max | OK | OK | OK | OK | OK | OK | OK | OK | DNS |
| Q3 | OK | OK | OK | OK | OK | OK | OK | OK | OK | |
| Median | OK | OK | OK | OK | DNS | OK | OK | OK | OK | |
| Q1 | OK | OK | OK | OK | DNS | OK | OK | OK | DNS | |
| Min | DNS | DNS | DNS | DNS | DNS | DNS | OK | DNS | DNS | |
| No. OK—All | 40 | 34 | 28 | |||||||
| No. DNS—All | 5 | 11 | 17 | |||||||
| No. OK—Median | 9 | 6 | 5 | |||||||
| No. DNS—Median | 0 | 3 | 4 | |||||||
| Statistics of | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data set amplitude d | 1 year | 3 years | Max | - | |||||
| Time horizon h | Sub-period | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 | 2003–2007 | 2008–2013 |
| 3 months | Max | DNS | OK | DNS | DNS | OK | OK | DNS | OK |
| Q3 | DNS | OK | DNS | OK | OK | DNS | DNS | OK | |
| Median | OK | OK | DNS | OK | OK | DNS | OK | OK | |
| Q1 | OK | OK | DNS | OK | OK | DNS | OK | OK | |
| Min | OK | DNS | DNS | OK | OK | DNS | OK | DNS | |
| 6 months | Max | OK | OK | DNS | OK | OK | OK | OK | OK |
| Q3 | OK | OK | DNS | OK | OK | OK | OK | OK | |
| Median | OK | OK | DNS | OK | DNS | DNS | OK | OK | |
| Q1 | OK | OK | OK | DNS | OK | DNS | OK | OK | |
| Min | OK | OK | OK | DNS | OK | DNS | OK | OK | |
| 12 months | Max | DNS | OK | DNS | OK | DNS | OK | DNS | OK |
| Q3 | OK | OK | DNS | OK | OK | OK | OK | OK | |
| Median | OK | OK | DNS | OK | DNS | OK | OK | OK | |
| Q1 | OK | OK | DNS | OK | DNS | OK | OK | OK | |
| Min | DNS | DNS | DNS | OK | DNS | OK | DNS | DNS | |
| No. OK—All | 11 | 13 | 2 | 12 | 10 | 8 | 11 | 13 | |
| No. DNS—All | 4 | 2 | 13 | 3 | 5 | 7 | 4 | 2 | |
| No. OK—Median | 3 | 3 | 0 | 3 | 1 | 1 | 3 | 3 | |
| No. DNS—Median | 0 | 0 | 3 | 0 | 2 | 2 | 0 | 0 | |
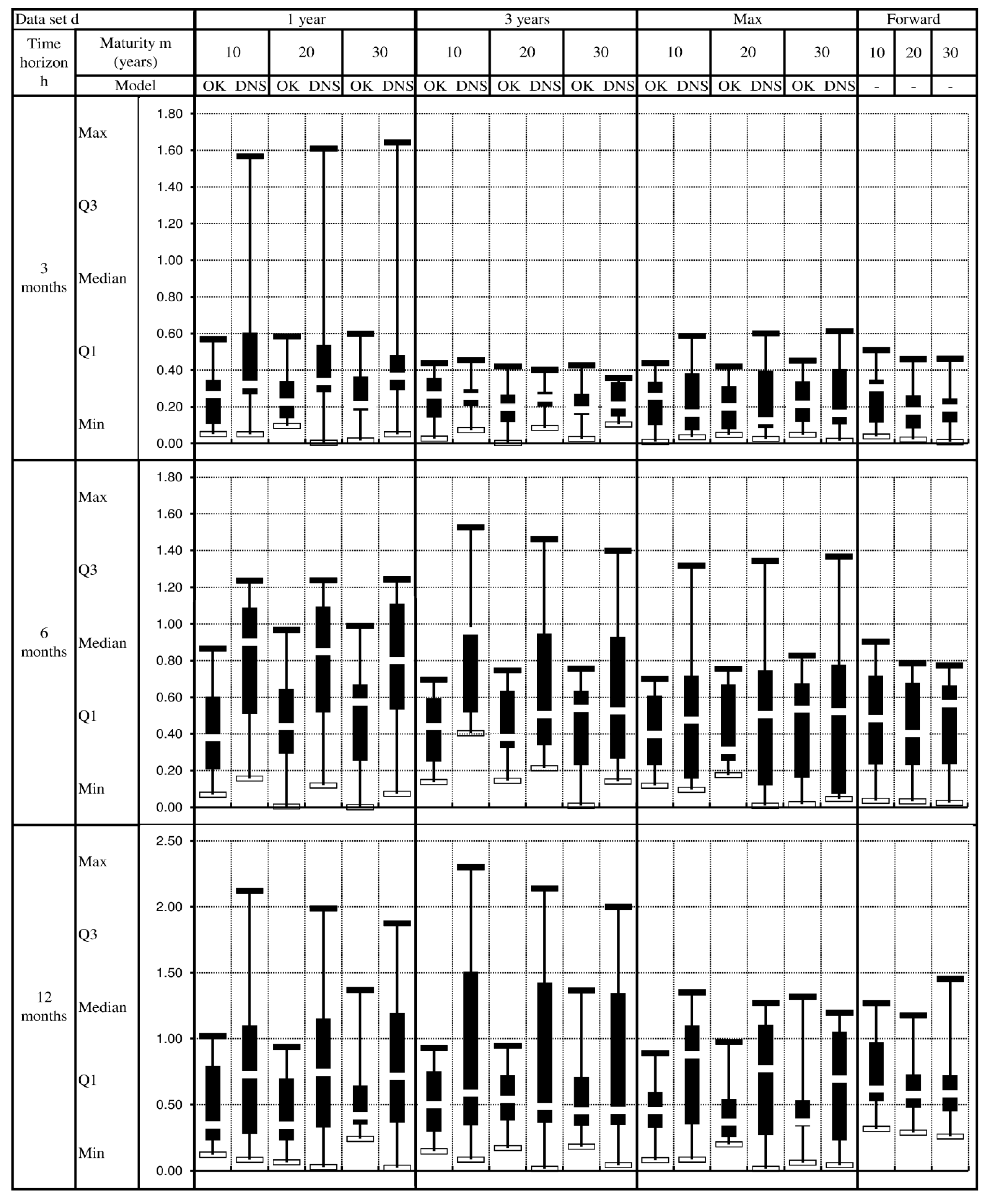
6. Conclusions
Author Contributions
Conflicts of Interest
References
- P. Hunt, J. Kennedy, and A. Pelsser. “Markov-Functional Interest Rate Models.” Financ. Stoch. 4 (2000): 391–408. [Google Scholar] [CrossRef]
- J.D. Hamilton. Time Series Analysis. Princeton, NJ, USA: Princeton University Press, 1994. [Google Scholar]
- N. Cressie. Statistics for Spatial Data. New York, NY, USA: Wiley, 1993. [Google Scholar]
- O. Shabenberger, and C. Gotway. Statistical Methods for Spatial Data Analysis. Boca Raton, FL, USA: Chapman & Hall/CRC, 2005. [Google Scholar]
- G. Fernández-Avilés, J.M. Montero, and A.G. Orlov. “Spatial modeling of stock market comovements.” Financ. Res. Lett. 9 (2012): 202–212. [Google Scholar] [CrossRef]
- E.M. Remolona, and P.D. Wooldridge. “The euro interest rate swap market.” BIS Q. Rev. March (2003): 47–56. [Google Scholar]
- D. Brigo, and F. Mercurio. Interest Rate Models-Theory and Practice: With Smile, Inflation and Credit. Berlin, Germany: Springer Finance, 2007. [Google Scholar]
- M.G. Subrahmanyam. “The Term Structure of Interest Rates: Alternative Approaches and their Implications for the Valuation of Contingent Claims.” Geneva Pap. Risk. Insur. Theory 21 (1996): 7–28. [Google Scholar] [CrossRef]
- F. Black, and M. Scholes. “The Pricing of Options and Corporate Liabilities.” J. Political Econ. 81 (1973): 637–654. [Google Scholar] [CrossRef]
- R.C. Merton. “An Intertemporal Capital Asset Pricing Model.” Econometrica 41 (1973): 867–887. [Google Scholar] [CrossRef]
- M.J. Brennan, and E.S. Schwartz. “A Continuous Time Approach to the Pricing of Bonds.” J. Bank. Financ. 3 (1979): 133–155. [Google Scholar] [CrossRef]
- T.S. Ho, and S.B. Lee. “Term Structure Movements and Pricing Interest Rate Contingent Claims.” J. Financ. 41 (1986): 1011–1029. [Google Scholar] [CrossRef]
- J. Hull, and A. White. “Pricing Interest-Rate-Derivative Securities.” Rev. Financ. Stud. 3 (1990): 573–592. [Google Scholar] [CrossRef]
- D. Heath, R. Jarrow, and A. Morton. “Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation.” Econometrica 60 (1992): 77–105. [Google Scholar] [CrossRef]
- A. Brace, D. Gatarek, and M. Musiela. “The Market Model of Interest Rate Dynamics.” Math. Financ. 7 (1997): 127–155. [Google Scholar] [CrossRef]
- A. Brace, and M. Musiela. “A Multifactor Gauss Markov Implementation of Heath, Jarrow, and Morton.” Math. Financ. 4 (1994): 259–283. [Google Scholar] [CrossRef]
- B. Goldys, M. Musiela, and D. Sondermann. “Lognormality of Rates and Term Structure Models.” Stoch. Anal. Appl. 18 (2000): 375–396. [Google Scholar] [CrossRef]
- M. Musiela. “General Framework for Pricing Derivative Securities.” Stoch. Proc. Appl. 55 (1995): 227–251. [Google Scholar] [CrossRef]
- M. Musiela, and M. Rutkowski. “Continuous-Time Term Structure Models: Forward Measure Approach.” Financ. Stoch. 1 (1997): 261–291. [Google Scholar] [CrossRef]
- D. Duffie, and K.J. Singleton. “Modeling Term Structures of Defaultable Bonds.” Rev. Financ. Stud. 12 (1999): 687–720. [Google Scholar] [CrossRef]
- F. Jamshidian. “LIBOR and Swap Market Models and Measures.” Financ. Stoch. 1 (1997): 293–330. [Google Scholar] [CrossRef]
- F. De Jong, J. Driessen, and A. Pelsser. “Libor Market Models versus Swap Market Models for Pricing Interest Rate Derivatives: An Empirical Analysis.” Eur. Financ. Rev. 5 (2001): 201–237. [Google Scholar] [CrossRef]
- F.A. Longstaff, and E.S. Schwartz. “Interest Rate Volatility and the Term Structure: A Two-Factor General Equilibrium Model.” J. Financ. 47 (1992): 1259–1282. [Google Scholar] [CrossRef]
- J.C. Cox, J.E. Ingersoll, and S.A. Ross. “A Re-Examination of Traditional Hypotheses about the Term Structure of Interest Rates.” J. Financ. 36 (1981): 769–799. [Google Scholar] [CrossRef]
- J.C. Cox, J.E. Ingersoll, and S.A. Ross. “An Intertemporal General Equilibrium Model of Asset Prices.” Econometrica 53 (1985): 363–384. [Google Scholar] [CrossRef]
- J.C. Cox, J.E. Ingersoll, and S.A. Ross. “A Theory of the Term Structure of Interest Rates.” Econometrica 53 (1985): 385–407. [Google Scholar] [CrossRef]
- O. Vasicek. “An Equilibrium Characterization of the Term Structure.” J. Financ. Econ. 5 (1977): 177–188. [Google Scholar] [CrossRef]
- F. Black, and P. Karasinski. “Bond and Option Pricing when Short Rates are Lognormal.” Financ. Anal. J. 47 (1991): 52–59. [Google Scholar] [CrossRef]
- L.U. Dothan. “On the Term Structure of Interest Rates.” J. Financ. Econ. 6 (1978): 59–69. [Google Scholar] [CrossRef]
- J. Hull, and A. White. “One-Factor Interest-Rate Models and the Valuation of Interest-Rate Derivative Securities.” J. Financ. Quant. Anal. 28 (1993): 235–254. [Google Scholar] [CrossRef]
- L. Broze, O. Scaillet, and J.M. Zakoian. “Testing for Continuous-Time Models of the Short-Term Interest Rate.” J. Empir. Financ. 2 (1995): 199–223. [Google Scholar] [CrossRef]
- K.C. Chan, G.A. Karolyi, F.A. Longstaff, and A.B. Sanders. “An Empirical Comparison of Alternative Models of the Short-Term Interest Rate.” J. Financ. 47 (1992): 1209–1227. [Google Scholar] [CrossRef]
- A. Monsalve-Cobis, W. González-Manteiga, and M. Febrero-Bande. “Goodness-of-Fit Test for Interest Rate Models: An Approach Based on Empirical Processes.” Comput. Stat. Data Anal. 55 (2011): 3073–3092. [Google Scholar] [CrossRef]
- G.R. Duffee. “Term Premia and Interest Rate Forecasts in Affine Models.” J. Financ. 57 (2002): 405–443. [Google Scholar] [CrossRef]
- D. Duffie, and R. Kan. “A Yield-Factor Model of Interest Rates.” Math. Financ. 6 (1996): 379–406. [Google Scholar] [CrossRef]
- S.M. Schaefer, and E.S. Schwartz. “A Two-Factor Model of the Term Structure: An Approximate Analytical Solution.” J. Financ. Quant. Anal. 19 (1984): 413–424. [Google Scholar] [CrossRef]
- V. Jakas. “Theory and empirics of an affine term structure model applied to European data.” Aestimatio IEB Int. J. Financ. 2 (2011): 2–19. [Google Scholar]
- V. Jakas. “Discrete Affine Term Structure Models Applied to German and Greek Government Bonds.” Aestimatio IEB Int. J. Financ. 5 (2012): 2–31. [Google Scholar]
- V. Jakas, and M. Jakas. “Are Economic Fundamentals Unable to Explain Current European Benchmark Yields? Empirical Evidence from a Continuous Time Affine Term Structure Model. Empirical Evidence from a Continuous Time Affine Term Structure Model.” Aestimatio IEB Int. J. Financ. 6 (2013): 2–27. [Google Scholar]
- V. Jakas. “Discrete Affine Term Structure Models Applied to the Government Debt and Fiscal Imbalances.” Aestimatio IEB Int. J. Financ. 7 (2013): 48–93. [Google Scholar]
- V. Jakas. “The Term Structure, Latent Factors and Macroeconomic Data: A Local Linear Level Model.” Aestimatio IEB Int. J. Financ. 8 (2014): 2–31. [Google Scholar]
- C.R. Nelson, and A.F. Siegel. “Parsimonious Modeling of Yield Curves.” J. Bus. 60 (1987): 473–489. [Google Scholar] [CrossRef]
- L.E.O. Svensson. Estimating and Interpreting Forward Interest Rates: Sweden 1992–1994. Working Paper 4871; Cambridge, MA, USA: National Bureau of Economic Research, 1994. [Google Scholar]
- R. Gimeno, and J.M. Nave. “A Genetic Algorithm Estimation of the Term Structure of Interest Rates.” Comput. Stat. Data Anal. 53 (2009): 2236–2250. [Google Scholar] [CrossRef]
- F.X. Diebold, and C. Li. “Forecasting the Term Structure of Government Bond Yields.” J. Econom. 130 (2006): 337–364. [Google Scholar] [CrossRef]
- Q. Dai, and K.J. Singleton. “Specification Analysis of Affine Term Structure Models.” J. Financ. 55 (2000): 1943–1978. [Google Scholar] [CrossRef]
- F. De Jong. “Time Series and Cross-Section Information in Affine Term-Structure Models.” J. Bus. Econ. Stat. 18 (2000): 300–314. [Google Scholar] [CrossRef]
- E.F. Fama, and R.R. Bliss. “The Information in Long-Maturity Forward Rates.” Am. Econ. Rev. 77 (1987): 680–692. [Google Scholar]
- A.B. Galvao, and S. Costa. “Does the Euro Area Forward Rate Provide Accurate Forecasts of the Short Rate? ” Int. J. Forecast. 29 (2013): 131–141. [Google Scholar] [CrossRef]
- Y. Chen, and L. Niu. “Adaptive Dynamic Nelson–Siegel Term Structure Model with Applications.” J. Econom. 180 (2014): 98–115. [Google Scholar] [CrossRef]
- J. Xiang, and X. Zhu. “A Regime-Switching Nelson–Siegel Term Structure Model and Interest Rate Forecasts.” J. Financ. Econom. 11 (2013): 522–555. [Google Scholar] [CrossRef]
- J.H. Cochrane, and M. Piazzesi. Bond Risk Premia (No. w9178). Cambridge, MA, USA: National Bureau of Economic Research, University of Chicago and UCLA, 2002. [Google Scholar]
- G.R. Duffee. “Forecasting Interest Rates.” In Handbook of Economic Forecasting. Edited by G. Elliott and A. Timmermann. Amsterdam, The Netherlands: Elsevier, 2013, Volume 2, Part A; pp. 385–426. [Google Scholar]
- J.G. Gasha, Y. He, C.I. Medeiros, M. Rodriguez Waldo, J. Salvati, and J. Yi. On the Estimation of Term Structure Models and an Application to the United States. IMF Working Papers; Washington, WA, USA: IMF, 2010, pp. 1–62. [Google Scholar]
- E. Moench. “Forecasting the yield curve in a data-rich environment. A no-arbitrage factor-augmented VaR approach.” J. Econom. 146 (2008): 26–43. [Google Scholar] [CrossRef]
- V. Bolotnyy, R. Edge, and L. Guerrieri. Stressing Bank Profitability for Interest Rate Risk; Washington, WA, USA: Federal Reserve Board Mimeo, 2014.
- K. Nyholm, and R. Vidova-Koleva. “Nelson-Siegel, Affine and Quadratic Yield Curve Specifications: Which One is Better at Forecasting? ” J. Forecast. 31 (2012): 540–564. [Google Scholar] [CrossRef]
- G. Matheron. “Principles of Geostatistics.” Econ. Geol. 58 (1963): 1246–1266. [Google Scholar] [CrossRef]
- B.D. Ripley. Spatial Statistics. New York, NJ, USA: John Wiley & Sons, 1981. [Google Scholar]
- D. Kennedy. Stochastic Financial Models. Boca Raton, FL, USA: CRC Press, 2010. [Google Scholar]
- L. Bauwens, and N. Hautsch. “Stochastic Conditional Intensity Processes.” J. Financ. Econom. 4 (2006): 450–493. [Google Scholar] [CrossRef]
- L. Bauwens, and N. Hautsch. “Modelling Financial High Frequency Data Using Point Processes.” In Handbook of Financial Time Series. Edited by T.G. Andersen, R.A. Davis, J.-P. Kreiss and T. Mikosch. Berlin, Germany: Springer-Verlag, 2009, pp. 953–979. [Google Scholar]
- N. Hautsch. Modeling Irregularly Spaced Financial Data. Berlin, Germany: Springer, 2004. [Google Scholar]
- N. Hautsch. Econometrics of Financial High-Frequency Data. Berlin, Germany: Springer, 2012. [Google Scholar]
- S.I. Resnick. Extreme Values, Regular Variation, and Point Processes. Berlin, Germany: Springer-Verlag, 2007. [Google Scholar]
- B.N. Boots, and A. Getis. Point Pattern Analysis. Newbury Park, CA, USA: Sage Publication, 1988. [Google Scholar]
- P. Diggle. Statistical Analysis of Spatial Point Patterns. London, UK: Academic Press, 1983. [Google Scholar]
- D.G. Krige. “A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand.” J. Chem. Met. Min. Soc. S. Afr. 52 (1951): 119–139. [Google Scholar]
- J.C. Hull. Options, Futures, and Other Derivatives. Upper Saddle River, NJ, USA: Pearson Education, 2011. [Google Scholar]
- R.T. Baillie. “Long Memory Processes and Fractional Integration in Econometrics.” J. Econom. 73 (1996): 5–59. [Google Scholar] [CrossRef]
- J.C. Duan, and K. Jacobs. “Is Long Memory Necessary? An Empirical Investigation of Nonnegative Interest Rate Processes.” J. Empir. Financ. 15 (2008): 567–581. [Google Scholar] [CrossRef]
- J.H. Christensen, F.X. Diebold, and G.D. Rudebusch. “The affine arbitrage-free class of Nelson-Siegel term structure models.” J. Econom. 164 (2011): 4–20. [Google Scholar] [CrossRef]
- W.C. Yu, and E. Zivot. “Forecasting the term structures of Treasury and corporate yields using dynamic Nelson-Siegel models.” Int. J. Forecast. 27 (2011): 579–591. [Google Scholar] [CrossRef]
- L. Coroneo, K. Nyholm, and R. Vidova-Koleva. “How arbitrage-free is the Nelson-Siegel model? ” J. Empir. Financ. 18 (2011): 393–407. [Google Scholar] [CrossRef]
- 1All computations were performed using the software R.
- 2Using the “EstimateAnisotropy” function of the software R (package “Intamap”).
- 3Using the “Nelson.Siegel” function of the software R (package “YieldCurve”).
- 4The information of date is expressed as (Day/Month/Year).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arbia, G.; Di Marcantonio, M. Forecasting Interest Rates Using Geostatistical Techniques. Econometrics 2015, 3, 733-760. https://doi.org/10.3390/econometrics3040733
Arbia G, Di Marcantonio M. Forecasting Interest Rates Using Geostatistical Techniques. Econometrics. 2015; 3(4):733-760. https://doi.org/10.3390/econometrics3040733
Chicago/Turabian StyleArbia, Giuseppe, and Michele Di Marcantonio. 2015. "Forecasting Interest Rates Using Geostatistical Techniques" Econometrics 3, no. 4: 733-760. https://doi.org/10.3390/econometrics3040733
APA StyleArbia, G., & Di Marcantonio, M. (2015). Forecasting Interest Rates Using Geostatistical Techniques. Econometrics, 3(4), 733-760. https://doi.org/10.3390/econometrics3040733





