A One Line Derivation of EGARCH

Abstract

One of the most popular univariate asymmetric conditional volatility models is the exponential GARCH (or EGARCH) specification. In addition to asymmetry, which captures the different effects on conditional volatility of positive and negative effects of equal magnitude, EGARCH can also accommodate leverage, which is the negative correlation between returns shocks and subsequent shocks to volatility. However, the statistical properties of the (quasi-) maximum likelihood estimator of the EGARCH parameters are not available under general conditions, but rather only for special cases under highly restrictive and unverifiable conditions. It is often argued heuristically that the reason for the lack of general statistical properties arises from the presence in the model of an absolute value of a function of the parameters, which does not permit analytical derivatives, and hence does not permit (quasi-) maximum likelihood estimation. It is shown in this paper for the non-leverage case that: (1) the EGARCH model can be derived from a random coefficient complex nonlinear moving average (RCCNMA) process; and (2) the reason for the lack of statistical properties of the estimators of EGARCH under general conditions is that the stationarity and invertibility conditions for the RCCNMA process are not known.

1. Introduction

In the world of univariate conditional volatility models, the ARCH model of Engle [1] and the generalization to the GARCH model by Bollerslev [2] are the two most widely estimated symmetric models of time-varying conditional volatility, where symmetry refers to the identical effects on volatility of positive and negative shocks of equal magnitude.

The asymmetric effects on conditional volatility of positive and negative shocks of equal magnitude can be captured in different ways by the exponential GARCH (or EGARCH) model of Nelson [3,4], and the GJR (alternatively, asymmetric or threshold) model of Glosten, Jagannathan and Runkle [5]. These are the two most widely estimated asymmetric univariate models of conditional volatility.

A special case of asymmetry is that of leverage. As defined by Black [6] in terms of the debt-to-equity ratio, leverage is associated with increases in volatility for negative shocks to returns and decreases in volatility for positive shocks to returns. In short, leverage captures the negative correlation between returns shocks and subsequent shocks to volatility. The EGARCH model is capable of capturing leverage, depending on appropriate restrictions on the parameters of the model.

Although the GJR model can capture asymmetry, leverage is not possible, unless the short run persistence effect (that is, the ARCH parameter) is negative. Such a restriction is not consistent with the standard sufficient condition for conditional volatility to be positive.

The univariate GARCH model has been extended to its multivariate counterpart in, for example, the BEKK model of Baba et al. [7] and Engle and Kroner [8], and the VARMA-GARCH model of Ling and McAleer [8]. The GJR model has a multivariate counterpart in the VARMA-AGARCH model of McAleer, Hoti and Chan [10].

However, the EGARCH model has not yet been developed formally for multivariate processes, with appropriate regularity conditions. Kawakatsu [11] examined a matrix exponential GARCH model and its estimation under alternative multivariate distributions, but did not provide any asymptotic theory.

Although it is not essential, leverage is an attractive feature of the EGARCH model. Since EGARCH is derived as a discrete-time approximation to a continuous-time stochastic volatility process, and is expressed in logarithms, the exponential operator is required to obtain conditional volatility, which is guaranteed to be positive. Therefore, no restrictions are required for conditional volatility to be positive.

However, the statistical properties for the (quasi-) maximum likelihood estimator of the EGARCH parameters are not available under general conditions, but rather only for special cases under highly restrictive and unverifiable conditions. It is often argued heuristically that the reason for the lack of general statistical properties arises from the presence in the model of an absolute value of a function of the parameters, which does not permit analytical derivatives, and hence does not permit (quasi-) maximum likelihood estimation.

Some specific statistical results are available under highly restrictive assumptions that cannot readily be verified. For example, Straumann and Mikosch [12] assume that conditional volatility models are solutions to stochastic recurrence equations which satisfy a contraction property, and derive some asymptotic results for the EGARCH(1,0), or EARCH(1) model. However, their regularity conditions are difficult to interpret or verify.

Wintenberger [13] proves consistency using continuous invertibility, which is assumed to hold for the EGARCH(1,1) model, and shows asymptotic normality for the quasi-maximum likelihood estimator of EGARCH(1,1) under “non-verifiable” conditions, and asymptotic normality for the stable quasi-maximum likelihood estimator of an invertible EGARCH(1,1) model. However, the sufficient conditions for invertibility seem to be restrictive on the admissible parameter space, and cannot be verified.

Demos and Kyriakopoulou [14] present sufficient conditions under which the EGARCH(1,1) processes have bounded first- and second-order variance derivatives, and the expectation of the supremum norm of the second order log-likelihood derivative is finite. These sufficient conditions for asymptotic normality also restrict the admissible parameter space, and are difficult to verify.

It is shown in this paper for the non-leverage case that the EGARCH model can be derived from a random coefficient complex nonlinear moving average (RCCNMA) process, and that the reason for the lack of statistical properties of the estimators of EGARCH under general conditions is that the stationarity and invertibility conditions for the RCCNMA process are not known.

The remainder of the paper is organized as follows. In Section 2, the EGARCH model is discussed. Section 3 presents a RCCNMA process, from which EGARCH is derived in Section 4. Some concluding comments are given in Section 5.

2. EGARCH

Let the conditional mean of financial returns be given as:

y_t = E (y_t | I_t−1) + ε_t

(1)

where y_t = Δlog P_t represents the log-difference in stock prices (P_t), I_t−1 is the information set at time t−1, and ε_t is conditionally heteroskedastic.

The EGARCH specification of Nelson [3,4] is given as:

log h_t = ω + α |η_t−1| + γη_t−1 + β log h_t−1, |β|<1

(2)

where the standardized shocks, η_t, are given by , η_t ~ iid (0, ω), |β|<1 and is the stability condition when log h_t−1 is included in the model. Asymmetry exists if γ ≠ 0, while leverage exists if γ < 0 and γ < α < −γ. The specification in Equation (2) is EGARCH(1,1), but this can easily be extended to EGARCH(p,q).

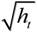As η_t−1 is a function of both ε_t and , each of which is a function of the parameters through Equations (1) and (2), it is clear that quasi-maximum likelihood estimation of EGARCH is problematic as |η_t−1| is not differentiable with respect to the parameters. Moreover, invertibility of EGARCH is also problematic because of the presence of the logarithmic transformation as well as the absolute value function.

3. Random Coefficient Complex Nonlinear Moving Average Process

Consider a random coefficient complex nonlinear moving average (RCCNMA) process given by:

(3)

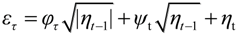
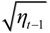Where is a complex-valued function of η_t−1, φ_t ~ iid (0, α), and ψ_t ~ iid (0, γ).

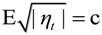If η_t is a standard normal variable, then , which is a known constant. Moreover:

Where and E[I(η_t ≥ 0)] = E[I(η_t < 0)] = 0.5 are the expectations of two indicator functions. As the mean of the complex-valued function is a finite constant, it follows that both the unconditional and conditional means of ε_t in Equation (3) are zero.

As the RCCNMA process given in Equation (3) is not in the class of random coefficient linear moving average models examined in Marek [15], the sufficient conditions for stationarity and invertibility of the RCCNMA process are not known.

4. One Line Derivation of EGARCH

It follows from Equation (3) that:

(4)

The use of an infinite lag for the RCCNMA process in Equation (3) would yield the EGARCH model in Equation (2).

It is worth noting that the transformation of h_t in Equation (4) is not logarithmic, but the approximation given by:

log h_t = log(1 + (h_t − 1)) ≈ h_t − 1

can be used to replace h_t in Equation (4) with 1 + log h_t.

The interpretation of leverage, whereby γ < 0 and γ < α < −γ, is lost in the above derivation because both α and γ are required to be positive.

More importantly, in terms of interpreting the model, the derivation of EGARCH, albeit without the logarithmic transformation, in Equation (4) shows that the statistical properties of the (quasi-) maximum likelihood estimator of the EGARCH parameters do not exist under general conditions because the model is based on a RCCNMA process, for which the stationarity and invertibility conditions are not known.

5. Conclusion

The paper was concerned with one of the most popular univariate asymmetric conditional volatility models, namely the exponential GARCH (or EGARCH) specification. The EGARCH model is popular, among other reasons, because it can capture both asymmetry, namely the different effects on conditional volatility of positive and negative effects of equal magnitude, and leverage, which is the negative correlation between returns shocks and subsequent shocks to volatility.

The statistical properties for the (quasi-) maximum likelihood estimator of the EGARCH parameters are not available under general conditions, but rather only for special cases under highly restrictive and unverifiable conditions. It is often argued heuristically that the reason for the lack of general statistical properties arises from the presence in the model of an absolute value of a function of the parameters, which does not permit analytical derivatives, and hence does not permit (quasi-) maximum likelihood estimation.

It was shown in the paper for the non-leverage case that the EGARCH model could be derived from a random coefficient complex nonlinear moving average (RCCNMA) process, and that the reason for the lack of statistical properties of the estimators of EGARCH under general conditions is that the stationarity and invertibility conditions for the RCCNMA process are not known.