Counterfactual Duration Analysis

Abstract

This article introduces new counterfactual standardization techniques for comparing duration distributions subject to random censoring through counterfactual decompositions. The counterfactual distribution of one population relative to another is computed after estimating the conditional distribution, using either a semiparametric or a nonparametric specification. We consider both the semiparametric proportional hazard model and a fully nonparametric partition-based estimator. The finite-sample performance of the proposed methods is evaluated through Monte Carlo experiments. We also illustrate the methodology with an application to unemployment duration in Spain during the period between 2004 and 2007, focusing on gender differences. The results indicate that observable characteristics account for only a small portion of the observed gap.

1. Introduction

When comparing a phenomenon across populations, it is essential to account for differences in population composition in order to avoid drawing misleading conclusions. For example, in analyzing differences in unemployment duration between men and women, it is necessary to control for differences in human capital and job tenure to ensure comparability. This can be carried out by estimating the outcome of interest in both populations under a common composition, i.e., the unemployment duration distribution that would arise if men and women shared the same levels of human capital and tenure.

Neison (1844) introduced standardization techniques to compare crude death rates across districts in Great Britain, accounting for differences in age structure. In this context, standardization entails re-estimating counterfactual values of the outcome under a common distribution of covariates. Typically, this distribution corresponds to that of one of the populations, although it may also be defined as the pooled distribution or another external benchmark. Later, Kitagawa (1955) formalized this approach and proposed decomposing the total difference in mortality rates into a composition effect, driven by differences in population characteristics, and a structure effect reflecting differences in group-specific risks. The latter term captures disparities in returns to observable characteristics and is often interpreted as reflecting institutional factors, behavioral responses, or potential discrimination (Fortin et al., 2011; Neumark, 1988; Oaxaca & Ransom, 1999). The structural effect should therefore be interpreted as a statistical measure of unexplained heterogeneity rather than as evidence of a specific causal mechanism. Kitagawa (1964) extended this framework to decomposing the differences between the characteristics of the cumulative distribution functions (CDFs) of two populations.

In the context of unemployment duration gender gaps, the composition effect measures the share of the observed difference that arises solely from disparities in observable characteristics. In contrast, the structure effect captures the residual difference that would remain even if both groups shared identical covariate distributions. Moreover, the composition effect can be further decomposed to assess the relative contribution of each covariate (Oaxaca & Ransom, 1999; Rothe, 2015).

In economics, counterfactual decompositions became prominent through their application to the analysis of gender wage gaps. The Oaxaca–Blinder (OB) decomposition, introduced independently by Oaxaca (1973) and Blinder (1973), partitions the difference between sample means into two counterfactual components based on a linear specification of the regression function. In this framework, the counterfactual mean is obtained as the average of fitted values using coefficient estimates from one population and covariate observations from the other. The OB approach has been extended to other features of the cumulative distribution function and applied widely in the study of gender wage differentials (e.g., Cain, 1986; Blau & Kahn, 1992; Oaxaca & Ransom, 1999; and Machado & Mata, 2005). Related work has analyzed other wage differentials, including racial (Reimers, 1983; Melly, 2005), union (Freeman, 1980), skill-related (Juhn et al., 1991), cross-country (Donald & Hsu, 2014), policy-induced (Rothe, 2015), and immigrant–native (Chiquiar & Hanson, 2005) gaps. Lemieux (2002) provides a comprehensive review of methodologies for decomposing changes in wage distributions.

Nonparametric and semiparametric extensions relax the linearity assumption to address mean and distributional decompositions, often relying on kernel regression or density estimation (e.g., Stock, 1989; DiNardo et al., 1996). For other distributional features, decompositions employ flexible nonparametric or semiparametric specifications of the conditional CDF. Fortin et al. (2011) provide an extensive overview of these methodological developments. Despite their broad use, only a limited number of studies have examined duration outcomes such as unemployment spells. More recent contributions include Guo and Basse (2021), who generalize the OB framework to nonlinear models, and Charpentier and Flachaire (2024), who propose a simultaneous decomposition of means and inequality.

Although these methods are widely used in applied work, relatively few studies focus on duration outcomes, such as unemployment spells. Analyzing duration data requires stronger identification assumptions, particularly concerning the censoring mechanism. We propose counterfactual decomposition techniques for right-censored duration outcomes that encompass alternative standardizations of the distribution function, using both nonparametric and semiparametric specifications of the underlying cumulative distribution function. We also provide a detailed discussion of how to implement OB-type decompositions in this setting. The original OB proposal cannot be directly extended to other distributional features that are nonlinear in the underlying conditional CDF. In particular, the cumulative hazard rate (CHR) is defined as the integral of the conditional CDF over the corresponding survival function. The averaged CHR (ACHR) is not directly related to the HR, and the two can exhibit very different shapes, as shown in the empirical example. Furthermore, the interpretation of the ACHR is not obvious. The HR is the main research tool in duration analysis, providing valuable information on the underlying duration distribution. In the context of unemployment spells, it measures the instantaneous probability of finding a job after remaining unemployed for a period of length t. Nevertheless, as we show in this article, the counterfactual HR can be derived from the counterfactual CDF, and this estimator can be used to decompose the difference between the HR estimates in the two populations.

The Cox proportional cumulative hazard rate (PCHR) model has been widely used to study gender gaps in unemployment duration, typically through the averaged cumulative hazard function (ACHF), i.e., the conditional hazard function integrated with respect to the marginal distribution of covariates, see, e.g., Ham et al. (1999), Du and Dong (2009), and Tansel and Tasci (2010). Since the ACHF and the marginal hazard function (HF) are generally unrelated, inference based on the ACHF may be misleading. To our knowledge, no studies have implemented direct standardization of the HF or other distributional features under right censoring, nor have these methods been applied beyond unemployment. The counterfactual decomposition methodology presented in this article is directly transferable to these domains, offering a unified framework for analyzing differences in censored duration outcomes. Beyond unemployment analysis, the proposed methods can be applied to a wide range of outcomes that can be expressed as duration times. Examples include time to school dropout, time to credit default or repayment, duration until job promotion or contract termination, patient recovery times in medical studies, or the length of stay in migration.

Because the mean duration cannot be consistently estimated in the presence of censoring, comparisons based on the restricted mean survival time (RMST), i.e., the expected duration within a fixed time window, are more appropriate. For example, comparisons over the first 12 months (short-run unemployment) or 24 months (long-run unemployment) are meaningful. We extend our framework to incorporate RMST-based standardization and counterfactual decomposition. Our analysis connects to this broader research agenda, complementing recent work on counterfactual survival analysis (Chapfuwa et al., 2021), on the role of heterogeneous survival expectations in shaping structural effects (de Bresser, 2024), and on semiparametric methods for counterfactual inference in duration models (Hausman & Woutersen, 2014).

We evaluate the performance of the proposed methods through Monte Carlo simulations under alternative data-generating processes, and we illustrate their empirical application by decomposing gender gaps in unemployment duration in Spain during 2004–2007, using data from the European Union Statistics on Income and Living Conditions (EU-SILC). The results indicate that composition effects account for only a small fraction of the observed gender gap. Moreover, estimates based on ACHR and HR differ substantially, with nonparametric approaches providing more robust and reliable insights.

The remainder of this article is structured as follows. Section 2 introduces the main notation, standardization techniques, and counterfactual decomposition methods. Section 3 develops estimators based on both the PCHR model and nonparametric specifications of the conditional distribution. Section 4 evaluates the finite-sample performance through Monte Carlo simulations. Section 5 applies the proposed methods to Spanish unemployment duration data. Finally, Section 6 concludes with key findings and remarks.

2. Standardization Under Censoring

Consider the duration random variable $T^{\left(j\right)}$ for populations observed under right censoring according to variable $C^{\left(j\right)}$, $j=0,1$. Counterfactual decompositions must be performed from the observed random vector $\left(Z^{\left(j\right)},{\delta }^{\left(j\right)},{\mathit{X}}^{\left(j\right)}\right),$ where ${\mathit{X}}^{\left(j\right)}$ is the observed vector of population components, or characteristics, with explanatory power for $T^{\left(j\right)},$$Z^{\left(j\right)}=min\left(T^{\left(j\right)},C^{\left(j\right)}\right)$, and ${\delta }^{\left(j\right)}=1_{\left\{T^{\left(j\right)}\le C^{\left(j\right)}\right\}}$ indicates whether or not the observed duration is censored with $1_{\left\{A\right\}}$, the indicator function of event A. Censoring appears due to the lack of follow-up for the individuals. When individuals are observed over a fixed period, complete durations are not always available because the relevant event did not occur at the end of the observation period (administrative censoring) or because the individual drops out before completion (loss to follow-up).

Let $F_{T,\mathit{X}}^{\left(j\right)}$ be the joint cumulative distribution function (CDF) of $\left(T^{\left(j\right)},\mathit{X}\right)$ and $F_{T\mid \mathit{X}}^{\left(j\right)}\left(·\mid \mathit{X}\right)$ the corresponding CDF of $T^{\left(j\right)}$ given $\mathit{X}$, i.e.,

$$F^{\left(j\right)}\left(t,\mathit{x}\right)={\int }_{\left\{\overline{\mathit{x}}\le \mathit{x}\right\}}{F}_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.t\right|\overline{\mathit{x}}\right)F_{\mathit{X}}^{\left(j\right)}\left(d\overline{\mathit{x}}\right),$$

for all $\left(t,\mathit{x}\right)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^k$ and $j=0,1,$ where $F_{\xi }^{\left(j\right)}\left(v\right)={\mathbb{P}}^{\left(j\right)}\left({\xi }^{\left(j\right)}\le v\right)$ is the corresponding CDF of a generic random variable, or random vector, ${\xi }^{\left(j\right)}$, and ${\tau }_{\xi }^{\left(j\right)}=inf\left(t:F_{\xi }^{\left(j\right)}\left(t\right)=1\right)$ is the upper bound of its support. Note that the sample does not provide information beyond ${\tau }_Z^{\left(j\right)}=min\left({\tau }_C^{\left(j\right)},{\tau }_T^{\left(j\right)}\right)$, which implies that $F^{\left(j\right)}\left(t,\mathit{x}\right)$ cannot be identified from the CDF of the observable random vector $\left(Z^{\left(j\right)},{\mathit{X}}^{\left(j\right)},{\delta }^{\left(j\right)}\right)$. Thus, the consistent estimation of the sub-DF,

$$F_{*}^{\left(j\right)}\left(t,\mathit{x}\right)=\left\{\begin{array}{c}{F}^{\left(j\right)}\left(t,\mathit{x}\right)\mathrm{for}t<{\tau }_Z^{\left(j\right)}\hfill \\ F^{\left(j\right)}\left({\tau }_Z^{\left(j\right)}-,\mathit{x}\right)+1_{\left\{{\tau }_Z^{\left(j\right)}\in A^{\left(j\right)}\right\}}{F}^{\left(j\right)}\left(\left\{{\tau }_Z^{\left(j\right)}\right\},\mathit{x}\right),t\ge {\tau }_Z^{\left(j\right)},\hfill \end{array}\right.$$

is the best we can hope for, where for any generic CDF $G,$$G\left\{t\right\}=G\left(t\right)-G(t-),$ and $A^{\left(j\right)}=\left\{z:{\mathbb{P}}^{\left(j\right)}\left(Z^{\left(j\right)}=z\right)>0\right\}$ is the number of jumps in $F_Z^{\left(j\right)}.$ Notice that $F_{*}^{\left(j\right)}(t,·)=F^{\left(j\right)}(t,·)$ for all $t<{\tau }_Z^{\left(j\right)}$, and also for all $t\le {\tau }_Z^{\left(j\right)},$ when either, $F^{\left(j\right)}\left(\left\{t\right\},·\right)=0\mathrm{or}{F}^{\left(j\right)}\left(\left\{t\right\},·\right)>0\mathrm{and}{\mathbb{P}}^{\left(j\right)}\left(C^{\left(j\right)}\le {\tau }_Z^{\left(j\right)}\right)<1$.

The standardized version of $F_T^{\left(j\right)}\left(t\right)$, taking population s as standard, is

$$F_T^{(j,s)}\left(t\right)={\int }_0^{\infty }{F}_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.t\right|\overline{\mathit{x}}\right)F_{\mathit{X}}^{\left(s\right)}\left(d\overline{\mathit{x}}\right)\mathrm{for}t\le {\tau }_Z^{\left(j\right)},$$

(1)

which represents the distribution that population j would exhibit if it had the covariate distribution of population s. For instance, in the context of gender differences in unemployment duration, this would correspond to the distribution of unemployment duration for women if they had the same observable characteristics as men. Henceforth, we take for granted that integrals in (1) are well defined, which requires that the support of the components ${\mathit{X}}^{\left(s\right)}$ in the standard population is contained in the support of the standardized population. Notice that $F_T^{\left(j\right)}=F_T^{(j,j)}.$ The counterfactual distribution $F_T^{(j,s)}$ is the basis for identifying their moments or other characteristics. In particular, the standardized cumulative HR is

$$\begin{array}{lll}{\mathsf{\Lambda }}^{(j,s)}\left(t\right)& =& {\int }_0^t{\displaystyle \frac{F_T^{(j,s)}\left(d\overline{t}\right)}{1-F_T^{(j,s)}(\overline{t}-)}},t\le {\tau }_Z^{\left(j\right)},\hfill \\ & =& {\int }_0^t{\lambda }^{(j,s)}\left(\overline{t}\right)d\overline{t}\mathrm{for}{F}_T^{(j,s)}\mathrm{absolutely}\mathrm{continuous},\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& =& \sum _{\ell =0}^t{\lambda }^{(j,s)}(\ell ),\mathrm{for}{F}_T^{(j,s)}\mathrm{discrete}\mathrm{with}\mathrm{jumps}\mathrm{at}\ell =0,1,...\hfill \end{array}$$

(3)

where ${\lambda }^{(j,s)}$ is the standarized HR. This is interpreted, in the context of unemployment duration analysis, as the instant probability of finding a job that would have a worker unemployed during a period of length t, taken at random from population j, if population j had the same distribution of covariates than population s.

As it was mentioned in the introduction, the existing applied work on counterfactual duration analysis of unemployment duration gender gaps is based on the ACHR, ${\gamma }^{(j,s)}\left(t\right)=\mathbb{E}\left({\lambda }_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.t\right|{\mathit{X}}^{\left(s\right)}\right)\right),$ where ${\lambda }_{\left.T\right|\mathit{X}}^{\left(j\right)}$ is the CHR, defined as (2) in terms of the cumulative CHR

$${\mathsf{\Lambda }}_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.t\right|\mathit{x}\right)={\int }_0^t{\displaystyle \frac{F_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.d\overline{t}\right|\mathit{x}\right)}{1-F_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.\overline{t}\right|\mathit{x}\right)}}.$$

Obviously, the ${\gamma }^{(j,s)}$ and ${\lambda }^{(j,s)}$ shapes are not necessarily related.

Alternative estimators can also be considered, relying on different specifications of the conditional CDF, which is equivalently characterized by the conditional hazard rate (CHR) for censored duration variables. Examples include semiparametric approaches such as the accelerated failure time (AFT) model (Kalbfleisch & Prentice, 1973), the proportional odds (PO) model (Clayton, 1976), or, more recently, the distributional regression framework for censored duration data proposed by Delgado et al. (2022). These alternatives to the Cox model may be preferred depending on the context. In this article, we have focused on Cox’s specification because it is by far the most popular. The advantage of a nonparametric model is that the underlying CHR is not specified, and the regularity conditions needed to justify the consistency of the proposed partition estimate are minimal taking a fixed number of partitions. Notice that, because we are estimating integrals using KM weights, independence between the survival variable T and the censoring variable C is needed. Naturally, other nonparametric estimators could also be employed.

While the hazard rate remains the central distributional feature in duration analysis, mean-based comparisons are often of interest from a policy perspective. Since the unconditional mean of duration cannot be consistently estimated under censoring, a natural alternative is the restricted mean survival time (RMST), defined as,

$${\mu }_{{\tau }^{*}}^{\left(j\right)}={\int }_0^{{\tau }^{*}}\left(1-F_T^{\left(j\right)}\left(t\right)\right)dt=\mathbb{E}\left(\min \left(T^{\left(j\right)},{\tau }^{*}\right)\right),\mathrm{for}\mathrm{any}{\tau }^{*}\le {\tau }_Z^{\left(j\right)}.$$

The RMST is the average duration in the first ${\tau }^{*}$ periods. For instance, if ${\tau }^{*}=12$, this is the average unemployment duration during the first 12 months, which is related to short-term unemployment. Chen and Tsiatis (2001), Karrison (1987), Zhang and Schaubel (2011), and Zucker (1998) provide applications of RMST to different contexts. The parameter of the corresponding counterfactual CDF is

$${\mu }_{{\tau }^{*}}^{(j,s)}={\int }_0^{{\tau }^{*}}\left(1-F_T^{(j,s)}\left(t\right)\right)dt={\int }_0^{\infty }min\left(t,{\tau }^{*}\right)F_T^{(j,s)}\left(dt\right),\mathrm{for}\mathrm{any}{\tau }^{*}\le {\tau }_Z^{\left(j\right)}.$$

(4)

The crucial step to estimate the standardized quantities, either $F_T^{(j,s)}$, ${\lambda }^{(j,s)}$, or ${\mu }_{{\tau }^{*}}^{(j,s)},$ requires the prior estimation of $F_{\left.T\right|\mathit{X}}^{\left(j\right)}$. To this end, we consider two possibilities. One is based on the PCHR specification, which assumes that the underlying CHR, ${\mathsf{\Lambda }}_{\left.T\right|\mathit{X}}^{\left(j\right)},$ belongs to the family of monotonically increasing functions $\left(t,x\right)\to {\mathsf{\Lambda }}_0\left(t\right)·exp\left({\mathit{x}}^T\mathit{\beta }\right)$ where $\mathit{\beta }\in \mathsf{\Theta }$ and $t\to {\mathsf{\Lambda }}_0\left(t\right)\in {\mathbb{R}}^{+}$.

When the CHR specification is correct, there exists a ${\mathsf{\Lambda }}_0^{\left(j\right)}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ and ${\mathit{\beta }}_0^{\left(j\right)}\in \mathsf{\Theta },$ such that

$$F_{\left.T\right|\mathit{X}}^{\left(j\right)}\left(\left.t\right|{\mathit{X}}^{\left(j\right)}\right)=1-exp\left\{-{\mathsf{\Lambda }}_0^{\left(j\right)}\left(t\right)·exp\left({\mathit{X}}^{\left(j\right)\mathrm{T}}{\mathit{\beta }}_0^{\left(j\right)}\right)\right\}a.s.$$

The identification of ${\mathsf{\Lambda }}_0$ and ${\mathit{\beta }}_0$ requires that

A.0.

$T^{\left(j\right)}$ is independent of $C^{\left(j\right)}$ conditionally on ${\mathit{X}}^{\left(j\right)},$$j=0,1.$

The standardized $F_T^{\left(j\right)}$ with respect to population $s,$ assuming that ${\mathsf{\Lambda }}_{\left.T\right|\mathit{X}}^{\left(j\right)}\in \mathcal{G}$, is

$$F_{T\mathcal{G}}^{(j,s)}\left(t\right)=1-\mathbb{E}\left[exp\left\{-{\mathsf{\Lambda }}_0^{\left(j\right)}\left(t\right)·exp\left({\mathit{X}}^{\left(s\right)\mathrm{T}}{\mathit{\beta }}_0^{\left(j\right)}\right)\right\}\right],\mathrm{for}\mathrm{any}t\le {\tau }_Z^{\left(j\right)},$$

with corresponding cumulative HR

$${\mathsf{\Lambda }}_{\mathcal{G}}^{(j,s)}\left(t\right)={\int }_0^t{\displaystyle \frac{F_{T\mathcal{G}}^{(j,s)}\left(d\overline{t}\right)}{1-F_{T\mathcal{G}}^{(j,s)}\left(\overline{t}-\right)}},$$

with HR ${\lambda }_{\mathcal{G}}^{(j,s)},$ which is typically unrelated to the ACHR ${\gamma }_{\mathcal{G}}^{(j,s)}=\mathbb{E}\left({\mathsf{\Lambda }}_0^{\left(j\right)}\left(t\right)·exp\left({\mathit{X}}^{\left(s\right)\prime }{\mathit{\beta }}^{\left(j\right)}\right)\right).$ The corresponding standardized RMST is,

$${\mu }_{{\tau }^{*}\mathcal{G}}^{(j,s)}={\int }_0^{\infty }min\left(t,{\tau }^{*}\right)F_{T\mathcal{G}}^{(j,s)}\left(dt\right).$$

Note that $F_{T\mathcal{G}}^{(j,j)}=F_T^{\left(j\right)}$ for all $j=0,1$ under a correct specification, but this is not necessarily the case under misspecification.

We can avoid specifying the CDF by noticing that standardizations can also be performed from any given partition ${\mathbb{A}}_m={\left\{{\mathcal{A}}_{\ell }\right\}}_{\ell =1}^m$ of ${\mathbb{R}}^k,$ such that $\mathbb{P}\left({\mathit{X}}^{\left(j\right)}\in {\mathcal{A}}_{\ell }\right)>0$ for all $\ell =1,...,m,$ since

$$F_T^{\left(j\right)}\left(t\right)=\sum _{\ell =1}^m{F}_{\left.T\right|{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(\left.t\right|{\mathcal{A}}_{\ell }\right)q_{{\mathcal{A}}_{\ell }}^{\left(j\right)}=\sum _{\ell =1}^m{p}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(t\right)\mathrm{for}t\le {\tau }_Z^{\left(j\right)},$$

with

$$F_{\left.T\right|\mathcal{A}}^{\left(j\right)}\left(\left.t\right|\mathcal{A}\right)={\mathbb{P}}^{\left(j\right)}\left(\left.T^{\left(j\right)}\le t\right|{\mathit{X}}^{\left(j\right)}\in \mathcal{A}\right)={\displaystyle \frac{p_{\mathcal{A}}^{\left(j\right)}\left(t\right)}{q_{\mathcal{A}}^{\left(j\right)}}},$$

$p_{\mathcal{A}}^{\left(j\right)}\left(t\right)={\int }_{\mathit{x}\in \mathcal{A}}{F}^{\left(j\right)}\left(t,d\mathit{x}\right)$ and $q_{\mathcal{A}}^{\left(j\right)}=p_{\mathcal{A}}^{\left(j\right)}(\infty ).$ This suggests the standardization

$$F_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)=\sum _{\ell =1}^m{F}_{\left.T\right|{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(\left.t\right|{\mathcal{A}}_{\ell }\right)q_{{\mathcal{A}}_{\ell }}^{\left(s\right)}=\sum _{\ell =1}^m{\displaystyle \frac{p_{{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(t\right)}{q_{{\mathcal{A}}_{\ell }}^{\left(j\right)}}}{q}_{{\mathcal{A}}_{\ell }}^{\left(s\right)},t\le {\tau }_Z^{\left(j\right)}.$$

(5)

Thus, it is not needed to specify $F_{\left.T\right|\mathit{X}}^{\left(j\right)}$ to obtain the components in the counterfactual decomposition, but only $p_{\mathcal{A}}^{\left(j\right)}.$ Notice that, unlike the semiparametric standardization $F_{T\mathcal{G}}^{(j,s)},$ we always have that $F_{T{\mathbb{A}}_m}^{(j,j)}=F_T^{\left(j\right)},$ despite the actual underlying CDF shape, but $F_T^{(j,s)}\ne F_{T{\mathbb{A}}_m}^{(j,s)}$ for $j\ne s.$ In order to identify $p_{\mathcal{A}}^{\left(j\right)}\left(t\right)$ for $t\le {\tau }_Z^{\left(j\right)},$ we need to assume that,

A.1

$T^{\left(j\right)}$ is independent of $C^{\left(j\right)},$$j=0,1.$

A.2

${\delta }^{\left(j\right)}$ and ${\mathit{X}}^{\left(j\right)}$ are independent conditional on $T^{\left(j\right)}$ a.s., $j=0,1.$

Condition A.1 is the standard identification condition for the nonparametric $F_{*T}^{\left(j\right)},$ which justifies the consistency of the Kaplan–Meier (KM) product limit estimator using censored data (Kaplan & Meier, 1958). Assumption A.2 is the extra condition, provided by Stute (1993) to identify $F_{*}^{\left(j\right)}$, which establishes the relation between the covariates and the censoring mechanism. Notice that we have a different standardization $F_{T{\mathbb{A}}_m}^{(j,s)}$ for each possible partition, which is the cost that one must pay for not imposing a more restrictive specification.

The standardized RMST using partitions ${\mathbb{A}}_m$ is

$${\mu }_{{\tau }^{*}{\mathbb{A}}_m}^{(j,s)}={\int }_0^{\infty }min\left(t,{\tau }^{*}\right)F_{T{\mathbb{A}}_m}^{(j,s)}\left(dt\right)=\sum _{\ell =1}^m{\displaystyle \frac{q_{{\mathcal{A}}_{\ell }}^{\left(s\right)}}{q_{{\mathcal{A}}_{\ell }}^{\left(j\right)}}}{\int }_0^{\infty }min\left(t,{\tau }^{*}\right)·p_{{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(dt\right).$$

An alternative standardization for the RMST relies on a semiparametric specification of the conditional mean of the restricted version of the outcome $min\left(T^{\left(j\right)},{\tau }^{*}\right)$, i.e., imposing restrictions on $m_{{\tau }^{*}}^{\left(j\right)}\left(\mathit{x}\right)=\mathbb{E}\left(\left.min\left(T^{\left(j\right)},{\tau }^{*}\right)\right|\mathit{X}=\mathit{x}\right),$ since

$${\mu }_{{\tau }^{*}}^{(j,s)}={\int }_{{\mathbb{R}}^k}{m}_{{\tau }^{*}}^{\left(j\right)}\left(\mathit{x}\right)F_{\mathit{X}}^{\left(s\right)}\left(d\mathit{x}\right)=\mathbb{E}\left(m_{{\tau }^{*}}^{\left(j\right)}\left({\mathit{X}}^{\left(s\right)}\right)\right).$$

In particular, a linear specification of $m_{{\tau }^{*}}^{\left(j\right)}$ produces the OB standardization analog for the RMST. That is, taking into account that ${\mu }_{{\tau }^{*}}^{\left(j\right)}={\alpha }_0^{\left(j\right)}+{\eta }_0^{\left(j\right)\mathrm{T}}\mathbb{E}\left({\mathit{X}}^{\left(j\right)}\right),$ with parameters ${\left({\alpha }_0^{\left(j\right)},{\eta }_0^{\left(j\right)\mathrm{T}}\right)}^{\mathrm{T}}$ such that $min\left(T^{\left(j\right)},{\tau }^{*}\right)-{\alpha }_0^{\left(j\right)}-{\eta }_0^{\left(j\right)\mathrm{T}}{\mathit{X}}^{\left(j\right)}$ has zero mean and is uncorrelated with ${\mathit{X}}^{\left(j\right)},$ the OB standardization of ${\mu }_{{\tau }^{*}}^{(j,s)}$ is ${\ell }_{{\tau }^{*}}^{(j,s)}={\alpha }_0^{\left(j\right)}+{\eta }_0^{\left(j\right)\mathrm{T}}\mathbb{E}\left({\mathit{X}}^{\left(s\right)}\right)$.

The total CDF difference $F_T^{\left(j\right)}\left(t\right)-F_T^{\left(s\right)}\left(t\right)$ can be written in terms of the counterfactual effects using $F_{T{\mathbb{A}}_m}^{(j,s)}$ as

$$\begin{array}{ccc}\hfill F_T^{\left(j\right)}\left(t\right)-F_T^{\left(s\right)}\left(t\right)={\Delta }^{(j,s)}\left(t\right)& =& \left[F_{T{\mathbb{A}}_m}^{(j,j)}\left(t\right)-F_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)\right]+\left[F_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)-F_{T{\mathbb{A}}_m}^{(s,s)}\left(t\right)\right]\hfill \\ & =& {\Delta }_{T{\mathbb{A}}_m}^{(j,s)C}\left(t\right)+{\Delta }_{T{\mathbb{A}}_m}^{(j,s)S}\left(t\right),t\le {\tau }_Z,\hfill \end{array}$$

(6)

where ${\Delta }_{T{\mathbb{A}}_m}^{(j,s)S}$ is the counterfactual structural effect, ${\Delta }_{T{\mathbb{A}}_m}^{(j,s)C}$ is the counterfactual composition effect, and ${\tau }_Z=min\left({\tau }_Z^{\left(j\right)},{\tau }_Z^{\left(s\right)}\right)$. We can perform a similar decomposition using $F_{T\mathcal{G}}^{(j,s)},$ but we must take into account that the decomposition is for ${\Delta }_{\mathcal{G}}^{(j,s)}=F_{T\mathcal{G}}^{(j,j)}-F_{T\mathcal{G}}^{(s,s)},$ which is different than ${\Delta }^{(j,s)}$ under the misspecification of the conditional CDF $F_{\left.T\right|\mathit{X}}^{\left(j\right)}$.

The HR or the RMST differences can be decomposed differently from (6). That is, if ${\theta }_T^{\left(j\right)}$ represents a particular distributional feature of population $j,$ e.g., ${\theta }_T^{\left(j\right)}$ can be ${\mu }_{{\tau }^{*}}^{\left(j\right)}$, ${\ell }_{{\tau }^{*}}^{\left(j\right)}$, or ${\lambda }_T^{\left(j\right)}\left(t\right),$

$${\Delta }_{\theta }^{(j,s)}={\theta }_T^{\left(j\right)}-{\theta }_T^{\left(s\right)}=\left[{\theta }_T^{(j,j)}-{\theta }_T^{(j,s)}\right]+\left[{\theta }_T^{(j,s)}-{\theta }_T^{(s,s)}\right]={\Delta }_{\theta }^{(j,s)C}+{\Delta }_{\theta }^{(j,s)S}.$$

(7)

3. Estimation

The sample observed consists of $iid$${\left\{Z_i^{\left(j\right)},{\mathit{X}}^{\left(j\right)},{\delta }_i^{\left(j\right)}\right\}}_{i=1}^{n_j}$ as $\left(Z^{\left(j\right)},{\mathit{X}}^{\left(j\right)},{\delta }^{\left(j\right)}\right),$ $j=0,1$. Henceforth, ties within censored or uncensored duration times are ordered arbitrarily, and ties among uncensored and censored durations are treated as if the former precedes the latter.

Assuming a PCHR specification, $F_{T\mathcal{G}}^{(j,s)}$ is estimated by

$${\tilde{F}}_{T\mathcal{G}}^{(j,s)}\left(t\right)=1-{\displaystyle \frac{1}{n_s}}\sum _{i=1}^{n_s}exp\left(-{\tilde{\mathsf{\Lambda }}}^{\left(j\right)}\left(t\right)·exp\left({\tilde{\mathit{\beta }}}^{\left(j\right)\mathrm{T}}{\mathit{X}}_i^{\left(s\right)}\right)\right),$$

where ${\tilde{\mathsf{\Lambda }}}_b^{\left(j\right)}$ is the Breslow (1974) estimator of ${\mathsf{\Lambda }}_0^{\left(j\right)}$ and ${\tilde{\mathit{\beta }}}^{\left(j\right)}$ is the Partial Maximum Likelihood (PML) estimator of ${\mathit{\beta }}_0$ (Cox, 1972). Henceforth, we avoid references to the sample size.

The weak convergence of ${\tilde{F}}_T^{(j,s)}$ is an immediate consequence of the well-developed asymptotic theory for ${\left({\tilde{\mathsf{\Lambda }}}_b^{\left(j\right)},{\tilde{\mathit{\beta }}}^{\left(j\right)\mathrm{T}}\right)}^{\mathrm{T}}$. Tsiatis (1981) showed that, under $A.0,$${\tilde{\mathit{\beta }}}^{\left(j\right)}={\mathit{\beta }}_0^{\left(j\right)}+O_p\left(n_j^{-1/2}\right)$ and ${sup}_{t\in \left[0,{\tau }_Z\right]}\left|\left({\tilde{\mathsf{\Lambda }}}^{\left(j\right)}-{\mathsf{\Lambda }}_0^{\left(j\right)}\right)\left(t\right)\right|=O_p\left(n_j^{-1/2}\right).$ Thus, applying Theorem 4.1 in Chernozhukov et al. (2013), for $j,s=0,1,$ when the PCHR specification is correct,

$$\begin{array}{ccc}\hfill \underset{t\in \left[0,{\tau }_Z\right]}{sup}\left|{\tilde{F}}_{T\mathcal{G}}^{(j,s)}-F_T^{(j,s)}\right|\left(t\right)& =& O_p\left(\sqrt{{\displaystyle \frac{n_0+n_1}{n_0{n}_1}}}\right)\mathrm{as}{n}_0,n_1\to \infty ,\hfill \end{array}$$

(8)

where $n_j/(n_0+n_1)\to s_j\in (0,1),$ as $n_0,n_1\to \infty ,j=0,1$.

Asymptotic confidence intervals for ${\tilde{F}}_{T\mathcal{G}}^{(j,s)}$ can be obtained applying results in Andersen and Gill (1982). Bootstrap confidence intervals can also be obtained using techniques designed for the PCHR model, as in Burr (1994), which can be justified in the lines of Theorem 4.2 in Chernozhukov et al. (2013).

The Cox estimator adapted to the counterfactual context is consistent when the CHR is correctly specified but inconsistent under misspecification. The formal justification of inferences based on the proposed counterfactual decompositions is beyond the scope of this article. The results in Chernozhukov et al. (2013) can be used to derive a functional central limit theorem (CLT) for the counterfactual estimator of the HR based on the Cox’s specification. Inferences using the nonparametric CDF estimator based on partitions and KM weights can be carried out using results in Stute (1993) and Stute et al. (2000). These partition estimators can be implemented when regressors are not necessarily random variables, but other random objects such as those used when dealing with spatial, networks, or functional data. Inferences of the counterfactual CDF estimator when the number of sets in the partitions diverges and the size of the sets converges to zero as the sample size diverges could be justified using universal consistency results (Stone, 1980), as implemented for partition estimators of conditional moments by Györfi et al. (2002).

Under A.1, $F_T^{\left(j\right)}$ is consistently estimated by the KM estimator,

$${\widehat{F}}_T^{\left(j\right)}\left(t\right)=1-\prod _{i=1}^{n_j}{\left[1-{\displaystyle \frac{{\delta }_{\left[i:n_j\right]}^{\left(j\right)}}{n_j-i+1}}\right]}^{1_{\{Z_{i:n_j}^{\left(j\right)}\le t\}}}=\sum _{i=1}^n{\widehat{\omega }}_i^{\left(j\right)}{1}_{\left\{Z_{i:n_j}^{\left(j\right)}\le t\right\}},\mathrm{for}\mathrm{all}t\le {\tau }_Z^{\left(j\right)},$$

where

$${\widehat{\omega }}_i^{\left(j\right)}={\displaystyle \frac{{\delta }_{\left[i:n_j\right]}^{\left(j\right)}}{n_j-i+1}}\prod _{\ell =1}^{i-1}{\left[{\displaystyle \frac{n_{\ell }-\ell }{n_{\ell }-\ell +1}}\right]}^{{\delta }_{[\ell :n_j]}^{\left(j\right)}},i=1,...,n,j=0,1,$$

are KM weights, and for any generic sequence ${\left\{{\xi }_i\right\}}_{i=1}^n,$${\xi }_{\left[i:n\right]}$ is the $i-th$$\xi -$concomitant of the ordered $Z-values,$ i.e., ${\xi }_{\left[i:n\right]}={\xi }_j$ if $Z_{i:n}=Z_j$. Then, ${\widehat{\omega }}_i^{\left(j\right)}$ is the mass attached to $\left(Z_{i:n_j}^{\left(j\right)},{\mathit{X}}_{[i:n_j]}^{\left(j\right)}\right)$. Likewise, under A.1 and A.2, $F^{\left(j\right)}\left(t,\mathit{x}\right)$ is consistently estimated by

$${\widehat{F}}^{\left(j\right)}\left(t,\mathit{x}\right)=\sum _{i=1}^{n_j}{\widehat{\omega }}_i^{\left(j\right)}{1}_{\left\{Z_{i:n_j}^{\left(j\right)}\le t,{\mathit{X}}_{[i:n_j]}^{\left(j\right)}\le \mathit{x}\right\}}\mathrm{for}t\le {\tau }_Z^{\left(j\right)}.$$

Therefore, the estimator of $F_{T{\mathbb{A}}_m}^{(j,s)}$ in (5) is estimated by

$${\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)=\sum _{\ell =1}^m{\displaystyle \frac{{\widehat{p}}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(t\right)}{{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}}}{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(s\right)},t\le {\tau }_Z^{\left(j\right)},$$

with ${\widehat{p}}_{\mathcal{A}}^{\left(j\right)}\left(t\right)={\sum }_{i=1}^{n_j}{\widehat{\omega }}_i^{\left(j\right)}{1}_{\left\{Z_{i:n_j}^{\left(j\right)}\le t,{\mathit{X}}_i^{\left(j\right)}\in \mathcal{A}\right\}}$ and ${\widehat{q}}_{\mathcal{A}}^{\left(j\right)}={\widehat{p}}_{\mathcal{A}}^{\left(j\right)}(\infty ).$

Any of the above DF standardizations results in alternative estimates of the cumulative HR. Let ${\check{F}}^{(j,s)}$ denote either ${\tilde{F}}_{T\mathcal{G}}^{(j,s)}$ or ${\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)},$ and the ${\mathsf{\Lambda }}^{(j,s)}$estimator is

$${\check{\mathsf{\Lambda }}}^{(j,s)}\left(t\right)={\int }_0^t{\displaystyle \frac{{\check{F}}_T^{(j,s)}\left(d\overline{t}\right)}{1-{\check{F}}_T^{(j,s)}(\overline{t}-)}},t<{\tau }_Z^{\left(j\right)},$$

which is a jump function in both cases. The corresponding ${\lambda }^{(j,s)}$ estimate is the value of the jump

$${\check{\lambda }}^{(j,s)}={\displaystyle \frac{{\check{F}}_T^{(j,s)}\left\{t\right\}}{1-{\check{F}}_T^{(j,s)}(t-)}},t\le {\tau }_Z^{\left(j\right)},$$

or the smooth version

$${\check{\lambda }}^{(j,s)}\left(t\right)={\int }_0^{\infty }{K}_h\left(\overline{t}-t\right){\check{\mathsf{\Lambda }}}^{(j,s)}\left(d\overline{t}\right),t<{\tau }_Z^{\left(j\right)},$$

where $K_h\left(t\right)=h^{-1}K(t/h),$ and K is a kernel function integrating to one.

Each standarized DF results in alternative ${\mu }_{{\tau }^{*}}^{(j,s)}$ estimates, i.e.,

$${\tilde{\mu }}_{{\tau }^{*}\mathcal{G}}^{(j,s)}={\int }_0^{\infty }min\left(t,{\tau }^{*}\right){\tilde{F}}_{T\mathcal{G}}^{(j,s)}\left(dt\right)=\sum _{i=1}^{n_j}min\left(Z_{i:n_j}^{\left(j\right)},{\tau }^{*}\right)\left[{\tilde{F}}_T^{(j,s)}\left(Z_{i:n_j}^{\left(j\right)}\right)-{\tilde{F}}_T^{(j,s)}\left(Z_{i-1:n_j}^{\left(j\right)}\right)\right]$$

using the PCHR specification, and

$$\begin{array}{ccc}\hfill {\widehat{\mu }}_{{\tau }^{*}{\mathbb{A}}_m}^{(j,s)}& =& {\int }_0^{\infty }min\left(t,{\tau }^{*}\right){\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)}\left(dt\right)\hfill \\ & =& \sum _{\ell =1}^m{\displaystyle \frac{{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(s\right)}}{{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}}}{\int }_0^{\infty }min\left(t,{\tau }^{*}\right)·{\widehat{p}}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}\left(dt\right)\hfill \\ & =& \sum _{i=1}^{n_j}{Z}_{i:n_j}^{\left(j\right)}{\widehat{\omega }}_i^{\left(j\right)}·\sum _{\ell =1}^m{\displaystyle \frac{{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(s\right)}}{{\widehat{q}}_{{\mathcal{A}}_{\ell }}^{\left(j\right)}}}{1}_{\left\{{\mathit{X}}_i^{\left(j\right)}\in {\mathcal{A}}_{\ell }\right\}},{\tau }^{*}\le {\tau }_Z^{\left(j\right)},j=0,1\hfill \end{array}$$

when $m_{{\tau }^{*}}^{\left(j\right)}$ is nonparametric, using the estimator based on grouped data.

An OB estimator of ${\mu }_{{\tau }^{*}}^{(j,s)}$ can be obtained after noticing that

$${\widehat{\mu }}_{{\tau }^{*}}^{\left(j\right)}=\sum _{i=1}^{n_j}min\left(T_i^{\left(j\right)},{\tau }^{*}\right){\widehat{\omega }}_i^{\left(j\right)}={\widehat{\alpha }}_{{\tau }^{*}}^{\left(j\right)}+{\widehat{\eta }}_{{\tau }^{*}}^{\left(j\right)\mathrm{T}}{\widehat{\mu }}_X^{\left(j\right)}$$

with ${\widehat{\mu }}_X^{\left(j\right)}=n_j^{-1}{\sum }_{i=1}^{n_j}$${\mathit{X}}^{\left(j\right)}{\widehat{\omega }}_i^{\left(j\right)}$ and ${\sum }_{i=1}^{n_j}\left[min\left(T_i^{\left(j\right)},{\tau }^{*}\right)-{\widehat{\ell }}_{{\tau }^{*}}^{\left(j\right)}\right]{\mathit{X}}_i^{\left(j\right)}=\mathbf{0}$ with ${\widehat{\ell }}_{{\tau }^{*}}^{\left(j\right)}={\widehat{\alpha }}^{\left(j\right)}+{\widehat{\eta }}_{{\tau }^{*}}^{\left(j\right)\mathrm{T}}{\mathit{X}}_i^{\left(j\right)}.$ This suggests applying the OB approach by estimating ${\mu }_{{\tau }^{*}}^{(j,s)}$ as ${\widehat{\ell }}_{{\tau }^{*}}^{(j,s)}={\widehat{\alpha }}_{{\tau }^{*}}^{\left(j\right)}+{\widehat{\eta }}_{{\tau }^{*}}^{\left(j\right)\mathrm{T}}{\widehat{\mu }}_X^{\left(s\right)},$ which is inconsistent when $m_{{\tau }^{*}}$ is nonlinear.

Stute (1993) shows, under $A.1$ and $A.2,$ that ${sup}_{t\le {\tau }^{*}}\left|{\widehat{F}}^{\left(i\right)}\left(t\right)-F_{*}^{\left(i\right)}\left(t\right)\right|=o_p\left(1\right)$ and that for any function $\phi :{\mathbb{R}}^{+}\times {\mathbb{R}}^k\to \mathbb{R}$ and $S_{\phi }^{\left(j\right)}=\phi \left(T^{\left(j\right)},{\mathit{X}}^{\left(j\right)}\right),$ such that $\mathbb{E}{S}_{\phi }^{\left(j\right)}<\infty$, ${\widehat{S}}_{\phi }^{\left(j\right)}={\sum }_{i=1}^{n_j}\phi \left(Z_{i:n_j}^{\left(j\right)},{\mathit{X}}_{\left[i:n_j\right]}^{\left(j\right)}\right){\widehat{\omega }}_i^{\left(j\right)}$ is a consistent estimator of ${\overline{S}}_{\phi }^{\left(j\right)}={\int }_{\mathbb{R}}\phi \left(t,x\right)\left(dt,d\mathit{x}\right)$ for $t\le {\tau }^{*},$ which shows that ${\widehat{\ell }}_{{\tau }^{*}}^{(j,s)}$ and ${\widehat{p}}_{{\mathcal{A}}_k}^{\left(j\right)}\left(t\right)$ are consistent estimators of ${\ell }_{{\tau }^{*}}^{(j,s)}$ and $p_{\mathcal{A}}^{\left(j\right)}\left(t\right),$ respectively. This justifies that ${\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)}$ is a consistent estimator of $F_{T{\mathbb{A}}_m}^{(j,s)}.$ Stute (1993) derives the asymptotic distribution of ${\widehat{S}}_{\phi }$. Bootstrap confidence intervals can be obtained following the procedure described in Stute et al. (2000). A formal justification of the inferential properties is beyond the scope of this paper.

Regarding the decompositions, we estimate ${\Delta }^{(j,s)}=F_T^{\left(j\right)}-F_T^{\left(s\right)}$ by ${\widehat{\Delta }}^{(j,s)}={\widehat{F}}_{T{\mathbb{A}}_m}^{(j,j)}\left(t\right)-{\widehat{F}}_{T{\mathbb{A}}_m}^{(s,s)}$ and the corresponding decomposition is

$$\begin{array}{ccc}\hfill {\widehat{\Delta }}^{(j,s)}\left(t\right)& =& \left[{\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)-{\widehat{F}}_{T{\mathbb{A}}_m}^{(s,s)}\left(t\right)\right]+\left[{\widehat{F}}_{T{\mathbb{A}}_m}^{(j,j)}\left(t\right)-{\widehat{F}}_{T{\mathbb{A}}_m}^{(j,s)}\left(t\right)\right]\hfill \\ & =& {\widehat{\Delta }}_{{\mathbb{A}}_m}^{(i,s)S}\left(t\right)+{\widehat{\Delta }}_{{\mathbb{A}}_m}^{(i,s)C}\left(t\right),t\le {\tau }_Z^{*}.\hfill \end{array}$$

The estimated counterfactual structural and composition effects, ${\widehat{\Delta }}_{{\mathbb{A}}_m}^{(i,s)S}$ and ${\widehat{\Delta }}_{{\mathbb{A}}_m}^{(i,s)C},$ are consistent estimates of ${\Delta }_{T{\mathbb{A}}_m}^{(j,s)S}$ and ${\Delta }_{T{\mathbb{A}}_m}^{(j,s)C},$ respectively. Decompositions based on ${\tilde{F}}_{T\mathcal{G}}^{(j,s)}$ are performed in the same way, but consistent ${\Delta }^{(j,s)}$ estimation requires the correct specification of the underlying CHR. Likewise, we can perform decomposition of the differences between HR and RSTM estimates.

4. Monte Carlo Simulations

This section provides evidence on the finite sample performance of the alternative standardization methods for the RMST using only one component ($k=1$). Henceforth, PML stands for the method using the Partial Maximum Likelihood estimator assuming a PCHR specification, OB-KM and OB-KM-Pol3 for the method based on the classical OB decomposition, using KM weights, under a linear and polynomial of order 3 specifications, respectively, and NP$\left(m\right)$ for the nonparametric method with $m=3$ and 10 with classes of equal size.

We consider the following designs,

DGP1:

$\left.T^{\left(j\right)}\right|X^{\left(j\right)}\sim N\left(5+X^{\left(j\right)},1\right),$  $j=0,1;$  $X^{\left(0\right)}\sim N(1.5,0.5),$  $X^{\left(1\right)}\sim N(1,0.5),$  $C^{\left(0\right)}\sim N(7.5,1.5),$  $C^{\left(1\right)}\sim N(7,1.5).$

DGP2:

$\left.T^{\left(j\right)}\right|X^{\left(j\right)}\sim Weibull\left(e^{2-X^{\left(j\right)}},5\right),$  $j=0,1;$  $C^{\left(0\right)}\sim Weibull(e^{2.26},5),$  $C^{\left(1\right)}\sim Weibull(e^{2.22},5),$  $X^{\left(0\right)}\sim U(0,1),$  $X^{\left(1\right)}$  $X^{\left(1\right)}\sim {\sum }_{i=1}^{3}U\left(0,1/3\right).$

DGP3:

$\left.T^{\left(j\right)}\right|X^{\left(j\right)}\sim N\left(5+2\left|X^{\left(j\right)}\right|,1\right),$  $j=0,1;$  $C^{\left(0\right)}\sim N(9.5,2),$  $C^{\left(1\right)}\sim N(7.7,1.5),$  $X^{\left(0\right)}\sim U(-3,3),$  $X^{\left(1\right)}\sim N(0,1).$

Monte Carlo experiments are based on 1000 replications with sample sizes of 200, 800, and 3200. We report the root mean squared error (RMSE) for the different estimators. Simulations are performed using ${\mu }_{{\tau }_Z}^{\left(j\right)}$ as the target parameter and without exploiting the fact that, in the three designs, $T^{\left(j\right)}$ and $C^{\left(j\right)}$ are unbounded, i.e., ${\tau }_Z=\infty$ and ${\mu }_{{\tau }_Z}^{\left(j\right)}={\mu }_{\infty }^{\left(j\right)},$$j=0,1.$ Parameter ${\tau }_Z$ is consistently estimated by ${\widehat{\tau }}_Z=min\left(Z_{n_0:n_0}^{\left(0\right)},Z_{n_1:n_1}^{\left(1\right)}\right)$ and the RMST is calculated with ${\tau }^{*}={\widehat{\tau }}_{Zn}.$

Table 1. Comparison of alternative procedures under DGP1.

Method	Sample Size	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{C}}$	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{S}}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(0\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(1\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{(0,1)}$
PML	200	0.481	0.457	0.080	0.087	0.476
	800	0.492	0.492	0.042	0.044	0.492
	3200	0.497	0.493	0.022	0.022	0.495
NP(3)	200	0.313	0.315	0.081	0.084	0.312
	800	0.184	0.189	0.043	0.042	0.186
	3200	0.128	0.128	0.022	0.022	0.128
NP(10)	200	0.321	0.327	0.081	0.084	0.320
	800	0.169	0.174	0.043	0.042	0.170
	3200	0.084	0.086	0.022	0.022	0.084
OB-KM	200	0.099	0.142	0.088	0.087	0.127
	800	0.057	0.082	0.046	0.044	0.072
	3200	0.029	0.040	0.023	0.023	0.035
OB-KM-Pol3	200	0.114	0.148	0.087	0.085	0.136
	800	0.064	0.087	0.046	0.044	0.077
	3200	0.030	0.041	0.023	0.023	0.036

reports results under DGP1 design. Since the PCHR specification is incorrect, the PML estimator is inconsistent for ${\mu }_{\infty }^{(j,s)}$, $j,s=0,1$, which explains the large biases. The regression function is linear and hence both OB-KM and OB-KM-Pol3 are consistent. As expected, OB-KM, which is asymptotically the most efficient, performs best in finite samples, but there are no significant loses using the overparameterized OB-KM-Pol3. As expected, the nonparametric NP(3) and NP(10) estimators are inefficient.

Table 2. Comparison of alternative procedures under DGP2.

Method	Sample Size	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{C}}$	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{S}}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(0\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(1\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{(0,1)}$
PML	200	0.017	0.132	0.101	0.088	0.106
	800	0.011	0.072	0.058	0.043	0.058
	3200	0.007	0.036	0.030	0.022	0.029
NP(3)	200	0.207	0.196	0.106	0.088	0.198
	800	0.116	0.114	0.060	0.044	0.110
	3200	0.075	0.073	0.031	0.023	0.072
NP(10)	200	0.353	0.339	0.106	0.088	0.340
	800	0.177	0.172	0.060	0.044	0.168
	3200	0.089	0.086	0.031	0.023	0.084
OB-KM	200	0.102	0.150	0.125	0.088	0.143
	800	0.097	0.120	0.071	0.044	0.120
	3200	0.102	0.114	0.036	0.022	0.114
OB-KM-Pol3	200	0.123	0.150	0.118	0.088	0.138
	800	0.076	0.083	0.070	0.044	0.077
	3200	0.040	0.045	0.036	0.022	0.041

reports results under the DGP2 specification. The OB-KM and OB-KM-Pol3 are still consistent estimators of ${\mu }_{\infty }^{\left(j\right)}={\mu }_{\infty }^{(j,j)}$, but they are inconsistent estimators of ${\mu }_{\infty }^{(j,s)}$ for $j\ne s$. In turn, since the PCHR specification is correct, the PML is consistent and efficient. This is confirmed by the simulations. Interestingly, OB-KM-Pol3 is a fairly robust alternative to OB-KM and performs similarly to NP(m).

Table 3. Comparison of alternative procedures under DGP3.

Method	Sample Size	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{C}}$	${\mathbf{\Delta }}_{{\mathit{\mu }}_{\mathit{\infty }}}^{(0,1)\mathit{S}}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(0\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{\left(1\right)}$	${\mathit{\mu }}_{\mathit{\infty }}^{(0,1)}$
PML	200	1.224	1.125	0.131	0.128	1.183
	800	1.298	1.289	0.070	0.063	1.300
	3200	1.348	1.343	0.036	0.033	1.350
NP(3)	200	0.590	0.496	0.134	0.120	0.536
	800	0.576	0.568	0.070	0.062	0.574
	3200	0.601	0.598	0.036	0.033	0.601
NP(10)	200	0.262	0.221	0.134	0.120	0.228
	800	0.139	0.124	0.070	0.062	0.121
	3200	0.077	0.071	0.036	0.033	0.072
OB-KM	200	1.217	1.336	0.206	0.115	1.332
	800	1.296	1.426	0.151	0.065	1.409
	3200	1.347	1.417	0.081	0.034	1.411
OB-KM-Pol3	200	0.247	0.244	0.138	0.114	0.219
	800	0.158	0.190	0.072	0.069	0.168
	3200	0.144	0.169	0.041	0.037	0.158

reports results under the DGP3. In this case, NP(m), OB-KM, and OB-KM-Pol3 are consistent for ${\mu }_{\infty }^{\left(j\right)}={\mu }_{\infty }^{(j,j)},$ but the PML is inconsistent. However, OB-KM and OB-KM-Pol3 are inconsistent for ${\mu }_{\infty }^{(j,s)},$ but NP(m) consistently estimates ${\mu }_{\infty {\mathbb{A}}_m}^{(j,s)}.$ NP(m) performs much better than both PML and OB-KM in this case. However, there is sensitivity with respect to the number of classes chosen, i.e., NP(3) versus NP(10). OB-KM-Pol3 shows to be a robust alternative to OB-KM that fairly captures nonlinearities in the underlying regression.

We also study the effect of ignoring censoring. First, assessing the effect on the estimates when censoring is not taken into account, and second, analyzing the effect of trying to estimate the mean, which is not identified because $C^{\left(j\right)}$ is bounded.

Table 4. Effect of ignoring censoring.

RMSE
		No Censoring			Censoring
	Sample Size	200	800	3200	200	800	3200
${\Delta }_{{\ell }_{{\widehat{\tau }}_{Zn}}}^{(j,s)C}$	Ignoring censoring	0.090	0.044	0.022	0.169	0.153	0.149
	Dropping censored obs.	0.090	0.044	0.022	0.123	0.088	0.077
	OB-KM	0.090	0.044	0.022	0.108	0.058	0.028
${\Delta }_{{\ell }_{{\widehat{\tau }}_{Zn}}}^{(j,s)S}$	Ignoring censoring	0.121	0.062	0.029	0.191	0.160	0.152
	Dropping censored obs.	0.121	0.062	0.029	0.158	0.103	0.082
	OB-KM	0.121	0.062	0.029	0.153	0.078	0.040

provides the RMSEs under DGP1 based on OLS fits using censored and uncensored observations, i.e., assuming that $Z^{\left(j\right)}$ is the actual duration. These biased estimates are compared with the corresponding OB-KM estimator. Simulation results show serious biases when ignoring censoring.

Table 5. Estimation of RMST and mean with ${\tau }_C^{\left(j\right)}<{\tau }_T^{\left(j\right)}$.

	$\mathit{\mu }$			${\mathit{\mu }}_{{\mathit{\tau }}^{*}}$
Sample Size	200	800	3200	200	800	3200
${\Delta }_{{\mu }_{{\tau }^{*}}}^{(0,1)C}$	0.084	0.076	0.076	0.016	0.008	0.004
${\Delta }_{{\mu }_{{\tau }^{*}}}^{(0,1)S}$	0.127	0.065	0.032	0.118	0.065	0.031
${\mu }_{{\tau }^{*}}^{(0,0)}$	0.089	0.048	0.029	0.084	0.044	0.022
${\mu }_{{\tau }^{*}}^{(1,1)}$	0.137	0.106	0.098	0.097	0.051	0.025
${\mu }_{{\tau }^{*}}^{(0,1)}$	0.126	0.102	0.097	0.078	0.041	0.020

illustrates the effect of neglecting the fact that ${\tau }_T^{\left(j\right)}>{\tau }_C^{\left(j\right)}$ when estimating the duration mean. In this case, $F_T$ cannot be consistently estimated beyond ${\tau }_Z^{\left(j\right)}$, and unlike previous experiments, where ${\tau }_T={\tau }_C=\infty ,$ it is not possible to estimate ${\mu }_{\infty }^{(j,s)}$ or ${\mu }_{{\tau }^{*}}^{(j,s)}$ for ${\tau }^{*}>{\tau }_Z^{\left(j\right)}.$ We compare the PML estimators of ${\mu }_{{\tau }_Z}^{(j,s)}$ under design DGP2, i.e., PML is efficient, when $C^{\left(j\right)}$ is censored, using ${\tilde{C}}^{\left(j\right)}=min\left(C^{\left(j\right)},6.5\right)$ as the censoring variable, i.e., ${\tau }_C^{\left(0\right)}={\tau }_C^{\left(1\right)}=6.5<{\tau }_T^{\left(0\right)}={\tau }_T^{\left(1\right)}=\infty$. Table 5 confirms high biases for estimating the mean when ${\tau }_T^{\left(j\right)}>{\tau }_C^{\left(j\right)}$, but the PML estimator still performs well as an estimator of ${\mu }_{{\tau }_Z}^{(j,s)}$. This illustrates the importance of focusing the statistical inference in truncated or restricted parameters as the RMST.

5. Unemployment Duration Gender Gaps in Spain

This section investigates the causes of unemployment duration gender gaps in Spain using counterfactual decompositions of HR and RMST differences. We also provide a comparison between ACHR and HR estimates using the alternative specifications. The Spanish case is particularly interesting because it has experienced one of the highest unemployment rates among OECD countries in recent decades. According to official statistics, for the period 1995–2005, the average unemployment rate was around 6.8% in OECD countries and 5% in the US while it was 14% in Spain. Moreover, the difference in unemployment rates by gender has also been important. For the same period, women exhibited an unemployment rate 9 percentage points (p.p.) higher, while in the US this gap was around 0.04 p.p.

The existing literature has mainly paid attention to gender gaps in the aggregated unemployment rate (Azmat et al., 2006; Johnson, 1983; Niemi, 1974; Queneau & Sen, 2007), but gender gaps in other unemployment features, like spells of unemployment duration, have received less attention. Research on unemployment duration gender gaps has almost exclusively focused in explaining the gender differences in the ACHR rather than HR. See Section 1 for a discussion.

We implement the proposed methodology to perform counterfactual decompositions of the HR and RMST differences using data from the Survey of Income and Living Conditions (SILC) for the period 2004–2007. Data is available on the website of the Spanish National Institute of Statistics https://www.ine.es/dyngs/INEbase/operacion.htm?c=Estadistica_C&cid=1254736176807&menu=resultados&idp=1254735976608#_tabs-1254736195153 (accessed on 15 october 2022). This survey, carried out by the European Commission, is a rotative household panel that collects information on socioeconomic characteristics, including the occupational status (monthly) for a period of 4 years. Our population consists of unemployed workers older than 25 starting a spell of unemployment during the period 2004–2007. All data used in this study are publicly available from the Spanish National Statistics Institute (INE). We measure unemployment duration as the number of months that a worker is not employed, which is usually referred to as non-employment duration.

We consider as composition variables those commonly used in unemployment duration analysis such as age, educational level, tenure, marital status, whether the individual is the head of the household, the number of unemployed in the household, city size (according to three levels of urbanization in the SILC as big city, medium size city, and small city), and region (Addison & Portugal, 2003; Kuhn & Skuterud, 2004; Tansel & Tasci, 2010). The first three variables refer to human capital characteristics, while the others are related to the opportunity cost of being unemployed and the reservation wage.

Table 6. Descriptive statistics of composition variables.

Variable	Total	Women	Men
Age	39.727	40.014	39.218
	(0.322)	(0.381)	(0.585)
Household head	0.323	0.237	0.476
	(0.012)	(0.014)	(0.022)
Tenure	13.466	11.003	17.834
	(0.320)	(0.334)	(0.615)
Marital status	0.640	0.680	0.569
	(0.013)	(0.015)	(0.022)
High education (dummy)	0.182	0.193	0.162
	(0.010)	(0.013)	(0.016)
No. unemployed	1.129	1.120	1.145
	(0.010)	(0.012)	(0.016)
Big city	0.330	0.316	0.354
	(0.012)	(0.015)	(0.021)
Medium size city	0.244	0.236	0.260
	(0.011)	(0.014)	(0.019)
No. observations	1473	942	531

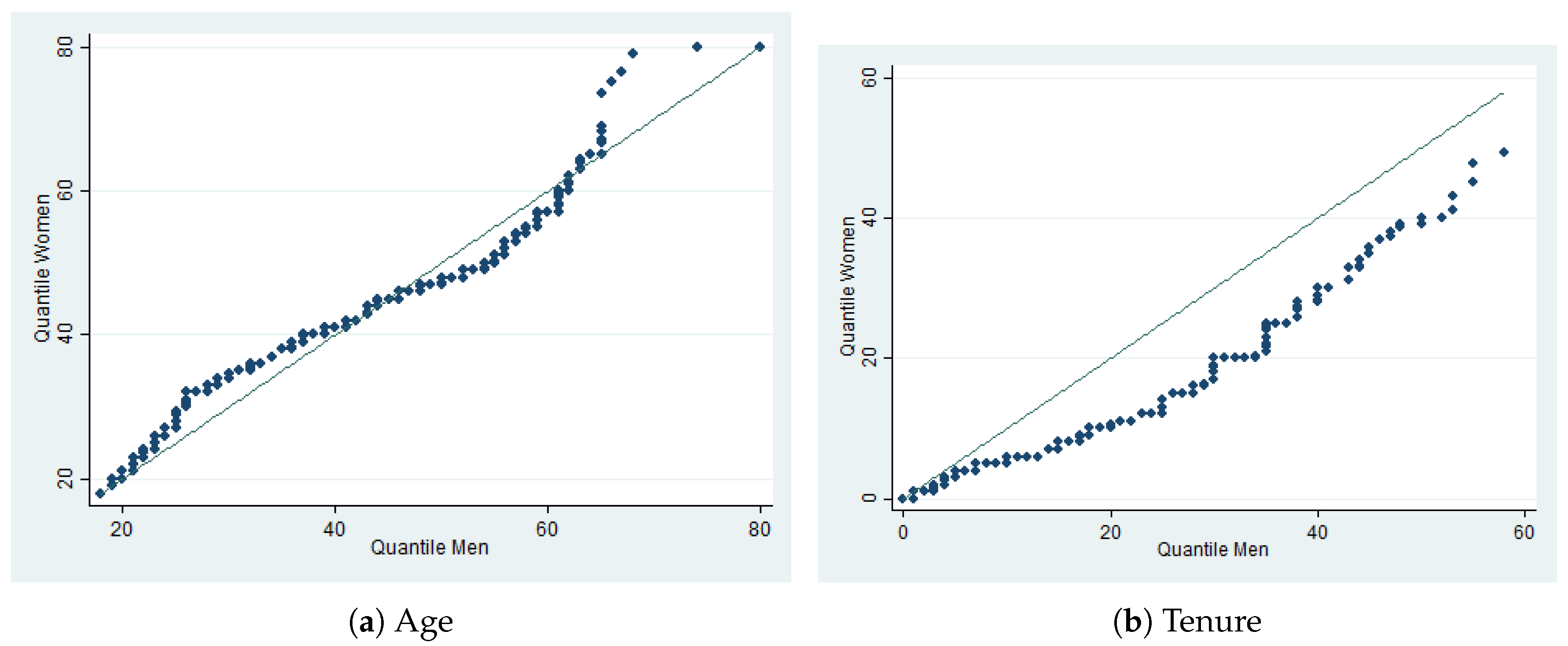
Standard errors in parentheses.

provides summary statistics for the discrete explanatory variables and Figure 1 the corresponding QQ plots for the continuous variables, i.e., age and tenure. Compositions are similar in the two populations, except for tenure. Therefore, the composition effect should not be particularly important. We observe censoring levels of 21.4% for women and 16.2% for men.

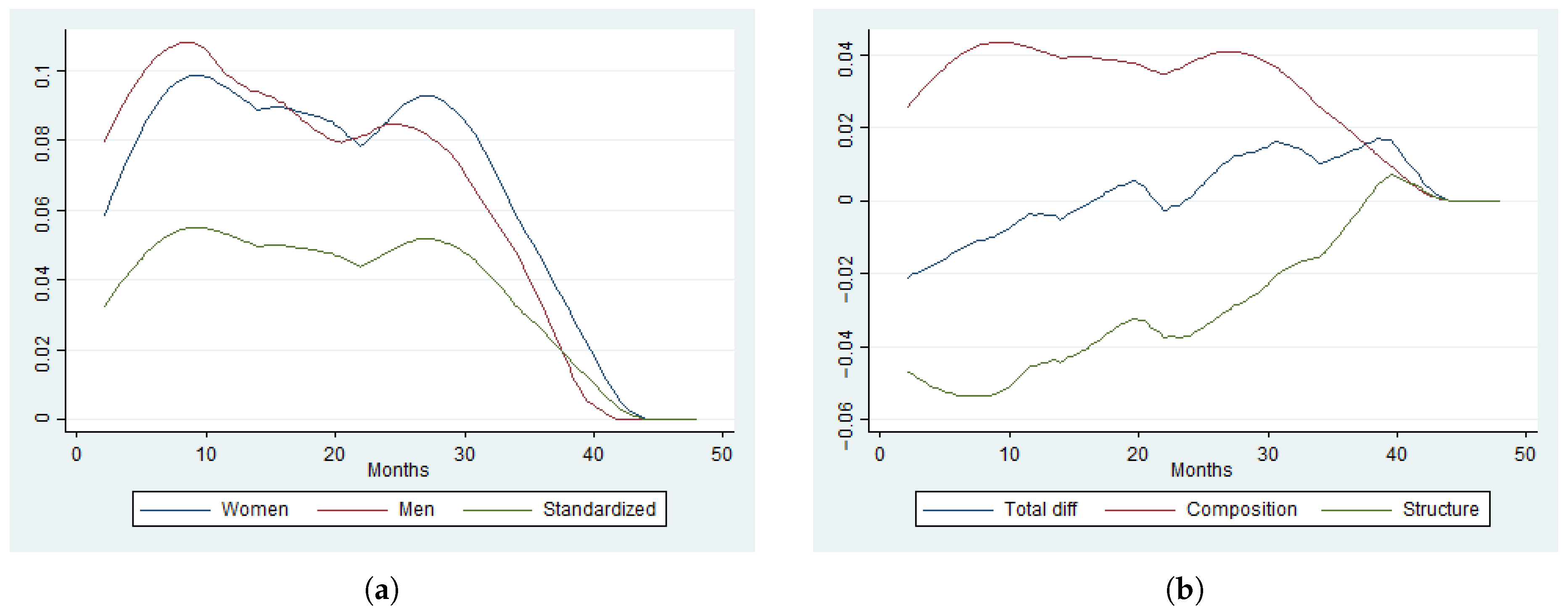
Henceforth, population 0 corresponds to women and population 1 to men. First, we analyze the HR differences between the two populations. Figure 2 provides KM estimates of the marginal HR, ${\lambda }^{\left(j\right)},$ and the corresponding nonparametric estimates of ${\lambda }_{{\mathbb{A}}_m}^{(0,1)}$ based on a partition ${\mathbb{A}}_m$, as well as the HR difference, ${\Delta }_{\lambda }^{(0,1)},$ into counterfactual effects. The partition is based on $m=8$ classes and ${\lambda }_{{\mathbb{A}}_8}$ is estimated using kernel smoothing, ${\breve{\lambda }}_{{\mathbb{A}}_8}^{(0,1)}$, with an Epanechnikov kernel and the bandwidth chosen by the classical plug-in method. The number of classes in the partition was established according to the structure of the composition variables using some natural thresholds for the continuous variables. For instance, we grouped workers between 25 and 40 years old (prime-age workers) and workers with less than 10 years tenure. If the number of partitions is too high, some classes could contain very few observations, particularly when there is a high dependence on covariates, e.g., there are few observations in a partition class with young workers of more than 10 years tenure, married, and with a high education level. Therefore, by using age, labor market size, and marital status, we construct eight classes. This method has the advantage that the classes in a partition can be chosen in a natural way, accounting for the observed relation between duration and covariates.

The nonparametric KM estimates of the HR show an acceleration of women HR after 24 months of unemployment, which is consistent with the unemployment compensation normative in Spain during the analyzed period. Unemployment benefits expired after 24 months and workers received 70% of their salary during the first 6 months and 60% for up to 24 months. Figure 2 suggests that, on average, women exhaust all unemployment benefits, producing a spike in the HR starting around the expiration rate. That is, women and men exhibit different optimal delays in job acceptance. This phenomenon has also been documented by Roed and Zhang (2003) and Boone and van Ours (2012) using Norwegian and Slovenian data, respectively. We observe that the estimated composition effect is very small at any period. That is, HR differences between women and men do not seem to be explained by the socioeconomic characteristics considered in this study, which are almost identical, but by anything else, like circumstances of the labor market’s tightness and discrimination related to institutional factors, labor circumstances, or behavioral aspects (Bachmann & Sinning, 2016).

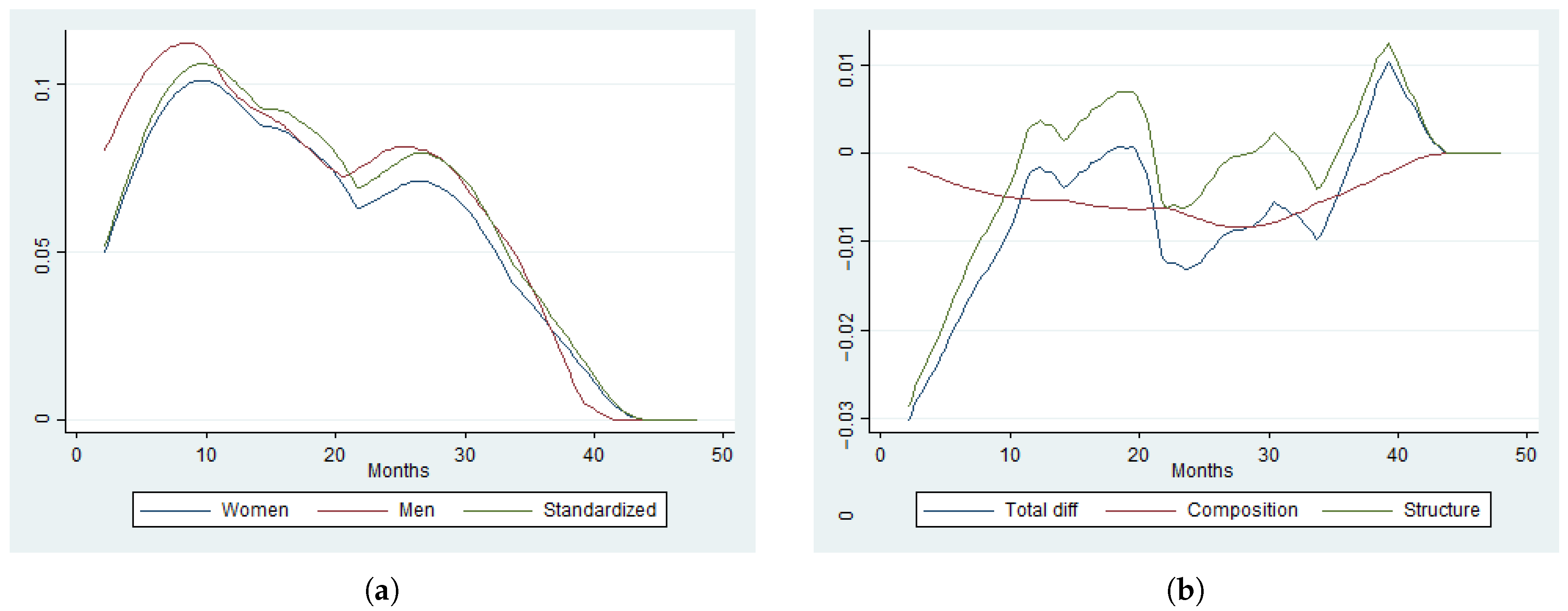
We have checked Cox’s model specification for the two populations using the popular Schoenfeld (1982) residual based goodness-of-fit test, which results in p-values of 0.031 and 0.654 for women and men, respectively. Therefore, Cox’s specification is rejected for women but not for men, at 5% significance. Figure 3 shows the smooth version of PML standardized HR estimates, ${\check{\lambda }}^{(0,1)},$ with the same kernel and bandwidths used in the nonparametric case. The estimates are quantitatively very different to the nonparametric ones in Figure 2, possibly because of misspecification, though it also shows a composition effect close to zero at any period and an acceleration of the HR for women after 24 months of unemployment.

Figure 4 and Figure 5 provide the ACHR estimates and its standardizations using NP(8) and PML, respectively. The HR and ACHR shapes are very different for each estimator. However, the counterfactual composition effect of both HR and ACHR are close to zero. The ACHR estimates of the counterfactual decompositions using PML is particularly hard to interpret.

Next, we analyze the ${\mu }_{{\tau }^{*}}^{\left(j\right)}$ and ${\mu }_{{\tau }^{*}}^{(0,1)}$ estimates for ${\tau }^{*}={\widehat{\tau }}_{Zn}=42$ using OB-KM, PML, and NP(8), which produces estimates of the duration means when ${\tau }_C^{\left(j\right)}\ge {\tau }_T^{\left(j\right)},$ and also for ${\tau }^{*}=24,36$, which are of interest when studying short- and medium-term unemployment differences. RMST estimates and their corresponding counterfactual decompositions can be found in

Table 7. Standardized RMST.

	${\widehat{\mathit{\tau }}}_{\mathbf{Zn}}=42$			${\mathit{\tau }}^{*}=36$			${\mathit{\tau }}^{*}=24$
Method	Women	Men	${\mathbf{\mu }}_{{\mathbf{Z}}_{\mathbf{n}}}^{(\mathbf{0},\mathbf{1})}$	Women	Men	${\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}^{(\mathbf{0},\mathbf{1})}$	Women	Men	${\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}^{(\mathbf{0},\mathbf{1})}$
PML	10.721	8.090	10.275	10.398	7.886	10.016	9.463	7.258	9.220
NP(8)	10.864	7.804	10.831	10.594	7.596	10.476	9.726	7.043	9.545
OB-KM	10.864	7.804	10.427	10.594	7.596	10.094	9.726	7.043	9.193

RMST estimates by gender for different ${\tau }^{*}$.

and

Table 8. Decomposition components’ RMST.

	${\widehat{\mathit{\tau }}}_{{\mathit{Z}}_{\mathit{n}}}=42$			${\mathit{\tau }}^{*}=36$			${\mathit{\tau }}^{*}=24$
Method	${\Delta }_{{\mathbf{\mu }}_{{\widehat{\mathbf{\tau }}}_{\mathbf{Zn}}}}^{(\mathbf{0},\mathbf{1})}$	${\Delta }_{{\mathbf{\mu }}_{{\widehat{\mathbf{\tau }}}_{\mathbf{Zn}}}}^{(\mathbf{0},\mathbf{1})\mathbf{C}}$	${\Delta }_{{\mathbf{\mu }}_{{\widehat{\mathbf{\tau }}}_{\mathbf{Zn}}}}^{(\mathbf{0},\mathbf{1})\mathbf{S}}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})\mathbf{C}}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})\mathbf{S}}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})\mathbf{C}}$	${\Delta }_{{\mathbf{\mu }}_{{\mathbf{\tau }}^{*}}}^{(\mathbf{0},\mathbf{1})\mathbf{S}}$
PML	2.631	0.446	2.185	2.512	0.382	2.130	2.204	0.242	1.962
NP(8)	3.060	0.033	3.027	2.997	0.118	2.880	2.683	0.180	2.502
OB-KM	3.060	0.438	2.622	2.997	0.499	2.498	2.683	0.533	2.150

RMST decomposition effects for different values of ${\tau }^{*}$.

, respectively. The estimate of the non-standardized RMST during the first 42 months is around 10.8 months for women and 7.9 months for men. The standardized RMST estimate, which is interpreted as the average unemployment duration during the first 42 months if women would have the same components than men is around 10.3 months, close to the corresponding nonstandardized value. Results across methods are qualitatively similar and reveal a reduction in the corresponding standardized RMST.

The counterfactual decompositions of RMST using OB-KM and PML for ${\tau }^{*}={\widehat{\tau }}_{Zn}=42$ (see Table 8) are fairly different compared to the NP(8), which may indicate a misspecification of the underlying assumed structures. For instance, the OB-KM estimator might be biased because $\mathbb{E}\left(\left.min({\tau }^{*},Z^{\left(j\right)})\right|{\mathit{X}}^{\left(j\right)}\right)$ is nonlinear and the PML is also biased because the underlying CDF does not follow a PCHR model, which was confirmed by Schoenfeld’s test.

The counterfactual composition effect for any ${\tau }^{*}$ is close to zero for any of the three methods. This indicates that the difference in worker characteristics slightly increases the severity of women’s unemployment duration compared to men, which might be driven mainly because of tenure, as suggested in previous descriptive analyses. Notice that the counterfactual effects using the OB-KM and PML methods are similar, but the composition effect using NP(8) is much smaller, as we have already seen for the HR in Figure 2 and Figure 3. Similar results are obtained for ${\tau }^{*}=24$ and ${\tau }^{*}=36$. However, based on NP(8) and OB-KM, it seems that the composition effect is more important when explaining unemployment duration gender gaps in the first stages of unemployment, but this is always much smaller than the structure effect.

6. Conclusions

We have presented a new methodology for standardizing duration distributions using right-censored data. To this end, we introduced the counterfactual hazard function, as well as parameters that summarize the characteristics of the duration CDF, such as the RMST. These are nonlinear functionals of the underlying conditional CDF, and we have shown that the OB technique for obtaining counterfactual means cannot, in general, be extrapolated to this setting. In particular, the ACHR—obtained by averaging certain conditional hazard rates, typically under a proportional hazards specification—lacks a clear interpretation and may lead to misleading conclusions.

We proposed the following two types of counterfactual estimators of the conditional CDF: on the one hand, nonparametric estimators are based on partitioning the support of the explanatory variables into a fixed number of classes, and consistently estimate the joint CDF of durations and covariates using Kaplan–Meier (KM) weights; on the other hand, semiparametric estimators are based on a Cox proportional hazard specification, which are inconsistent under model misspecification.

The finite-sample properties of these estimators and the resulting decompositions—evaluated through Monte Carlo simulations and an application to gender gaps in unemployment duration using Spanish data—show that the nonparametric approach performs reasonably well in finite samples. Moreover, the OB approach using KM weights proves robust for RMST decompositions when a flexible functional form (such as a polynomial) is used for the underlying regression. In contrast, estimates based on the semiparametric PCHR specification perform very poorly under misspecification.

The empirical application shows that decompositions of hazard rate (HR) differences, rather than of averaged hazard rates (ACHR), yield more reliable results. The analysis suggests that the gender gap is mainly driven by the structure effect.

There are several potential applications and extensions of the proposed methods that are of interest. For example, the counterfactual estimators developed in this study can be applied across a broad range of disciplines such as health, labor and education economics, finance, management, and public policy. From a methodological standpoint, future work could refine the proposed estimators by incorporating more flexible frameworks for conditional distribution estimation and by developing data-driven partition selection rules in the nonparametric context.