Daily Emissions of CO2 in the World: A Fractional Integration Approach
Abstract
1. Introduction
2. Review of the Literature
3. Methodology and Data
3.1. Methodology
- (i)
- The case of anti-persistence, if d < 0;
- (ii)
- Short-memory processes or I(0), if d = 0;
- (iii)
- Long-memory stationary processes, if 0 < d < 0.5;
- (iv)
- Processes which are nonstationary, though with mean-reverting behavior, if 0.5 ≤ d < 1;
- (v)
- Unit roots or I(1) behavior, if d = 1;
- (vi)
- Explosive patterns, if d ≥ 1.
3.2. Data Description
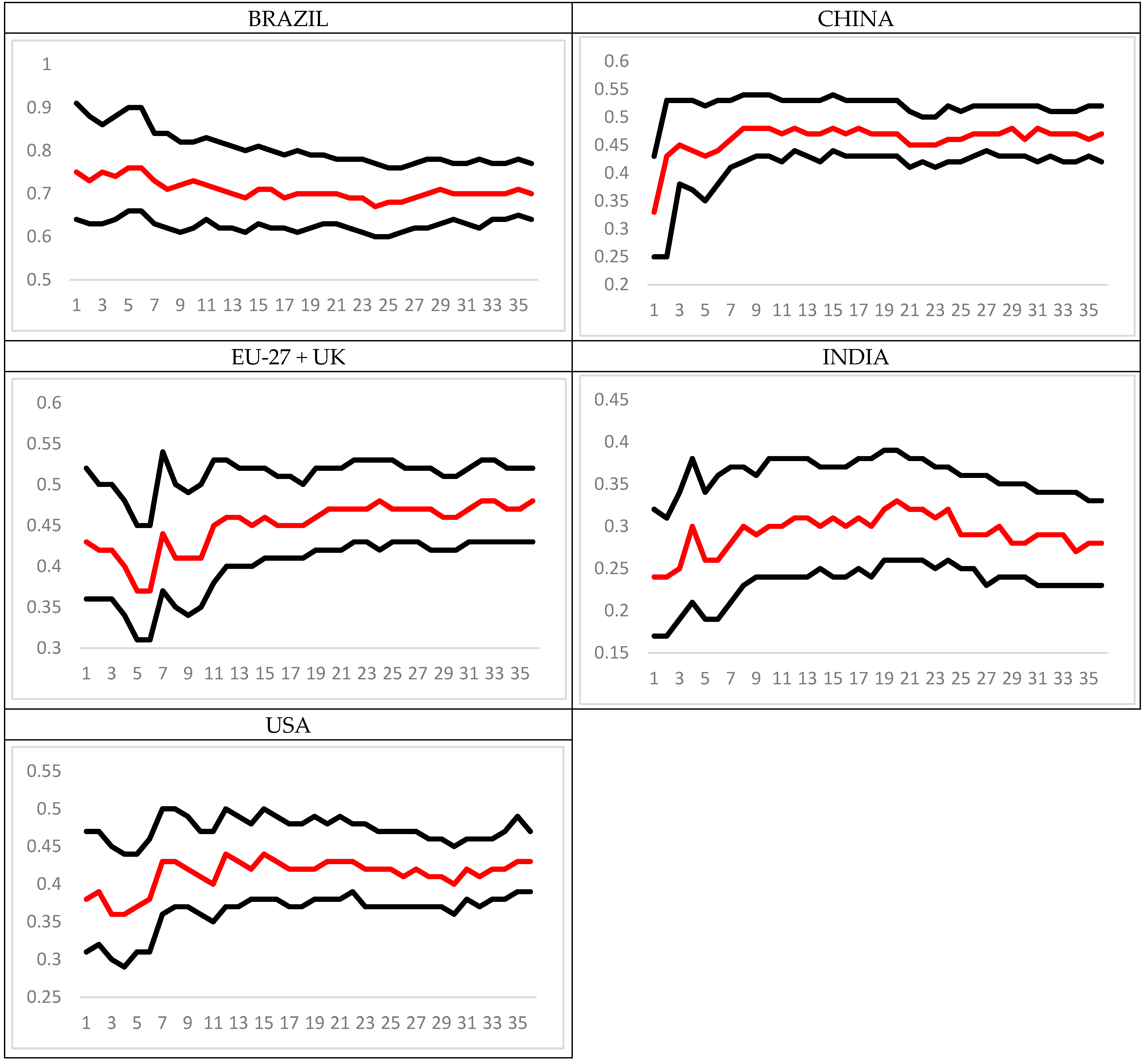
4. Empirical Results and Discussion
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Acharya, J. (2009). FDI, growth and the environment: Evidence from India on CO2 emissions during the last two decades. Journal of Economic Development, 34(1), 43–58. [Google Scholar] [CrossRef]
- Al-Shboul, M., & Anwar, S. (2016). Fractional integration in daily stock market indices at Jordan’s Amman stock exchange. The North American Journal of Economics and Finance, 37, 16–37. [Google Scholar] [CrossRef]
- Apergis, N., & Payne, J. E. (2009a). CO2 emissions, energy usage, and output in Central America. Energy Policy, 37(8), 3282–3286. [Google Scholar] [CrossRef]
- Apergis, N., & Payne, J. E. (2009b). Energy consumption and economic growth: Evidence from the Commonwealth of Independent States. Energy Economics, 31(5), 641–647. [Google Scholar] [CrossRef]
- Aye, G. C., & Edoja, P. E. (2017). Effect of economic growth on CO2 emission in developing countries: Evidence from A dynamic panel threshold model. Cogent Economics and Finance, 5(1), 1379239. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D., Shahbaz, M., Roubaud, D., & Farhani, S. (2018). How economic growth, renewable electricity and natural resources contribute to CO2 emissions? Energy Policy, 113, 356–367. [Google Scholar] [CrossRef]
- Banerjee, A., & Urga, G. (2005). Modelling structural breaks, long memory and stock market volatility: An overview. Journal of Econometrics, 129(1–2), 1–34. [Google Scholar] [CrossRef]
- Bloomfield, P. (1973). An exponential model in the spectrum of a scalar time series. Biometrika, 60, 217–226. [Google Scholar] [CrossRef]
- Boopen, S., & Vinesh, S. (2011). On the relationship between CO2 emissions and economic growth: The Mauritian experience. In Mauritius environment outlook report. University of Mauritius. [Google Scholar]
- Box, G. E. P., & Pierce, D. A. (1970). Distribution of residual autocorrelations in autoregressive integrated moving average time series models. Journal of the American Statistical Association, 65, 1509–1526. [Google Scholar] [CrossRef]
- Breusch, T. S. (1978). Testing for autocorrelation in dynamic linear models. Australian Economic Papers, 17, 334–355. [Google Scholar] [CrossRef]
- Caporale, G. M., Gil-Alana, L. A., & Poza, C. (2020). Persistence, non-linearities and structural breaks in European stock market indices. The Quarterly Review of Economics and Finance, 77, 50–61. [Google Scholar] [CrossRef]
- Claudio-Quiroga, G., & Poza, C. (2024). Measuring the circular economy in Europe: Big differences among countries, great opportunities to converge. Sustainable Development, 32(5), 4707–4725. [Google Scholar] [CrossRef]
- Cuestas, J. C., & Gil-Alana, L. A. (2016). Testing for long memory in the presence of non-linear Chebyshev polynomials in time. Studies in Nonlinear Dynamics and Econometrics, 20(1), 57–74. [Google Scholar]
- Dash, R. K. (2009). Revisited export-led growth hypothesis: An empirical study on India. South Asia Economic Journal, 10(2), 305–324. [Google Scholar] [CrossRef]
- Diebold, F. X., & Inoue, A. (2001). Long memory and regime switching. Journal of Econometrics, 105(1), 1–39. [Google Scholar] [CrossRef]
- Du, L., Wei, C., & Cai, S. (2012). Economic development and carbon dioxide emissions in China: Provincial panel data analysis. China Economics Review, 23(2), 371–384. [Google Scholar] [CrossRef]
- Furuoka, F., Gil-Alana, L. A., Yaya, O. S., Aruchunan, E., & Ogbonna, A. E. (2024). A new fractional integration approach based on neural network nonlinearity with an application to testing unemployment hysteresis. Empirical Economics, 66, 2471–2499. [Google Scholar] [CrossRef]
- Giancaterini, F., Hecq, A., & Morana, C. (2022). Is climate change time-reversible? Econometrics, 10(4), 36. [Google Scholar] [CrossRef]
- Gil-Alana, L. A., & Trani, T. (2019). Time trends and persistence in the global CO2 emissions across Europe. Environmental and Resource Economics, 73, 213–228. [Google Scholar] [CrossRef]
- Godfrey, L. G. (1978). Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica, 46(6), 1293–1301. [Google Scholar] [CrossRef]
- Granger, C. W. J., & Hyung, N. (2004). Occasional structural breaks and long memory with an application to the S&P 500 absolute stock returns. Journal of Empirical Finance, 11(3), 399–421. [Google Scholar] [CrossRef]
- Han, P., Cai, O., Oda, T., Zeng, N., Shan, Y., Lin, X., & Liu, D. (2021). Assessing the recent impact of COVID-19 on carbon emissions from China using domestic economic data. Science of The Total Environment, 750, 141688. [Google Scholar] [CrossRef] [PubMed]
- International Energy Agency (IEA). (2020). Global energy review 2020: The impacts of the COVID-19 crisis on global energy demand and CO2 emissions. Available online: https://www.iea.org/reports/global-energy-review-2020 (accessed on 1 June 2024).
- Kalmaz, D. B., & Kirikkaleli, D. (2019). Modeling CO2 emissions in an emerging market: Empirical finding from ARDL-based bounds and wavelet coherence approaches. Environmental Science and Pollution Research, 26(5), 5210–5220. [Google Scholar] [CrossRef] [PubMed]
- Kirikkaleli, D. (2020). New insights into an old issue: Exploring the nexus between economic growth and CO2 emissions in China. Environmental Science and Pollution Research, 27(32), 40777–40786. [Google Scholar] [CrossRef] [PubMed]
- Le Quéré, C., Jackson, R. B., Jones, M. W., Smith, A. J., Abernethy, S., Andrew, R. M., De-Gol, A. J., Willis, D. R., Shan, Y., Canadell, J. G., Friedlingstein, P., Creutzig, F., & Peters, G. P. (2020). Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement. Natural Climate Change, 10, 647–653. [Google Scholar] [CrossRef]
- Lee, J. W. (2013). The contribution of foreign direct investment to clean energy use, carbon emissions and economic growth. Energy Policy, 55, 483–489. [Google Scholar] [CrossRef]
- Liu, Z., Ciais, P., & Schellnhuber, H. J. (2020). Near-real-time monitoring of global CO2 emissions reveals the effects of the COVID-19 pandemic. Nature Communications, 11, 5172. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z., Deng, Z., Davis, S. J., Giron, C., & Ciais, P. (2022). Monitoring global carbon emissions in 2021. Natural Reviews Earth & Environment, 3, 217–219. [Google Scholar] [CrossRef]
- Ljung, G. M., & Box, G. E. P. (1978). On a Measure of Lack of Fit in Time Series Models. Biometrika, 65(2), 297–303. [Google Scholar] [CrossRef]
- McMillan, D. G., & Wohar, M. E. (2013). The relationship between temperature and CO2 emissions: Evidence from a short and very long dataset. Applied Economics, 45(26), 3683–3690. [Google Scholar] [CrossRef]
- Nguyen, Q. T., Diaz, J. F., Chen, J. H., & Lee, M. Y. (2019). Social responsibility indices: A FIGARCH and HYGARCH approach. Asian Economic and Financial Review, 9, 7. [Google Scholar] [CrossRef]
- Nguyen, X. P., Hoang, A. T., Ölçer, A. I., & Huynh, T. T. (2021). Record decline in global CO2 emissions prompted by COVID-19 pandemic and its implications on future climate change policies. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 47(1), 4699–4702. [Google Scholar] [CrossRef]
- Robinson, P. M. (1994). Efficient tests of nonstationary hypotheses. Journal of the American Statistical Association, 89, 1420–1437. [Google Scholar] [CrossRef]
- Rume, T., & Islam, S. M. D. U. (2020). Environmental effects of COVID-19 pandemic and potential strategies of sustainability. Heliyon, 6(9), e04965. [Google Scholar] [CrossRef] [PubMed]
- Sephton, P. (2008). Exchange rates and fractional integration revisited. Applied Financial Economics Letters, 4(6), 383–387. [Google Scholar] [CrossRef]
- Shahbaz, M., Loganathan, N., Muzaffar, A. T., Ahmed, K., & Jabran, M. A. (2016a). How urbanization affects CO2 emissions in Malaysia? The application of STIRPAT model. Renewable and Sustainable Energy Reviews, 57, 83–93. [Google Scholar] [CrossRef]
- Shahbaz, M., Mahalik, M. K., Shah, S. H., & Sato, J. R. (2016b). Time-varying analysis of CO2 emissions, energy consumption, and economic growth nexus: Statistical experience in next 11 countries. Energy Policy, 98, 33–48. [Google Scholar] [CrossRef]
- Shahbaz, M., Sharma, R., Sinha, A., & Jiao, Z. (2021). Analyzing nonlinear impact of economic growth drivers on CO2 emissions: Designing an SDG framework for India. Energy Policy, 148, 111965. [Google Scholar] [CrossRef]
- Tiseo, I. (2023). Global historical CO2 emissions from fossil fuels and industry 1750–2020. Statista, Energy & Environment. [Google Scholar]
- Udemba, E. N., Güngör, H., Bekun, F. V., & Kirikkaleli, D. (2021). Economic performance of India amidst high CO2 emissions. Sustainable Production and Consumption, 27, 52–60. [Google Scholar] [CrossRef]
- Xiong, J., & Xu, D. (2021). Relationship between energy consumption, economic growth and environmental pollution in China. Environmental Research, 194, 110718. [Google Scholar] [CrossRef] [PubMed]
- Yao, J., & Zhao, Y. (2022). Structural breaks in carbon emissions: A machine learning analysis. IMF Working Paper, WP/22/9. Strategy, Policy, and Review Department. International Monetary Fund. [Google Scholar]
- Zhao, W., Yin, C., Hua, T., Meadows, M. E., Li, Y., Liu, Y., Cherubini, F., Pereira, P., & Fu, B. (2022). Achieving the sustainable development goals in the post-pandemic era. Humanities and Social Sciences Communications, 9, 258. [Google Scholar] [CrossRef] [PubMed]
- Zickfeld, K., Arora, V. K., & Gillett, N. P. (2012). Is the climate response to CO2 emissions path dependent? Geophysics Resources Letters, 39(5), L05703. [Google Scholar] [CrossRef]
- Zickfeld, K., Eby, M., Weaver, A. J., Alexander, K., Crespin, E., Edwards, N. R., Eliseev, A. V., Feulner, G., Fichefet, T., Forest, C. E., Friedlingstein, P., Goosse, H., Holden, P. B., Joos, F., Kawamiya, M., Kicklighter, D., Kienert, H., Matsumoto, K., Mokhov, I. I., … Zhao, F. (2013). Long-term climate change commitment and reversibility: An EMIC intercomparison. Journal of Climate, 26(16), 5782–5809. [Google Scholar] [CrossRef]
- Zickfeld, K., MacDougall, A. H., & Matthews, H. D. (2016). On the proportionality between global temperature change and cumulative CO2 emissions during periods of net negative CO2 emissions. Environmental Resources Letters, 11(5), 055006. [Google Scholar] [CrossRef]
| N | Total Sum | Minimum | Maximum | Mean | Stand. Deviation | |
|---|---|---|---|---|---|---|
| CHINA | 1430 | 1,986,514,518 | 476,259 | 4,504,574 | 1,389,170.99 | 516,818.89 |
| USA | 1430 | 2,902,279,760 | 890,340 | 3,244,791 | 2,029,566.27 | 469,126.30 |
| INDIA | 1430 | 2,778,759,248 | 542,567 | 3,585,520 | 1,943,188.29 | 403,080.67 |
| EU-27 and UK | 1430 | 2,380,424,821 | 562,451 | 3,294,981 | 1,664,632.74 | 448,737.16 |
| BRAZIL | 1430 | 3,031,259,948 | 601,802 | 3,592,567 | 2,119,762.20 | 609,542.09 |
| N valid | 1430 |
| Series | No Terms | Intercept | Linear Time Trend |
|---|---|---|---|
| BRAZIL | 0.94 (0.91, 0.98) | 0.56 (0.53, 0.59) | 0.56 (0.53, 0.59) |
| CHINA | 0.89 (0.85, 0.92) | 0.37 (0.34, 0.40) | 0.36 (0.34, 0.39) |
| EU-27 + UK | 0.91 (0.87, 0.94) | 0.34 (0.32, 0.37) | 0.34 (0.32, 0.37) |
| INDIA | 0.90 (0.87, 0.94) | 0.22 (0.19, 0.25) | 0.22 (0.19, 0.25) |
| USA | 0.92 (0.89, 0.96) | 0.32 (0.29, 0.35) | 0.32 (0.29, 0.35) |
| Series | d | Intercept (t-Value) | Time Trend (t-Value) |
|---|---|---|---|
| BRAZIL | 0.56 (0.53, 0.59) | 6.295 (117.91) | --- |
| CHINA | 0.36 (0.34, 0.39) | 6.225 (169.67) | −0.00012 (−2.74) |
| EU-27 + UK | 0.34 (0.32, 0.37) | 6.217 (290.67) | --- |
| INDIA | 0.22 (0.19, 0.25) | 6.279 (581.78) | --- |
| USA | 0.32 (0.29, 0.35) | 6.290 (350.82) | --- |
| Series | No Terms | Intercept | Linear Time Trend |
|---|---|---|---|
| BRAZIL | 0.98 (0.92, 1.05) | 0.70 (0.64, 0.77) | 0.70 (0.64, 0.77) |
| CHINA | 0.95 (0.89, 1.00) | 0.47 (0.42, 0.52) | 0.47 (0.42, 0.52) |
| EU-27 + UK | 0.97 (0.92, 1.04) | 0.48 (0.43, 0.52) | 0.48 (0.43, 0.52) |
| INDIA | 0.95 (0.90, 1.01) | 0.28 (0.23, 0.33) | 0.28 (0.23, 0.33) |
| USA | 0.97 (0.92, 1.04) | 0.43 (0.39, 0.47) | 0.43 (0.39, 0.47) |
| Series | d | Intercept (t Value) | Time Trend (t Value) |
|---|---|---|---|
| BRAZIL | 0.70 (0.64, 0.77) | 6.297 (90.39) | --- |
| CHINA | 0.47 (0.42, 0.52) | 6.235 (127.33) | −0.00012 (−1.98) |
| EU-27 + UK | 0.48 (0.43, 0.52) | 6.227 (144.80) | --- |
| INDIA | 0.28 (0.23, 0.33) | 6.278 (397.14) | --- |
| USA | 0.43 (0.39, 0.47) | 6.282 (193.41) | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-Alana, L.A.; Poza, C. Daily Emissions of CO2 in the World: A Fractional Integration Approach. Econometrics 2025, 13, 26. https://doi.org/10.3390/econometrics13030026
Gil-Alana LA, Poza C. Daily Emissions of CO2 in the World: A Fractional Integration Approach. Econometrics. 2025; 13(3):26. https://doi.org/10.3390/econometrics13030026
Chicago/Turabian StyleGil-Alana, Luis Alberiko, and Carlos Poza. 2025. "Daily Emissions of CO2 in the World: A Fractional Integration Approach" Econometrics 13, no. 3: 26. https://doi.org/10.3390/econometrics13030026
APA StyleGil-Alana, L. A., & Poza, C. (2025). Daily Emissions of CO2 in the World: A Fractional Integration Approach. Econometrics, 13(3), 26. https://doi.org/10.3390/econometrics13030026







