Government Subsidies and Industrial Productivity in South Africa: A Focus on the Channels
Abstract
1. Introduction
2. Review of the Literature
2.1. Theoretical Literature
2.2. Empirical Literature
3. Materials and Methods
3.1. Data Description
3.2. Model Specification
3.3. Estimation Strategy
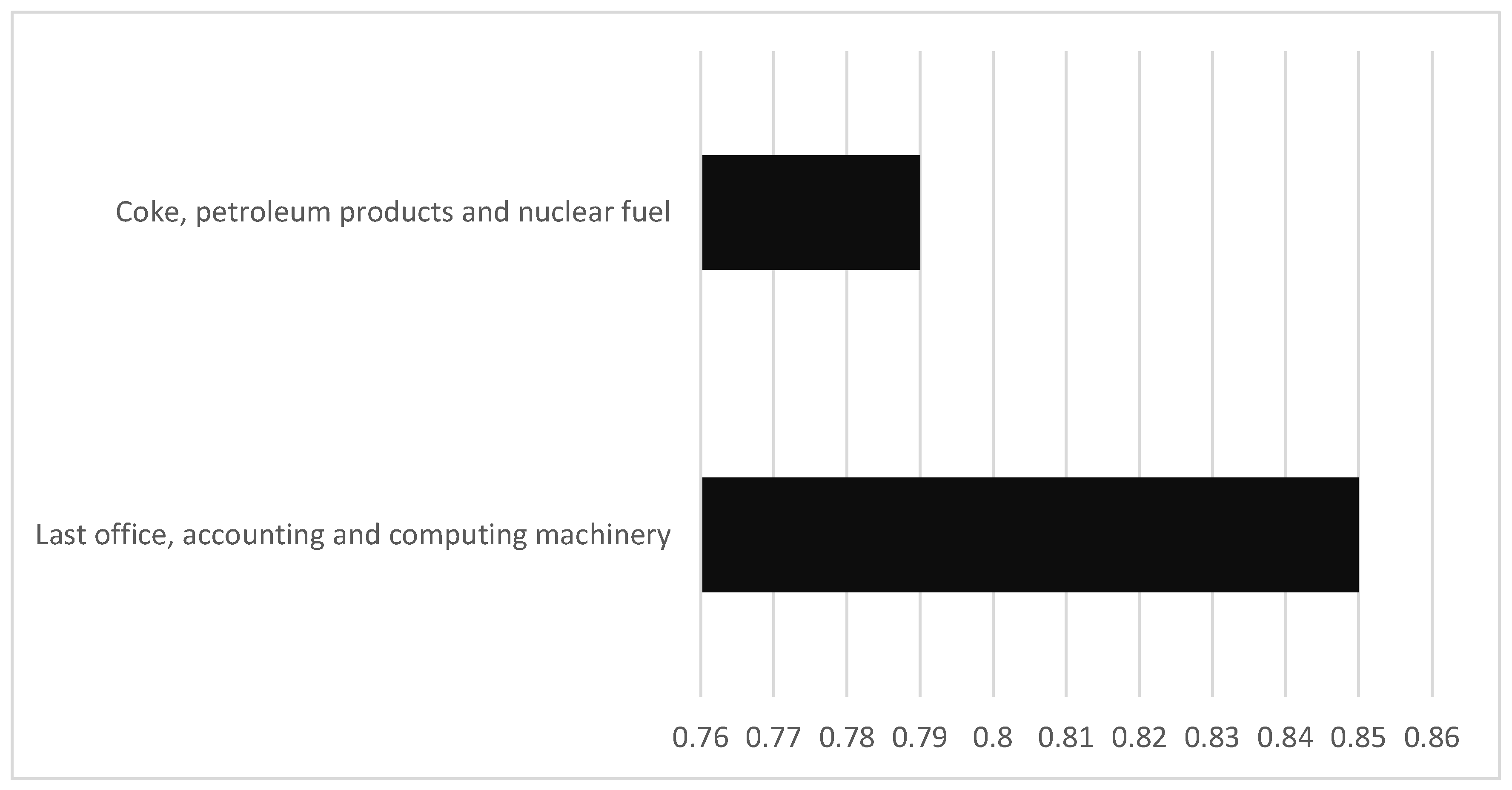
4. Results and Discussion
Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agostino, M., Comert, E. E., Demaria, F., & Ruberto, S. (2024). What kinds of subsidies affect technical efficiency? The case of Italian dairy farms. Agribusiness, 40(1), 116–138. [Google Scholar] [CrossRef]
- Aiginger, K., & Rodrik, D. (2020). Rebirth of industrial policy and an agenda for the twenty-first century. Journal of Industry, Competition and Trade, 20, 189–207. [Google Scholar] [CrossRef]
- Arellano, M., & Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. The Review of Economic Studies, 58(2), 277–297. [Google Scholar] [CrossRef]
- Baltagi, B. H. (2010). Fixed effects and random effects. In Microeconometrics (pp. 59–64). Palgrave Macmillan. [Google Scholar]
- Battese, G. E., & Coelli, T. J. (1988). Prediction of firm-level technical efficiencies with a generalized frontier production function and panel data. Journal of Econometrics, 38(3), 387–399. [Google Scholar] [CrossRef]
- Battese, G. E., & Coelli, T. J. (1992). Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. Journal of Productivity Analysis, 3, 153–169. [Google Scholar] [CrossRef]
- Battese, G. E., & Coelli, T. J. (1995). A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empirical Economics, 20, 325–332. [Google Scholar] [CrossRef]
- Beason, R., & Weinstein, D. E. (1996). Growth, economies of scale, and targeting in Japan (1955–1990). The Review of Economics and Statistics, 78, 286–295. [Google Scholar] [CrossRef]
- Bernini, C., Cerqua, A., & Pellegrini, G. (2017). Public subsidies, TFP and efficiency: A tale of complex relationships. Research Policy, 46(4), 751–767. [Google Scholar] [CrossRef]
- Branstetter, L. G., Li, G., & Ren, M. (2023). Picking winners? Government subsidies and firm productivity in China. Journal of Comparative Economics, 51(4), 1186–1199. [Google Scholar] [CrossRef]
- Bruno, G. S. (2005). Approximating the bias of the LSDV estimator for dynamic unbalanced panel data models. Economics Letters, 87(3), 361–366. [Google Scholar] [CrossRef]
- Burns, J., Edwards, L., & Pauw, K. (2013). Revisiting wage subsidies: How pro-poor is a South African wage subsidy likely to be? Development Southern Africa, 30(2), 186–210. [Google Scholar] [CrossRef]
- Camino-Mogro, S., & Carrillo-Maldonado, P. (2023). Do imports of intermediate inputs generate higher productivity? Evidence from Ecuadorian manufacturing firms. The World Economy, 46(5), 1471–1521. [Google Scholar] [CrossRef]
- Cin, B. C., Kim, Y. J., & Vonortas, N. S. (2017). The impact of public R&D subsidy on small firm productivity: Evidence from Korean SMEs. Small Business Economics, 48, 345–360. [Google Scholar]
- Cornwell, C., Schmidt, P., & Sickles, R. C. (1990). Production frontiers with cross-sectional and time-series variation in efficiency levels. Journal of Econometrics, 46(1–2), 185–200. [Google Scholar] [CrossRef]
- de Jorge, J., & Suárez, C. (2011). Influence of R&D subsidies on efficiency: The case of Spanish manufacturing firms. Cuadernos de Economía y Dirección de la Empresa, 14(3), 185–193. [Google Scholar]
- Devlin, R., & Moguillansky, G. (2013). What’s new in the new industrial policy in Latin America? In The industrial policy revolution I: The role of government beyond ideology (pp. 276–317). Palgrave Macmillan. [Google Scholar]
- Fox, K. J. (1996). Specification of functional form and the estimation of technical progress. Applied Economics, 28(8), 947–956. [Google Scholar] [CrossRef]
- Gilles, E., Deaza, J., & Vivas, A. (2023). The role of imported intermediates in productivity change. Economic Systems Research, 35(2), 211–227. [Google Scholar] [CrossRef]
- Go, D. S., Kearney, M., Korman, V., Robinson, S., & Thierfelder, K. (2010). Wage subsidy and labour market flexibility in South Africa. The Journal of Development Studies, 46(9), 1481–1502. [Google Scholar] [CrossRef]
- Greene, W. (2005). Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. Journal of Econometrics, 126(2), 269–303. [Google Scholar] [CrossRef]
- Greenwald, B., & Stiglitz, J. E. (2006). Helping infant economies grow: Foundations of trade policies for developing countries. American Economic Review, 96(2), 141–146. [Google Scholar] [CrossRef]
- Grossman, G. M., & Helpman, E. (1991). Trade, knowledge spillovers, and growth. European Economic Review, 35(2–3), 517–526. [Google Scholar] [CrossRef]
- Jin, X. (2018). Government subsidies, resource misallocation and manufacturing productivity. China Finance and Economic Review, 7(3), 74–95. [Google Scholar]
- Jin, Z., Shang, Y., & Xu, J. (2018). The impact of government subsidies on private R&D and firm performance: Does ownership matter in China’s manufacturing industry? Sustainability, 10(7), 2205. [Google Scholar] [CrossRef]
- Jongwanich, J., & Kohpaiboon, A. (2020). Effectiveness of industrial policy on firm productivity: Evidence from Thai manufacturing. Asian-Pacific Economic Literature, 34(2), 39–63. [Google Scholar] [CrossRef]
- Juhász, R., Lane, N., & Rodrik, D. (2023). The new economics of industrial policy. Annual Review of Economics, 16, 213–242. [Google Scholar] [CrossRef]
- Karakaplan, M. U. (2022). Panel stochastic frontier models with endogeneity. The Stata Journal, 22(3), 643–663. [Google Scholar] [CrossRef]
- Karakaplan, M. U., & Kutlu, L. (2017). Endogeneity in panel stochastic frontier models: An application to the Japanese cotton spinning industry. Applied Economics, 49(59), 5935–5939. [Google Scholar] [CrossRef]
- Karhunen, H., & Huovari, J. (2015). R&D subsidies and productivity in SMEs. Small Business Economics, 45, 805–823. [Google Scholar]
- Köhler, T., Bhorat, H., & Hill, R. (2023). The effect of wage subsidies on job retention in a developing country: Evidence from South Africa (No. 2023/114) (WIDER Working Paper). UNU-WIDER. [Google Scholar]
- Krueger, A. O., & Tuncer, B. (1982). An empirical test of the infant industry argument. The American Economic Review, 72(5), 1142–1152. [Google Scholar]
- Krugman, P. R. (1983). Targeted industrial policies: Theory and evidence. Industrial Change and Public Policy, 123–155. Available online: https://www.kansascityfed.org/documents/7641/1983-S83-full-publication.pdf#page=139 (accessed on 2 April 2025).
- Kumbhakar, S. C. (1990). Production frontiers, panel data, and time-varying technical inefficiency. Journal of Econometrics, 46, 201–211. [Google Scholar] [CrossRef]
- Kumbhakar, S. C. (2002). Specification and estimation of production risk, risk preferences and technical efficiency. American Journal of Agricultural Economics, 84(1), 8–22. [Google Scholar] [CrossRef]
- Kumbhakar, S. C., Li, M., & Lien, G. (2023). Do subsidies matter in productivity and profitability changes? Economic Modelling, 123, 106264. [Google Scholar] [CrossRef]
- Kumbhakar, S. C., & Wang, D. (2007). Economic reforms, efficiency and productivity in Chinese banking. Journal of Regulatory Economics, 32, 105–129. [Google Scholar] [CrossRef]
- Kumbhakar, S. C., Wang, H. J., & Horncastle, A. P. (2015). A practitioner’s guide to stochastic frontier analysis using Stata. Cambridge University Press. [Google Scholar]
- Latruffe, L., Bravo-Ureta, B. E., Carpentier, A., Desjeux, Y., & Moreira, V. H. (2017). Subsidies and technical efficiency in agriculture: Evidence from European dairy farms. American Journal of Agricultural Economics, 99(3), 783–799. [Google Scholar] [CrossRef]
- Lee, Y. H., & Schmidt, P. (1993). A production frontier model with flexible temporal variation in technical efficiency. The Measurement of Productive Efficiency: Techniques and Applications, 237, 255. [Google Scholar]
- Levinsohn, J., & Petrin, A. (2003). Estimating production functions using inputs to control for unobservables. The Review of Economic Studies, 70(2), 317–341. [Google Scholar] [CrossRef]
- Levinsohn, J., Rankin, N., Roberts, G., & Schöer, V. (2014). Wage subsidies and youth employment in South Africa: Evidence from a randomised control trial. Stellenbosch Economic Working Papers, 2, 14. [Google Scholar]
- Li, M., Jin, M., & Kumbhakar, S. C. (2022). Do subsidies increase firm productivity? Evidence from Chinese manufacturing enterprises. European Journal of Operational Research, 303(1), 388–400. [Google Scholar] [CrossRef]
- Lin, B., & Okyere, M. A. (2023). Race and energy poverty: The moderating role of subsidies in South Africa. Energy Economics, 117, 106464. [Google Scholar] [CrossRef]
- Lin, B., & Xie, Y. (2024). Effect of renewable energy subsidy policy on firms’ total factor productivity: The threshold effect. Energy Policy, 192, 114241. [Google Scholar] [CrossRef]
- Liu, D., Chen, T., Liu, X., & Yu, Y. (2019). Do more subsidies promote greater innovation? Evidence from the Chinese electronic manufacturing industry. Economic Modelling, 80, 441–452. [Google Scholar] [CrossRef]
- Liu, Z., & Zhou, X. (2023). Can direct subsidies or tax incentives improve the R&D efficiency of the manufacturing industry in China? Processes, 11(1), 181. [Google Scholar] [CrossRef]
- Martin, J. P., & Page, J. M. (1983). The impact of subsidies on X-efficiency in LDC industry: Theory and an empirical test. The Review of Economics and Statistics, 65, 608–617. [Google Scholar] [CrossRef]
- Masunda, S. (2011). Real exchange rate misalignment and sectoral output in Zimbabwe. International Journal of Economic Research, 2(4), 59–74. [Google Scholar]
- Mattsson, P. (2019). The impact of labour subsidies on total factor productivity and profit per employee. Economic Analysis and Policy, 62, 325–341. [Google Scholar] [CrossRef]
- Minviel, J. J., Sipiläinen, T., Latruffe, L., & Bravo-Ureta, B. E. (2024). Impact of public subsidies on persistent and transient technical efficiency: Evidence from French mixed crop-livestock farms. Applied Economics, 56(55), 7286–7301. [Google Scholar] [CrossRef]
- Mohsen, A. S., Chua, S. Y., & Sab, C. N. C. (2015). Determinants of industrial output in Syria. Journal of Economic Structures, 4, 1–12. [Google Scholar] [CrossRef]
- Moulay Ali, H., Guellil, M. S., Mokhtari, F., & Tsabet, A. (2024). The effect of subsidies on tecnical efficiency of Algerian agricultural sector: Using stochastic frontier model (SFA). Discover Sustainability, 5(1), 98. [Google Scholar] [CrossRef]
- Nickell, S. (1981). Biases in dynamic models with fixed effects. Econometrica: Journal of the Econometric Society, 49, 1417–1426. [Google Scholar] [CrossRef]
- Obeng, K., & Sakano, R. (2008). Public transit subsidies, output effect and total factor productivity. Research in Transportation Economics, 23(1), 85–98. [Google Scholar] [CrossRef]
- Papke, L. E., & Wooldridge, J. M. (2008). Panel data methods for fractional response variables with an application to test pass rates. Journal of Econometrics, 145(1–2), 121–133. [Google Scholar] [CrossRef]
- Pitt, M. M., & Lee, L. F. (1981). The measurement and sources of technical inefficiency in the Indonesian weaving industry. Journal of Development Economics, 9(1), 43–64. [Google Scholar] [CrossRef]
- Rizov, M., Pokrivcak, J., & Ciaian, P. (2013). CAP subsidies and productivity of the EU farms. Journal of Agricultural Economics, 64(3), 537–557. [Google Scholar] [CrossRef]
- Rodrik, D. (1995). Getting interventions right: How South Korea and Taiwan grew rich. Economic Policy, 10(20), 53–107. [Google Scholar] [CrossRef]
- Rodrik, D. (2019). Where are we in the economics of industrial policies? 1. Frontiers of Economics in China, 14(3), 329–335. [Google Scholar]
- Rodrik, D. (2022). An industrial policy for good jobs. In Hamilton project—Policy proposal. Brookings Institution. [Google Scholar]
- Salustiano, S. F. M., Barbosa, N., & Moreira, T. B. S. (2020). Do subsidies drive technical efficiency? The case of Portuguese firms in the agribusiness sector. Revista de Economia e Sociologia Rural, 58(3), e216150. [Google Scholar] [CrossRef]
- Schmidt, P., & Sickles, R. C. (1984). Production frontiers and panel data. Journal of Business & Economic Statistics, 2(4), 367–374. [Google Scholar]
- Schwartz, G., & Clements, B. (1999). Government subsidies. Journal of Economic Surveys, 13(2), 119–148. [Google Scholar] [CrossRef]
- Wang, H. J. (2002). Heteroscedasticity and non-monotonic efficiency effects of a stochastic frontier model. Journal of Productivity Analysis, 18, 241–253. [Google Scholar] [CrossRef]
- Wang, H. J., & Ho, C. W. (2010). Estimating fixed-effect panel stochastic frontier models by model transformation. Journal of Econometrics, 157(2), 286–296. [Google Scholar] [CrossRef]
- Wooldridge, J. M. (2014). Quasi-maximum likelihood estimation and testing for nonlinear models with endogenous explanatory variables. Journal of Econometrics, 182(1), 226–234. [Google Scholar] [CrossRef]
- Zhang, X., Gong, D., Huang, Y., & Li, Y. (2024). The government’s fiscal and taxation policy effect on enterprise productivity: Policy choice and optimal allocation. International Review of Economics & Finance, 93, 28–41. [Google Scholar]
- Zhu, M., Zheng, K., Liu, B., & Jin, F. (2024). Can agricultural support and protection subsidy policies promote high-quality development of grain industry? A case study of China. Agriculture, 14(10), 1664. [Google Scholar] [CrossRef]
- Zhu, X., Zuo, F., Wang, S., Yang, Q., & Shi, X. (2024). Can government subsidies facilitate TFP growth? From the perspective of dynamic capability. International Journal of Innovation and Technology Management (IJITM), 21(5), 2450035. [Google Scholar] [CrossRef]





| Model EX | Model EN | |
|---|---|---|
| Dep.var: logoutput | ||
| Constant | 5.748 *** (0.922) | 6.274 *** (0.970) |
| Log (labour) | 0.127 *** (0.010) | 0.128 *** (0.010) |
| Log (capital stock) | 0.005 (0.018) | 0.006 (0.018) |
| Log (intermediate inputs) | 0.544 *** (0.012) | 0.545 *** (0.012) |
| Log (subsidies) | −0.055 *** (0.014) | −0.061 *** (0.014) |
| Log (intermediate imports) | 0.055 *** (0.016) | 0.059 *** (0.016) |
| Year | −0.000 (0.000) | −0.001 (0.001) |
| Dep.var: ln(σ2_u) | ||
| Constant | 2.301 *** (0.209) | 2.293 *** (0.209) |
| Log (subsidies) | 0.029 (0.018) | 0.030 (0.018) |
| Export intensity (%) | 0.001 † (0.000) | 0.001 † (0.000) |
| Log (intermediate imports) | −0.191 *** (0.022) | −0.192 *** (0.022) |
| ICTs (share of total capital stock) | −1.607 *** (0.156) | −1.640 *** (0.159) |
| Unit labour costs | −0.001 *** (0.000) | −0.001 *** (0.000) |
| Informal employment | −0.398 *** (0.060) | −0.383 *** (0.061) |
| Dep.var: ln(σ2_v) | ||
| Constant | −4.690 *** (0.033) | |
| Dep.var: ln(σ2_w) | ||
| Constant | −4.693 *** (0.033) | |
| eta1 (logsubsidies) | 0.022 * (0.010) | |
| eta Endogeneity test | X2 = 4.58 *** (0.032) | |
| Observations | 1920 | 1920 |
| Log likelihood | 1540.80 | 1554.29 |
| Mean technical efficiency | 0.2881 | 0.2899 |
| Median technical efficiency | 0.2610 | 0.2630 |
| iv1_Logsubsidies | Coefficient |
|---|---|
| Log (subsidies) (−1) | 0.877 *** (0.008) |
| Log (labour) | −0.017 *** (0.005) |
| Log (capital) | 0.022 *** (0.006) |
| Log (intermediate inputs) | 0.052 *** (0.012) |
| Log (intermediate imports) | 0.069 *** (0.009) |
| Year | −0.003 *** (0.001) |
| Export intensity | −0.001 (0.003) |
| ICTs (share of total capital stock) | 0.100 (0.076) |
| Unit labour costs | 0.0003 * (0.0002) |
| Informal employment | 0.197 *** (0.037) |
| Constant | 4.018 (1.705) |
| Ch12 (2) | 148.58 |
| Prob > chi2 | 0.0000 |
| Coefficients | |
|---|---|
| Log (subsidies) (−1) | 0.762 *** |
| (0.0149) | |
| Log (labour) | 0.0592 ** |
| (0.0259) | |
| Log (capital) | −0.00425 |
| (0.0447) | |
| Log (intermediates) | 0.0354 |
| (0.0283) | |
| Log (intermediate imports) | 0.181 *** |
| (0.0317) | |
| Export intensity | −0.000589 |
| (0.000594) | |
| ICTs (share of total capital stock) | 0.156 |
| (0.190) | |
| Unit labour costs | 0.000364 * |
| (0.000218) | |
| Informal employment | 0.177 ** |
| (0.0735) | |
| Year | −0.00885 *** |
| (0.00116) | |
| Observations | 1920 |
| Number of industries | 64 |
| (1) | (2) | |
|---|---|---|
| TFE-CFA | TFE | |
| Frontier model | ||
| loglabour | 0.117 *** | 0.105 *** |
| (0.0100) | (0.0101) | |
| logcapital | 0.0787 *** | 0.0818 *** |
| (0.0231) | (0.0236) | |
| logintermediates | 0.478 *** | 0.467 *** |
| (0.0120) | (0.0122) | |
| loginterimports | 0.113 *** | 0.0913 *** |
| (0.0114) | (0.0113) | |
| Residual | 0.339 | |
| (0.214) | ||
| logsubsidies | −0.0569 *** (0.00793) | −0.0217 *** (0.00659) |
| Year | 0.00136 ** (0.000537) | 0.00311 *** (0.000495) |
| Inefficiency model | ||
| logsubsidies | −0.0924 | −0.0530 |
| (0.078) | (0.0631) | |
| Export | 0.00168 | 0.00183 |
| (0.00210) | (0.00186) | |
| loginterimports | −0.157 * | −0.153 ** |
| (0.0844) | (0.0752) | |
| ICTshare | −7.701 ** | −6.505 ** |
| (3.256) | (2.694) | |
| ulc | 0.00373 ** | 0.00353 *** |
| (0.00153) | (0.00133) | |
| informal_share | −12.82 *** | −11.58 *** |
| (3.912) | (3.314) | |
| Residual | 0.0973 *** | |
| (0.0126) | ||
| Constant | 1.529 *** | 1.436 *** |
| (0.523) | (0.456) | |
| Mean technical efficiency | 0.83 | 0.84 |
| Observations | 1920 | 1920 |
| Number of industries | 64 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazorodze, B.T. Government Subsidies and Industrial Productivity in South Africa: A Focus on the Channels. Econometrics 2025, 13, 20. https://doi.org/10.3390/econometrics13020020
Mazorodze BT. Government Subsidies and Industrial Productivity in South Africa: A Focus on the Channels. Econometrics. 2025; 13(2):20. https://doi.org/10.3390/econometrics13020020
Chicago/Turabian StyleMazorodze, Brian Tavonga. 2025. "Government Subsidies and Industrial Productivity in South Africa: A Focus on the Channels" Econometrics 13, no. 2: 20. https://doi.org/10.3390/econometrics13020020
APA StyleMazorodze, B. T. (2025). Government Subsidies and Industrial Productivity in South Africa: A Focus on the Channels. Econometrics, 13(2), 20. https://doi.org/10.3390/econometrics13020020






