Relationship Between Coefficients in Parametric Survival Models for Exponentially Distributed Survival Time—Registered Unemployment in Poland
Abstract
:1. Introduction
2. Methods of Survival Analysis
- t—time to the event,
- —cumulative distribution function of random variable T,
- —probability density function,
- —probability.
2.1. Proportional Hazards (PH) Models
- —baseline hazard,
- —vector of covariates,
- —vector of coefficients,
- n—number of covariates in the model.
- —hazard function,
- —time to the event
- —vector of covariates for the i-th unit,
- —vector of covariates for the j-th unit,
- n—number of covariates in the model.
2.2. Accelerated Failure Time (AFT) Models
- —the acceleration factor,
- —survival functions for group 1 and group 2, respectively.
- —survival time of group 1,
- —survival time of group 2.
- —vector of covariates,
- —vector of coefficients,
- n—number of covariates in the model.
- If , the effect of covariate is decelerated.
- If , the effect of covariate is accelerated.
- —vector of covariates,
- —vector of coefficients,
- —the intercept,
- —random errors that does not depend on ,
- —an unknown scale parameter,
- n—number of covariates in the model.
2.3. Main Differences Between PH and AFT Models
- 1.
- Basic assumptions of the models:
- 2.
- Different interpretation of coefficients:
2.4. Application of Survival Analysis Methods in the Study of Socio-Economic Phenomena
3. Symmetry of Coefficients in PH and AFT Models for Exponential Distribution of Survival Time T
- If γ > 1, then the time to the event is higher than in the reference group. In this case, HR < 1, i.e., the intensity of the event, is lower compared to the reference group.
- If γ < 1, then the time to the event is lower than in the reference group. In this case, HR > 1, i.e., the intensity of the event is higher than in the reference group.
- In the case, when γ = HR = 1, then the time to the incident and the intensity of the incident are the same as in the reference group.
4. Analysis of Duration in Registered Unemployment—An Empirical Example
- —number of events at the time ti,
- —number of units at the time ti.
5. Discussion and Conclusions
- Answer to Q1: In the case of an exponential distribution of survival time, there is a symmetric relation between the coefficients of the PH and AFT models.
- Answer to Q2: The symmetric relation between the coefficients of the PH and AFT models (for exponential survival) indicates the opposite direction of the effects of the variables on hazard and the duration of the phenomenon.
Funding
Data Availability Statement
Conflicts of Interest
References
- Aalen, O. O., Borgan, Ø., & Gjessing, H. K. (2008). Survival and event history analysis: A process point of view. Springer. [Google Scholar]
- Addison, J. T., & Portugal, P. (1998). Some specification issues in unemployment duration analysis. Labour Economics, 5(1), 53–66. [Google Scholar] [CrossRef]
- Babucea, A. G., & Danacica, D. E. (2007). Using kaplan—Meier curves for preliminary evaluation the duration of unemployment spells, MPRA paper 7854. University Library of Munich. Available online: https://core.ac.uk/download/pdf/7296501.pdf (accessed on 14 November 2024).
- Basha, L., & Gjika, E. D. (2022). Accelerated failure time models in analyzing duration of employment. Journal of Physics: Conference Series, 2287, 012014. [Google Scholar] [CrossRef]
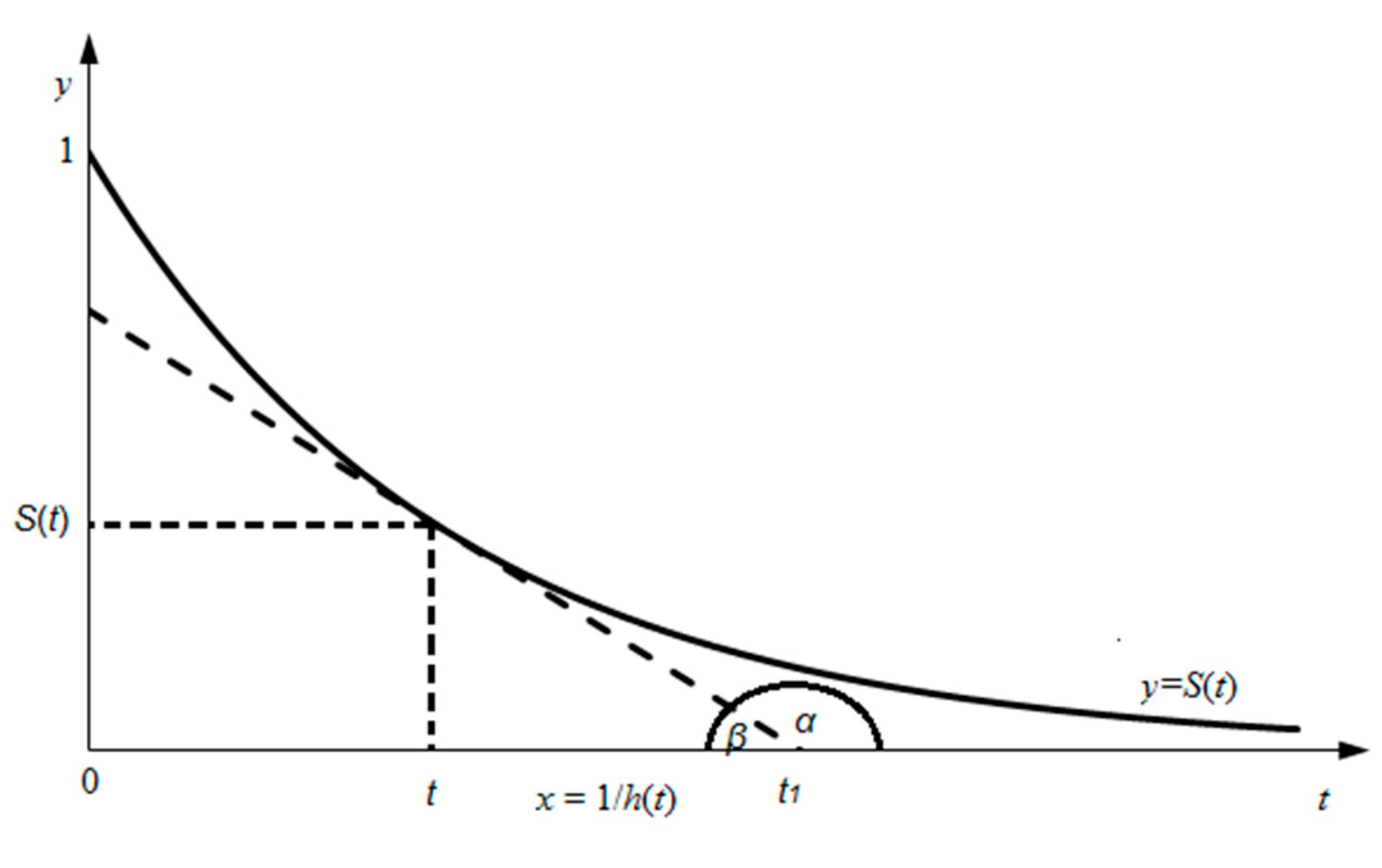
- Bieszk-Stolorz, B. (2015). Geometric method of determining hazard for the continuous survival function. Folia Oeconomica Stetinensia, 15, 22–33. [Google Scholar] [CrossRef]
- Bieszk-Stolorz, B. (2017). Cumulative incidence function in studies on the duration of the unemployment exit process. Folia Oeconomica Stetinensia, 17, 138–150. [Google Scholar] [CrossRef]
- Bieszk-Stolorz, B., & Dmytrów, K. (2021). Evaluation of changes on world stock exchanges in connection with the SARS-CoV-2 pandemic. survival analysis methods. Risks, 9(7), 121. [Google Scholar] [CrossRef]
- Bieszk-Stolorz, B., & Markowicz, I. (2022). The impact of the COVID-19 pandemic on the situation of the unemployed in Poland. A study using survival analysis methods. Sustainability, 14(19), 12677. [Google Scholar] [CrossRef]
- Biggs, N. L. (2002). Discrete mathematics (2nd ed.). Oxford University Press. [Google Scholar]
- Box-Steffensmeier, J. M., & Jones, B. S. (2004). Event history modeling a guide for social scientists. Cambridge University Press. [Google Scholar]
- Box-Steffensmeier, J. M., & Zorn, C. J. W. (2001). Duration models and proportional hazards in political science. American Journal of Political Science, 45, 972–988. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J. M., Reiter, D., & Zorn, C. J. W. (2003). Nonproportional hazards and event history analysis in international relations. The Journal of Conflict Resolution, 47, 33–53. [Google Scholar] [CrossRef]
- Bradburn, M., Clark, T. G., Love, S., & Altman, D. (2003). Survival analysis part II: Multivariate data analysis—An introduction to concepts and methods. British Journal of Cancer, 89, 431–436. [Google Scholar] [CrossRef]
- Calabuig, J. M., Jiménez-Fernández, E., Sánchez-Pérez, E. A., & Manzanares, S. (2021). Modeling hospital resource management during the COVID-19 pandemic: An experimental validation. Econometrics, 9(4), 38. [Google Scholar] [CrossRef]
- Ciucă, V., & Matei, M. (2011). Survival rates in unemployment. International Journal of Mathematical Models and Methods in Applied Sciences, 5, 362–370. [Google Scholar]
- Collett, D. (2023). Modelling survival data in medical research (4th ed.). CRC Press. [Google Scholar]
- Cox, D. R., & Snell, E. J. (1968). A general definition of residuals. Journal of the Royal Statistical Society. Series B (Methodological), 30, 248–265. [Google Scholar] [CrossRef]
- Dendir, S. (2006). Unemployment duration in poor developing economies: Evidence from urban Ethiopia. The Journal of Developing Areas, 40, 181–201. [Google Scholar] [CrossRef]
- Doğan, F. İ. (2019). Unemployment benefits and unemployment duration in France and Poland. Marmara Journal of European Studies, 27, 191–216. [Google Scholar] [CrossRef]
- Doğan, F. İ. (2020). Social transfers and unemployment duration: An empirical evidence of the EU and Turkey. Marmara Üniversitesi İktisadi ve İdari Bilimler Dergisi, 42, 247–264. [Google Scholar] [CrossRef]
- Enderton, H. B. (1977). Elements of set theory. Academic Press. [Google Scholar]
- Faruk, A. (2018). The comparison of proportional hazards and accelerated failure time models in analyzing the first birth interval survival data. Journal of Physics: Conference Series, 974, 012008. [Google Scholar] [CrossRef]
- Gelfand, L. A., MacKinnon, D. P., DeRubeis, R. J., & Baraldi, A. N. (2016). Mediation analysis with survival outcomes: Accelerated failure time vs. proportional hazards models. Frontiers in Psychology, 7, 423. [Google Scholar] [CrossRef]
- Grzenda, W. (2023). Estimating the probability of leaving unemployment for older people in Poland using survival models with censored data. Statistics in Transition. New Series, 24, 241–256. [Google Scholar] [CrossRef]
- Han, A., & Hausman, J. A. (1990). Flexible parametric estimation of duration and competing risk models. Journal of Applied Econometrics, 5, 1–28. [Google Scholar] [CrossRef]
- Kavkler, A., Danacica, D. E., Babucea, A. G., Bicanic, I., Bohm, B., Tevdovski, D., Tosevska, K., & Borsic, D. (2009). Cox regression models for unemployment duration in Romania, Austria, Slovenia, Croatia, and Macedonia. Romanian Journal of Economic Forecasting, 10, 81–104. [Google Scholar]
- Khamis, A., Hamat, C. A. C., & Abdullah, M. A. A. (2020). Modeling students’ performance using Cox and parametric accelerated failure time models. Scientific Research Journal, 8, 44–49. [Google Scholar] [CrossRef]
- Khanal, S. P., Sreenivas, V., & Acharya, S. K. (2014). Accelerated failure time models: An application in the survival of acute liver failure patients in India. International Journal of Science and Research, 6, 161–166. [Google Scholar]
- Khanal, S. P., Sreenivas, V., & Acharya, S. K. (2019). Comparison of Cox proportional hazards model and lognormal accelerated failure time model: Application in time to event analysis of acute liver failure patients in India. Nepalese Journal of Statistics, 3, 21–40. [Google Scholar] [CrossRef]
- Klein, J. P., & Moeschberger, M. L. (2003). Survival analysis techniques for censored and truncated data (2nd ed.). Springer. [Google Scholar]
- Kleinbaum, D. G., & Klein, M. (2005). Survival analysis a self-learning text (2nd ed.). Springer. [Google Scholar]
- Lalive, R. (2008). How do extended benefits affect unemployment duration? A regression discontinuity approach. Journal of Econometrics, 142, 785–806. [Google Scholar] [CrossRef]
- Landmesser, J. M. (2007). Wykorzystanie modeli ryzyka konkurencyjnego w celu szacowania czasu trwania aktywności zawodowej. Prace Naukowe Akademii Ekonomicznej im. Oskara Langego we Wrocławiu. Taksonomia, 14, 542–550. [Google Scholar]
- Landmesser, J. M. (2009). Econometric analysis of unemployment duration using hazard models. Studia Ekonomiczne, 1–2, 79–92. [Google Scholar]
- Landmesser, J. M. (2010). A dynamic approach to the study of unemployment duration. Metody Ilościowe w Badaniach Ekonomicznych, 11, 212–222. [Google Scholar]
- Landmesser, J. M. (2013). Wykorzystanie metod analizy czasu trwania do badania aktywności ekonomicznej ludności w Polsce. Wydawnictwo SGGW. [Google Scholar]
- Machin, D., Cheung, Y. B., & Parmar, M. (2006). Survival analysis: A practical approach (2nd ed.). John Wiley & Sons. [Google Scholar]
- Marcassa, S. (2012). Unemployment duration of spouses: Evidence from France. THEMA working papers 2012-31. Université de Cergy-Pontoise. [Google Scholar]
- Matuszyk, A. (2017). Credit scoring. CeDeWu. [Google Scholar]
- Meyer, B. D. (1990). Unemployment insurance and unemployment spells. Econometrica, 58, 757–782. [Google Scholar] [CrossRef]
- Mishra, N., & Misra, S. (2022). Comparison of Cox proportional hazard model and accelerated failure time (AFT) models: An application to under-five mortality in Uttar Pradesh. Indian Journal of Applied Research, 12, 83–87. [Google Scholar] [CrossRef]
- Moffitt, R. (1985). Unemployment insurance and the distribution of unemployment spells. Journal of Econometrics, 28, 85–101. [Google Scholar] [CrossRef]
- Nickell, S. (1979). Estimating the probability of leaving unemployment. Econometrica, 47, 1249–1266. [Google Scholar] [CrossRef]
- Olive, D. J. (2003). Available online: http://parker.ad.siu.edu/Olive/survbook.pdf (accessed on 12 July 2024).
- Orbe, J., Ferreira, E., & Núñez-Antón, V. (2002). Comparing proportional hazards and accelerated failure time models for survival analysis. Statistics in Medicine, 21, 3493–3510. [Google Scholar] [CrossRef]
- Pang, M., Platt, R. W., Schuster, T., & Abrahamowicz, M. (2021). Spline-based accelerated failure time model. Statistics in Medicine, 40, 481–497. [Google Scholar] [CrossRef] [PubMed]
- Patel, K., Kay, R., & Rowell, L. (2006). Comparing proportional hazards and accelerated failure time models: An application in influenza. Pharmaceutical Statistics: The Journal of Applied Statistics in the Pharmaceutical Industry, 5, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Pourhoseingholi, M. A., Hajizadeh, E., Dehkordi, B. D. M., Safaee, A., Abadi, A., & Zali, M. R. (2007). Comparing Cox regression and parametric models for survival of patients with gastric carcinoma. Asian Pacific Journal of Cancer Prevention, 8, 412–416. [Google Scholar] [PubMed]
- Putek-Szeląg, E., & Gdakowicz, A. (2021). Application of duration analysis methods in the study of the exit of a real estate sale offer from the offer database system. In K. Jajuga, K. Najman, & M. Walesiak (Eds.), Data analysis and classification. Methods and applications (pp. 153–169). Springer. [Google Scholar] [CrossRef]
- Qi, J. (2009). Comparison of proportional hazards and accelerated failure time models [Ph.D. Thesis, University of Saskatchewan]. [Google Scholar]
- Rashidi, T. H., & Mohammadian, A. (Kouros). (2011). Parametric hazard functions: Overview. Transportation Research Record, 2230, 48–57. [Google Scholar] [CrossRef]
- Sączewska-Piotrowska, A. (2015). Poverty duration of households of the self-employed. Econometrics. Ekonometria, 1, 44–55. [Google Scholar] [CrossRef]
- Saikia, R., & Barman, M. P. (2017). A review on accelerated failure time models. International Journal of Statistics and Systems, 12, 311–322. [Google Scholar]
- Statistics Poland. (n.d.). Available online: https://stat.gov.pl/en/poland-macroeconomic-indicators/ (accessed on 16 November 2024).
- Swindell, W. R. (2009). Accelerated failure time models provide a useful statistical framework for aging research. Experimental gerontology, 44, 190–200. [Google Scholar] [CrossRef]
- Tansel, A., & Taşçı, H. M. (2010). Hazard analysis of unemployment duration by gender in developing county: The case of Turkey. Labour, 24, 501–530. [Google Scholar] [CrossRef]
- Urbańczyk, D. M. (2020). Competing risks models for an enterprises duration on the market. Folia Oeconomica Stetinensia, 20, 456–473. [Google Scholar] [CrossRef]
- Wycinka, E. (2019). Competing risk models of default in the presence of early repayments. Econometrics. Ekonometria. Advances in Applied Data Analytics, 23, 99–120. [Google Scholar] [CrossRef]



| Characteristic | Category | Variable Name |
|---|---|---|
| Gender | males * | – |
| females | gender | |
| Seniority | without seniority * | – |
| with seniority | seniority | |
| Level of education | at most lower secondary * | – |
| basic vocational | education2 | |
| general secondary | education3 | |
| vocational secondary | education4 | |
| higher | education5 | |
| Age | 18–24 * | – |
| 25–34 | age2 | |
| 35–44 | age3 | |
| 45–54 | age4 | |
| 55–59 | age5 | |
| 60–64 | age6 |
| Characteristic | Category | Total Size | Starting Work | Right-Censored Observations |
|---|---|---|---|---|
| Gender | males * | 4766 | 2765 | 2001 |
| females | 4112 | 2856 | 1256 | |
| Seniority | without seniority * | 3457 | 1892 | 1565 |
| with seniority | 5421 | 3729 | 1692 | |
| Level of education | at most lower secondary * | 1929 | 850 | 1079 |
| basic vocational | 1648 | 943 | 705 | |
| general secondary | 1264 | 823 | 441 | |
| vocational secondary | 1647 | 1139 | 508 | |
| higher | 2390 | 1866 | 524 | |
| Age | 18–24 * | 948 | 586 | 362 |
| 25–34 | 2598 | 1762 | 836 | |
| 35–44 | 2442 | 1631 | 811 | |
| 45–54 | 1620 | 1053 | 567 | |
| 55–59 | 587 | 360 | 227 | |
| 60–64 | 683 | 229 | 454 | |
| Total | 8878 | 5621 | 3257 |
| Variable | Coef. | Std. Err. | z | p > |z| | 95% Conf. Interval |
|---|---|---|---|---|---|
| gender | −0.1884 | 0.0276 | −6.83 | 0.000 | [−0.2424, −0.1344] |
| seniority | 0.0755 | 0.0305 | 2.48 | 0.013 | [0.0158, 0.1352] |
| education2 | 0.3490 | 0.0484 | 7.22 | 0.000 | [0.2543, 0.4438] |
| education3 | 0.3506 | 0.0499 | 7.03 | 0.000 | [0.2529, 0.4483] |
| education4 | 0.5234 | 0.0460 | 11.37 | 0.000 | [0.4332, 0.6136] |
| education5 | 0.7268 | 0.0435 | 16.72 | 0.000 | [0.6416, 0.8121] |
| age2 | −0.2793 | 0.0493 | −5.66 | 0.000 | [−0.3760, −0.1825] |
| age3 | −0.4754 | 0.0509 | −9.34 | 0.000 | [−0.5751, −0.3757] |
| age4 | −0.5887 | 0.0543 | −10.84 | 0.000 | [−0.6951, −0.4822] |
| age5 | −0.6632 | 0.0695 | −9.54 | 0.000 | [−0.7994, −0.5269] |
| age6 | −1.8166 | 0.0807 | −22.51 | 0.000 | [−1.9748, −1.6585] |
| Const. | −2.3460 | 0.0515 | −45.54 | 0.000 | [−2.4470, −2.2450] |
| LR chi2(11) | 1188.07 | ||||
| Log likelihood | −12,364.40 | ||||
| Prob > chi2 | 0.0000 | ||||
| AIC | 24,752.8 | ||||
| BIC | 24,837.9 |
| Variable | Coef. | Std. Err. | z | p > |z| | 95% Conf. Interval |
|---|---|---|---|---|---|
| gender | 0.1884 | 0.0276 | 6.83 | 0.000 | [0.1344, 0.2424] |
| seniority | −0.0755 | 0.0305 | −2.48 | 0.013 | [−0.1352, −0.0158] |
| education2 | −0.3490 | 0.0484 | −7.22 | 0.000 | [−0.4438, −0.2543] |
| education3 | −0.3506 | 0.0499 | −7.03 | 0.000 | [−0.4483, −0.2529] |
| education4 | −0.5234 | 0.0460 | −11.37 | 0.000 | [−0.6136, −0.4332] |
| education5 | −0.7268 | 0.0435 | −16.72 | 0.000 | [−0.8121, −0.6416] |
| age2 | 0.2793 | 0.0493 | 5.66 | 0.000 | [0.1825, 0.3760] |
| age3 | 0.4754 | 0.0509 | 9.34 | 0.000 | [0.3757, 0.5751] |
| age4 | 0.5887 | 0.0543 | 10.84 | 0.000 | [0.4822, 0.6951] |
| age5 | 0.6632 | 0.0695 | 9.54 | 0.000 | [0.5270, 0.7994] |
| age6 | 1.8166 | 0.0807 | 22.51 | 0.000 | [1.6585, 1.9748] |
| Const. | 2.3460 | 0.0515 | 45.54 | 0.000 | [2.2450, 2.4470] |
| LR chi2(11) | 1188.07 | ||||
| Log likelihood | −12,364.40 | ||||
| Prob > chi2 | 0.0000 | ||||
| AIC | 24,752.8 | ||||
| BIC | 24,837.9 |
| Variable | PH Model ) | AFT Model ) | PH Model ) | AFT Model |
|---|---|---|---|---|
| gender | −0.1884 | 0.1884 | 0.8283 | 1.2073 |
| seniority | 0.0755 | −0.0755 | 1.0784 | 0.9273 |
| education2 | 0.3490 | −0.3490 | 1.4177 | 0.7054 |
| education3 | 0.3506 | −0.3506 | 1.4199 | 0.7043 |
| education4 | 0.5234 | −0.5234 | 1.6877 | 0.5925 |
| education5 | 0.7268 | −0.7268 | 2.0685 | 0.4834 |
| age2 | −0.2793 | 0.2793 | 0.7563 | 1.3221 |
| age3 | −0.4754 | 0.4754 | 0.6216 | 1.6087 |
| age4 | −0.5887 | 0.5887 | 0.5551 | 1.8016 |
| age5 | −0.6632 | 0.6632 | 0.5152 | 1.9409 |
| age6 | −1.8166 | 1.8166 | 0.1626 | 6.1512 |
| Const. | −2.3460 | 2.3460 | 0.0958 | 10.444 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieszk-Stolorz, B. Relationship Between Coefficients in Parametric Survival Models for Exponentially Distributed Survival Time—Registered Unemployment in Poland. Econometrics 2025, 13, 1. https://doi.org/10.3390/econometrics13010001
Bieszk-Stolorz B. Relationship Between Coefficients in Parametric Survival Models for Exponentially Distributed Survival Time—Registered Unemployment in Poland. Econometrics. 2025; 13(1):1. https://doi.org/10.3390/econometrics13010001
Chicago/Turabian StyleBieszk-Stolorz, Beata. 2025. "Relationship Between Coefficients in Parametric Survival Models for Exponentially Distributed Survival Time—Registered Unemployment in Poland" Econometrics 13, no. 1: 1. https://doi.org/10.3390/econometrics13010001
APA StyleBieszk-Stolorz, B. (2025). Relationship Between Coefficients in Parametric Survival Models for Exponentially Distributed Survival Time—Registered Unemployment in Poland. Econometrics, 13(1), 1. https://doi.org/10.3390/econometrics13010001







