Abstract
Predicting stock market movement direction is a challenging task due to its fuzzy, chaotic, volatile, nonlinear, and complex nature. However, with advancements in artificial intelligence, abundant data availability, and improved computational capabilities, creating robust models capable of accurately predicting stock market movement is now feasible. This study aims to construct a predictive model using news headlines to predict stock market movement direction. It conducts a comparative analysis of five supervised classification machine learning algorithms—logistic regression (LR), support vector machine (SVM), random forest (RF), extreme gradient boosting (XGBoost), and artificial neural network (ANN)—to predict the next day’s movement direction of the close price of the Nepal Stock Exchange (NEPSE) index. Sentiment scores from news headlines are computed using the Valence Aware Dictionary for Sentiment Reasoning (VADER) and TextBlob sentiment analyzer. The models’ performance is evaluated based on sensitivity, specificity, accuracy, and the area under the receiver operating characteristic (ROC) curve (AUC). Experimental results reveal that all five models perform equally well when using sentiment scores from the TextBlob analyzer. Similarly, all models exhibit almost identical performance when using sentiment scores from the VADER analyzer, except for minor variations in AUC in SVM vs. LR and SVM vs. ANN. Moreover, models perform relatively better when using sentiment scores from the TextBlob analyzer compared to the VADER analyzer. These findings are further validated through statistical tests.
1. Introduction
The stock market facilitates the buying and selling of ownership units in companies, known as stocks, allowing investors to profit from increases in a company’s profitability and causing them to suffer losses when it declines. The evolution of the stock market is remarkable, transitioning from handwritten transactions in coffee shops to today’s digital platforms, providing instant access to global markets. This advancement fosters economic growth by fostering competition and innovation across various sectors such as business, education, and the labor market (Bosworth et al. 1975; Jones 2002). However, selecting the right stocks at the right time remains a daunting challenge due to various factors and circumstances influencing stock prices. The inherently nonlinear, volatile, fuzzy, noisy, nonparametric, and deterministic chaotic nature of stock behavior (Ahangar et al. 2010; Bhandari et al. 2022; Gandhmal and Kumar 2019; Weng et al. 2017) adds complexity. Utilizing reliable sources of public sentiment regarding stock prices can enhance investment decisions by employing stock price prediction models, thereby aiding in mitigating market uncertainty.
Several schools of thought have been employed in predicting the direction of stock price movements. Traditionally, the first school subscribes to the efficient market hypothesis theory, emphasizing the significant influence of historical stock data in forecasting future price movement (Hansen et al. 1999). In contrast, the random walk (Fama 1995) theory posits that a stock’s current price already encompasses all relevant information, with any price changes attributed to the release of new information or random noise. The second school focuses on statistical modeling, aiming to predict future price movement based on the relationship between past and present data (Bisoi et al. 2019; Devi et al. 2013; Dhyani et al. 2020; Garlapati et al. 2021). However, many of these models assume a linear relationship between variables, despite stock market data often exhibiting nonlinear patterns. The third and most advanced school emerged with technological advancements, heightened computational power, and the development of rule-based artificial intelligence algorithms (Chen and Ge 2019; Derakhshan and Beigy 2019; Long et al. 2019; Nelson et al. 2017; Xu and Cohen 2018; Zhao and Yang 2023). These models excel in capturing the nonlinear behavior inherent in stock market data.
With rare exceptions, most models developed within any paradigm rely on structured numerical data to forecast stock price movements (Ismail et al. 2020; Kara et al. 2011; Khoa and Huynh 2022; Wang 2014). However, in the past decade, the trajectory of the stock market has been significantly influenced by information disseminated through various digital media platforms such as Facebook, Twitter, and financial forums. These channels of communication contribute to heightened stock market volatility as they often reflect the psychological inclinations of individuals. When considering human sentiment, the landscape becomes intricate and multifaceted. For instance, on 27 January 2023, the Nepalese Supreme Court’s decision to invalidate the election of Rabi Lamichhane (the former deputy prime minister and home minister of Nepal) to the House of Representatives impacted investor sentiment, resulting in an 88.67 point or 4.06 percent drop in the Nepal Stock Exchange (NEPSE) index between 29 January and 2 February, see https://thehimalayantimes.com/business/political-uncertainty-weighs-on-nepse (The Himalayan). Similarly, a tweet by Elon Musk announcing Tesla’s acceptance of Bitcoin as payment on 24 March 2021 caused a 5.2% increase in Bitcoin’s stock price, see https://www.bloomberg.com/news/articles/2021-03-24/you-can-now-buy-a-tesla-with-bitcoin-elon-musk-says?embedded-checkout=true (Bloomberg.com). Furthermore, President Donald Trump’s tweet on 5 January 2017 threatening to impose heavy taxes on Toyota Motor for manufacturing Corolla cars in Mexico led to a significant decline in Toyota’s stock price (Ge et al. 2017, 2018). Similarly, a series of tweets by President Trump on August 1, 2019, regarding tariffs on Chinese goods resulted in a drop in stock prices, with the Dow Jones Industrial Average closing 98.41 points lower and the S&P 500, losing 0.7% by the end of the day, see https://www.cnbc.com/2019/08/02/stock-market-dow-futures-slightly-lower-after-trumps-tariff-threat.html (CNBC).
Numerous research articles have been released employing different machine learning models, showcasing a spectrum of assertions regarding their accuracy and robustness (Joshi 2023; Tang et al. 2024; Zhao 2021). Each new publication highlights the accuracy and robustness of its model with enthusiasm. However, their implementation approaches, operational frameworks, underlying assumptions, feature sets, and data origins vary considerably, making an impartial comparison between previously published works utilizing identical models for predicting stock index price movements unfeasible. Additionally, there is a noticeable gap in the literature regarding a comprehensive comparative examination of predicting stock price movements exclusively through unstructured data, such as news headlines or social media posts.
In this research, LR, SVM, RF, XGBoost, and ANN machine learning models are evaluated within a standardized framework, employing uniform conditions and relying solely on financial news headlines as input. Access to financial news from developing nations like Nepal is constrained to a few media sources. However, given the consistency in sentiment analysis of news affecting stock markets across certain periods, it is logical to choose data from developing nations to align with this study’s objectives.
Our complete vision to achieve the stated goal can be conceptualized from the broader spectrum via the schematic diagram in Figure 1. The proposed study uses close price and financial news data to build the model. We calculate the movement direction of the closing price and the sentiment score of news headlines. Subsequently, the data undergo normalization via the min-max technique. LR, SVM, RF, XGBoost, and ANN models are then created using financial news data as the input. Following the tuning of hyperparameters, the ultimate model forecasts the movement direction of the stock market index’s closing price for the subsequent day. Finally, the accuracy and robustness of the proposed model are evaluated using four distinct performance metrics: sensitivity, specificity, accuracy, and area under the receiver operating characteristic (ROC) curve (AUC).
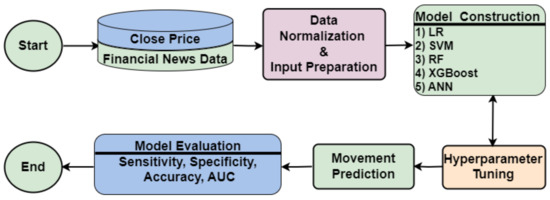
Figure 1.
Schematic diagram of the proposed research framework.
The primary contributions of this research encompass the following: (a) Addressing the core inquiry. Given uniform circumstances, which model—LR, SVM, RF, XGBoost, or ANN—is the optimal selection for predicting stock price movement direction when utilizing news headlines as the sole input? (b) Identifying the sentiment analyzer that exhibits optimal alignment with the machine learning models. (c) Executing a sequence of statistical hypotheses to confirm the experiment’s reliability.
The remainder of this paper is structured as follows: Section 2 delves into the related work within this domain. Section 3 provides a concise overview of the machine learning models. Standard assessment metrics are explained in Section 4. Section 5 discusses the experimental design, encompassing data preprocessing and partitioning, the hyperparameter tuning process, model comparisons, and subsequent statistical analysis. Section 6 explains the ethics and implications of the subject area. Finally, Section 7 provides the conclusion and future work followed by acknowledgments and the list of references.
2. Related Work
In recent years, there has been significant growth in the research focusing on the stock price movements of diverse financial sectors. Both academic scholars and industry practitioners have dedicated considerable efforts to forecasting future movements of the stock market index or its returns and developing financial trading strategies to capitalize on these forecasts (Chen et al. 2003; Kara et al. 2011). This section focuses on reviewing prior studies that have utilized machine learning algorithms for predicting stock price movements.
Wang (2014) compared PCA-SVM, a hybrid model combining principal component analysis (PCA) and a support vector machine (SVM), with four other machine learning algorithms: SVM, an artificial neural network (ANN), random walk (RW), and a PCA-ANN, using fundamental data to predict market index and stock price direction. The study encompassed empirical research on the Korean Composite Stock Price Index (KOSPI), Hang Seng Index (HSI), and their constituent stocks, demonstrating notably high hit ratios for the PCA-SVM in predicting individual stock movements. Similarly, Kara et al. (2011) investigated ANN and SVM models for predicting movement direction in the Istanbul Stock Exchange National 100 Index, with the ANN showing significantly better average performance than the SVM. Meanwhile, Khoa and Huynh (2022) conducted a comparison of a support vector machine, artificial neural networks, and logistic regression models in predicting the VNI30 index. Ultimately, the SVM emerged as the most effective model. Moreover, Huang et al. (2005) evaluated an SVM’s performance in forecasting the NIKKEI 225 index movement against other methods, with the SVM outperforming other classification techniques. Additionally, Ballings et al. (2015) compared ensemble methods against single classifier models for stock price prediction, with random forest emerging as the top-performing algorithm. These studies collectively highlight the efficacy of various machine learning approaches in predicting stock market movements across different indices and markets.
The study by Ismail et al. (2020) introduced a hybrid method combining logistic regression, artificial neural networks, support vector machines, and random forest with persistent homology to enhance prediction performance, focusing on three stock prices from the Kuala Lumpur Stock Exchange. Their findings indicated that employing machine learning methods with persistent homology led to improved prediction accuracy. Similarly, Ren et al. (2018) integrated sentiment analysis into a support vector machine-based model, achieving a notable increase in forecasting accuracy for the Shanghai Stock Exchange (SSE) 50 Index. In another study, Qiu and Song (2016) investigated the predictive capability of a hybrid model incorporating an optimized artificial neural network with genetic algorithms for the Nikkei 225 index, demonstrating enhanced forecast accuracy through proper input variable selection. Meanwhile, Imandoust and Bolandraftar (2014) compared decision tree, random forest, and naïve Bayes for predicting movement direction in the Tehran Stock Exchange index, with the decision tree model outperforming the others. Additionally, Chandola et al. (2023) proposed a hybrid deep learning model called Word2Vec-LSTM, which integrates Word2Vec and long short-term memory (LSTM) algorithms. This model was designed for forecasting stock market prices using financial time series and news headlines. Their study demonstrated enhanced accuracy compared to prior models, highlighting the temporal influence of news headlines on investor behavior.
In their study, Ampomah et al. (2020) compared various tree-based ensemble machine learning models, including random forest, extreme gradient boosting, bagging classifier, AdaBoost, extra trees, and a voting classifier, for predicting stock price movements across eight different stocks from the NYSE, NASDAQ, and NSE exchanges. They utilized forty technical indicators grouped into momentum, volume, and price transform as input features and assessed the models’ performance using Kendall’s W test of concordance. Their findings indicated that the extra tree model outperformed the others. In their endeavor to predict the price trends of the S&P 500 stock market index, Fazlija and colleagues (Fazlija and Harder 2022) utilized financial news headlines and moving averages as primary inputs. They employed pretrained transformer networks to compute sentiment scores. The results derived from the random forest classifier emphasized that news headlines stand out as the most significant predictor in forecasting stock price movements. Additionally, Rustam et al. (2018) compared support vector machines (SVMs) and fuzzy kernel C-means (FKCMs) for predicting Indonesian stock market movement, finding that SVMs with trend-based technical indicators outperformed other models. Meanwhile, Kim et al. (2020) investigated the use of effective transfer entropy (ETE) as a market explanatory variable, showing its efficacy in improving prediction performance when integrated into logistic regression, multilayer perceptron, random forest, extreme gradient boosting, and long short-term memory network models. Moreover, Kim et al. (2020) proposed a deep stock trend prediction neural network (DSPNN), leveraging desensitized transaction records and public market information to predict stock price trends, with experiments demonstrating its superior performance over random forest, AdaBoost, and long short-term memory models.
In their paper, Zhang et al. (2021) developed a convolutional neural network called FA-CNN, integrating a deep factorization machine and attention mechanism to enhance feature learning for predicting stock price movement. Their model outperformed competing models such as long short-term memory (LSTM), hybridization of LSTM and deep factorization machines (DeepFM), a convolutional neural network based on an attention mechanism (ATT-CNN), and a multifilter neural network (MFNN). Similarly, Zhao and Yang (2023) proposed SA-DLSTM, a hybrid model combining an emotion-enhanced convolutional neural network (ECNN), a denoising autoencoder (DAE), and LSTM, which demonstrated superior prediction accuracy compared to alternative models including a wavelet PCA neural network (WPCA-NN), wavelet neural network (WNN), and hybridization of random forest and LSboost (LS_RF) when applied to the Hang Seng Index. Additionally, Zhang et al. (2021) introduced a DBN-LSTM (fusion of deep belief network and LSTM) model for predicting stock price movements, which outperformed multilayer perceptron (MLP) and traditional LSTM when tested on data from the Shanghai and Shenzhen Stock Exchanges. Furthermore, Kumar et al. (2022) proposed a generative adversarial network (GAN)-based model for forecasting stock markets, which showed improved performance over LSTM when evaluated using data from some companies. Moreover, Gao et al. (2020) examined the performance of MLP, LSTM, CNN, and uncertainty-aware attention (UA) in predicting stock market prices across different market types, with UA demonstrating the best performance, particularly in developed financial markets.
Shahi et al. (2020) explored whether incorporating financial news sentiments could enhance stock price predictions using LSTM and GRU models. Using historical data from Nepal’s Agricultural Development Bank Limited (ADBL) and financial news headlines, they found that including financial news sentiments as input features significantly improved the performance of both models. Similarly, Kunwar and Khati (2023) conducted a comparative analysis of the effectiveness of technical indicators in predicting the stock market, using LSTM neural networks. Their findings indicated that technical indicators combined with fundamental and sentimental data yielded more effective results than using fundamental and sentimental data alone.
Prasad and Kadariya (2022) examined the benefits of global diversification by analyzing the differing behaviors of the Nepalese and US stock markets, using descriptive and causal-comparative research designs and content analysis of newspaper headlines classified as ‘bad’, ‘good’, or ‘informational’. Their regression models revealed that ‘bad’ news negatively impacts stock returns, ‘good’ news has a positive effect, and ‘informational’ news has an inconsistent effect, with ‘bad’ news having the strongest impact. Illia et al. (2021) analyzed public sentiment towards an application using Twitter data collected from 31 August to 7 September 2021 during vaccine data leaks associated with the PeduliLindung app, employing TextBlob and VADER libraries, and found VADER performed better due to its social media lexicon. Abiola et al. (2023) analyzed 1,048,575 tweets with the hashtag ‘COVID-19’, using a Twitter tokenizer, TextBlob for text mining, VADER for sentiment analysis, and latent Dirichlet allocation for topic modeling, finding 39.8% positive, 31.3% neutral, and 28.9% negative sentiments with VADER and 46.0% neutral, 36.7% positive, and 17.3% negative with TextBlob. Nemes and Kiss (2021) performed sentiment analysis on company news headlines using BERT, VADER, TextBlob, and a recurrent neural network (RNN), finding BERT and the RNN more accurate at identifying stock value change timings by comparing sentiment results with stock changes, noting significant differences in the impact of emotional values across models.
In summary, the extensive range of methodologies and models explored in the cited studies reflects the ongoing pursuit of refined and accurate stock market prediction. From hybrid machine learning approaches to sentiment analysis integration and deep learning architectures, the diverse strategies underscore the multifaceted nature of forecasting in financial markets, offering insights and advancements that pave the way for more effective investment decision making in the future.
3. Modeling Approach
3.1. Logistic Regression (LR)
Logistic regression (LR) is a widely employed statistical technique for representing binary data. As part of the generalized linear models category, LR is a potent method for categorizing binary outcome variables using a collection of independent variables. Extensive studies have‘ illustrated its effectiveness and application across a range of disciplines, encompassing medicine, social sciences, and economics (DeMaris 1995; Field 2009; Kleinbaum et al. 2002; LaValley 2008; Menard 2002; Pampel 2020; Sperandei 2014; Wright 1995).
Consider a scenario with a dataset containing n observations and k features, represented as an input matrix X. Alongside this, there is a binary outcome vector Y where each response for every input can be either 1 or 0. Based on these outcomes, we categorize instances into either a positive or a negative class. Assuming instances with are positive and those with are negative, we can utilize the LR model with a sigmoid activation function to classify an instance as positive or negative. The sigmoid function is defined as follows:
where is a vector of parameters and is estimated by the maximum likelihood method. Instead of supplying the exact values 0 and 1, the fitted model provides the probabilistic values that lie between 0 and 1. So, the predicted values are assigned 1 if is greater than or equal to some threshold and 0 otherwise.
LR is beneficial for stock prediction because it is well suited for scenarios where the prediction task can be framed as binary classification, such as forecasting whether a stock price will rise or fall. Its simplicity and interpretability are advantageous for analyzing historical data and identifying key features that influence stock price movements. Furthermore, logistic regression provides probability estimates for outcomes, enabling investors to make informed decisions based on the likelihood of specific stock price changes (Dutta et al. 2012; Gong and Sun 2009). Its straightforward nature makes logistic regression a widely utilized tool in various fields, including medicine, biology, and epidemiology (Abreu et al. 2009; Binder et al. 2019; Kleinbaum et al. 1982; Lemon et al. 2003; Peterson et al. 1995; Stoltzfus 2011; Thompson et al. 2018). The authors (Budhathoki et al. 2023; Christodoulou et al. 2019; Jiang et al. 2021; Musa 2013) have shown that LR competes effectively with other models.
3.2. Support Vector Machine (SVM)
The support vector machine (SVM) is a highly utilized, robust, and potent machine learning algorithm known for its compelling features and impressive practical performance across diverse domains. Initially introduced by Vapnik and Chervonenkis in 1963, the SVM is versatile, serving purposes in both classification and regression tasks. In its classification role, the SVM is alternatively referred to as the support vector classifier (SVC) (Boser et al. 1992; Chervonenkis 2013; Durgesh and Lekha 2010; Li et al. 2009; Vapnik 1995).
The SVC predicts the class for each input in the range of 1 to p by identifying a hyperplane that separates the different types of data. This hyperplane represents a flat subspace with a dimension of within a p-dimensional space. The input matrix X is structured as an matrix, where n denotes the number of observations and p represents the number of features. The binary outcome vector Y belongs to either of the classes . The SVC model predicts the class by determining the hyperplane described by
where is a vector of parameters and is estimated by an optimization method with the property if and if . The SVC provides various kernels like linear, radial, polynomial, and more, along with hyperparameters such as cost and gamma. These elements collaborate to manage the model’s performance and ensure accurate outcomes. For example, the SVC’s linear kernel is effective when the class boundary is linear. Furthermore, adjusting the tuning of hyperparameters is crucial for balancing bias and variance trade-offs. Improper tuning can lead to underfitting (with small parameter values) or overfitting (with large parameter values) the data (Claesen and De Moor 2015; Géron 2019; Wang et al. 2018).
SVCs are advantageous for predicting stock price movement due to their ability to handle nonlinear relationships and high-dimensional data. SVCs work by identifying the optimal hyperplane that separates data points into different classes, making them suitable for classification tasks such as predicting whether a stock price will rise or fall. They have demonstrated superior performance compared to various other machine learning models, such as artificial neural networks, across a range of fields including pattern recognition, text categorization, biomedicine, and financial regression (Byvatov et al. 2003; Dahal and Gautam 2020; Doniger et al. 2002; Shao et al. 2014).
3.3. Random Forest (RF)
Random forest (RF) is an ensemble learning method that combines multiple decision trees to improve the accuracy and robustness of predictions (Seni and Elder 2010). In an RF model, a collection of decision trees is trained on random subsets of the training data and random subsets of features. During prediction, each tree in the forest independently makes a prediction, and the final output is determined by aggregating the predictions of all the trees, typically by taking the mode (for classification) or average (for regression) of the individual predictions. This ensemble approach helps to mitigate overfitting and increases the model’s generalization ability, making RF a powerful algorithm for various machine learning tasks (Biau and Scornet 2016; Rigatti 2017).
Analytically, RF can be represented as a weighted sum of decision trees, where each tree contributes to the final prediction based on its individual performance and the correlation between trees. The randomness introduced in the training process, such as bootstrapping the data and selecting random subsets of features for each tree, promotes diversity among the trees, reducing the likelihood of overfitting. Moreover, RF provides a measure of feature importance, indicating the contribution of each feature to the model’s predictions. This insight helps in feature selection and understanding the underlying patterns in the data (Ahmad et al. 2017; Chen et al. 2018; Kocev et al. 2013).
RF is an excellent model for predicting stock price movement direction due to its ability to handle large datasets with high dimensionality and its robustness to overfitting. By constructing multiple decision trees and aggregating their predictions, RF captures complex patterns and interactions within the data that may not be apparent with simpler models. This ensemble method enhances predictive accuracy and generalization by averaging out the biases of individual trees, making it particularly effective in the noisy and volatile environment of stock markets. Additionally, RF can handle missing values and maintain performance even when dealing with unbalanced datasets, which are common challenges in financial data analysis (Hatwell et al. 2020; Menze et al. 2009; Pereira et al. 2018; Statnikov et al. 2008; Yin et al. 2023; Zien et al. 2009).
3.4. Extreme Gradient Boosting (XGBoost)
Extreme gradient boosting (XGBoost) is a popular machine learning model that employs gradient-boosted decision trees and is recognized for its scalability and distribution functionalities. It is extensively utilized for regression, classification, and ranking tasks because of its capacity to execute parallel tree boosting, which is more effective than sequential tree boosting. XGBoost utilizes supervised learning, decision trees, ensemble learning, and gradient boosting, establishing it as a dependable and precise library for a wide range of applications (Bekkerman et al. 2011; Chen and Guestrin 2016).
The design of XGBoost employs a step-by-step approach to gradually minimize residuals from preceding trees in order to train subsequent trees until reaching a satisfactory level. The ultimate predicted outcome is derived by aggregating the outcomes from all trees within the ensemble. This iterative procedure enhances the model’s predictive capability and enables it to capture intricate data relationships more effectively. The mathematical representation for XGBoost is expressed in the following equation:
In this context, F represents the domain of the classification tree, and denotes a specific tree. Thus, signifies the outcome generated by tree k for input , while represents the predicted value for the i-th instance of . A detailed mathematical derivation of this model can be found in the research article by Chen and Guestrin (2016).
XGBoost is a highly effective model for predicting stock price movement direction due to its advanced handling of overfitting and high predictive accuracy. XGBoost leverages gradient boosting techniques to iteratively improve model performance by focusing on minimizing errors of previous models, resulting in a robust ensemble of weak learners that excel in capturing complex patterns within financial data. Its built-in regularization mechanisms prevent overfitting, ensuring that the model generalizes well to unseen data. Moreover, XGBoost’s ability to handle missing values, its scalability to large datasets, and its feature importance metrics make it particularly suited for the dynamic and intricate nature of stock market predictions (Dey et al. 2016).
3.5. Artificial Neural Network (ANN)
Artificial neural networks (ANNs), also known as neural networks (NNs), are computational systems inspired by the biological neural networks found in animal brains (Bland et al. 2020; Moayedi et al. 2020). These systems consist of layers of interconnected neurons, with adjustable weights facilitating connections between different layers (Dahal et al. 2021; Mohandes et al. 1998). An ANN typically comprises three key components: an input layer, one or more hidden layers, and an output layer. Various parameters such as weights, bias, optimizer, learning rate, number of hidden layers, number of neurons per hidden layer, and batch size are integral to an ANN’s architecture. During training, certain parameters like weights and bias are optimized, while others such as the optimizer, learning rate, number of neurons per hidden layer, and batch size must be carefully chosen using validation data. Additionally, selecting an appropriate activation function significantly impacts the model’s accuracy. The most commonly used activation functions include the sigmoid (Nwankpa et al. 2018; Turian et al. 2009), rectified linear unit (Nair and Hinton 2010), and softplus (Glorot et al. 2011).
A diagram representing a typical fully connected neural network is shown in Figure 2, consisting of n predictors, one hidden layer with m neurons, and an output layer with one neuron. In the input layer, the n predictors are denoted by an input vector . and are weight matrices of dimensions and , respectively. and represent biases, while f and g are activation functions. The output of the hidden layer, represented by the vector , serves as the input for the output layer. Finally, the network’s final output is given by .
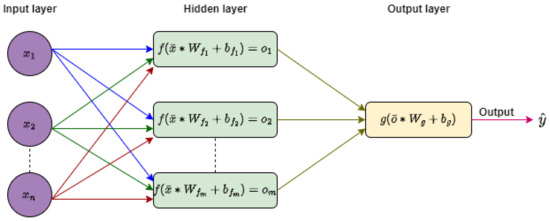
Figure 2.
General architecture of neural network with n predictors, a single hidden layer with m neurons, and an output layer.
ANNs are an excellent model for predicting stock price movement direction due to their ability to learn and model complex, nonlinear relationships within financial data (Bhandari et al. 2022; Dahal et al. 2023; Pokhrel et al. 2022, 2024). ANNs, inspired by the human brain, consist of interconnected layers of nodes that can automatically detect intricate patterns and interactions in the data. This capability allows ANNs to capture underlying trends and signals in stock price movements that traditional models might miss (Bhandari et al. 2022; Duda et al. 1973; Zhang 2000). Additionally, with the advent of deep learning, neural networks can handle large datasets and leverage vast amounts of historical market data, improving their predictive power. The flexibility and adaptability of ANNs make them particularly well suited for the highly dynamic and volatile nature of stock markets. Neural networks have been successfully utilized in various real-world classification tasks, including medical diagnosis, crime classification, fault detection, and speech recognition, showcasing their superiority over classical models (Baxt 1990, 1991; Bourlard and Morgan 1993; Burke 1994; Burke et al. 1997; Dahal et al. 2020; Dahal and Gautam 2020; Hoskins et al. 1990; Lippmann 1989).
4. Performance Measures
NEPSE movement direction predictions from the constructed models are assessed through the four different performance metrics: sensitivity, specificity, accuracy, and area under the receiver operating characteristic (ROC) curve (AUC). These metrics help determine the best model in terms of accuracy and reliability (Ampomah et al. 2020; Ballings et al. 2015; Basak et al. 2019). The elements of the confusion matrix are utilized to find three important metrics: sensitivity, specificity, and accuracy. The analytical form of a confusion matrix is defined in Table 1.

Table 1.
Confusion matrix.
Sensitivity represents the proportion of actual positive cases (NEPSE moving upward) that are correctly predicted as positive. Specificity represents the proportion of actual negative cases (NEPSE moving downward) that are correctly predicted to be negative. Accuracy represents the proportion of cases that are predicted accurately (predicted positive for NEPSE moving upward and predicted negative for NEPSE moving downward). The analytical form of these metrics is defined by
Sensitivity and specificity are inversely proportional to each other. The receiver operating characteristic (ROC) curve is commonly used to characterize the sensitivity/specificity trade-offs for a binary classifier. The ROC curve is obtained by plotting the false-positive rate (1-specificity) on the x axis against the sensitivity on the y axis at various threshold settings. Area under the ROC curve (AUC) is one of the most important metrics to measure the performance of the model. Its value lies between 0 and 1. A model is said to be excellent if its AUC is close to 1. The higher the AUC, the better the model, while the lower the AUC, the worse the model. The best model is determined by prioritizing statistics in the following order: AUC (first priority), accuracy (second priority), sensitivity, and specificity (equal and lower priority compared to the other two).
5. Experimental Design
This study compared the performance of LR, SVM, RF, XGBoost, and ANN models in NEPSE movement direction prediction. The experiment was divided into five phases: setting up the environment, data description and input preparation, data normalization and partition, hyperparameter tuning, model comparison, and statistical analysis, as illustrated in Figure 3.
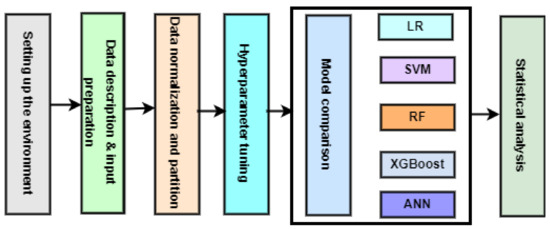
Figure 3.
Experimental design.
5.1. Setting Up the Environment
Table 2 summarizes the computational framework of the experiments. The experiments were conducted using the Python 3.6.0 programming environment, with the TensorFlow 2.x and Keras 2.x APIs. Furthermore, the machine configuration and employed architecture used in the experiments are listed in the table.

Table 2.
Computing environmental setup.
5.2. Data Description and Preparation
The Nepal Stock Exchange (NEPSE) serves as the primary stock market in Nepal, facilitating the trading of securities and promoting investment opportunities within the country. Established in 1993 under the Securities Exchange Act, NEPSE plays a crucial role in fostering economic growth and development by providing a platform for companies to raise capital and for investors to participate in the financial markets. As the sole stock exchange in Nepal, NEPSE oversees the listing and trading of various financial instruments, including stocks, bonds, and mutual funds, contributing to the country’s financial infrastructure and market stability (Shrestha and Lamichhane 2021, 2022).
The close price of the NEPSE index and the financial news headlines from 1 January 2019 to 31 December 2023 were scraped from the portal Share Sansar (www.sharesansar.com) using a web crawler. Share Sansar is a prominent online platform in Nepal dedicated to stock market news and analysis, providing a wealth of data, including stock prices, market trends, company financials, and news articles.
This study aimed to perform a comparative analysis of the performance of machine learning models in predicting the next day’s movement direction of the NEPSE index, the sole stock exchange of Nepal. Figure 4 illustrates the original time series data of the index closing prices from 1 January 2019 to 31 December 2023. The time span covers both bear and bull markets. The vertical dotted line in the graph indicates the maximum close price, which occurred on 9 September 2021 just before the spread of COVID-19 in Nepal. The time span was selected intentionally to train the models to capture the patterns in both normal and volatile market situations and then to test their performance in similar environments. We defined the direction, a dichotomous variable, using the following equation:
where represents the closing price of the current day, while represents the closing price of the following day. Over the five years from the beginning of 2019 through the end of 2024, there were 551 instances of the NEPSE moving upward (positive direction) and 584 instances of it moving downward (negative direction).
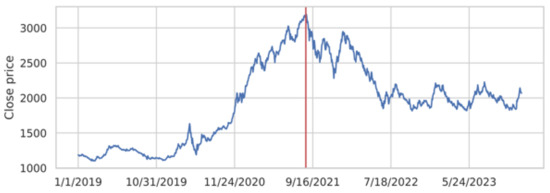
Figure 4.
NEPSE closing price between 1 January 2019 to 31 December 2023.
Before computing sentiment scores, raw text data should undergo preprocessing steps such as removing stop words, handling punctuation, and stemming or lemmatization to enhance the accuracy and effectiveness of sentiment analysis algorithms. We cleaned up the raw text data (news headlines) using the functions , , , , , , stopwords.words(‘english’), , and sequentially, which were extracted from the library (Bird 2006).
Now, the text data were ready (clean) for sentiment analysis. Valence Aware Dictionary and Sentiment Reasoning (VADER) (Hutto and Gilbert 2014) and TextBlob (Loria 2018) are the most common and reliable tools to compute the sentiment score (Aljedaani et al. 2022; Al-Natour and Turetken 2020; Bonta et al. 2019). VADER is a pretrained model that analyzes people’s opinions, sentiments, evaluations, attitudes, and emotions via computational treatment regarding polarity (positive/negative) and intensity (strength) in text. It relies on an English dictionary that maps lexical features to their semantic orientation as positive or negative (Liu 2010). TextBlob is a powerful and user-friendly Python library for natural language processing (NLP). Built on the (Bird 2006) and Pattern libraries, TextBlob simplifies the complexities of working with textual data by providing a simple API for common NLP tasks. It offers a range of functionalities, including part-of-speech tagging, noun-phrase extraction, sentiment analysis, classification, translation, and more. TextBlob’s strength lies in its ease of use, making it an excellent choice for beginners and researchers alike. With its straightforward syntax and extensive documentation, TextBlob enables developers to quickly implement NLP features in their applications without the need for extensive background knowledge in linguistics or machine learning.
Both tools (VADER and TextBlob) have their strengths and weaknesses, and the choice between them depends on factors such as the specific use case, the type of text data being analyzed, and the desired level of accuracy and flexibility. After preprocessing, the data were fed into TextBlob and VADER to determine their corresponding sentiment scores. We labeled the sentiment score from TextBlob as TextBlob sentiment data and the sentiment score from VADER as VADER sentiment data. This labeling will help readers easily identify and understand the source of the data.
The news data contained a large amount of news published in a single day. So, we computed the average news score for each day. The NEPSE runs from Sunday to Thursday, but financial news headlines are published seven days a week. We believe that news on Thursday and the weekend has an impact on the stock price on Sunday (the first trading day of the next week). Therefore, we computed the mean sentiment score of Thursday, Friday, and Saturday, which we used to predict the movement direction of the NEPSE index for Sunday. Finally, the sentiment scores for the financial news data were aligned with the movement direction of the index date, as shown in Figure 5.
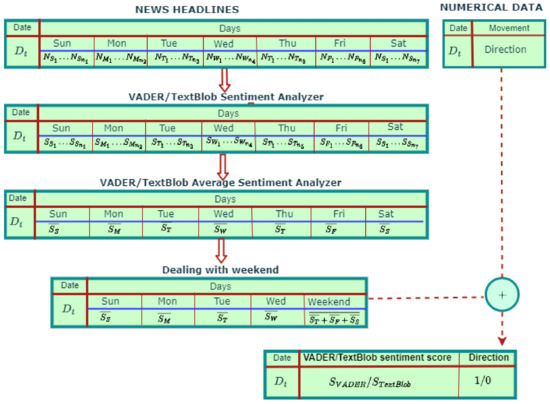
Figure 5.
Concatenation of movement direction and news sentiment score.
5.3. Data Normalization and Partition
The range of values for input features can vary significantly, negatively impacting our results’ accuracy. Thus, we implemented a min-max normalization technique that scales each feature to the [0, 1] range. The mathematical formulation of the normalization procedure is defined as
where x is the original value and z is the normalized value of the input variable. Similarly, and are the minimum and the maximum values, respectively. The normalized data were split into training and test sets in a ratio of 4:1, with 908 observations for training and 227 for testing. Within the training set, 25% of the data were separated for validation (227 observations whenever needed), which corresponds to 20% of the total data.
5.4. Hyperparameter Tuning
A machine learning model is a mathematical model with several parameters that need to be learned from the data during the training process. However, there are some parameters, known as hyperparameters, that cannot be directly learned. These hyperparameters play a crucial role in shaping the performance and behavior of the machine learning models. Researchers commonly choose the hyperparameters based on some intuition, previous study, hit and trial, or cross validation before the actual training begins. These parameters exhibit their importance by improving the model’s performance such as its complexity or its learning rate. Models can have many hyperparameters, and finding their best combination can be treated as a search problem.
The standard LR contains no hyperparameter. On the other hand, an SVM is equipped with three hyperparameters: kernel, gamma, and C. The kernel defines the type of decision boundary the SVM will use, while adjusting gamma is crucial for controlling the SVM’s flexibility and avoiding overfitting. The regularization parameter C influences the trade-off between achieving a smooth decision boundary and accurately classifying the training data. Higher C values encourage the SVM to fit the training data more closely, while lower values promote a smoother decision boundary that generalizes better to new data. Balancing these hyperparameters is essential for optimizing SVM performance across different datasets and tasks.
These hyperparameters of the SVM were tuned by using the grid search algorithm of sklearn (Hao and Ho 2019). In the initial phase, we experimented with four possible kernels: linear, sigmoid, radial basis function (RBF), and polynomial (degree 3). For each kernel, we varied C and gamma between 1 and 51 and 0.01 to 1 with an increment of 1 and 0.01, respectively. For each possible combination of kernel, C, and gamma, the SVM was fitted using 10 cross-validation methods, and the results are presented in Table 3 and Table 4 for TextBlob sentiment data and VADER sentiment data, respectively. According to the findings presented in these tables, the most optimal hyperparameters for TextBlob sentiment data are as follows: a kernel of RBF, a C value of 1.0, and a gamma value of 0.5. For VADER sentiment data, the optimal settings of hyperparameters are a sigmoid kernel, a C value of 13, and a gamma value of 0.83. In order to enhance readability for the readers, these outcomes are highlighted within the tables.

Table 3.
List of best hyperparameters for support vector machine (SVM) with respect to kernels obtained using ten-fold cross validation on TextBlob sentiment data.

Table 4.
List of best hyperparameters for support vector machine (SVM) with respect to kernels obtained using ten-fold cross validation on VADER sentiment data.
Similar to the SVM, random forest (RF) is also equipped with hyperparameters. Three key hyperparameters in RF are n_estimators, max_depth, and max_leaf_nodes. The n_estimators parameter determines the number of trees in the forest, and a higher value generally leads to a more robust model but increases computational cost. Max_depth controls the maximum depth of each decision tree in the ensemble, regulating the complexity of individual trees. A deeper tree can capture more complex relationships in the data but may lead to overfitting. Finally, max_leaf_nodes limits the total number of terminal nodes or leaves in each tree, aiding in the prevention of overfitting by restricting the granularity of the tree structure. Tuning these hyperparameters allows practitioners to strike a balance between model complexity and generalization, tailoring the RF for optimal performance on diverse datasets.
These hyperparameters of RF were tuned by using the grid search algorithm of sklearn (Hao and Ho 2019). We varied n_ estimators, max_depth, and max_leaf_nodes between 1 and 101, 1 and 21, and 1 and 21 with an increment of 5, 2, and 2, respectively. For each possible combination of these hyperparameters, the RF was fitted using ten-fold cross-validation methods, and the results are presented in Table 5. Based on the results showcased in Table 5, the most optimal hyperparameters for TextBlob sentiment data are outlined as follows: max_depth = 3, max_leaf_nodes = 3, and n_estimators = 71. As for VADER sentiment data, the ideal hyperparameter settings are max_depth = 11, max_leaf_nodes = 11, and n_estimators = 6.

Table 5.
List of best hyperparameters for random forest classifier (RFC) obtained using ten-fold cross validation.
XGBoost, an efficient and scalable implementation of gradient boosting, boasts several critical hyperparameters that significantly impact its performance. The n_estimators hyperparameter determines the number of boosting rounds or trees to be built, affecting the overall complexity and predictive power of the model. The max_depth parameter controls the maximum depth of each tree, regulating the model’s capacity and potential for overfitting. The learning_rate, often denoted as eta, scales the contribution of each tree, influencing the step size during optimization. A smaller learning rate typically requires more boosting rounds but can enhance generalization. Lastly, the min_child_weight hyperparameter sets the minimum sum of instance weight needed in a child, impacting tree partitioning and addressing imbalances in the data. These hyperparameters collectively play a crucial role in fine-tuning the XGBoost algorithm for optimal performance, balancing model complexity and generalization across diverse datasets.
These hyperparameters of XGBoost were also tuned by using the grid search algorithm of sklearn (Hao and Ho 2019). In the initial phase, we experimented with four possible eta values: 0.0001, 0.001, 0.01, and 0.1. For each eta, we varied n_ estimators, max_depth, and min_child_weight between 1 and 101, 1 and 21, and 1 and 10 with an increment of 5, 2, and 2, respectively. For each possible combination of these four hyperparameters, the XGBoost was fitted using ten-fold cross-validation methods, and the results are presented in Table 6. According to the findings presented in Table 6, the most favorable hyperparameters for TextBlob sentiment data are delineated as follows: max_depth = 3, eta = 0.1, n_estimators = 21, and min_child_weight = 9. Meanwhile, for VADER sentiment data, the optimal hyperparameter configurations consist of max_depth = 13, eta = 0.1, n_estimators = 36, and min_child_weight = 5.

Table 6.
List of best hyperparameters for XGBoost classifier (XGBoost) obtained using ten-fold cross validation.
Hyperparameters play a crucial role in shaping the performance and behavior of a neural network model. The number of neurons in the hidden layer determines the model’s capacity to capture complex patterns in the data, with larger numbers potentially enabling better representation but also increasing the risk of overfitting. The learning rate influences the size of steps taken during the optimization process, affecting the convergence speed and stability of the model. Batch size determines the number of data points used in each iteration of training, impacting the efficiency and generalization ability of the network. The choice of optimizer, such as stochastic gradient descent (SGD) or Adam, affects how the model adjusts its weights to minimize the loss function. Finding the optimal combination of these hyperparameters is often a challenging task, requiring careful tuning to achieve optimal model performance.
Due to the small size of the data, a single hidden layer NN model was used. The rest of the hyperparameters of the network were tuned by using the grid search algorithm of sklearn (Hao and Ho 2019). In the initial phase, we constructed all possible combinations of hyperparameters. This includes five different optimizers (adam, rmsprop, adagrad, nadam, and adadelta); three different learning rates (0.1, 0.01, and 0.001); four options for batch sizes (8, 16, 32, and 64); and seven different possible values of neurons in the hidden layer (1, 5, 10, 15, 20, 25, and 50). Therefore, 5 × 3 × 4 × 7 = 420 possible choices were available for each model to identify its best combination. We then constructed a neural network architecture with an input layer, a hidden layer with relu activation, followed by a fully connected output layer with sigmoid activation. This network was fitted with all 420 possible combinations of the hyperparameters using ten-fold cross-validation methods, and the results are presented in Table 7. Based on the results displayed in Table 7, the best set of optimal hyperparameters for TextBlob sentiment data are as follows: # neurons = 50, eta = 0.1, optimizer = adam, and batch_size = 8. In contrast, for VADER sentiment data, the most favorable set of hyperparameters are as follows: # neurons = 25, eta = 0.001, optimizer = nadam, and batch_size = 8.

Table 7.
List of best hyperparameters for neural network (NN) obtained using ten-fold cross validation.
5.5. Model Comparison
The models LR, SVM, RF, and XGBoost were tested on the test dataset with their respective optimized hyperparameters obtained in Section 5.4 in place. The performance scores achieved by the models are presented in Table 8 for TextBlob sentiment data and Table 9 for VADER sentiment data, demonstrating the approaches’ effectiveness.

Table 8.
Model performance matrices obtained using test TextBlob sentiment data.

Table 9.
Model performance matrices obtained using test VADER sentiment data.
Once the hyperparameters of the NN model were tuned, the models were set with their corresponding optimized hyperparameters obtained in Section 5.4. The epochs were set to 500, and an early stopping criterion was implemented to address the consequences of underfitting and overfitting that can occur when training neural networks. It allowed us to specify a large number of epochs and stop training when the model’s performance stopped improving on the validation data (Brownlee 2018). Furthermore, a 10% dropout was implemented between the hidden and fully connected output layers to prevent overfitting. The binary cross entropy was used as the loss function during the training process. During the training of the ANN, the loss function behaved on the number of epochs, as illustrated in Figure 6. The model overfitted after 300 epochs on TextBlob sentiment data, whereas there was no further improvement after 250 epochs on VADER sentiment data.
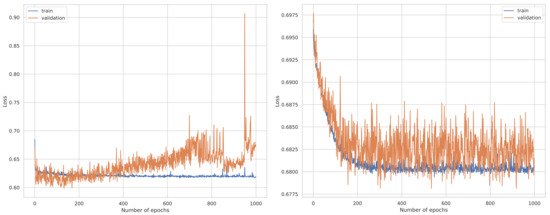
Figure 6.
Plot of loss function vs. the number of epochs on the TextBlob sentiment data on the left and VADER sentiment data on the right.
To address the stochastic behavior of the ANNs, we replicated each of the models 50 times, and the corresponding metrics were computed on the test dataset. The average metrics together with their respective standard deviation are presented in Table 8 for TextBlob sentiment data and Table 9 for VADER sentiment data.
The standard deviations of 0.0202, 0.0135, 0.0050, and 0.0032 on sensitivity, specificity, accuracy, and AUC in Table 8 are comparatively very small, which reveals the fact that the NN model looks consistent on the TextBlob sentiment data. On the other hand, the standard deviations of 0.3727 and 0.3028 on sensitivity and specificity in Table 9 are comparatively large, which reveals the fact that the NN model looks inconsistent on the VADER sentiment data.
The metrics of sensitivity, specificity, accuracy, and AUC of the models LR, SVM, RF, XGBoost, and ANN are provided in Table 8 for TextBlob sentiment data and in Table 9 for VADER sentiment data. These matrices are further visualized by the multiple bar plots in Figure 7.
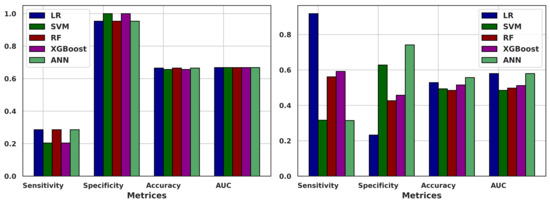
Figure 7.
Multiple bar plots of the metrics on the test dataset using ML models: TextBlob sentiment data on the left and VADER sentiment data on the right.
The sensitivity values provided (0.2857 for LR, 0.2041 for SVM, 0.3469 for RF, 0.3163 for XGBoost, and 0.2806 for ANN) for the TextBlob sentiment data represent the ability of each machine learning model to correctly identify the proportion of the actual positive cases (NEPSE moving upward) that were correctly predicted as positive. A higher sensitivity indicates a better ability to detect positive instances. In this comparison, the RF model had the highest sensitivity of 0.3469, followed by XGBoost with a sensitivity of 0.3163. LR and ANN had sensitivities of 0.2857 and 0.2806, respectively, and SVM showed the lowest sensitivity of 0.2041. On the other hand, for the VADER sentiment data, the LR model had the highest sensitivity of 0.9184, followed by XGBoost with a sensitivity of 0.5918. RF and SVM had sensitivities of 0.5612 and 0.3163, respectively, while ANN showed the lowest sensitivity at 0.3143. These sensitivity values are crucial metrics for evaluating the performance of classification models, especially in scenarios where correctly identifying positive cases is important.
The specificity values provided (0.9535 for LR, 1.0000 for SVM, 0.9147 for RF, 0.9302 for XGBoost, and 0.9603 for ANN) for the TextBlob sentiment data represent the ability of each machine learning model to correctly identify the proportion of the actual negative cases (NEPSE moving downward) that were correctly predicted as negative. A higher specificity indicates a better ability to detect negative instances. In this comparison, the SVM model had the highest specificity of 1.0, indicating perfect performance in identifying negative cases. ANN followed closely with a specificity of 0.9603, while LR, RF, and XGBoost had specificities of 0.9535, 0.9147, and 0.9302, respectively. On the other hand, for the VADER sentiment data, the ANN model had the highest specificity of 0.7414, followed by SVM with a specificity of 0.6279. XGBoost and RF had a specificity of 0.4574 and 0.4264, respectively, while LR showed the lowest specificity at 0.3143. These specificity values are important metrics for evaluating the overall accuracy and performance of classification models, especially in scenarios where correctly identifying negative cases is crucial.
The accuracy values provided (0.6652 for LR, 0.6564 for SVM, 0.6696 for RF, 0.6652 for XGBoost, and 0.6669 for ANN) for TextBlob data represent the overall correctness of predictions made by each machine learning model. A higher accuracy indicates better overall performance in correctly predicting both positive (NEPSE moving upward) and negative (NEPSE moving downward) cases. In this comparison, the RF model had the highest accuracy of 0.6696, followed closely by the ANN with an accuracy of 0.6669. LR and XGBoost both had accuracies of 0.6652, while SVM showed the lowest accuracy at 0.6564. On the other hand, for the VADER sentiment data, the ANN model had the highest accuracy of 0.5572, followed by LR with an accuracy of 0.5286. XGBoost and SVM had accuracies of 0.5154 and 0.4934, respectively, while RF showed the lowest accuracy of 0.4846. These accuracy values are fundamental metrics for assessing the general effectiveness and reliability of classification models in making correct predictions across different classes.
For the TextBlob sentiment data, in the provided AUC values (0.6682 for LR, 0.6682 for SVM, 0.6772 for RF, 0.6942 for XGBoost, and 0.6682 for ANN), the differences between LR, SVM, and ANN were negligible as they all had the same AUC score. However, RF and XGBoost stood out with higher AUC values. XGBoost led with an AUC of 0.6942, indicating superior discriminative ability, while RF followed closely with an AUC of 0.6772. On the other hand, for the VADER sentiment data, the ANN and LR model had the highest AUC of 0.5800, followed by XGBoost with an AUC of 0.5122. RF had an AUC of 0.4977, while SVM showed the lowest AUC of 0.4816. These AUC values are critical metrics for evaluating the overall performance and discriminative power of classification models in binary classification tasks.
Comparing the ROC curves for TextBlob sentiment data depicted in Figure 8 (left) for the machine learning models LR, SVM, RF, XGBoost, and ANN with their associated AUC values offers valuable insights into their discriminatory capabilities. The ROC curves visually portray the balance between the true-positive rate (sensitivity) and false-positive rate (1-specificity) across varying threshold settings. Models with higher AUC values typically showcase ROC curves that approach the top-left corner, indicating superior discrimination between positive and negative classes. In this assessment, XGBoost emerges as the standout performer with the highest AUC of 0.6942, likely corresponding to a ROC curve close to the ideal top-left corner. RF follows closely with an AUC of 0.6772, signaling slightly lesser but still effective discriminatory performance. LR, SVM, and ANN exhibit similar AUC values of 0.6682, reflecting comparable discriminatory power evident in their ROC curves that lie closer to the diagonal line. Additionally, comparing the ROC curves for VADER sentiment data in Figure 8 (right) for the same models with their AUC values further elucidates their discriminatory prowess, where LR and ANN show moderate discrimination with AUC values of 0.58, while SVM and RF demonstrate weaker discriminatory performance with AUC values of 0.4816 and 0.4977, respectively. XGBoost falls between these extremes with an AUC of 0.5122, indicating a moderate level of discrimination compared to the other models.
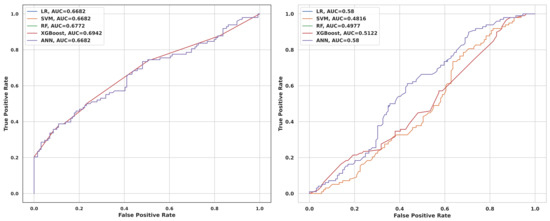
Figure 8.
Left: ROC curves of the five models for TextBlob data. Right: ROC curves of the five models for VADER sentiment data.
Moreover, although all five models exhibit greater sensitivity when applied to VADER sentiment data, they excel in terms of specificity, accuracy, and AUC when operating on TextBlob sentiment data. This suggests that the overall performance of all five models is superior when analyzing TextBlob sentiment data as opposed to VADER sentiment data.
5.6. Statistical Analysis
To evaluate the reliability of the models’ outcomes, a statistical analysis was conducted to determine significant performance differences among the five models. This analysis followed a hypothesis testing approach for two populations, as recommended by the authors (Agresti and Caffo 2000; Dahal and Amezziane 2020; Wald and Wolfowitz 1940). The Wald test, renowned for its simplicity and widespread use, was utilized to compare population proportions between the models. The test aims to detect meaningful differences in proportions between groups or populations, with statistical significance determined through a p-value derived from the standard normal distribution. In this study, the Wald method’s effectiveness was contingent upon a sufficiently large sample size (no. of observations on test data = 227), ensuring that the product of the sample size, accuracy percentage, and its complement is at least 10. The null hypothesis () posits that model prediction accuracies are not significantly different, while the alternative hypothesis () suggests the opposite. The results of multiple pairwise comparisons using the Wald test, along with corresponding p-values, are presented in Table 10 and Table 11 for TextBlob sentiment data and in Table 12 and Table 13 for VADER sentiment data.

Table 10.
p-values of the Wald test for pairwise comparisons within the models for accuracy on TextBlob sentiment data.

Table 11.
p-values of the Wald test for pairwise comparisons within the models for AUC on TextBlob sentiment data.

Table 12.
p-values of the Wald test for pairwise comparisons within the models for accuracy on VADER sentiment data.

Table 13.
p-values of the Wald test for pairwise comparisons within the models for AUC on VADER sentiment data.
Examining Table 10 and Table 11, we find no evidence to reject the null hypothesis, as none of the p-values are below the 0.05 threshold. This lack of significant p-values indicates insufficient evidence to claim significant differences in model performance. Put simply, it is reasonable to conclude that all five models exhibit similar accuracy and AUC on TextBlob sentiment data. Similar conclusions are drawn from Table 12, suggesting statistical similarity in accuracy across the models on VADER sentiment data. However, Table 13 presents mixed results; specifically, LR versus SVM and SVM versus ANN show p-values below 0.05. This signifies statistically significant differences in AUC performance between these pairs on VADER sentiment data, while the remaining pairs exhibit similar performances.
6. Ethics and Implications
Cultivating high ethical standards, transparency, integrity, and honesty is imperative for upholding investors’ trust in the financial market. This study utilizes publicly available web information without any form of manipulation. The models’ reported performance is based on out-of-sample data chosen randomly. Therefore, the results can be supplementary information for investment decisions, maintaining investors’ confidence. Nevertheless, investment decisions must not be solely reliant on the research findings. Investors are encouraged to conduct thorough due diligence and consider their risk tolerance across various market conditions. The reliability of forecasts hinges not only on a specific model’s output but also on the volatile nature of the stock market, particularly during geopolitical tensions, global supply chain disruptions, conflicts, pandemics, and other market risks. Thus, stakeholders stand to benefit from an appropriate analysis of the current market behavior fused with the model’s outcomes.
Equity traders, individual investors, and portfolio managers inherently seek to predict stock prices and projected returns. This research indicates the promising potential of machine learning architecture in delineating the cone of uncertainty in stock price prediction. Furthermore, academic researchers can extend the applicability of machine learning algorithms in the financial market.
7. Conclusions
The detection of stock price movements is becoming increasingly crucial for all stakeholders involved in making the foremost financial decisions, whether directly or indirectly. However, achieving precise and consistent predictions is challenging due to the stock market’s volatile, nonlinear, noisy, chaotic, nonparametric, and fuzzy nature. Notably, the existing literature lacks a comparative analysis focusing solely on human sentiment for predicting stock price movement direction using unstructured data.
This article aims to address this gap by conducting a comparative study of machine learning models under uniform conditions, leveraging financial news headlines to discern the influence of textual data on predicting stock price movement direction. The study evaluates the effectiveness of logistic regression, support vector machine, random forest, extreme gradient boosting, and artificial neural network models in detecting stock price movement using news headlines. Sentiment scores, derived from the Valence Aware Dictionary for Sentiment Reasoning (VADER) and the TextBlob analyzers, serve as the sole input for these models.
Model performance is assessed using sensitivity, specificity, accuracy, and the area under the receiver operating characteristic (ROC) curve (AUC). Experimental results indicate that when utilizing sentiment scores from the TextBlob analyzer, model performances do not exhibit significant differences. Similarly, when employing sentiment scores from the VADER analyzer, model accuracy remains relatively consistent across the board. However, minor discrepancies in AUC performance arise, particularly between the LR versus SVM and SVM versus ANN pairs when using sentiment scores from the VADER analyzer, while other pairs demonstrate similar performances. Furthermore, it is observed that all models perform better when utilizing sentiment scores computed from the TextBlob analyzer compared to those obtained from the VADER analyzer.
In our upcoming endeavors, we aim to fuse the existing models with neural network architectures like transformers to create hybrid predictive models. We also plan to explore integrating traditional and deep learning model structures to develop a novel predictive model. Additionally, we intend to introduce a hybrid optimization algorithm that combines local and global optimizers to train model parameters. Expanding the scope of our model development, we will consider incorporating sentiments from various media sources beyond financial news. Furthermore, we are committed to exploring the implementation of evolutionary algorithms to achieve cutting-edge performance.
Author Contributions
K.R.D.: conceptualization, methodology, software, validation, formal analysis, investigation, writing—original draft, writing—review and editing. A.G.: software, writing—original draft, writing—review and editing. N.R.P.: methodology, investigation, writing—original draft, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are publicly available on the website of the ShareSansar: https://www.sharesansar.com/ (accessed on 1 May 2024).
Acknowledgments
The authors would like to thank ShareSansar for making Nepal Stock Exchange (NEPSE) data available online through the website.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abiola, Odeyinka, Adebayo Abayomi-Alli, Oluwasefunmi Arogundade Tale, Sanjay Misra, and Olusola Abayomi-Alli. 2023. Sentiment analysis of covid-19 tweets from selected hashtags in nigeria using vader and text blob analyser. Journal of Electrical Systems and Information Technology 10: 5. [Google Scholar] [CrossRef]
- Abreu, Mery Natali Silva, Arminda Lucia Siqueira, and Waleska Teixeira Caiaffa. 2009. Ordinal logistic regression in epidemiological studies. Revista de Saude Publica 43: 183–94. [Google Scholar] [CrossRef]
- Agresti, Alan, and Brian Caffo. 2000. Simple and effective confidence intervals for proportions and differences of proportions result from adding two successes and two failures. The American Statistician 54: 280–88. [Google Scholar] [CrossRef]
- Ahangar, Reza Gharoie, Mahmood Yahyazadehfar, and Hassan Pournaghshband. 2010. The comparison of methods artificial neural network with linear regression using specific variables for prediction stock price in tehran stock exchange. arXiv arXiv:1003.1457. [Google Scholar]
- Ahmad, Muhammad Waseem, Monjur Mourshed, and Yacine Rezgui. 2017. Trees vs neurons: Comparison between random forest and ann for high-resolution prediction of building energy consumption. Energy and Buildings 147: 77–89. [Google Scholar] [CrossRef]
- Aljedaani, Wajdi, Furqan Rustam, Mohamed Wiem Mkaouer, Abdullatif Ghallab, Vaibhav Rupapara, Patrick Bernard Washington, Ernesto Lee, and Imran Ashraf. 2022. Sentiment analysis on twitter data integrating textblob and deep learning models: The case of us airline industry. Knowledge-Based Systems 255: 109780. [Google Scholar] [CrossRef]
- Al-Natour, Sameh, and Ozgur Turetken. 2020. A comparative assessment of sentiment analysis and star ratings for consumer reviews. International Journal of Information Management 54: 102132. [Google Scholar] [CrossRef]
- Ampomah, Ernest Kwame, Zhiguang Qin, and Gabriel Nyame. 2020. Evaluation of tree-based ensemble machine learning models in predicting stock price direction of movement. Information 11: 332. [Google Scholar] [CrossRef]
- Ballings, Michel, Dirk Van den Poel, Nathalie Hespeels, and Ruben Gryp. 2015. Evaluating multiple classifiers for stock price direction prediction. Expert Systems with Applications 42: 7046–56. [Google Scholar] [CrossRef]
- Basak, Suryoday, Saibal Kar, Snehanshu Saha, Luckyson Khaidem, and Sudeepa Roy Dey. 2019. Predicting the direction of stock market prices using tree-based classifiers. The North American Journal of Economics and Finance 47: 552–67. [Google Scholar] [CrossRef]
- Baxt, William G. 1990. Use of an artificial neural network for data analysis in clinical decision-making: The diagnosis of acute coronary occlusion. Neural Computation 2: 480–89. [Google Scholar] [CrossRef]
- Baxt, William G. 1991. Use of an artificial neural network for the diagnosis of myocardial infarction. Annals of Internal Medicine 115: 843–48. [Google Scholar] [CrossRef]
- Bekkerman, Ron, Mikhail Bilenko, and John Langford. 2011. Scaling up Machine Learning: Parallel and Distributed Approaches. Cambridge: Cambridge University Press. [Google Scholar]
- Bhandari, Hum Nath, Binod Rimal, Nawa Raj Pokhrel, Ramchandra Rimal, and Keshab R. Dahal. 2022. Lstm-sdm: An integrated framework of lstm implementation for sequential data modeling. Software Impacts 14: 100396. [Google Scholar] [CrossRef]
- Bhandari, Hum Nath, Binod Rimal, Nawa Raj Pokhrel, Ramchandra Rimal, Keshab R. Dahal, and Rajendra K. C. Khatri. 2022. Predicting stock market index using lstm. Machine Learning with Applications 9: 100320. [Google Scholar] [CrossRef]
- Biau, Gérard, and Erwan Scornet. 2016. A random forest guided tour. Test 25: 197–227. [Google Scholar] [CrossRef]
- Binder, Torsten, Angela Sandmann, Bernd Sures, Gunnar Friege, Heike Theyssen, and Philipp Schmiemann. 2019. Assessing prior knowledge types as predictors of academic achievement in the introductory phase of biology and physics study programmes using logistic regression. International Journal of STEM Education 6: 1–14. [Google Scholar] [CrossRef]
- Bird, Steven. 2006. Nltk: The natural language toolkit. Paper presented at COLING/ACL 2006 Interactive Presentation Sessions, Sydney, Australia, July 17–18; pp. 69–72. [Google Scholar]
- Bisoi, Ranjeeta, Pradipta Kishore Dash, and Ajaya Kumar Parida. 2019. Hybrid variational mode decomposition and evolutionary robust kernel extreme learning machine for stock price and movement prediction on daily basis. Applied Soft Computing 74: 652–78. [Google Scholar] [CrossRef]
- Bland, Charles, Lucio Tonello, Elia Biganzoli, David Snowdon, Piero Antuono, and Michele Lanza. 2020. Advances in Artificial Neural Networks. 119p, Available online: https://www.scirp.org/book/detailedinforofabook?bookid=2716&booktypeid=1 (accessed on 1 May 2024).
- Bonta, Venkateswarlu, Nandhini Kumaresh, and Naulegari Janardhan. 2019. A comprehensive study on lexicon based approaches for sentiment analysis. Asian Journal of Computer Science and Technology 8: 1–6. [Google Scholar] [CrossRef]
- Boser, Bernhard E., Isabelle M. Guyon, and Vladimir N. Vapnik. 1992. A training algorithm for optimal margin classifiers. Paper presented at Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, July 27–29; pp. 144–152. [Google Scholar]
- Bosworth, Barry, Saul Hymans, and Franco Modigliani. 1975. The stock market and the economy. Brookings Papers on Economic Activity 1975: 257–300. [Google Scholar] [CrossRef]
- Bourlard, Herve, and Nelson Morgan. 1993. Continuous speech recognition by connectionist statistical methods. IEEE Transactions on Neural Networks 4: 893–909. [Google Scholar] [CrossRef]
- Brownlee, Jason. 2018. Better Deep Learning: Train Faster, Reduce Overfitting, and Make Better Predictions. Machine Learning Mastery. Available online: https://machinelearningmastery.com/better-deep-learning/ (accessed on 1 May 2024).
- Budhathoki, Nirajan, Ramesh Bhandari, Suraj Bashyal, and Carl Lee. 2023. Predicting asthma using imbalanced data modeling techniques: Evidence from 2019 michigan brfss data. PLoS ONE 18: e0295427. [Google Scholar] [CrossRef] [PubMed]
- Burke, Harry B. 1994. Artificial neural networks for cancer research: Outcome prediction. Seminars in Surgical Oncology 10: 73–79. [Google Scholar] [CrossRef] [PubMed]
- Burke, Harry B., Philip H Goodman, David B. Rosen, Donald E. Henson, John N. Weinstein, Frank E. Harrell, Jr., Jeffrey R. Marks, David P. Winchester, and David G. Bostwick. 1997. Artificial neural networks improve the accuracy of cancer survival prediction. Cancer 79: 857–862. [Google Scholar] [CrossRef]
- Byvatov, Evgeny, Uli Fechner, Jens Sadowski, and Gisbert Schneider. 2003. Comparison of support vector machine and artificial neural network systems for drug/nondrug classification. Journal of Chemical Information and Computer Sciences 43: 1882–89. [Google Scholar] [CrossRef]
- Chandola, Deeksha, Akshit Mehta, Shikha Singh, Vinay Anand Tikkiwal, and Himanshu Agrawal. 2023. Forecasting directional movement of stock prices using deep learning. Annals of Data Science 10: 1361–78. [Google Scholar] [CrossRef]
- Chen, An-Sing, Mark T. Leung, and Hazem Daouk. 2003. Application of neural networks to an emerging financial market: Forecasting and trading the taiwan stock index. Computers & Operations Research 30: 901–23. [Google Scholar]
- Chen, Shun, and Lei Ge. 2019. Exploring the attention mechanism in lstm-based hong kong stock price movement prediction. Quantitative Finance 19: 1507–15. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. Xgboost: A scalable tree boosting system. Paper presented at the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17; pp. 785–794. [Google Scholar]
- Chen, Wei, Shuai Zhang, Renwei Li, and Himan Shahabi. 2018. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Science of the Total Environment 644: 1006–18. [Google Scholar] [CrossRef] [PubMed]
- Chervonenkis, Alexey Ya. 2013. Early history of support vector machines. In Empirical Inference. Cham: Springer, pp. 13–20. [Google Scholar]
- Christodoulou, Evangelia, Jie Ma, Gary S. Collins, Ewout W. Steyerberg, Jan Y. Verbakel, and Ben Van Calster. 2019. A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. Journal of Clinical Epidemiology 110: 12–22. [Google Scholar] [CrossRef]
- Claesen, Marc, and Bart De Moor. 2015. Hyperparameter search in machine learning. arXiv arXiv:1502.02127. [Google Scholar]
- Dahal, Keshab Raj, J. N. Dahal, H. Banjade, and S. Gaire. 2021. Prediction of wine quality using machine learning algorithms. Open Journal of Statistics 11: 278–89. [Google Scholar] [CrossRef]
- Dahal, Keshab R., and Mohamed Amezziane. 2020. Exact distribution of difference of two sample proportions and its inferences. Open Journal of Statistics 10: 363. [Google Scholar] [CrossRef]
- Dahal, Keshab R., Jiba N. Dahal, Kenneth R. Goward, and Oluremi Abayami. 2020. Analysis of the resolution of crime using predictive modeling. Open Journal of Statistics 10: 600. [Google Scholar] [CrossRef]
- Dahal, Keshab R., and Yadu Gautam. 2020. Argumentative comparative analysis of machine learning on coronary artery disease. Open Journal of Statistics 10: 694–705. [Google Scholar] [CrossRef]
- Dahal, Keshab Raj, Nawa Raj Pokhrel, Santosh Gaire, Sharad Mahatara, Rajendra P. Joshi, Ankrit Gupta, Huta R. Banjade, and Jeorge Joshi. 2023. A comparative study on effect of news sentiment on stock price prediction with deep learning architecture. PLoS ONE 18: e0284695. [Google Scholar] [CrossRef]
- DeMaris, Alfred. 1995. A tutorial in logistic regression. Journal of Marriage and the Family, 956–68. [Google Scholar]
- Derakhshan, Ali, and Hamid Beigy. 2019. Sentiment analysis on stock social media for stock price movement prediction. Engineering Applications of Artificial Intelligence 85: 569–78. [Google Scholar] [CrossRef]
- Devi, B. Uma, Darshan Sundar, and P. Karappan Alli. 2013. An effective time series analysis for stock trend prediction using arima model for nifty midcap-50. International Journal of Data Mining & Knowledge Management Process 3: 65. [Google Scholar]
- Dey, Shubharthi, Yash Kumar, Snehanshu Saha, and Suryoday Basak. 2016. Forecasting to classification: Predicting the direction of stock market price using xtreme gradient boosting. PESIT South Campus, 1–10. [Google Scholar]
- Dhyani, Bijesh, Manish Kumar, Poonam Verma, and Abhisheik Jain. 2020. Stock market forecasting technique using arima model. International Journal of Recent Technology and Engineering 8: 2694–97. [Google Scholar] [CrossRef]
- Doniger, Scott, Thomas Hofmann, and Joanne Yeh. 2002. Predicting cns permeability of drug molecules: Comparison of neural network and support vector machine algorithms. Journal of Computational Biology 9: 849–64. [Google Scholar] [CrossRef]
- Duda, Richard O., Peter E. Hart, and David G. Stork. 1973. Pattern Classification and Scene Analysis. New York: Wiley, vol. 3. [Google Scholar]
- Durgesh, K. Srivastava, and Bhambhu Lekha. 2010. Data classification using support vector machine. Journal of Theoretical and Applied Information Technology 12: 1–7. [Google Scholar]
- Dutta, Avijan, Gautam Bandopadhyay, and Suchismita Sengupta. 2012. Prediction of stock performance in the indian stock market using logistic regression. International Journal of Business and Information 7: 105. [Google Scholar]
- Fama, Eugene F. Fama 1995. Random walks in stock market prices. Financial Analysts Journal 51: 75–80.
- Fazlija, Bledar, and Pedro Harder. 2022. Using financial news sentiment for stock price direction prediction. Mathematics 10: 2156. [Google Scholar] [CrossRef]
- Field, Andy. 2009. Logistic regression. Discovering Statistics Using SPSS 264: 315. [Google Scholar]
- Gandhmal, Dattatray P., and Kannan Kumar. 2019. Systematic analysis and review of stock market prediction techniques. Computer Science Review 34: 100190. [Google Scholar] [CrossRef]
- Gao, Penglei, Rui Zhang, and Xi Yang. 2020. The application of stock index price prediction with neural network. Mathematical and Computational Applications 25: 53. [Google Scholar] [CrossRef]
- Garlapati, Anusha, Doredla Radha Krishna, Kavya Garlapati, Udayagiri Rahul, and Gayathri Narayanan. 2021. Stock price prediction using facebook prophet and arima models. Paper presented at 2021 6th International Conference for Convergence in Technology (I2CT), Pune, India, April 2–4; Piscatway: IEEE, pp. 1–7. [Google Scholar]
- Ge, Qi, Alexander Kurov, and Marketa Halova Wolfe. 2017. Stock Market Reactions to Presidential Social Media Usage: Evidence from Company-Specific Tweets. SSRN Electronic Journal. Available online: https://www.researchgate.net/publication317796867_Stock_Market_Reactions_to_Presidential_Social_Media_Usage_Evidence_from_Company-Specific_Tweets (accessed on 1 May 2024). [CrossRef]
- Ge, Qi, Alexander Kurov, and Marketa Halova Wolfe. 2018. Stock Market Reactions to Presidential Statements: Evidence from Company-Specific Tweets. Available online: https://creativematter.skidmore.edu/econ_fac_schol/2/ (accessed on 1 May 2024).
- Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. Sebastopol: O’Reilly Media, Inc. [Google Scholar]
- Glorot, Xavier, Antoine Bordes, and Yoshua Bengio. 2011. Deep sparse rectifier neural networks. Paper presented at Fourteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Lauderdale, FL, USA, April 11–13; pp. 315–23. [Google Scholar]
- Gong, Jibing, and Shengtao Sun. 2009. A new approach of stock price prediction based on logistic regression model. Paper presented at 2009 International Conference on New Trends in Information and Service Science, Beijing, China, June 30–July 2; Piscatway: IEEE, pp. 1366–71. [Google Scholar]
- Hansen, James V., James B. McDonald, and Ray D. Nelson. 1999. Time series prediction with genetic-algorithm designed neural networks: An empirical comparison with modern statistical models. Computational Intelligence 15: 171–84. [Google Scholar] [CrossRef]
- Hao, Jiangang, and Tin Kam Ho. 2019. Machine learning made easy: A review of scikit-learn package in python programming language. Journal of Educational and Behavioral Statistics 44: 348–61. [Google Scholar] [CrossRef]
- Hatwell, Julian, Mohamed Medhat Gaber, and R. Muhammad Atif Azad. 2020. Chirps: Explaining random forest classification. Artificial Intelligence Review 53: 5747–88. [Google Scholar] [CrossRef]
- Hoskins, J. C., K. M. Kaliyur, and David M. Himmelblau. 1990. Incipient fault detection and diagnosis using artificial neural networks. Paper presented at 1990 IJCNN International Joint Conference on Neural Networks, Washington, DC, USA, January 15–19; Piscatway: IEEE, pp. 81–86. [Google Scholar]
- Huang, Wei, Yoshiteru Nakamori, and Shou-Yang Wang. 2005. Forecasting stock market movement direction with support vector machine. Computers & Operations Research 32: 2513–22. [Google Scholar]
- Hutto, Clayton, and Eric Gilbert. 2014. Vader: A parsimonious rule-based model for sentiment analysis of social media text. Paper presented at International AAAI Conference on Web and Social Media, Buffalo, NY, USA, June 3–6, vol. 8, pp. 216–25. [Google Scholar]
- Illia, Fathonah, Migunani Puspita Eugenia, and Sita Aliya Rutba. 2021. Sentiment analysis on pedulilindungi application using textblob and vader library. International Conference on Data Science and Official Statistics 2021: 278–88. [Google Scholar] [CrossRef]
- Imandoust, Sadegh Bafandeh, and Mohammad Bolandraftar. 2014. Forecasting the direction of stock market index movement using three data mining techniques: The case of tehran stock exchange. International Journal of Engineering Research and Applications 4: 106–17. [Google Scholar]
- Ismail, Mohd Sabri, Mohd Salmi Md Noorani, Munira Ismail, Fatimah Abdul Razak, and Mohd Almie Alias. 2020. Predicting next day direction of stock price movement using machine learning methods with persistent homology: Evidence from kuala lumpur stock exchange. Applied Soft Computing 93: 106422. [Google Scholar] [CrossRef]
- Jiang, Yunxing, Xianghui Zhang, Rulin Ma, Xinping Wang, Jiaming Liu, Mulatibieke Keerman, Yizhong Yan, Jiaolong Ma, Yanpeng Song, and Jingyu Zhang. 2021. Cardiovascular disease prediction by machine learning algorithms based on cytokines in kazakhs of china. Clinical Epidemiology 13: 417. [Google Scholar] [CrossRef] [PubMed]
- Jones, Charles M. 2002. A Century of Stock Market Liquidity and Trading Costs. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=313681 (accessed on 1 May 2024).
- Joshi, Dushyant Lal. 2023. Enhancing investment strategies: A comprehensive technical analysis approach for informed buy-sell-hold decisions in nepse (nepal stock exchange). Nepal Journal of Multidisciplinary Research 6: 72–80. [Google Scholar] [CrossRef]
- Kara, Yakup, Melek Acar Boyacioglu, and Ömer Kaan Baykan. 2011. Predicting direction of stock price index movement using artificial neural networks and support vector machines: The sample of the istanbul stock exchange. Expert Systems with Applications 38: 5311–19. [Google Scholar] [CrossRef]
- Khoa, Bui Thanh, and Tran Trong Huynh. 2022. Forecasting stock price movement direction by machine learning algorithm. International Journal of Electrical and Computer Engineering 12: 6625. [Google Scholar] [CrossRef]
- Kim, Sondo, Seungmo Ku, Woojin Chang, and Jae Wook Song. 2020. Predicting the direction of us stock prices using effective transfer entropy and machine learning techniques. IEEE Access 8: 111660–82. [Google Scholar] [CrossRef]
- Kleinbaum, David G., K. Dietz, M. Gail, Mitchel Klein, and Mitchell Klein. 2002. Logistic Regression. New York: Springer. [Google Scholar]
- Kleinbaum, David G., Lawrence L. Kupper, and Lloyd E. Chambless. 1982. Logistic regression analysis of epidemiologic data: Theory and practice. Communications in Statistics-Theory and Methods 11: 485–547. [Google Scholar] [CrossRef]
- Kocev, Dragi, Celine Vens, Jan Struyf, and Sašo Džeroski. 2013. Tree ensembles for predicting structured outputs. Pattern Recognition 46: 817–33. [Google Scholar] [CrossRef]
- Kumar, Ashish, Abeer Alsadoon, PWC Prasad, Salma Abdullah, Tarik A. Rashid, Duong Thu Hang Pham, and Tran Quoc Vinh Nguyen. 2022. Generative adversarial network (GAN) and enhanced root mean square error (ERMSE): Deep learning for stock price movement prediction. Multimedia Tools and Applications 81: 3995–4013. [Google Scholar] [CrossRef]
- Kunwar, Bikash, and Paras Khati. 2023. Predictive analysis of nepse using lstm and technical indicators. International Research Journal of Innovations in Engineering and Technology 7: 1. [Google Scholar] [CrossRef]
- LaValley, Michael P. 2008. Logistic regression. Circulation 117: 2395–99. [Google Scholar] [CrossRef]
- Lemon, Stephenie C., Jason Roy, Melissa A. Clark, Peter D. Friedmann, and William Rakowski. 2003. Classification and regression tree analysis in public health: Methodological review and comparison with logistic regression. Annals of behavioral medicine 26: 172–81. [Google Scholar] [CrossRef] [PubMed]
- Li, Qiong, Qinglin Meng, Jiejin Cai, Hiroshi Yoshino, and Akashi Mochida. 2009. Applying support vector machine to predict hourly cooling load in the building. Applied Energy 86: 2249–56. [Google Scholar] [CrossRef]
- Lippmann, Richard P. 1989. Review of neural networks for speech recognition. Neural Computation 1: 1–38. [Google Scholar] [CrossRef]
- Liu, Bing. 2010. Sentiment analysis and subjectivity. Handbook of Natural Language Processing 2: 627–66. [Google Scholar]
- Long, Jiawei, Zhaopeng Chen, Weibing He, Taiyu Wu, and Jiangtao Ren. 2020. An integrated framework of deep learning and knowledge graph for prediction of stock price trend: An application in chinese stock exchange market. Applied Soft Computing 91: 106205. [Google Scholar] [CrossRef]
- Long, Wen, Zhichen Lu, and Lingxiao Cui. 2019. Deep learning-based feature engineering for stock price movement prediction. Knowledge-Based Systems 164: 163–73. [Google Scholar] [CrossRef]
- Loria, Steven. 2018. Textblob documentation. Release 0.15 2: 269. [Google Scholar]
- Menard, Scott. 2002. Applied Logistic Regression Analysis. Number 106. Thousand Oaks: Sage. [Google Scholar]
- Menze, Bjoern H., B. Michael Kelm, Ralf Masuch, Uwe Himmelreich, Peter Bachert, Wolfgang Petrich, and Fred A. Hamprecht. 2009. A comparison of random forest and its gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinformatics 10: 1–16. [Google Scholar] [CrossRef] [PubMed]
- Moayedi, Hossein, Mansour Mosallanezhad, Ahmad Safuan A. Rashid, Wan Amizah Wan Jusoh, and Mohammed Abdullahi Muazu. 2020. A systematic review and meta-analysis of artificial neural network application in geotechnical engineering: Theory and applications. Neural Computing and Applications 32: 495–18. [Google Scholar] [CrossRef]
- Mohandes, Mohamed A., Shafiqur Rehman, and Talal O. Halawani. 1998. A neural networks approach for wind speed prediction. Renewable Energy 13: 345–54. [Google Scholar] [CrossRef]
- Musa, Abdallah Bashir. 2013. Comparative study on classification performance between support vector machine and logistic regression. International Journal of Machine Learning and Cybernetics 4: 13–24. [Google Scholar] [CrossRef]
- Nair, Vinod, and Geoffrey E. Hinton. 2010. Rectified linear units improve restricted boltzmann machines. Paper presented at 27th International Conference on Machine Learning (ICML 2010), Haifa, Israel, June 21–24. [Google Scholar]
- Nelson, David M. Q., Adriano C. M. Pereira, and Renato A. De Oliveira. 2017. Stock market’s price movement prediction with lstm neural networks. Paper presented at 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, May 14–19; Piscatway: IEEE, pp. 1419–26. [Google Scholar]
- Nemes, László, and Attila Kiss. 2021. Prediction of stock values changes using sentiment analysis of stock news headlines. Journal of Information and Telecommunication 5: 375–94. [Google Scholar] [CrossRef]
- Nwankpa, Chigozie, Winifred Ijomah, Anthony Gachagan, and Stephen Marshall. 2018. Activation functions: Comparison of trends in practice and research for deep learning. arXiv arXiv:1811.03378. [Google Scholar]
- Pampel, Fred C. 2020. Logistic Regression: A Primer. Thousand Oaks: Sage Publications, vol. 132. [Google Scholar]
- Pereira, Sérgio, Raphael Meier, Richard McKinley, Roland Wiest, Victor Alves, Carlos A. Silva, and Mauricio Reyes. 2018. Enhancing interpretability of automatically extracted machine learning features: Application to a rbm-random forest system on brain lesion segmentation. Medical Image Analysis 44: 228–44. [Google Scholar] [CrossRef]
- Peterson, Lars-Erik, Alf L. Nachemson, D. S. Bradford, R. G. Burwell, M. Duhaime, M. A. Edgar, M. M. Eppig, A. D. H. Gardner, D. K. Kehl, J. Lidstrom, and et al. 1995. Prediction of progression of the curve in girls who have adolescent idiopathic scoliosis of moderate severity. logistic regression analysis based on data from the brace study of the scoliosis research society. Journal of Bone and Joint Surgery-Series A 77: 823–27. [Google Scholar] [CrossRef]
- Pokhrel, Nawa Raj, Keshab Raj Dahal, Ramchandra Rimal, Hum Nath Bhandari, Rajendra K. C. Khatri, Binod Rimal, and William Edward Hahn. 2022. Predicting nepse index price using deep learning models. Machine Learning with Applications 9: 100385. [Google Scholar] [CrossRef]
- Pokhrel, Nawa Raj, Keshab Raj Dahal, Ramchandra Rimal, Hum Nath Bhandari, and Binod Rimal. 2024. Deep-sdm: A unified computational framework for sequential data modeling using deep learning models. Software 3: 47–61. [Google Scholar] [CrossRef]
- Prasad, Dev, and Sudarshan Kadariya. 2022. Stock returns: Nepalese investors’ reactions to news coverage. Journal of Accounting and Finance 22. [Google Scholar] [CrossRef]
- Qiu, Mingyue, and Yu Song. 2016. Predicting the direction of stock market index movement using an optimized artificial neural network model. PLoS ONE 11: e0155133. [Google Scholar] [CrossRef]
- Ren, Rui, Desheng Dash Wu, and Tianxiang Liu. 2018. Forecasting stock market movement direction using sentiment analysis and support vector machine. IEEE Systems Journal 13: 760–70. [Google Scholar] [CrossRef]
- Rigatti, Steven J. 2017. Random forest. Journal of Insurance Medicine 47: 31–39. [Google Scholar] [CrossRef] [PubMed]
- Rustam, Z., D. F. Vibranti, and D. Widya. 2018. Predicting the direction of indonesian stock price movement using support vector machines and fuzzy kernel c-means. In AIP Conference Proceedings. Melville: AIP Publishing, vol. 2023. [Google Scholar]
- Seni, Giovanni, and John Elder. 2010. Ensemble Methods in Data Mining: Improving Accuracy through Combining Predictions. San Rafael: Morgan & Claypool Publishers. [Google Scholar]
- Shahi, Tej Bahadur, Ashish Shrestha, Arjun Neupane, and William Guo. 2020. Stock price forecasting with deep learning: A comparative study. Mathematics 8: 1441. [Google Scholar] [CrossRef]
- Shao, Yuan-Hai, Wei-Jie Chen, and Nai-Yang Deng. 2014. Nonparallel hyperplane support vector machine for binary classification problems. Information Sciences 263: 22–35. [Google Scholar] [CrossRef]
- Shrestha, Purna Man, and Pitambar Lamichhane. 2021. Macroeconomic factors and stock market performance in nepal. PYC Nepal Journal of Management 14: 79–92. [Google Scholar] [CrossRef]
- Shrestha, Purna Man, and Pitambar Lamichhane. 2022. Effect of firm-specific variables on stock returns: Evidence from nepal. Quest Journal of Management and Social Sciences 4: 249–59. [Google Scholar] [CrossRef]
- Sperandei, Sandro. 2014. Understanding logistic regression analysis. Biochemia Medica 24: 12–18. [Google Scholar] [CrossRef]
- Statnikov, Alexander, Lily Wang, and Constantin F. Aliferis. 2008. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinformatics 9: 1–10. [Google Scholar] [CrossRef] [PubMed]
- Stoltzfus, Jill C. 2011. Logistic regression: A brief primer. Academic Emergency Medicine 18: 1099–104. [Google Scholar] [CrossRef]
- Tang, Pan, Cheng Tang, and Keren Wang. 2024. Stock movement prediction: A multi-input lstm approach. Journal of Forecasting. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/for.3071 (accessed on 1 May 2024). [CrossRef]
- Thompson, E. David, Bethany V. Bowling, and Ross E. Markle. 2018. Predicting student success in a major’s introductory biology course via logistic regression analysis of scientific reasoning ability and mathematics scores. Research in Science Education 48: 151–63. [Google Scholar] [CrossRef]
- Turian, Joseph, James Bergstra, and Yoshua Bengio. 2009. Quadratic features and deep architectures for chunking. Paper presented at Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Boulder, CO, USA, May 31–June 5; pp. 245–48. [Google Scholar]
- Vapnik, Vladimir N. 1995. The Nature of Statistical Learning. Theory. Available online: https://www.bibsonomy.org/bibtex/198898576dfede7a15fcbf60cad98f9c0 (accessed on 1 May 2024).
- Wald, Abraham, and Jacob Wolfowitz. 1940. On a test whether two samples are from the same population. The Annals of Mathematical Statistics 11: 147–62. [Google Scholar] [CrossRef]
- Wang, Siqi, Qiang Liu, En Zhu, Fatih Porikli, and Jianping Yin. 2018. Hyperparameter selection of one-class support vector machine by self-adaptive data shifting. Pattern Recognition 74: 198–211. [Google Scholar] [CrossRef]
- Wang, Yanshan. 2014. Stock price direction prediction by directly using prices data: An empirical study on the kospi and hsi. International Journal of Business Intelligence and Data Mining 9: 145–60. [Google Scholar] [CrossRef]
- Weng, Bin, Mohamed A. Ahmed, and Fadel M. Megahed. 2017. Stock market one-day ahead movement prediction using disparate data sources. Expert Systems with Applications 79: 153–63. [Google Scholar] [CrossRef]
- Wright, Raymond E. 1995. Logistic Regression. Available online: https://psycnet.apa.org/record/1995-97110-007 (accessed on 1 May 2024).
- Xu, Yumo, and Shay B. Cohen. 2018. Stock movement prediction from tweets and historical prices. Paper presented at 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, July 15–20; pp. 1970–79. [Google Scholar]
- Yin, Lili, Benling Li, Peng Li, and Rubo Zhang. 2023. Research on stock trend prediction method based on optimized random forest. CAAI Transactions on Intelligence Technology 8: 274–84. [Google Scholar] [CrossRef]
- Zhang, Guoqiang Peter. 2000. Neural networks for classification: A survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 30: 451–62. [Google Scholar] [CrossRef]
- Zhang, Xiaoci, Naijie Gu, Jie Chang, and Hong Ye. 2021. Predicting stock price movement using a dbn-rnn. Applied Artificial Intelligence 35: 876–92. [Google Scholar] [CrossRef]
- Zhang, Xiaodong, Suhui Liu, and Xin Zheng. 2021. Stock price movement prediction based on a deep factorization machine and the attention mechanism. Mathematics 9: 800. [Google Scholar] [CrossRef]
- Zhao, Shunan. 2021. Nepal stock market movement prediction with machine learning. Paper presented at 2021 5th International Conference on Information System and Data Mining, Honolulu, HI, USA, July 23–29; pp. 1–7. [Google Scholar]
- Zhao, Yanli, and Guang Yang. 2023. Deep learning-based integrated framework for stock price movement prediction. Applied Soft Computing 133: 109921. [Google Scholar] [CrossRef]
- Zien, Alexander, Nicole Krämer, Sören Sonnenburg, and Gunnar Rätsch. 2009. The feature importance ranking measure. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2009, Bled, Slovenia, 7–11 September 2009, Proceedings, Part II 20. Cham: Springer, pp. 694–709. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).