Exponential Time Trends in a Fractional Integration Model
Abstract
1. Introduction
2. The Model
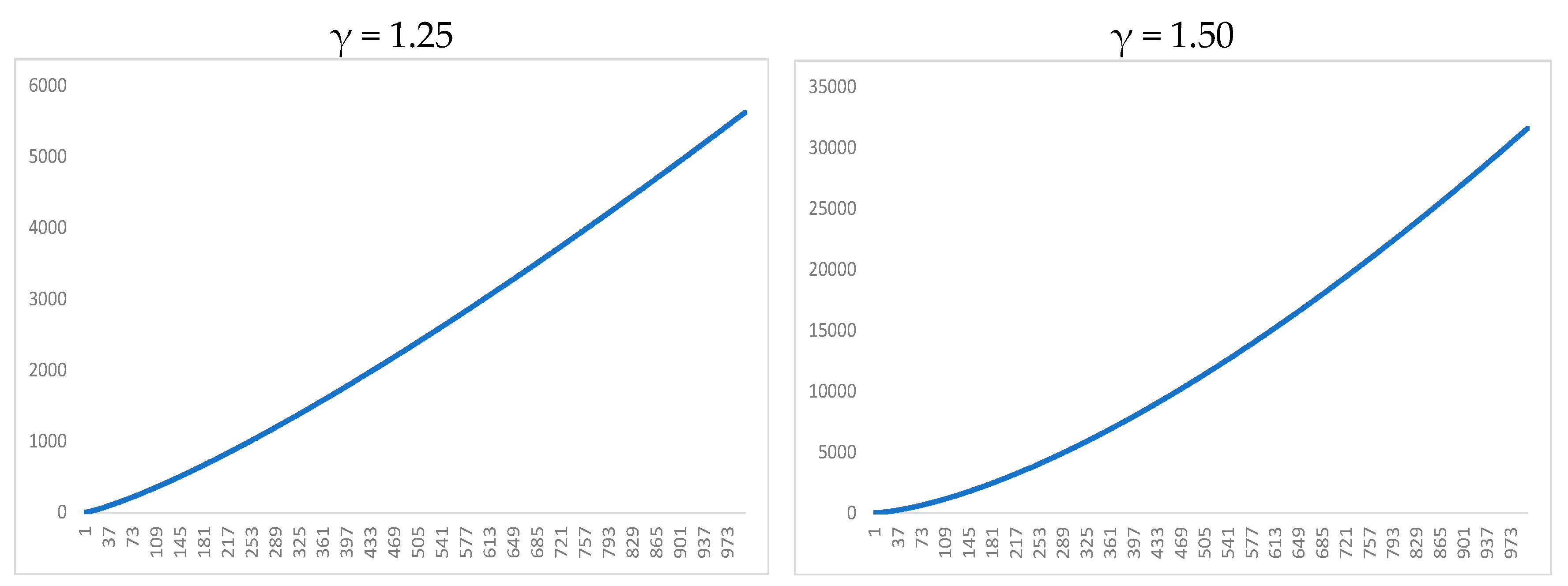
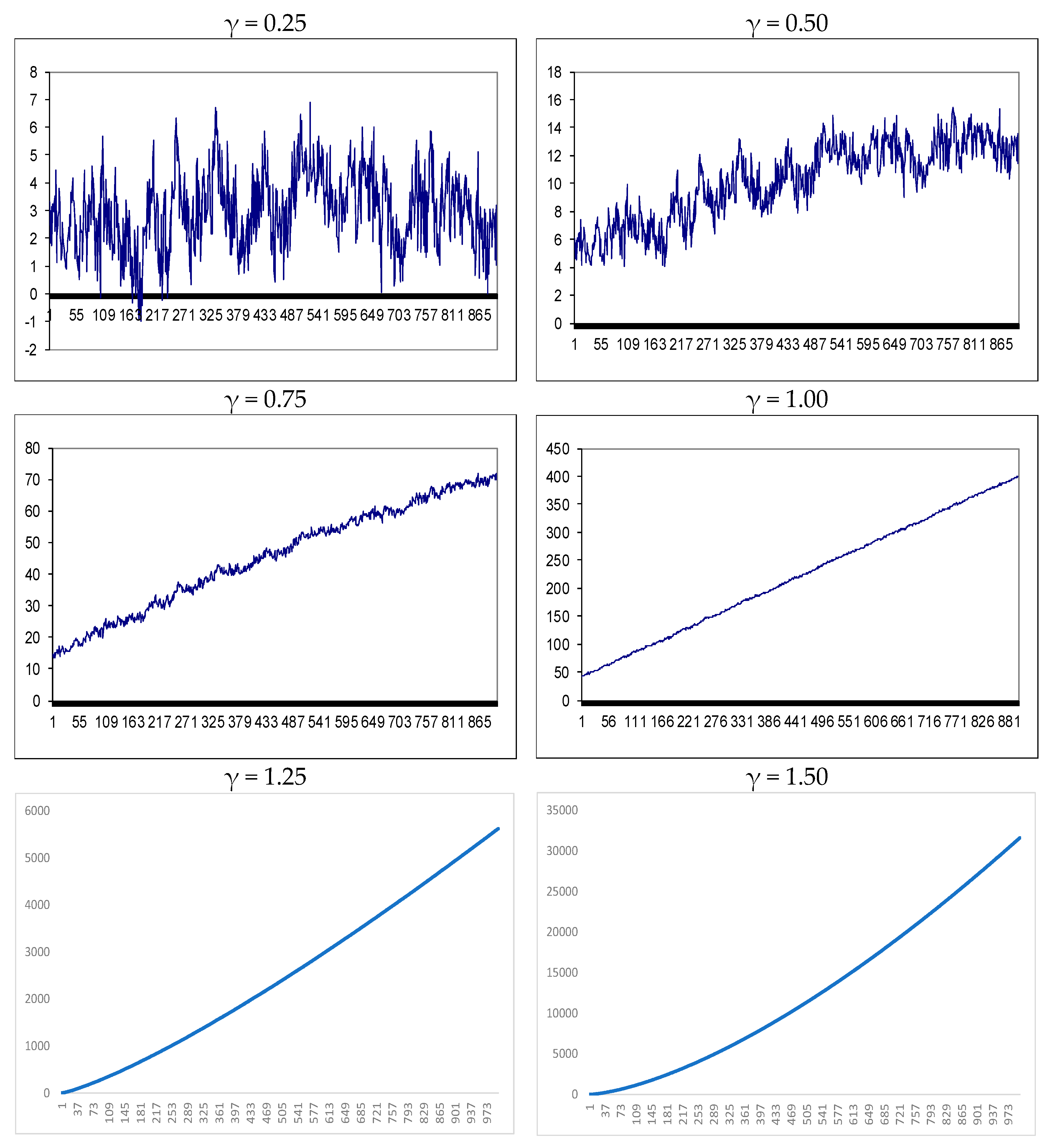
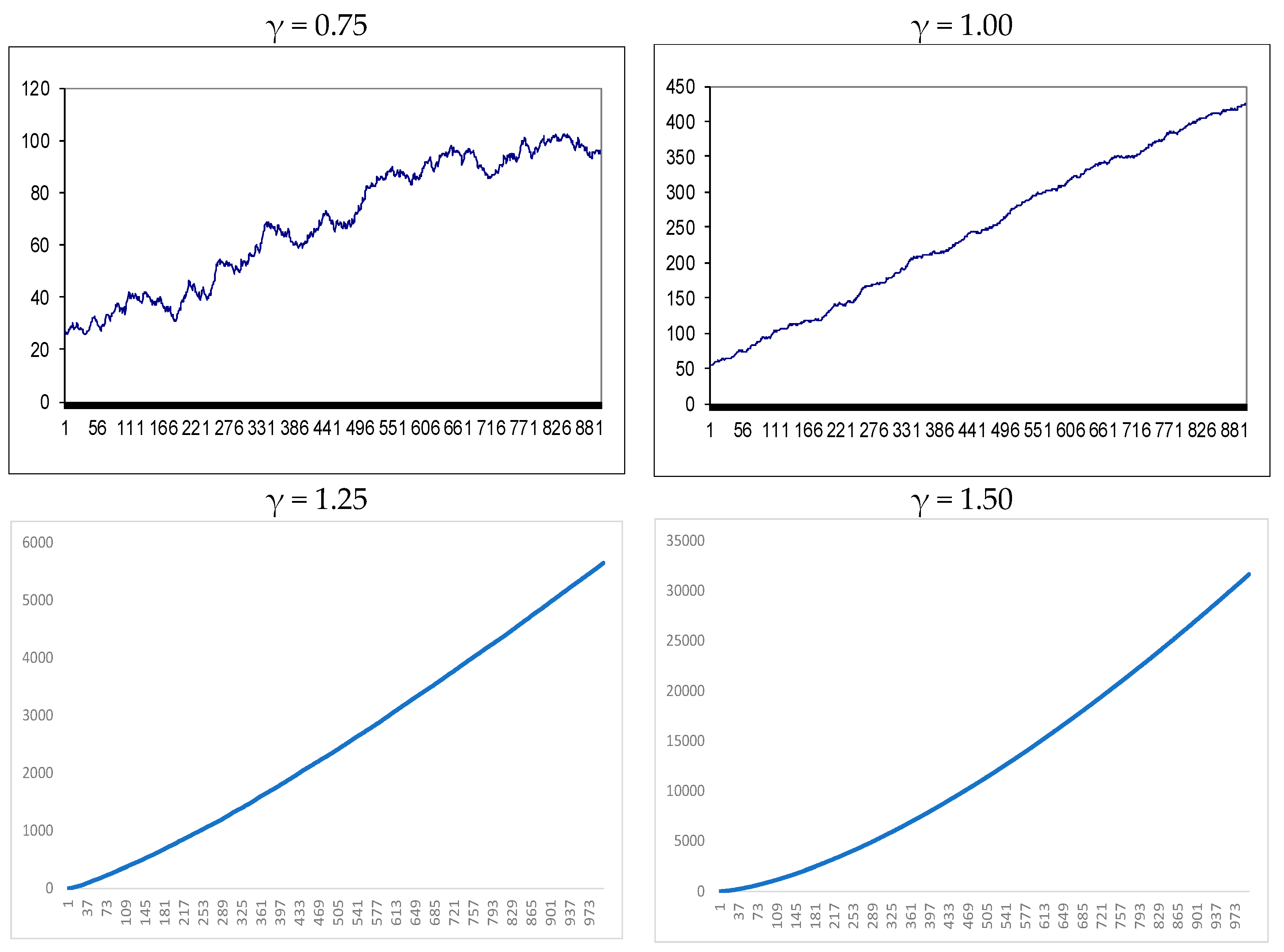
3. Simulation Results
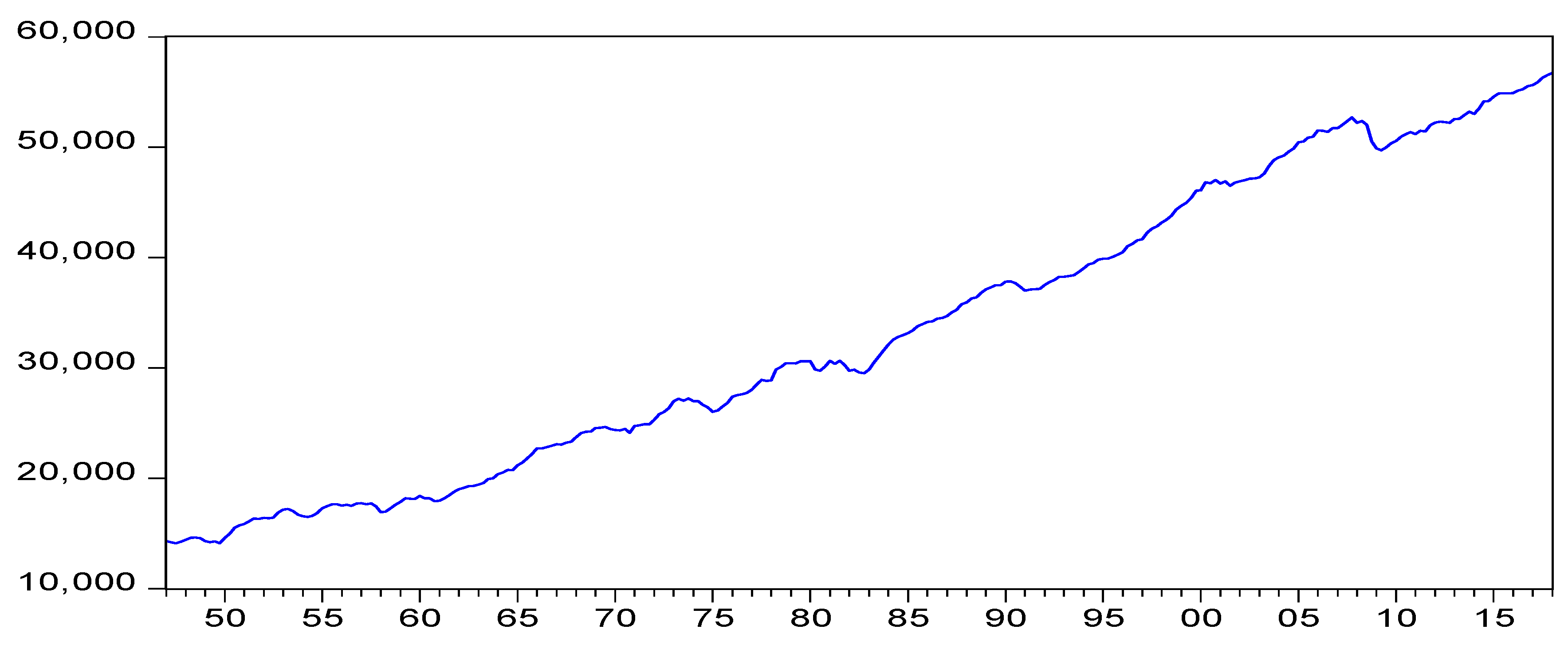
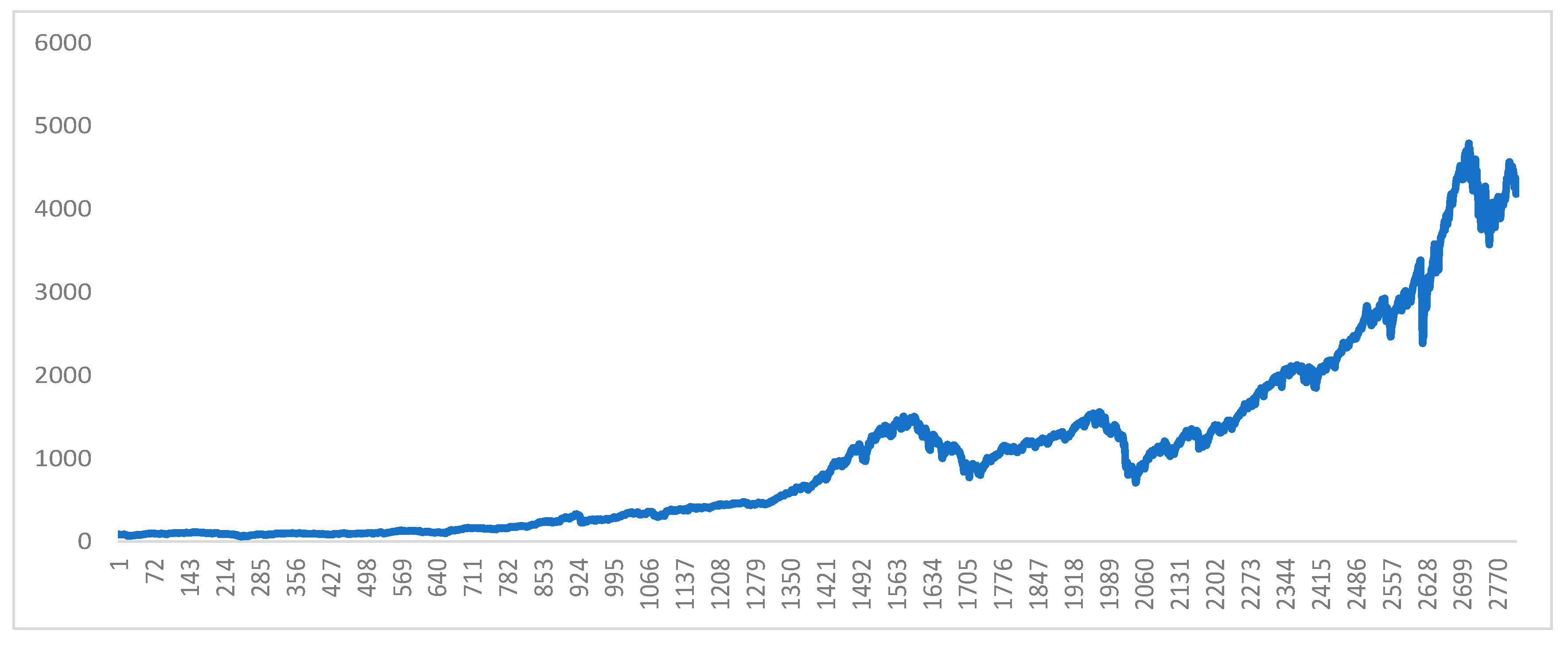
4. Three Empirical Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Proof of Theorem 1
| 1 | Alternatively, an I(0) process can be defined in the time domain as one for which the sum of all autocorrelation coefficients is finite. |
| 2 | Note that becomes 0 for t > 1 only if do = 1. |
| 3 | For this particular version of Robinson’s (1994) tests, based on Equation (2), the spectrum has a singularity at the zero frequency; therefore, j runs from 1 to T-1. |
| 4 | Note that shorter sample sizes, such as T = 50, though of interest in some cases, are not relevant in the context of fractional integration and long-memory processes, which require large samples for meaningful statistical inference. |
| 5 | Although seasonal and cyclical fractional integration has already been analysed in a linear context in Gil-Alana and Robinson (2001) and Gil-Alana (2001), respectively, no attempt has yet been made to incorporate non-linearities. |
References
- Bhargava, Alok. 1986. On the Theory of Testing for Unit Roots in Observed Time Series. The Review of Economics Studies 53: 369–84. [Google Scholar] [CrossRef]
- Brown, Bruce M. 1971. Martingale central limit theorems. Annals of Mathematical Statistics 53: 59–66. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient Capital Markets: A Review of Theory and Empirical Work. Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Gil-Alana, Luis A. 1997. Testing of Fractional Integration in Macroeconomic Time Series. Ph.D. thesis, London School of Economics, LSE, London, UK. [Google Scholar]
- Gil-Alana, Luis A. 2001. Testing Stochastic Cycles in Macroeconomic Time Series. Journal of Time Series Analysis 22: 411–30. [Google Scholar] [CrossRef]
- Gil-Alana, Luis A., and Peter M. Robinson. 2001. Testing of seasonal fractional integration in UK and Japanese consumption and income. Journal of Applied Econometrics 16: 95–114. [Google Scholar] [CrossRef]
- Omay, Tolga, Rangan Gupta, and Giovanni Bonaccolto. 2017. The US real GNP is trend stationary after all. Applied Economics Letters 24: 510–14. [Google Scholar] [CrossRef]
- Press, William H., Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. 1986. Numerical Recipes. The Art of Scientific Computing. Cambridge: Cambridge University Press. [Google Scholar]
- Robinson, Peter M. 1991. Testing for strong serial correlation and dynamic conditional heteroskedasticity in multiple regression. Journal of Econometrics 47: 67–84. [Google Scholar] [CrossRef]
- Robinson, Peter M. 1994. Efficient tests of nonstationary hypotheses. Journal of the American Statistical Association 89: 1420–37. [Google Scholar] [CrossRef]
- Schmidt, Peter, and Peter CB Phillips. 1992. LM tests for a unit root in the presence of deterministic trends. Bulletin of Economcis and Statistics 53: 257–87. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 1988. Variable Trends in Economic Time Series. Journal of Economic Perspectives 2: 147–74. [Google Scholar] [CrossRef]
- Tanaka, Katsuto. 1999. Nonstationary fractional unit root. Econometric Theory 15: 549–82. [Google Scholar] [CrossRef]
- Yaya, Olaoluwa, Ahamuefula Ogbonna, Luis Alberiko Gil-Alana, and Fumitaka Furuoka. 2021. A new unit root analysis for testing hysteresis in unemployment. Oxford Bulletin of Economics and Statistics 83: 960–81. [Google Scholar] [CrossRef]




| do | T = 100 | T = 500 | T = 1000 | |
|---|---|---|---|---|
| Ho: d > do | 0.20 | 0.688 | 0.983 | 1.000 |
| 0.30 | 0.478 | 0.688 | 0.808 | |
| 0.40 | 0.296 | 0.354 | 0.499 | |
| 0.50 | 0.099 | 0.069 | 0.057 | |
| Ho: d < do | 0.50 | 0.104 | 0.099 | 0.068 |
| 0.60 | 0.319 | 0.449 | 0.676 | |
| 0.70 | 0.665 | 0.883 | 0.997 | |
| 0.80 | 0.997 | 1.000 | 1.000 |
| do | T = 100 | T = 500 | T = 1000 | |
|---|---|---|---|---|
| Ho: d > do | 0.20 | 0.709 | 0.878 | 0.998 |
| 0.30 | 0.526 | 0.735 | 0.910 | |
| 0.40 | 0.314 | 0.359 | 0.651 | |
| 0.50 | 0.112 | 0.089 | 0.067 | |
| Ho: d < do | 0.50 | 0.127 | 0.109 | 0.083 |
| 0.60 | 0.414 | 0.565 | 0.712 | |
| 0.70 | 0.727 | 0.899 | 1.000 | |
| 0.80 | 1.000 | 1.000 | 1.000 |
| Γ | d | 95% Band | α (t-Value) | β (t-Value) | Stastistic |
|---|---|---|---|---|---|
| 0 | 1.29 | (1.18, 1.42) | 9.568 (1120.32) | --- | 0.02218 |
| 0.10 | 1.29 | (1.18, 1.43) | 9.625 (80.19) | −0.00584 (−0.47) | 0.04994 |
| 0.20 | 1.29 | (1.18, 1.43) | 9.585 (172.36) | −0.01811 (−0.31) | 0.04412 |
| 0.30 | 1.29 | (1.18, 1.43) | 9.572 (299.66) | −0.00473 (−0.13) | 0.03298 |
| 0.40 | 1.29 | (1.18, 1.43) | 9.565 (404.95) | 0.00347 (0.14) | 0.00959 |
| 0.50 | 1.29 | (1.18, 1.43) | 9.561 (550.26) | 0.00823 (0.46) | 0.02218 |
| 0.60 | 1.29 | (1.17, 1.42) | 9.559 (712.56) | 0.01068 (0.83) | -0.05273 |
| 0.70 | 1.28 | (1.17, 1.42) | 9.559 (882.03) | 0.01165 (1.33) | 0.05811 |
| 0.80 | 1.28 | (1.17, 1.42) | 9.561 (1008.38) | 0.00981 (1.68) | 0.00337 |
| 0.90 | 1.28 | (1.17, 1.42) | 9.583 (1079.09) | 0.00709 (1.92) | 0.01557 |
| 1.00 | 1.28 | (1.17, 1.42) | 9.565 (1107.19) | 0.00453 (2.04) | 0.01978 |
| 1.10 | 1.28 | (1.17, 1.42) | 9.567 (1115.28) | 0.02653 (2.05) | 0.05558 |
| 1.20 | 1.29 | (1.18, 1.42) | 9.567 (1119.87) | 0.00147 (1.91) | -0.03381 |
| 1.30 | 1.29 | (1.19, 1.42) | 9.568 (1119.53) | 0.00079 (1.83) | 0.02787 |
| 1.40 | 1.30 | (1.19, 1.42) | 9.568 (1122.12) | 0.00041 (1.63) | -0.06320 |
| 1.50 | 1.30 | (1.20, 1.43) | 9.568 (1121.49) | 0.02166 (1.54) | -0.01687 |
| Γ | d | 95% Band | α (t-Value) | β (t-Value) | Stastistic |
|---|---|---|---|---|---|
| 0 | 0.96 | (0.93, 1.02) | 41.119 (0.171) | --- | 0.227 |
| 0.10 | 0.96 | (0.93, 1.02) | 42.633 (0.143) | 49.836 (0,16) | 0.219 |
| 0.20 | 0.97 | (0.92, 1.23) | 52.366 (0.399 | 39.924 (0.31) | 0.203 |
| 0.30 | 0.97 | (0.92, 1.23) | 54.121 (0.70) | 37.914 (0.56) | 0.239 |
| 0.40 | 0.95 | (0.91, 1.22) | 57.445 (1.09) | 34.327 80.90) | 0.202 |
| 0.50 | 0.95 | (0.91, 1.22) | 59.009 (1.18) | 34.327 (0.90) | 0.200 |
| 0.60 | 0.96 | (0.92, 1.22) | 73.080 (1.99) | 18.523 (1.71) | 0.188 |
| 0.70 | 0.97 | (0.92, 1.23) | 80.733 (2.28) | 10.997 (2.08) | 0.161 |
| 0.80 | 0.97 | (0.92, 1.23) | 85.950 (2.46) | 5.941 (2.38) | 0.091 |
| 0.90 | 0.97 | (0.92, 1.23) | 89.053 (2.55) | 3.004 (2.62) | 0.006 |
| 1.00 | 0.97 | (0.92, 1.22) | 90.718 (2.60) | 1.461 (2.81) | −0.001 |
| 1.10 | 0.97 | (0.92, 1.23) | 91.577 (2.63) | 0.693 (2.96) | −0.154 |
| 1.20 | 0.98 | (0.92, 1.22) | 92.010 (2.64) | 0.324 (3.09) | −0.225 |
| 1.30 | 0.97 | (0.92, 1.23) | 92.228 (2.65) | 0.149 (3.20) | −0.289 |
| 1.40 | 0.98 | (0.93, 1.23) | 92.341 (2.65) | 0.068 (3.30) | −0.346 |
| 1.50 | 0.97 | (0.92, 1.24) | 92.042 (2.61) | 0.031 (3.39) | −0.398 |
| Γ | d | 95% Band | α (t-Value) | β (t-Value) | Stastistic |
|---|---|---|---|---|---|
| 0 | 1.43 | (1.36, 1.51) | 9.921 (3.13) | --- | 0.144 |
| 0.10 | 1.43 | (1.36, 1.51) | 9.938 (1.71) | −0.144 (−0.02) | 0.147 |
| 0.20 | 1.42 | (1.36, 1.50) | 9.851 (3.60) | −0.056 (−0.01) | 0.129 |
| 0.30 | 1.43 | (1.36, 1.52) | 9.814 (5.81) | −0.018 (−0.03) | 0.122 |
| 0.40 | 1.43 | (1.35, 1.52) | 9.784 (8.36) | −0.015 (−1.21) | 0.124 |
| 0.50 | 1.42 | (1.37, 1.50) | 9.871 (4.44) | −0.017 (−1.22) | 0.108 |
| 0.60 | 1.43 | (1.36, 1.51) | 9.742 (4.26) | 0.123 (−0.02) | 0.119 |
| 0.70 | 1.42 | (1.36, 1.50) | 9.796 (7.88) | 0.125 (0.59) | 0.114 |
| 0.80 | 1.43 | (1.37, 1.52) | 9.475 (5.76) | 0.166 (0.60) | 0.094 |
| 0.90 | 1.44 | (1.38, 1.52) | 9.697 (24.36) | 0.171 (0.87) | 0.088 |
| 1.00 | 1.44 | (1.37, 1.50) | 9.722 (26.15) | 0.151 (1.11) | 0.079 |
| 1.10 | 1.44 | (1.38, 1.52) | 9.755 (26.85) | 0.106 (1.32) | −0.055 |
| 1.20 | 1.44 | (1.38, 1.50) | 9.780 (27.05) | 0.064 (1.91) | −0.079 |
| 1.30 | 1.44 | (1.37, 1.51) | 9.741 (27.11) | 0.034 (1.93) | −0.087 |
| 1.40 | 1.44 | (1.38, 1.51) | 9.799 (26.14) | 0.018 (1.98) | −0.119 |
| 1.50 | 1.44 | (1.37, 1.51) | 9.801 (27.13) | 0.009 (1.65) | −0.145 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caporale, G.M.; Gil-Alana, L.A. Exponential Time Trends in a Fractional Integration Model. Econometrics 2024, 12, 15. https://doi.org/10.3390/econometrics12020015
Caporale GM, Gil-Alana LA. Exponential Time Trends in a Fractional Integration Model. Econometrics. 2024; 12(2):15. https://doi.org/10.3390/econometrics12020015
Chicago/Turabian StyleCaporale, Guglielmo Maria, and Luis Alberiko Gil-Alana. 2024. "Exponential Time Trends in a Fractional Integration Model" Econometrics 12, no. 2: 15. https://doi.org/10.3390/econometrics12020015
APA StyleCaporale, G. M., & Gil-Alana, L. A. (2024). Exponential Time Trends in a Fractional Integration Model. Econometrics, 12(2), 15. https://doi.org/10.3390/econometrics12020015







