Abstract
The COVID-19 pandemic is characterized by a recurring sequence of peaks and troughs. This article proposes a regime-switching unobserved components (UC) approach to model the trend of COVID-19 infections as a function of this ebb and flow pattern. Estimated regime probabilities indicate the prevalence of either an infection up- or down-turning regime for every day of the observational period. This method provides an intuitive real-time analysis of the state of the pandemic as well as a tool for identifying structural changes ex post. We find that when applied to U.S. data, the model closely tracks regime changes caused by viral mutations, policy interventions, and public behavior.
JEL Classification:
C32; C51; I10
1. Introduction
Since its onset in late 2019, the COVID-19 pandemic has permeated next to all facets of public life. Even in the transition of the COVID-19 pandemic to an endemic state, the by now well-known routine of alternating infection peaks and troughs will demand close observation for the foreseeable future (Telenti et al. 2021). However, analyzing and monitoring the state and development of the pandemic is complicated by the nature of the data on COVID-19 case numbers: a glimpse at Figure 1 reveals key characteristics include the strong persistence and nonstationarity of case numbers (Dolton 2021), as well as alternating regimes of increasing and decreasing infections caused by policy interventions, medical innovations, seasonal climate conditions, and the evolution of the virus itself (Doornik et al. 2022; Fiscon et al. 2021). In addition, infection dynamics are overlapped by a seasonal pattern of increasing volatility, generated by a varying number of tests over the days of the week (Bergman et al. 2020), as well as by measurement errors (Hortaçsu et al. 2021).
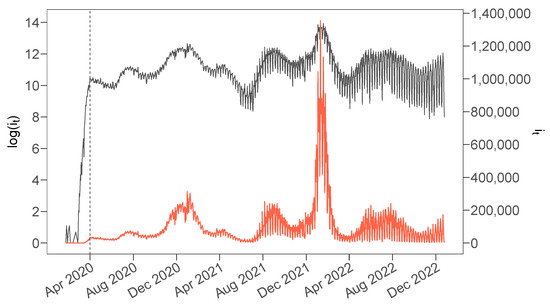
Figure 1.
Daily U.S. COVID-19 infections (orange, right scale) and logarithm of daily infections (gray, left scale). The vertical line (gray, dashed) indicates the 1st of April 2020, the start of the observational period.
While a variety of econometric tools have been utilized to study the dynamics of COVID-19 case numbers, in particular, unobserved components (UC) models have been found successful in capturing the aforementioned characteristics of COVID-19-related data.1 In the early stages of the pandemic, UC models were used to fit linear deterministic trends to COVID-19 case numbers and to identify structural breaks (Hartl et al. 2020; Lee et al. 2021; Liu et al. 2021). With an increasing number of observations available, UC models with stochastic trends have been considered by Moosa (2020) and Doornik et al. (2022), while (stationary) seasonal components were added by Navas Thorakkattle et al. (2022) and Xie (2022), among others. However, appropriately accounting for the alternating peaks and troughs in the trend of COVID-19 case numbers remains an open challenge.
We contribute to the UC literature by explicitly modeling the peak and trough pattern of infection numbers, which has emerged as one of the defining features of the COVID-19 pandemic. For this purpose, we introduce a regime-switching UC model that decomposes log daily COVID-19 infections into trend, seasonal, and cyclical components. While the trend is formulated as a random walk (RW) with drift to capture the long-run dynamics of log new infections, the novelty of our model is that the drift term is made regime-dependent to account for alternating periods of increasing and decreasing infections, as well as for the strong persistence of the respective regime. A seasonal component is added to model the weekly recurring pattern of case numbers, while an autoregressive (AR) term accounts for short-term dependencies in the data.
Regime-switching and mixture models have been studied extensively in the past. We refer to Frühwirth-Schnatter (2006); Kim and Nelson (2017) for an overview. As proposed in Kim (1994); Kim and Nelson (2017, ch. 5), we estimate the trend, seasonal, and cyclical components via the Kim filter, which is an extension of the Kalman filter to regime-switching models: between the prediction and updating step of the Kalman filter, it executes the recursions of Hamilton (1989) to estimate the regime probabilities and thus allows for regime switching in a state-space framework. Parameter estimation is carried out by numerical optimization of the likelihood function, where we make use of an extensive grid search to be robust against local optima. As an alternative, one could also utilize the Expectation–Maximization (EM) algorithm, which has recently been derived for the Kim filter by Degras et al. (2022). As an alternative estimation strategy, we also consider a Bayesian–Gibbs sampling approach. Markov chain Monte Carlo (MCMC) techniques have been widely employed for state-space and especially regime-switching models (see Frühwirth-Schnatter 2006). In contrast to the Kim filter, inference is based on the joint distribution of the state vector, regime probabilities, and additional parameters, rather than on conditional distributions (Frühwirth-Schnatter 2006, ch. 13).
The model is applied to daily U.S. infection data provided by the Johns Hopkins University Center for Systems Science and Engineering (JH/CSSE) (Dong et al. 2020). We found that the estimated regime probabilities closely track the pattern of infection waves throughout the whole chronology of the pandemic. This allows for easy ex post evaluation of the effectiveness of public health interventions or the severity of viral mutations: whereas significant changes tip the system into the opposite regime, harmless mutations or insignificant interventions do not trigger a switch. Moreover, we introduce a nowcasting application that provides an easy-to-understand and concise monitoring tool for the current state of the pandemic.
The plan of this paper is as follows. Section 2 describes the data and methodology. Section 3 presents empirical findings and examines the nowcasting application. Section 4 discusses alternative model specifications, contrasts the Kim filter with a Bayesian–Gibbs sampling approach, and presents a Monte Carlo study to evaluate the reliability of parameter estimates for the preferred specification. Section 5 concludes. All R code to replicate this paper is available at the Github repository https://github.com/Paul-Haimerl/Regime-SW-UC-COVID-19 Repository accessed on 2 April 2023.
2. Data and Methodology
To analyze the state and dynamics of the COVID-19 pandemic, we consider data from the JH/CSSE, which can be downloaded from https://github.com/CSSEGISandData/COVID-19 (accessed on 14 March 2023). Figure 1 sketches the data on reported daily COVID-19 infections from the 22nd of January 2020 to the 25th of December 2022 for the U.S. in both levels and logarithms.
As can be seen, data on daily infections in the early phase of the pandemic are downward-biased due to limited test capacities. As test availability increases, one sees a rapid increase in case numbers in March 2020.2
Accounting for this bias, we select the 1st of April 2020 as the start date for our study. Tracking the pandemic until the end of 2022 provides a total of daily observations.3
To set up our model, let denote new daily U.S. COVID-19 infections and define . The measurement equation of the unobserved components model is then given by
where denotes the trend, models the seasonal component, and is a stationary cyclical component. As Figure 1 suggests, the model is formulated in terms of logarithmic case numbers to reflect the exponential growth of COVID-19. Furthermore, taking logs allows for proportional seasonal effects and measurement errors rather than additive effects (see e.g., Doornik et al. 2021; Lee et al. 2021; Liu et al. 2021).
As typical in the literature, the seasonal component is modeled as a mean-zero deterministic process (Durbin and Koopman 2012; Navas Thorakkattle et al. 2022, ch. 3.2.2)
The cyclical component is to capture short-run dynamics in the data. Therefore, we define as a stationary AR(2) process
L denotes the lag operator . The motivation behind (3) is to allow for some additional short-term dependencies and thus for autocorrelated measurement errors instead of a purely unsystematic additive component with no temporal correlation. Such short-term fluctuations can arise, e.g., due to testing bottlenecks, large-scale public events, the gradual introduction of new policies, or time lags in the reporting of new cases.
Turning to the trend, we specify as a random walk with drift to capture the permanent, smooth low-frequency dynamics, as displayed in Figure 1.
The drift term depends on the current regime indicator . In order to uniquely identify the system, we impose , which declares as the infection down-turning regime and as the infection up-turning regime. Consequently, (4) allows for alternating regimes of increasing and decreasing infections, as well as for different rates of growth and decay. Specification (4) can be justified by visual inspection of Figure 1, which shows that log infections are driven by persistent but alternating phases of increasing and decreasing case numbers. Regime switches may be triggered by major epidemic events that have a persistent impact, such as virus mutations, policy changes, or medical innovations, among others.
The switching behavior between the two states is modeled by a first-order stationary Markov process (Hamilton 1989, ch. 2), with the transition probabilities
The transition probabilities are constrained to satisfy , which resembles the path-dependent behavior of infection-increasing and infection-decreasing regimes.4
In the following, we refer to the specification in (1) to (5) as the D.Seas.C. model. To estimate the parameters we proceed similarly to the UC literature: First, the model is cast in state-space form. Based on the Kim filter, we obtain a conditional likelihood function that combines the prediction and updating steps of the Kalman filter with the regime-switching recursions of Hamilton (1989) (see Kim 1994, ch. 2 for details). Maximizing the conditional likelihood yields the desired parameter estimates and is analogous to the usual prediction error decomposition in the UC literature, which involves the Kalman filter instead of the Kim filter (see Harvey 1989, ch. 4).5 While the estimation results for the D.Seas.C model are presented in the next section, we also discuss generalizations, including a stochastic specification of the seasonal term and the inclusion of a third state in Section 4.
3. Empirical Results
To initiate the Kim filter, we initialize with the number of reported COVID-19 cases on the 31st of May 2020, one day prior to the start of the observational period. The remaining entries to the state vector and the diagonal of the state covariance matrix are initialized diffusely, as is common in the UC literature (see Durbin and Koopman 2012, ch. 5).
To ensure stable estimates of all parameters in and to avoid convergence to local optima, we employ an extensive three-step grid search that covers the relevant parameter space while remaining computationally feasible: In a first global grid search, 30,000 parameter combinations are randomly drawn from uniform distributions with sufficiently wide support to encompass the entire parameter space. To narrow down the locations of local and global optima, we pick the 50 -vectors corresponding to the greatest likelihood values. For each parameter, we store the minimum and maximum value of these 50 combinations, which gives us the range of the relevant parameter space. In the second step, these minimum and maximum values are employed as bounds to construct a finer parameter grid. After computing the likelihood of each grid point, we use the 50 grid points yielding the greatest likelihood as starting values for numerical optimization via the Nelder–Mead algorithm. The optimized parameters corresponding to the greatest log likelihood are then chosen as the final parameter estimate . Figure 2 outlines the parameter distributions as generated by these 50 optimization results.
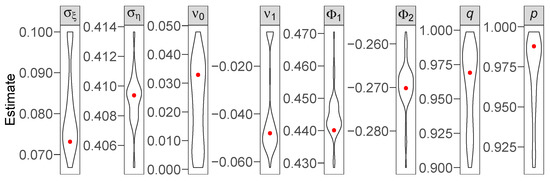
Figure 2.
Parameter-specific kernel densities of the final-step grid search results. The respective best estimate is marked in red. Note that p and q are floored at 90% (see Section 2).
As all parameters of our model (1) to (5) feature a narrow distribution around their best estimate, they appear accurately identified.
Table 1 presents the estimation results and corresponding standard errors.

Table 1.
Maximum likelihood estimation result for the D.Seas.C specification.
Based on the transition probabilities and , it is straightforward to calculate the regime durations. The model estimates an expected duration of days for the down-turning regime and days for the up-turning state. The drift estimates and are interpreted as the average day-to-day change in the trend in log COVID-19 cases. Transforming back into levels gives an average daily decrease of for the down-turning regime on the one hand, and a daily increase of in periods of the up-turning regime on the other. Whereas the COVID-19 infections double roughly every days in an up-turning state, approximately days are required to halve these case numbers again in a subsequent down-turning regime.
Executing the Kim filter and smoothing recursions yields estimates for the state vector. Figure 3 displays the smoothed trend and regime probabilities , together with the noisy measurement of log COVID-19 infections.
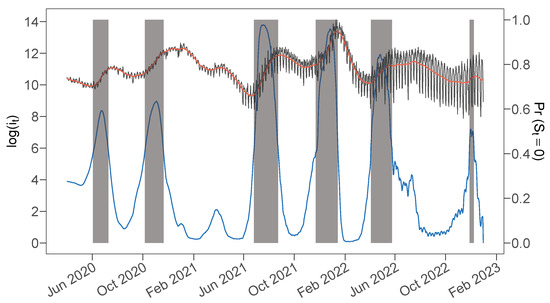
Figure 3.
Smoothed trend estimates (orange, left scale), smoothed regime probabilities (blue, right scale), and log COVID-19 cases (gray, left scale). The smoothed trend is a probability-weighted average of the two regime-specific trend estimates. Infection waves (up-turning regime) as identified by are shaded.
As Figure 3 shows, the model allows for the identification of episodes of up- and down-turning regimes. In particular, it assigns a strong path dependence to the infection regimes, such that long episodes of containment are followed by new infection waves. The increasing proportion of seasonal distortions is attributed to the seasonal and short-run component, and thus does not deteriorate the smoothed trend nor the smoothed regime probabilities. It is only towards the end of the observational horizon that lateral dynamics, strong seasonal fluctuations, and the limited number of future observations complicate the separation of trend, seasonal, and cyclical dynamics. As a consequence, the smoothed trend and regime probabilities appear more erratic.
To illustrate the benefits from our UC model for identifying structural changes ex post, we select a simple threshold of the smoothed regime probability in order to indicate up-turning states. While we leave the choice of a policy rule up to the experts in the field, our arbitrarily chosen threshold is rather cautious (i.e., the probability threshold is set below ) and allows to identify several infectious waves that are shaded in Figure 3. A chosen list of policy measures and events, as reported by the U.S. Centers for Disease Control and Prevention in proximity of the six identified infection waves, is presented below.6
- 3 June 2020–10 July 2020 10.04.: The U.S. is the country with the most reported COVID-19 cases and deaths worldwide. 13.04.: Most states in the U.S. report widespread cases of COVID-19. 13.06.: CDC releases consolidated COVID-19 testing guidelines. 22.06.: The U.S. President extends the temporary suspension on new immigrant visas through the end of the year. 30.06.: Dr. Anthony Fauci warns of new infections overwhelming the healthcare system. 01.07.: The U.S. has more than 50 K new daily COVID-19 cases. 14.07.: The CDC again calls on all people to wear cloth face masks when leaving their homes.
- 6 October 2020–20 November 2020 04.11.: New U.S. COVID-19 cases surpass 100 K in a day. 10.11.: Total cases of COVID-19 in the U.S. surge past 10 M. 13.11.: COVID-19 case numbers spike across the U.S. after Halloween celebrations. 20.11.: The CDC recommends to stay home for Thanksgiving and to avoid contact as case numbers surge.
- 26 June 2021–23 August 2021 27.07.: Amid a Delta variant surge, the CDC releases updated guidance recommending that everyone in areas with high transmission wears a mask. 30.07.: The CDC releases data suggesting that vaccinated people infected with Delta can transmit the virus to others. 23.08.: The FDA fully approves the Pfizer–BioNTech COVID-19 vaccine for all people ages 18 years and older.
- 22 November 2021–14 January 2022 26.11.: The WHO designates the COVID-19 Omicron variant as a “variant of concern”. 20.12.: The CDC releases data estimating that the Omicron variant is around 1.6 times more transmissible than the Delta variant. 27.12.: The CDC shortens the recommended isolation period for people with COVID-19 to six days.
- 4 April 2022–25 May 2022 13.04.: The Omicron subvariant BA.2 makes up more than 85% of all new COVID-19 infections in the U.S. 18.04.: The CDC’s mask mandate for indoor public transportation is struck down in court. 21.04.: The DHS extends the COVID-19 vaccine requirement for all noncitizens entering the U.S.
- 28 November 2022–8 December 2022 08.12.: The FDA authorizes bivalent COVID-19 vaccines for children as young as 6 months of age. 15.12.: The Biden administration announces the COVID-19 Winter Preparedness plan.
In addition to an ex post analysis, we also propose the use of the prediction step of the Kim filter as an easy real-time monitoring device for the pandemic. In case the one-step-ahead prediction of entering the up-turning regime exceeds the aforementioned threshold of 40%, policies may be triggered to quickly shorten the duration of the incoming up-turning regime.
In the following, we evaluate the appropriateness of this monitoring application based on its past propensity for type I (false-positive) and type II (false-negative) errors, as well as on the time lag of filtered predictions relative to the smoothed estimates. To mimic the situation of a decision maker in real time, we start with 150 observations and estimate the parameters , as described at the beginning of this section. We then obtain one-step-ahead predictions for the conditional probability for the up-turning state from the Kim filter. Next, an additional observation is added to the sample, and the procedure repeats. To speed up the procedure, we update the parameter estimates only every two iterations and use the estimates from the previous iteration as starting values for the numerical optimization. Every 500 iterations, an additional grid search, as described at the beginning of this section, is performed to robustify the procedure.
Figure 4 compares the smoothed estimates and the filtered one-step-ahead regime probabilities. Time periods where the one-step-ahead prediction exceeds the 40% threshold are shaded.
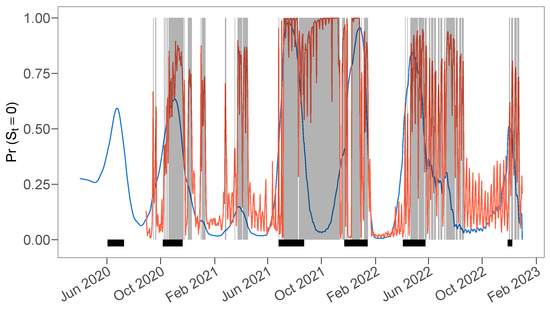
Figure 4.
Smoothed regime probabilities (blue) and filtered regime probabilities (orange) for the up-turning regime. Days on which the filtered predictions exceed a threshold of are shaded. Horizontal black bars denote infection waves based on the smoothed estimates from Figure 3.
As expected, the filtered regime probabilities are significantly more jagged and slightly lag the smoothed estimates due to their smaller information set. Nonetheless, all of the previously established up-turning periods that fall within the scope of the nowcasting exercise are identified by the monitoring device. A feature that underpins the rather conservative nature of the monitoring device is that it detects the onset of an up-turning regime almost in real time. However, this comes at the cost of a higher type I error, i.e., the detection of an up-turning regime that contradicts the smoothed estimates, e.g., at the end of 2021. During the summer of 2022, the monitoring device detected several additional up-turning regimes that are classified as down-turning ones based on the smoothed regime probabilities. However, as Figure 3 indicates, the smoothed trend is actually increasing during that period; however, the magnitude of the increase is small compared with other up-turning periods.
Table 2 contrasts the infection waves, as identified by the smoothed regime probabilities (shaded periods in Figure 3), with those derived from the filtered one-step-ahead predictions (shaded periods in Figure 4).

Table 2.
Periods of the up-turning regime as identified by smoothed estimates and corresponding nowcasting one-step-ahead predictions.
4. Robustness and Discussion
The daily observations of COVID-19 case numbers in Figure 1 display an increasing seasonal variation over time. The deterministic seasonality of the D.Seas.C. model in Equation (2) is not equipped to handle such dynamic behavior. As a result, some of the increasing seasonality may be captured by the estimated cyclical and trend component, which subsequently distorts the regime-switching behavior of the system. A straightforward extension of the model would therefore be to substitute (2) with a stochastic specification capable of assuming seasonal behavior with a progressively increasing variance. One process with such properties is a seasonal unit root (see Bauer and Wagner 2012 for details). It can be added to the state-space model by specifying the new seasonal component
Similar to the traditional UC literature, is set to be a stochastic process with expected average equal to zero (see e.g., Durbin and Koopman 2012, ch. 3.2.2). However, contrary to the deterministic seasonality in (2), the stochastic specification (6) introduces nonstationary dynamics at lag seven. By plugging in and rearranging, (6) can be expressed as , and thus . Therefore, the unit root at lag seven links the current seasonal dynamics to those of the previous week, which generates a repeating seasonal pattern. In each period, a shock is added to , which yields an ever-increasing volatility over time. Figure 5 sketches 100 simulations of and illustrates the oscillating property and nonstationary nature of this seasonal component. Note that (6) differs from unit root seasonal components in the spirit of Harrison and Stevens (1976), which are rather to allow for time-variant seasonal dummies instead of generating an oscillating, diverging behavior.
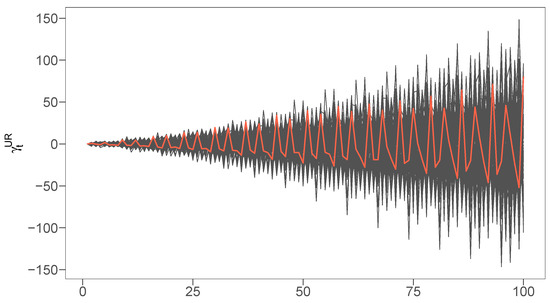
Figure 5.
One hundred simulated paths of the seasonal component , as given in (6) (gray). The orange sample path depicts a single exemplary trajectory.
Table 3 presents the estimation results for substituting the deterministic seasonal term (2) with the unit root specification (6), where the parameter estimates are obtained as before. Furthermore, we provide estimates for specifications that exclude the cyclical component (3) in favor of an unsystematic error term for both the deterministic and stochastic seasonality, respectively.

Table 3.
Maximum likelihood parameter estimates for different model specifications.
Another point of concern is the lateral behavior of infection numbers towards the end of the observational horizon. Ambiguous time periods that cannot be fully attributed to either the up-turning or the down-turning regime may lead to incoherent regime probabilities and thus bias the regime estimates at an earlier stage of the pandemic. As a potential remedy, we introduce a specification involving a third state , during which the drift term of the trend component in (4) is set to zero. Thus, the third state is intended to reflect periods that feature neither a strong upward nor downward trend in the reported case numbers. Table 3 provides estimates of the proposed extensions together with the preferred D.Seas.C. specification displayed in Section 3.
All information criteria clearly favor the more general specifications that include a seasonal unit root process over the D.Seas.C. model presented in Section 3. This is due to the seasonal unit root component, which better grasps the oscillating seasonal pattern along with its increasing volatility over time, as compared with the deterministic seasonal specification. The latter attributes the strong short-run fluctuations to the cyclical component. Since cannot adequately capture the strong seasonal patterns due to its stationary nature, the smoothed cyclical shocks appear to be autocorrelated, which reduces the likelihood and thus increases the information criteria.7 However, even though the observed series can be fitted more accurately overall when the seasonal component is generalized to include a seasonal unit root, it is striking that the trend and regime-switching characteristics vary little across specifications: as illustrated by Figure 6, the smoothed regime probabilities of the different models almost coincide, and only minimal differences between the smoothed trends can be spotted. Therefore, smoothed trend and regime probabilities appear robust to the specification of seasonal and short-run components.
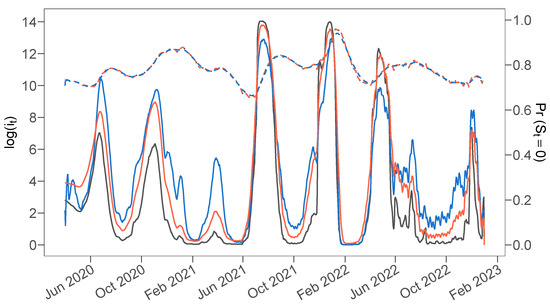
Figure 6.
Smoothed trend (dashed, left scale) and regime probability (right scale) estimates for the preferred D.Seas.C. specification (orange, see Table 1), as well as for the seasonal unit root UR.Seas. model (grey, see Table 3) using the Kim filter. Averaged posterior draws of the trend and regime probabilities for the D.Seas.C. model as derived by the Gibbs sampler are shown in blue (see Table 4).
The introduction of a third state, reflecting episodes of stable case numbers, is able to improve upon the fit of the two-state D.Seas.C. model, but this refinement is not sufficient enough as to be favored by the BIC and HQ information criteria. In addition, the constraint is binding, indicating that the model is not suitable to depict the regime path persistence that is inherent to the pandemic.8 Consequently, we choose the simpler D.Seas.C. model for the remainder of our analysis.
Additional consideration is given to the general estimation strategy. Numerical optimization of a likelihood function, as employed by the Kim filter, has been traditionally regarded as the standard technique for state-space models (Durbin and Koopman 2012, ch. 7). However, Bayesian approaches, especially MCMC techniques, are also a well-developed field in the literature (Frühwirth-Schnatter 2006; Kim and Kang 2019; Luginbuhl and de Vos 1999). In the Bayesian estimation of UC models, the state vector and additional parameters are drawn from a joint distribution, rather than treating the unknown parameters as fixed when maximizing the likelihood numerically. As a consequence, the Bayesian approach bears the advantage that the posteriors incorporate any underlying uncertainty regarding the additional parameters (Luginbuhl and de Vos 1999). Moreover, in order for the Kim filter to account for all possible regime permutations, individual predictions need to be produced in a single time period for a model with M states. Since the path dependencies grow at a rate of , the Kim filter exploits regime probabilities to collapse state vector posteriors into M posteriors at the end of each time period in order to remain computationally feasible (Kim and Nelson 2017, ch. 5.2). Although previous studies have shown that this approximation entails only a small effect on the final estimates, some bias may be introduced by using weighted averages to collapse the posteriors (Kim and Kang 2019). The Bayesian approach, on the other hand, relies on draws from the joint distribution of the state vector, regime probabilities, and additional parameters. The need for a similar approximation step in an effort to track all conditional distributions is eliminated. Inference only requires the convergence of the Markov chain (Frühwirth-Schnatter 2006, ch. 13).
To robustify our findings, we therefore also estimate the preferred D.Seas.C. model using a Gibbs sampling approach. Table 4 portrays the results. Furthermore, Figure 6 includes the averaged trend and regime probability posterior draws.

Table 4.
Gibbs sampling posterior draws for the preferred D.Seas.C. model specification.
Comparing the Kim filter estimates in Table 1 with the Bayesian inference in Table 4, the cyclical dynamics almost perfectly match. However, when analyzing the trend component, the Gibbs sampler provides a lower estimate of the innovation variance while, in parallel, specifying the regimes as less persistent and more dissimilar. Therefore, more variance of the data-generating process is attributed to the regime-switching behavior, driving more frequent regime switches and a greater regime-dependent effect. Nevertheless, even with more volatile regime probability estimates, inference based on the Gibbs sampler exhibits only marginal differences, as Figure 6 reveals.
Regime-switching models are notoriously difficult to estimate. In particular, inference regarding the regime transitions is often based on only a small number of observed switches; thus, it presents a substantial challenge to the practitioner. Therefore, it is a sensible exercise to evaluate and test the performance of the specification at hand via a Monte Carlo simulation study. We simulate a sample path over 1000 time periods for 1000 iterations, where the parameter values as well as the length of the data-generating process are chosen to mimic the reported number of COVID-19 infections. The results of the Monte Carlo study are shown in Table 5.

Table 5.
Result from 1000 Monte Carlo simulations.
Considering the confounding factors that complicate the estimation of regime-switching state-space models, the D.Seas.C. specification in (1) to (5) seems to accurately identify the data-generating process. Only the mean of the estimates of the additional drift parameter deviates from its true value, together with a very high standard deviation. The drift parameter materializes only during episodes where the down-turning regime is turned on (see Equation (4)). As a consequence, in iterations where the randomly generated sample path contains only very few and brief periods of the down-turning regime, any parameter estimate will be imprecise and subject to a high variance. This is also evident from the median of point estimates in Table 5, which is robust against such outlier cases.
Regarding the robustness of the D.Seas.C. model, it can be inferred that a sufficient data history, as well as a sufficient exposure to both regimes, are required in order to accurately estimate a regime-switching model. Examining Figure 1, these conditions appear to be satisfied.
5. Conclusions
In this article, we employ a regime-switching UC model to decompose log daily COVID-19 infections and estimate the probabilities of alternating regimes of up- and down-turning case numbers over an extensive period, spanning from the 1st of April 2020 to the 25th of December 2022.
Our findings indicate that a regime-switching UC model is capable of capturing many characteristics of the COVID-19 pandemic that more inflexible approaches cannot absorb: a regime-dependent drift assumes persistent long-run dynamics; the weekly patterns of reported COVID-19 infections are modeled by a seasonal component; and a stationary autoregressive component captures short-run dynamics and measurement errors.
The results show that: (i) our approach is well-suited to asses ex post the severity and or efficacy of structural changes, such as viral mutations, regulatory loosening and tightening, behavioral changes, and novel therapeutic approaches ex post; (ii) the model can be applied as a policy tool to monitor the state of the pandemic by nowcasting the current propensity of either the up- or down-turning regime being switched on.
Remaining issues arising from highly inconsistent and erratic seasonality could be overcome by extending the model to allow for fractionally integrated components. In particular, this would allow for gradual adjustments of the trend to structural changes (see e.g., Hartl and Jucknewitz 2022). Another possible extension could be the use of time-inhomogeneous transition probabilities, as proposed in Kaufmann (2015). There, an exogenous variable drives the transition matrix over time, allowing for changes in the frequency of regime switches over the course of the pandemic. However, identifying a candidate exogenous variable is difficult and remains an open question for future research.
Author Contributions
Conceptualization, P.H. and T.H.; methodology, P.H. and T.H.; software, P.H.; validation, T.H.; writing—original draft preparation, P.H. and T.H.; writing—review and editing, P.H. and T.H.; visualization, P.H.; supervision, T.H.; funding acquisition, T.H. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by the Institute for Employment Research, 90478 Nuremberg, Germany. Tobias Hartl gratefully acknowledges support through the project 356439312 financed by the German Research Foundation (DFG).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found at the Github COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University https://github.com/CSSEGISandData/COVID-19 (accessed on 14 March 2023).
Acknowledgments
We wish to thank the editor and the anonymous referees for helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AR | Autoregressive |
| EM | Expectation-Maximization |
| JH/CSSE | Johns Hopkins University Center for Systems Science and Engineering |
| RW | Random Walk |
| UC | Unobserved Components |
Notes
| 1 | Harvey (1989) refers to these models as structural time series models. To avoid confusion, the term UC model is used for any state-space model that specifies one or multiple time series as a function of latent components and assigns an interpretation to these components by imposing assumptions on their spectra. |
| 2 | Carvalho et al. (2021) and the U.S. Centers for Disease Control and Prevention (https://www.cdc.gov/museum/timeline/covid19.html, accessed on 14 March 2023), provide an exhaustive timeline regarding the development of the COVID-19 pandemic. Additional data on the number of performed tests, as well as on a wide range of other indicators, can be found at https://ourworldindata.org/coronavirus (accessed on 14 March 2023) (Ritchie et al. 2020). |
| 3 | It is reasonable to assume that the number of reported COVID-19 cases in the last week of the year is again biased downward due to the holiday period. We therefore omit the last week of 2022 and end the observational horizon of our analysis on the 25th of December. |
| 4 | Constraining the parameter space to implies a maximum expected value of three regime switches per 30 days. This is a reasonable constraint given the realized dynamics of the COVID-19 pandemic and, furthermore, speeds up the parameter optimization. |
| 5 | Note that we estimate as part of the state vector. However, the state-space representation of the model in (1) to (5) is not uniquely defined. Different, albeit observationally identical approaches, such as, e.g., the estimation of via ML or constraining to be >0 and flipping labels with , are possible. |
| 6 | A more detailed and extensive overview can be seen at https://www.cdc.gov/museum/timeline/covid19.html (accessed on 14 March 2023) as well as https://www.defense.gov/Spotlights/Coronavirus-DOD-Response/Timeline/ (accessed on 14 March 2023). |
| 7 | Another way to get rid of the strong seasonal pattern would be to take seven-day averages of the log case numbers before estimating the model, which would yield a smooth series and eliminate the seasonal variation. |
| 8 | Since the focus of the analysis lies on identifying coherent periods of up- or down-turning infection regimes, we do not constrain to be >90%. |
References
- Bauer, Dietmar, and Martin Wagner. 2012. A state space canonical form for unit root processes. Econometric Theory 28: 1313–49. [Google Scholar] [CrossRef]
- Bergman, Aviv, Yehonatan Sella, Peter Agre, and Arturo Casadevall. 2020. Oscillations in U.S. COVID-19 incidence and mortality data reflect diagnostic and reporting factors. mSystems 5: e00544–20. [Google Scholar] [CrossRef]
- Carvalho, Thiago, Florian Krammer, and Akiko Iwasaki. 2021. The first 12 months of COVID-19: A timeline of immunological insights. Nature Reviews Immunology 21: 245–56. [Google Scholar] [CrossRef] [PubMed]
- Degras, David, Chee-Ming Ting, and Hernando Ombao. 2022. Markov-switching state-space models with applications to neuroimaging. Computational Statistics & Data Analysis 174: 107525. [Google Scholar] [CrossRef]
- Dolton, Peter. 2021. The statistical challenges of modelling COVID-19. National Institute Economic Review 257: 46–82. [Google Scholar] [CrossRef]
- Dong, Ensheng, Hongru Du, and Lauren Gardner. 2020. An interactive web-based dashboard to track COVID-19 in real time. The Lancet Infectious Diseases 20: 533–34. [Google Scholar] [CrossRef] [PubMed]
- Doornik, Jurgen A., Jennifer L. Castle, and David F. Hendry. 2021. Modeling and forecasting the COVID-19 pandemic time-series data. Social Science Quarterly 102: 2070–87. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., Jennifer L. Castle, and David F. Hendry. 2022. Short-term forecasting of the Coronavirus pandemic. International Journal of Forecasting 38: 453–66. [Google Scholar] [CrossRef]
- Durbin, James, and Siem Jan Koopman. 2012. Time Series Analysis by State Space Methods: Second Edition. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Fiscon, Giulia, Francesco Salvadore, Valerio Guarrasi, Anna Rosa Garbuglia, and Paola Paci. 2021. Assessing the impact of data-driven limitations on tracing and forecasting the outbreak dynamics of COVID-19. Computers in Biology and Medicine 135: 104657. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, Sylvia. 2006. Finite Mixture and Markov Switching Models. New York: Springer. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Harrison, Peter J., and C. F. Stevens. 1976. Bayesian forecasting. Journal of the Royal Statistical Society: Series B 38: 205–28. [Google Scholar] [CrossRef]
- Hartl, Tobias, and Roland Jucknewitz. 2022. Approximate state space modelling of unobserved fractional components. Econometric Reviews 41: 75–98. [Google Scholar] [CrossRef]
- Hartl, Tobias, Klaus Wälde, and Enzo Weber. 2020. Measuring the impact of the German public shutdown on the spread of COVID-19. Covid Economics: Vetted and Real-Time Papers 1: 25–32. [Google Scholar]
- Harvey, Andrew C. 1989. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge: Cambridge University Press. [Google Scholar]
- Hortaçsu, Ali, Jiarui Liu, and Timothy Schwieg. 2021. Estimating the fraction of unreported infections in epidemics with a known epicenter: An application to COVID-19. Journal of Econometrics 220: 106–29. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, Sylvia. 2015. K-state switching models with time-varying transition distributions—Does loan growth signal stronger effects of variables on inflation? Journal of Econometrics 187: 82–94. [Google Scholar] [CrossRef]
- Kim, Chang-Jin. 1994. Dynamic linear models with Markov-switching. Journal of Econometrics 60: 1–22. [Google Scholar] [CrossRef]
- Kim, Chang-Jin, and Charles R. Nelson. 2017. State-Space Models with Regime Switching: Classical and Gibbs-Sampling Approaches with Applications. Cambridge: MIT Press. [Google Scholar] [CrossRef]
- Kim, Young Min, and Kyu Ho Kang. 2019. Likelihood inference for dynamic linear models with Markov switching parameters: On the efficiency of the Kim filter. Econometric Reviews 38: 1109–30. [Google Scholar] [CrossRef]
- Lee, Sokbae, Yuan Liao, Myung Hwan Seo, and Youngki Shin. 2021. Sparse HP filter: Finding kinks in the COVID-19 contact rate. Journal of Econometrics 220: 158–80. [Google Scholar] [CrossRef] [PubMed]
- Liu, Laura, Hyungsik Roger Moon, and Frank Schorfheide. 2021. Panel forecasts of country-level COVID-19 infections. Journal of Econometrics 220: 2–22. [Google Scholar] [CrossRef] [PubMed]
- Luginbuhl, Rob, and Aart de Vos. 1999. Bayesian analysis of an unobserved-component time series model of GDP with Markov-switching and time-varying growths. Journal of Business & Economic Statistics 17: 456–65. [Google Scholar] [CrossRef]
- Moosa, Imad A. 2020. The effectiveness of social distancing in containing COVID-19. Applied Economics 52: 6292–05. [Google Scholar] [CrossRef]
- Navas Thorakkattle, Muhammed, Shazia Farhin, and Athar Ali Khan. 2022. Forecasting the trends of COVID-19 and causal impact of vaccines using Bayesian structural time series and ARIMA. Annals of Data Science 9: 1025–47. [Google Scholar] [CrossRef]
- Ritchie, Hannah, Edouard Mathieu, Lucas Rodés-Guirao, Cameron Appel, Charlie Giattino, Esteban Ortiz-Ospina, Joe Hasell, Bobbie Macdonald, Diana Beltekian, and Max Roser. 2020. Coronavirus pandemic (COVID-19). Our World in Data. Available online: https://ourworldindata.org/coronavirus (accessed on 14 March 2023).
- Telenti, Amalio, Ann Arvin, Lawrence Corey, Davide Corti, Michael S. Diamond, Adolfo García-Sastre, Robert F. Garry, Edward C. Holmes, Phillip S. Pang, and Herbert W. Virgin. 2021. After the pandemic: Perspectives on the future trajectory of COVID-19. Nature 596: 495–504. [Google Scholar] [CrossRef]
- Xie, Liming. 2022. The analysis and forecasting COVID-19 cases in the United States using Bayesian structural time series models. Biostatistics & Epidemiology 6: 1–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).