Modelling and Diagnostics of Spatially Autocorrelated Counts
Abstract
1. Introduction
2. Spatial Lag Models for Count Data
3. Diagnostics
3.1. Non-Randomised Probability Integral Transform
3.2. Scoring Rules
3.3. Relative Deviations Plot
4. Monte Carlo Study
4.1. Data Generating Process
4.2. Monte Carlo Results
5. Empirical Application
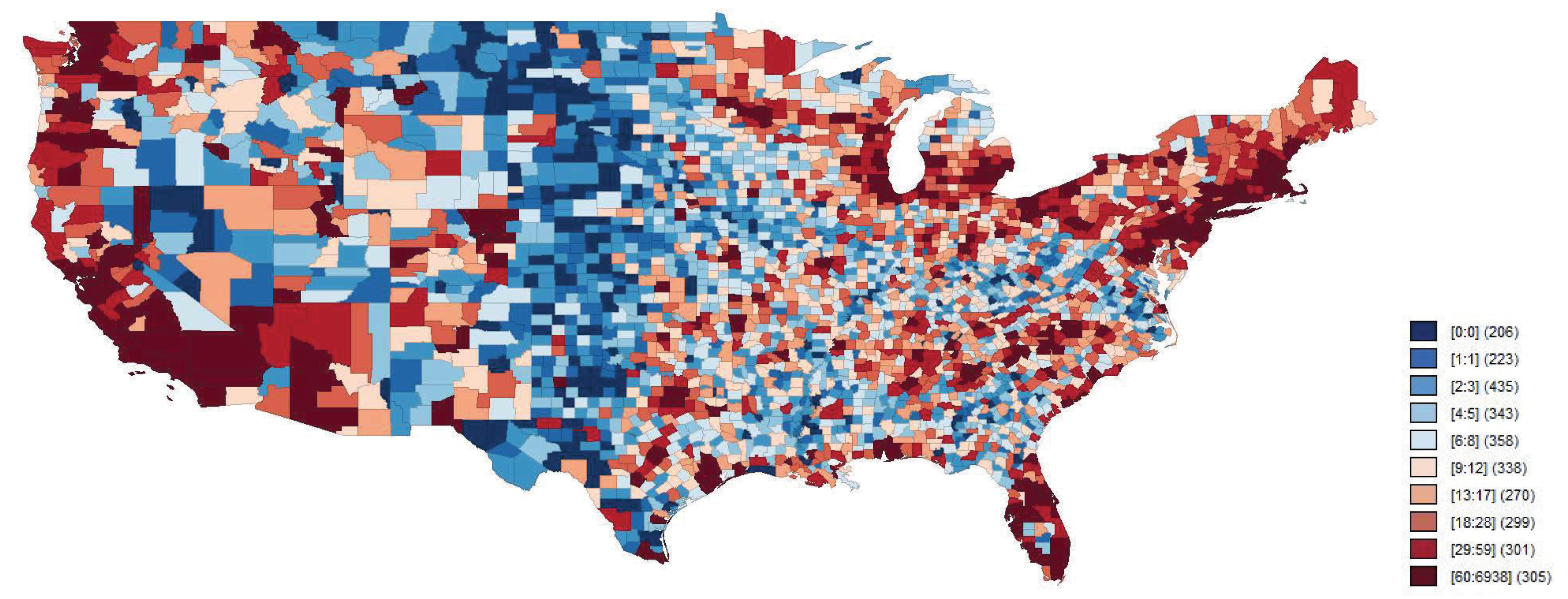
5.1. Data
5.2. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Proença and Glórias (2021) also employed the SAR-Poisson specification (1), but proposed an alternative two-step Poisson pseudo-maximum likelihood approach to solve the problem of taking logarithms from zero counts. See also Simões et al. (2017), who employed the SAR-Poisson model of Lambert et al. (2016) to analyse the spatial correlation of calls to the Portugese National Healthline. The authors proposed a spatial lag Poisson Bayesian model to be estimated by a suitably augmented Nested Laplace Approximation (INLA) developed by Gómez-Rubio et al. (2015). |
| 2 | Besag’s model has been used frequently to model spatial heterogeneity in context of a count data model (see, e.g., Gschlößl and Czado 2007; Gschlößl and Czado 2008; Apardian and Smirnov 2020). |
| 3 | See the very instructive discussion on this in Lambert et al. (2016). |
References
- Apardian, Rebecca E., and Oleg Smirnov. 2020. An analysis of pedestrian crashes using a spatial count data model. Papers in Regional Science 99: 1317–38. [Google Scholar] [CrossRef]
- Besag, Julian. 1974. Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society Series B 36: 192–236. [Google Scholar] [CrossRef]
- Besag, Julian. 1975. Statistical Analysis of Non-lattice Data. The Statistician 24: 179–95. [Google Scholar] [CrossRef]
- Billé, Anna Gloria, and Giuseppe Arbia. 2019. Spatial limited dependent variable models: A review focused on specification, estimation, and health economics applications. Journal of Economic Surveys 33: 1531–54. [Google Scholar] [CrossRef]
- Blundell, Richard, Rachel Griffith, and Frank Windmeijer. 2002. Individual effects and dynamics in count data models. Journal of Econometrics 108: 113–31. [Google Scholar] [CrossRef]
- Cox, David R. 1981. Statistical analysis of time series: Some recent developements. Scandinavian Journal of Statistics 8: 93–115. [Google Scholar]
- Czado, Claudia, Tilmann Gneiting, and Leonhard Held. 2009. Predictive model assessment for count data. Biometrics 65: 1254–61. [Google Scholar] [CrossRef] [PubMed]
- Diebold, Francis X., Todd A. Gunther, and Anthony S. Tay. 1998. Evaluating Density Forecasts with Applications to Financial Risk Management. International Economic Review 39: 863. [Google Scholar] [CrossRef]
- Geman, Stuart, and Donald Geman. 1984. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6: 721–41. [Google Scholar] [CrossRef] [PubMed]
- Glaser, Stephanie. 2017. A review of spatial econometric models for count data. In Hohenheim Discussion Papers in Business, Economics and Social Sciences, No. 19-2017. Stuttgart: Universität Hohenheim. [Google Scholar]
- Gómez-Rubio, Virgilio, Roger Bivand, and Håvard Rue. 2015. A New Latent Class to Fit Spatial Econometrics Models with Integrated Nested Laplace Approximations. Procedia Environmental Sciences 27: 116–18. [Google Scholar] [CrossRef][Green Version]
- Gschlößl, Susanne, and Claudia Czado. 2007. Spatial modelling of claim frequency and claim size in non-life insurance. Scandinavian Actuarial Journal 2007: 202–25. [Google Scholar] [CrossRef]
- Gschlößl, Susanne, and Claudia Czado. 2008. Modelling count data with overdispersion and spatial effects. Statistical Papers 49: 531–52. [Google Scholar] [CrossRef]
- Jensen, Jens Ledet, and Jasper Moller. 1991. Pseudolikelihood for exponential family models of spatial point processes. Annals of Applied Probability 1: 445–61. [Google Scholar] [CrossRef]
- Jung, Robert C., Brendan P. M. McCabe, and Andrew R. Tremayne. 2016. Model validation and diagnostics. In Handbook of Discrete Valued Time Series. Edited by Richard A. Davis, Scott H. Holan, Robert Lund and Nalini Ravishanker. Boca Raton: Chapman and Hall, pp. 189–218. [Google Scholar]
- Jung, Robert C., and Andrew R. Tremayne. 2011. Useful models for time series of counts or simply wrong ones? AStA Advances in Statistical Analysis 95: 59–91. [Google Scholar] [CrossRef]
- Lambert, Dayton M., Jason P. Brown, and Raymond J. G. M. Florax. 2016. A two-step estimator for a spatial lag model of counts: Theory, small sample performance and an application. Regional Science and Urban Economics 40: 241–52. [Google Scholar] [CrossRef]
- LeSage, James P., and R. Kelley Pace. 2009. Introduction to Spatial Econometrics. New York: Chapman and Hall/CRC-Press. [Google Scholar]
- Liesenfeld, Roman, Jean-François Richard, and Jan Vogler. 2016. Likelihood Evaluation of High-Dimensional Spatial Latent Gaussian Models with Non–Gaussian Response Variables. In Spatial Econometrics: Qualitative and Limited Dependent Variables. Advances in Econometrics. Bingley: Emerald Group Publishing Limited, vol. 37, pp. 35–77. [Google Scholar]
- Long, J. Scott. 1997. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks: Sage Publications, Inc. [Google Scholar]
- Proença, Isabel, and Ludgero Glórias. 2021. Revisiting the spatial autoregressive exponential model for counts and other nonnegative variables, with application to the knowledge production function. Sustainability 13: 2843. [Google Scholar] [CrossRef]
- Rosenblatt, Murray. 1952. Remarks on a multivariate transformation. Annals of Mathematical Statistics 23: 470–72. [Google Scholar] [CrossRef]
- Simões, Paula, M. Lucília Carvalho, Sandro Aleixo, Sérgio Gomes, and Isabel Natário. 2017. A spatial econometric analysis of the calls to the Portugese national health line. Econometrics 5: 24. [Google Scholar] [CrossRef]
- Varin, B. Cristiano, and Paolo Vidoni. 2005. A note on composite likelihood inference and model selection. Biometrika 92: 519–28. [Google Scholar] [CrossRef]
- Vecchia, A. V. 1998. Estimation and model identification for continuous spatial processes. Journal of the Royal Statistical Society Series B 50: 297–312. [Google Scholar] [CrossRef]




| 100 | 250 | 500 | 1000 | 5000 | 10,000 | |
|---|---|---|---|---|---|---|
| RMSE | ||||||
| 0 | 0.0444 | 0.0159 | 0.0141 | 0.0090 | 0.0040 | 0.0023 |
| 0.2 | 0.0233 | 0.0221 | 0.0210 | 0.0146 | 0.0059 | 0.0041 |
| 0.4 | 0.0417 | 0.0350 | 0.0205 | 0.0136 | 0.0059 | 0.0044 |
| 0.6 | 0.0497 | 0.0291 | 0.0175 | 0.0139 | 0.0058 | 0.0038 |
| 0.8 | 0.0455 | 0.0224 | 0.0152 | 0.0082 | 0.0050 | 0.0043 |
| BIAS | ||||||
| 0 | −0.0034 | −0.0007 | −0.0006 | −0.0002 | 0.0001 | −0.0001 |
| 0.2 | −0.0009 | −0.0018 | −0.0021 | −0.0016 | −0.0010 | −0.0010 |
| 0.4 | −0.0040 | −0.0041 | −0.0018 | −0.0015 | −0.0009 | −0.0012 |
| 0.6 | −0.0048 | −0.0030 | −0.0014 | −0.0010 | −0.0009 | −0.0007 |
| 0.8 | −0.0113 | −0.0045 | −0.0036 | −0.0030 | −0.0030 | −0.0031 |
| RMSE | ||||||
| 0 | 0.1493 | 0.0819 | 0.0624 | 0.0425 | 0.0188 | 0.0118 |
| 0.2 | 0.1174 | 0.0926 | 0.0778 | 0.0560 | 0.0239 | 0.0159 |
| 0.4 | 0.2378 | 0.1554 | 0.0842 | 0.0628 | 0.0281 | 0.0195 |
| 0.6 | 0.2951 | 0.1871 | 0.1042 | 0.0900 | 0.0351 | 0.0237 |
| 0.8 | 0.6341 | 0.2598 | 0.1649 | 0.0732 | 0.0447 | 0.0331 |
| BIAS | ||||||
| 0 | 0.0019 | 0.0012 | 0.0001 | 0.0007 | −0.0011 | 0.0001 |
| 0.2 | −0.0007 | 0.0045 | 0.0051 | 0.0049 | 0.0040 | 0.0042 |
| 0.4 | 0.0058 | 0.0103 | 0.0056 | 0.0058 | 0.0047 | 0.0055 |
| 0.6 | −0.0002 | 0.0083 | 0.0051 | 0.0057 | 0.0062 | 0.0054 |
| 0.8 | −0.0104 | 0.0026 | 0.0011 | −0.0011 | 0.0027 | 0.0032 |
| RMSE | ||||||
| 0 | 0.0645 | 0.0422 | 0.0296 | 0.0206 | 0.0093 | 0.0062 |
| 0.2 | 0.0763 | 0.0426 | 0.0346 | 0.0238 | 0.0107 | 0.0071 |
| 0.4 | 0.0955 | 0.0569 | 0.0356 | 0.0269 | 0.0114 | 0.0084 |
| 0.6 | 0.1021 | 0.0704 | 0.0401 | 0.0326 | 0.0130 | 0.0096 |
| 0.8 | 0.1683 | 0.0844 | 0.0550 | 0.0360 | 0.0173 | 0.0123 |
| BIAS | ||||||
| 0 | −0.0002 | −0.0004 | 0.0002 | −0.0001 | 0.0006 | 0.0001 |
| 0.2 | 0.0014 | −0.0012 | −0.0005 | −0.0009 | −0.0010 | −0.0007 |
| 0.4 | −0.0008 | −0.0017 | −0.0012 | −0.0008 | −0.0008 | −0.0009 |
| 0.6 | −0.0029 | −0.0008 | 0.0001 | −0.0013 | −0.0016 | −0.0006 |
| 0.8 | 0.0057 | −0.0012 | −0.0003 | 0.0005 | −0.0008 | −0.0008 |
| RMSE | ||||||
| 0 | 0.0274 | 0.0135 | 0.0119 | 0.0075 | 0.0033 | 0.0021 |
| 0.2 | 0.0131 | 0.0145 | 0.0140 | 0.0096 | 0.0040 | 0.0027 |
| 0.4 | 0.0323 | 0.0263 | 0.0141 | 0.0099 | 0.0045 | 0.0029 |
| 0.6 | 0.0594 | 0.0257 | 0.0149 | 0.0136 | 0.0054 | 0.0037 |
| 0.8 | 0.1056 | 0.0401 | 0.0254 | 0.0090 | 0.0064 | 0.0046 |
| BIAS | ||||||
| 0 | −0.0006 | −0.0003 | −0.0001 | −0.0001 | 0.0001 | 0.0001 |
| 0.2 | −0.0003 | −0.0007 | −0.0011 | −0.0008 | −0.0006 | −0.0007 |
| 0.4 | −0.0013 | −0.0020 | −0.0009 | −0.0011 | −0.0008 | −0.0008 |
| 0.6 | 0.0008 | −0.0016 | −0.0012 | −0.0009 | −0.0008 | −0.0010 |
| 0.8 | 0.0023 | −0.0008 | −0.0005 | −0.0001 | −0.0005 | −0.0004 |
| 100 | 250 | 500 | 1000 | 5000 | 10,000 | |
|---|---|---|---|---|---|---|
| RMSE | ||||||
| 0 | 0.0581 | 0.0352 | 0.0162 | 0.0102 | 0.0041 | 0.0031 |
| 0.2 | 0.0705 | 0.0438 | 0.0333 | 0.0229 | 0.0125 | 0.0102 |
| 0.4 | 0.0653 | 0.0580 | 0.0413 | 0.0276 | 0.0148 | 0.0108 |
| 0.6 | 0.1113 | 0.0652 | 0.0391 | 0.0291 | 0.0129 | 0.0103 |
| 0.8 | 0.0910 | 0.0539 | 0.0429 | 0.0305 | 0.0129 | 0.0100 |
| BIAS | ||||||
| 0 | −0.0101 | −0.0064 | −0.0009 | −0.0008 | 0.0001 | −0.0001 |
| 0.2 | −0.0189 | −0.0116 | −0.0103 | −0.0095 | −0.0080 | −0.0079 |
| 0.4 | −0.0099 | −0.0132 | −0.0129 | −0.0096 | −0.0087 | −0.0074 |
| 0.6 | −0.0299 | −0.0157 | −0.0087 | −0.0067 | −0.0049 | −0.0054 |
| 0.8 | −0.0291 | −0.0118 | −0.0108 | −0.0102 | −0.0057 | −0.0056 |
| RMSE | ||||||
| 0 | 0.2771 | 0.1549 | 0.0990 | 0.0653 | 0.0300 | 0.0196 |
| 0.2 | 0.3330 | 0.1987 | 0.1498 | 0.1091 | 0.0594 | 0.0493 |
| 0.4 | 0.3564 | 0.2672 | 0.1868 | 0.1402 | 0.0864 | 0.0706 |
| 0.6 | 0.7309 | 0.4176 | 0.2675 | 0.1958 | 0.1069 | 0.0908 |
| 0.8 | 1.2300 | 0.6524 | 0.5012 | 0.3573 | 0.1637 | 0.1334 |
| BIAS | ||||||
| 0 | 0.0142 | 0.0124 | 0.0003 | 0.0017 | −0.0028 | 0.0016 |
| 0.2 | 0.0581 | 0.0419 | 0.0436 | 0.0460 | 0.0397 | 0.0395 |
| 0.4 | 0.0481 | 0.0562 | 0.0663 | 0.0617 | 0.0647 | 0.0590 |
| 0.6 | 0.0836 | 0.0804 | 0.0897 | 0.0761 | 0.0732 | 0.0726 |
| 0.8 | 0.0421 | 0.0439 | 0.0761 | 0.1181 | 0.0928 | 0.0951 |
| RMSE | ||||||
| 0 | 0.1297 | 0.0744 | 0.0527 | 0.0373 | 0.0172 | 0.0113 |
| 0.2 | 0.1598 | 0.0935 | 0.0679 | 0.0470 | 0.0222 | 0.0168 |
| 0.4 | 0.1734 | 0.1092 | 0.0767 | 0.0560 | 0.0290 | 0.0207 |
| 0.6 | 0.2461 | 0.1619 | 0.1071 | 0.0761 | 0.0368 | 0.0282 |
| 0.8 | 0.6660 | 0.2615 | 0.1854 | 0.1267 | 0.0574 | 0.0428 |
| BIAS | ||||||
| 0 | −0.0037 | −0.0024 | −0.0002 | −0.0003 | 0.0018 | −0.0007 |
| 0.2 | −0.0105 | −0.0078 | −0.0090 | −0.0096 | −0.0078 | −0.0075 |
| 0.4 | −0.0132 | −0.0126 | −0.0118 | −0.0108 | −0.0140 | −0.0112 |
| 0.6 | −0.0076 | −0.0132 | −0.0180 | −0.0165 | −0.0164 | −0.0157 |
| 0.8 | −0.0230 | −0.0058 | −0.0153 | −0.0221 | −0.0200 | −0.0198 |
| RMSE | ||||||
| 0 | 0.0572 | 0.0363 | 0.0202 | 0.0142 | 0.0061 | 0.0044 |
| 0.2 | 0.0601 | 0.0397 | 0.0311 | 0.0209 | 0.0118 | 0.0098 |
| 0.4 | 0.0628 | 0.0520 | 0.0367 | 0.0271 | 0.0163 | 0.0139 |
| 0.6 | 0.1147 | 0.0784 | 0.0436 | 0.0355 | 0.0195 | 0.0175 |
| 0.8 | 0.1742 | 0.1007 | 0.0779 | 0.0650 | 0.0278 | 0.0248 |
| BIAS | ||||||
| 0 | −0.0040 | −0.0033 | −0.0004 | −0.0004 | 0.0002 | −0.0003 |
| 0.2 | −0.0129 | −0.0095 | −0.0094 | −0.0091 | −0.0079 | −0.0079 |
| 0.4 | −0.0107 | −0.0131 | −0.0142 | −0.0133 | −0.0127 | −0.0121 |
| 0.6 | −0.0224 | −0.0198 | −0.0171 | −0.0156 | −0.0147 | −0.0146 |
| 0.8 | −0.0221 | −0.0167 | −0.0166 | −0.0250 | −0.0183 | −0.0198 |
| RMSE | ||||||
| 0 | 0.0554 | 0.0358 | 0.0243 | 0.0174 | 0.0075 | 0.0056 |
| 0.2 | 0.0503 | 0.0314 | 0.0225 | 0.0155 | 0.0077 | 0.0065 |
| 0.4 | 0.0424 | 0.0295 | 0.0213 | 0.0161 | 0.0098 | 0.0092 |
| 0.6 | 0.0406 | 0.0256 | 0.0195 | 0.0145 | 0.0095 | 0.0087 |
| 0.8 | 0.0353 | 0.0227 | 0.0165 | 0.0125 | 0.0079 | 0.0067 |
| BIAS | ||||||
| 0 | −0.0129 | −0.0050 | −0.0028 | −0.0012 | −0.0005 | −0.0002 |
| 0.2 | −0.0088 | −0.0020 | 0.0004 | 0.0022 | 0.0036 | 0.0042 |
| 0.4 | −0.0034 | −0.0002 | 0.0056 | 0.0071 | 0.0075 | 0.0081 |
| 0.6 | 0.0035 | 0.0025 | 0.0082 | 0.0074 | 0.0078 | 0.0077 |
| 0.8 | −0.0004 | 0.0040 | 0.0046 | 0.0058 | 0.0061 | 0.0056 |
| Dependent variable | subirths | Single unit start-ups in the lower 48 United States during 2000–2004 in the manufacturing sector (NAICS 31-33) |
| Agglomeration economies | msemp | Manufactoring share of employment |
| tfdense | Total establishment density (in 100 s) | |
| pel10emp | Percent of manufacturing establishments with less than 10 employees | |
| pem100emp | Percent of manufacturing establishments with more than 100 employees | |
| Market structure | mhhi | Median household income (in 1000 s) |
| pop | Population (in 10,000 s) | |
| cclass | Share of workers in creative occupations | |
| Labor availability and cost | uer | Unemployment rate |
| pedas | Pecent of adults with an associate’s degree | |
| avg_wage | Average wage per job (in 1000 s) | |
| netflow_emp | Net flow of wages per commuter (in 1000 s) | |
| Infrastucture | proad | Public road density |
| interst | Interstate highway miles | |
| hwy_pc | Government expenditures on highways per capita (in 100 s) | |
| avland | Percent of farmland to total county | |
| Fiscal policy | educ_pc | Government expenditures on education per capita (in 100 s) |
| bci | State tax business climate index (higher values indicate more favorable business climates) | |
| Area | metro | Dummy variable indentifying counties as belonging to metropolitan areas |
| micro | Dummy variable indentifying counties as belonging to micropolitan areas |
| Spatial | Non-Spatial | Spatial | Non-Spatial | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Poisson | NB | Poisson | NB2 | Poisson | NB | Poisson | NB2 | |
| 0.288 *** | 0.166 *** | awage | 0.033 *** | −0.058 *** | 0.019 *** | −0.038 *** | |||
| (0.043) | (0.022) | (0.008) | (0.012) | (0.007) | (0.007) | ||||
| const | −1.707 *** | −1.120 *** | −0.934 *** | −1.066 *** | netflow | 0.003 | −0.027 | 0.002 | −0.016 *** |
| (0.397) | (0.249) | (0.281) | (0.195) | (0.003) | (0.006) | (0.820) | (0.003) | ||
| msemp | 0.035 *** | 0.053 *** | 0.031 *** | 0.050 *** | proad | 0.093 *** | 0.084 *** | 0.103 *** | 0.083 *** |
| (0.006) | (0.003) | (0.004) | (0.002) | (0.023) | (0.024) | (0.018) | (0.022) | ||
| pelt10 | −0.007 ** | 0.005 *** | −0.002 | 0.005 *** | interst | 0.009 *** | 0.005 *** | 0.007 *** | 0.005 *** |
| (0.003) | (0.001) | (0.002) | (0.001) | (0.001) | (0.001) | (0.001) | (0.001) | ||
| pemt100 | −0.034 *** | −0.023 *** | −0.029 *** | −0.018 *** | avland | −0.007 *** | −0.006 *** | −0.009 *** | −0.007 *** |
| (0.006) | (0.003) | (0.004) | (0.002) | (0.002) | (0.001) | (0.001) | (0.001) | ||
| tfdens | −0.013 | −0.046 *** | 0.006 | −0.053 *** | bci | 0.128 *** | 0.032 | 0.080 | 0.034 |
| (0.011) | (0.016) | (0.010) | (0.013) | (0.042) | (0.021) | (0.037) | (0.015) | ||
| mhhi | −0.034 *** | 0.024 ** | 0.000 | 0.027 *** | educpc | 0.006 *** | 0.006 ** | 0.004 | 0.004 |
| (0.008) | (0.010) | (0.009) | (0.005) | (0.002) | (0.003) | (0.002) | (0.003) | ||
| pop | 0.002 *** | 0.017 *** | 0.002 *** | 0.018 *** | hwypc | −0.039 | −0.132 | −0.030 | −0.028 |
| (0.000) | (0.003) | (0.000) | (0.003) | (0.023) | (0.031) | (0.019) | (0.021) | ||
| cclass | 0.088 *** | 0.101 *** | 0.048 *** | 0.082 *** | metro | 1.630 *** | 1.017 *** | 1.265 *** | 0.845 *** |
| (0.011) | (0.007) | (0.013) | (0.005) | (0.157) | (0.081) | (0.092) | (0.054) | ||
| uer | 0.037 | 0.076 *** | 0.073 *** | 0.080 *** | micro | 0.839 *** | 0.645 *** | 0.573 *** | 0.546 *** |
| (0.037) | (0.021) | (0.022) | (0.013) | (0.119) | (0.055) | (0.063) | (0.038) | ||
| pedas | 0.150 *** | 0.062 *** | 0.130 *** | 0.044 *** | 0.403 *** | 0.437 *** | |||
| (0.022) | (0.011) | (0.021) | (0.009) | (0.026) | (0.024) | ||||
| Log L | −28,149 | −10,300 | −32,248 | −10,401 | |||||
| logs | 9.002 | 3.348 | 9.917 | 3.379 | |||||
| qs | −0.027 | −0.073 | −0.017 | −0.070 | |||||
| rps | 14.035 | 22.836 | 15.244 | 33.858 | |||||
| Poisson Spatial Reg. | NB Spatial Reg. | Poisson | NB2 | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Total M.E. | Direct M.E. | Indirect M.E. | Total M.E. | Direct M.E. | Indirect M.E. | Direct M.E. | Direct M.E. |
| msemp | 0.377 *** | 0.198 *** | 0.148 *** | 0.516 *** | 0.339 *** | 0.116 *** | 0.326 *** | 0.463 *** |
| (0.061) | (0.040) | (0.032) | (0.032) | (0.026) | (0.018) | (0.044) | (0.024) | |
| pelt10 | −0.065 ** | −0.034 ** | −0.025 ** | 0.050 *** | 0.033 *** | 0.011 *** | −0.022 | 0.048 *** |
| (0.028) | (0.014) | (0.013) | (0.013) | (0.009) | (0.003) | (0.020) | (0.011) | |
| pemt100 | −0.366 *** | −0.192 *** | −0.144 *** | −0.226 *** | −0.148 *** | −0.051 *** | −0.314 *** | −0.171 *** |
| (0.062) | (0.035) | (0.035) | (0.034) | (0.021) | (0.012) | (0.038) | (0.023) | |
| tfdens | −0.140 | −0.074 | −0.055 | −0.456 *** | −0.299 *** | −0.102 *** | 0.066 | −0.493 *** |
| (0.123) | (0.065) | (0.050) | (0.157) | (0.109) | (0.034) | (0.107) | (0.125) | |
| mhhi | −0.366 *** | −0.192 *** | −0.144 *** | 0.237 ** | 0.155 ** | 0.053 ** | 0.002 | 0.249 *** |
| (0.095) | (0.046) | (0.049) | (0.103) | (0.064) | (0.026) | (0.091) | (0.049) | |
| pop | 0.022 *** | 0.011 *** | 0.008 *** | 0.163 *** | 0.107 *** | 0.037 *** | 0.025 *** | 0.170 *** |
| (0.005) | (0.003) | (0.002) | (0.033) | (0.023) | (0.008) | (0.005) | (0.030) | |
| cclass | 0.948 *** | 0.498 *** | 0.373 *** | 0.987 *** | 0.648 *** | 0.222 *** | 0.516 *** | 0.764 *** |
| (0.125) | (0.075) | (0.082) | (0.069) | (0.055) | (0.037) | (0.136) | (0.049) | |
| uer | 0.399 | 0.209 | 0.157 | 0.745 *** | 0.489 *** | 0.167 *** | 0.779 *** | 0.750 *** |
| (0.398) | (0.212) | (0.159) | (0.215) | (0.133) | (0.059) | (0.236) | (0.124) | |
| pedas | 1.616 *** | 0.848 *** | 0.636 *** | 0.608 *** | 0.399 *** | 0.136 *** | 1.387 *** | 0.415 *** |
| (0.256) | (0.135) | (0.157) | (0.109) | (0.076) | (0.031) | (0.211) | (0.084) | |
| awage | 0.356 *** | 0.187 *** | 0.140 *** | −0.565 *** | −0.371 *** | −0.127 *** | 0.198 *** | −0.354 *** |
| (0.089) | (0.047) | (0.044) | (0.129) | (0.072) | (0.040) | (0.075) | (0.062) | |
| netflow | 0.032 | 0.017 | 0.013 | −0.267 *** | −0.175 *** | −0.060 *** | 0.025 | −0.146 |
| (0.027) | (0.014) | (0.011) | (0.063) | (0.035) | (0.020) | (0.024) | (0.025) | |
| proad | 1.002 *** | 0.526 *** | 0.395 *** | 0.825 *** | 0.542 *** | 0.185 *** | 1.097 *** | 0.776 *** |
| (0.251) | (0.147) | (0.114) | (0.236) | (0.155) | (0.064) | (0.194) | (0.213) | |
| interst | 0.086 *** | 0.045 *** | 0.034 *** | 0.049 *** | 0.032 *** | 0.011 *** | 0.078 *** | 0.044 *** |
| (0.014) | (0.008) | (0.008) | (0.009) | (0.006) | (0.003) | (0.011) | (0.007) | |
| avland | −0.075 *** | −0.040 *** | −0.030 *** | −0.056 *** | −0.037 *** | −0.013 *** | −0.092 *** | −0.062 *** |
| (0.018) | (0.010) | (0.008) | (0.009) | (0.006) | (0.003) | (0.016) | (0.007) | |
| bci | 1.368 *** | 0.718 *** | 0.539 *** | 0.313 | 0.206 | 0.070 | 0.855 ** | 0.316 ** |
| (0.450) | (0.230) | (0.207) | (0.211) | (0.136) | (0.050) | (0.400) | (0.137) | |
| educpc | 0.065 *** | 0.034 *** | 0.025 *** | 0.055 ** | 0.036 ** | 0.012 ** | 0.038 | 0.036 |
| (0.022) | (0.012) | (0.010) | (0.025) | (0.017) | (0.006) | (0.020) | (0.025) | |
| hwypc | −0.420 | −0.221 | −0.165 | −1.294 *** | −0.850 *** | −0.290 *** | −0.320 | −0.258 |
| (0.248) | (0.132) | (0.103) | (0.313) | (0.197) | (0.090) | (0.200) | (0.194) | |
| metro | 23.233 *** | 14.520 *** | 7.382 *** | 12.481 *** | 8.632 *** | 2.449 *** | 19.385 *** | 9.909 *** |
| (2.972) | (1.486) | (1.791) | (1.304) | (0.752) | (0.513) | (2.288) | (0.822) | |
| micro | 10.901 *** | 4.787 *** | 5.031 *** | 7.154 *** | 4.650 *** | 1.757 *** | 6.200 *** | 5.575 *** |
| (2.349) | (0.639) | (1.677) | (0.759) | (0.397) | (0.378) | (0.788) | (0.434) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, R.C.; Glaser, S. Modelling and Diagnostics of Spatially Autocorrelated Counts. Econometrics 2022, 10, 31. https://doi.org/10.3390/econometrics10030031
Jung RC, Glaser S. Modelling and Diagnostics of Spatially Autocorrelated Counts. Econometrics. 2022; 10(3):31. https://doi.org/10.3390/econometrics10030031
Chicago/Turabian StyleJung, Robert C., and Stephanie Glaser. 2022. "Modelling and Diagnostics of Spatially Autocorrelated Counts" Econometrics 10, no. 3: 31. https://doi.org/10.3390/econometrics10030031
APA StyleJung, R. C., & Glaser, S. (2022). Modelling and Diagnostics of Spatially Autocorrelated Counts. Econometrics, 10(3), 31. https://doi.org/10.3390/econometrics10030031






