Are Vaccinations Alone Enough to Curb the Dynamics of the COVID-19 Pandemic in the European Union?

Abstract

I use the data on the COVID-19 pandemic maintained by Our Word in Data to estimate a nonstationary dynamic panel exhibiting the dynamics of confirmed deaths, infections and vaccinations per million population in the European Union countries in the period of January–July 2021. Having the data aggregated on a weekly basis I demonstrate that a model which allows for heterogeneous short-run dynamics and common long-run marginal effects is superior to that allowing only for either homogeneous or heterogeneous responses. The analysis shows that the long-run marginal death effects with respect to confirmed infections and vaccinations are positive and negative, respectively, as expected. Since the estimate of the former effect compared to the latter one is about 71.67 times greater, only mass vaccinations can prevent the number of deaths from being large in the long-run. The success in achieving this is easier for countries with the estimated large negative individual death effect (Cyprus, Denmark, Ireland, Portugal, Estonia, Lithuania) than for those with the large but positive death effect (Bulgaria, Hungary, Slovakia). The speed of convergence to the long-run equilibrium relationship estimates for individual countries are all negative. For some countries (Bulgaria, Denmark, Estonia, Greece, Hungary, Slovakia) they differ in the magnitude from that averaged for the whole EU, while for others (Croatia, Ireland, Lithuania, Poland, Portugal, Romania, Spain), they do not.

1. Introduction

The COVID-19 pandemic painfully hit individuals and nations around the world. By the time of writing it had infected over 235 million people, out of which nearly 5 million had died from infection and related diseases (Worldometer 2021). In response to increasing viral transmission, governments have implemented many nonpharmaceutical interventions including the use of masks, social distancing, restrictions on movement, tests, contact tracking, quarantine, business and school closures, and country-wide lockdowns (Hale et al. 2021). Despite them, the intensity of the pandemic, as reflected in the number of confirmed infections and deaths, has alternately increased and decreased depending on the severity of restrictions, their extent, duration, and occasional mitigation, but still remains high, particularly in non-peripheral countries (Rossman et al. 2021). Even though the mass vaccinations started in early 2021 have elicited the immune response and reduced deaths in many high-income countries, the fourth wave of infection is either under way or is expected by this fall.1 Thus, the research into the dynamics of the pandemic and its causes remains of vital importance.

Most attempts in this regard undertaken to this point have been based on the epidemiological models matched to the COVID-19 data in which the trajectory of the pandemic is assumed to be caused by a mix of factors related to pathogen contagiousness, human behaviour and government intervention (Bhouri et al. 2021; Gumel et al. 2021; Liu et al. 2021; Moore et al. 2021; Musa et al. 2021; Shayak et al. 2021; Xu et al. 2021; Zhong 2021). Since the solution to these models hinges on an extensive set of parameters and initial conditions, predictions made on them lead to a wide spectra of outcomes ranging from sustained epidemics to near elimination (Saad-Roy et al. 2020).2 More interestingly, the performed simulations suggest that vaccinations alone are not enough to curb the current and the next waves of infection (Cot et al. 2021), especially in the presence of peoples’ resistance to vaccination (Burke et al. 2021; Kessels et al. 2021; Hyland et al. 2021; Mondal et al. 2021; Schmelz and Bowles 2021; Wang et al. 2021).

This paper aims to validate the above claim about the role of vaccinations in breaking the pandemic in the European Union countries on a purely empirical basis. In what follows, the dynamics of the pandemic is solely exhibited by variables related to the number of con-firmed deaths, infections and vaccinations. The data on those variables are extracted from the Data on COVID-19 (coronavirus) by Our World in Data, available at GitHub. They are then aggregated on a weekly basis to overcome the weekend effects and missing data points resulting from differences in the data collection systems at the country’s level. To circumvent the problem of epidemiological model choice and its calibration on the available data and include a large number of countries at the same time, the analysis is nested within an autoregressive distributive lag (ARDL) dynamic panel setup. Since the variables of interest are found to be nonstationary and cointegrated, a relevant error correction representation is estimated, as in Pesaran et al. (1999), by applying the mean group (MG), pooled mean group (PMG) and dynamic fixed effect (DFE) estimators, which enables us to infer about the long and the short-run nature of the pandemic. Next, based on the Hausman test, it is determined whether the long-run and the short-run death responses to the infections and vaccinations are country specific or not. Finally, the intensity of vaccinations to prevent the number of fatal cases from being large in the long-run is computed. To the best of the author’s knowledge, such a panel approach to modelling the COVID-19 pandemic dynamics is a new one.3

The reminder of the paper proceeds as follows. Section 2 describes the employed methodology. Section 3 summarizes the empirical findings. The last section concludes the paper.

2. Model

Assume that the long-run ”deaths” function is

$$d_{it}={\theta }_{i0}+{\theta }_i^c{c}_{it}+{\theta }_i^v{v}_{it}+{ϵ}_{it},$$

(1)

where $d_{it}$, $c_{it}$ and $v_{it}$ stand for the number of confirmed new deaths, infections (cases) and vaccinations per million population, respectively, ${\theta }_i^c$ and ${\theta }_i^v$ are marginal death effects with respect to confirmed infections and vaccinations such that ${\theta }_i^c>0$ and ${\theta }_i^v<0$, ${ϵ}_{it}$ is a random error, $i=1, 2,\dots , N$ and $t=1, 2,\dots , T$ characterize the number of countries and time periods (weeks) in question. The ARDL($p$, $q_c$, $q_v$) dynamic panel specification of (1) reads

$$d_{it}={\Sigma }_{j=1}^p{\lambda }_{ij}{d}_{i,t-j}+{\Sigma }_{k=0}^{q_c}{\delta }_{ik}^c{c}_{i,t-k}+{\Sigma }_{l=0}^{q_v}{\delta }_{il}^v{v}_{i,t-l}+{\mu }_i+{ϵ}_{it},$$

(2)

where ${\lambda }_{ij}$, ${\delta }_{ik}^c$ and ${\delta }_{il}^v$ are coefficients pertaining the right hand side variables and ${\mu }_i$ is the country specific effect. In the case $d_{it}$, $c_{it}$ and $v_{it}$ are integrated of order one variables and cointegrated making ${ϵ}_{it}$ a stationary process for all $i$, the relevant panel error correction representation becomes

$$\begin{gathered} \mathsf{\Delta }{d}_{it}={\varphi }_i\left(d_{i,t-1}-{\theta }_{i0}-{\theta }_i^c{c}_{it}-{\theta }_i^v{v}_{it}\right)+{\Sigma }_{j=1}^{p-1}{\lambda }_{ij}^{*}\mathsf{\Delta }{d}_{i,t-j}+{\Sigma }_{k=0}^{q_c-1}{\delta }_{ik}^{c*}\mathsf{\Delta }{c}_{i,t-k} \\ +{\Sigma }_{l=0}^{q_{v-1}}{\delta }_{il}^{v*}\mathsf{\Delta }{v}_{i,t-l}+{ϵ}_{it}, \end{gathered}$$

(3)

where ${\varphi }_i=-\left(1-{\Sigma }_{j=1}^p{\lambda }_{ij}\right)$ exhibits the speed of convergence to the long-run equilibrium relationship, ${\theta }_{i0}={\mu }_i/\left(1-{\Sigma }_{j=1}^p{\lambda }_{ij}\right)$, ${\theta }_i^c={\Sigma }_{k=0}^{q_c}{\delta }_{ik}^c/\left(1-{\Sigma }_{j=1}^p{\lambda }_{ij}\right)$, ${\theta }_i^v={\Sigma }_{l=0}^{q_v}{\delta }_{il}^v/\left(1-{\Sigma }_{j=1}^p{\lambda }_{ij}\right)$, ${\lambda }_{ij}^{*}=-{\Sigma }_{m=j+1}^p{\lambda }_{im}$, ${\delta }_{ik}^{c*}=-{\Sigma }_{m=k+1}^{q_c}{\delta }_{il}^c$, ${\delta }_{il}^{v*}=-{\Sigma }_{m=l+1}^{q_v}{\delta }_{il}^v$.

Equation (3) allows to address explicitly four research questions (RQ) about the nature of the COVID-19 pandemic and the role of vaccinations in breaking it in the European Union countries:

• RQ1—Is the pandemic dynamics homogeneous ${\lambda }_{ij}^{*}={\lambda }_{rj}^{*}, {\delta }_{ik}^{c*}={\delta }_{rk}^{c*}$, ${\delta }_{il}^{v*}={\delta }_{rl}^{v*}$ ${\varphi }_i={\varphi }_r$ for all $i\ne r$) or heterogeneous (${\lambda }_{ij}^{*}\ne {\lambda }_{rj}^{*}, {\delta }_{ik}^{c*}\ne {\delta }_{rk}^{c*}$, ${\delta }_{il}^{v*}\ne {\delta }_{rl}^{v*}$ ${\varphi }_i\ne {\varphi }_t$ for at least some $i\ne r$?
• RQ2—Is the speed of convergence to the long-run equilibrium relationship the same in the whole EU (${\varphi }_i={\varphi }_r$ for all $i\ne r$) or it is country specific (${\varphi }_i\ne {\varphi }_r$ for at least some $i\ne r$)?
• RQ3—Whether the same applies to the long-run marginal death effects with respect to the number of new infections and vaccinations (equal marginal effects: ${\theta }_i^c={\theta }_r^c$, ${\theta }_i^v={\theta }_r^v$ for all $i\ne r$; country specific marginal effects: ${\theta }_i^c\ne {\theta }_r^c$, ${\theta }_i^v\ne {\theta }_r^v$ for at least some $i\ne r$)?
• RQ4—What the intensity of vaccination shall be ($v_i^0$) to prevent the number of fatal cases from being large ($d_i^{*}$) in the case the number of infections reaches a $c_i^{*}$ level ($v_i^0=\left(d_i^{*}-{\theta }_{i0}-{\theta }_i^c{c}_i^{*}\right)/{\theta }_i^v)$?

Its estimation is performed in Stata 16 using xtpmg2 command, which enables the application of the MG, PMG and DFE estimators to nonstationary panels (Blackburne and Frank 2007). The PMG estimator constrains the long-run coefficients across all panels and averages their short-run panel counterparts, while the DFE estimator constrains all coefficients except for a country specific effect ${\mu }_i$. If, however, the true model is heterogeneous, they both are inconsistent. The MG estimator which averages both the long-run and the short-run panel coefficients is consistent regardless of the model heterogeneity. Thus the choice of a proper model specification resulting in answering research questions RQ1–RQ3 is made upon the Hausman test in which the significance of a distance between the MG estimator and one of the PMG and DFE pair is tested for.

The estimation of Equation (3) is preceded by testing for the nature of variables of interest using the heteroskedasticity-robust panel unit-root tests suggested in Herwartz and Siedenburg (2008), Demetrescu and Hanck (2012), and Herwartz et al. (2019), as time-varying volatility may be a characteristic of the series exhibiting the pandemic. In case the panel unit-root null hypothesis is not rejected, the error-correction-based cointegration tests for panel data invented by Westerlund (2007) are applied (Persyn and Westerlund 2008). The lags $p$, $q_c$ and $q_v$ are set upon the Akaike information criterion computed for the least restricted model given by Equation (3), i.e., the full MG model consisted from $N$ equations.

3. Results

The series of weekly new deaths, infections and vaccinations per million population in the European Union countries, except for Sweden and the Netherlands, are depicted in Figure 1, Figure 2 and Figure 3.4 They cover the period 31 December 2020–11 July 2021. The first time point exhibits the week at which the vaccinations in many EU countries either begun or had been just initiated. With $N=25$ (number of countries) and $T=30$ (number of time points), each panel is strongly balanced. The visual inspection of the new deaths and infections series for particular countries shows that they peak at different time points as the consecutive waves of the pandemic have spread across the EU countries at a little different pace, partly due to the diversity of locally undertaken interventions. For many countries the new vaccinations series dramatically decrease at the end of the period in question exhibiting a halt and a failure of the intended mass vaccinations. Lastly, all three series rarely pass through their mean levels, indicating that they are very likely nonstationary.

The results of testing for non-stationarity of the new deaths, infections and vaccinations per million population series are gathered in

Table 1. Results of the heteroskedasticity-robust panel unit-root tests.

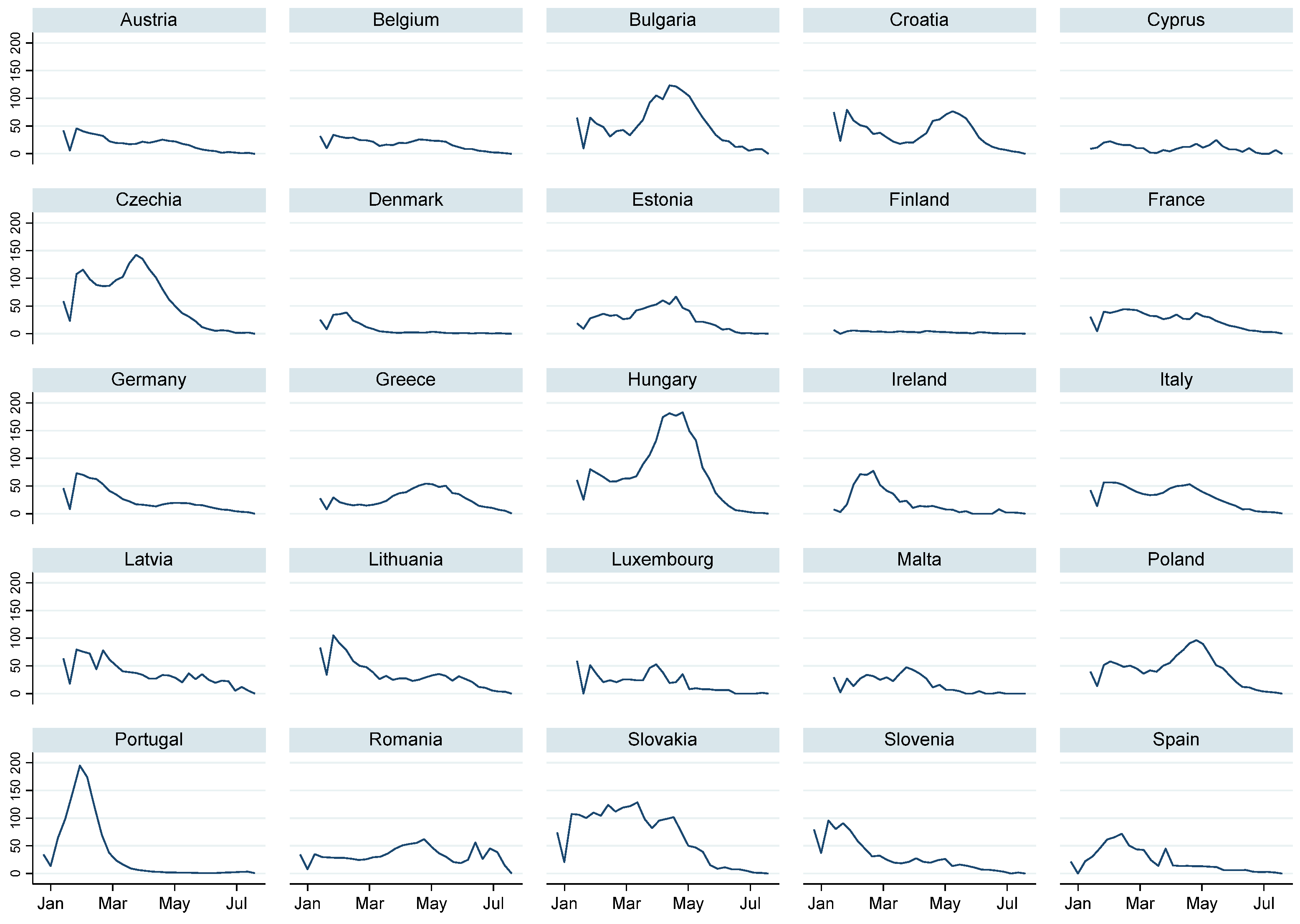
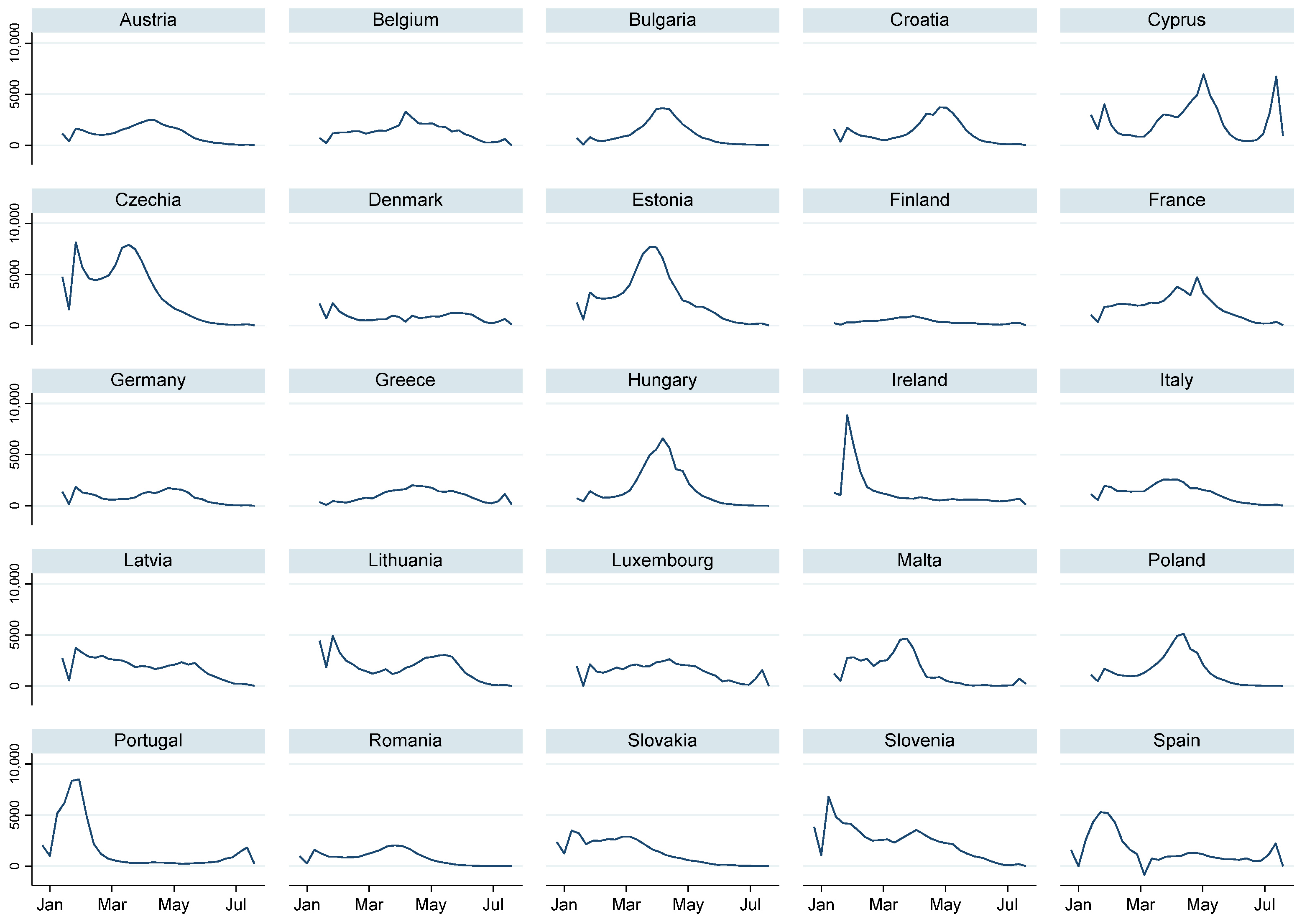
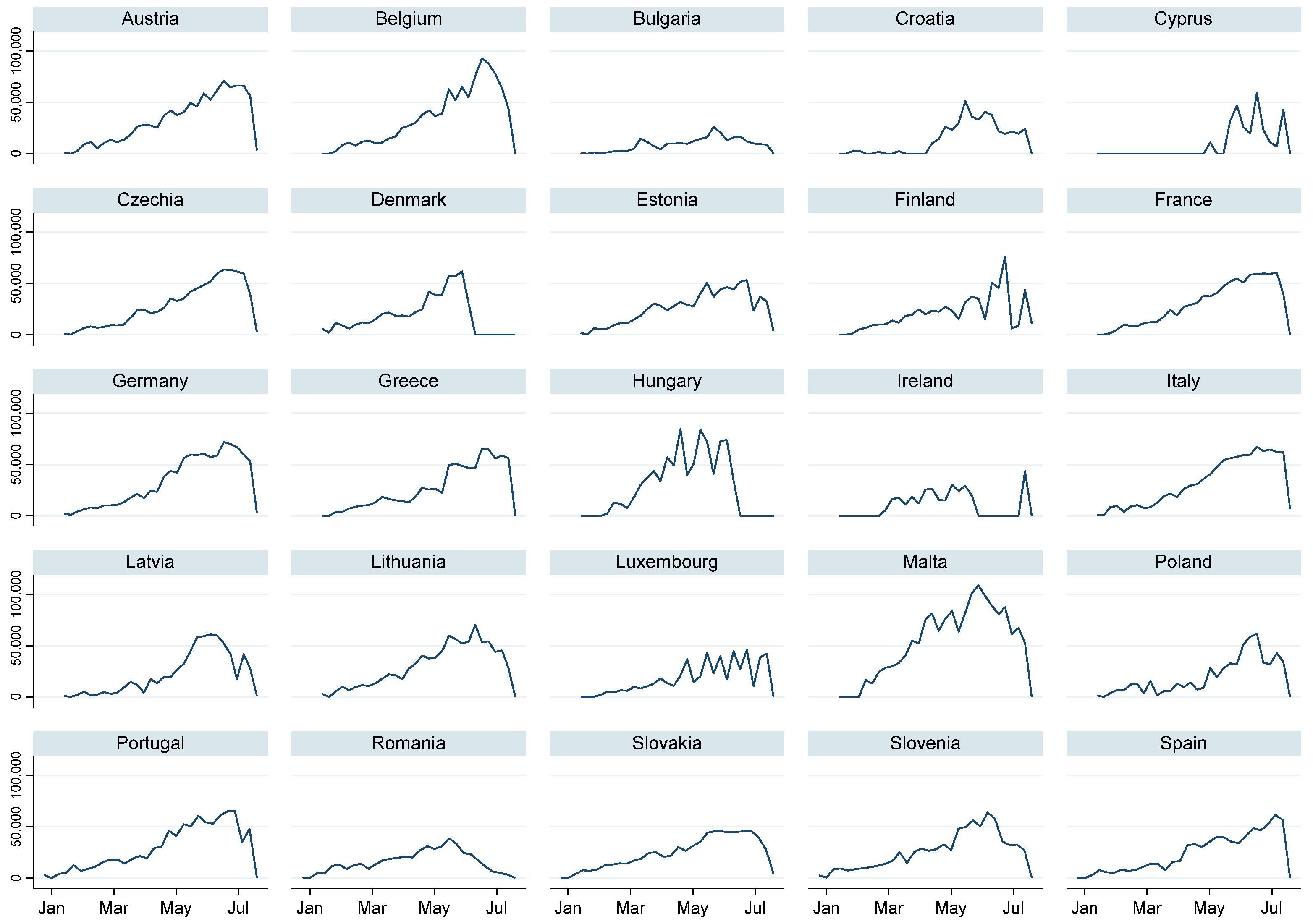
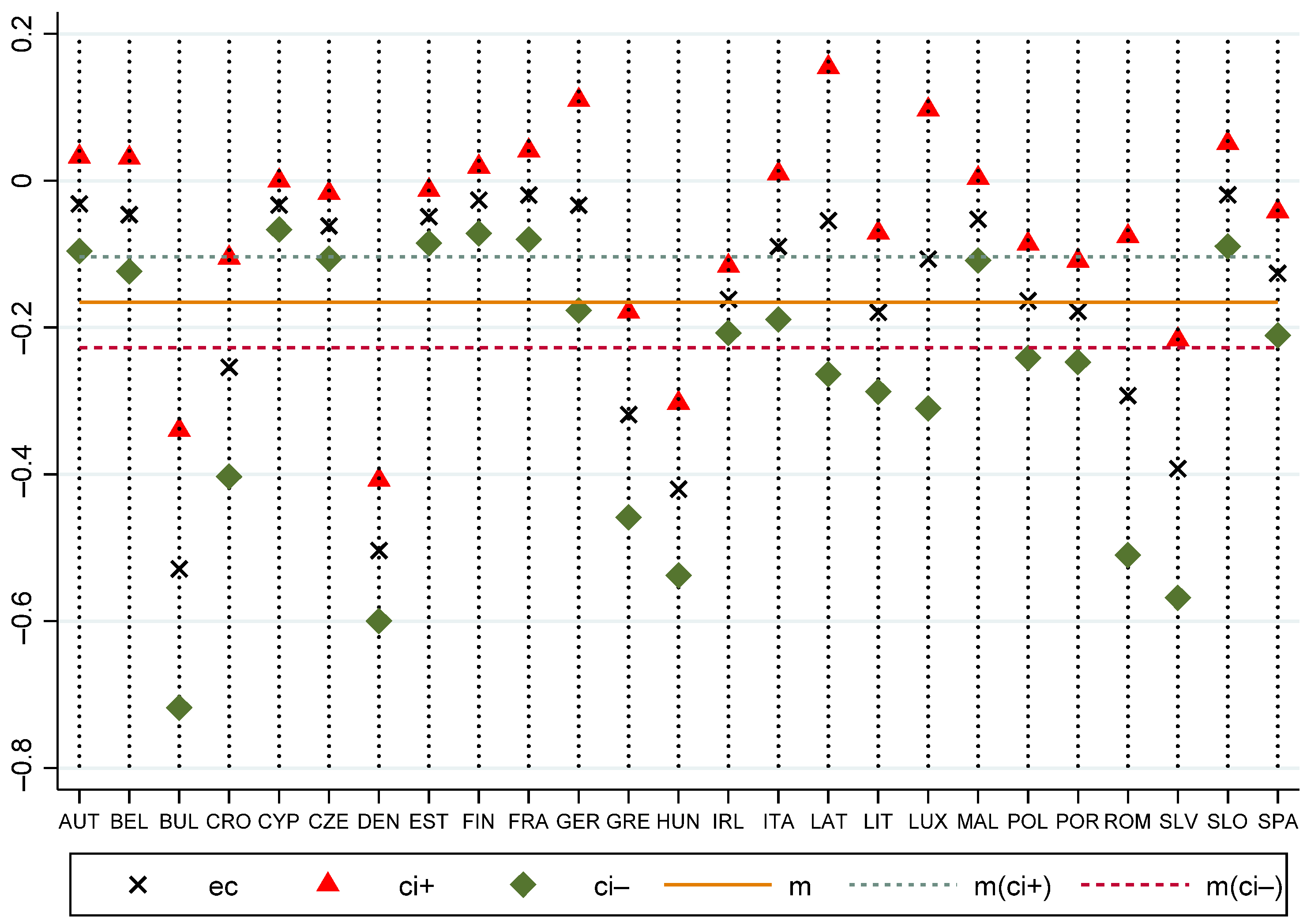
Variable	Test
	HS		DH		HMW
	${\mathit{t}}_{\mathit{H}\mathit{S}}$	$\mathit{p}.\mathit{v}.$	${\mathit{t}}_{\mathit{D}\mathit{H}}$	$\mathit{p}.\mathit{v}.$	${\mathit{t}}_{\mathit{H}\mathit{M}\mathit{W}}$	$\mathit{p}.\mathit{v}.$
$d_t$	2.2015	0.9862	1.8514	0.9679	4.9722	1.0000
$c_t$	−0.4447	0.3283	0.7841	0.7835	0.9002	0.8160
$v_t$	−1.2598	0.1039	−0.4875	0.3129	1.8952	0.9710
$\mathsf{\Delta }{d}_t$	−2.8223	0.0024	−2.4767	0.0066	−0.4312	0.3332
$\mathsf{\Delta }{c}_t$	−1.8154	0.0347	−2.1283	0.0167	−1.5431	0.0614
$\mathsf{\Delta }{v}_t$	−1.7507	0.0400	−2.2255	0.0130	−1.0741	0.1414

. In two tests, namely those of Herwartz and Siedenburg (HS), and Demetrescu and Hanck (DH), the panel unit root null hypothesis of driftless random walk against the alternative hypothesis of a stationary process with individual specific intercept terms is tested for, while in the third one, that of Herwartz, Maxand and Walle (HMW), the same is done for the random walk with drift null against the trend stationarity alternative (Herwartz et al. 2018). Thus the tests are left-sided. Under the null of a panel unit root, each test statistic is asymptotically distributed as $N\left(0,1\right)$. The results for levels suggest that a panel unit root in $d_t$, $c_t$ and $v_t$ cannot be rejected at 5% significance level. The results for the first differences, except for the HMW test, indicate its rejection. Consequently, all variables of interest may be treated as being $I\left(1\right)$.

Next, the tests of Westerlund (2007) are applied to $d_t$, $c_t$ and $v_t$ to decide upon whether they are cointegrated and may be included in the error correction form given by Equation (3). In the first two out of four tests—the group mean tests ($G_{\tau }$, $G_{\alpha }$)—the null hypothesis of no cointegration in all panels against the alternative of cointegration in at least one panel is tested for, while in the remaining two tests—the panel tests ($P_{\tau }$, $P_{\alpha }$)—the same null is accompanied by the alternative of cointegration in all panels. In what follows, the bootstrapped versions of those tests are employed to account for any possible dependence between the cross-sectional units. The null of no cointegration is rejected if the calculated sample value of the relevant test statistic is smaller than the lower 5% quantile of its bootstrapped distribution. The results gathered in

Table 2. Results of the Westerlund tests for panel cointegration.

Variable	Group Mean Tests				Panel Tests
	${\mathit{G}}_{\mathit{\tau }}$	$\mathit{p}.\mathit{v}.$ a	${\mathit{G}}_{\mathit{\alpha }}$	$\mathit{p}.\mathit{v}.$ a	${\mathit{P}}_{\mathit{\tau }}$	$\mathit{p}.\mathit{v}.$ a	${\mathit{P}}_{\mathit{\alpha }}$	$\mathit{p}.\mathit{v}.$ a
	No constant in the cointegration relationship
$d_t, c_t, v_t$	−3.097	0.000	−10.699	0.000	−14.915	0.000	−9.259	0.000
	With constant in the cointegration relationship
$d_t, c_t, v_t$	−2.514	0.000	−9.474	0.040	−12.198	0.000	−9.168	0.010

^a The p-values are for a one-sided test based on the bootstrapped distribution with 100 bootstrap replications.

indicate that the null of no cointegration of $d_t$, $c_t$ and $v_t$ is to be rejected in favour of the alternative of cointegration in at least one panel as well as in all panels regardless of whether a constant is or is not included in the cointegration relationship.

The Akaike information criterion, when computed for the least restricted version of the panel error correction model given by Equation (3), consisted from $N=25$ equations, i.e., the MG version suggests the choice of $p=1$ and $q_c=q_v=2$ (see

Table 3. Estimates of the Akaike information criterion for the full MG model given by Equation (3).

$(\mathit{p}, {\mathit{q}}_{\mathit{c}}, {\mathit{q}}_{\mathit{v}})$	AIC	$\mathit{d}\mathit{f}$	$(\mathit{p}, {\mathit{q}}_{\mathit{c}}, {\mathit{q}}_{\mathit{v}})$	AIC	$\mathit{d}\mathit{f}$	$(\mathit{p}, {\mathit{q}}_{\mathit{c}}, {\mathit{q}}_{\mathit{v}})$	AIC	$\mathit{d}\mathit{f}$
1, 0, 0	5132.936	100	1, 2, 0	4686.905	150	2, 1, 0	4708.890	150
1, 0, 1	5142.862	125	1, 2, 1	4647.197	175	2, 1, 1	4683.162	175
1, 1, 0	5009.580	125	1, 2, 2	4641.517	200	2, 1, 2	4696.016	200
1, 1, 1	5020.774	150	2, 0, 0	4773.425	125	2, 2, 1	4649.488	200
1, 1, 2	4741.771	175	2, 0, 1	4749.394	150	2, 2, 2	4644.836	225

). Thus, the further inference on the dynamics of the COVID-19 pandemic is based on the ARDL(1, 2, 2) nonstationary panel.

The estimation results for the corresponding error correction form using the MG, PMG and DFE estimators are stacked in

Table 4. Estimation results for Equation (3).

Regressor	Estimator
	MG	PMG	DFE
	Long-run
$c_t$	0.0198 ***	0.0371 ***	0.0228 ***
	(4.78)	(23.48)	(6.19)
$v_t$	−0.000368 **	−0.000518 ***	−0.000266 *
	(−3.81)	(−10.58)	(−2.16)
	Short-run
$e{c}_{t-1}$	−0.4914 ***	−0.1657 ***	−0.275 ***
	(−8.72)	(−5.24)	(−7.49)
$\mathsf{\Delta }{c}_t$	0.002	0.00603 ***	0.00179
	(1.00)	(3.58)	(0.95)
$\mathsf{\Delta }{c}_{t-1}$	−0.00572 ***	−0.00462 ***	−0.00205 *
	(−5.14)	(−3.81)	(−2.32)
$\mathsf{\Delta }{v}_t$	0.000133 *	0.0000202	0.0000227
	(2.10)	(0.63)	(0.61)
$\mathsf{\Delta }{v}_{t-1}$	0.0000526	−0.0000182	0.0000135
	(1.11)	(−0.38)	(0.47)
const.	5.024 *	−0.165	0.426
	(1.98)	(−0.20)	(0.19)

Figures in brackets under the parameter estimates refer to $z$ statistics; * (**, ***)—significant at 10% (5%, 1%) level.

. The long-run marginal death effect with respect to the number of new infections is estimated at 0.0198, 0.0371 and 0.0228, while that with respect to the number of new vaccinations is $-0.000368$, $-0.000518$ and $-0.000266$, respectively. The signs of the first and the second effect are positive and negative, as expected. All effects are found different from zero to at least a 10% significance level. Out of all short run estimates, those for the coefficient exhibiting the speed of convergence to the long run equilibrium relationship differ the most. That obtained on the MG estimator ($-0.4914)$ is in absolute terms almost two and three times as large as those obtained on its DFE ($-0.275$) and PMG ($-0.1657$) counterparts. The calculated Hausman statistic for the MG and PMG pair (${\chi }^2\left(7\right)=5.11$, $p.v.=0.6461$) indicates that the PMG estimator, the efficient estimator under the null hypothesis, is preferred. When the same procedure is repeated for the MG and DFE pair, the result (${\chi }^2\left(7\right)=103.30$, $p.v.=0.0$) favours the MG estimator. Thus, the PMG model allowing for homogenous long-run and heterogenous short-run death responses to the infections and vaccinations is preferred over the MG and DFE models in which either both the long-run and the short-run responses are heterogeneous or so is a constant term exhibiting the country specific effect ${\mu }_i$. The homogeneity of the long-run death effects with respect to the infections and vaccinations provides strong evidence of the commonality in the COVID-19 dynamics in the European Union (EU) countries regardless of the diversity of locally undertaken nonpharmaceutical interventions and the social responses to the restrictions.

Since the long-run marginal death effect with respect to confirmed infections ($0.0371$) is in absolute terms about 71.62 times greater than that with respect to confirmed vaccinations (−0.000518), only mass vaccinations can prevent the number of deaths from being large in the long-run. Figures exhibiting the intensity of recommended vaccinations $v_i^0$ are given in

Table 5. Figures exhibiting the intensity of recommended vaccinations, $v_i^0$.

Infections	$\mathbf{Deaths},{\mathit{d}}_{\mathit{i}}^{*}$
${\mathit{c}}_{\mathit{i}}^{*}$	1	2	5	10	20	30	40	50	100	150	200	250
20
50	2
100	5	3
200	12	10	5
500	36	32	26	17	3
1000	72	68	62	52	33	14
2000	143	139	134	124	105	85	66	47
5000	358	354	348	339	319	300	281	262	165	69
10,000	716	712	707	697	678	658	639	620	523	427	330	234
20,000	1432	1429	1423	1413	1394	1374	1355	1336	1239	1143	1046	950
50,000	3581	3577	3571	3562	3542	3523	3504	3484	3388	3291	3195	3098

. Particular entries show a minimal weekly number of new vaccinations per million population × 1000 in a EU country to keep the number of new deaths per million population at $d_i=d_i^{*}$ in the case where the number of new infections per million population reaches the $c_i^{*}$ level ($v_i^0=\left(d_i^{*}-{\theta }_{i0}-{\theta }_i^c{c}_i^{*}\right)/{\theta }_i^v)$. For instance, in the case of $d_i^{*}=10$ and $c_i^{*}=5000$, which for a 10-million population country indicates 100 weekly deaths and 50,000 infections, the weekly minimal number of vaccinations shall be 3,390,000 (10 × 339,000). If the weekly number of infections increases to 100,000 ($c_i^{*}=\mathrm{10,000}$), the weekly minimal number of vaccinations shall be 6,970,000 (10 × 697,000). In the same circumstances, the number of vaccinations for a country with a population of 25 million shall be 8,475,000 (25 × 339,000) and 17,425,000 (25 × 697,000), respectively.5 Since the vaccination of such large parts of the country’s population in the consecutive weeks given the limited resources of the health system is very unlikely, figures from Table 5 must be interpreted with care. Those from its upper rows give a more plausible explanation of the long-run dependence between the number of deaths and vaccinations suggesting that the mass vaccinations can curb the COVID-19 pandemic only when they are initiated before the infections climb to a high level. For instance, when the weekly number of new infections in a 10-million population country reaches 10,000 ($c_i^{*}=1000$), only as many as 520,000 people have to be vaccinated per week to keep the number of weekly deaths at 100 ($d_i^{*}=10$). Such an intensity of vaccinations is fairly achievable.

Keeping the number of vaccinations at the recommended level may be easier for countries with a large negative individual death effect ${\mu }_i$ estimated from the full PMG model (Cyprus, Denmark, Ireland, Portugal, Estonia, Lithuania) than for those with a large but positive such effect (Bulgaria, Hungary, Slovakia). The required corrections for ($c_i^{*}$, $d_i^{*}$) entries from Table 5, equal to $-{\theta }_{i0}/{\theta }_i^v=-{\mu }_i/\left(1-{\lambda }_i\right){\theta }_i^v$, are given in

Table 6. Corrections for the intensity of recommended vaccinations, $-{\theta }_{i0}/{\theta }_i^v$.

Country	Estimate		Correction
	${\mathit{\mu }}_{\mathit{i}}$	$1-{\mathit{\lambda }}_{\mathit{i}}$
Bulgaria	8.2068	0.5288	29,961
Cyprus	−2.7628	0.0332	−160,650
Denmark	−7.0520	0.5036	−27,033
Estonia	−3.2903	0.0490	−129,631
Hungary	9.3993	0.4203	43,172
Ireland	−3.9769	0.1618	−47,450
Lithuania	−3.1295	0.1792	−33,714
Portugal	−2.5767	0.1781	−27,930
Slovakia	11.5474	0.3922	56,839

. For instance, the correction in the number of vaccinations for the 1.3 million people in Estonia is $-\mathrm{168,520} \left(1.3\times \left(\left(3.2903\right)/\left(0.049\times \left(-0.000518\right)\right)\right)\right)$, while the correction for the 10 million people of Hungary is 431,720 $\left(10\times \left(-9.3993/\left(0.4203\times \left(-0.000518\right)\right)\right)\right)$.

Although the long-run equilibrium relationship among the deaths, cases and vaccinations per million population is the same for all EU countries included in the sample, the speed of convergence to this pattern is country specific. The estimates of relevant convergence coefficients with 95% confidence intervals for the whole EU and its particular countries are depicted in Figure 4. The estimate of the convergence coefficient for the whole EU, $m=-0.1657$, is marked with a dark orange horizontal line, while those for its upper, $m\left(ci+\right)=-0.2277$, and its lower bound, $m\left(ci-\right)=-0.1038$—have teal and cranberry dashed horizontal lines. The relevant estimates for particular EU countries are marked with the dark crosses (convergence coefficients), red triangles (upper confidence bands) and green diamonds (lower confidence bands). The visual inspection reveals that the speed of convergence estimates for individual countries are all negative. For some countries (Bulgaria, Denmark, Estonia, Greece, Hungary, Slovakia) they differ significantly in the magnitude from that averaged for the whole EU, while for others (Croatia, Ireland, Lithuania, Poland, Portugal, Romania, Spain) they do not. More interestingly, testing for the equality of coefficients exhibiting the speed of convergence to the long-run equilibrium relationship in particular EU countries using the Wald test shows that the null of their equality cannot be rejected for Austria, Germany, Belgium, Luxembourg, France, Italy and Spain (${\chi }^2\left(6\right)=5.37$, $p.v.=0.4976)$, as well as for the Baltic States (Estonia, Latvia, Lithuania—${\chi }^2\left(2\right)=5.07$, $p.v.=0.0793$). The same conclusion for the whole EU (${\chi }^2\left(24\right)=165.17$, $p.v.=0.0$), its old (Austria, Belgium, Cyprus, Denmark, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg, Malta, Portugal, Spain—${\chi }^2\left(13\right)=135.45$, $p.v.=0.0)$ and new member states (Bulgaria, Croatia, Czechia, Estonia, Hungary, Latvia, Lithuania, Poland, Romania, Slovakia, Slovenia—${\chi }^2\left(10\right)=77.15$, $p.v.=0.0$), and the Visegrad group (Czechia, Hungary, Poland, Slovakia—${\chi }^2\left(3\right)=41.79$, $p.v.=0.0$) does not apply, however.

In what has followed so far, nonpharmaceutical interventions, a potentially important factor to curb the dynamics of the COVID-19 pandemic, have been absent. For a robustness check, the right-hand side of Equation (1) was appended by the stringency index, $s_{it}$, a composite measure of nine of the response metrics exhibiting the strictness of government policies (school closures, workplace closures, cancellation of public events, restrictions on public gatherings, closures of public transport, stay-at-home requirements, public information campaigns, restrictions on internal movements, international travel controls), and next the relevant model estimation and validation procedures were repeated with the ultimate goal being to determine the intensity of recommended vaccinations. The results of the heteroskedasticity-robust panel unit-root tests (HS, DH, HMW) showed that $s_{it}$ is integrated of order one.6 The results of three out of four error-correction-based cointegration tests ($G_{\tau }$, $G_{\alpha }$, $P_{\alpha }$) indicated that $d_{it}$, $c_{it}$, $v_{it}$ and $s_{it}$ did not cointegrate, so that the stringency index must not be included in the extended ”deaths” function given by Equation (1). What is more, feedback from the index to deaths was not found present in the case ${\mathsf{\Delta }\mathrm{s}}_{it}$ and its lags were included in the short-run part of the panel ARDL model given by Equation (3) regardless of its final specification and the employed estimation method (MG, PMG, DFE). On the other hand, since $d_{it}$ and $s_{it}$ alone were found to be cointegrated, a two variable panel error correction model may be suitable for testing for the direction of causality and assessing the effectiveness of interventions. The COVID-19 surveillance system may be of enough high quality for incoming information on the pandemic to be processed without delay into various restrictions. Checking that all, however, is left for future research.

4. Conclusions

In this paper I validated the claim that vaccinations alone would be hardly enough to curb the current and the next waves of the COVID-19 pandemic in the EU countries. Based on the panel exhibiting the weekly number of confirmed deaths, infections and vaccinations per million population in the period 31 December 2020–11 July 2021, I showed that the variables in question were integrated of order one and cointegrated, which allowed for the modelling of the COVID-19 pandemic dynamics within the ARDL nonstationary panel setup. Having estimated the relevant error correction form, I demonstrated that the PMG model allowing for homogenous long-run and heterogenous short-run death responses to the infections and vaccinations was superior over the MG and DFE models in which either both the long-run and the short-run responses were heterogeneous or so was a constant term exhibiting the country specific effect. The inclusion of the stringency index into the model to control for the nonpharmaceutical interventions was not supported by the data. That suggests that the long-run COVID-19 pandemic dynamics was the same across the EU countries no matter that they belonged to the Union’s core or its periphery, and presumably what type of interventions they undertook, as well as what the timing of interventions was. Since $d_{it}$ and $s_{it}$ alone were found cointegrated the last two conjectures, however, require further checking.

In particular, the analysis showed that the long-run marginal death effects with respect to confirmed infections and vaccinations were positive and negative, respectively, as expected. Since the estimate of the former effect compared to the latter one was found to be about 71.67 times greater, only the mass vaccinations could prevent the number of deaths from being large in the long-run provided they are initiated before the infections climb to a high level. The success in so achieving would be easier, if only possible, for countries with the estimated large negative individual death effect (Cyprus, Denmark, Ireland, Portugal, Estonia, Lithuania) than for those with the large but positive such effect (Bulgaria, Hungary, Slovakia). The speed of convergence to the long-run equilibrium relationship estimates for all countries was negative. For some of them (Bulgaria, Denmark, Estonia, Greece, Hungary, Slovakia), they differed in the magnitude from the average for the whole EU while for others (Croatia, Ireland, Lithuania, Poland, Portugal, Romania, Spain), they did not. More interestingly, for Austria, Germany, Belgium, Luxembourg, France, Italy and Spain, as well as for the Baltic States (Estonia, Latvia, Lithuania), the hypothesis stating that the convergence coefficients were equal could not be rejected, which allowed for the conjecture that the interventions undertaken in those countries in response to the growing number of active and critical cases, deaths, and the pessimistic hospital resource use projections were similar in type and equally effective.