1. Introduction
Information fusion when working with wireless sensor networks plays an important role. Sensors have evolved over time [
1]. WSNs are usually deployed in large numbers and in places where they are exposed to highly varying conditions making their sensed values sometimes imprecise. Even in ambient conditions, the sensed values could be far from precise due to the possible failures. Such inoperable nodes can be possible nodes for attack and subsequent compromise. A more common issue with using WSN is the limited spatial and temporal coverage they can have in the environment. To overcome the above-mentioned limitations, previous works have classified the information fusion into co-operative, complementary and redundant based on the relationship they have with the information source.
When information from multiple sources have to be aggregated to form the broader scene, the complementary algorithm is used. In cases when two or more sensor sources provide information about the same environment, we use the redundant algorithms. This provides the means for fault tolerance and pieces of the input source can be fused to increase associated confidence. Complementary fusion algorithms search for completeness by compounding new information from different pieces. This is highly applicable in a WSN-like environment. The most popular sensor fusion algorithms include Kalman filter (widely used in signal processing), Bayesian networks (used in Neural networks), Dempster–Shafer (probability calculus) and Brooks–Iyengar algorithm.
The Brooks–Iyengar algorithm being a distributed algorithm improves both the precision and accuracy of the sensor readings from a distributed WSN. This algorithm works well even in the presence of faulty inputs from sensors. This fault tolerance is achieved by exchanging the measured value and accuracy value at every node with every other node. These values are aggregated to calculate the accuracy range and a measured value for the whole network from all of the individual values collected. In 2016, the precision and accuracy bounds of this algorithm were proved. Because of its distributed and fault tolerant nature, it finds applications where the blockchains can be utilized. Various applications and dissertations based on the Brooks–Iyengar algorithm have proved this.
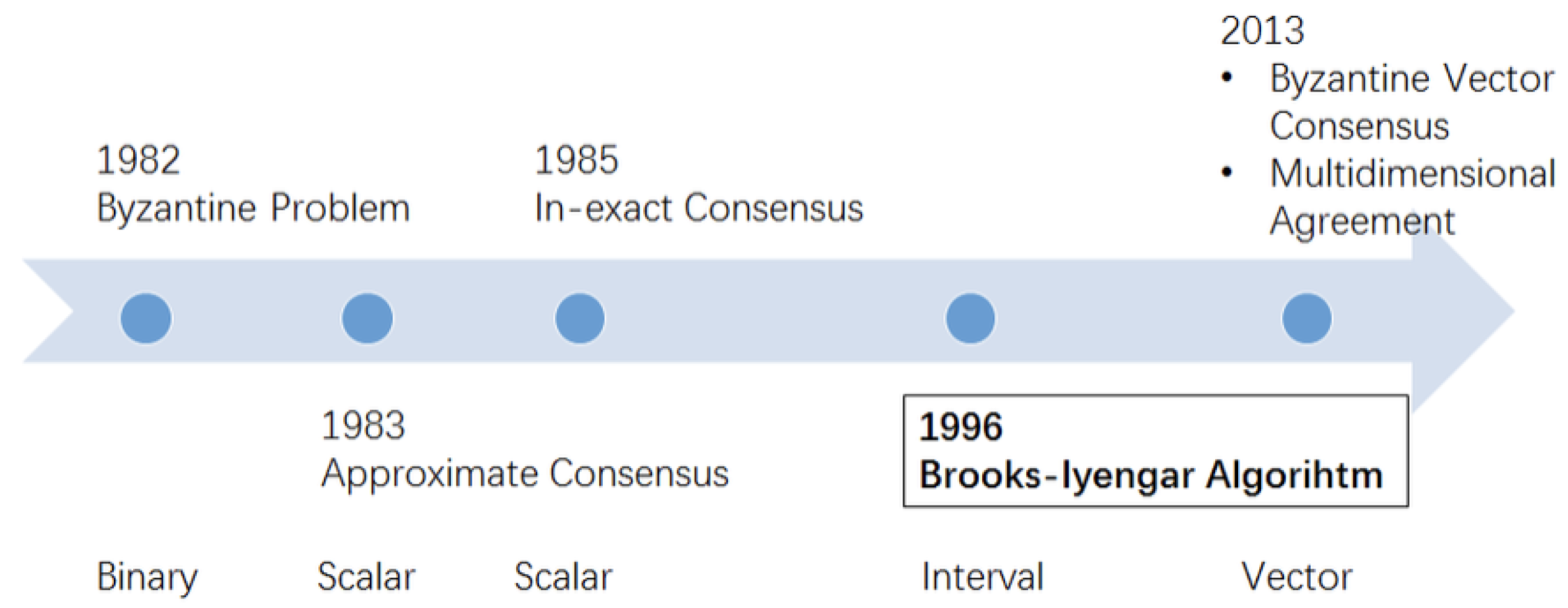
Figure 1 depicts the timeline of the various related algorithms. The list is as follows:
1982—The Byzantine General problem [
2] was defined as an extension of the Two-Generals problem so that it can be viewed as a binary problem.
1983—Approximate Consensus method [
3] was introduced that eliminated values from the set of scalars to tolerate faulty inputs.
1985—Inexact Consensus was introduced [
4] that used scalar inputs.
1996—Brooks–Iyengar algorithm [
5] is an interval based approach, is highly fault tolerant and has since then seen many applications even until the date.
2013—Byzantine vector consensus [
6] as a method that works on vector inputs was introduced. The multi-dimensional agreement method was also introduced with the added feature that included the usage of distance.
Blockchains are distributed, decentralized public ledgers that deals with the storage and subsequent manipulation of digital information (blocks) in public databases (chains). One of the key features of a blockchain system can be explained in the way it is used in a Bitcoin like crypto-currency with the solution it provides to the double-spending problem based on the consensus algorithms and confirmation mechanisms. Blockchain systems and the corresponding network protocols have great potential in many fields including Financial Technology (FinTech), Internet of Things (IoT), Smart Grid, etc.
The Blockchain system is a decentralized system, where every node has a complete copy of the blockchain data. This makes it more robust to malicious attacks and attempts to crack the system and extract information. Successful working without a centralized node which manages and maintains all the interactions showcases the lack of need for a specified official node to govern the database within the Blockchain. All of the historical transactions among users are recorded as blocks and stored immutably in the blockchain system [
7].
A typical blockchain system has the following features:
Every node has a full copy of the transactional records related to the application it is being used for right from the genesis of the application.
Participants are rewarded with a certain transaction fee or an incentive for any publicly-verifiable computational work they perform. This forms the basis for the consensus, which acts as the backbone of the blockchain technology.
Repeated verification of the works of others enhances the chances of gaining the benefits or rewards and thus lures new nodes to join the network of decentralized nodes. The larger the number of nodes, the more are the number of people verifying the transactions and the better is the integrity of the data.
In the Blockchain system, the transaction history is distributed to the decentralized peer-to-peer network. Each block has the details of transactions that have occurred. Hence, for a new block to be added to the parent chain and thus the blockchain system, it would need the consent of the participants in the chain. The new transaction that is reported is then packaged into a new block and awaits the successful acceptance by the participating nodes. After successful verification of the transaction recorded in the block, the block is added to the parent chain and every node updates its database with details of the new block.
Consensus in Blockchain
Consensus algorithms play an important role in the blockchain technology. It ensures that the integrity of the record in a block in the chain is maintained and the transaction is not tampered with or altered. In order to alter the transactional history in a block of an existing parent blockchain, the sub chain would have to be completely altered and is a very tedious task to be performed in the midst of the many peering eyes of the fellow nodes. Thus, the historical records are consistent in every node.
Many consensus algorithms have been introduced to support the Blockchain system. Some of the well known consensus algorithms are:
Each of these algorithms has its own set of advantages and disadvantages. The applicability of any of the above consensus algorithms depends on the application it is being used for. Thus, identifying the appropriate consensus algorithm that would fit the application is an important aspect of designing the blockchain system.
In this paper, we use references to multiple sensors and sensor data and provide a novel technique of using the Brooks–Iyengar algorithm to decentralize the data source, which is the value in the transaction of a block, in case the data source is dominated by one or few groups. The rest of the paper is organized as follows.
Section 2 gives a brief introduction to blockchains and the various structures that exist in blockchains. Principles related to the Blockchain technology are discussed in
Section 3. The succeeding sections highlight the applicability of the Brooks–Iyengar algorithm in combination with a multi-sensor environment while using the Blockchain system. The proposed procedure using the algorithm would provide a means to decentralize the data source. Finally, we give a theoretical analysis of the usage of the Brooks–Iyengar algorithm in this context and conclude the paper.
This paper describes a novel technique to explain the decentralization of a data source using a blockchain based approach. Information fusion from multiple sensors is explained using the seminal work of the Brooks–Iyengar Algorithm. The use of this algorithm when working with the Blockchain technology is the main contribution of this paper. The applicability of the design to a smart grid environment with possible seamless collaboration by a financial system energy system and the consumer is explained in this paper. A theoretical analysis of the performance of the algorithm has been explained in this paper and more experimentation is a part of the future research directions.
2. Blockchain Structures
Blocks in a blockchain system hold batches of valid transactions. These transactions are encoded by a Merkle Tree into hash values. Each block includes the hash values of the previous block and this chain runs until the path to the very first block of the chain can be traced. Thus, every two blocks in the system are linked like a chain giving it the name
Blockchain.
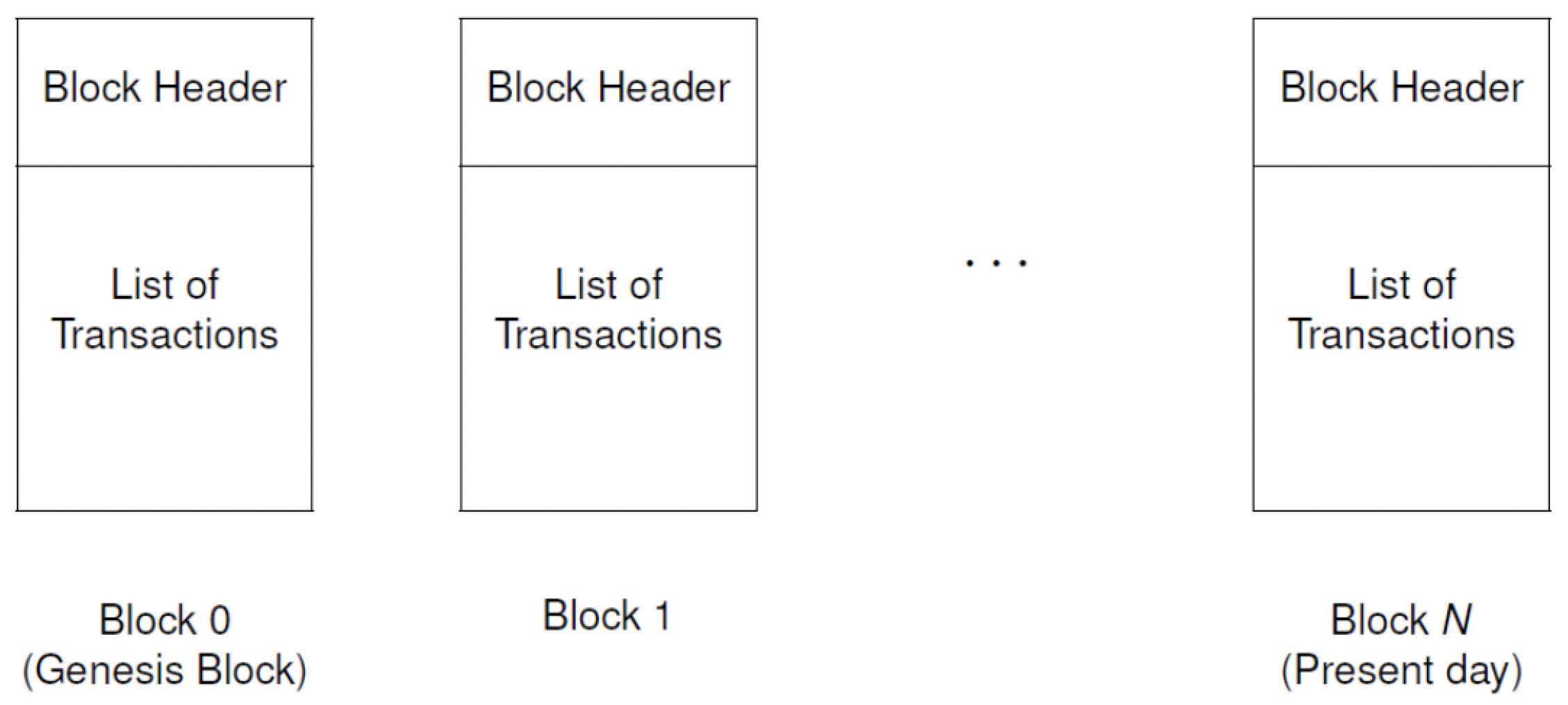
Figure 2 showcases the links between the individual blocks and how it grows into the complete blockchain. This chain of blocks is expected to have a great impact on the way things work. A good example of the applicability of blockchains is the way it has revolutionized the working of crypto-currencies. Many other researchers have discussed the various applications of blockchains. Newer versions or these have been introduced and implemented successfully.
As depicted in
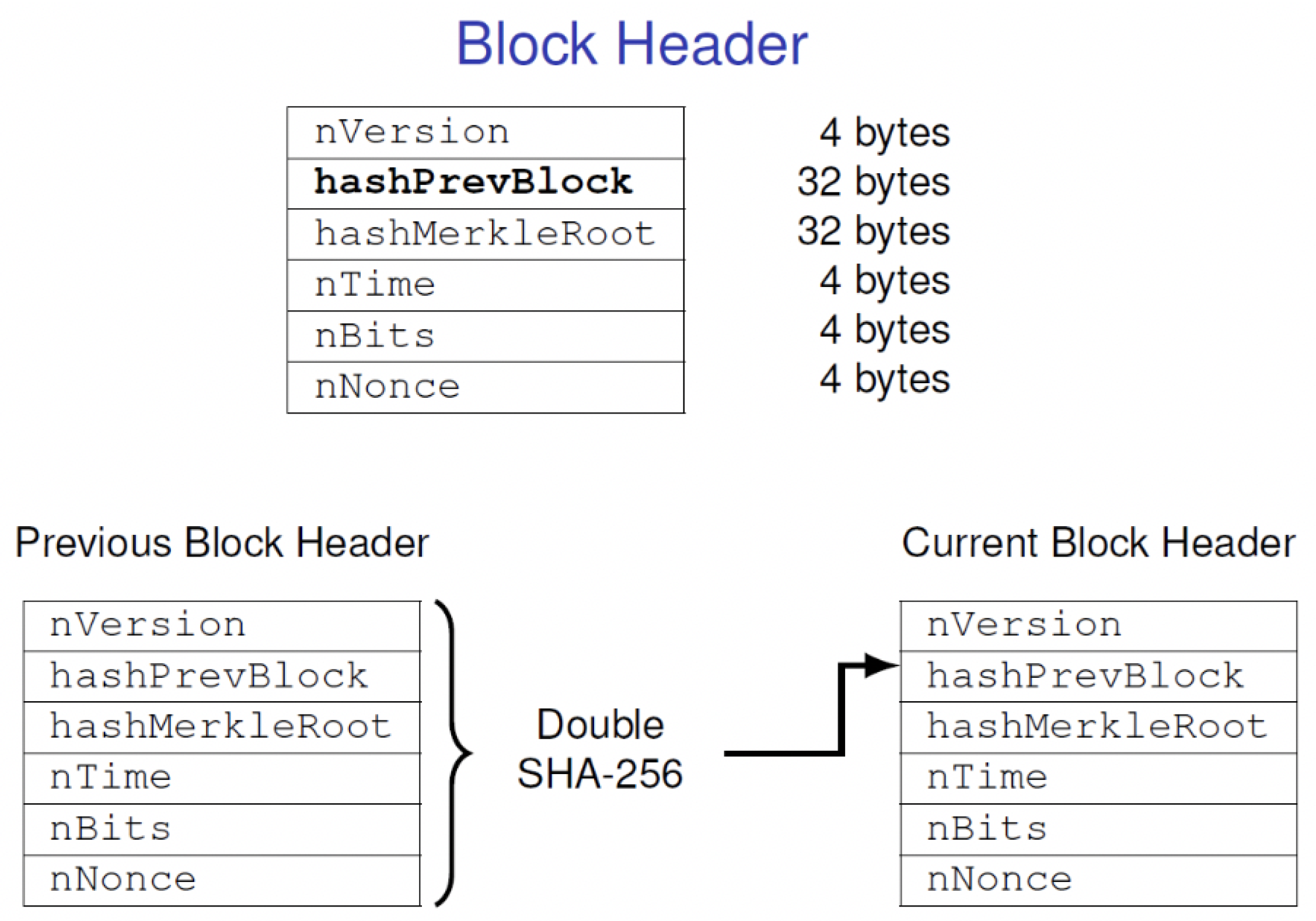
Figure 2, each block consists of a block header and a list of transactions. The block header has six parameters that include:
The blocks are linked by the item of the
hashPrevBlock. A detailed view of the Block Header with the various fields encompassed in it is depicted in
Figure 3, where the
hashPrevBlock of
th block is the Double SHA-256 hash value of the
nth block. Finally, all blocks are linked and all historical transactions is recorded in the blockchain.
Transaction Procedure in Blockchain
The transaction procedure adopted in Blockchains solved the double-spending problem by employing the consensus algorithm and replicating the confirmed stages. The process of finding a valid block is called mining, and and is accomplished by specialized nodes called the mining nodes. The participants involved in the consensus process perform the mining and the process involved in this is as discussed in the following loop:
New transactions are generated and broadcasted into the network;
Mining nodes collect these broadcasted transactions from the network;
The mining nodes then verify all transactions and package them into a block, making a record of all the inputs that have already been used previously;
Select the most recent block on the longest chain in the blockchain. This block would have the most votes from participant nodes. The hash value of the latest block determined in such a manner is inserted into the new block header;
Solve the Proof-of-Work (PoW) problem—If the PoW solution is checked indicating that all the transactions are verified, then the block is validated;
The new validated block is broadcasted to the network;
Each node that receives the new block will check the availability of the new block and verify the signature and PoW solution of theirs. If the block is checked and validated, the node will accept the new block and insert it into the blockchain where it becomes immutable and thus can not be altered.
Every transaction to be added to the blockchain will need to be confirmed and checked by six or more nodes. This means that, if some malicious node wants to alter the transactions, it must reconfirm the new transactions and the corresponding hash values; in addition, the PoW solutions to generate all the blocks in the chain after the block are altered.
3. Transaction Source of Blockchain
The historical transactions within the Blockchain and the transaction procedures have been proved robust through many applications. However, the most successful discussions in many years has been in the area of crypto-currencies. Introducing the blockchain architecture into new areas calls for more research and understanding of the system. Systems such as Smart Grids and Internet of Things (IoT), where the data produced or transmitted by the source of the transactions are not reliable, would need the use of other algorithms that could make the system more robust. For example,
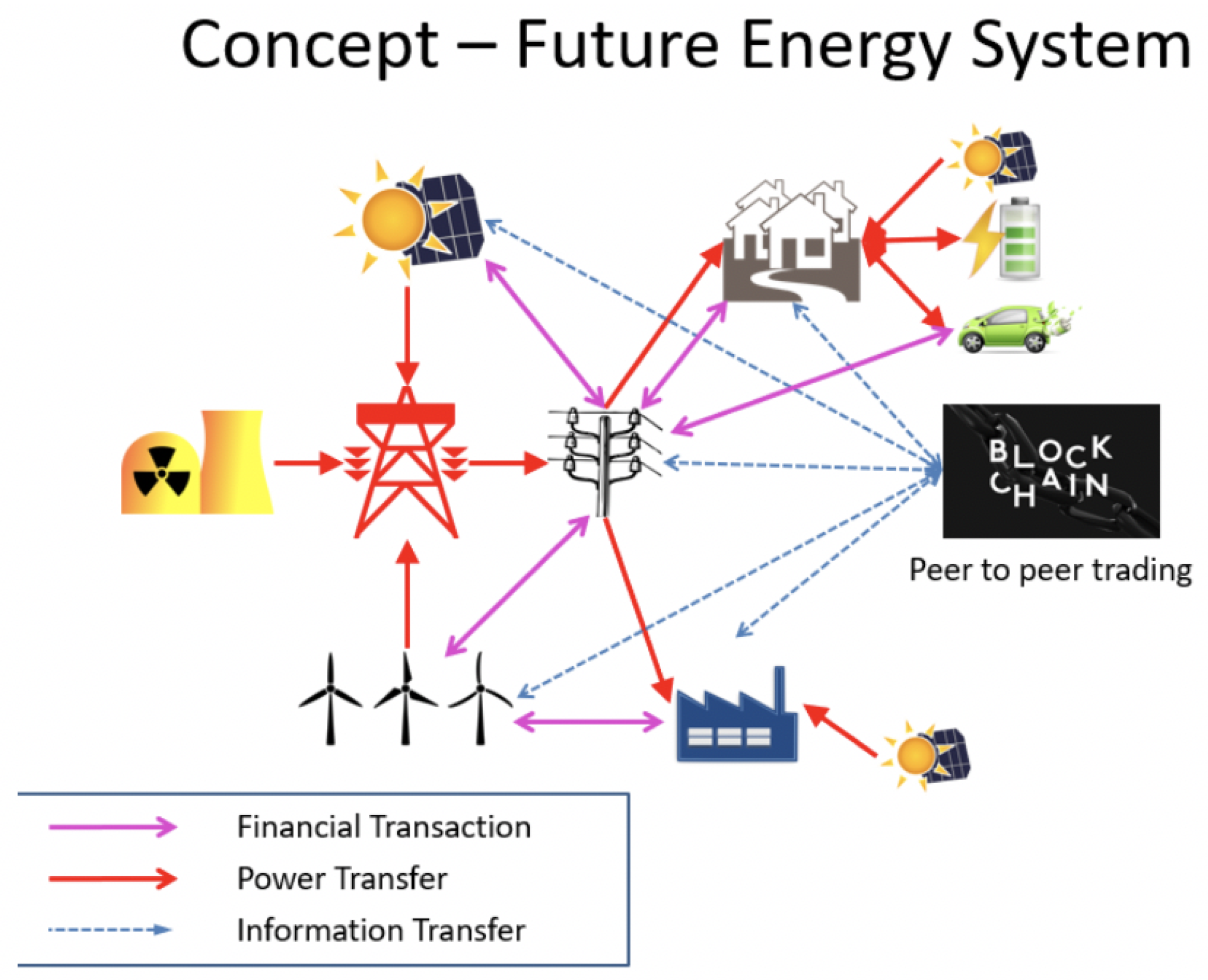
Figure 4 shows the Future Energy System with the Blockchain technology deployed in its functioning.
Figure 4 depicts a scenario wherein an energy supplier harnesses energy from multiple sources including nuclear, solar, wind, hydel, coal and other methods. This is the scenario with many suppliers who supply energy to a specific geographic area. With the advent of IoT and the benefits it has in collaboration with the Smart grids, we can expect the energy delivering process to the household automated. In such cases, there would be the use of multiple sensors that monitor the amount of energy being supplied and it can be argued that each of the suppliers would have their own set of sensors to d o this process.
In
Figure 4, the transactions need to be confirmed and consistent among all nodes such as users, financial institutes and power stations. However, the source of the transactions which refers to the amount of the electricity consumed by the user is not completely decentralized and robust. As an example, the amount of electricity consumed is usually measured by a sensor. Any issue with the sensor or its malfunctioning, or possibility of attack by some adversaries and thus the alteration of the input raw data, makes the source unreliable.
In addition, in such scenarios, falsification of data as the sensor reading and thus reported to the blockchain system could lead to catastrophes. Therefore, we need a solution that can make the data source for the transaction fully decentralized and robust.
Thus, it is necessary to have a novel technique of decentralizing the data source and also make sure the process is robust and highly immune to faulty transactions. There is also a need for a strong fusion algorithm that would help in harnessing all the benefits that a distributed ledger like blockchains has to offer. The following section provides a brief introduction to the seminal work on the Brooks–Iyengar algorithm that would be used in designing a novel technique to decentralizing the data source and thus make the blockchain system built for such applications more robust.
3.1. Brooks–Iyengar Algorithm
One of the seminal algorithms that has had a profound impact on sensor technology applications is the Brooks–Iyengar Distributed Sensing Algorithm [
5,
8,
9]. The Brooks–Iyengar hybrid algorithm for distributed control in the presence of noisy data combines Byzantine agreement with sensor fusion. It bridges the gap between sensor fusion and Byzantine fault tolerance. This seminal algorithm unified these disparate fields for the first time. Essentially, it combines Dolev’s algorithm for approximate agreement with Mahaney and Schneider’s fast convergence algorithm (FCA). The algorithm assumes N processing elements (PEs), t of which are faulty and can behave maliciously. It takes as input either real values with inherent inaccuracy or noise (which can be unknown), or a real value with a priori defined uncertainty, or an interval. The output of the algorithm is a real value with an explicitly specified accuracy. The algorithm runs in O (NlogN), where N is the number of PEs: see Big O notation. It is possible to modify this algorithm to correspond to Crusader’s Convergence Algorithm (CCA); however, the bandwidth requirement will also increase. The algorithm has applications in distributed control, software reliability and High-performance computing.
Initially, it was observed that mapping a group of sensor nodes to estimate its value accurately would need all the sensors to mutually exchange the values amongst themselves. This was a computationally expensive process. The algorithm utilized an array of sensors that sensed a similar environment and passed the collected data onto a virtual sensor node. This virtual node thus defined would collect data from all the sensors and aggregate the data from un-corrupted sensors. The Byzantine algorithm [
2] and its fault tolerant methodology when used in such situations provides the necessary solution when working with real-time data from multi-sensor applications. This brought the rise of the Brooks–Iyengar algorithm or the Brooks–Iyengar hybrid algorithm that provides solutions to enhance the precision and accuracy of the measurements taken by a distributed sensor network. This algorithm works well even in the presence of faulty sensors [
10].
The Brooks–Iyengar algorithm can fuse multiple sensors in a local system or reach consensus in distributed systems with the capability of fault tolerance. In case the source of data for the blockchain is unreliable, we would need the benefits of the Brooks–Iyengar algorithm to make the data source decentralized and robust to malicious attack or sensor errors.
3.2. Algorithm in Brief
The Brooks–Iyengar algorithm is executed in every processing element (PE) of a distributed sensor network. Each PE exchanges its measured interval with all other PEs in the network. The “fused” measurement is a weighted average of the midpoints of the regions found [
11]. The concrete steps of the Brooks–Iyengar algorithm are shown in this section. Each PE performs the algorithm separately:
Input:
The measurement sent by to is a closed interval , .
Output:
The output of includes a point estimate and an interval estimate.
receives measurements from all the other PEs.
Divide the union of collected measurements into mutually exclusive intervals based on the number of measurements that intersect, which is known as the weight of the interval.
Remove intervals with weight less than , where is the number of faulty PEs.
If there are L intervals left, let denote the set of the remaining intervals. We have , where interval and is the weight associated with interval . We also assume .
Calculate the point estimate of as and the interval estimate is .
The input and output of the Brooks–Iyengar algorithm can be depicted as:
where
- -
⋯ are the sensor readings in the specified interval;
- -
v is the output value;
- -
I is the output interval that defines the bounds of the output value.
Accurate detection of sensor values is one of the fundamental requirements to successful tracking when working with multi-target and multi-sensor applications. Key factors affecting the multi-target detection include
Detection in Wireless Sensor Networks (WSNs) must carefully address the possibility of a high correlation between nearby sensors and detached sensing by far away nodes, as this would play an important role in the overall outcome and the functioning of the system.
3.3. Combining the Brooks–Iyengar Algorithm with Blockchains
Since blockchains have no official node, and the application deals with decentralized network of nodes, there is a need for a robust consensus algorithm. By using such a consensus based approach in the smart grid example, we can introduce multiple suppliers to the measurement stage of the consumption by a user. More specifically, multiple sensors would have to be employed to measure the physical world and make a decentralized measurement that will ensure that the values in the transactions of the Blockchain is robust and the integrity is maintained even when distributed among all nodes in the network.
In similar lines, to visualize the application depicted in
Figure 4, we would use multiple heterogeneous sensors from different suppliers to measure the physical values in its surroundings. The Brooks–Iyengar algorithm would work in conjunction and attempt to fuse the measurements of the physical values. Redundant sensors from different suppliers measure the physical values according to their own criteria, and using the Brooks–Iyengar algorithm can make the sensor readings consistent.
Figure 5 shows the use of four sensors to measure the electricity flow and supply. Each of these sensors is installed by varying suppliers, who, with their independent sensors, can avoid the data source from being determined by one or few predominant groups that try to monopolize the system and its activities.
We combine the Brooks–Iyengar algorithm with Blockchain by adopting the following steps:
Each supply has an independent sensor or group of sensors to perform this action.
Redundant and independent sensors enhance the fault tolerance ability and make the data source decentralized.
Introducing the Proof of Work (PoW) consensus mechanism to provide each node with the permissions and ability to check and verify the raw sensor data.
After careful verification and with the consent of the multiple participating nodes, the raw data from different suppliers are saved into blocks and ascertained to be a part of the parent chain of the Blockchain.
The sensor node measures the physical values and computes a hash value of the raw data. These hash values are later uploaded to the Blockchain. The virtual node collects the sensor data from multiple sensors and computes to find the solution (raw sensor data) of the hash values and then uses the Brooks–Iyengar algorithm to get the result. Finally, a transaction that includes the solution (raw data), hash values and the result of the Brooks–Iyengar algorithm will be packaged into a block and broadcasted through the network.
The algorithm combines the benefits of the Brooks–Iyengar algorithm and Blockchain technology as follows:
Each sensor node encodes the measurements into a block of hash values and uploads it.
Each node collects the packets from sensor nodes and tries to identify the real measurements, following which, the Brooks–Iyengar algorithm is used to fuse the multiple sensors’ readings.
Real measurements, hash values and the result of the Brooks–Iyengar algorithm are packaged into a block.
Each node receives the new block and checks and verifies the authenticity of the transaction and decides to add it to the parent or dominant chain of the blockchain or not.
Figure 6 shows an example of the packet from sensor to block with four sensors, where
⋯
are the raw measurements and
are the outputs of the Brooks–Iyengar algorithm. The complexity of the encoding could be adapted to the real scenario, as well as the raw data could also be chained or linked one-by-one to be exempted from cracking or forging.
3.4. Example
There are various advantages of using the blockchain technology in Smart Grids [
12]. In this section, we give an example of the Brooks–Iyengar algorithm to blockchain and verify its applicability in Smart Grids. The platform used including software and hardware such as the smart metering module is open-source and decentralized i.e., anyone can set a sensor to measure the electricity consumption. Each user has an account that displays the records corresponding to the electricity balance and electricity consumption each day. The energy consumption is uploaded, validated and persisted in the blockchain where all the historical transactions are housed.
In a typical timeline of transactions, let us assume that the user has a balance of 100 units granted by the electricity plant. The user may consume a certain amount of electricity units and the transactions pertaining to this use should be synchronized and validated between the user and electricity supplier or plant. A sample of the timeline showing a series of transactions that depicts the events that occur based on the consumption is as shown in
Figure 7.
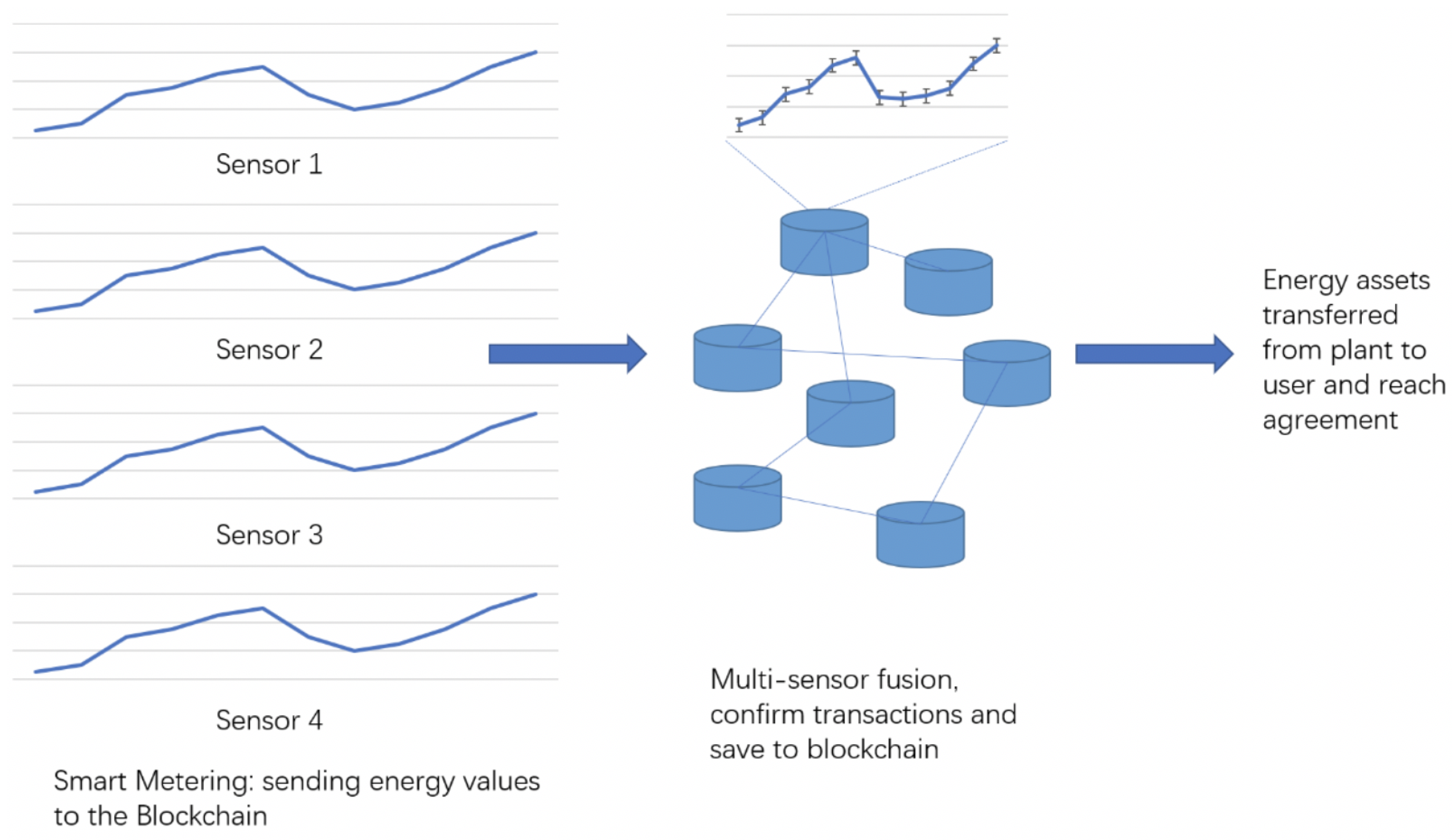
Since hardware and software of the sensors and the nodes are open-source, each measurement point may consist of multiple sensor metering nodes. The multiple sensor metering nodes may come from different manufacturers and vendors or the user could place his own sensor metering, making it highly heterogeneous. In
Figure 8, there are four sensors that may be placed by different companies to measure the electricity consumption. The sensor value after being collected is fused and stored as transactions in the parent chain of the blockchain.
As shown in
Figure 8, four sensors (assuming they are non-faulty) are used to measure the energy value and get the corresponding hash value. The hash value is then decoded by the nodes, which is a simplified Proof of Work (PoW) mechanism. After the hash value of the four sensors is decoded, the values are fused by the Brooks–Iyengar algorithm and a corresponding transaction is created. Following this, the transactions are broadcast into the whole network like a typical blockchain transaction. Finally, the transaction is stored in the blockchain and the user and the electricity plant will reach an agreement on the units consumed and remaining for the user.
Table 1 showcases an example of values from multiple sensors with one of them being faulty. A sensor senses and constantly measures the electricity consumption. We have selected a snapshot of the sensor readings as measured at time
. These are the readings that give an insight into the electricity consumption measurement from the user to the blockchain. At time
, we get values from five different sensors with
being faulty.
After the sensor values have been obtained, we pass it through a known hashing algorithm to get the hash value of the sensor values and the data packet is broadcast randomly to some of the participating nodes.
Table 2 depicts the hash values that have been created and the corresponding sensors that provided the input to the hashing algorithm. The hash values are then sent across to multiple participating nodes.
The node receives the hash value, decodes the hash value and tries to identify the real values. On identifying the initial value from the sensors, the Brooks–Iyengar algorithm is invoked to fuse the five sensors’ values, and gets
Table 3. In fact,
is faulty and deviates from the fused value.
is the value obtained after the Brooks–Iyengar algorithm based data fusion is performed.
A transaction includes the data (transaction values) as shown in
Table 3. Such transactions are broadcasted to other nodes, and is validated by the other nodes like a typical transaction process in a blockchain.
Figure 9 shows the various steps involved in fulfilling the transaction process of a blockchain. The transaction values are the fused electricity consumption values measured by multiple sensors and combined according to the Brooks–Iyengar algorithm. The Electricity Transmitter is the user and the Electricity Receiver could be the electricity supply plant; a transaction has the details of the transaction made between them. The process includes creation of a new block, which is usually validated by a miner and broadcast to all other nodes. Finally, the block contains transaction values that are to be added to the longest surviving parent chain of the blockchain.
4. Accuracy and Precision of the Brooks–Iyengar Algorithm
As depicted in the previous example, the faulty sensors such as
may have an impact and deviate the result, and we need to determine the precision and accuracy of the Brooks–Iyengar algorithm even in the presence of faulty sensors. We define the precision as:
where
,
are the two sensor values. The precision could be the disagreement of the fused result between two users when they both have faulty sensors.
In order to identify the disagreement between the fused result and the ground truth, we define the accuracy as:
where
is the ground truth.
Precision bound and accuracy bound are determined on the basis of the work published and described in [
7]. Let
denote the precision of the Brooks–Iyengar algorithm,
,
are the value of
ith and
jth Processing Elements (PEs). The largest possible disagreement about the fusion output between two Processing Elements (PEs) is as depicted in the below equation:
Accordingly, as per a well known theorem from [
7],
where
=
,
≤
,
N is the number of PEs,
is the number of faulty PEs, and
g is the set of non-faulty PEs.
Let
be the accuracy of the Brooks–Iyengar algorithm,
is the real value to be estimated, and then:
where
is the length of the
th smallest measurement of all non-faulty sensors.
Accuracy and precision bound describes the property of the final value stored in the blockchain, and could be used further as reliable transactions.
Fault Tolerance
Since some sensors could be faulty and deviate from the fused result, we will show the fault tolerant ability of the Brooks–Iyengar algorithm when it is used as a sensor fusion method. The Brooks–Iyengar algorithm could tolerate
faulty sensors and it is proved by [
13]; the output bound of the interval is:
| If <, then the output is bounded by |
where
is the faulty sensors number and
n is the number of all sensors, and
is the
th smallest values of all the input intervals.
5. Simulation
In this section, we will use an experiment [
14], which uses four sensors to measure a physical signal, in order to explain the fault tolerant ability of the Brooks–Iyengar algorithm. Give a ground truth signal:
where
= 1 and the sampling interval is 0.2.
The sensors measure the signal and output an interval , , where is the value and is the confidence range. Suppose is the ground truth and three sensors’ output values satisfy and X∼, which means that the distance between ith measurement and is continuous uniform distribution . One sensor is malfunction and , where is the sensor’s output value. Four sensors have the same quality and share the same confidence range .
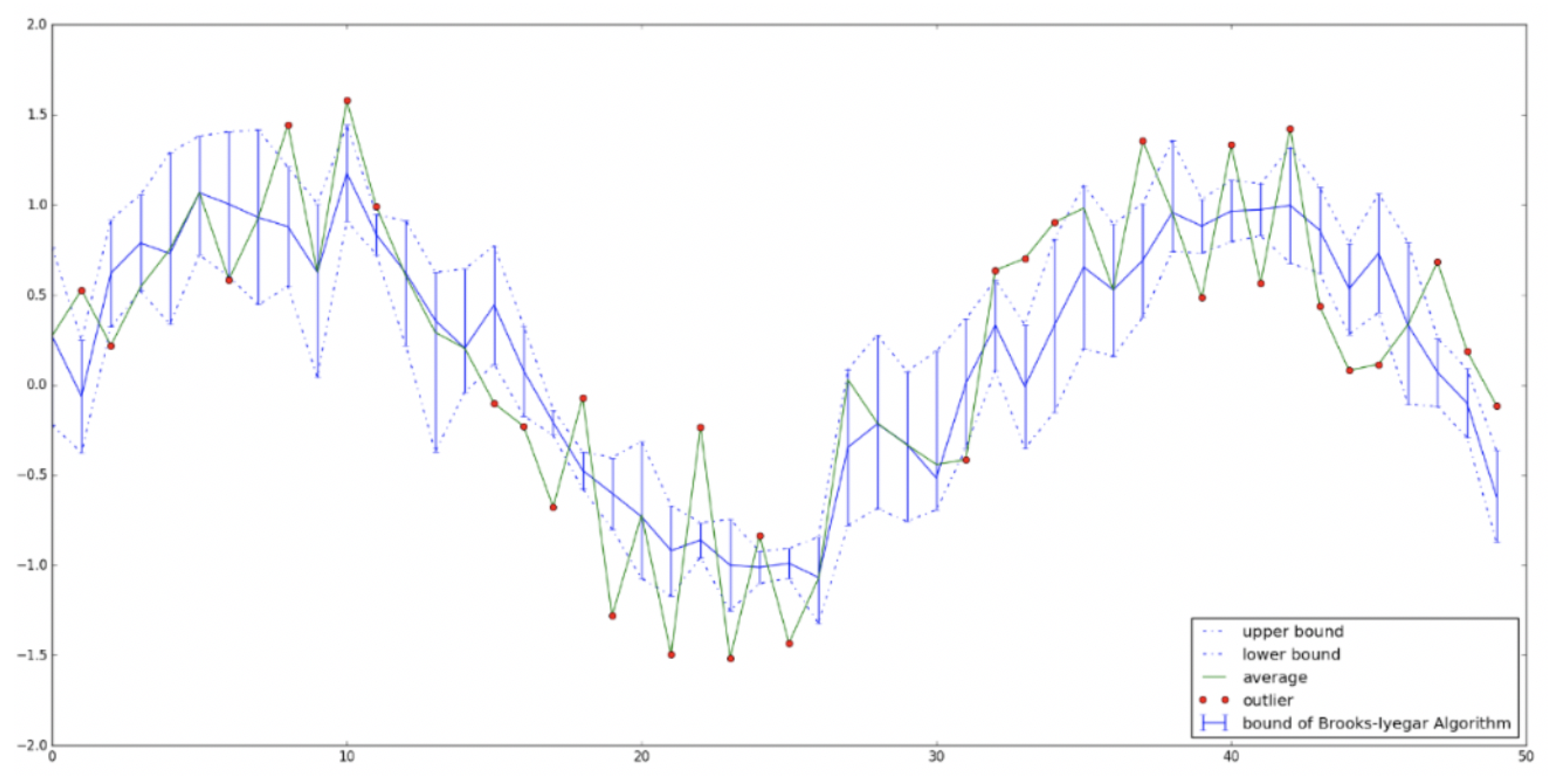
Given the above conditions,
Figure 10 shows a comparison between the Brooks–Iyengar algorithm and the naive average algorithm. Then, we run two algorithms in the same condition. From the simulation results, we find that the bound of the Brooks–Iyengar algorithm always contains the ground truth, while the output of naive average sometimes is far from the ground truth. Since the bound of the Brooks–Iyengar algorithm is the smallest bound to contain the ground truth, the green line that is not in the bound must be faulty outputs, which are denoted by the red points.
6. Conclusions
The paper describes the transaction protocol, consensus algorithm and Proof of Work based consensus algorithm of the common blockchain. However, the common blockchain with only one sensor in applications like IoT or Smart Grids can not decentralize the data source, thus making the transaction values in the Blockchain controlled by a centralized node. In this paper, we have introduced a novel technique that involves the Brooks–Iyengar algorithm and proposed a procedure of adapting it in a multi-sensor environment while decentralizing the data source. The paper also discusses the theoretical bound of the result of the Brooks–Iyengar algorithm, which is the value to be saved in the Blockchain. Information fusion from multiple sensors is explained using the seminal work of the Brooks–Iyengar algorithm. The use of this algorithm when working with the Blockchain technology is the main contribution of this paper. The applicability of the design to a smart grid environment with possible seamless collaboration by the financial system energy system and the consumer is explained in this paper. A theoretical analysis of the performance of the algorithm when used in a blockchain based decentralized environment has been explained in this paper and more experimentation is a part of the future research directions.
Author Contributions
All the authors have contributed equally towards the conceptualization, methodology, software, validation, analysis, investigation and resources. The original draft, changes post review were also performed by all the authors equally.
Funding
This research was funded by the US Army Research Office under the grant number W911NF-15-10572.
Acknowledgments
The authors would like to thank Prof. Garg from IIM Ahmedabad for giving us an opportunity to work on the problem of smart-grids funded by the Department of Science and Technology. The authors would also like to thank all the reviewers for their comments, which improved the presentation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PoW | Proof of Work |
| WSN | Wireless Sensor Networks |
| IoT | Internet of Things |
References
- Ramani, S.K.; Iyengar, S.S. Evolution of Sensors Leading to Smart Objects and Security Issues in IoT. In International Symposium on Sensor Networks, Systems and Security; Springer: Berlin, Germany, 2017; pp. 125–136. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The byzantine generals problem. ACM Trans. Programm. Lang. Syst. 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Dolev, D.; Lynch, N.A.; Pinter, S.S.; Stark, E.W.; Weihl, W.E. Reaching approximate agreement in the presence of faults. JACM 1986, 33, 499–516. [Google Scholar] [CrossRef]
- Mahaney, S.R.; Schneider, F.B. Inexact agreement: Accuracy, precision, and graceful degradation. In Proceedings of the Fourth Annual ACM Symposium on Principles of Distributed Computing, Minaki, ON, Canada, 5–7 August 1985; pp. 237–249. [Google Scholar]
- Brooks, R.R.; Iyengar, S. Robust distributed computing and sensing algorithm. Computer 1996, 29, 53–60. [Google Scholar] [CrossRef]
- Vaidya, N.H.; Garg, V.K. Byzantine vector consensus in complete graphs. In Proceedings of the 2013 ACM Symposium on Principles of Distributed Computing, Montréal, QC, Canada, 22–24 July 2013; pp. 65–73. [Google Scholar]
- Ao, B.; Wang, Y.; Yu, L.; Brooks, R.R.; Iyengar, S. On precision bound of distributed fault-tolerant sensor fusion algorithms. ACM Comput. Surv. 2016, 49, 5. [Google Scholar] [CrossRef]
- Iyengar, S.; Brooks, R.R. Multi-Sensor Fusion: Fundamentals And Applications With Software; Prentice-Hall International: Englewood Cliffs, NJ, USA, 1997. [Google Scholar]
- Krishnamachari, B.; Iyengar, S. Distributed bayesian algorithms for fault-tolerant event region detection in wireless sensor networks. IEEE Trans. Comput. 2004, 53, 241–250. [Google Scholar] [CrossRef]
- Kumar, V. Impact of brooks-iyengar distributedsensing algorithm on real time systems. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1370. [Google Scholar] [CrossRef]
- Sahni, S.; Xu, X. Algorithms for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2005, 1, 35–56. [Google Scholar] [CrossRef]
- Winter, T. The Advantages and Challenges of the Blockchain for Smart Grids; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]
- Marzullo, K. Tolerating failures of continuous-valued sensors. ACM Trans. Comput. Syst. 1990, 8, 284–304. [Google Scholar] [CrossRef]
- Ao, B. Robust fault tolerant rail door state monitoring systems: Applying the brooks-iyengar sensing algorithm to transportation applications. Int. J. Next Gener. Comput. 2017, 8, 108–114. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).