Development and Experimental Evaluation of a Low-Cost Cooperative UAV Localization Network Prototype
Abstract
1. Introduction
2. Materials and Methods
2.1. Cooperative UAV Swarm Network Prototype
2.2. Mathematical Details of Cooperative Localization in the Developed Prototype
2.2.1. Kinematic Mobility Model
2.2.2. Centralized Cooperative Localization
2.2.3. Distributed Cooperative Localization
2.2.4. Special Case: Infrastructure Based Cooperative Localization
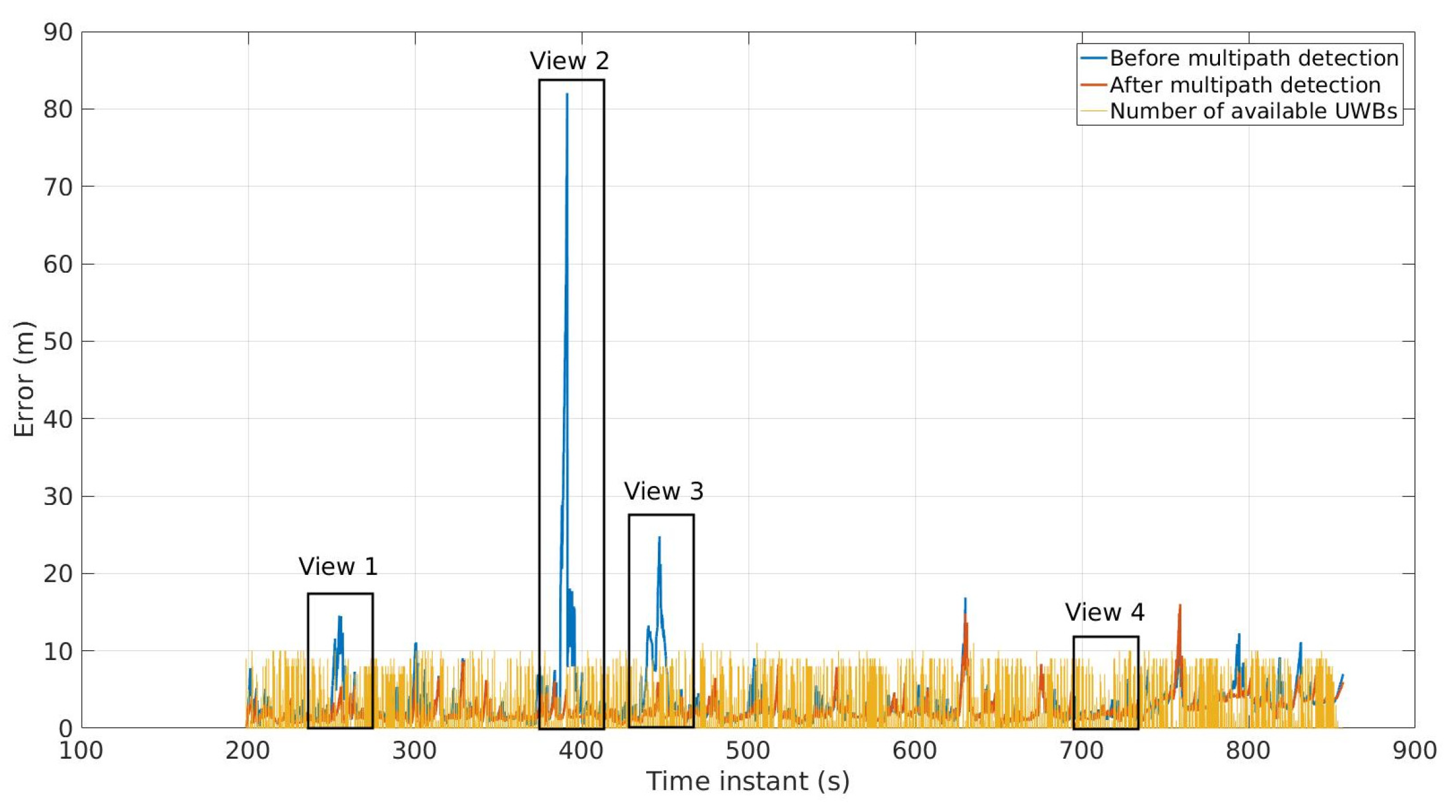
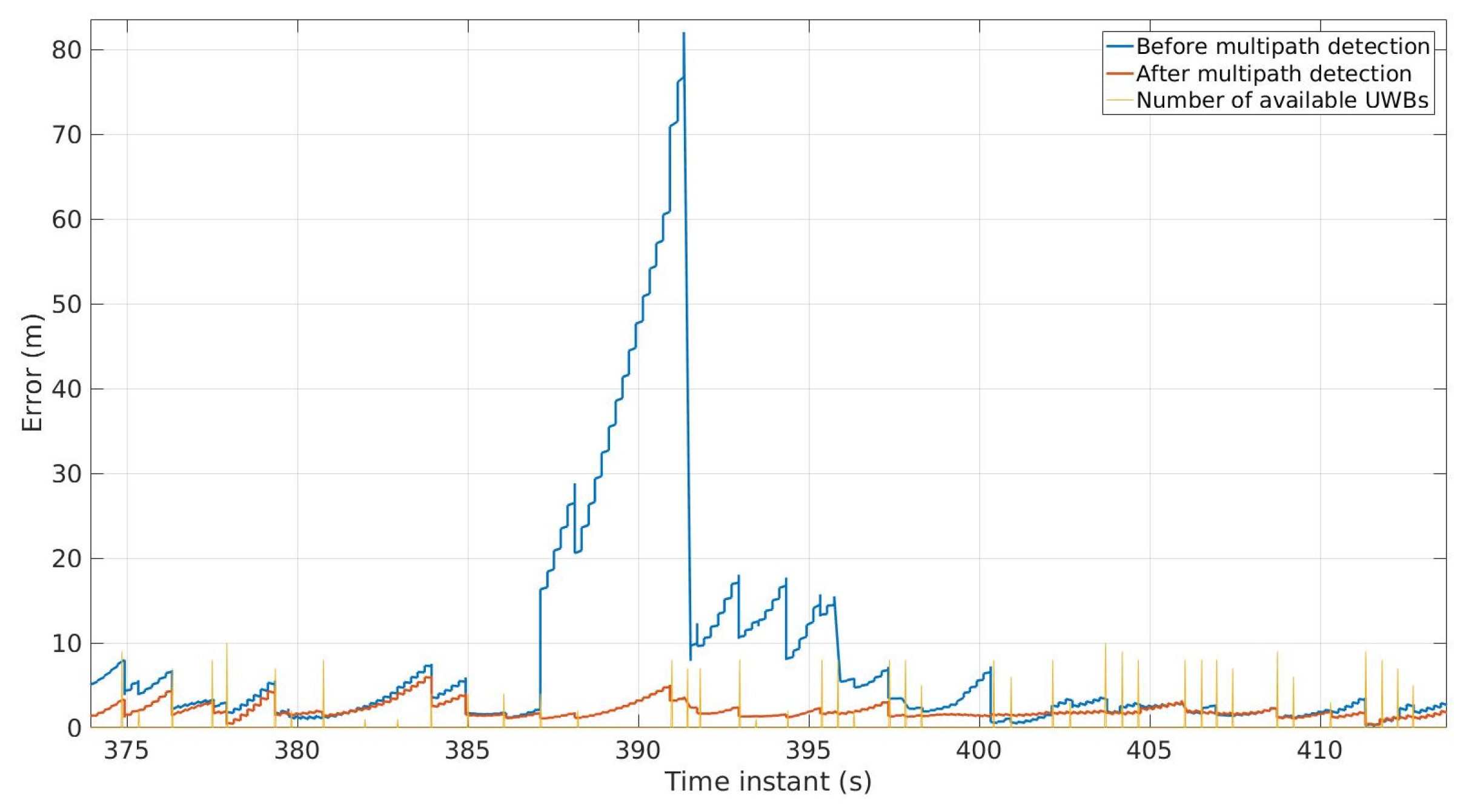
2.2.5. Adaptive Outlier and Multipath Rejection Algorithm
- : No range measurements affected by outliers are present in the dataset,
- : At least one range measurement affected by outliers is present.
2.3. Experimental Setup and Ground Truth Estimation
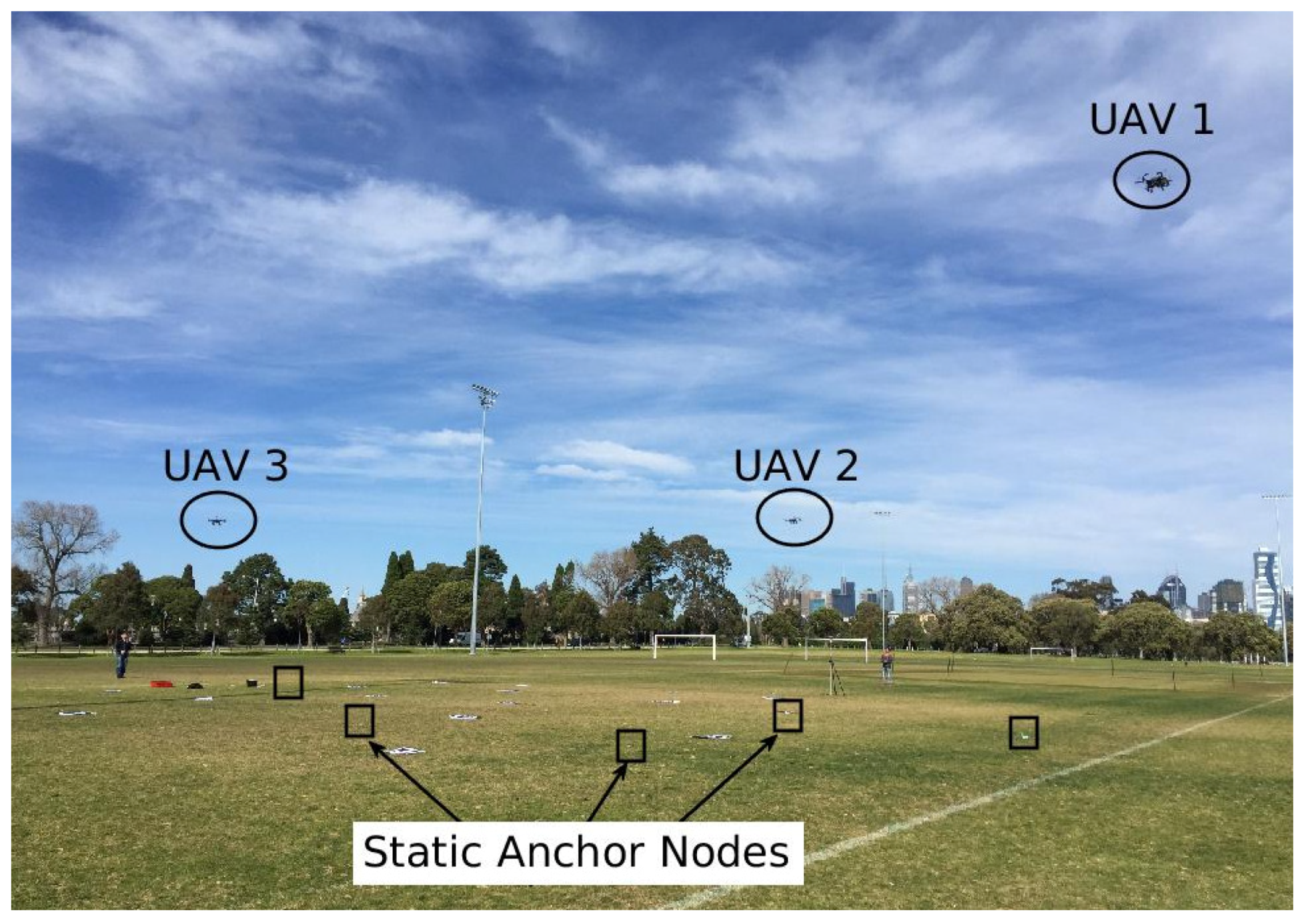
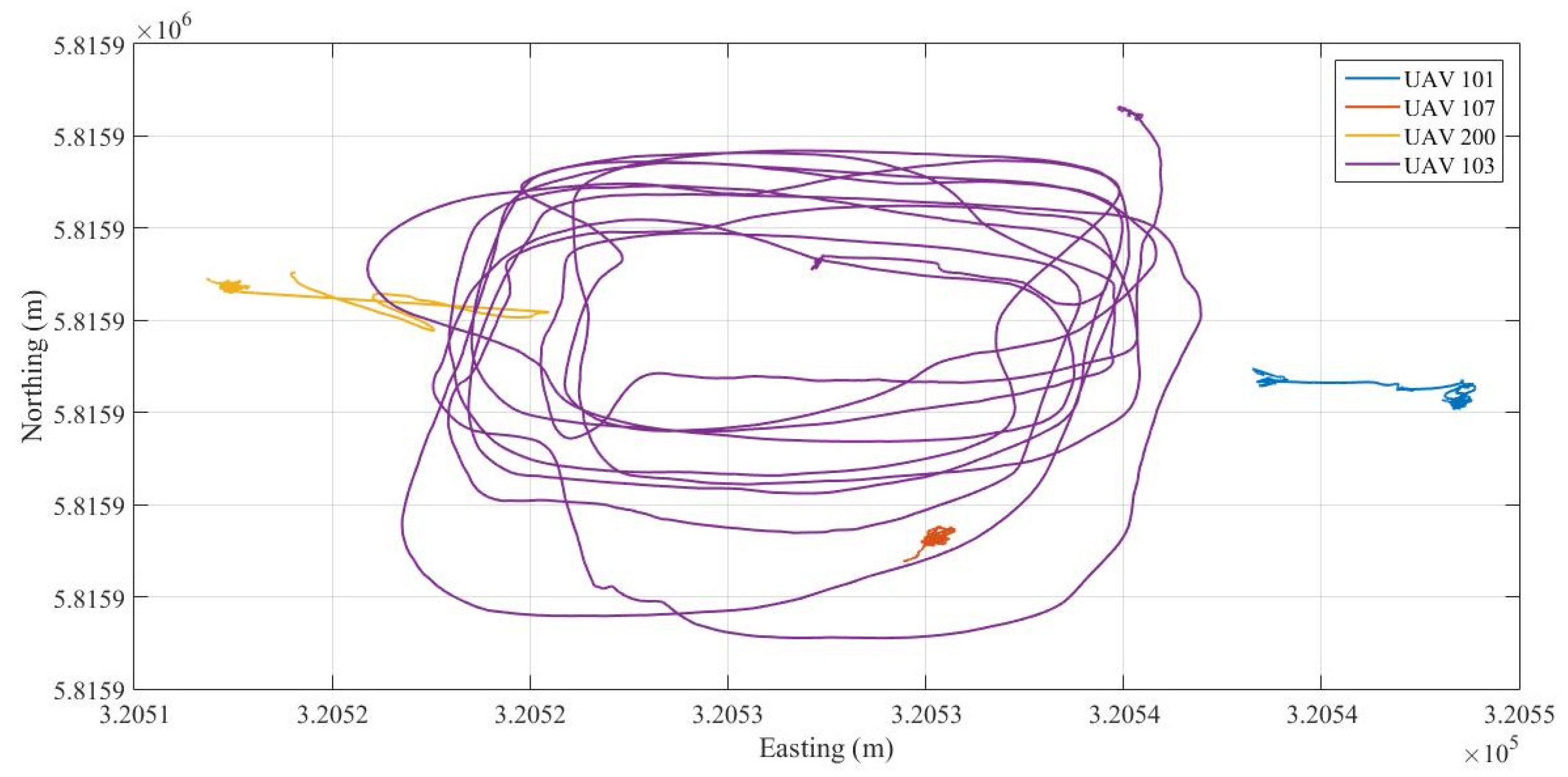
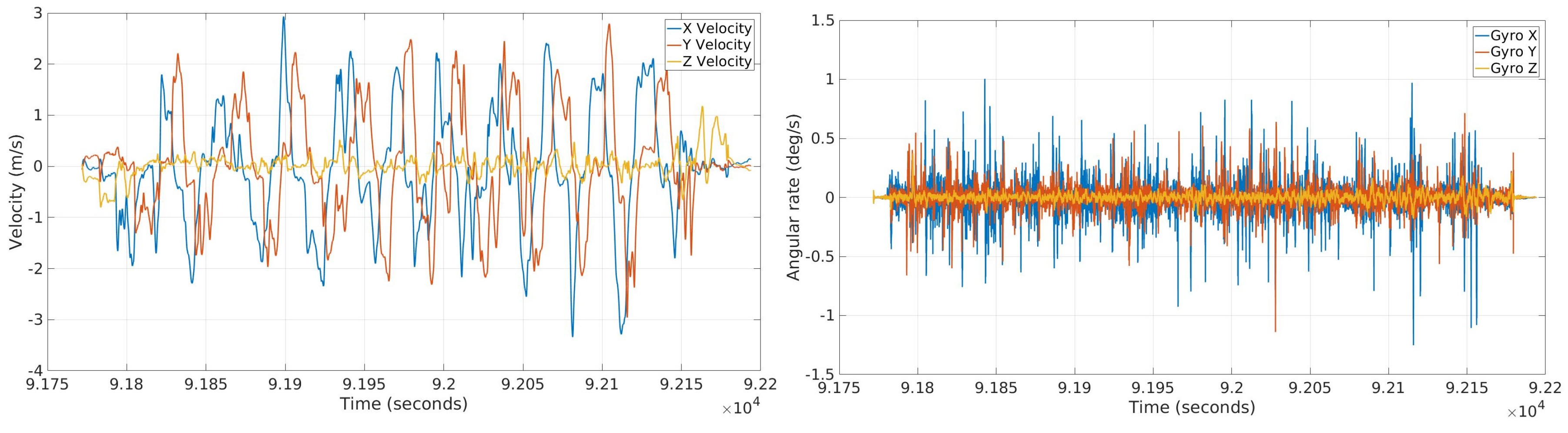
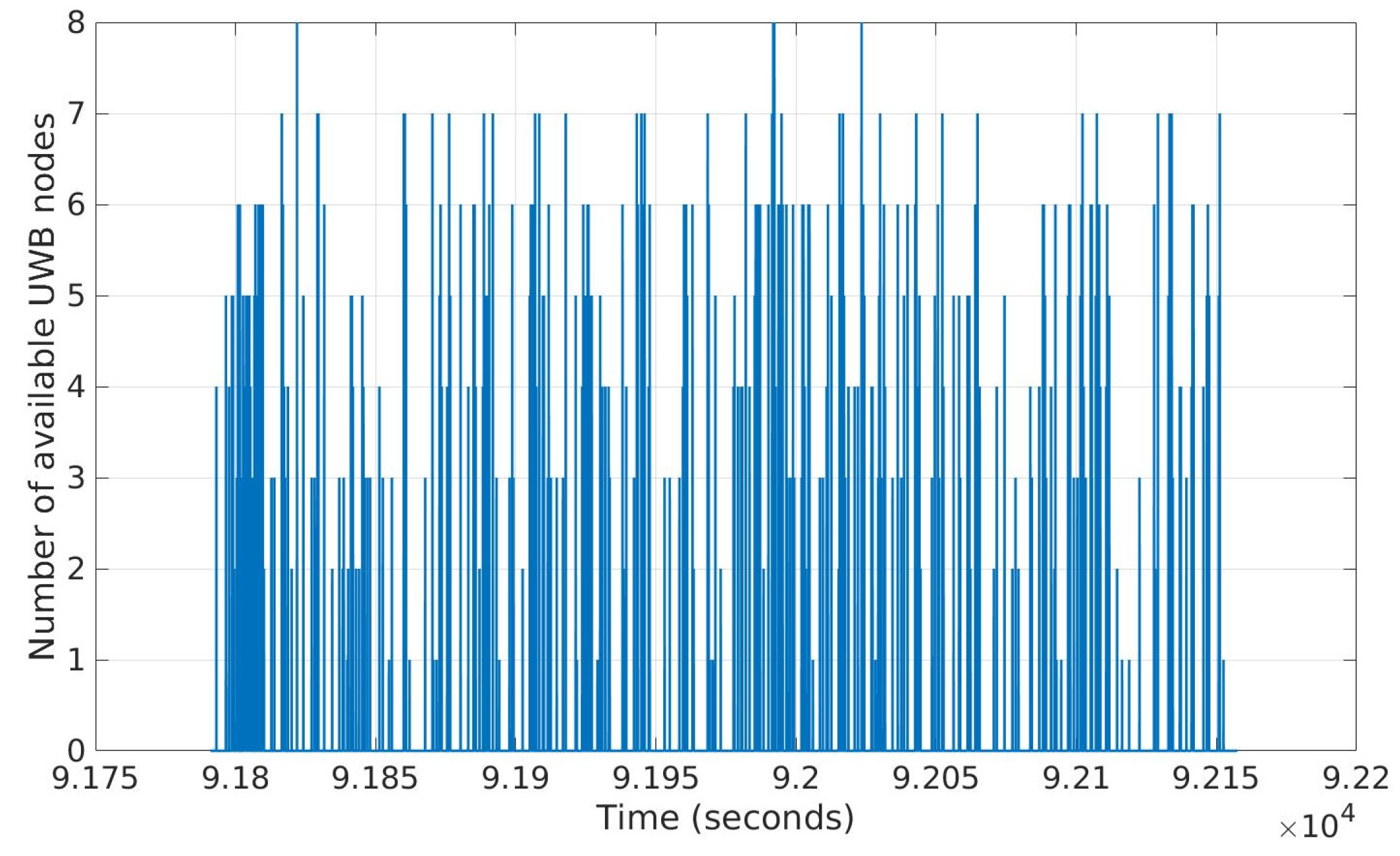
2.3.1. Experimental Setup of Cooperative Localization
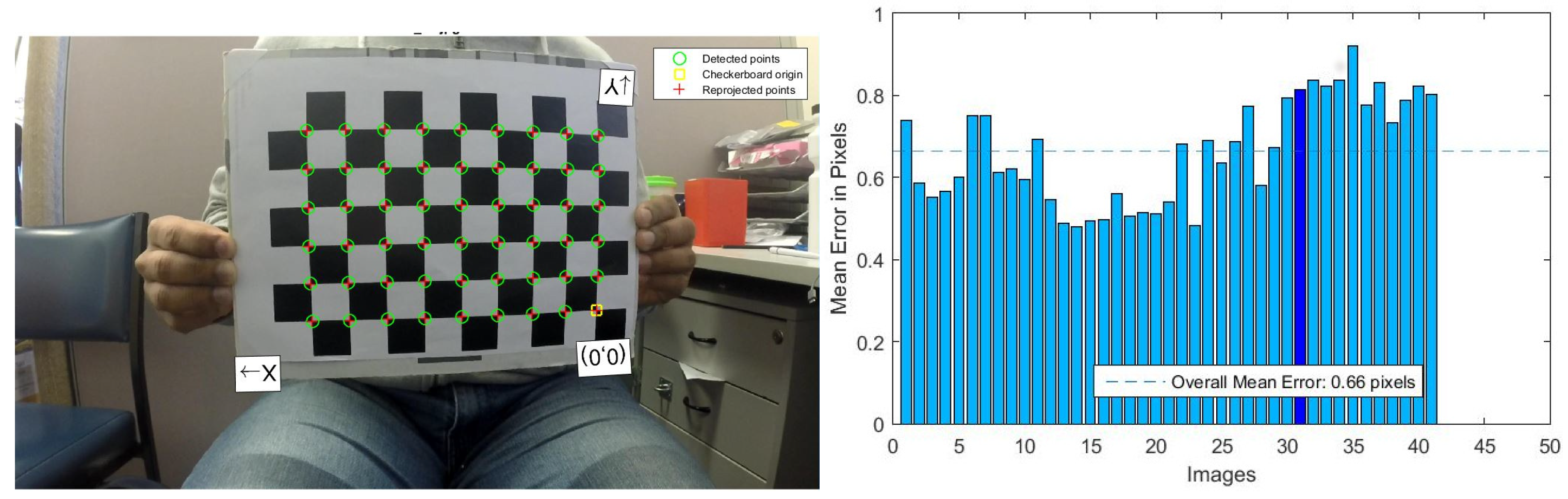
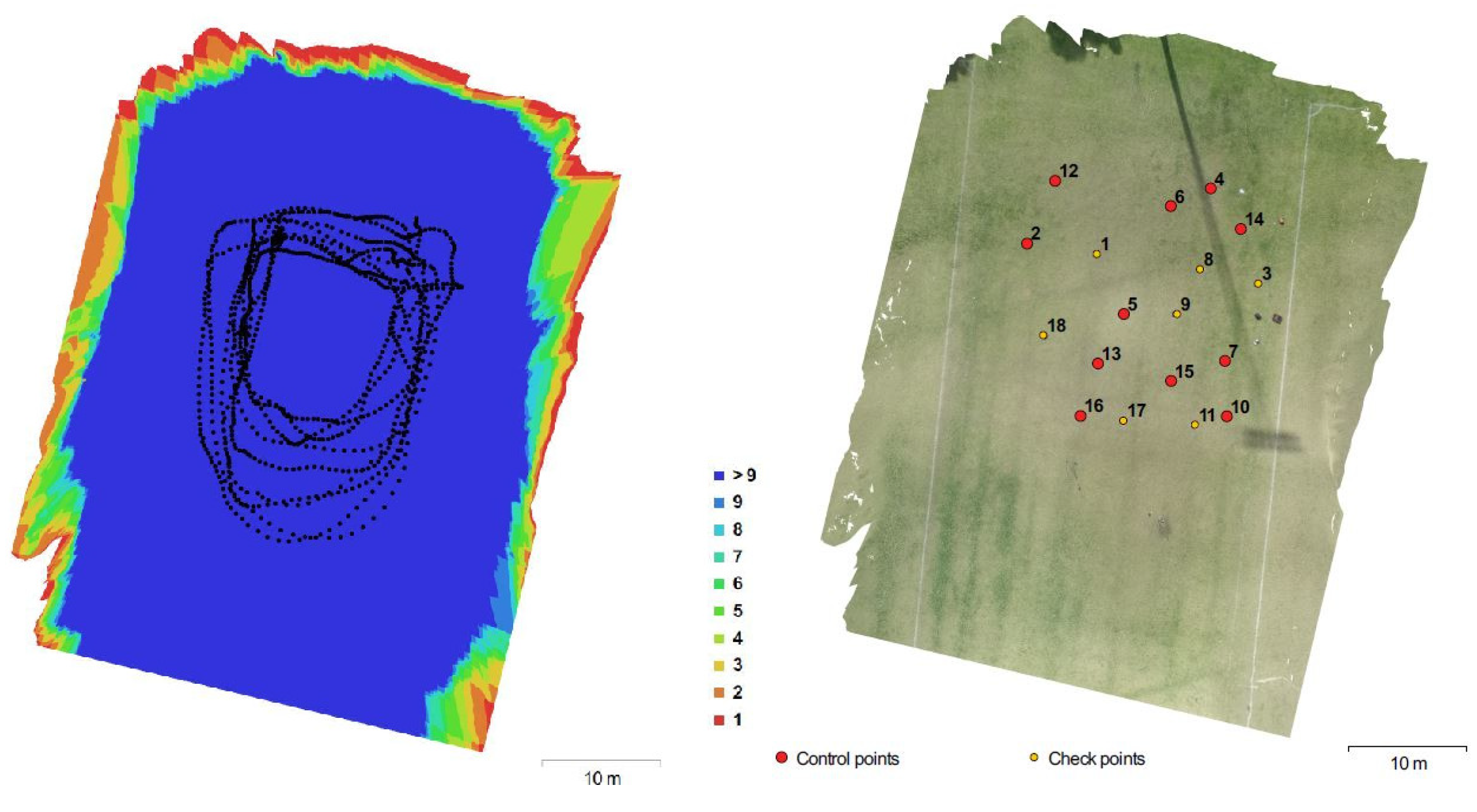
2.3.2. Ground Truth Estimation Using Photogrammetry
3. Results and Discussion
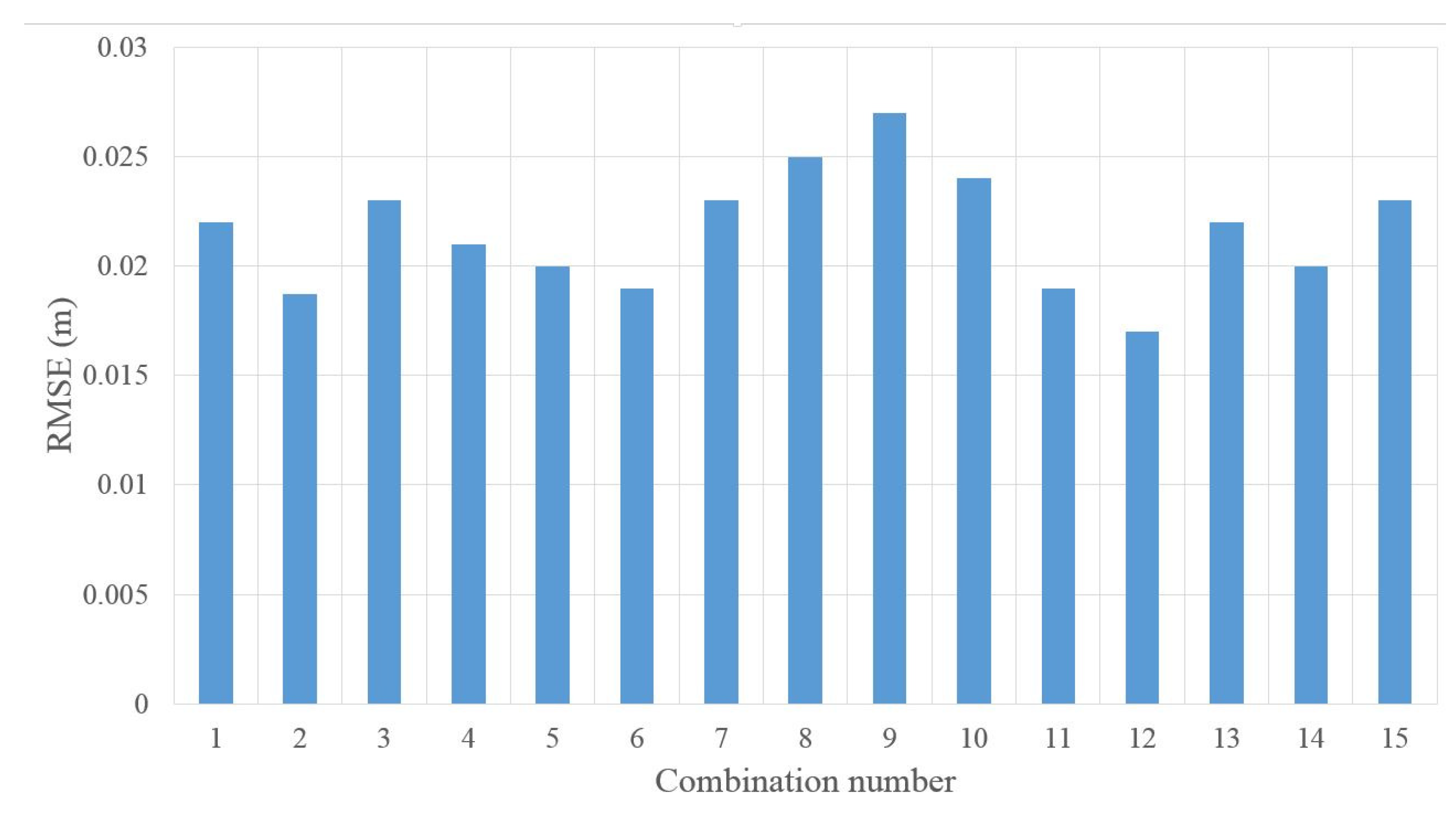
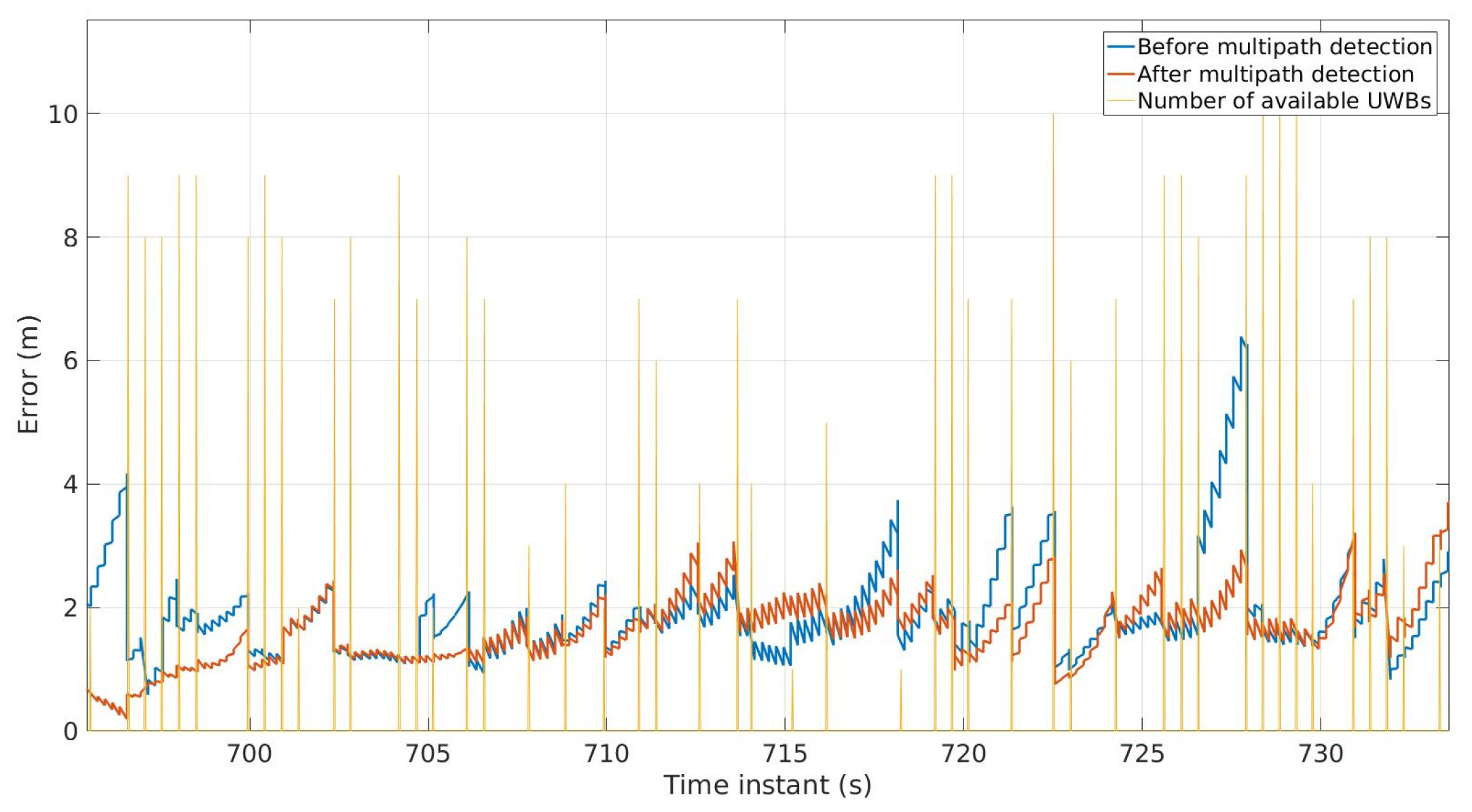
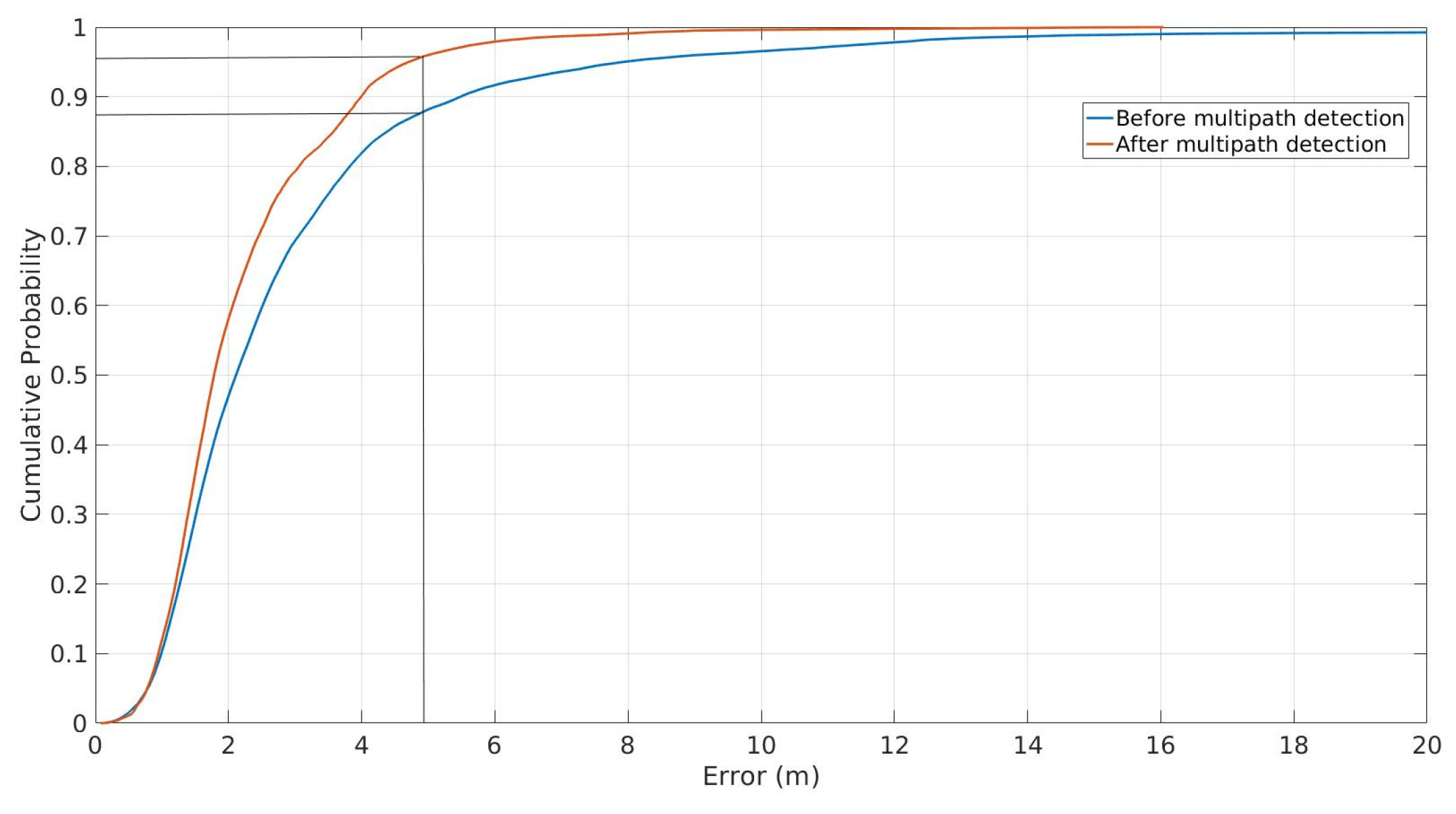
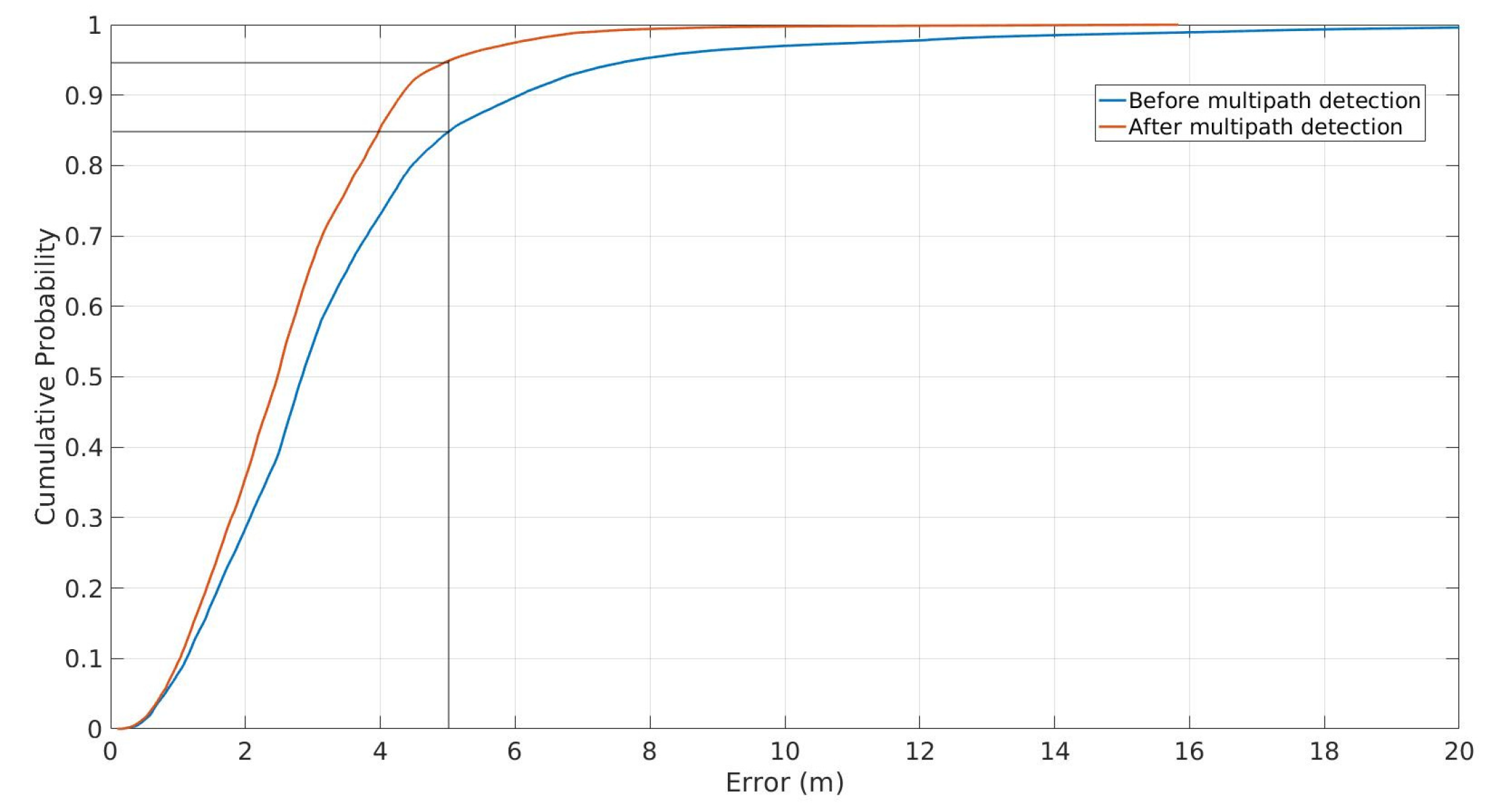
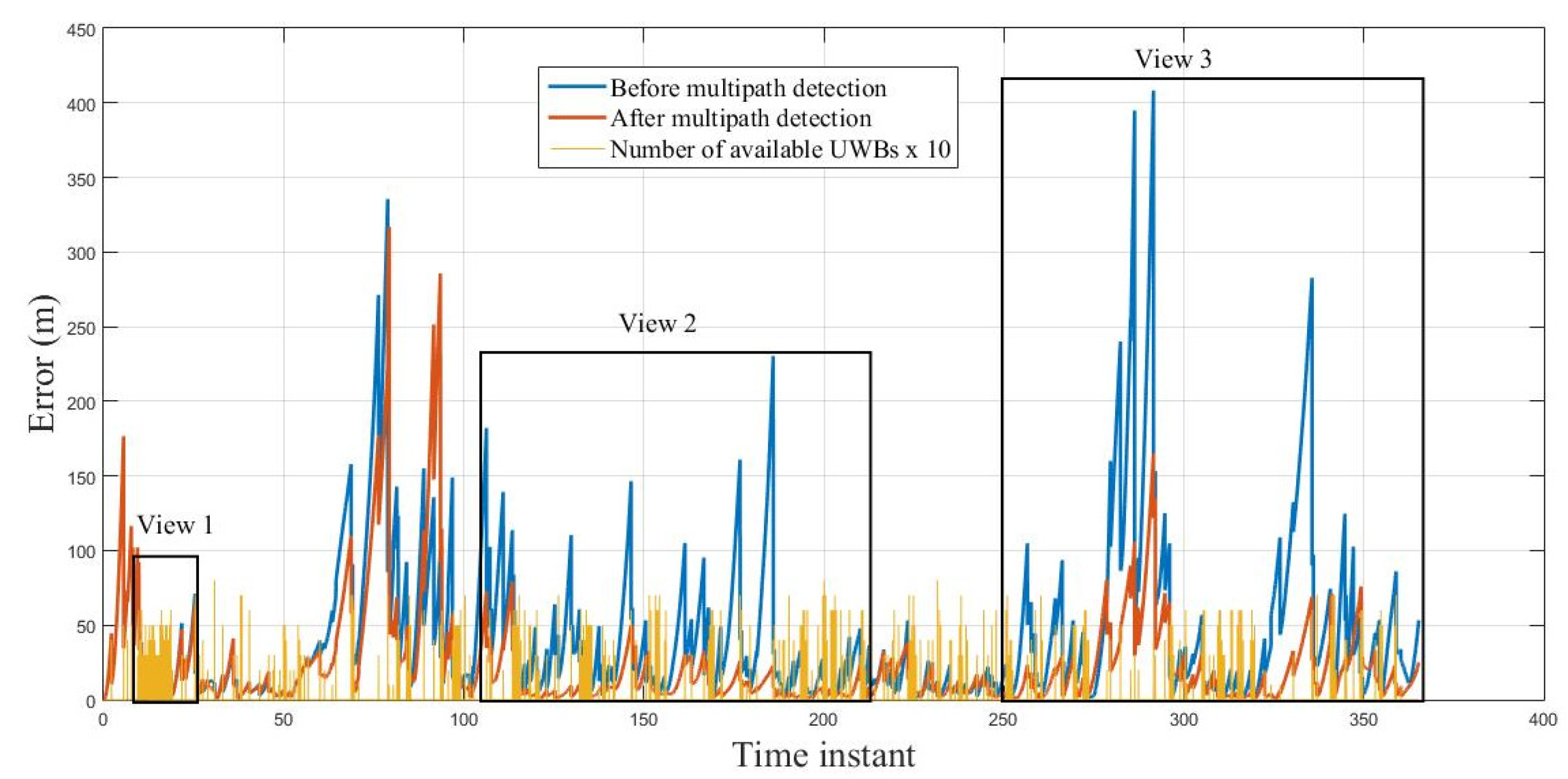
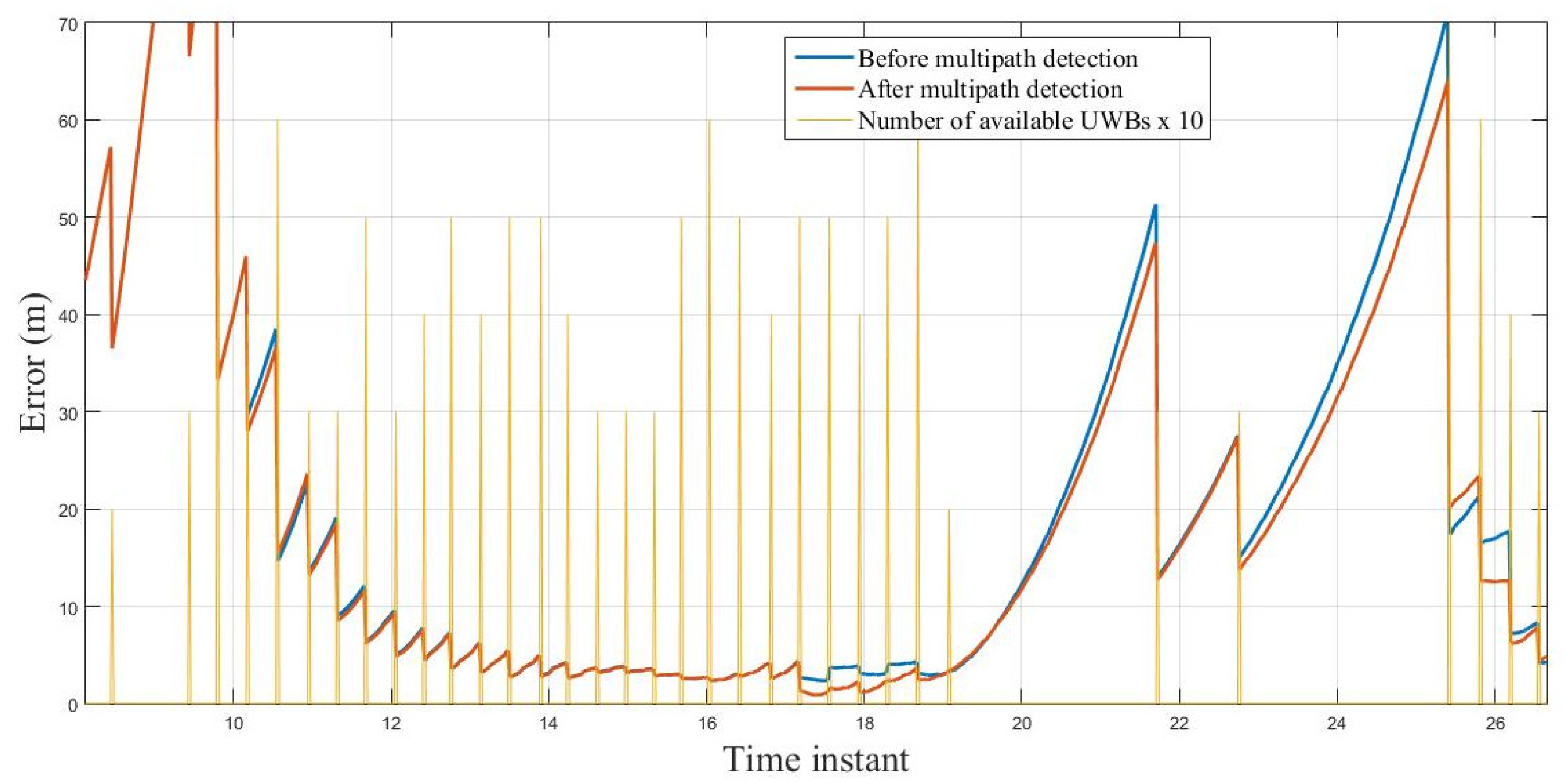
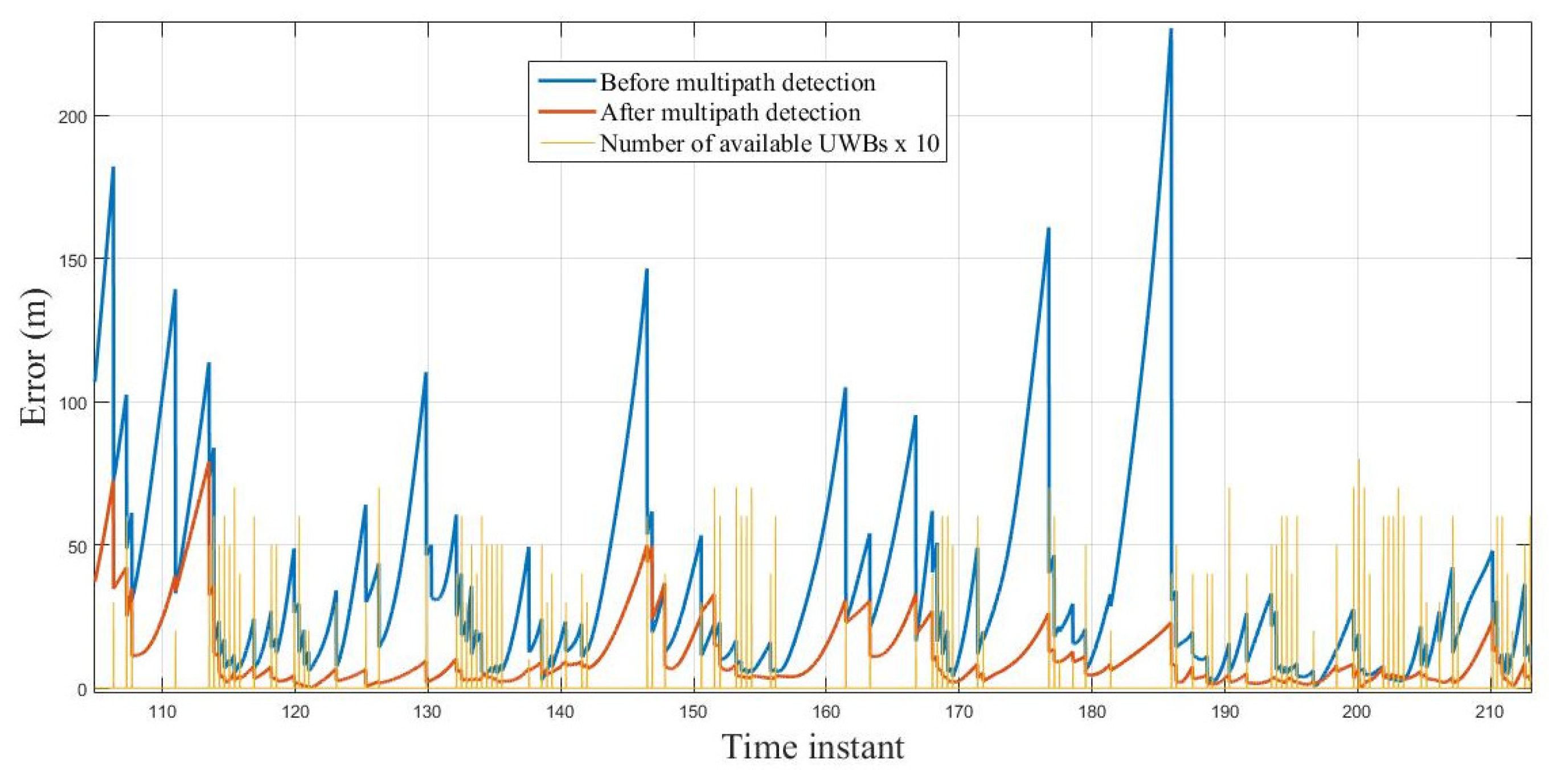
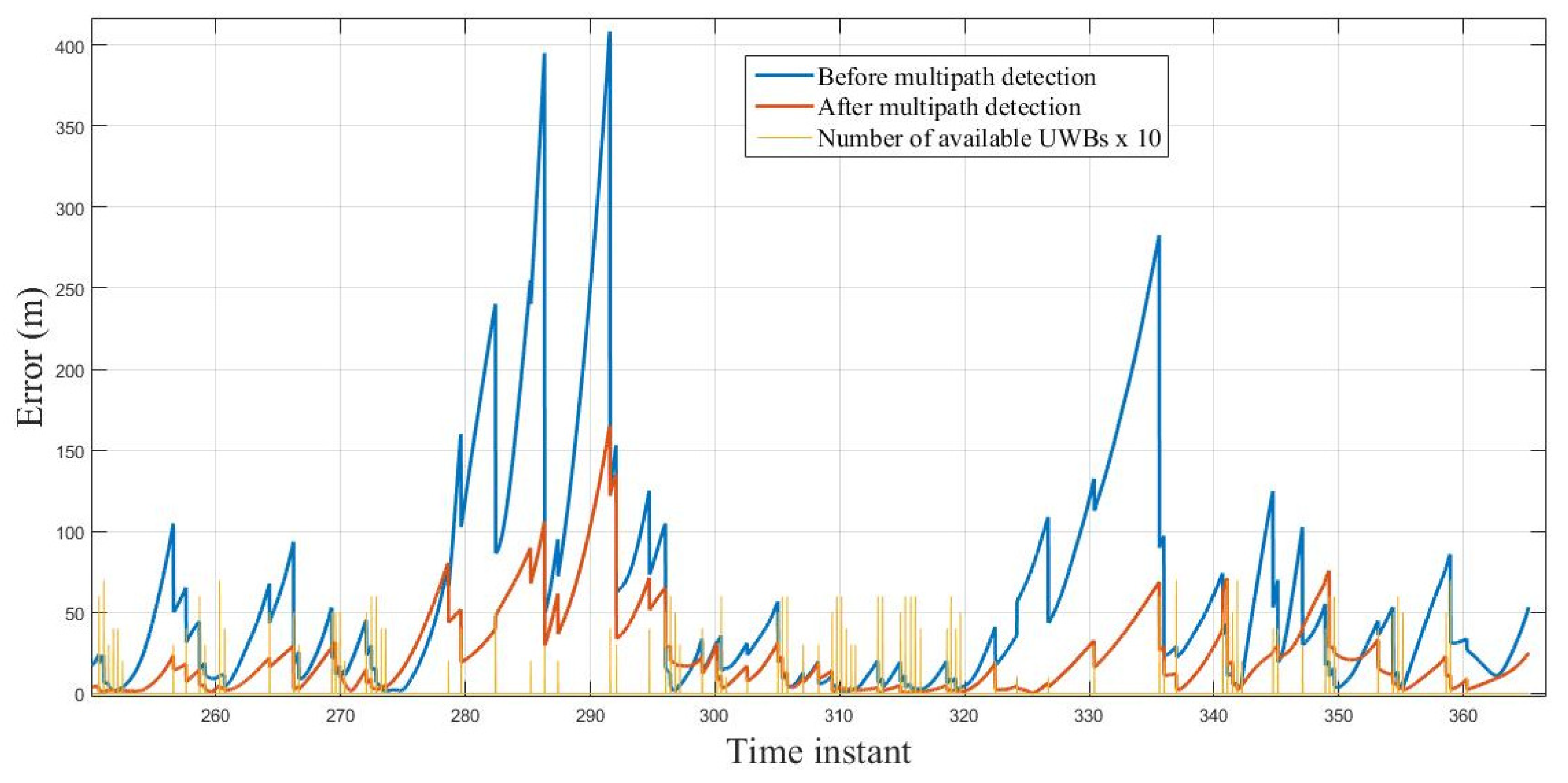
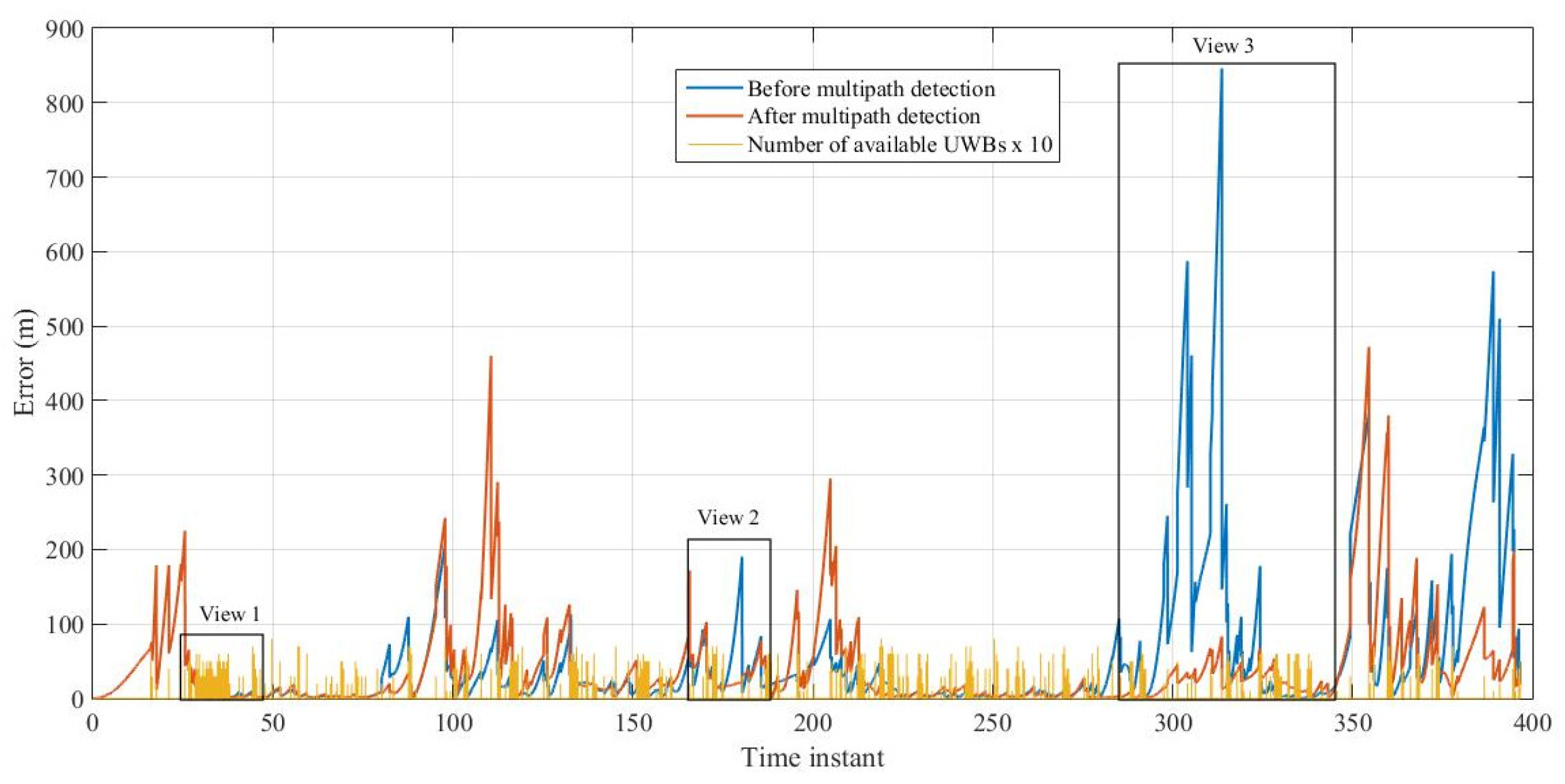
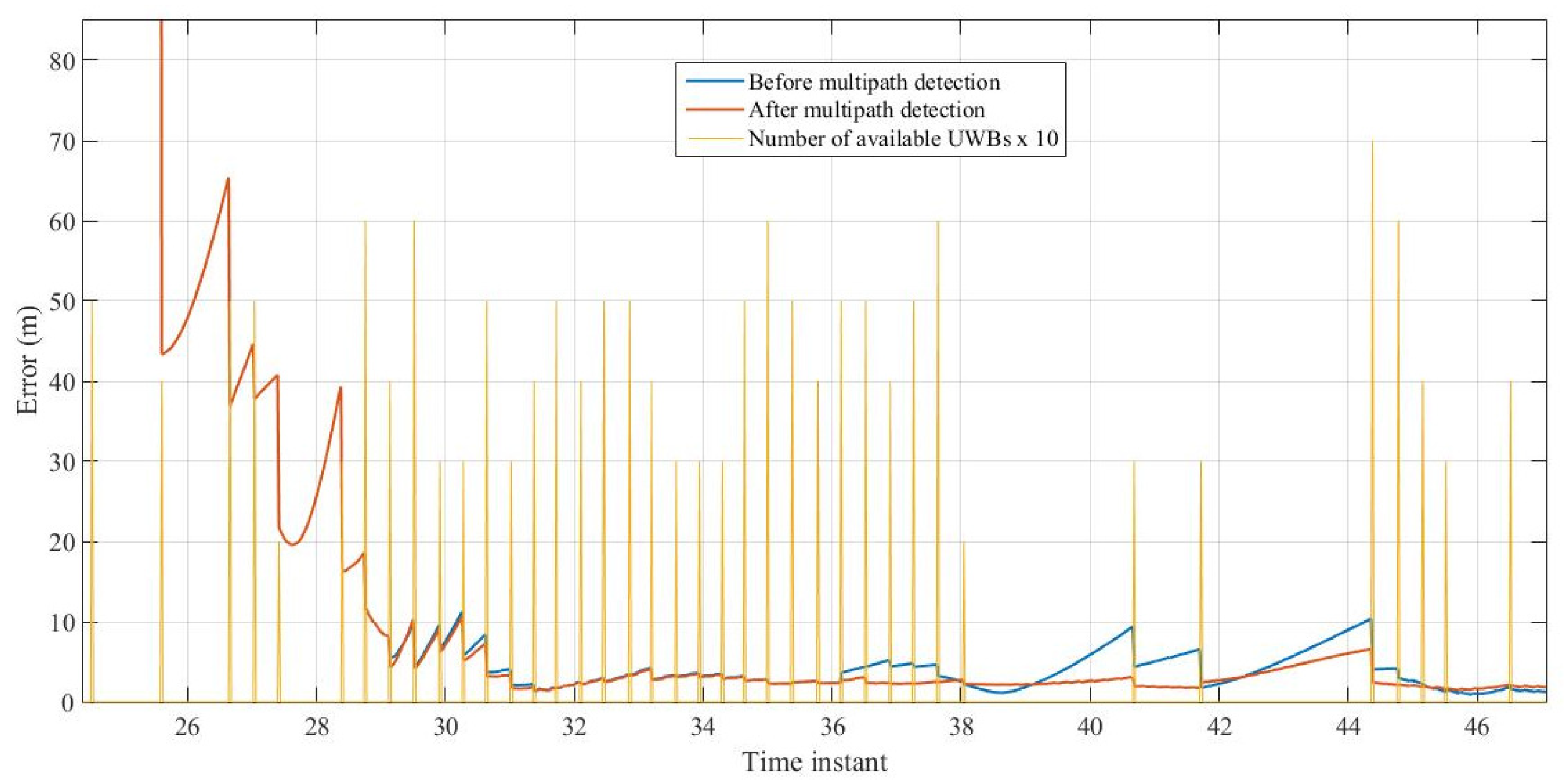
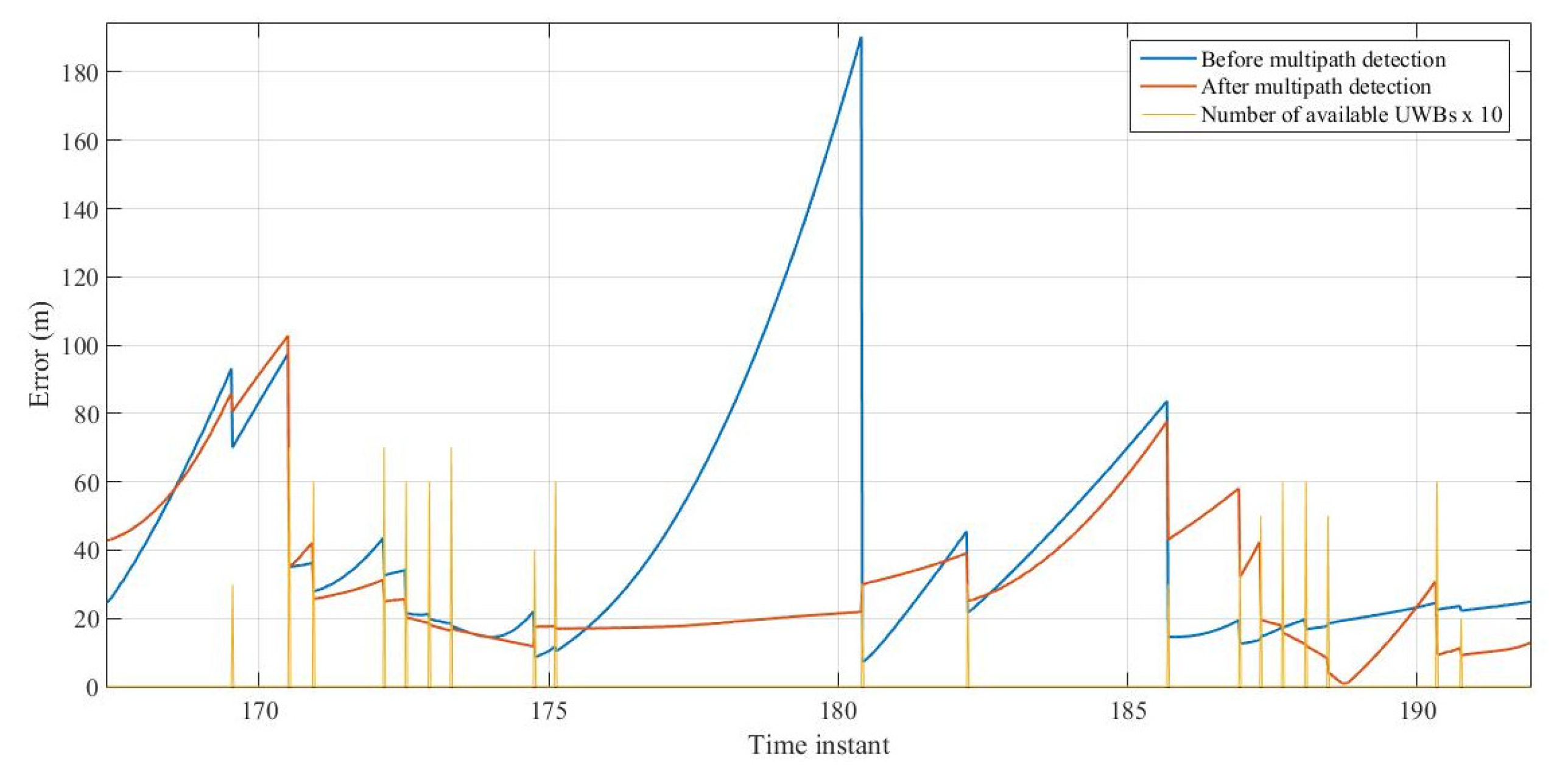
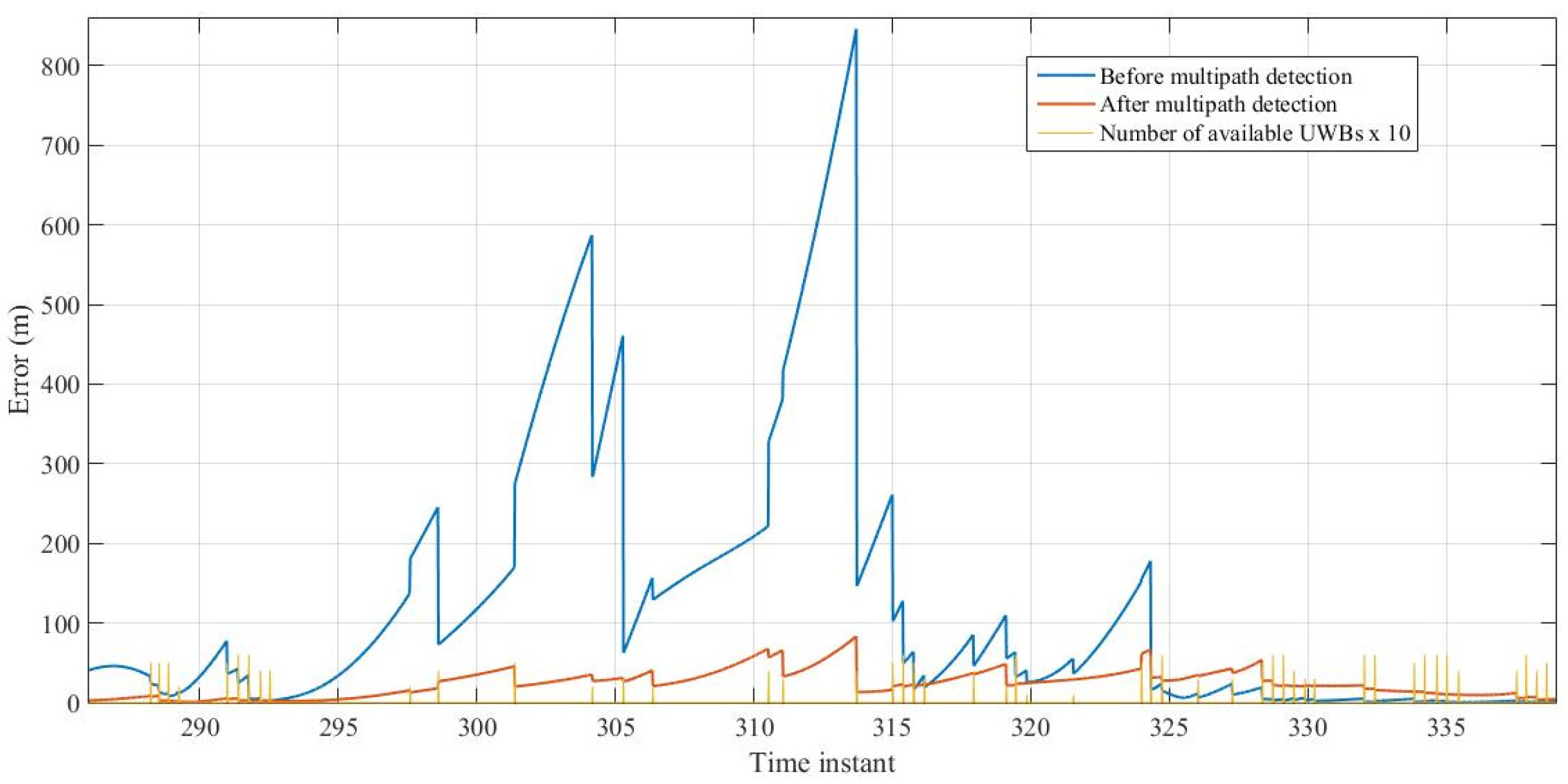
3.1. Infrastructure Based Localization
3.2. Centralized Cooperative Localization
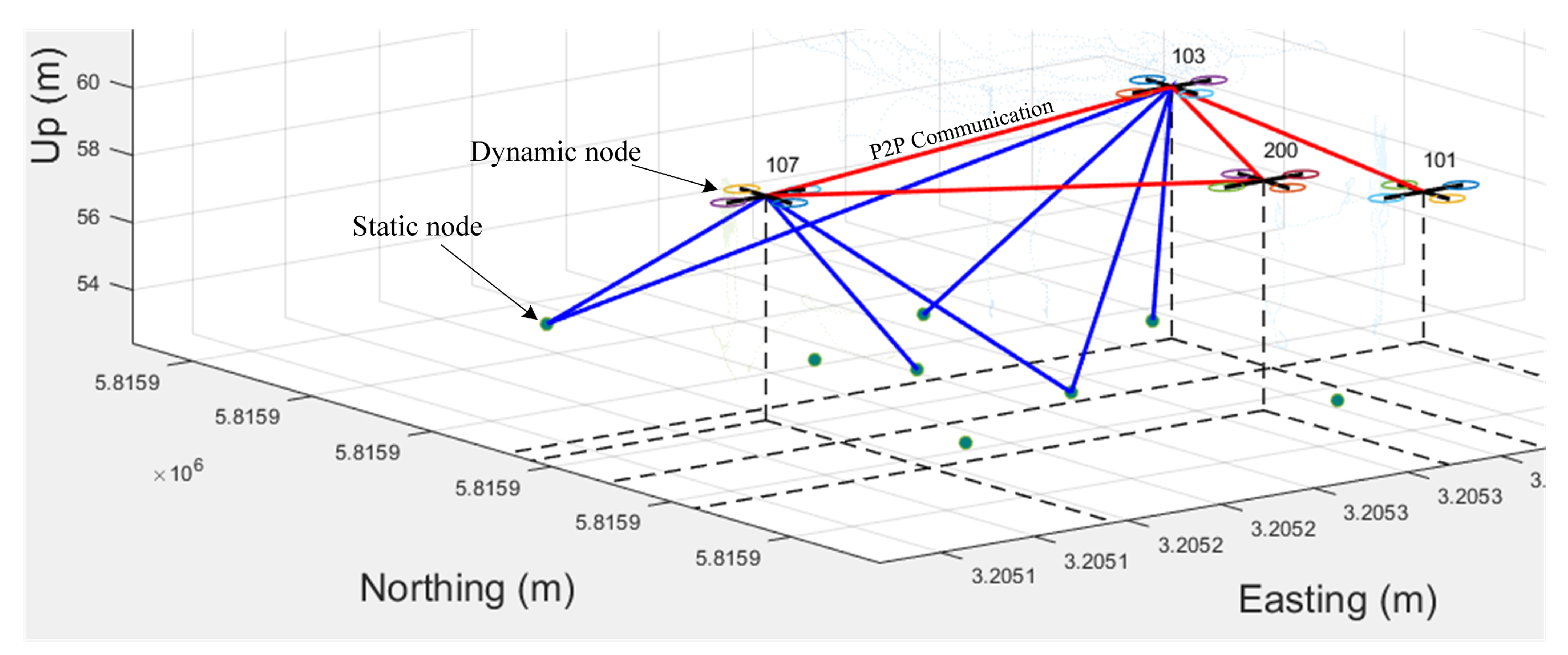
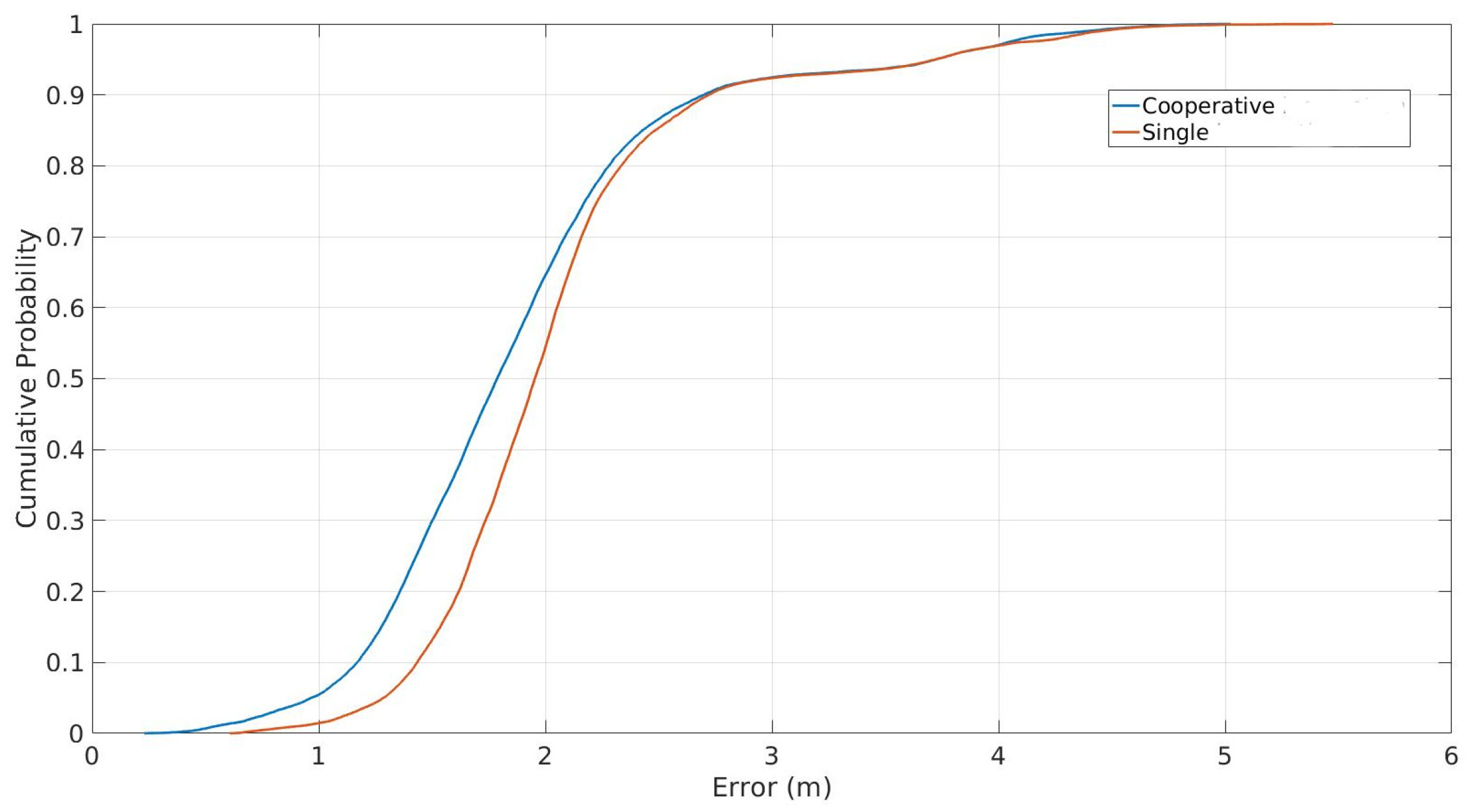
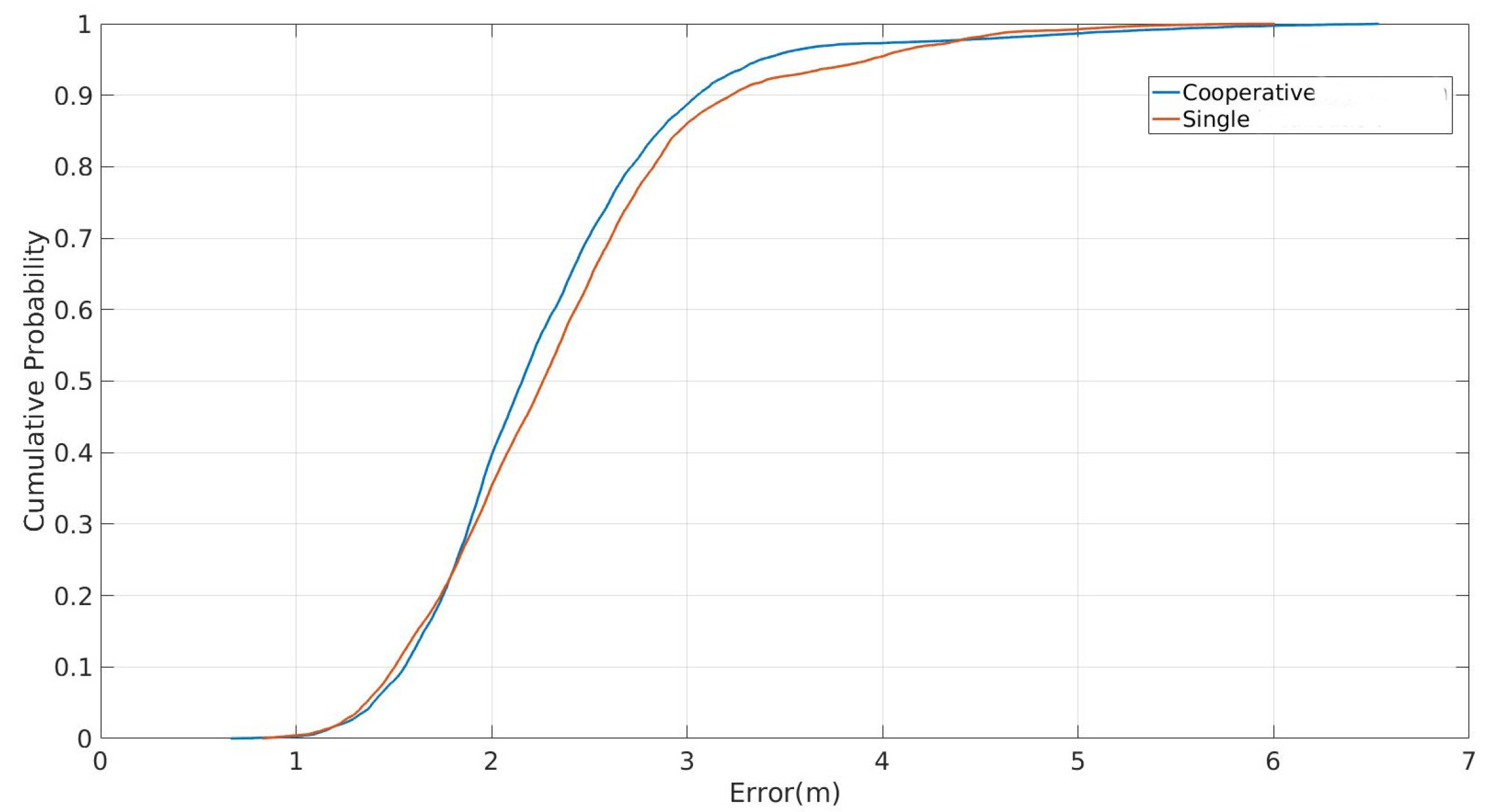
3.3. Distributed Cooperative Localization
3.4. Special Case: Cooperative Localization in Ideal GNSS Environments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EKF | Extended Kalman Filter |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| NLOS | Non-Line of Sight |
| P2I | Peer to Infrastructure |
| P2P | Peer to Peer |
| RMSE | Root Mean Square Error |
| SD | Secure Digital |
| UAVs | Unmanned Aerial Vehicles |
| UTM | Universal Transverse Mercator |
| UWB | Ultra Wide Band |
References
- Scherer, S.; Rehder, J.; Achar, S.; Cover, H.; Chambers, A.; Nuske, S.; Singh, S. River mapping from a flying robot: State estimation, river detection, and obstacle mapping. Auton. Robots 2012, 1, 189–214. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Georgopoulos, P.; McCarthy, B.; Edwards, C. Location Awareness Rescue System: Support for Mountain Rescue Teams. In Proceedings of the Ninth IEEE International Symposium on Network Computing and Applications, Cambridge, MA, USA, 15–17 July 2010; pp. 243–246. [Google Scholar]
- Ishikawa, T.; Fujiwara, H.; Imai, O.; Okabe, A. Wayfinding with a GPS-based mobile navigation system: A comparison with maps and direct experience. J. Environ. Psychol. 2008, 28, 74–82. [Google Scholar] [CrossRef]
- Fischer, J. The Role of GNSS in Driverless Cars, GPS World. Available online: http://gpsworld.com/the-role-of-gnss-in-driverless-cars/ (accessed on 31 September 2018).
- GNSS Market Report, European Global Navigation Satellite Systems Agency, Issue 5. Available online: https://www.gsa.europa.eu/system/files/reports/gnss_mr_2017.pdf (accessed on 20 June 2017).
- FAA Aerospace Forecast—Fiscal Years 2016–2036. 2016. Available online: https://www.faa.gov/data_research/aviation/aerospace_forecasts/media/FY2016-36_FAA_Aerospace_Forecast.pdf (accessed on 20 June 2017).
- Goel, S.; Kealy, A.; Gikas, V.; Retscher, G.; Toth, C.; Brzezinska, D.G.; Lohani, B. Cooperative Localization of Unmanned Aerial Vehicles using GNSS, MEMS Inertial and UWB Sensors. J. Surv. Eng. 2017, 143, 04017007. [Google Scholar] [CrossRef]
- Gabela, J.; Goel, S.; Kealy, A.; Hedley, M.; Moran, B.; Williams, S. Cramér Rao Bound Analysis for Cooperative Positioning in Intelligent Transportation Systems. In Proceedings of the 2018 Conference International Global Navigation Satellite Systems (IGNSS), Sydney, Australia, 7–9 February 2018; Available online: http://www.ignss2018.unsw.edu.au/sites/ignss2018/files/u80/Papers/IGNSS2018_paper_21.pdf (accessed on 8 May 2018).
- Goel, S.; Kealy, A.; Lohani, B. Cooperative UAS Localization using low cost sensors. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, III-1, 183–190. [Google Scholar] [CrossRef]
- Bal, M.; Liu, M.L.M.; Shen, W.S.W.; Ghenniwa, H. Localization in cooperative Wireless Sensor Networks: A review. In Proceedings of the 2009 13th International Conference on Computer Supported Cooperative Work in Design, Santiago, Chile, 22–24 April 2009; pp. 438–443. [Google Scholar]
- Goel, S. A Distributed Cooperative UAV Swarm Localization System: Development and Analysis. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 2501–2518. [Google Scholar]
- Roumeliotis, S.I.; Bekey, G.A. Distributed multirobot localization. IEEE Trans. Robot. Autom. 2002, 18, 781–795. [Google Scholar] [CrossRef]
- Gholami, M.R.; Gezici, S.; Rydström, M.; Ström, E.G. A distributed positioning algorithm for cooperative active and passive sensors. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–30 September 2010; pp. 1713–1718. [Google Scholar]
- Mourikis, A.I.; Roumeliotis, S.I. Performance analysis of multirobot cooperative localization. IEEE Trans. Robot. 2006, 22, 666–681. [Google Scholar] [CrossRef]
- Caceres, M.A.; Penna, F.; Wymeersch, H.; Garello, R. Hybrid GNSS-terrestrial cooperative positioning via distributed belief propagation. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Hlinka, O.; Sluciak, O.; Hlawatsch, F.; Rupp, M. Distributed data fusion using iterative covariance intersection. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1861–1865. [Google Scholar]
- Dong, J.; Nelson, E.; Indelman, V.; Michael, N.; Dellaert, F. Distributed real-time cooperative localization and mapping using an uncertainty-aware expectation maximization approach. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5807–5814. [Google Scholar]
- Indelman, V.; Gurfil, P.; Rivlin, E.; Rotstein, H. Distributed vision-aided cooperative localization and navigation based on three-view geometry. Robot. Auton. Syst. 2012, 60, 822–840. [Google Scholar] [CrossRef]
- Wanasinghe, T.R.; Mann, G.K.I.; Gosine, R.G. Decentralized Cooperative Localization for Heterogeneous Multi-robot System Using Split Covariance Intersection Filter. In Proceedings of the 2014 Canadian Conference on Computer and Robot Vision, Montreal, QC, Canada, 6–9 May 2014; pp. 167–174. [Google Scholar]
- Carrillo-Arce, L.C.; Nerurkar, E.D.; Gordillo, J.L.; Roumeliotis, S.I. Decentralized multi-robot cooperative localization using covariance intersection. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1412–1417. [Google Scholar]
- Savic, V.; Zazo, S. Cooperative localization in mobile networks using nonparametric variants of belief propagation. Ad Hoc Netw. 2013, 11, 138–150. [Google Scholar] [CrossRef]
- Wan, J.; Zhong, L.; Zhang, F. Cooperative Localization of Multi-UAVs via Dynamic Nonparametric Belief Propagation under GPS Signal Loss Condition. Int. J. Distrib. Sens. Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Priyantha, N.B.; Balakrishnan, H.; Demaine, E.; Teller, S. Anchor-Free Distributed Localization in Sensor Networks. In Proceedings of the 1st international conference on Embedded networked sensor systems (SenSys’03), Los Angeles, CA, USA, 5–7 November 2003; pp. 340–341. [Google Scholar]
- Leung, K.Y.K.; Barfoot, T.D.; Liu, H.H.T. Distributed and decentralized cooperative simultaneous localization and mapping for dynamic and sparse robot networks. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3841–3847. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. A non-divergent estimation algorithm in the presence of unknown correlations. In Proceedings of the 1997 American Control Conference (Cat. No.97CH36041), Albuquerque, NM, USA, 6 June 1997; pp. 2369–2373. [Google Scholar]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A New Method for the Nonlinear Transforamtion of Means and Covariances in Filters and Estimators. IEEE Trans. Automat. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Nerurkar, E.D.; Roumeliotis, S.I.; Martinelli, A. Distributed maximum a posteriori estimation for multi-robot cooperative localization. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Goel, S.; Kealy, A.; Lohani, B. Infrastructure vs Peer to Peer Cooperative Positioning: A Comparative Analysis. In Proceedings of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 1125–1137. [Google Scholar]
- Goel, S.; Kealy, A.; Retscher, G.; Lohani, B. Cooperative P2I Localization using UWB and Wi-Fi. In Proceedings of the International Global Navigation Satellite Systems (IGNSS) Conference 2016, Sydney, Australia, 6–8 December 2016. [Google Scholar]
- Goel, S.; Gabela, J.; Kealy, A.; Retscher, G. An Indoor Outdoor Cooperative Localization Framework for UAVs. In Proceedings of the International Global Navigation Satellite Systems (IGNSS) Conference 2018, Sydney, Australia, 7–9 February 2018. [Google Scholar]
- Goel, S.; Kealy, A.; Lohani, B.; Retscher, G. Cooperative Localization of Unmanned Aerial Vehicles: Prototype Development and Analysis. In Proceedings of the 10th International Symposium on Mobile Mapping Technology: Mobile Mapping for Sustainable Development, Cairo, Egypt, 6–8 May 2017. [Google Scholar]
- Penna, F.; Caceres, M.A.; Wymeersch, H. Cramér-Rao Bound for Hybrid GNSS-Terrestrial Cooperative Positioning. IEEE Commun. Lett. 2010, 14, 1005–1007. [Google Scholar] [CrossRef]
- Qu, Y.; Zhang, Y. Cooperative localization against GPS signal loss in multiple UAVs flight. J. Syst. Eng. Electron. 2011, 22, 103–112. [Google Scholar] [CrossRef]
- Giguere, P.; Rekleitis, I.; Latulippe, M. I see you, you see me: Cooperative localization through bearing-only mutually observing robots. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 863–869. [Google Scholar]
- Madhavan, R.; Fregene, K.; Parker, L.E. Distributed heterogeneous outdoor multi robot localization. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; pp. 374–381. [Google Scholar]
- Melnyk, I.V.; Hesch, J.A.; Roumeliotis, S.I. Cooperative vision-aided inertial navigation using overlapping views. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 936–943. [Google Scholar]
- Bryson, M.; Sukkarieh, S. Building a Robust Implementation of Bearing-Only Inertial SLAM for a UAV. J. Field Robot. 2007, 24, 113–143. [Google Scholar] [CrossRef]
- Bryson, M.; Sukkarieh, S. Cooperative Localisation and Mapping for Multiple UAVs in Unknown Environments. In Proceedings of the IEEE/AIAA Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–12. [Google Scholar]
- Ryde, J.; Hu, H. Cooperative Mutual 3D Laser Mapping and Localization. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 1048–1053. [Google Scholar]
- Wu, M.; Huang, F.; Wang, L.; Sun, J. Cooperative multi-robot monocular-SLAM using salient landmarks. In Proceedings of the 2009 International Asia Conference on Informatics in Control, Automation, and Robotics, Milan, Italy, 2–5 July 2009; pp. 151–155. [Google Scholar]
- Paull, L.; Huang, G.; Seto, M.; Leonard, J.J. Communication-constrained multi-AUV cooperative SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 509–516. [Google Scholar]
- Trujillo, J.C.; Munguia, R.; Guerra, E.; Grau, A. Cooperative Monocular-Based SLAM for Multi-UAV Systems in GPS-Denied Environments. Sensors 2018, 18, 1351. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Stewart, B.; Fox, D.; Konolige, K.; Limketkai, B. A practical, decision-theoretic approach to multi-robot mapping and exploration. In Proceedings of the International Conference on Intelligent Robots, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Trawny, N.; Roumeliotis, S.I.; Giannakis, G.B. Cooperative multi-robot localization under communication constraints. In Proceedings of the IEEE International Confererence on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Vetrella, A.R.; Fasano, G.; Accardo, D.; Moccia, A. Differential GNSS and Vision-Based Tracking to Improve Navigation Performance in Cooperative Multi-UAV Systems. Sensors 2016, 16, 2164. [Google Scholar] [CrossRef] [PubMed]
- Vetrella, A.R.; Fasano, G.; Renga, A.; Accardo, D. Cooperative UAV Navigation Based on Distributed Multi-Antenna GNSS, Vision, and MEMS Sensors. In Proceedings of the International Conference on Unmanned Aircraft Systems, Denver, CO, USA, 9–12 June 2015. [Google Scholar]
- Kenmogne, I.F.; Drevelle, V.; Marchand, E. Using constraint propagation for cooperative UAV localization from vision and ranging. In Proceedings of the Constraint Programming and Decision Making Workshop, Tokyo, Japan, 10 September 2018; pp. 1–5. [Google Scholar]
- Specifications of uBlox LEA-6H. Available online: https://goo.gl/HY4bC4 (accessed on 24 November 2017).
- Specifications of Pixhawk Autopilot. Available online: https://pixhawk.org/modules/pixhawk (accessed on 26 August 2016).
- Details of P410 UWB Radio. Available online: http://www.timedomain.com/ (accessed on 31 August 2018).
- Specifications and Details of GoPro Hero 3 Silver Edition. Available online: http://cbcdn1.gp-static.com/uploads/product_manual/file/55/HERO3_Silver_UM_ENG_RevC_web.pdf (accessed on 27 August 2016).
- Details of the Telemetry Radio. Available online: http://ardupilot.org/copter/docs/common-sik-telemetry-radio.html#common-sik-telemetry-radio (accessed on 31 August 2018).
- Grubbs, F.E. Procedures for Detecting Outlying Observations in Samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey vision conference, Manchester, UK, 31 August–2 September 1988; p. 50. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Moons, T.; Gool, L.V.; Vergauwen, M. 3D Reconstruction from Multiple Images, Part 1: Principles. Found. Trends Comput. Graph. Vis. 2009, 4, 287–404. [Google Scholar] [CrossRef]
- Larsson, V. Metric 3D-Reconstruction from Unordered and Uncalibrated Image Collections. Master’s Thesis, Lund University, Lund, Sweden, 2013. Available online: http://www2.maths.lth.se/vision/publdb/reports/pdf/larsson-master-13.pdf (accessed on 18 April 2017).
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 338–345. [Google Scholar]
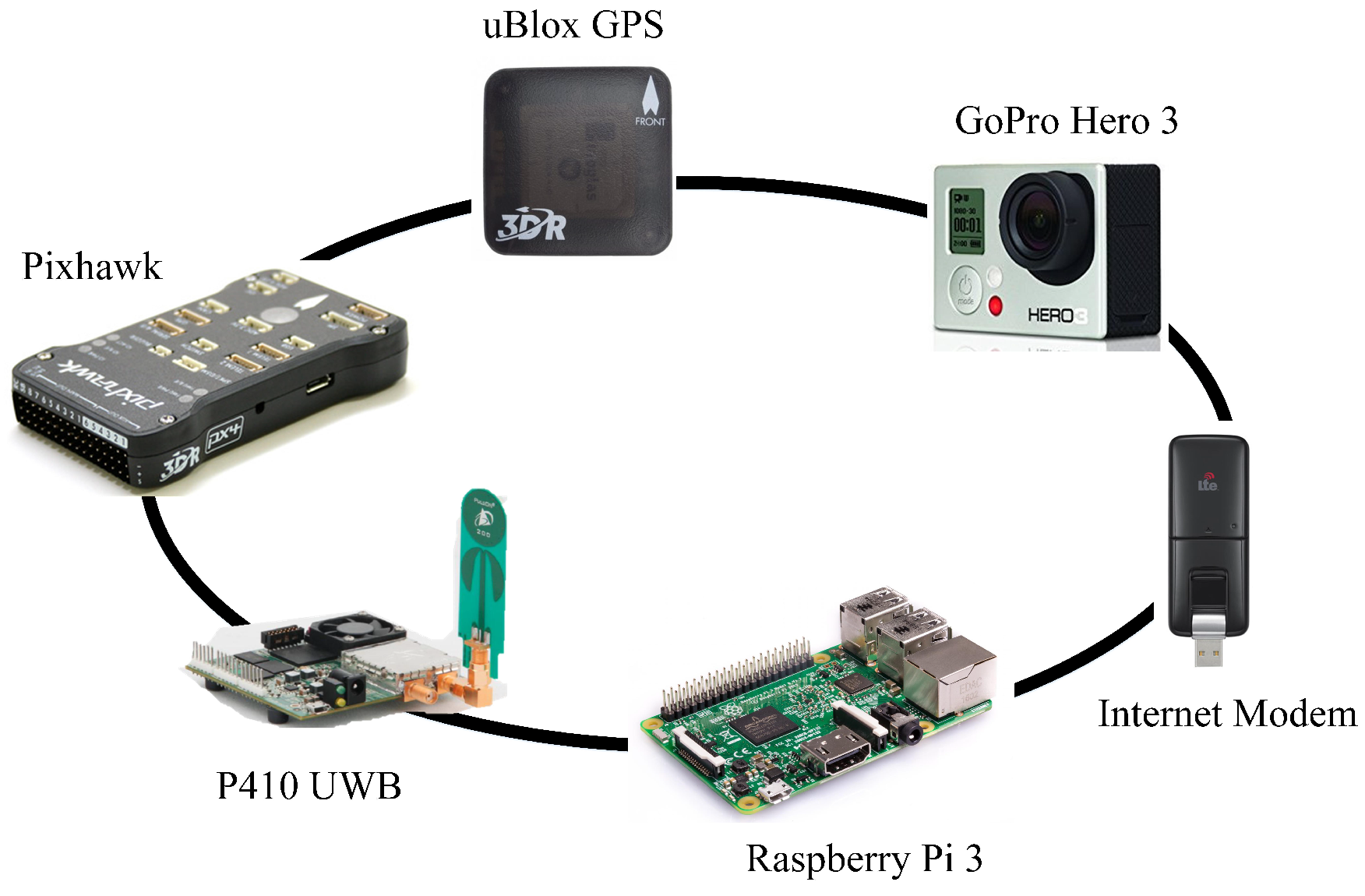
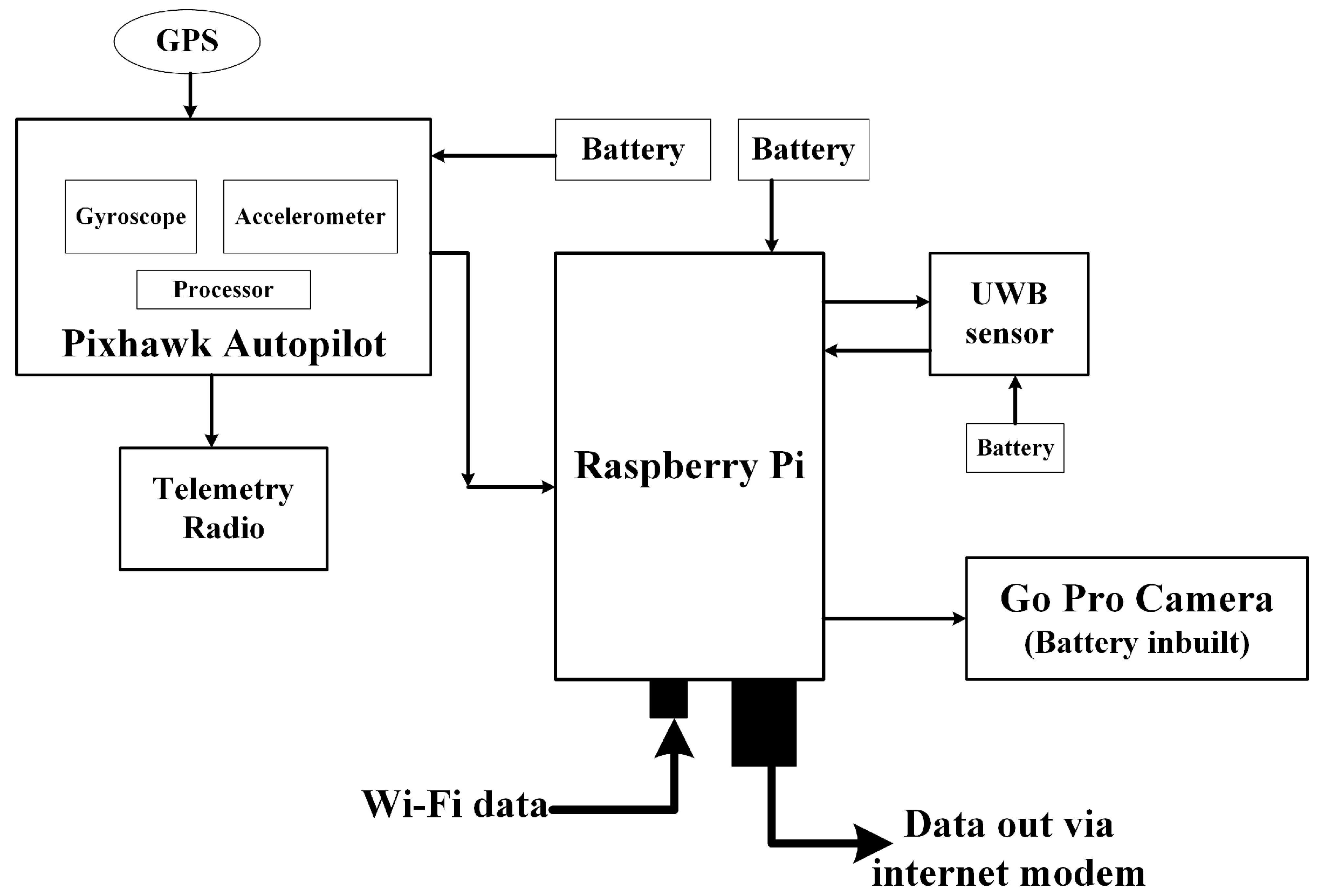






| Onboard Sensor | Dimension (L × W × H) | Weight (g) |
|---|---|---|
| uBlox GPS | 38 mm × 38 mm × 8.5 mm | 16.8 |
| P410 UWB | 76 mm × 80 mm × 16 mm | 58 |
| Raspberry Pi 3 | 85 mm × 56.5 mm | 45 |
| Pixhawk Autopilot | 81.5 mm × 50 mm × 15.5 mm | 38 |
| GoPro Camera | 60 mm × 42 mm × 30 mm | 74 |
| Measurement Type | Size of Vector | Size of Matrix |
|---|---|---|
| Pseudorange and relative range | ||
| Position and relative range | ||
| Relative range only | (or 16)N |
| ID | Observed Error (all in m) | 3D error (in m) | ||
|---|---|---|---|---|
| Easting | Northing | Up | ||
| 1 | 0.006 | 0.011 | −0.008 | 0.014 |
| 3 | −0.002 | 0.015 | 0.008 | 0.017 |
| 8 | −0.018 | −0.002 | −0.019 | 0.026 |
| 9 | −0.019 | −0.004 | 0.008 | 0.021 |
| 11 | 0.007 | 0.002 | 0.003 | 0.008 |
| 17 | 0.019 | 0.021 | −0.018 | 0.034 |
| 18 | −0.008 | 0.018 | 0.005 | 0.021 |
| Overall 3D RMSE (m) | 0.022 | |||
| Mode | Experiment Type | Operating Environment | |
|---|---|---|---|
| Infrastructure based Cooperative | Infrastructure based | GNSS denied | |
| P2P Cooperative | Centralized | Distributed | Partially GNSS denied |
| P2P Cooperative | Centralized | Full GNSS available | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goel, S.; Kealy, A.; Lohani, B. Development and Experimental Evaluation of a Low-Cost Cooperative UAV Localization Network Prototype. J. Sens. Actuator Netw. 2018, 7, 42. https://doi.org/10.3390/jsan7040042
Goel S, Kealy A, Lohani B. Development and Experimental Evaluation of a Low-Cost Cooperative UAV Localization Network Prototype. Journal of Sensor and Actuator Networks. 2018; 7(4):42. https://doi.org/10.3390/jsan7040042
Chicago/Turabian StyleGoel, Salil, Allison Kealy, and Bharat Lohani. 2018. "Development and Experimental Evaluation of a Low-Cost Cooperative UAV Localization Network Prototype" Journal of Sensor and Actuator Networks 7, no. 4: 42. https://doi.org/10.3390/jsan7040042
APA StyleGoel, S., Kealy, A., & Lohani, B. (2018). Development and Experimental Evaluation of a Low-Cost Cooperative UAV Localization Network Prototype. Journal of Sensor and Actuator Networks, 7(4), 42. https://doi.org/10.3390/jsan7040042





