A Framework for Multiple Object Tracking in Underwater Acoustic MIMO Communication Channels
Abstract
:1. Introduction
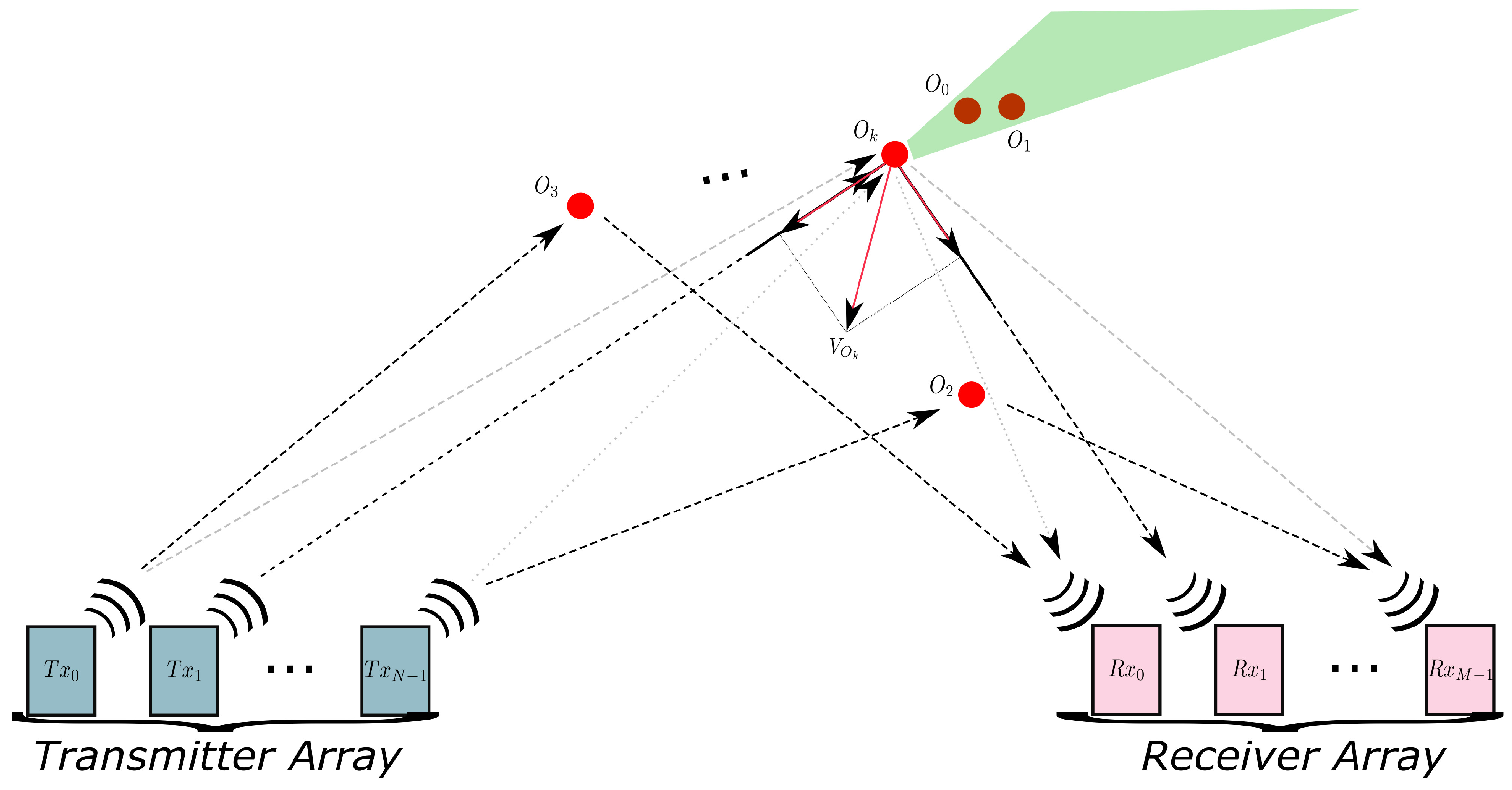
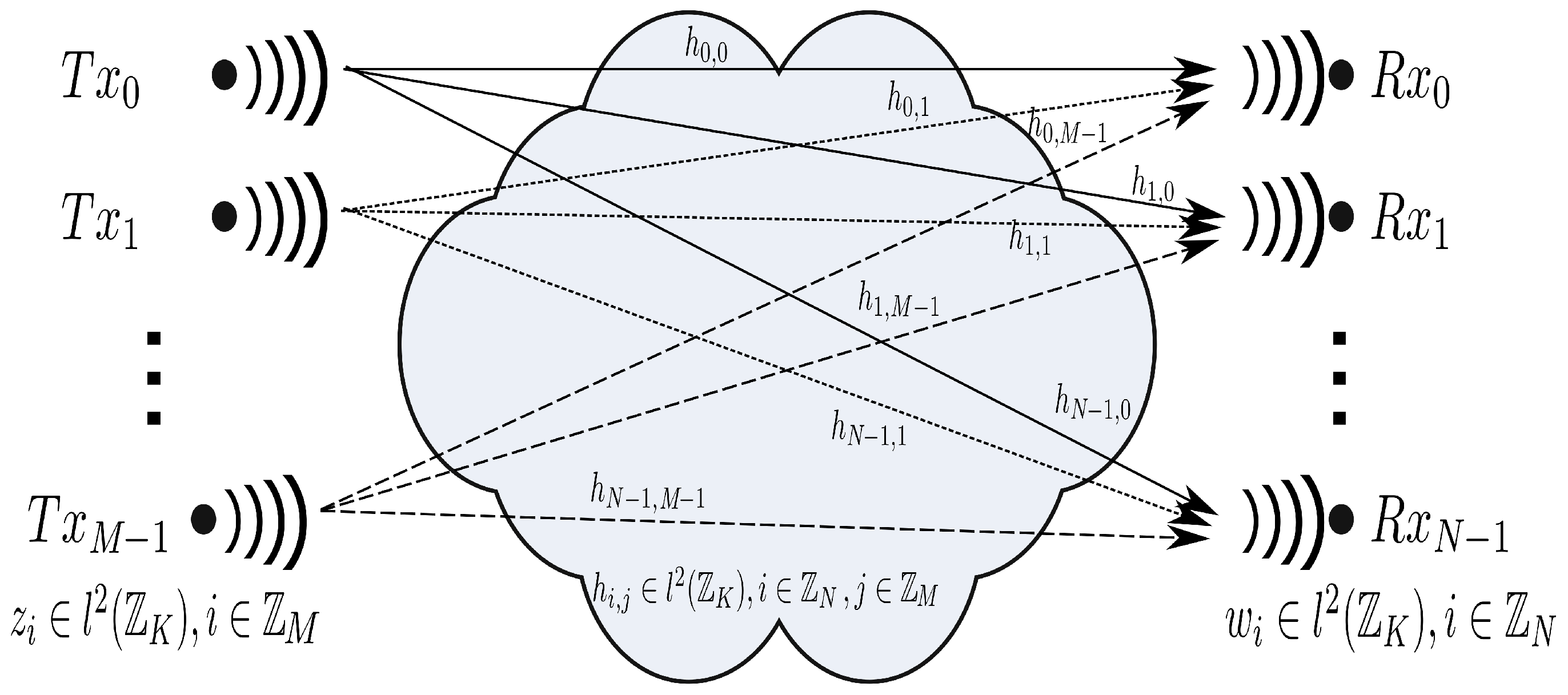
2. Delay-Doppler MIMO Channel Characterization
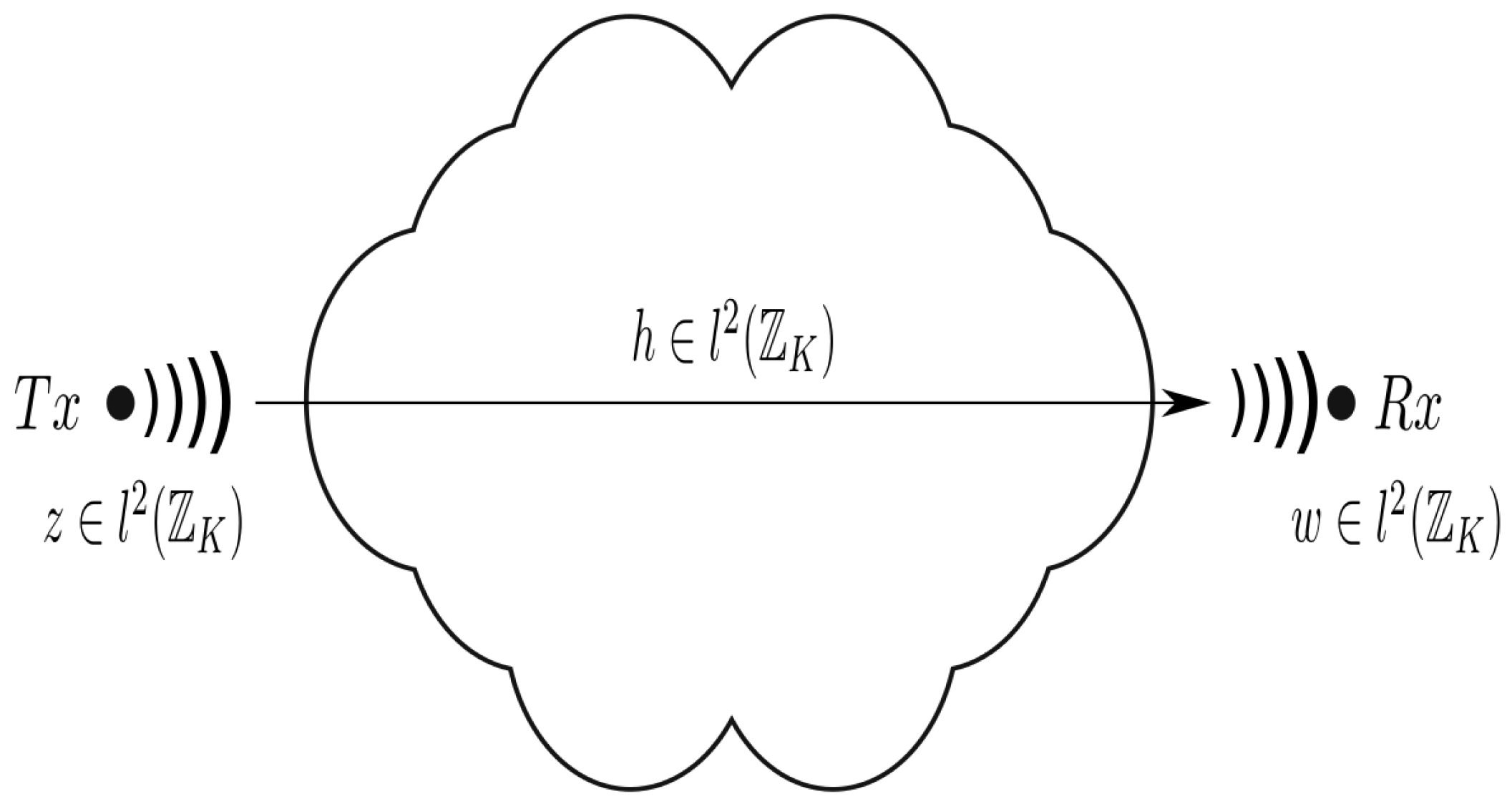
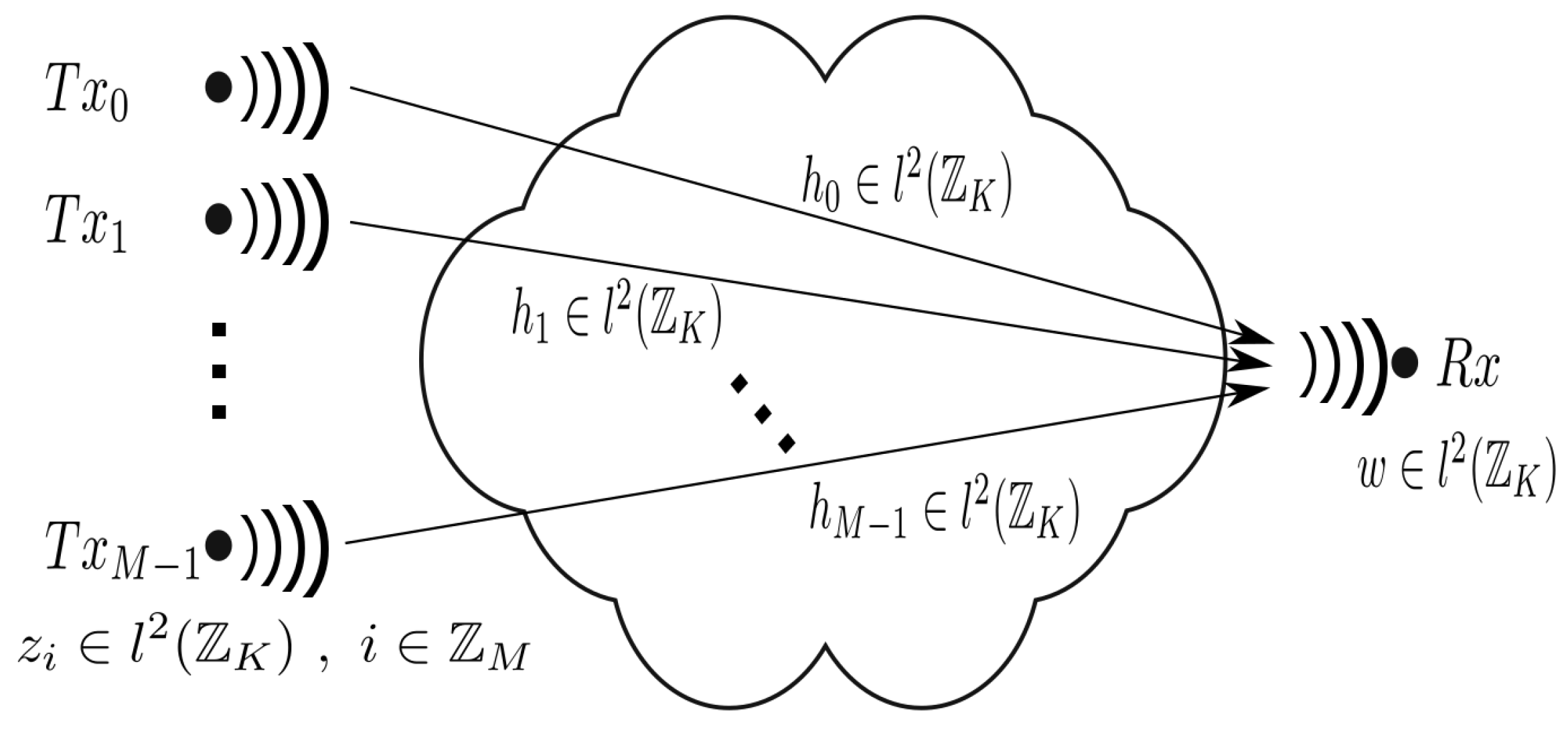
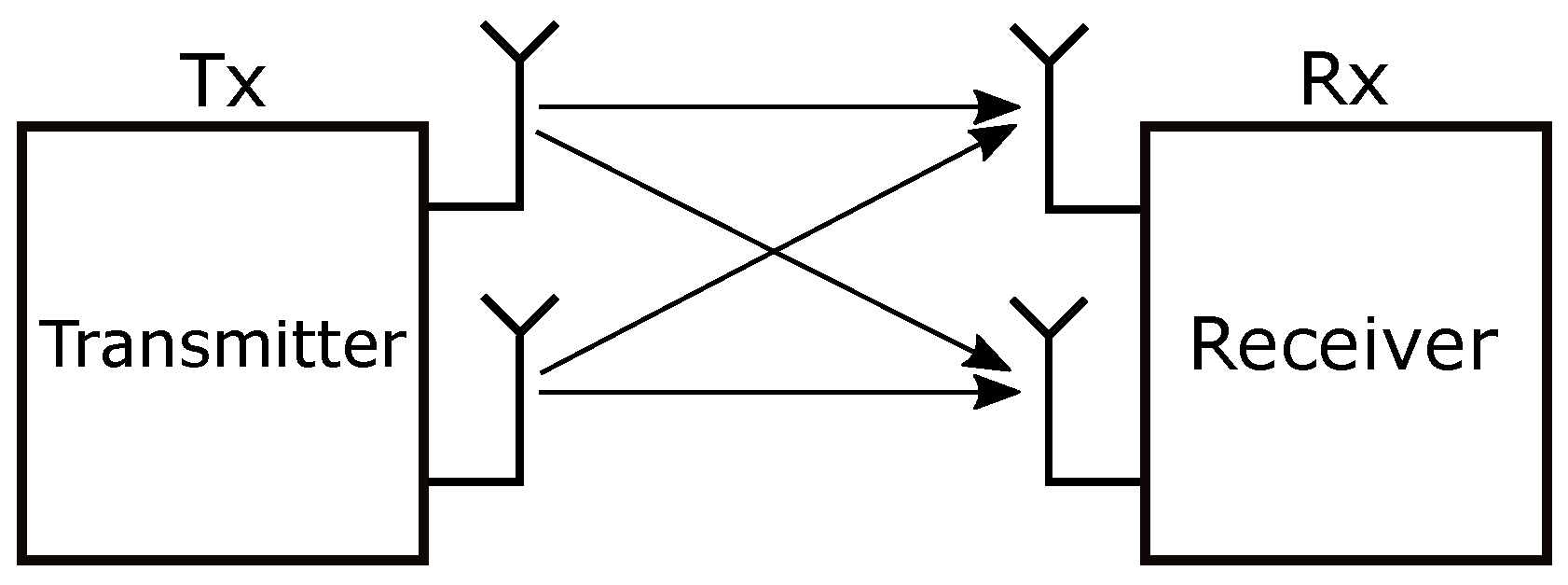
2.1. SISO, MISO and SIMO Channel Configurations
2.1.1. SISO Configuration
2.1.2. MISO Configuration
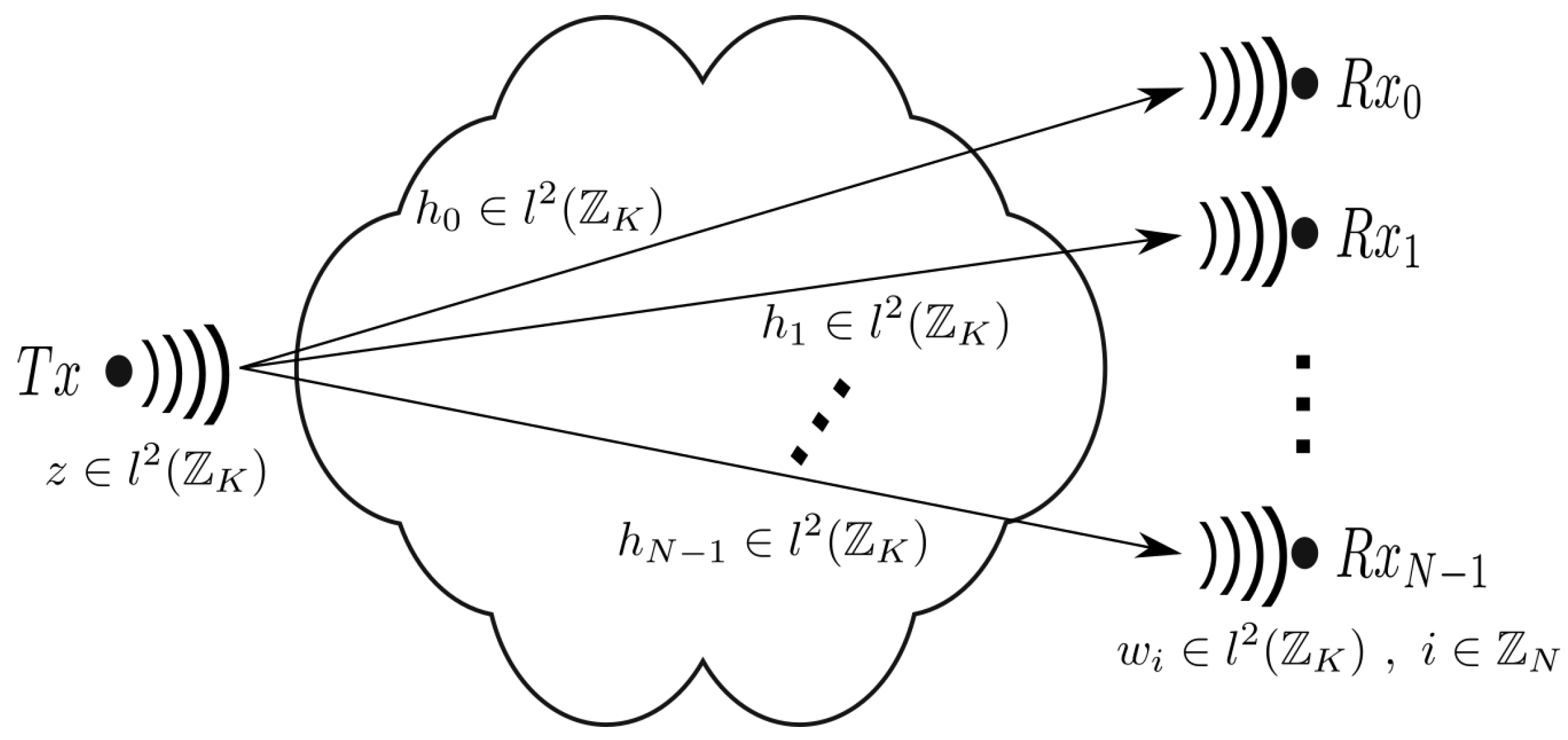
2.1.3. SIMO Configuration
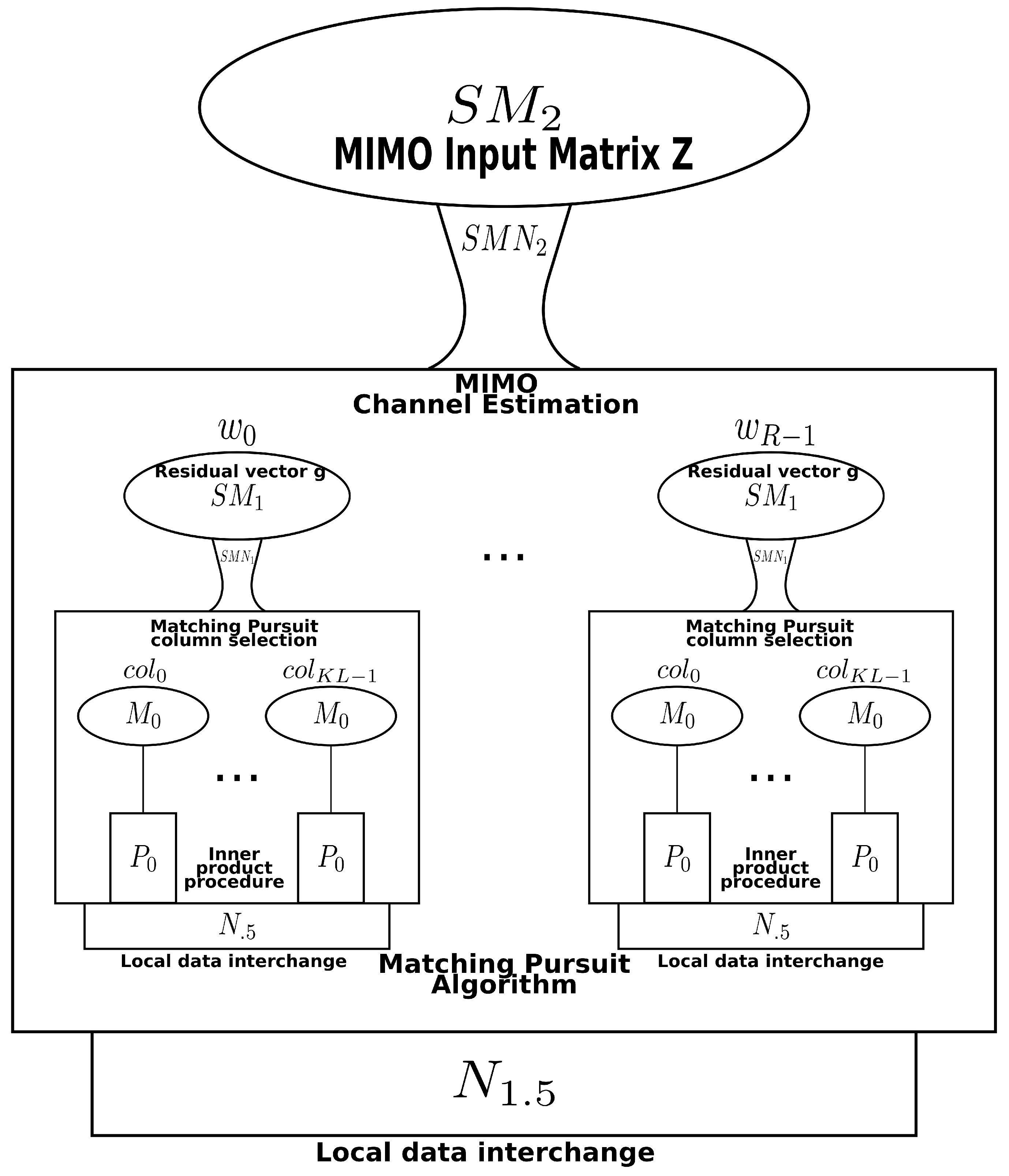
3. Kuck’s Paradigm of Computation
| Algorithm 1: Matching pursuit algorithmic core. Distributed max projection. |
|
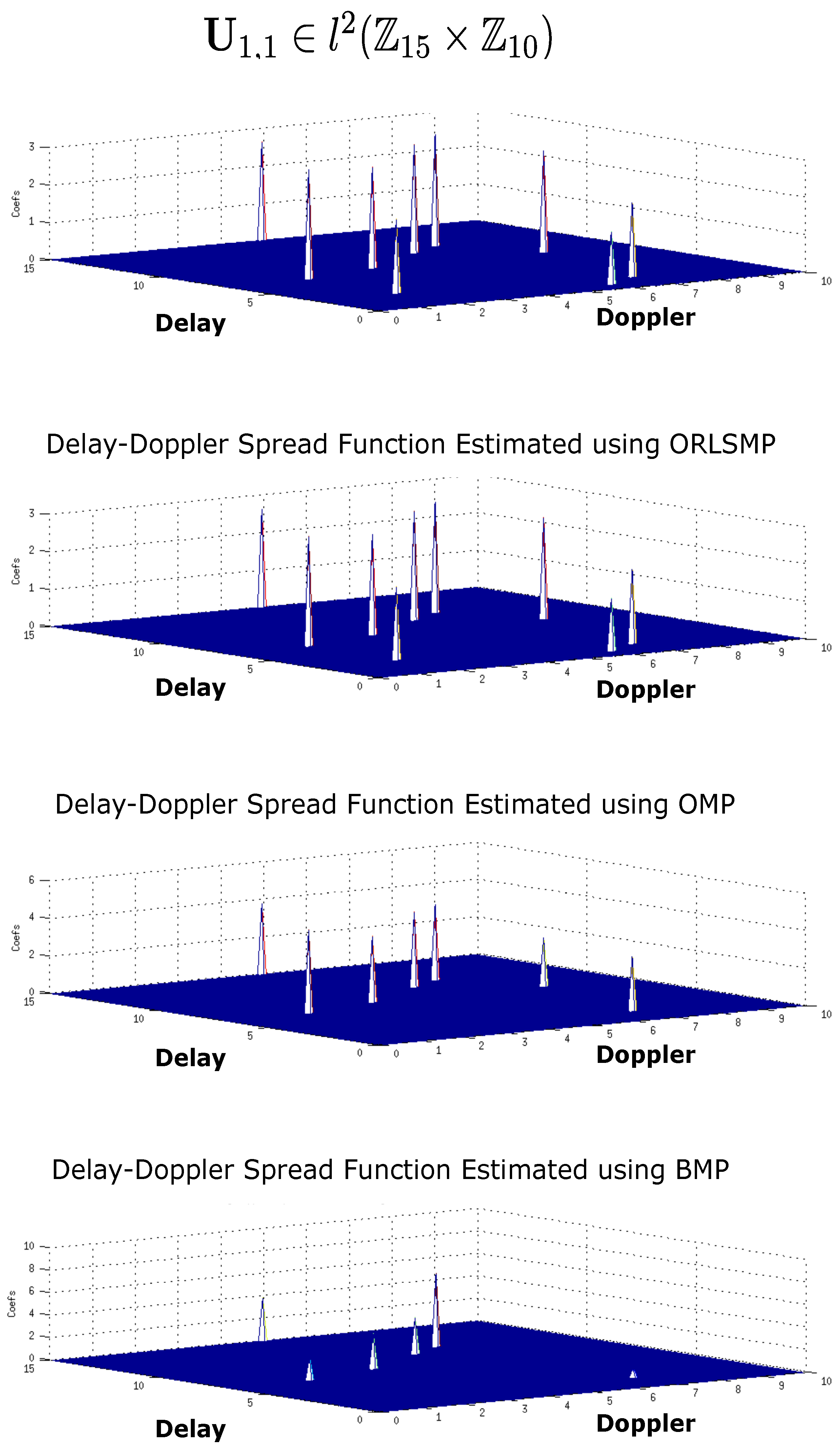
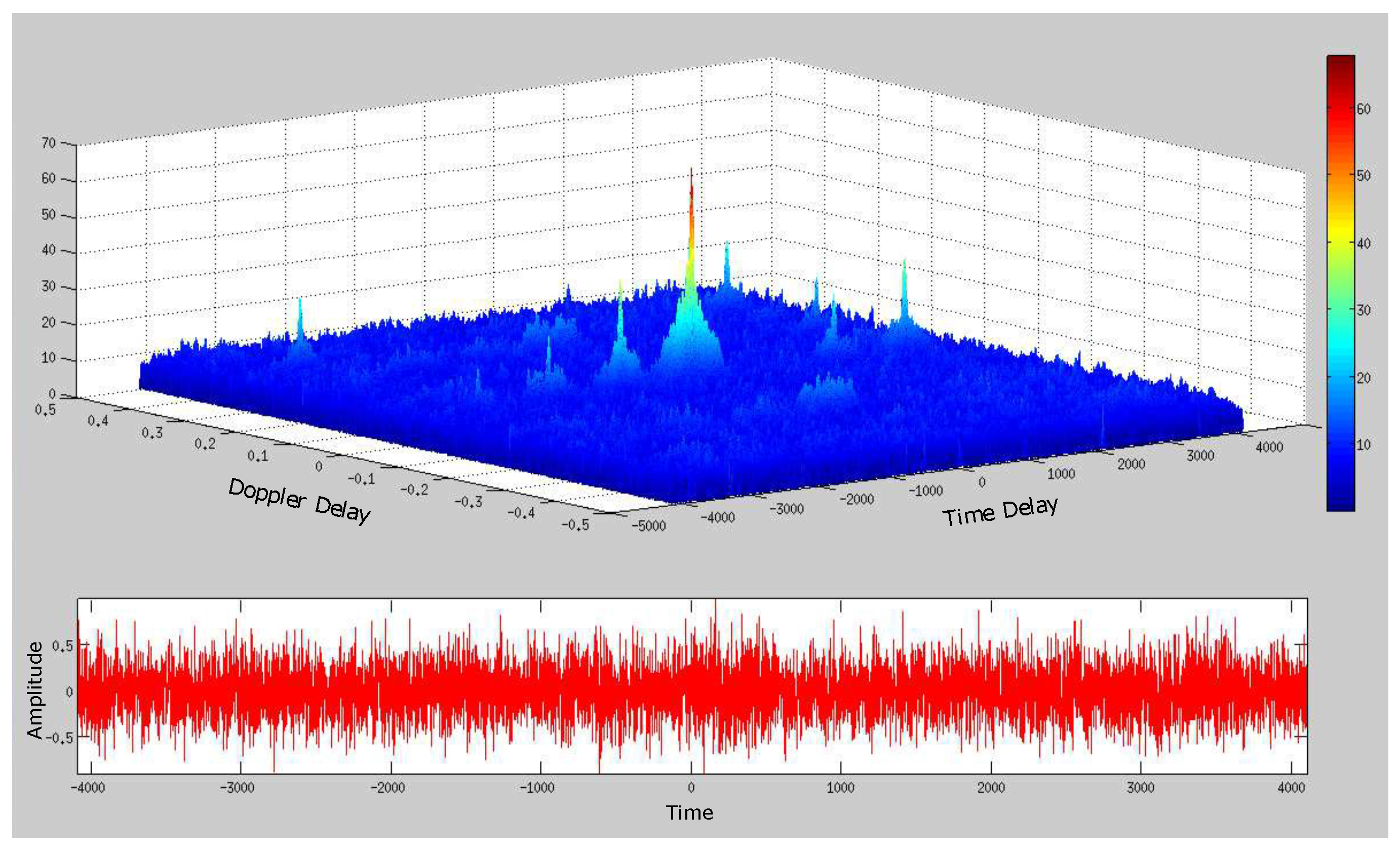
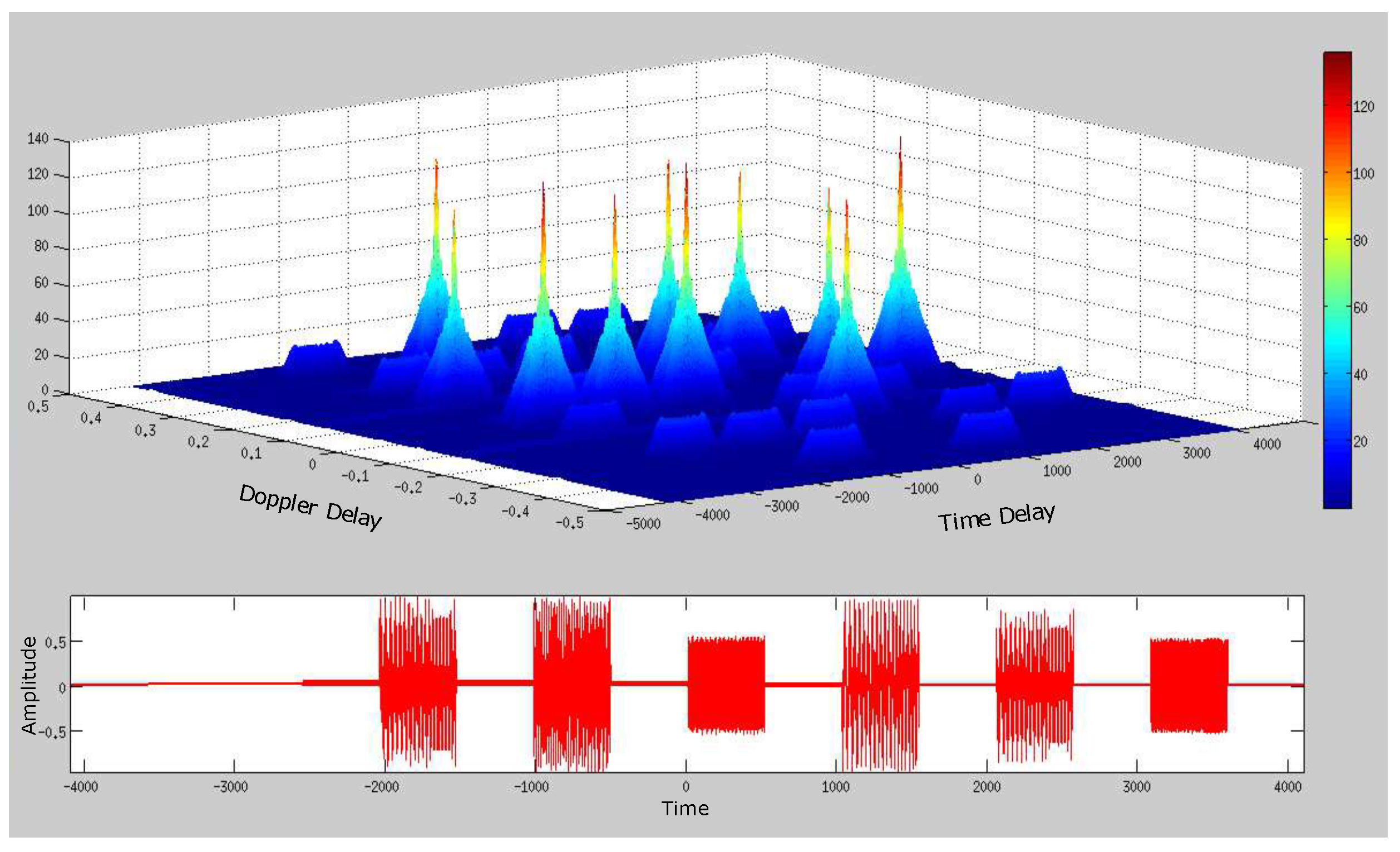
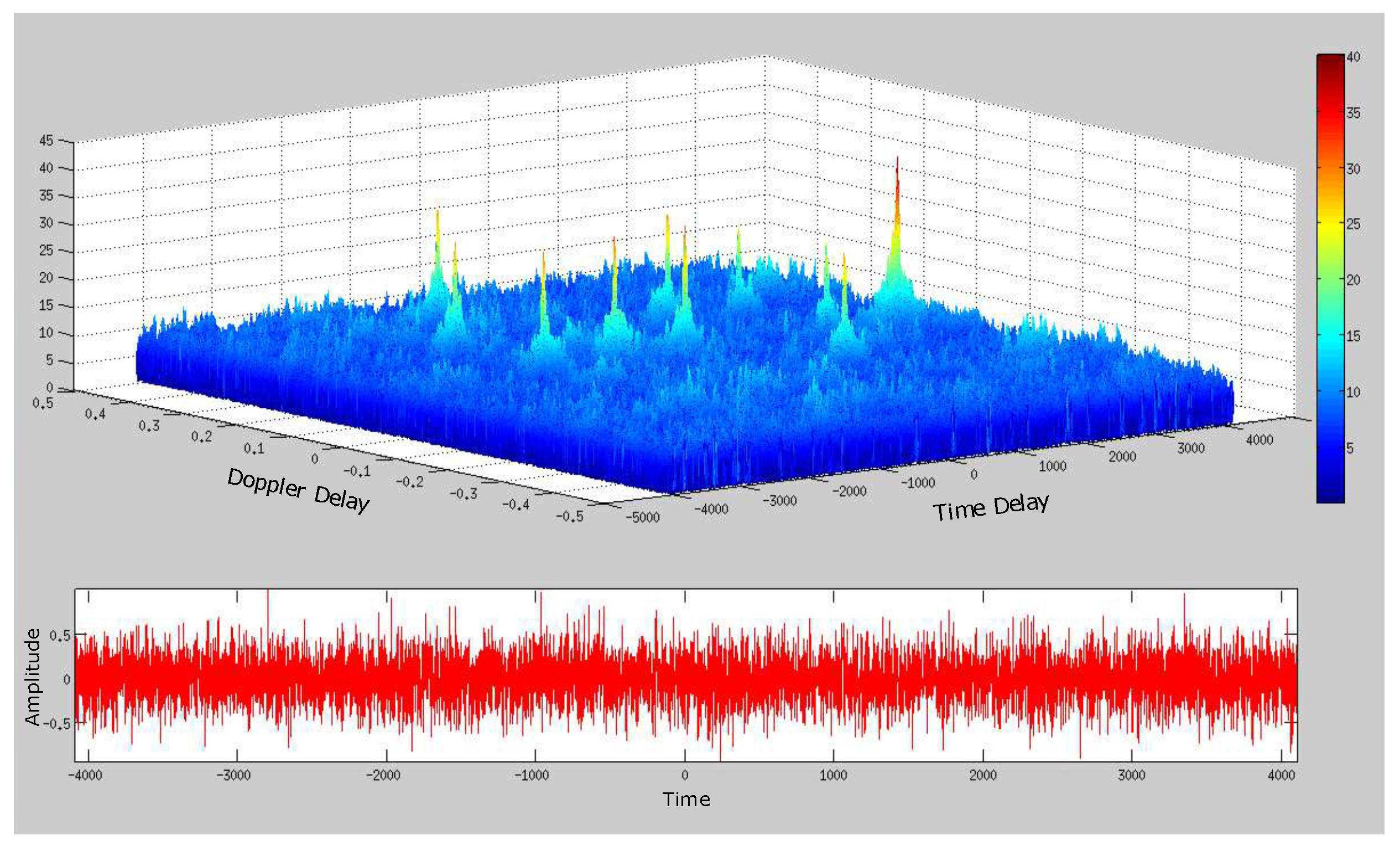
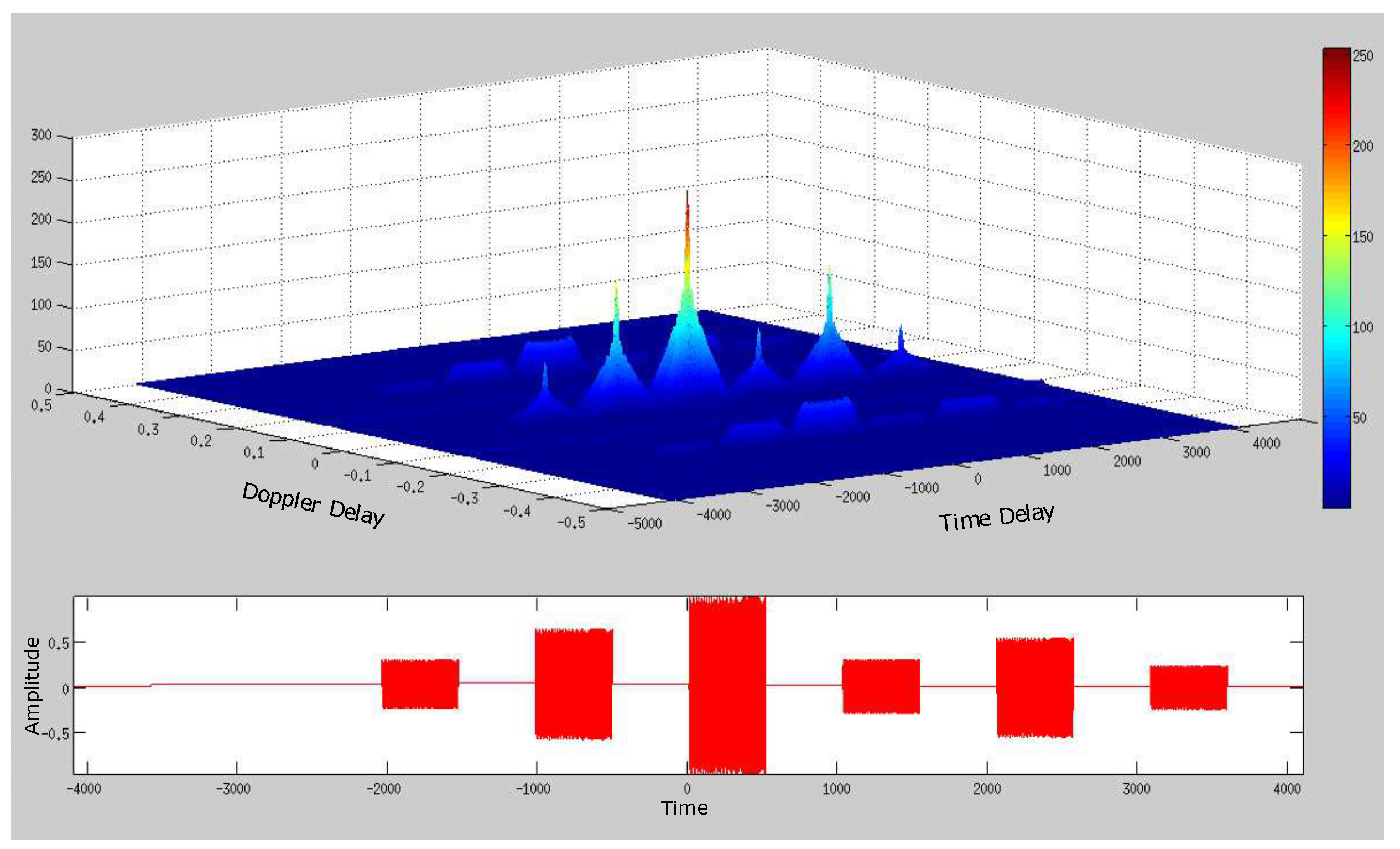
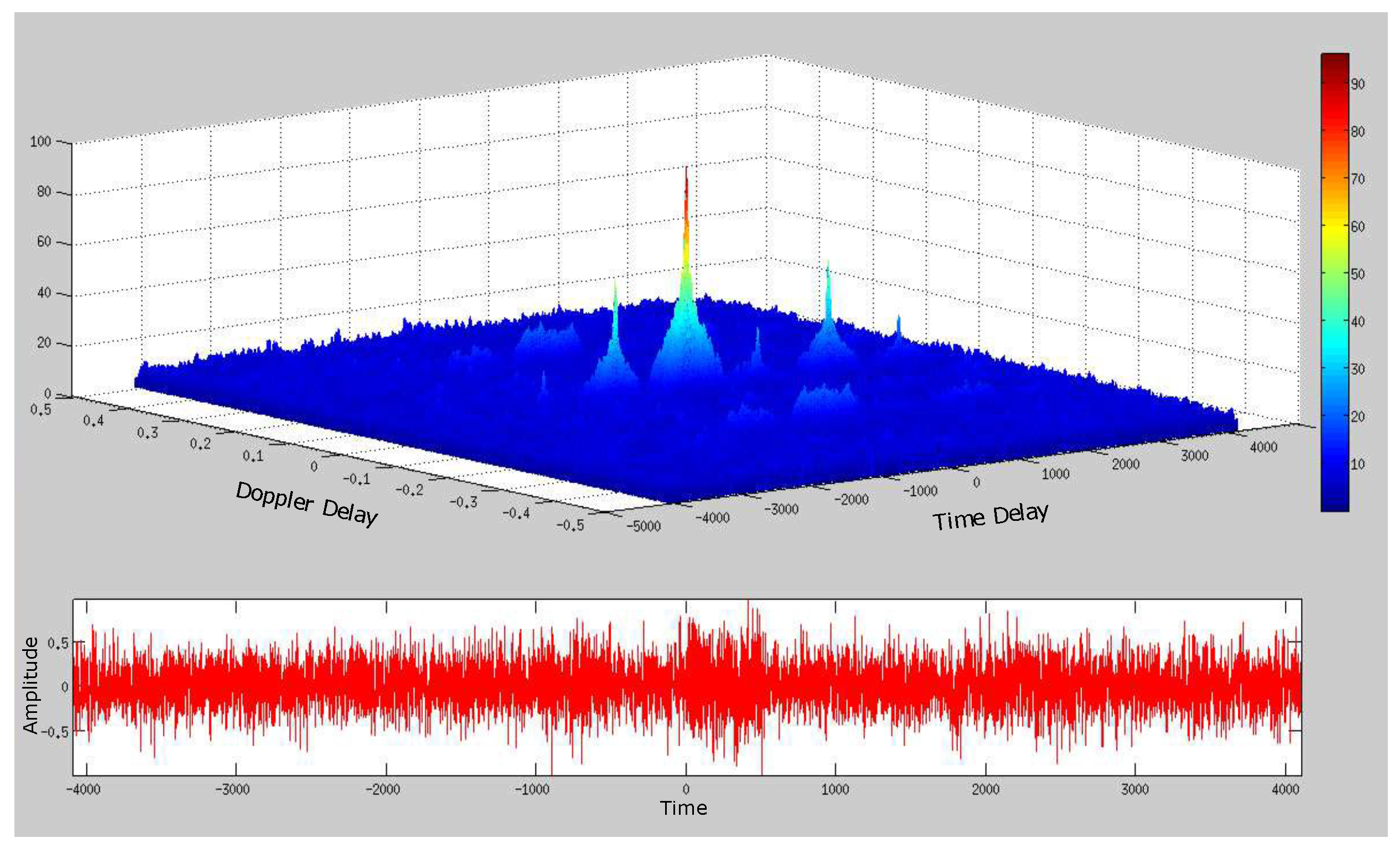
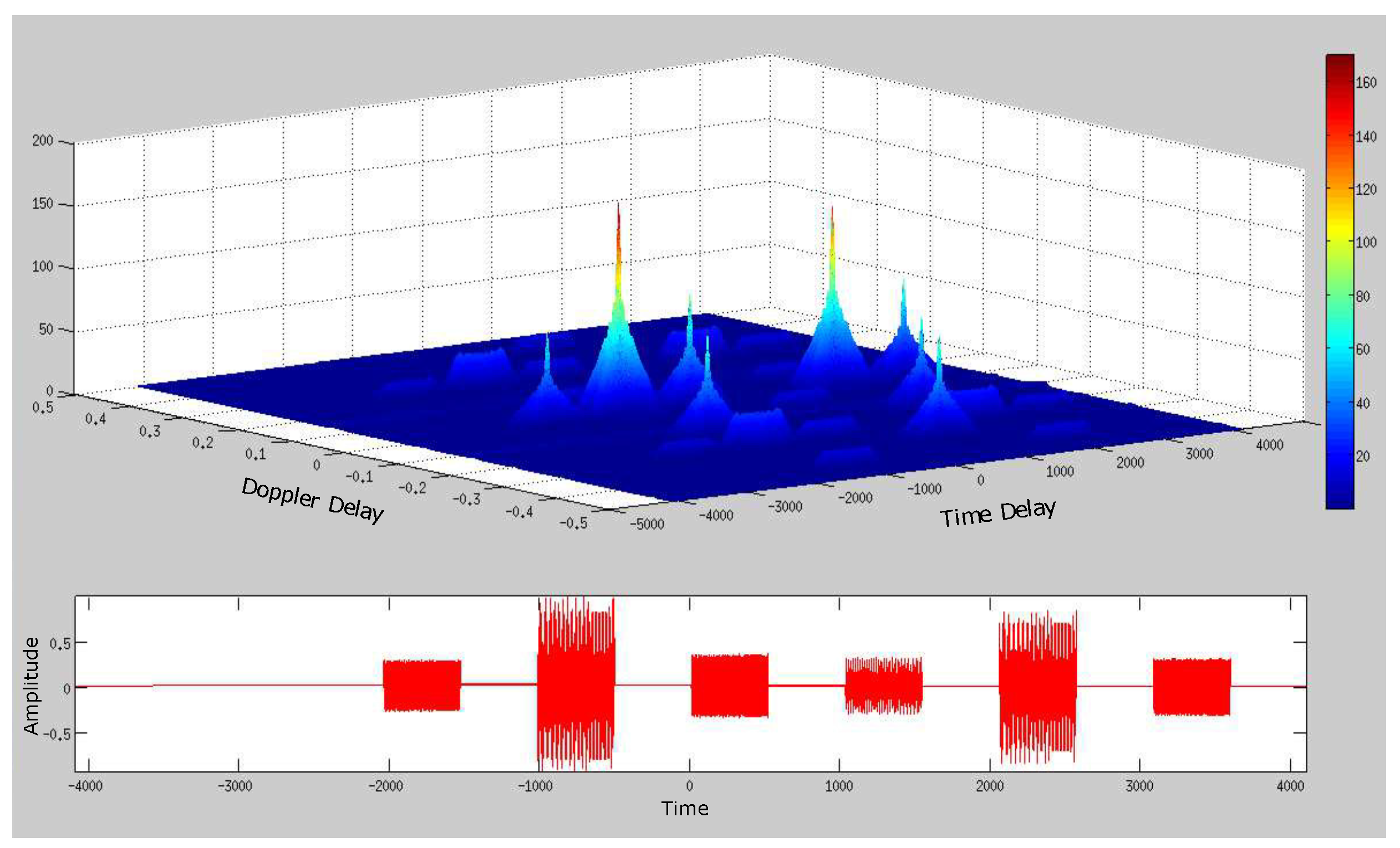
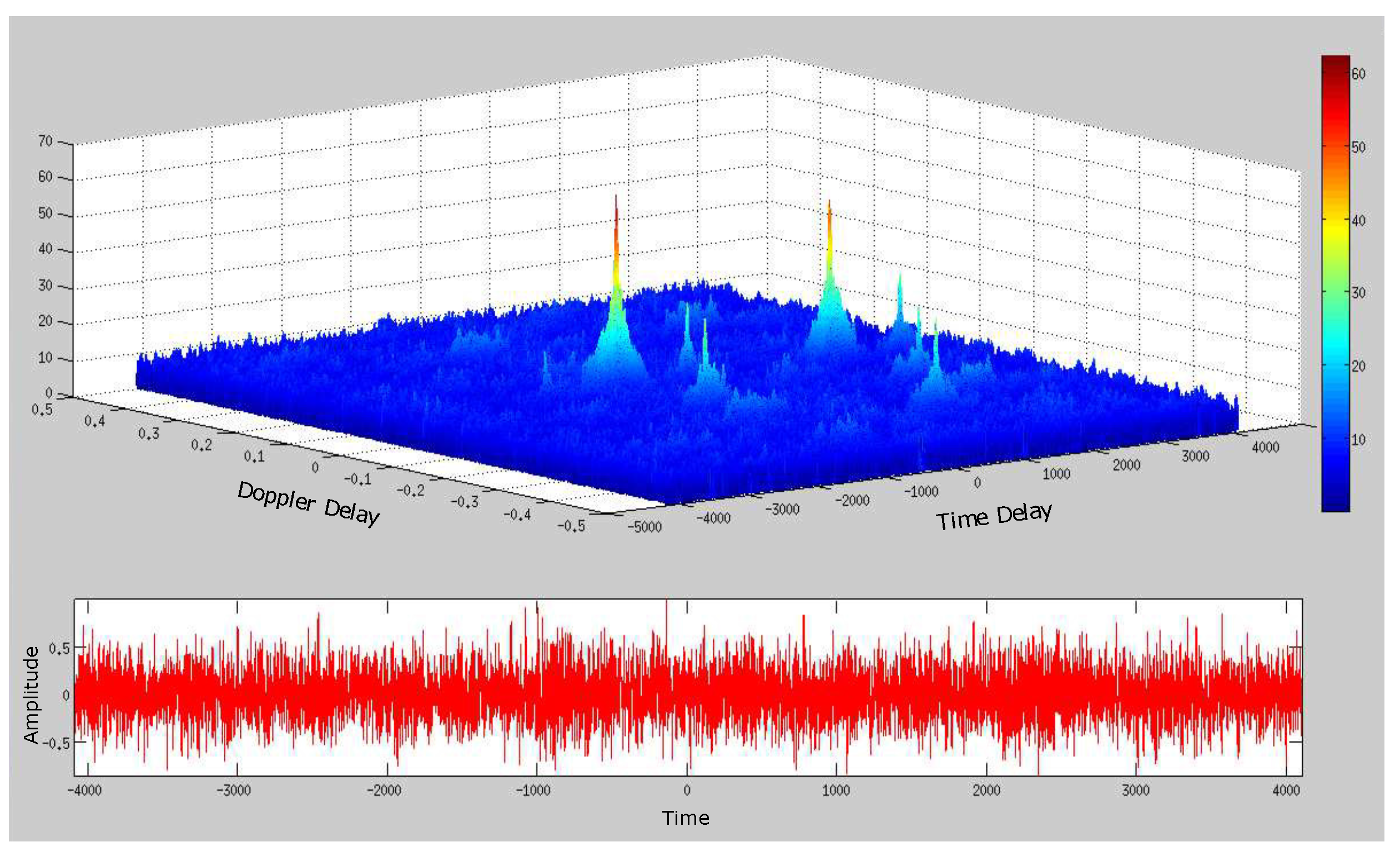
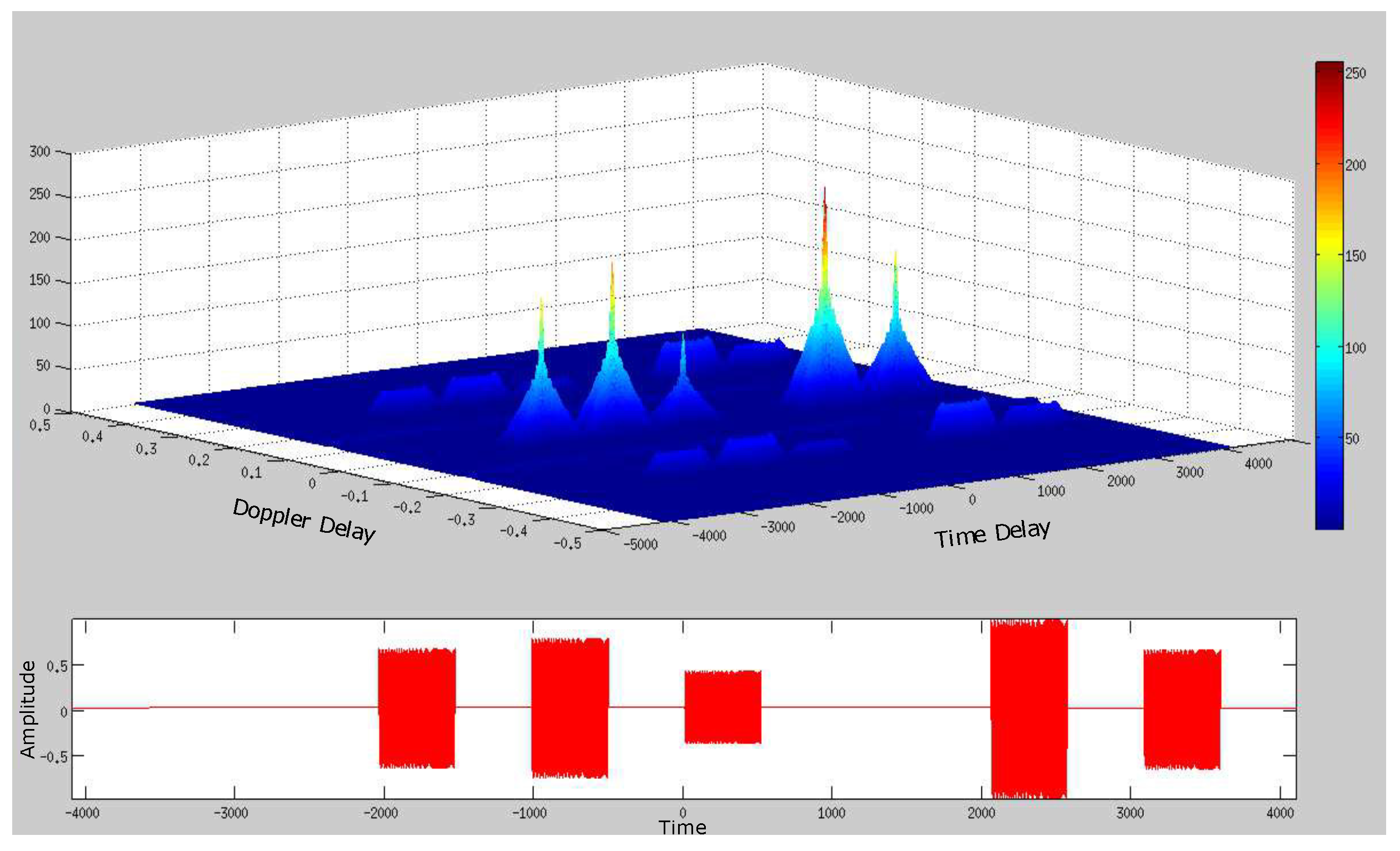
4. Simplified SDET Implementation Results
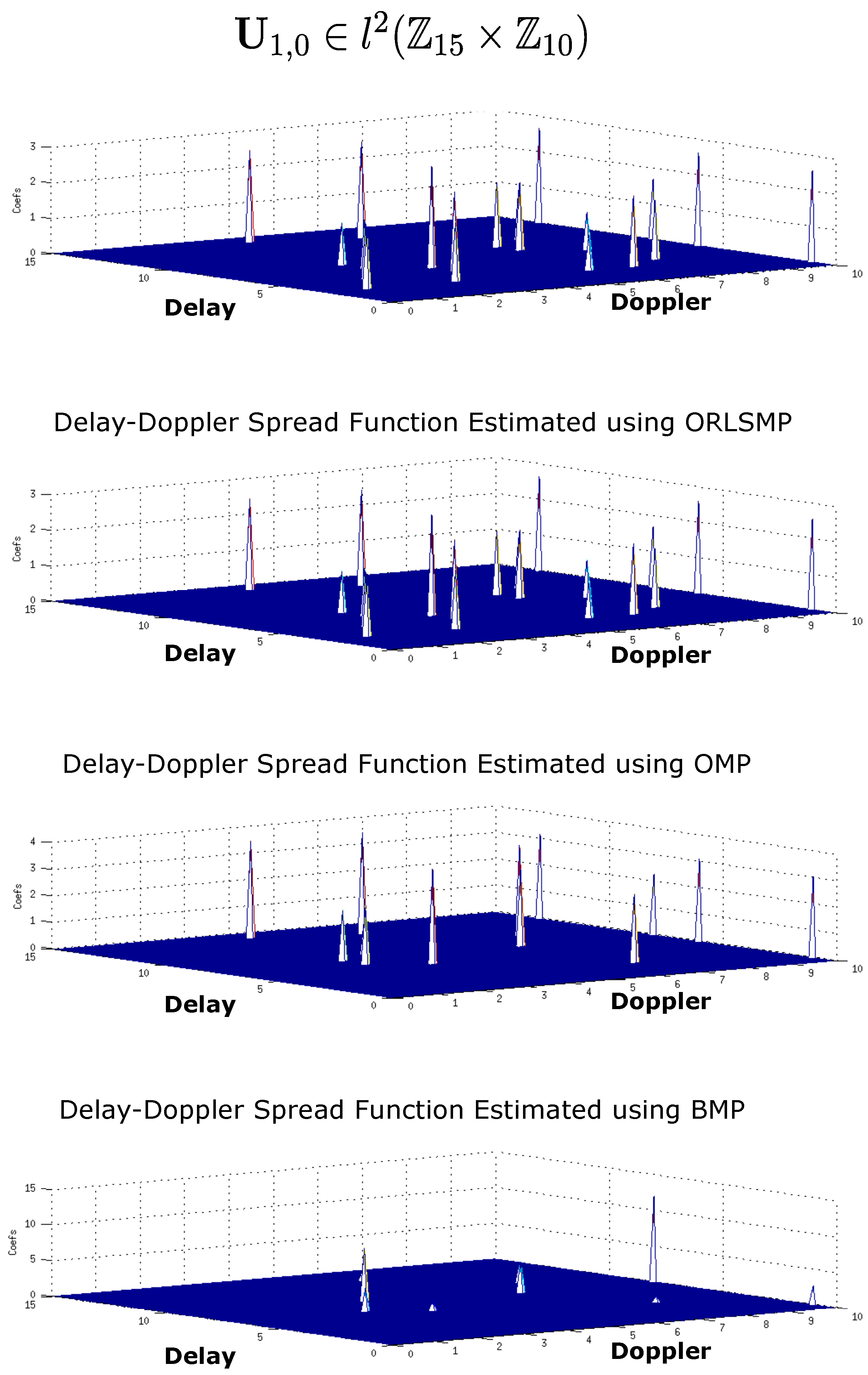
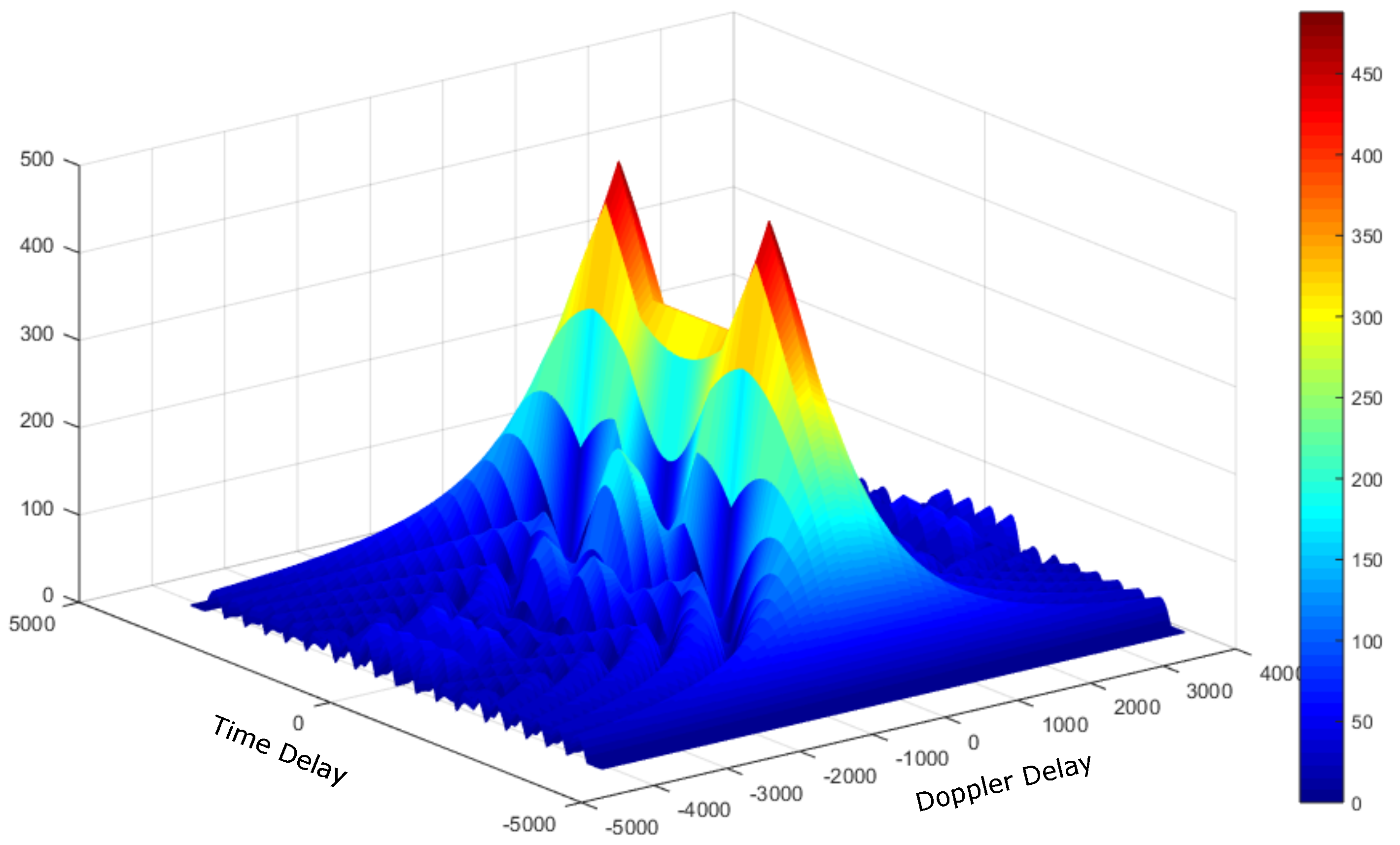
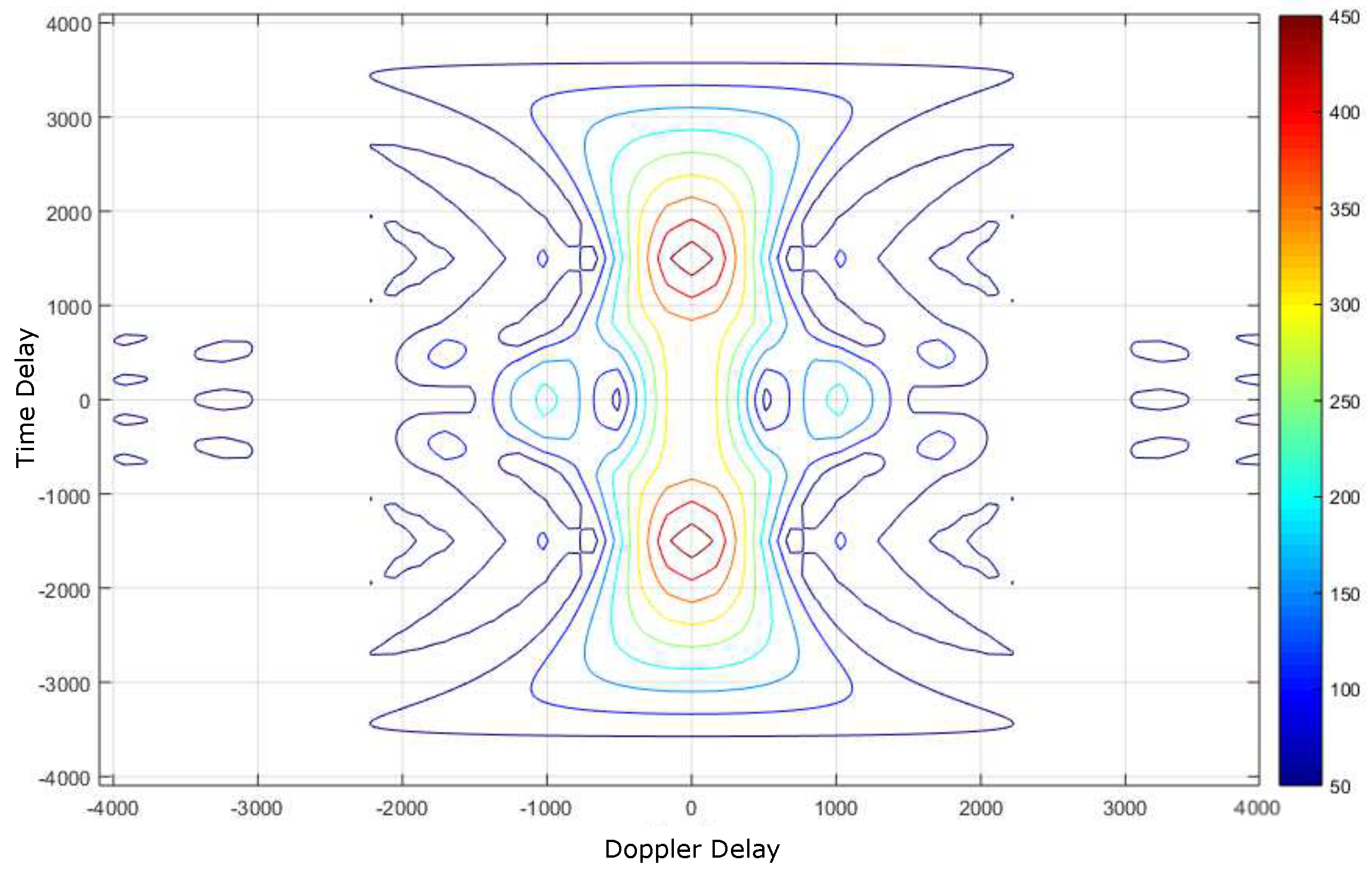
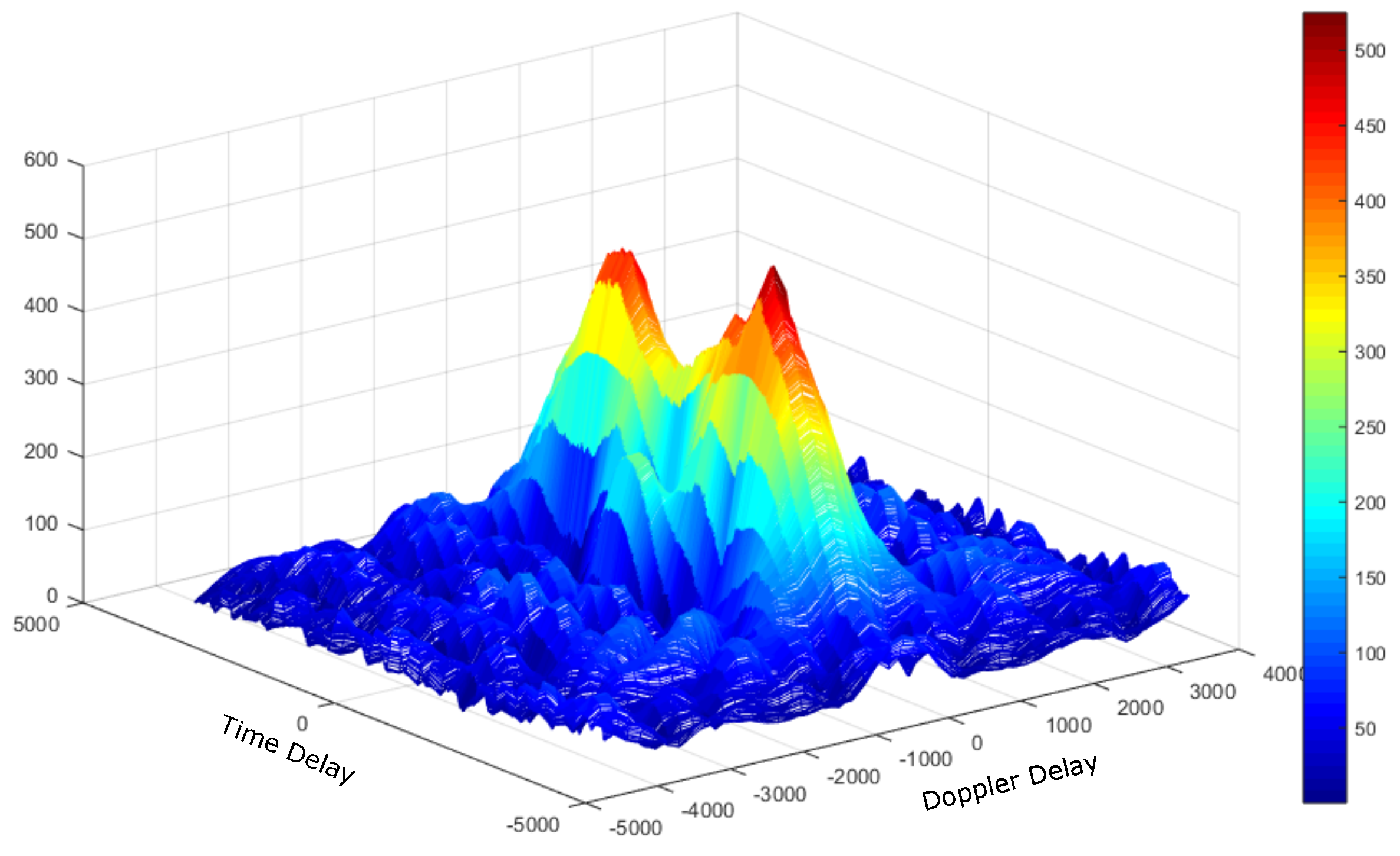
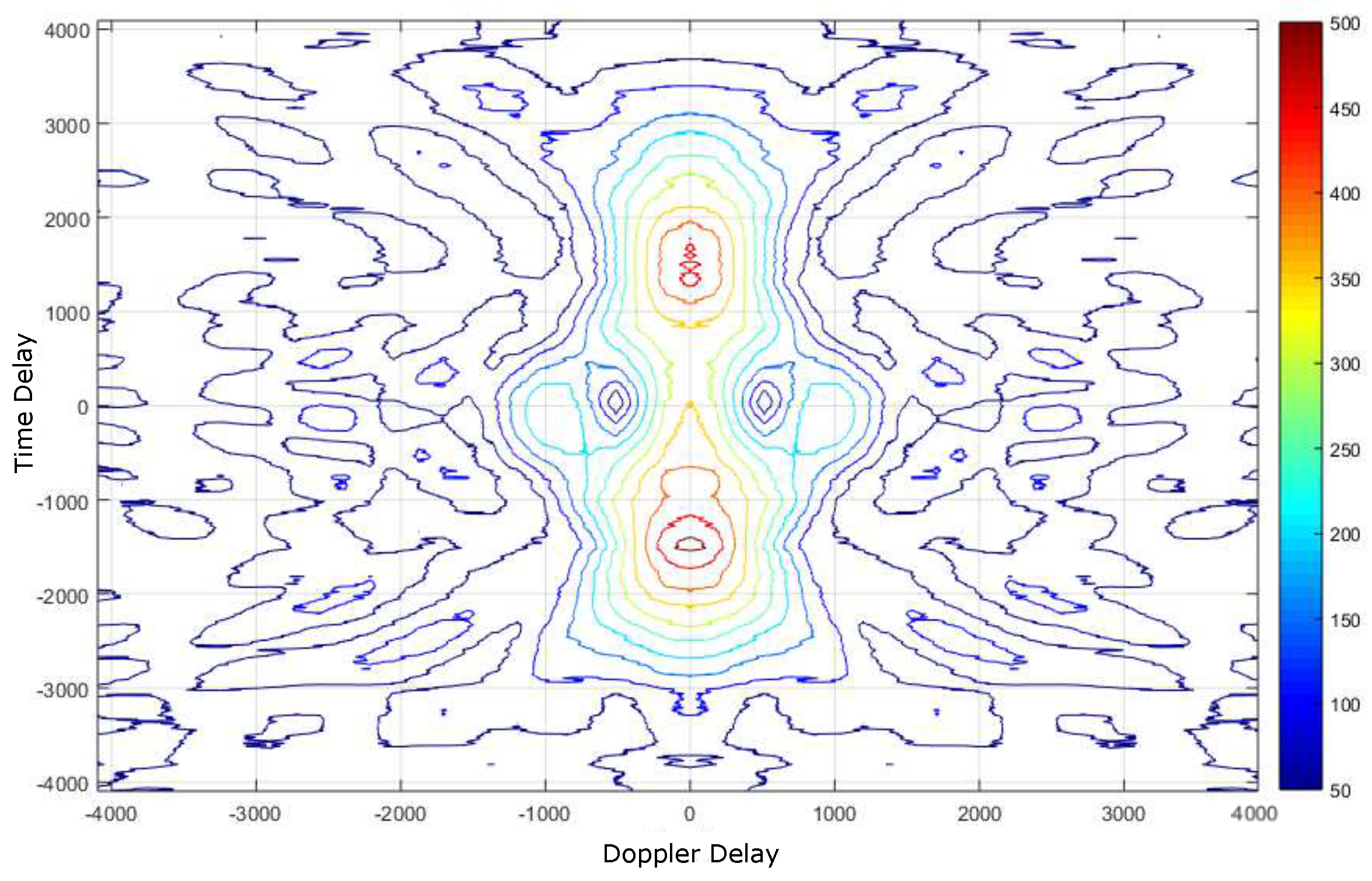
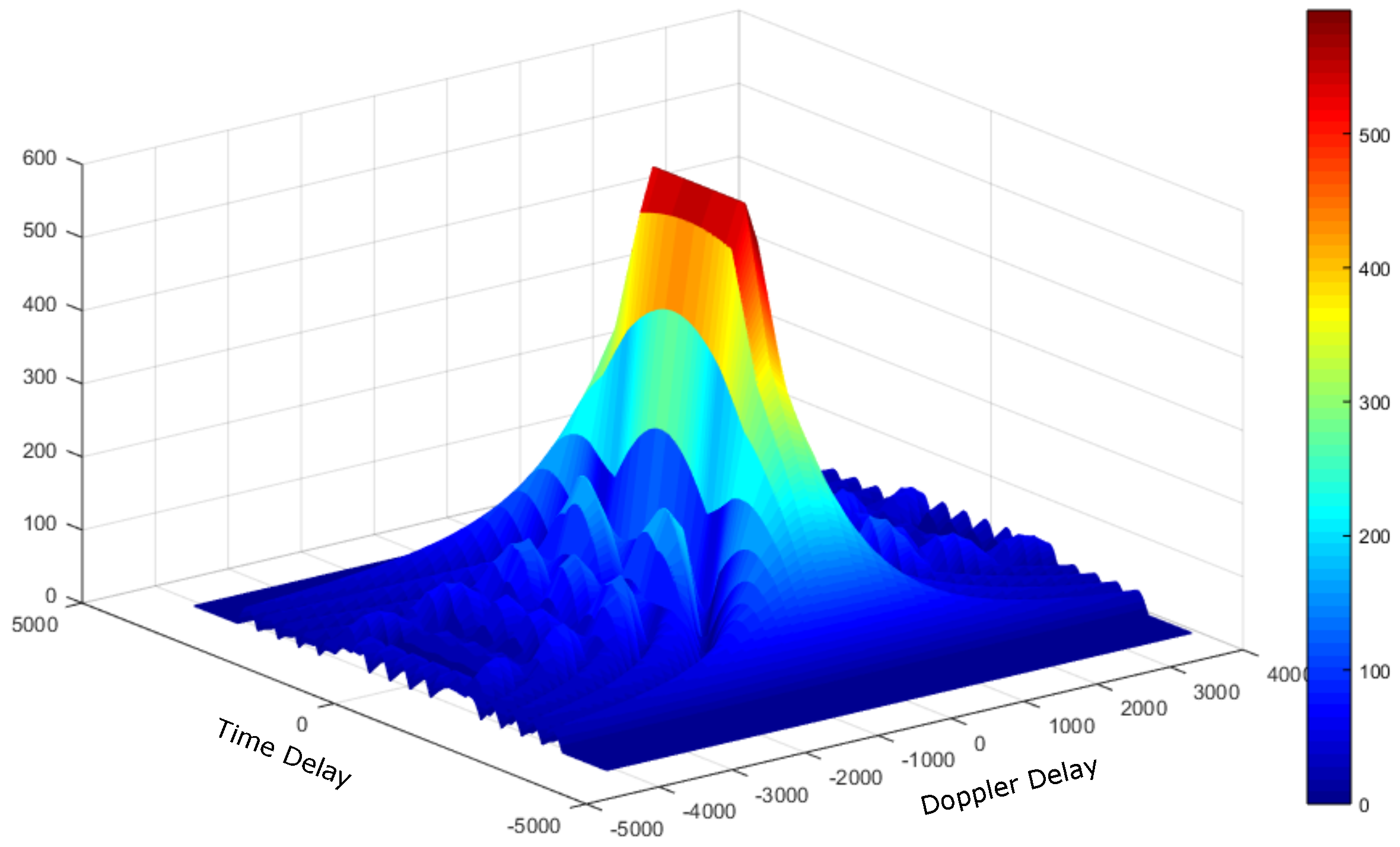
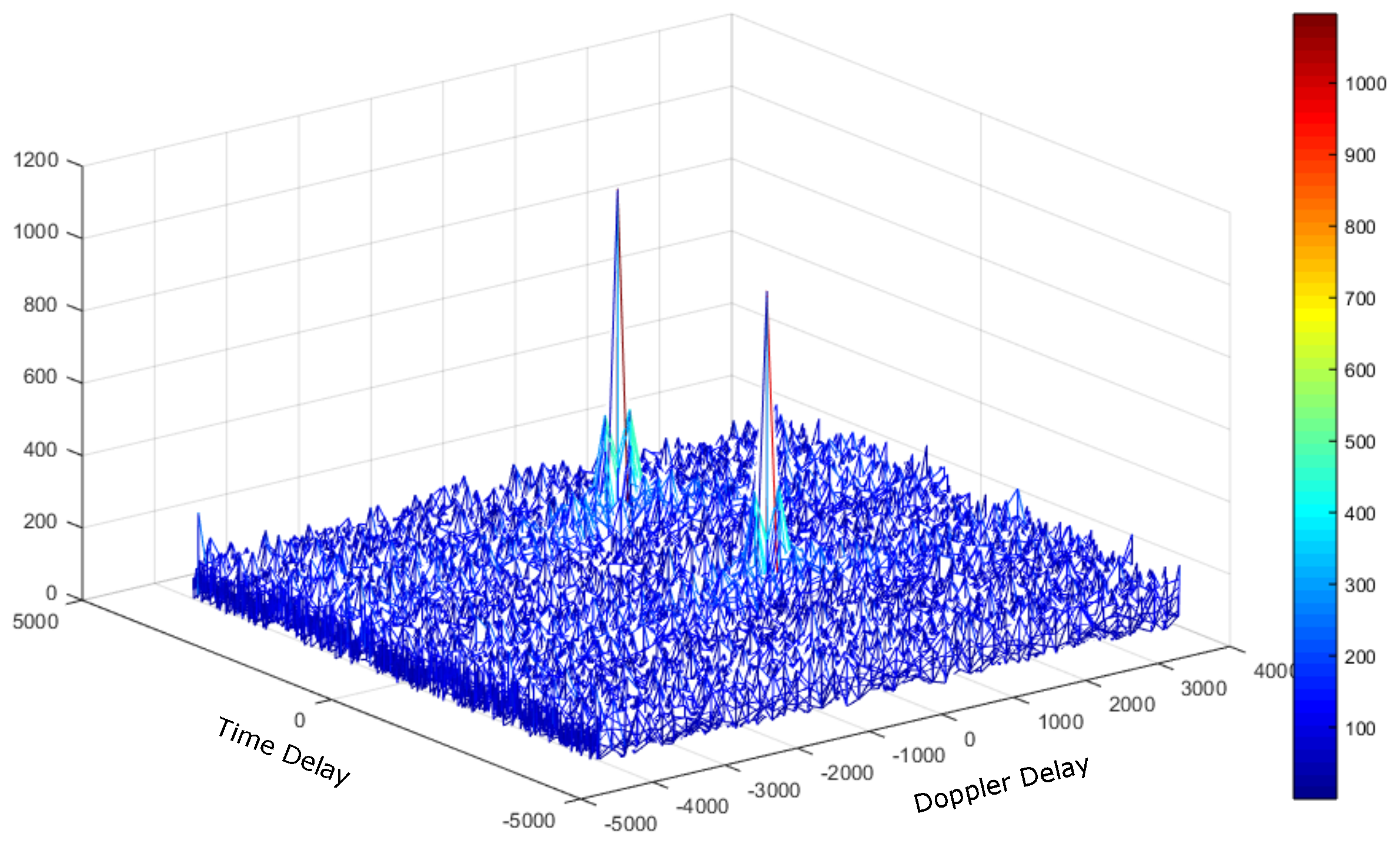
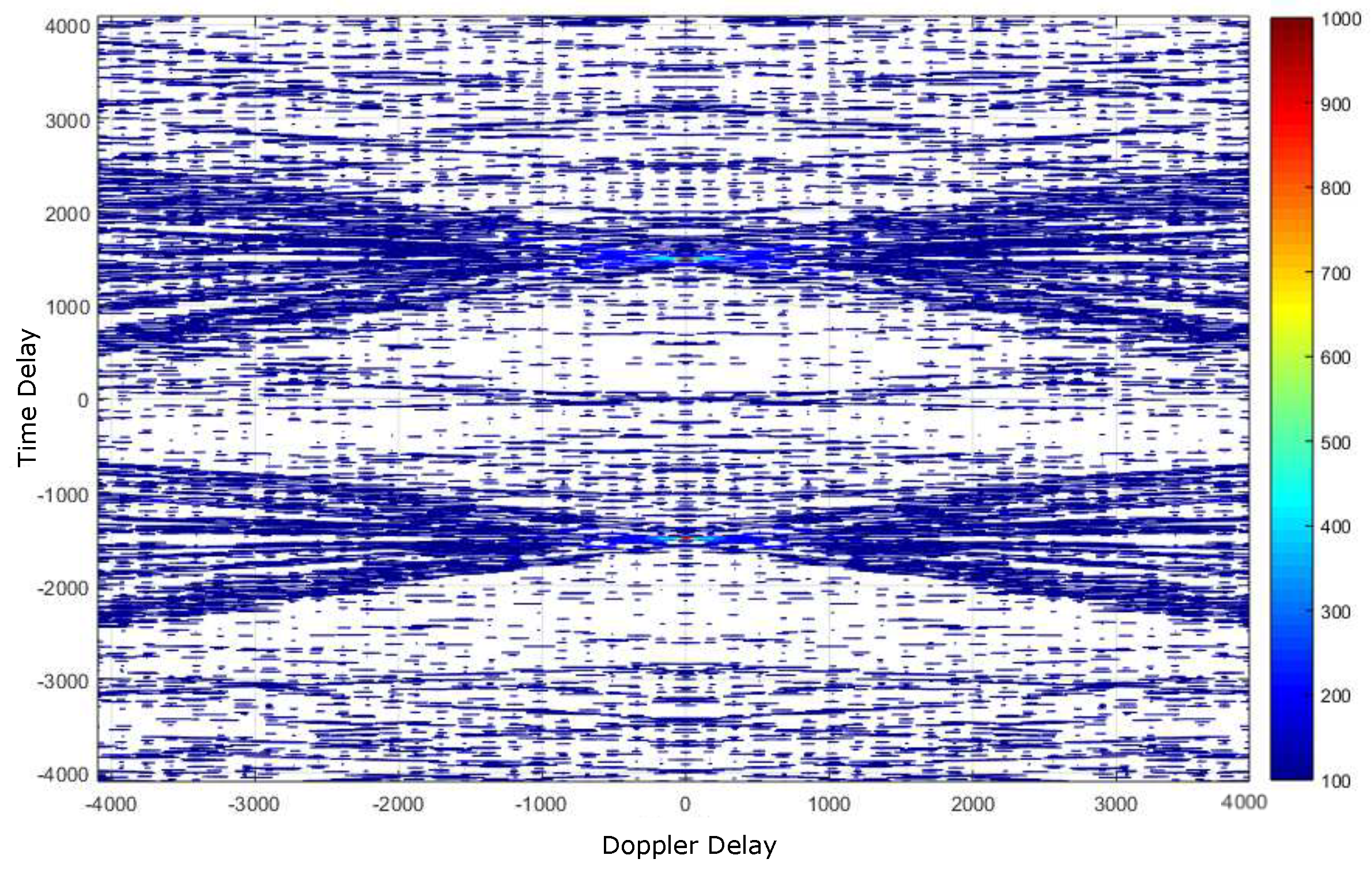
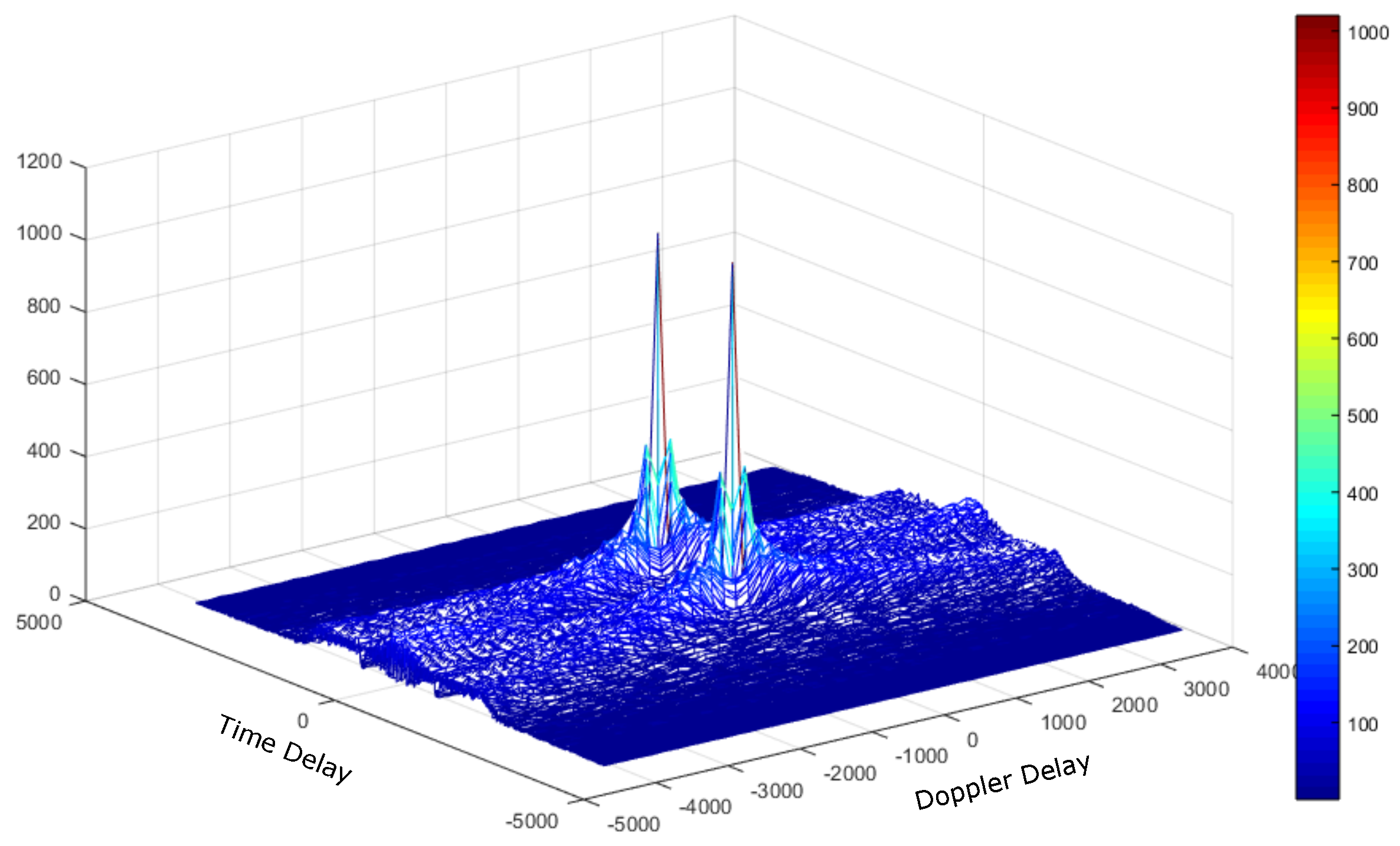
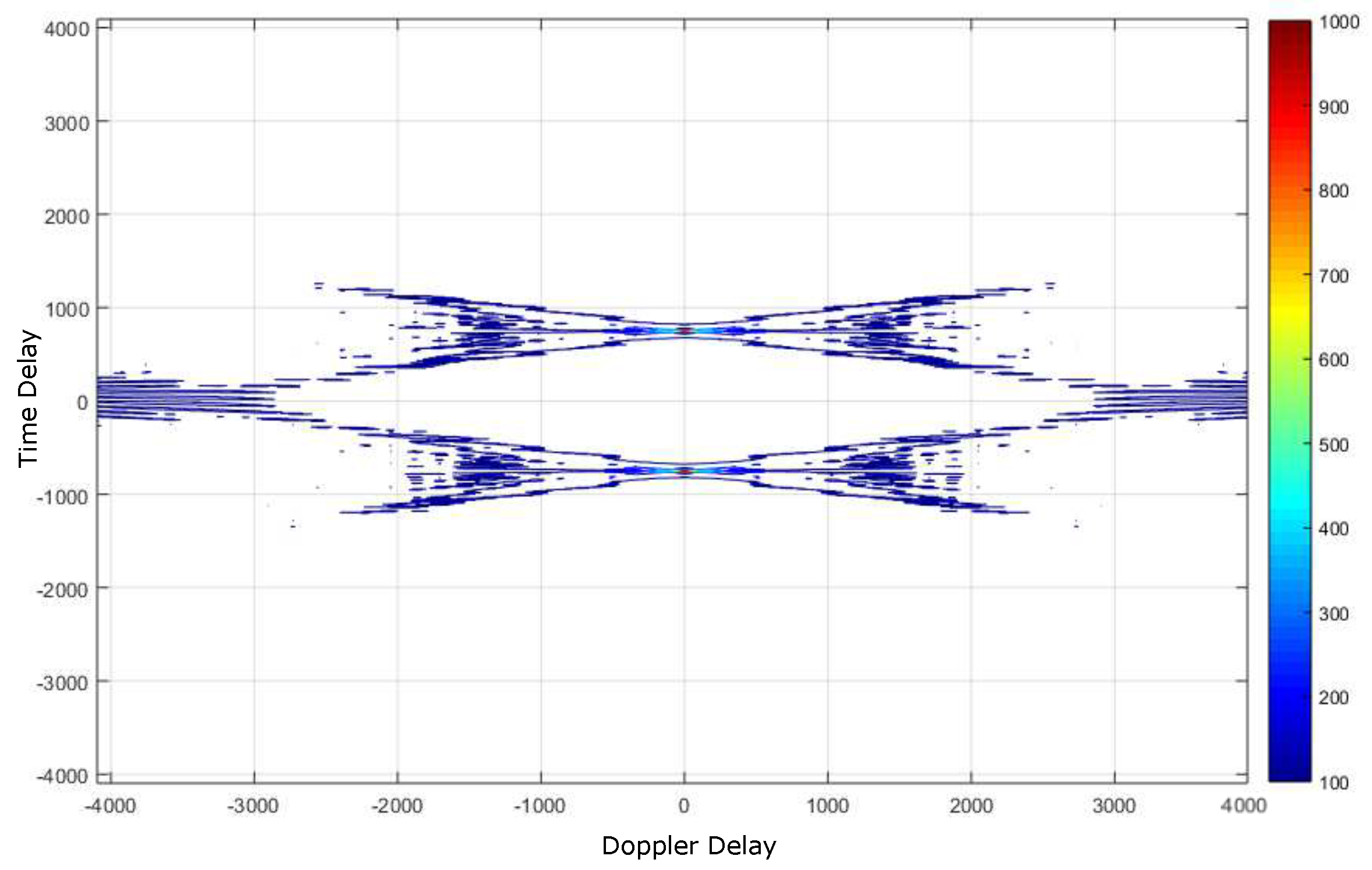
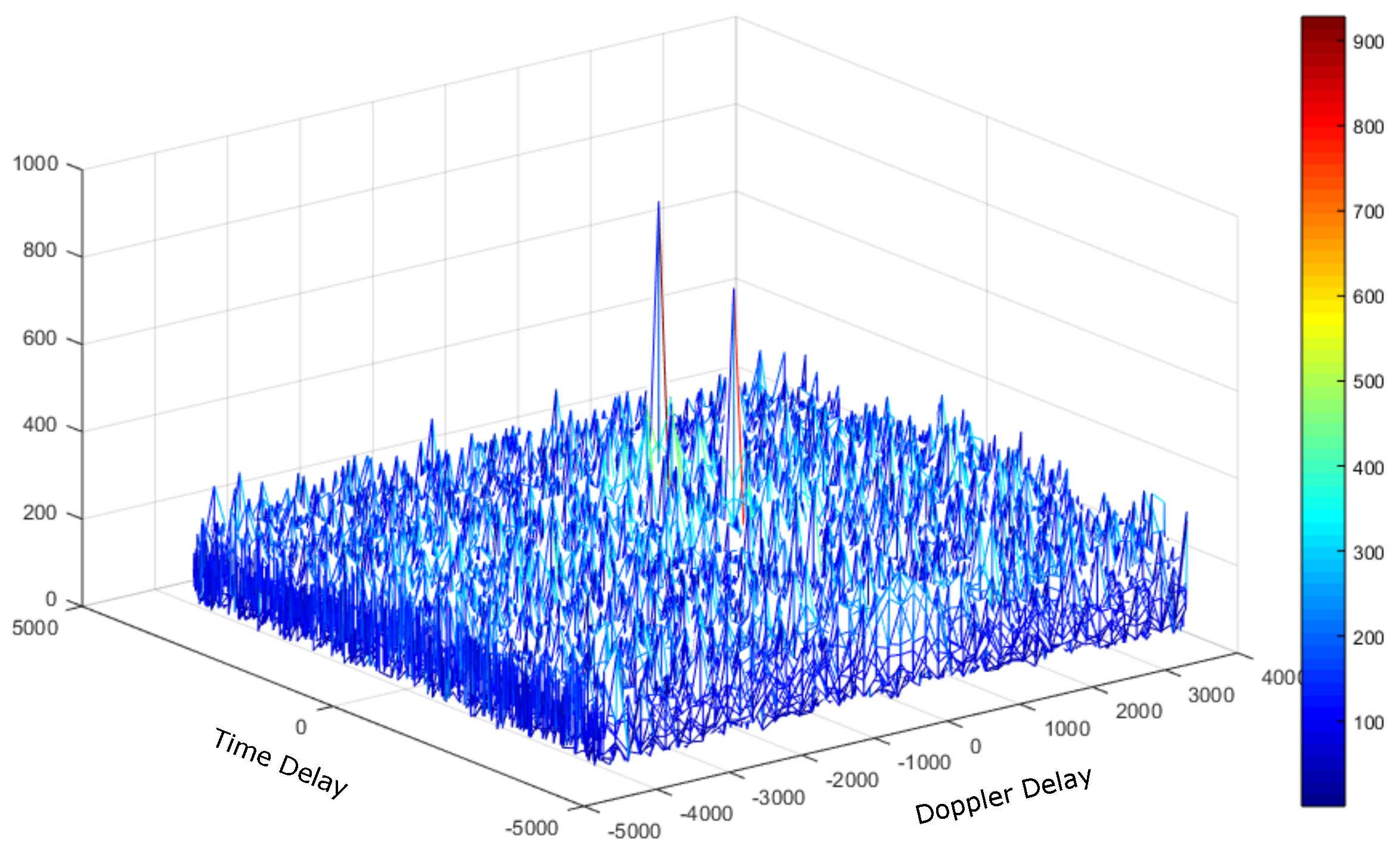
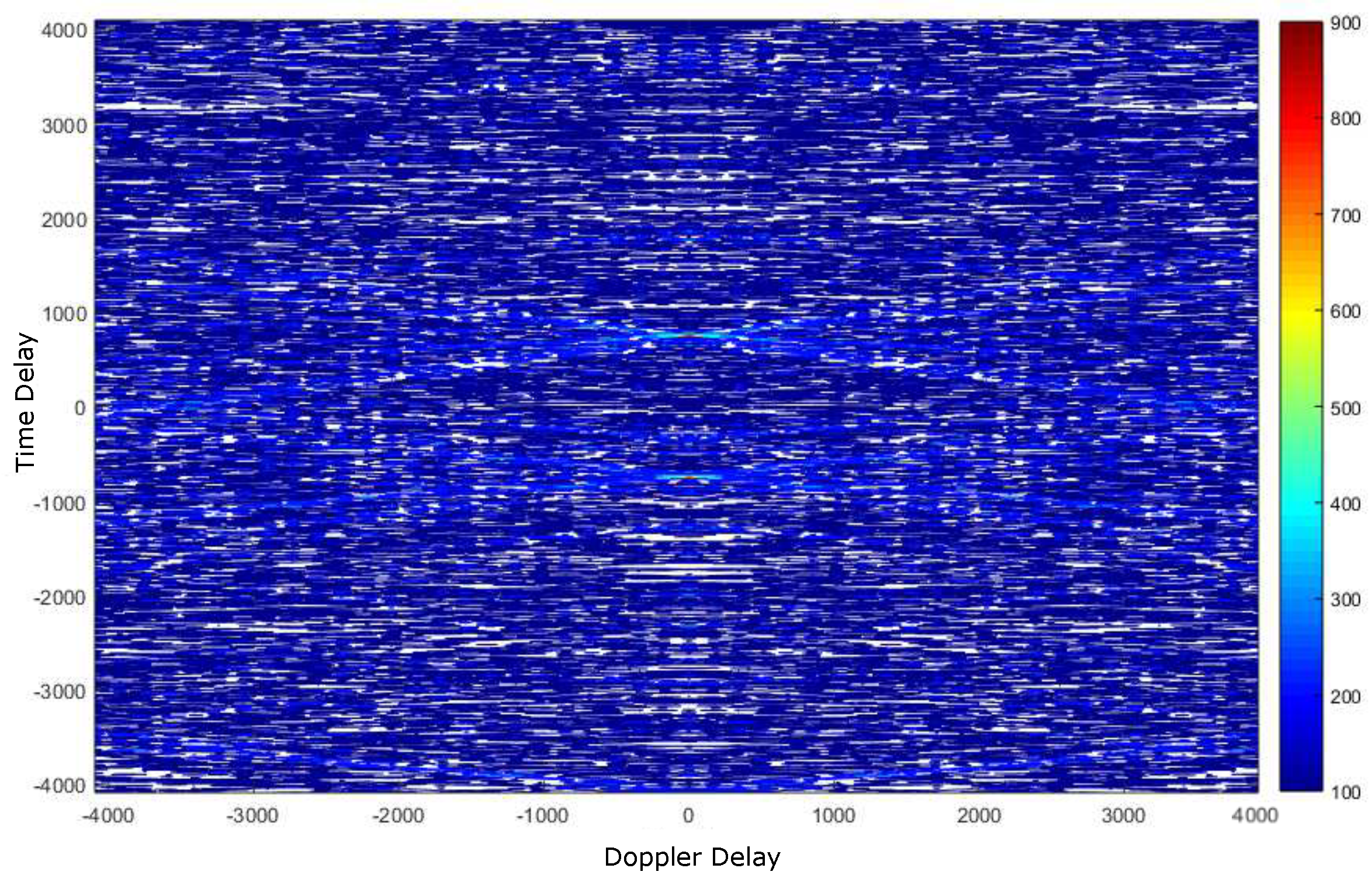
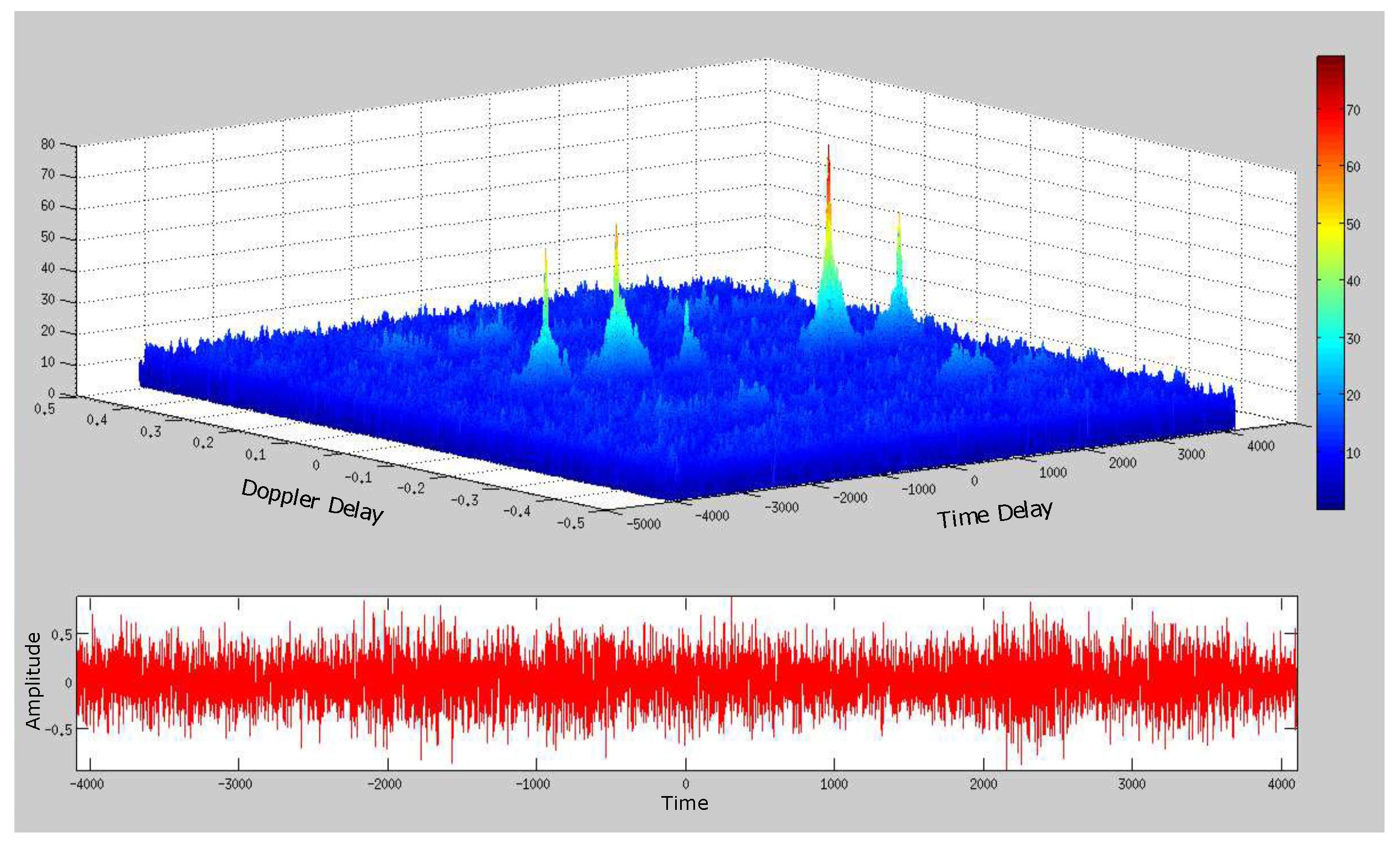
4.1. Deep Underwater Two-Object Tracking Example
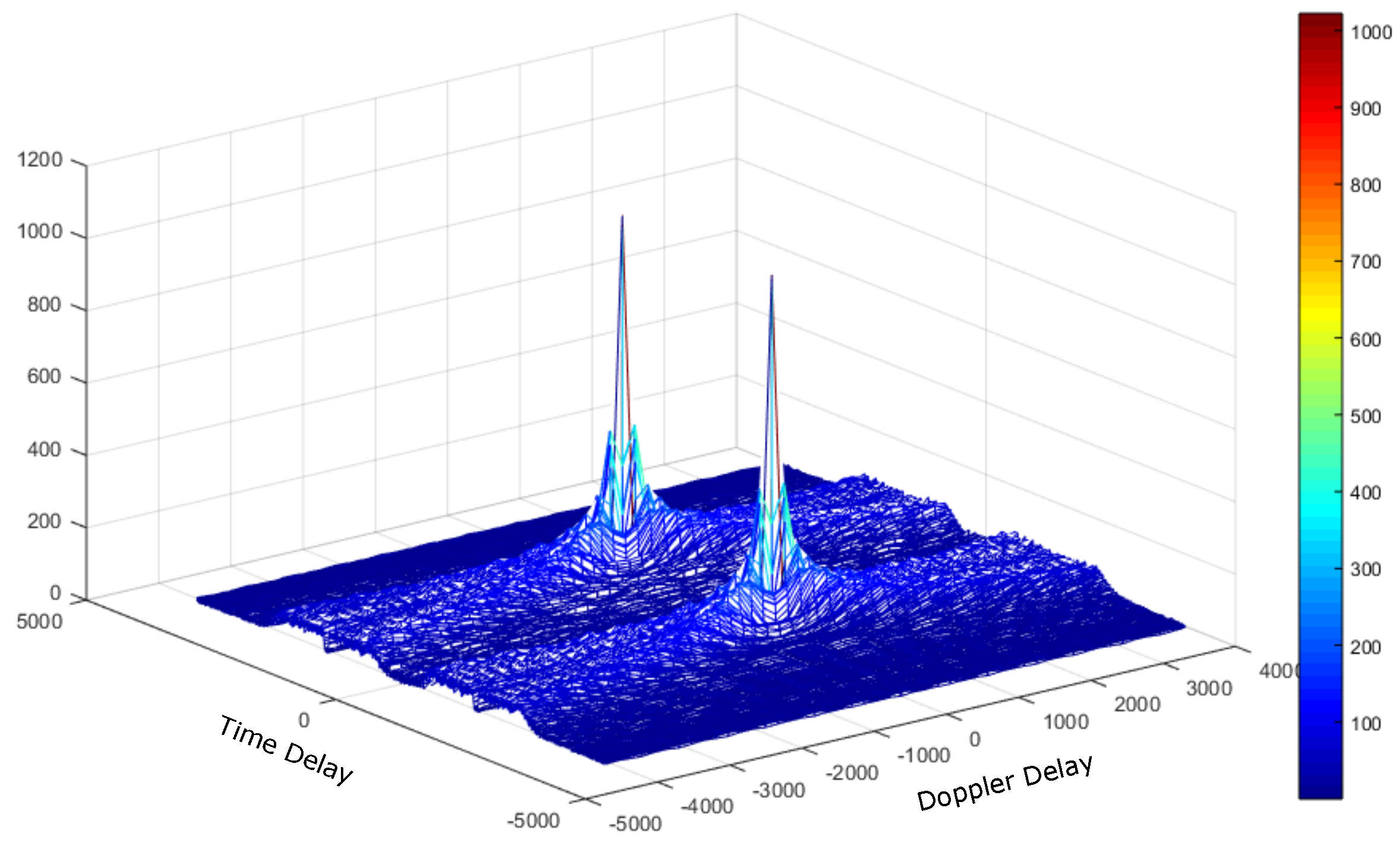
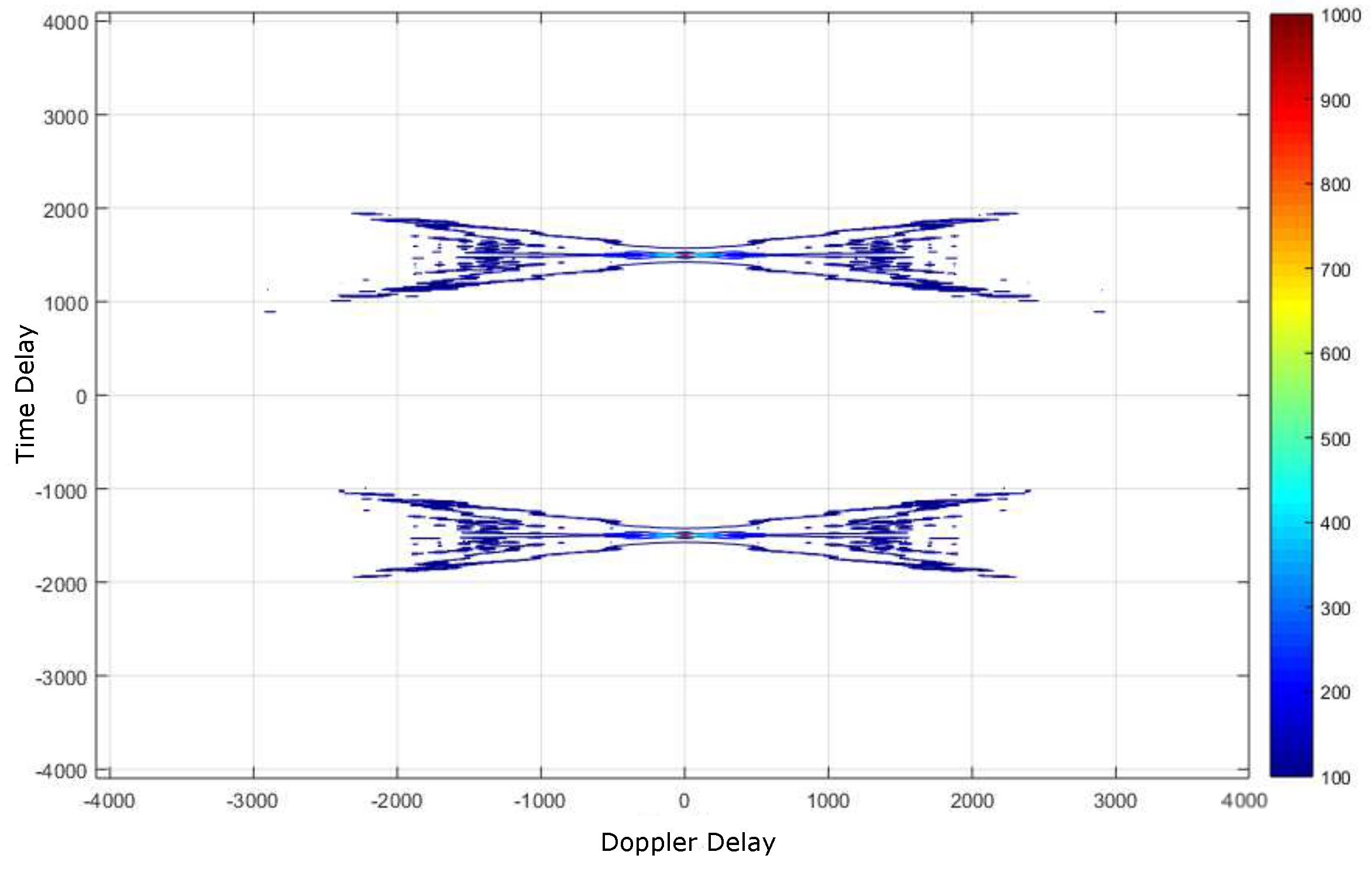
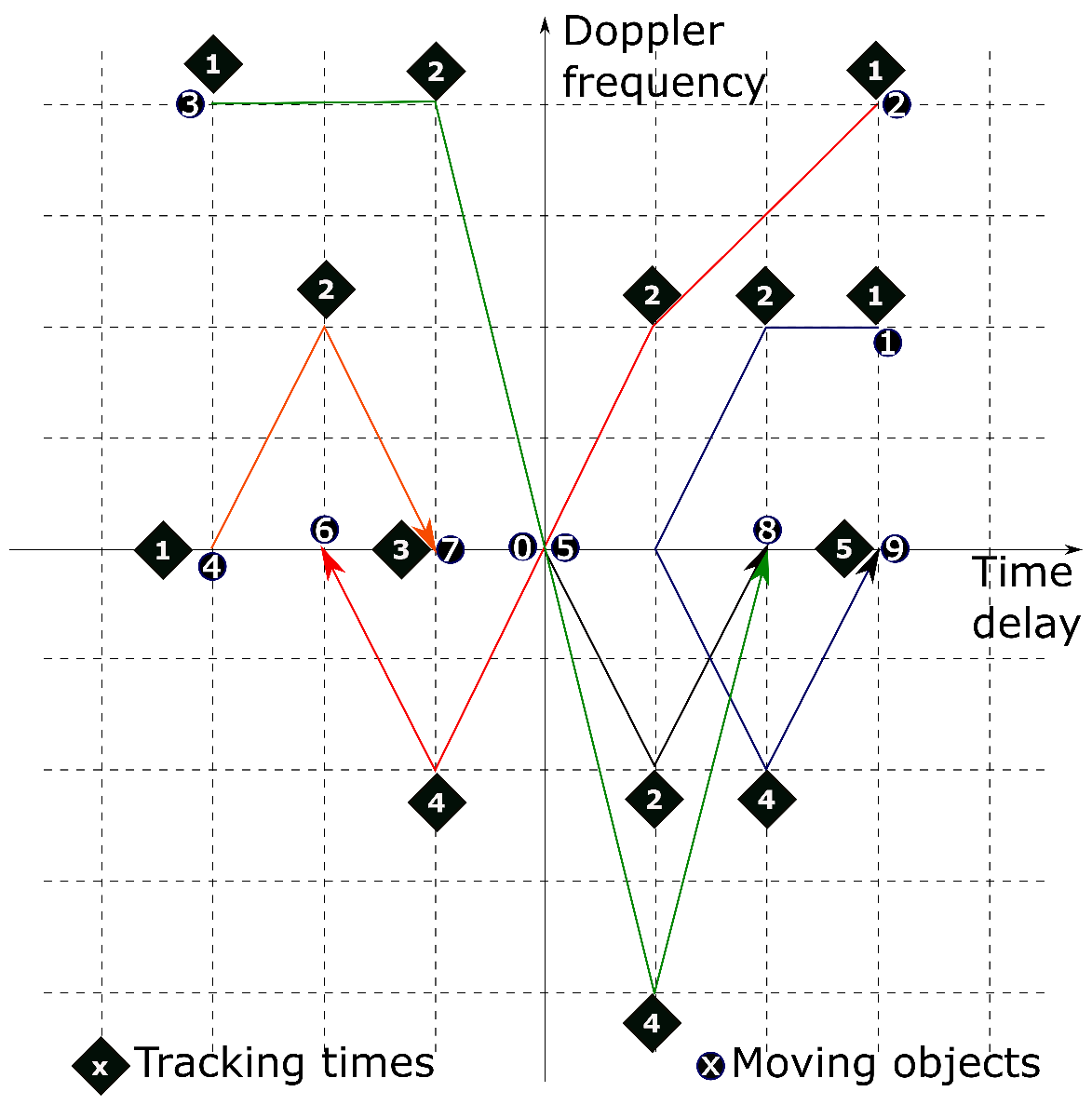
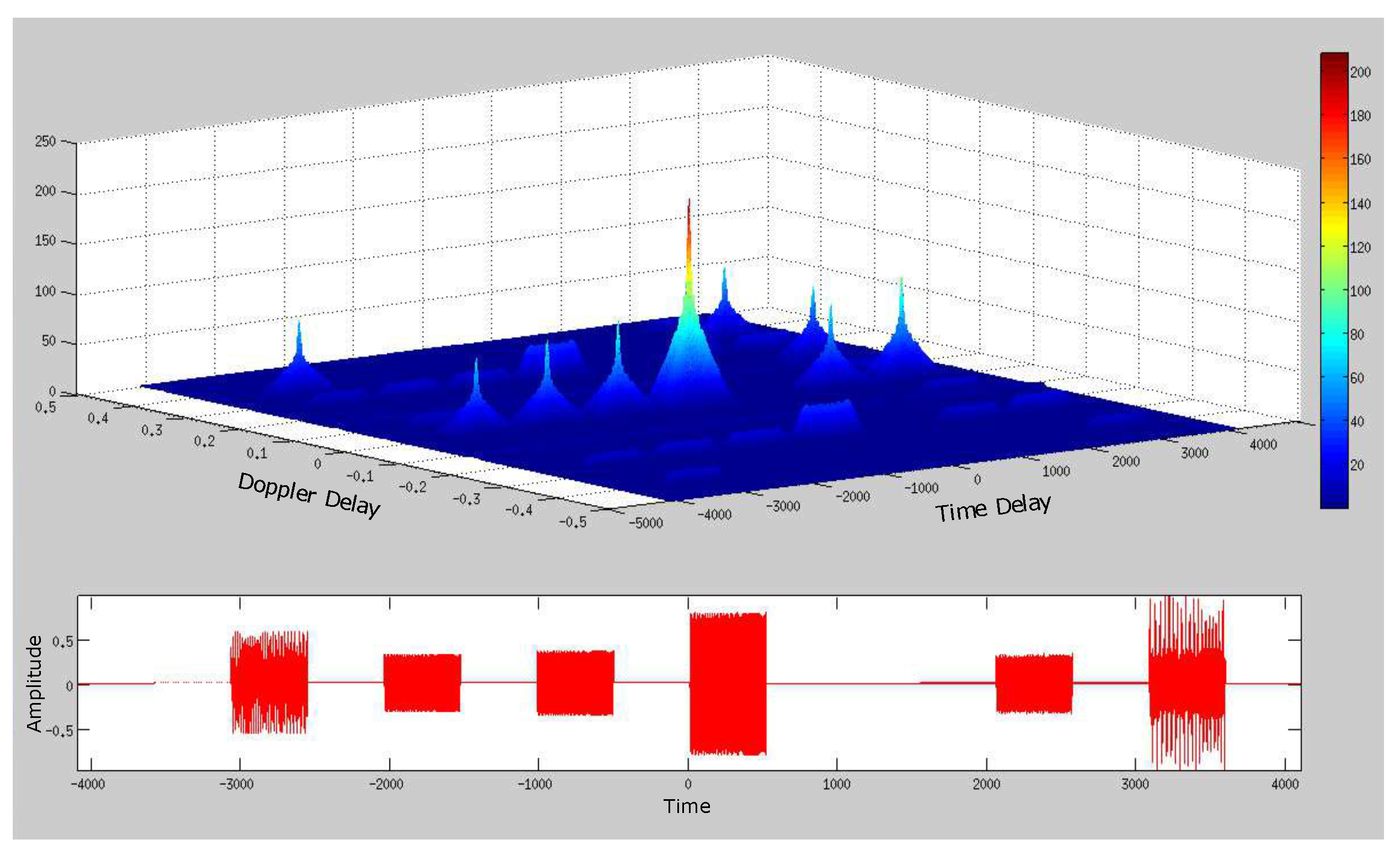
4.2. Deep Underwater Multiple Object Tracking Example
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Valera-Marquez, J. An Information-Based Complexity Approach to Acoustic Linear Stochastic Time-Variant Systems; ProQuest Dissertations and Theses; ProQuest: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Ray, S.; Lai, W.; Paschalidis, I.C. Statistical Location Detection with Sensor Networks. IEEE Trans. Inf. Theory 2006, 52, 2670–2683. [Google Scholar] [CrossRef]
- Karoui, I.; Quidu, I.; Legris, M. Automatic Sea-Surface Obstacle Detection and Tracking in Forward-Looking Sonar Image Sequences. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4661–4669. [Google Scholar] [CrossRef]
- Kreucher, C.; Shapo, B. Multitarget Detection and Tracking Using Multisensor Passive Acoustic Data. IEEE J. Ocean. Eng. 2011, 36, 205–218. [Google Scholar] [CrossRef]
- Daley, R.K.; Williams, A.; Green, M.; Barker, B.; Brodie, P. Can marine reserves conserve vulnerable sharks in the deep sea? A case study of Centrophorus zeehaani (Centrophoridae), examined with acoustic telemetry. Deep Sea Res. Part II Top. Stud. Oceanogr. 2015, 115, 127–136. [Google Scholar] [CrossRef]
- Qi, C.; Wang, X.; Wu, L. Underwater acoustic channel estimation based on sparse recovery algorithms. IET Signal Process. 2011, 5, 739–747. [Google Scholar] [CrossRef]
- Li, W.; Preisig, J. Estimation of Rapidly Time-Varying Sparse Channels. IEEE J. Ocean. Eng. 2007, 32, 927–939. [Google Scholar] [CrossRef]
- Johnson, J.R.; Johnson, R.W.; Rodriguez, D.; Tolimieri, R. A Methodology for Designing, Modifying, and Implementing Fourier Transform Algorithms on Various Architectures. Circ. Syst. Signal Process. 1990, 9, 449–500. [Google Scholar] [CrossRef]
- Carrascosa, P.C.; Stojanovic, M. Adaptive Channel Estimation and Data Detection for Underwater Acoustic MIMO-OFDM Systems. IEEE J. Ocean. Eng. 2010, 35, 635–646. [Google Scholar] [CrossRef]
- Li, B.; Huang, J.; Zhou, S.; Ball, K.; Stojanovic, M.; Freitag, L.; Willett, P. MIMO-OFDM for High-Rate Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2009, 34, 634–644. [Google Scholar]
- Yatawatta, S.; Petropulu, A.P. Blind channel estimation in MIMO OFDM systems with multiuser interference. IEEE Trans. Signal Process. 2006, 54, 1054–1068. [Google Scholar] [CrossRef]
- Van Loan, C. Computational Frameworks for the Fast Fourier Transform; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Franchetti, F.; Voronenko, Y.; Puschel, M. FFT Program Generation for Shared Memory: SMP and Multicore. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006; p. 51.
- Ali, A.; Johnsson, L.; Subhlok, J. Scheduling FFT Computation on SMP and Multicore Systems. In Proceedings of the 21st Annual International Conference on Supercomputing, Seattle, WA, USA, 17–21 June 2007; pp. 293–301.
- Arce-Nazario, R.A.; Jiménez, M.; Rodríguez, D. Mapping of Discrete Cosine Transforms onto Distributed Hardware Architectures. J. Signal Process. Syst. 2008, 53, 367–382. [Google Scholar] [CrossRef]
- Franchetti, F.; Puschel, M.; Voronenko, Y.; Chellappa, S.; Moura, J. Discrete Fourier Transform on Multicore. IEEE Signal Process. Mag. 2009, 26, 90–102. [Google Scholar] [CrossRef]
- Kepner, J. Parallel Matlab for Multicore and Multinode Computers. Software, Environments, and Tools; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2009; Volume 21. [Google Scholar]
- Bello, P. Characterization of Randomly Time-Variant Linear Channels. IEEE Trans. Commun. Syst. 1963, 11, 360–393. [Google Scholar] [CrossRef]
- Sandberg, J.; Hansson-Sandsten, M. Optimal Stochastic Discrete Time-Frequency Analysis in the Ambiguity and Time-Lag Domain. Signal Process. 2010, 90, 2203–2211. [Google Scholar] [CrossRef]
- Amini, P.; Chen, R.R.; Farhang-Boroujeny, B. Filterbank Multicarrier Communications for Underwater Acoustic Channels. IEEE J. Ocean. Eng. 2015, 40, 115–130. [Google Scholar] [CrossRef]
- Han, J.; Zhang, L.; Leus, G. Partial FFT Demodulation for MIMO-OFDM Over Time-Varying Underwater Acoustic Channels. IEEE Signal Process. Lett. 2016, 23, 282–286. [Google Scholar] [CrossRef]
- Wang, W.Q. MIMO SAR OFDM Chirp Waveform Diversity Design With Random Matrix Modulation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1615–1625. [Google Scholar] [CrossRef]
- Cheng, S.J.; Wang, W.Q.; Shao, H.Z. Spread Spectrum-Coded OFDM Chirp Waveform Diversity Design. IEEE Sens. J. 2015, 15, 5694–5700. [Google Scholar] [CrossRef]
- He, X.; Song, R.; Zhu, W.P. Pilot Allocation for Distributed-Compressed-Sensing-Based Sparse Channel Estimation in MIMO-OFDM Systems. IEEE Trans. Veh. Technol. 2016, 65, 2990–3004. [Google Scholar] [CrossRef]
- Duarte, M.F.; Baraniuk, R.G. Kronecker Compressive Sensing. IEEE Trans. Image Process. 2012, 21, 494–504. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Gil, G.T.; Lee, Y.H. Channel Estimation via Orthogonal Matching Pursuit for Hybrid MIMO Systems in Millimeter Wave Communications. IEEE Trans. Commun. 2016, 64, 2370–2386. [Google Scholar] [CrossRef]
- Kuck, D.J. High Performance Computing: Challenges for Future Systems; Oxford University Press, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. MIMO Radar Ambiguity Properties and Optimization Using Frequency-Hopping Waveforms. IEEE Trans. Signal Process. 2008, 56, 5926–5936. [Google Scholar] [CrossRef]
- Brookner, E. MIMO radars and their conventional equivalents. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 7–15.
- Pailhas, Y.; Petillot, Y. MIMO sonar systems for harbour surveillance. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–6.

| Algorithms | RTVSC | UWA-MIMO | BCE-MIMO | MOT-MIMO | |
|---|---|---|---|---|---|
| Features | |||||
| Authors | Li, W. | Carrascosa, P.C. | Yatawatta, S. | Rodriguez, D.; Aceros, C.; | |
| Preisig, J.C. | Stojanovic, M. | Petropulu, A. | Valera, J.; Anaya, E. | ||
| Reference | [7] | [9] | [11] | Proposed Work | |
| MIMO | × | ✓ | ✓ | ✓ | |
| Formulation | |||||
| Tracking | ✓ | ✓ | × | ✓ | |
| Capability | |||||
| Kronecker | ✓ | × | ✓ | ✓ | |
| Products | |||||
| Formulation | |||||
| MIMO Parallel | × | × | × | ✓ | |
| Algorithm | |||||
| Implementation | |||||
| MP Variant | Alg.Type | Computational Complexity |
|---|---|---|
| Basic MP | Greedy | |
| Orthogonal MP | Greedy | |
| Order Recur-sive LS-MP | Greedy | |
| Direct Computation | Pseudo Inverse |
| 512 | OLS0 | OLS1 | pOLS | OMP0 | OMP1 | pOMP | BMP0 | BMP1 | pBMP |
|---|---|---|---|---|---|---|---|---|---|
| SERIAL | 2.0459 | 2.0459 | 0.1913 | 0.1913 | 0.0585 | 0.0585 | |||
| 2-RANK | 0.9854 | 1.1937 | 1.0895 | 0.0842 | 0.1456 | 0.1149 | 0.0250 | 0.0324 | 0.0287 |
| 1024 | |||||||||
| SERIAL | 3.1667 | 3.1667 | 0.3677 | 0.3677 | 0.2100 | 0.2100 | |||
| 2-RANK | 1.6191 | 1.7272 | 1.6732 | 0.1877 | 0.2472 | 0.2175 | 0.1027 | 0.1172 | 0.1100 |
| 2048 | |||||||||
| SERIAL | 5.8147 | 5.8147 | 0.7511 | 0.7511 | 0.5094 | 0.5094 | |||
| 2-RANK | 2.9301 | 3.2614 | 3.0957 | 0.3816 | 0.4490 | 0.4153 | 0.3071 | 0.2832 | 0.2951 |
| 4096 | |||||||||
| SERIAL | 11.1109 | 11.1109 | 1.6114 | 1.6114 | 1.1871 | 1.1871 | |||
| 2-RANK | 5.4598 | 4.7954 | 5.1276 | 0.8156 | 0.8180 | 0.8168 | 0.6734 | 0.4850 | 0.5792 |
| 8192 | |||||||||
| SERIAL | 26.6413 | 26.6413 | 2.9315 | 2.9315 | 2.0470 | 2.0470 | |||
| 2-RANK | 18.4396 | 14.4820 | 16.4608 | 1.8021 | 1.5759 | 1.6890 | 1.2033 | 1.0748 | 1.1390 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, D.; Aceros, C.; Valera, J.; Anaya, E. A Framework for Multiple Object Tracking in Underwater Acoustic MIMO Communication Channels. J. Sens. Actuator Netw. 2017, 6, 2. https://doi.org/10.3390/jsan6010002
Rodriguez D, Aceros C, Valera J, Anaya E. A Framework for Multiple Object Tracking in Underwater Acoustic MIMO Communication Channels. Journal of Sensor and Actuator Networks. 2017; 6(1):2. https://doi.org/10.3390/jsan6010002
Chicago/Turabian StyleRodriguez, Domingo, Cesar Aceros, Juan Valera, and Edwin Anaya. 2017. "A Framework for Multiple Object Tracking in Underwater Acoustic MIMO Communication Channels" Journal of Sensor and Actuator Networks 6, no. 1: 2. https://doi.org/10.3390/jsan6010002
APA StyleRodriguez, D., Aceros, C., Valera, J., & Anaya, E. (2017). A Framework for Multiple Object Tracking in Underwater Acoustic MIMO Communication Channels. Journal of Sensor and Actuator Networks, 6(1), 2. https://doi.org/10.3390/jsan6010002





