Key Management in Wireless Sensor Networks
Abstract
:1. Introduction
1.1. Contributions
1.2. Related Work
| Proposed Schemes | Standard Algorithms | Cryptographic Technique | Simulation | Implementation | Verification |
|---|---|---|---|---|---|
| Chan et al. 2003 [22] | not specified | symmetric | none | none | none |
| Chan et al. 2005 [21] | not specified | symmetric | none | none | none |
| Chattopadhyay et al. 2012 [23] | not specified | symmetric | none | none | none |
| Chuang et al. 2010 [26] | yes | asymmetric | none | none | none |
| Dini et al. 2006 [25] | not specified | symmetric | none | none | none |
| Jiang et al. 2008 [24] | not specified | symmetric | none | none | none |
| Jolly et al. 2003 [31] | not specified | symmetric | yes | none | none |
| Purohit et al. 2011 [28] | not specified | symmetric | none | none | none |
| Wang et al. 2006 [29] | none | symmetric | none | none | none |
| Wang et al. 2010 [30] | not specified | symmetric | yes | none | none |
| Wang et al. 2007 [27] | not specified | symmetric | yes | none | none |
| All of our schemes | yes | symmetric/asymmetric | none | TelosB | automatic |
1.3. Outline
2. Authenticated Join Protocols
2.1. Cryptographic Primitives and Notations
- I: a new node that initiates the protocol,
- R: a neighbor of node I,
- S: the sink of the network (also called the base station),
- : a nonce generated by node A,
- : the encryption of message x with the symmetric or asymmetric key k,
- : the public key of node A,
- : the secret (private) key of node A,
- or : the symmetric session key between I and S,
- : the symmetric network key between all nodes of the network,
- or : the shared symmetric key between N and S using the Diffie–Hellman key exchange without the interaction described below.
- The sink knows its own secret key and the public key of any node N. The sink computes .
- Node N multiplies its secret key by the public key of the sink to get .
2.2. Join Protocols (DJS and IJS)

3. Renewal and Revocation Protocols
3.1. Key Revocation Protocol
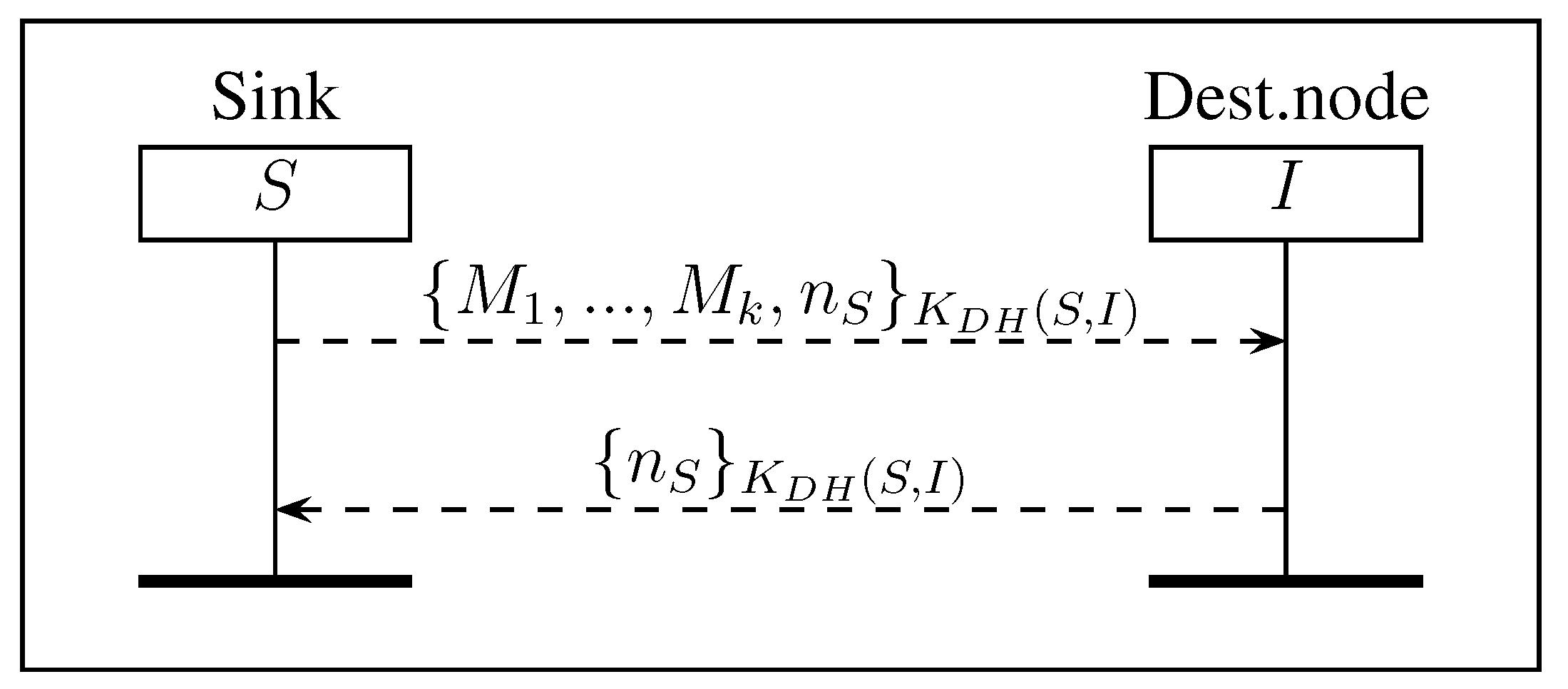
3.2. Renewing Symmetric Keys

| Protocol | Name | Figure | Time with S (ms) | Time without S (ms) | Gain | Standard Deviation (ms) |
|---|---|---|---|---|---|---|
| Join Protocols [11] | DJS | 1a | 10,112.62 | 04082.05 | 59% | 078.09 |
| IJS | 1b | 10,180.81 | 10,049.45 | 01% | 111.94 | |
| Revocation | KR | 2 | 00155.37 | 00087.58 | 44% | 003.82 |
| Renewing SymKey | RSK | 3 | 10,042.32 | 10,042.32 | 00% | 076.49 |
| Renewing AsymKey | RAKnk | 4a | 06797.75 | 03436.24 | 49% | 004.26 |
| RAKnk | 4b | 003646.05 | 00254.62 | 93% | 003.95 | |
| RAKdh | 5a | 06797.75 | 03436.24 | 49% | 004.26 | |
| RAKdh | 5b | 003646.05 | 00254.62 | 93% | 003.95 | |
| Renewing Network Key | RNK | 6 | 00221.09 | 00121.40 | 45% | 003.73 |
| Multihop Shared Key | MSK | 7a | 06893.76 | 06631.91 | 04% | 005.76 |
| MSK | 7b | 03682.53 | 00301.42 | 91% | 005.25 |
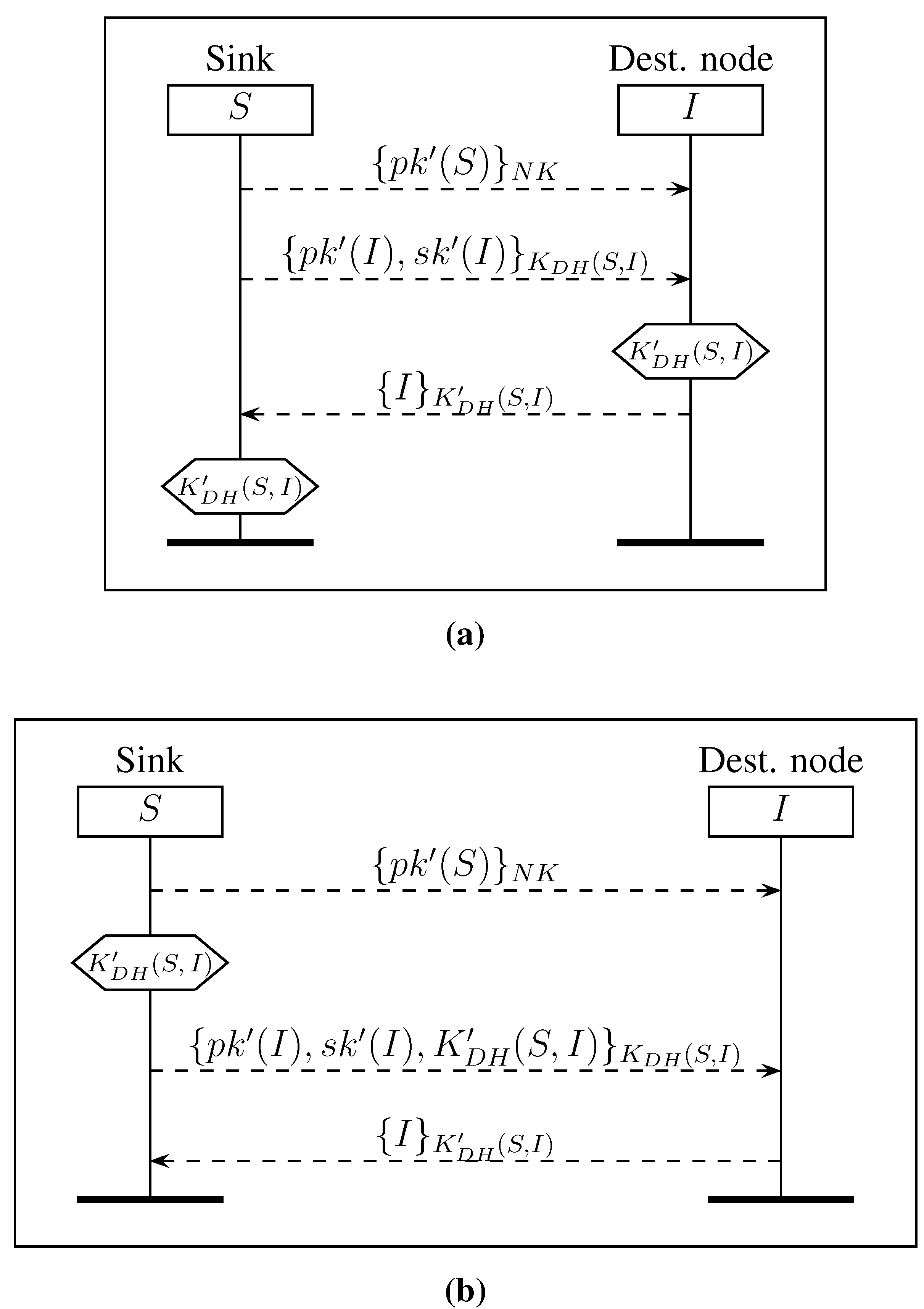
3.3. Renewing Asymmetric Keys

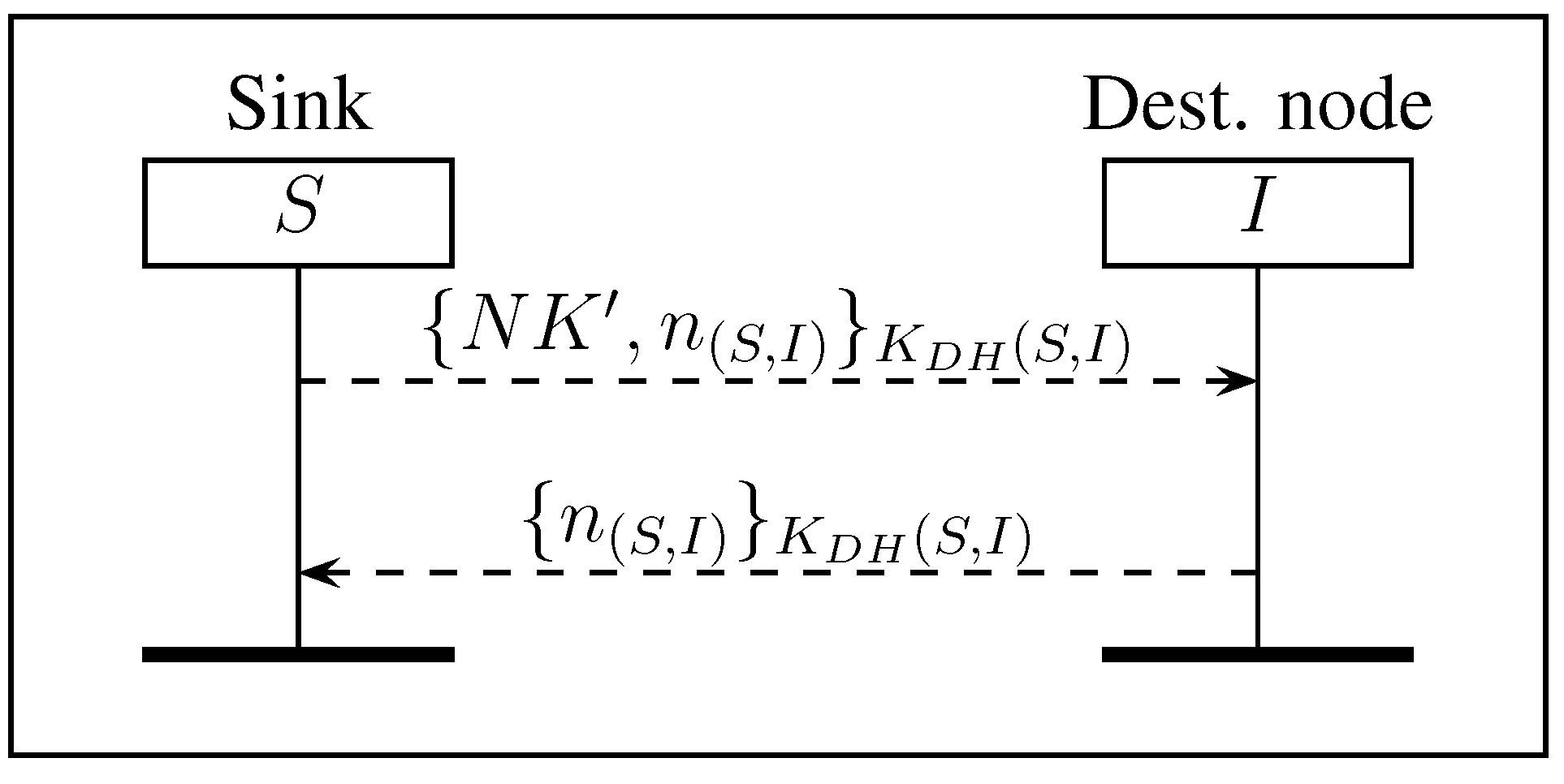
3.4. Renewing the Network Key
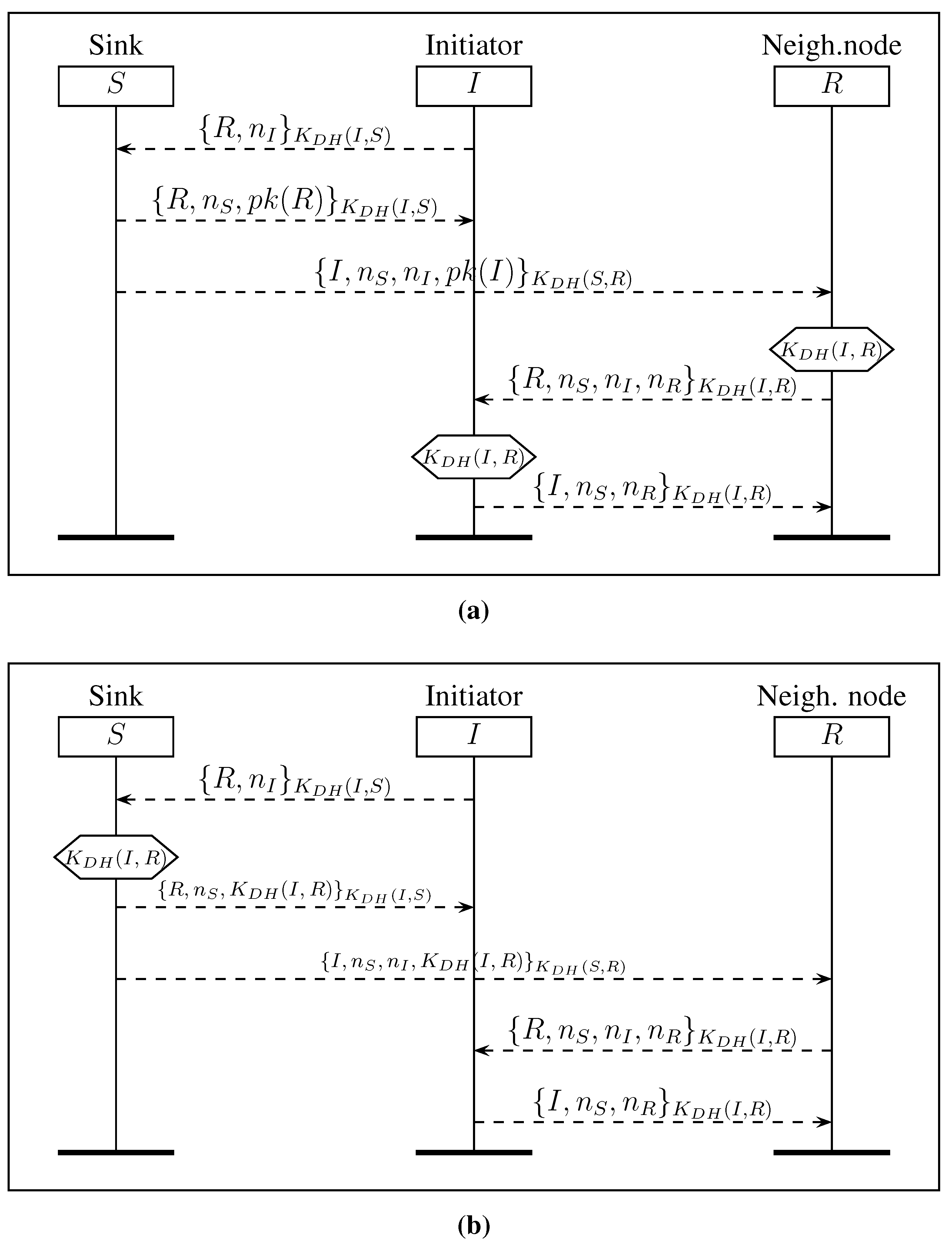
3.5. Multihop Shared Key Protocol
- to I, the identity of R, a nonce , the public key of R encrypted with the shared symmetric key ,
- to R, the identity of I, the same nonce , the nonce received from I and the public key of I encrypted with the shared symmetric key .
- Node I computes .
- Node R computes .
4. Key and Protocol Dependency
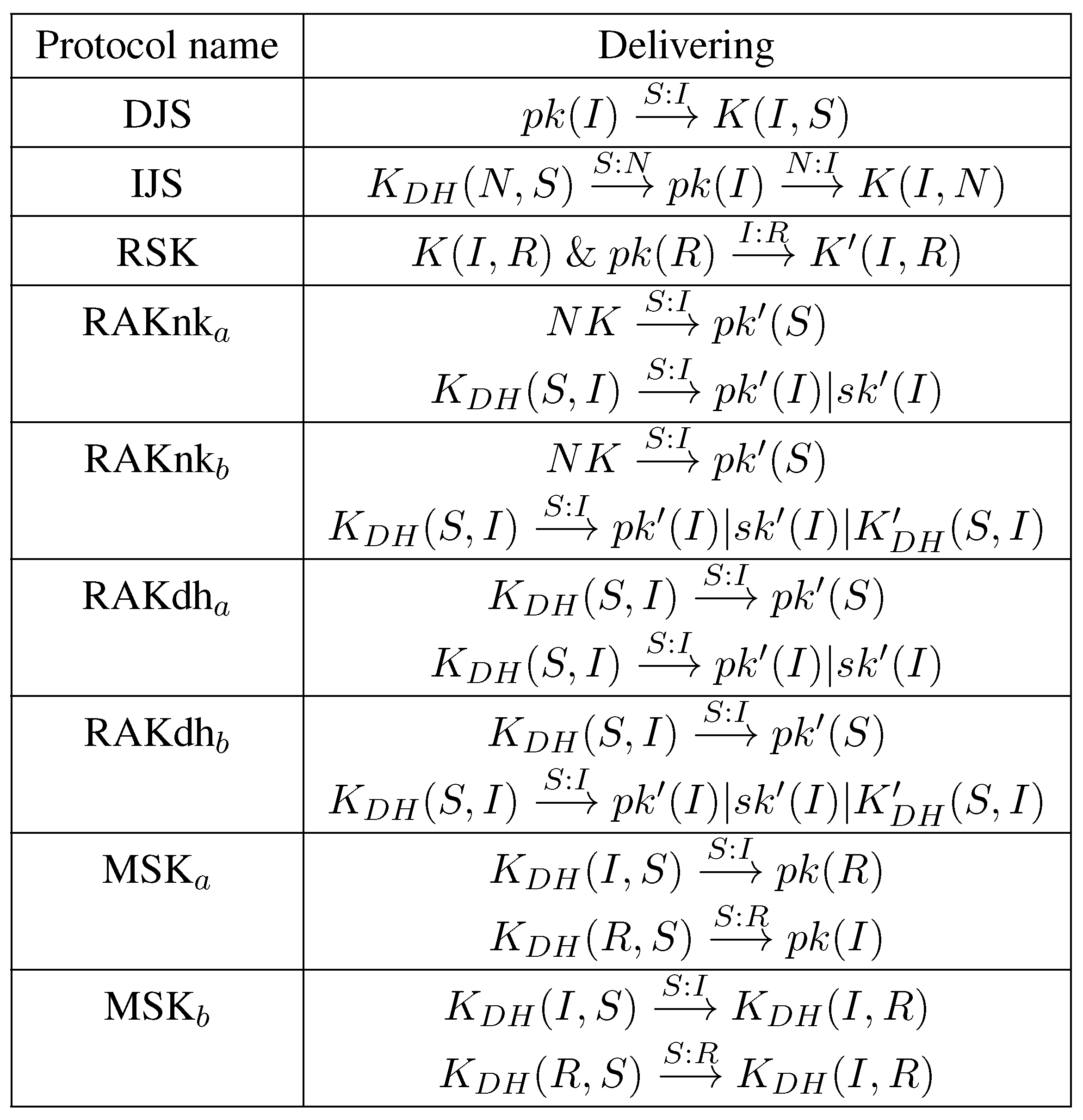
5. Formal Security Evaluation
5.1. Scyther Overview
5.2. Security Analysis
6. Experiments
6.1. Settings
6.2. Results and Discussion
7. Conclusions and Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hussain, M.A.; Khan, P.; Sup, K.K. WSN research activities for military application. In Proceedings of the 11th International Conference on Advanced Communication Technology, Phoenix Park, Korea, 15–18 February 2009; Volume 1, pp. 271–274.
- Debar, H.; Dacier, M.; Wespi, A. Towards a taxonomy of intrusion-detection systems. Comput. Netw. 1999, 31, 805–822. [Google Scholar] [CrossRef]
- Sun, B.; Osborne, L.; Xiao, Y.; Guizani, S. Intrusion detection techniques in mobile ad hoc and wireless sensor networks. IEEE Wirel. Commun. 2007, 14, 56–63. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. ACM Commun. 1978, 21, 120–126. [Google Scholar] [CrossRef]
- El Gamal, T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Eisenbarth, T.; Kumar, S.; Uhsadel, L.; Paar, C.; Poschmann, A. A Survey of Lightweight-Cryptography Implementations. IEEE Des. Test Comput. 2007, 24, 522–533. [Google Scholar] [CrossRef]
- Cazorla, M.; Marquet, K.; Minier, M. Survey and Benchmark of Lightweight Block Ciphers for Wireless Sensor Networks. In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT 2013), Reykjavík, Iceland, 29–31 July 2013; pp. 543–548.
- Jeong, K.; Lee, C.; Lim, J. Improved differential fault analysis on lightweight block cipher LBlock for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2013, 2013. [Google Scholar] [CrossRef]
- Couroussé, D.; Robisson, B.; Lanet, J.; Barry, T.; Noura, H.; Jaillon, P.; Lalevée, P. COGITO: Code Polymorphism to Secure Devices. In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT 2014), Vienna, Austria, 28–30 August 2014; pp. 451–456.
- Zhang, J.; Varadharajan, V. Wireless sensor network key management survey and taxonomy. J. Netw. Comput. Appl. 2010, 33, 63–75. [Google Scholar] [CrossRef]
- Mansour, I.; Chalhoub, G.; Misson, M. Security architecture for multi-hop wireless sensor networks. In Security for Multihop Wireless Networks; CRC Press: Boca Raton, FL, USA, 2014; pp. 157–178. [Google Scholar]
- Cremers, C. The Scyther Tool: Verification, Falsification, and Analysis of Security Protocols. In Proceedings of the 20th International Conference on Computer Aided Verification, Princeton, NJ, USA, 7–14 July 2008; pp. 414–418.
- Mansour, I.; Chalhoub, G.; Lafourcade, P.; Delobel, F. Secure Key Renewal and Revocation for Wireless Sensor Networks. In Proceedings of the 39th IEEE Conference on Local Computer Networks (LCN), Edmonton, AB, Cananda, 8–11 September 2014; pp. 382–385.
- Mansour, I.; Chalhoub, G.; Lafourcade, P. Evaluation of Secure Multi-Hop Node Authentication and Key Establishment Mechanisms for Wireless Sensor Networks. J. Sens. Actuator Netw. 2014, 3, 224–244. [Google Scholar] [CrossRef]
- Mansour, I.; Chalhoub, G.; Lafourcade, P. Secure Multihop Key Establishment Protocols for Wireless Sensor Networks. In Proceedings of International Conference on Cryptography and Security Systems, Lublin, Poland, 22–24 September 2014; pp. 166–177.
- Mehta, M.; Huang, D.; Harn, L. RINK-RKP: A scheme for key predistribution and shared-key discovery in sensor networks. In Proceedings of the 24th IEEE International on Performance, Computing, and Communications Conference, Phoenix, AZ, USA, 7–9 April 2005; pp. 193–197.
- Park, J.; Kim, Z.; Kim, K. State-based key management scheme for wireless sensor networks. In Proceedings of IEEE International Conference on Mobile Adhoc and Sensor Systems, Washington, DC, USA, 7 November 2005.
- Park, J.; Kim, Z.; Kim, K. Random key assignment for secure wireless sensor networks. In Proceedings of the 1st ACM workshop on Security of Ad Hoc and Sensor Networks, Washington, DC, USA, 27–30 October 2003; pp. 62–71.
- Cheng, Y.; Malik, M.; Xie, B.; Agrawal, D. Enhanced Approach for Random Key Pre-Distribution in Wireless Sensor Networks. In Proceedings of International Conference on Communication, Networking and Information Technology, Amman, Jordan, 6–8 December 2007.
- Cheng, Y.; Agrawal, D. An Improved Key Distribution Mechanism for Large-Scale Hierarchical Wireless Networks Key Distribution. AD HOC Netw. J. 2007, 5, 35–48. [Google Scholar] [CrossRef]
- Chan, H.; Gligor, V.; Perrig, A.; Muralidharan, G. On the distribution and revocation of cryptographic keys in sensor networks. IEEE Trans. Dependable Secur. Comput. 2005, 2, 233–247. [Google Scholar] [CrossRef]
- Chan, H.; Perrig, A.; Song, D. Random key predistribution schemes for sensor networks. In Proceedings of IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 11–14 May 2003.
- Chattopadhyay, S.; Turuk, A.K. A Scheme for Key Revocation in Wireless Sensor Networks. Int. J. Adv. Comput. Eng. Commun. Technol. 2012, 1, 16–20. [Google Scholar]
- Jiang, Y.; Shi, H. A Cluster-Based Random Key Revocation Protocol for Wireless Sensor Networks. J. Electron. Sci. Technol. China 2008, 6, 10–15. [Google Scholar]
- Dini, G.; Savino, I. An efficient key revocation protocol for wireless sensor networks. In Proceedings of International Symposium on a World of Wireless, Mobile and Multimedia Networks, Buffalo, NY, USA, 26–29 June 2006.
- Chuang, P.; Chang, S.; Lin, C. A Node Revocation Scheme Using Public-Key Cryptography in Wireless Sensor Networks. J. Inf. Sci. Eng. 2010, 26, 1859–1873. [Google Scholar]
- Wang, Y.; Ramamurthy, B.; Zou, X. KeyRev: An Efficient Key Revocation Scheme for Wireless Sensor Networks. In Proceedings of International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 1260–1265.
- Purohit, G.N.; Rawat, A.S. Revocation and Self-Healing of keys in Hierarchical Wireless Sensor Network. Int. J. Comput. Sci. Inf. Technol. 2011, 2, 2909–2914. [Google Scholar]
- Wang, C.; Hong, T.; Horng, G.; Wang, W. A Key Renewal Scheme under the Power Consumption for Wireless Sensor Networks. In Proceedings of the 4th International Conference on Photonics, Networking and Computing, Kaohsiung, Taiwan, 8–11 October 2006.
- Wang, G.; Kim, S.; Kang, D.; Choi, D.; Cho, G. Lightweight Key Renewals for Clustered Sensor Networks. J. Netw. 2010, 5, 300–312. [Google Scholar] [CrossRef]
- Jolly, G.; Kusçu, M.; Kokate, P.; Younis, M. A Low-Energy Key Management Protocol for Wireless Sensor Networks. In Proceedings of the Eighth IEEE International Symposium on Computers and Communications, Kiris-Kemer, Turkey, 30 June–3 July 2003.
- Standards for Efficient Cryptography Group. SEC 1: Elliptic Curve Cryptography. Available online: http://www.secg.org/2000 (accessed on 26 August 2015).
- Liu, A.; Ning, N. TinyECC: A Configurable Library for Elliptic Curve Cryptography in Wireless Sensor Networks. In Proceedings of 7th International Conference on Information Processing in Sensor Networks, St. Louis, MI, USA, 22–24 April 2008; pp. 245–256.
- Shoup, V. A Proposal for an ISO Standard for Public Key Encryption. IACR Cryptology ePrint Archive: Report 2001/112. Available online: http://eprint.iacr.org/2001/112 (accessed on 26 August 2015).
- Daemen, J.; Rijmen, V. The Design of Rijndael: AES—The Advanced Encryption Standard; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Manica, N.; Saloni, M.; Toldo, P. WSN—Secure comunications with AES algoritms. Faculty of Computer Science, University of Trento: Trento, Italy, 2008. [Google Scholar]
- Blake, I.F.; Seroussi, G.; Smart, N.P. Elliptic Curves in Cryptography; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Miller, V.S. Use of Elliptic Curves in Cryptography; Springer-Verlag New York, Inc.: New York, NY, USA, 1986; pp. 417–426. [Google Scholar]
- Meadows, C.; Poovendran, R.; Pavlovic, D.; Chang, L.; Syverson, P.F. Distance Bounding Protocols: Authentication Logic Analysis and Collusion Attacks. In Secure Localization and Time Synchronization for Wireless Sensor and Ad Hoc Networks; Poovendran, R., Roy, S., Wang, C., Eds.; Springer: Berlin, Germany, 2007; Volume 30, pp. 279–298. [Google Scholar]
- Arnaud, M.; Cortier, V.; Delaune, S. Modeling and Verifying Ad Hoc Routing Protocols. Inf. Comput. 2010, 238, 30–67. [Google Scholar] [CrossRef]
- Pura, M.L.; Patriciu, V.V.; Bica, I. Formal Verification of Secure Ad Hoc Routing Protocols Using AVISPA: ARAN Case Study. In Proceedings of the 4th Conference on European Computing Conference, Bucharest, Romania, 20–22 April 2010; pp. 200–206.
- Armando, A.; Basin, D.; Boichut, Y.; Chevalier, Y.; Compagna, L.; Cuellar, J.; Drielsma, P.H.; Heám, P.C.; Kouchnarenko, O.; Mantovani, J.; et al. The AVISPA Tool for the Automated Validation of Internet Security Protocols and Applications. In Proceedings of 17th International Conference, CAV 2005, Edinburgh, Scotland, UK, 6–10 July 2005; pp. 281–285.
- Blanchet, B. Automatic Proof of Strong Secrecy for Security Protocols. In Proceedings of IEEE Symposium on Security and Privacy, Oakland, CA, USA, 9–12 May 2004; pp. 86–100.
- Cremers, C.J.F.; Lafourcade, P.; Nadeau, P. Comparing State Spaces in Automatic Security Protocol Analysis. In Formal to Practical Security; Springer Berlin Heidelberg: Berlin, Germany, 2009; pp. 70–94. [Google Scholar]
- Mansour, I.; Lafourcade, P.; Chalhoub, G. Scyther code of our authentication protocols. Available online: http://sancy.univ-bpclermont.fr/~lafourcade/scyther-jsan-code.tar (accessed on 26 August 2015).
- Mansour, I.; Chalhoub, G. Evaluation of different cryptographic algorithms on wireless sensor network nodes. In Proceedings of International Conference on Wireless Communications in Unusual and Confined Areas, Clermont Ferrand, France, 28–30 August 2012; pp. 1–6.
- IoT-LAB. Available online: https://www.iot-lab.info/ (accessed on 26 August 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansour, I.; Chalhoub, G.; Lafourcade, P. Key Management in Wireless Sensor Networks. J. Sens. Actuator Netw. 2015, 4, 251-273. https://doi.org/10.3390/jsan4030251
Mansour I, Chalhoub G, Lafourcade P. Key Management in Wireless Sensor Networks. Journal of Sensor and Actuator Networks. 2015; 4(3):251-273. https://doi.org/10.3390/jsan4030251
Chicago/Turabian StyleMansour, Ismail, Gérard Chalhoub, and Pascal Lafourcade. 2015. "Key Management in Wireless Sensor Networks" Journal of Sensor and Actuator Networks 4, no. 3: 251-273. https://doi.org/10.3390/jsan4030251
APA StyleMansour, I., Chalhoub, G., & Lafourcade, P. (2015). Key Management in Wireless Sensor Networks. Journal of Sensor and Actuator Networks, 4(3), 251-273. https://doi.org/10.3390/jsan4030251





