Collaborative 3D Target Tracking in Distributed Smart Camera Networks for Wide-Area Surveillance
Abstract
:1. Introduction
- We define a target representation suitable for 3D tracking that includes the target state consisting of the position and orientation of the target in 3D space and the reference model consisting of multi-view feature histograms,
- We develop a probabilistic 3D tracker based on the target representation and implement the tracker based on sequential Monte Carlo methods,
- We develop and implement several variations of the base tracker that incur different computational and communication costs at each node, and produce different tracking accuracy. The variations include optimizations such as the use of mixture models, in-network aggregation and the use of image-plane based filtering where it is appropriate. We also present a qualitative comparison of the trackers according to their supported Quality-of-Service (QoS) and Quality-of-Information (QoI), and,
- We present quantitative evaluation of the trackers using synthetic targets in simulated camera networks, as well as using real targets (objects and people) in real-world camera network deployments. We also compare the proposed trackers with an implementation of a previous approach for 3D tracking, which is based on 3D ray intersection. The simulation results show robustness against target scale variation and rotation, while working within the bandwidth constraints.
2. Related Work
2.1. Feature Selection for Tracking
2.2. Target Tracking
2.3. Tracking with Camera Networks
3. Background
3.1. Target Representation
3.1.1. Target Model
3.1.2. Target Candidate
3.1.3. Similarity Measure
4. Probabilistic 3D Tracker
4.1. Target Representation
4.1.1. Target State
4.1.2. Target Model
4.1.3. Similarity Measure and Localization
4.1.4. Estimation of Target Orientation
4.2. Tracking Algorithm
4.2.1. Base Tracker (T0)
| Algorithm 1 Base tracker |
|
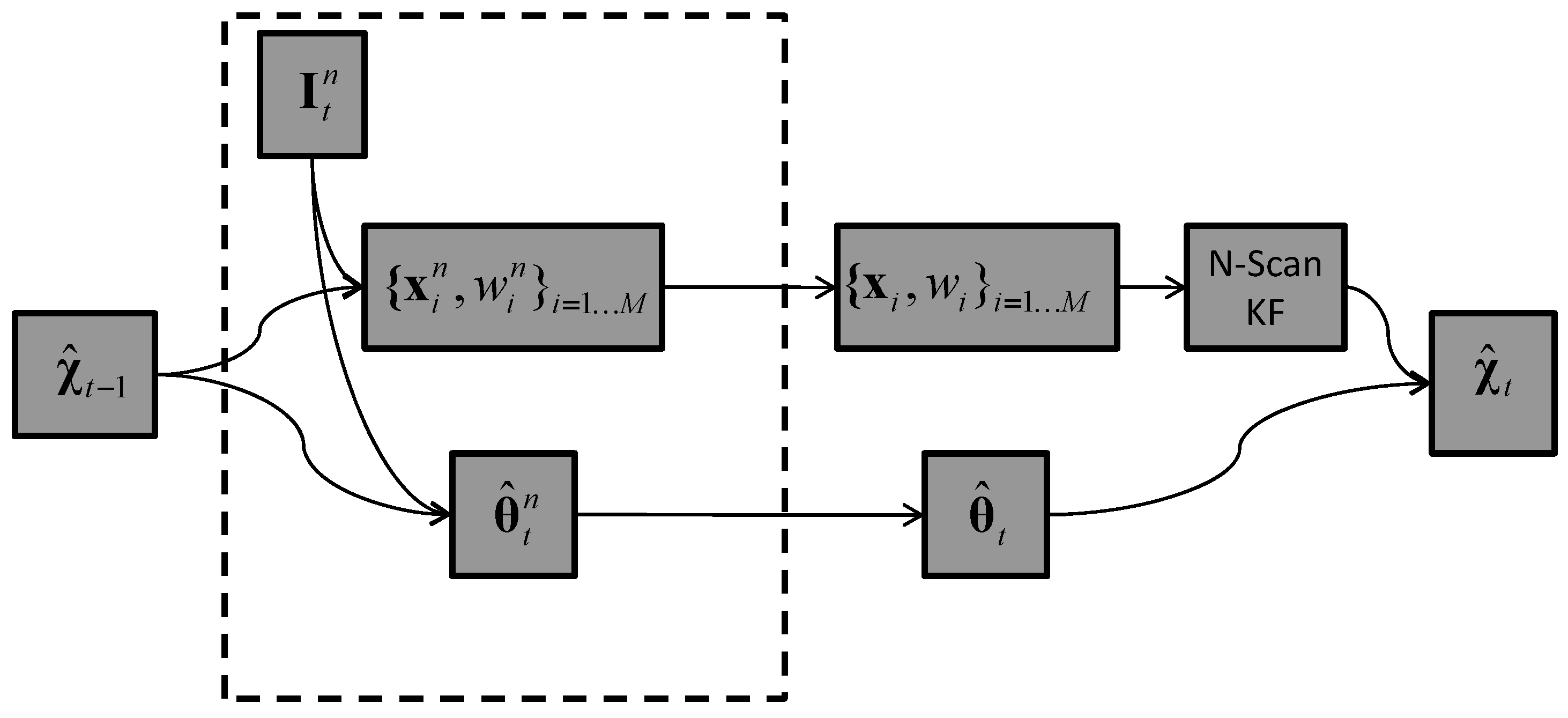
5. Tracker Variations
5.1. Tracker T1: 3D Kernel Density Estimate
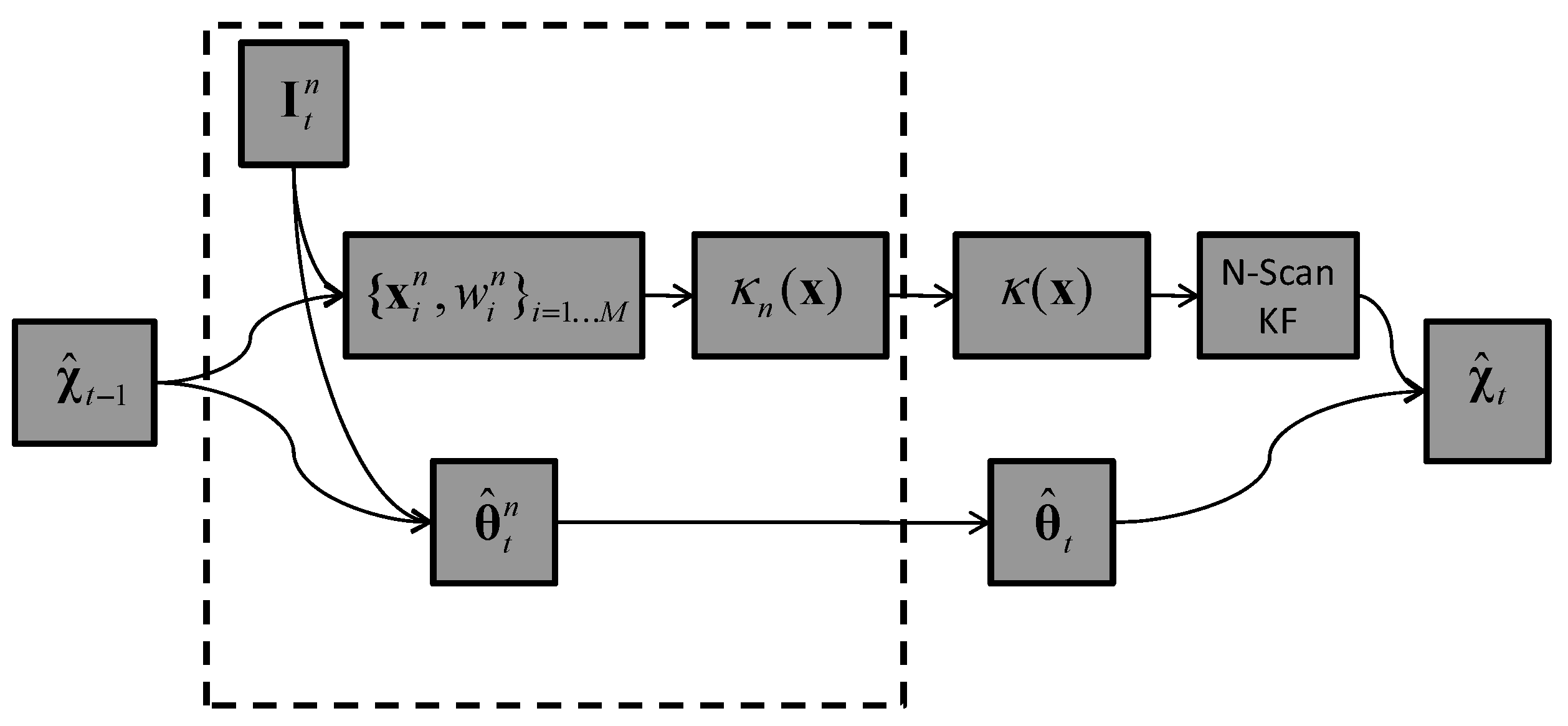
5.2. Tracker T2: In-Network Aggregation
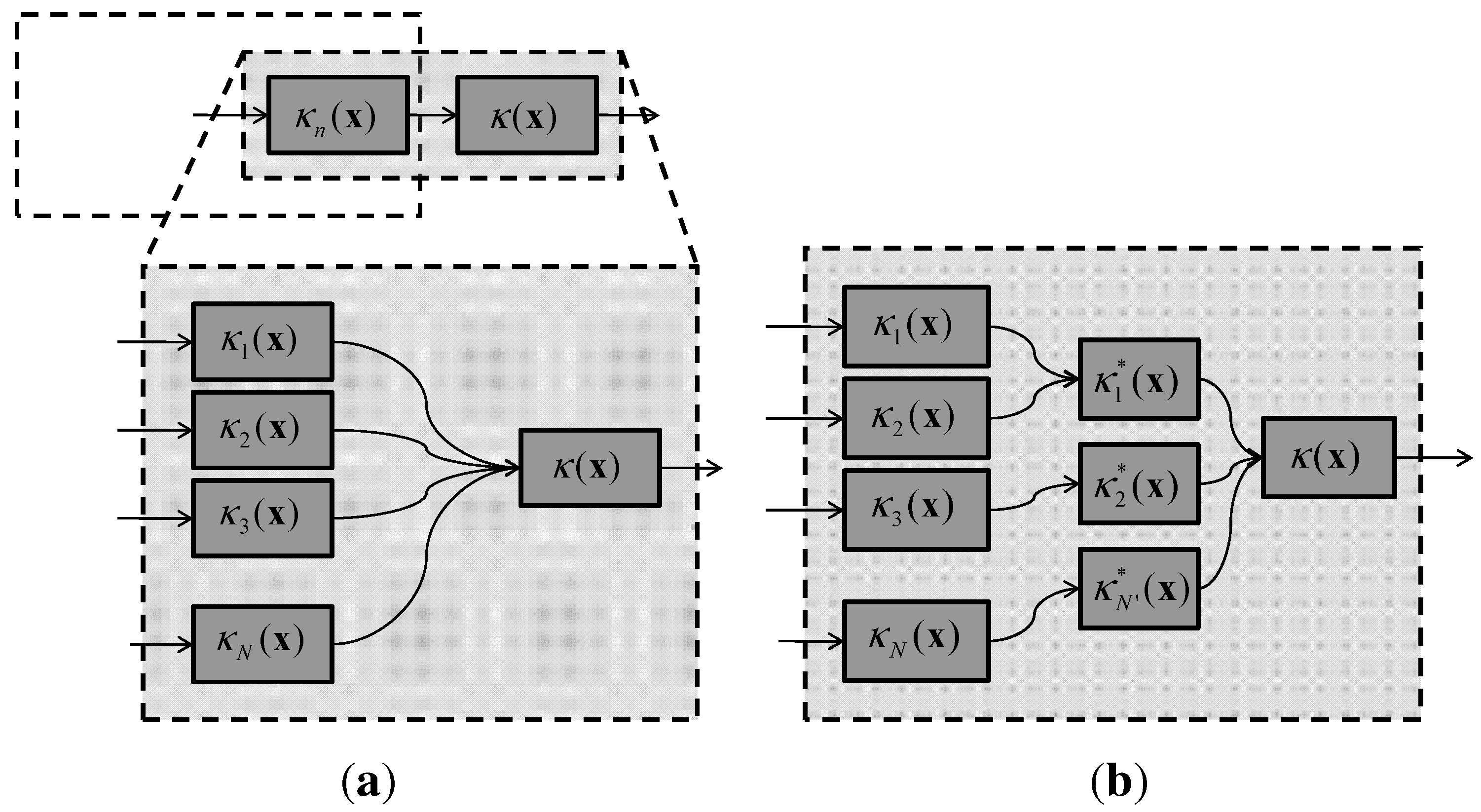
5.2.1. Step 1: Product of GMMs
5.2.2. Step 2: Model-Order Reduction
5.3. Tracker T3: Image-Plane Particle Filter & 3D Kernel Density
| Algorithm 2 T3 tracker |
|
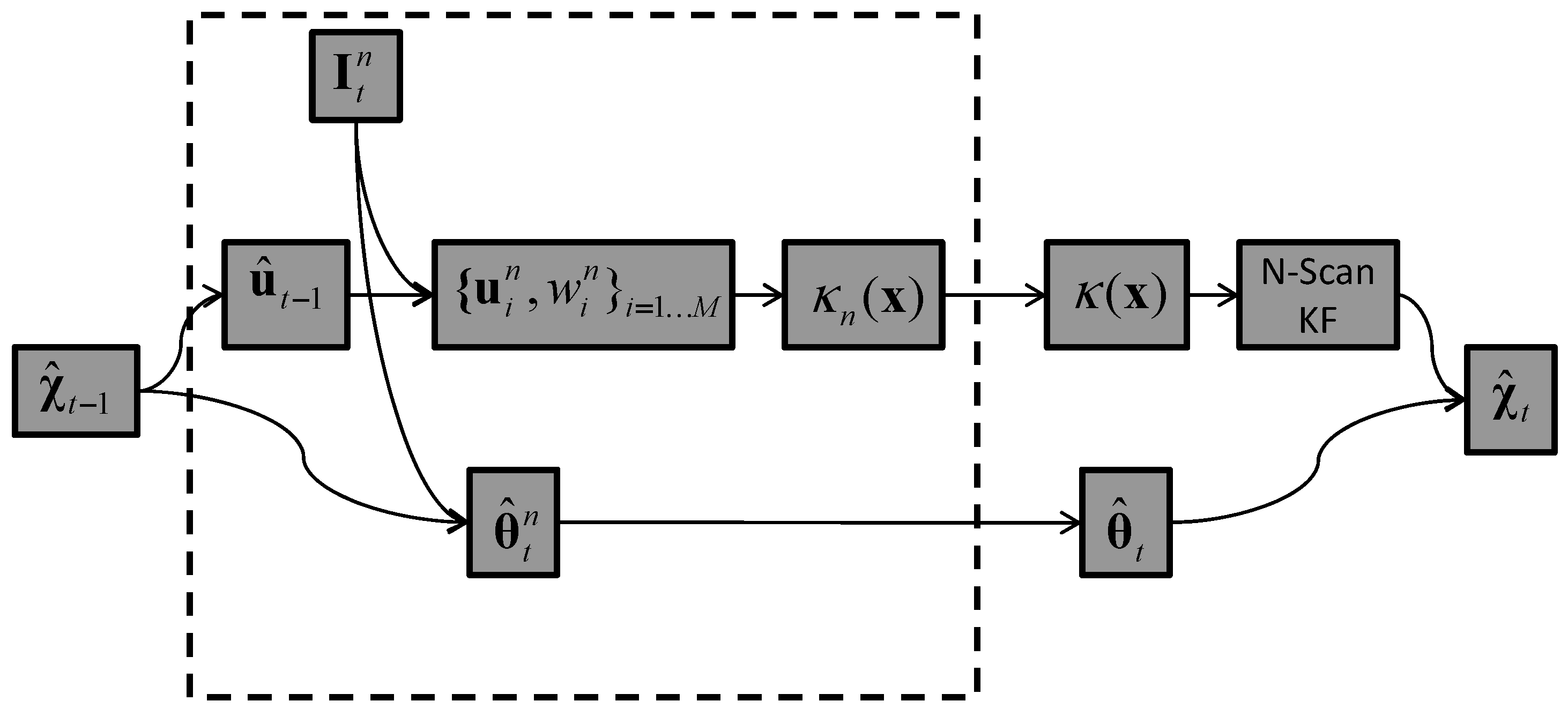
5.4. Tracker T4: Image-Plane Kernel Density
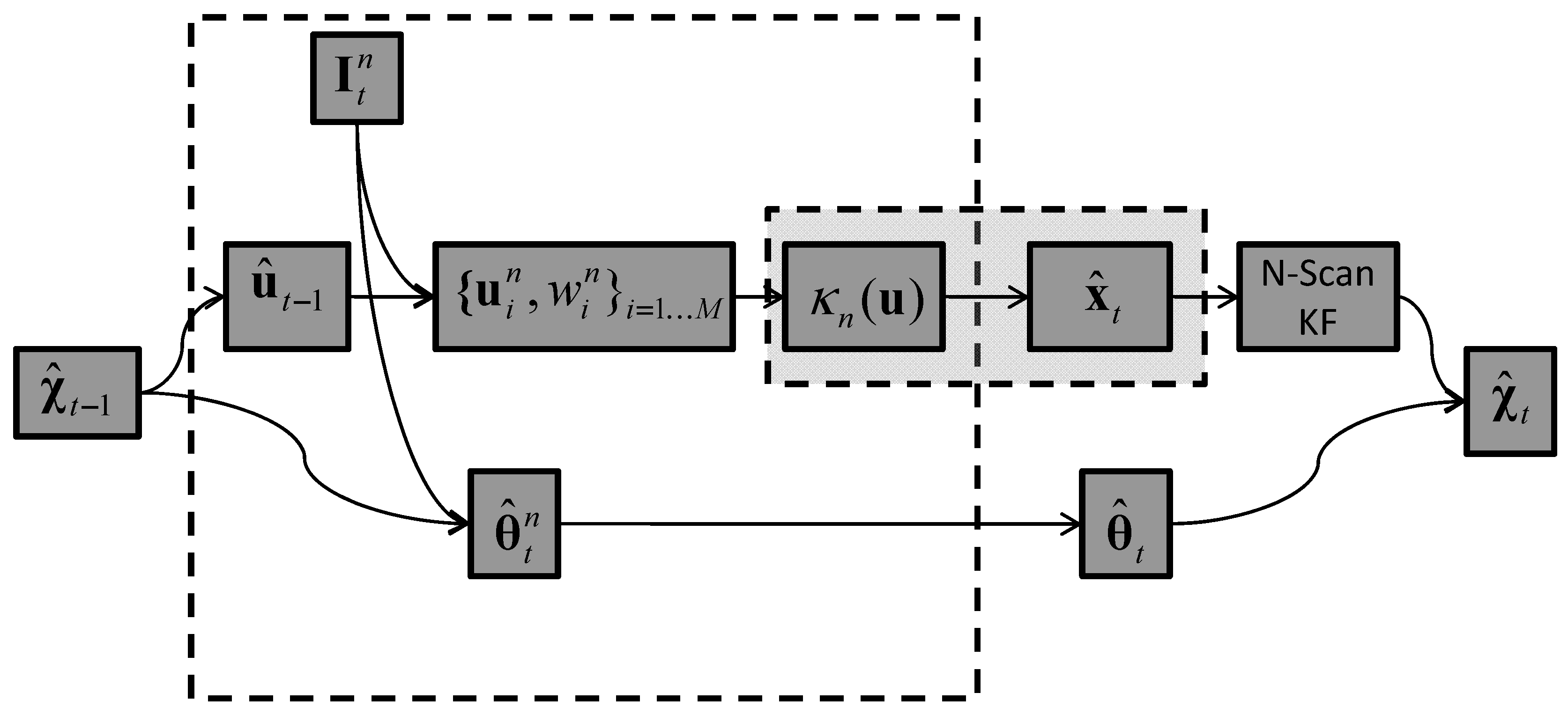
5.5. Comparison of All Trackers
| Tracker | Quality-of-Information (QoI) | Quality-of-Service (QoS) | Robustness to Target Size in Pixels | |
|---|---|---|---|---|
| tracking accuracy | number of particles | message size | ||
| (computational cost) | (communication cost) | |||
| Tracker P: | poor | low | low | no |
| (2D-to-3D) | ||||
| Base Tracker T0: | good | high | very high | yes |
| (Sync3DPF) | ||||
| Tracker T1: | medium | high | medium | yes |
| (3DPF & 3DKD) | ||||
| Tracker T2: | medium | high | low | yes |
| (3DPF & 3DKD & NetAggr) | ||||
| Tracker T3: | good | medium | low | no |
| (2DPF + 3DKD + NetAggr) | ||||
| Tracker T4: | good | medium | medium | no |
| (2DPF & 2DKD) | ||||
6. Performance Evaluation
6.1. Simulated Camera Network
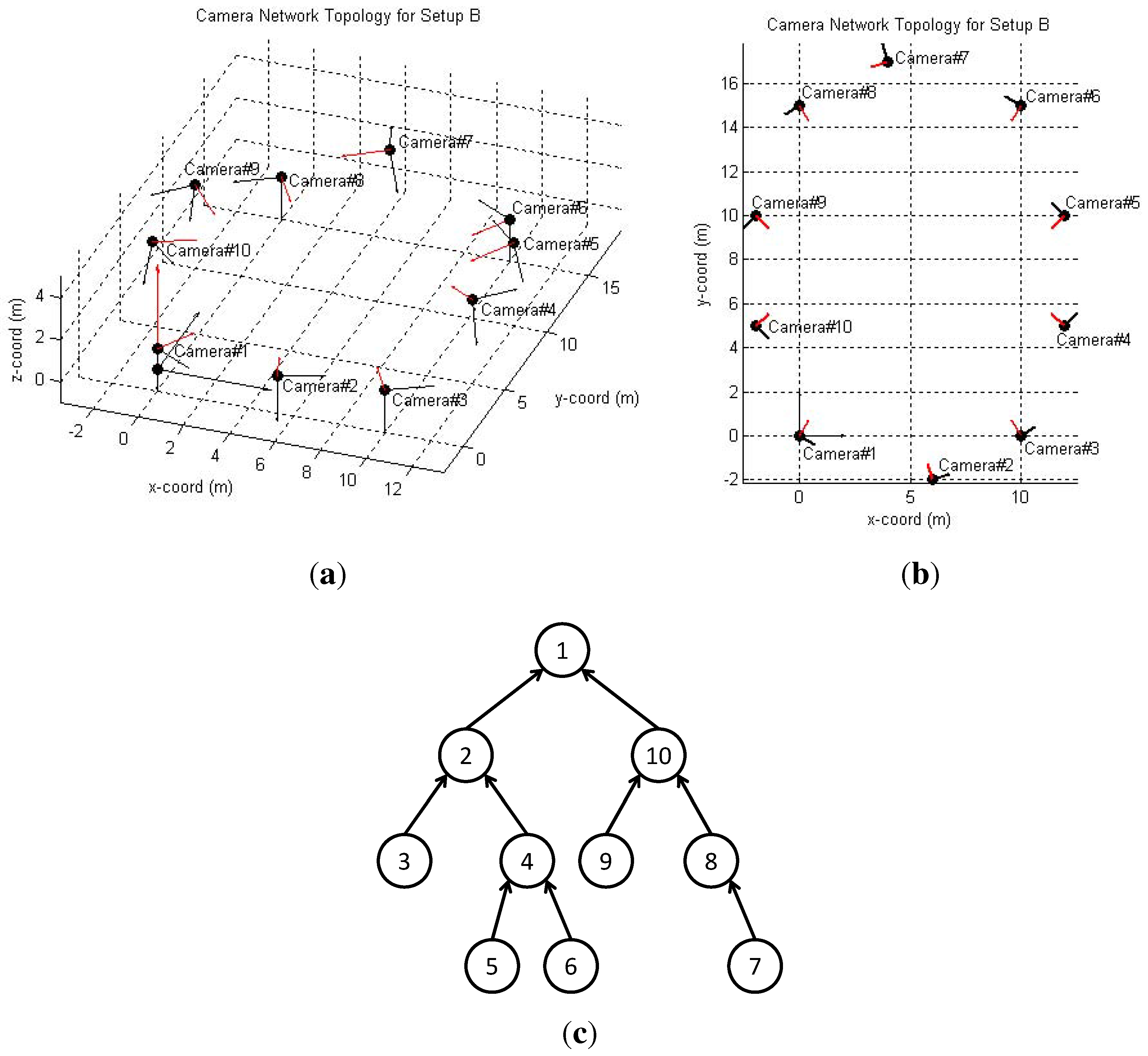


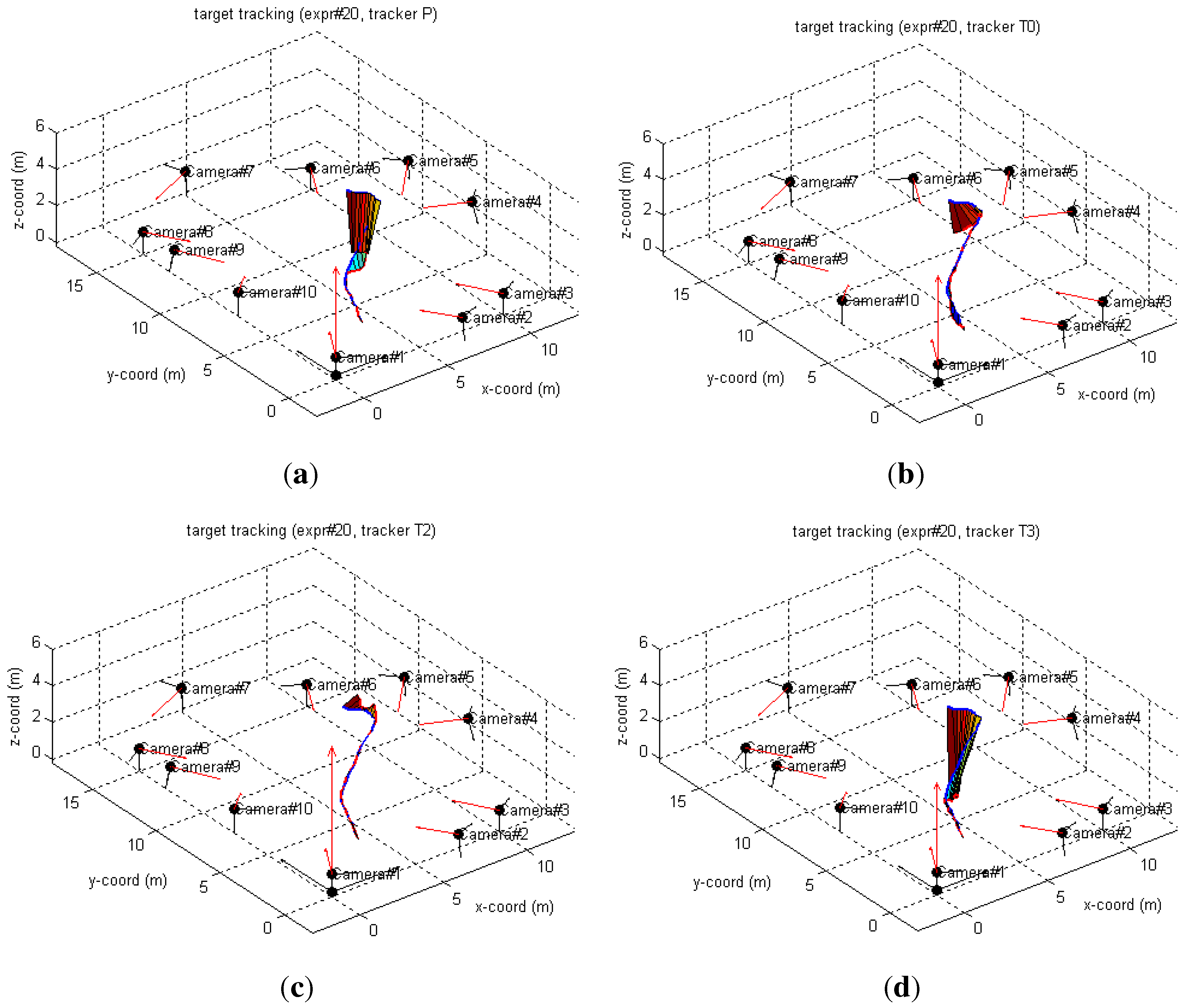
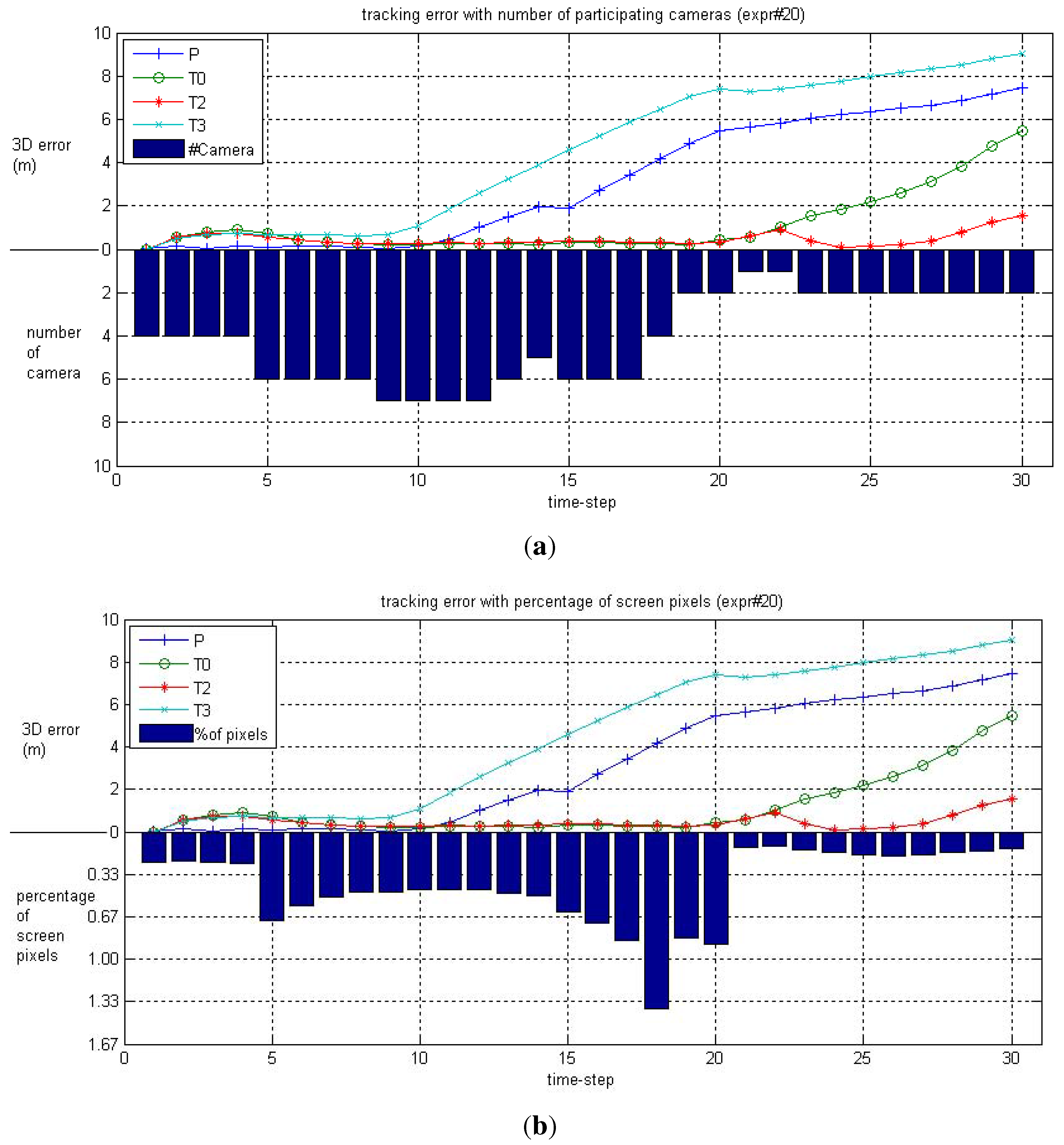
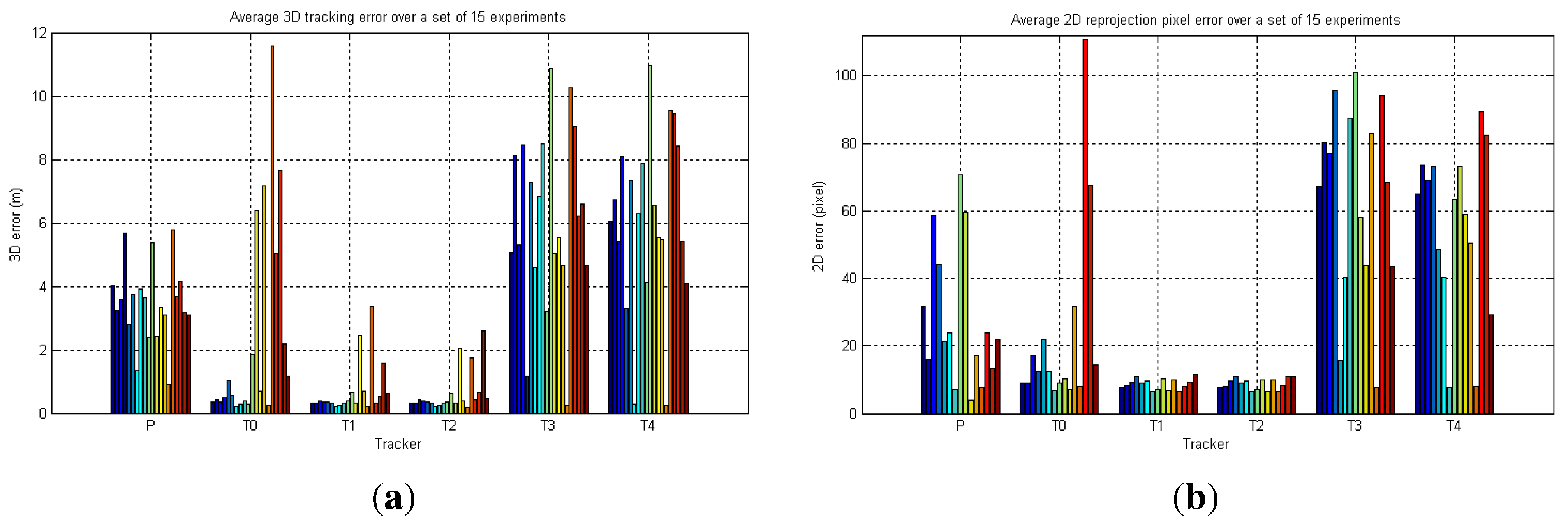
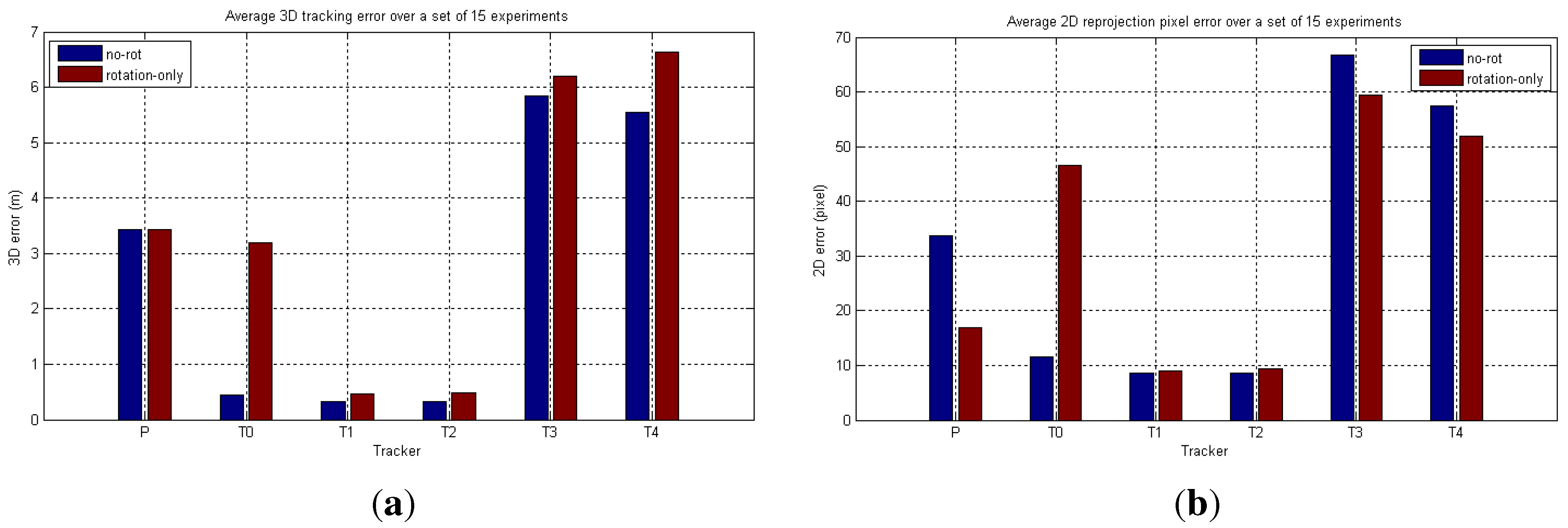
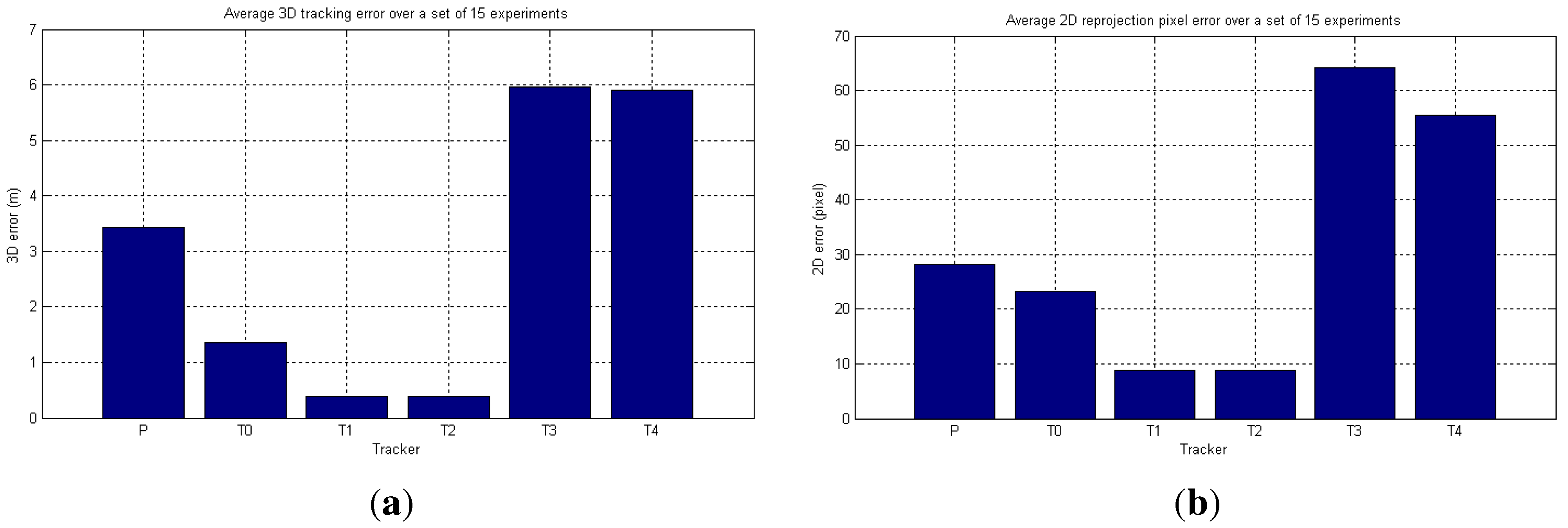
6.2. Real-World Camera Network
6.2.1. LCR Experiments
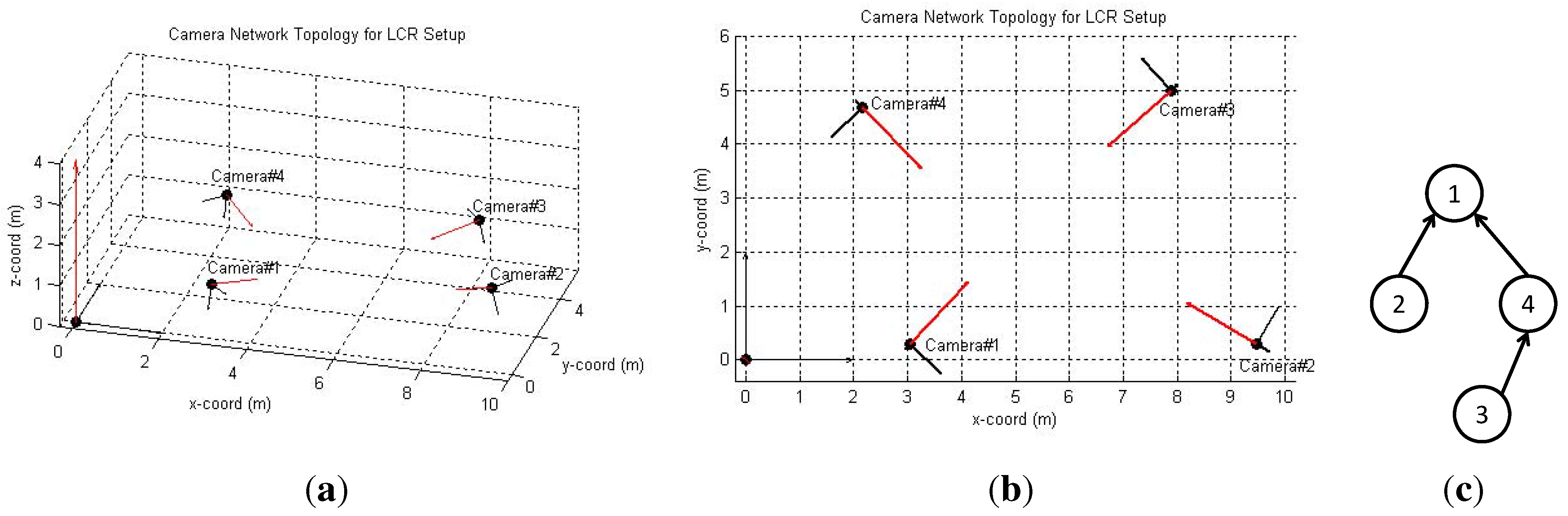

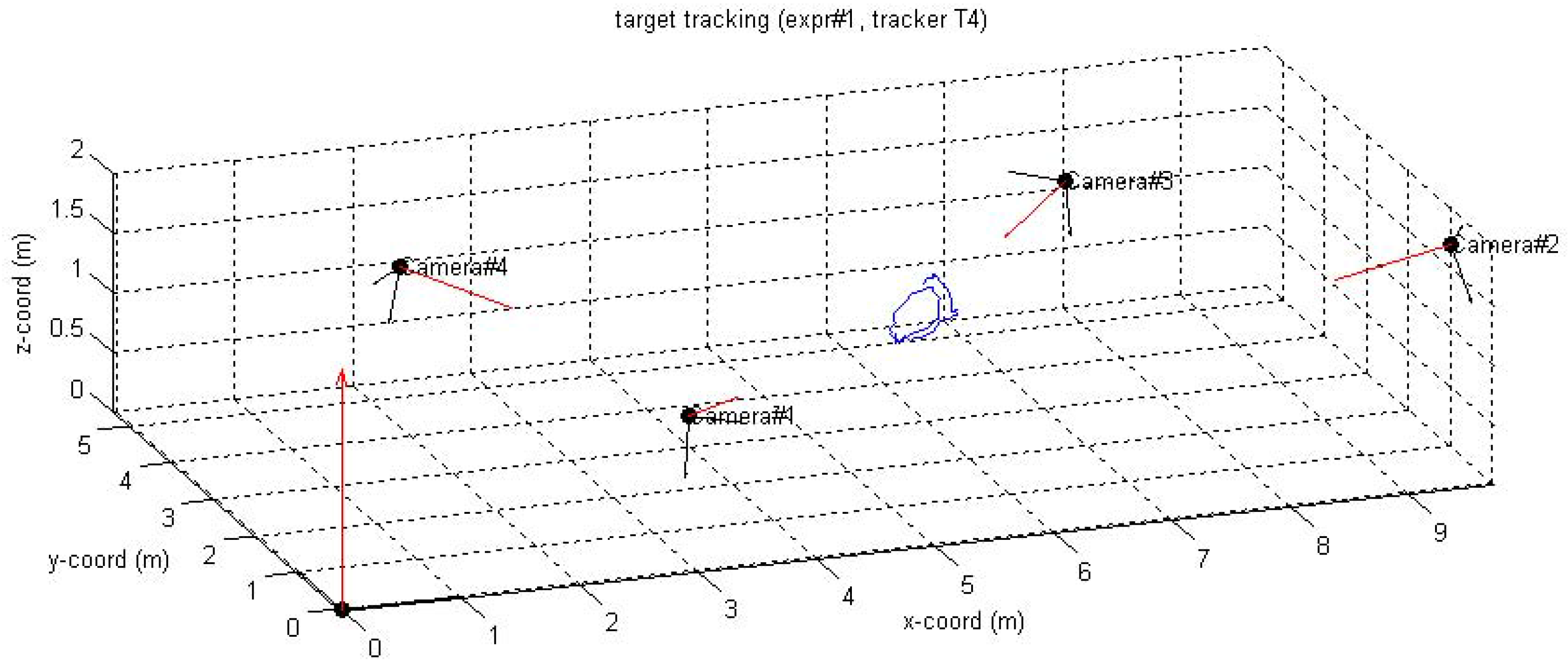
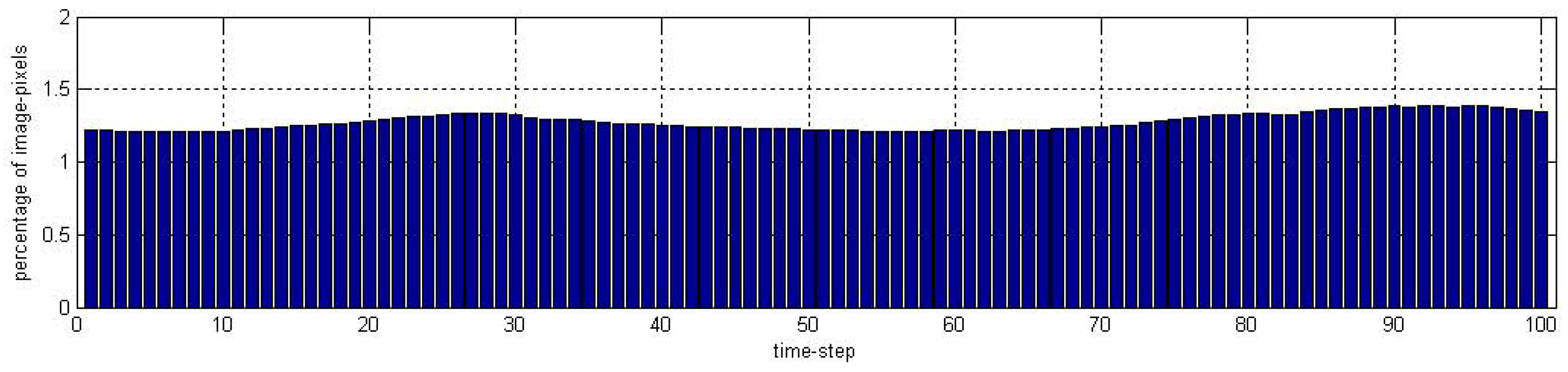
6.2.2. FGH Experiments
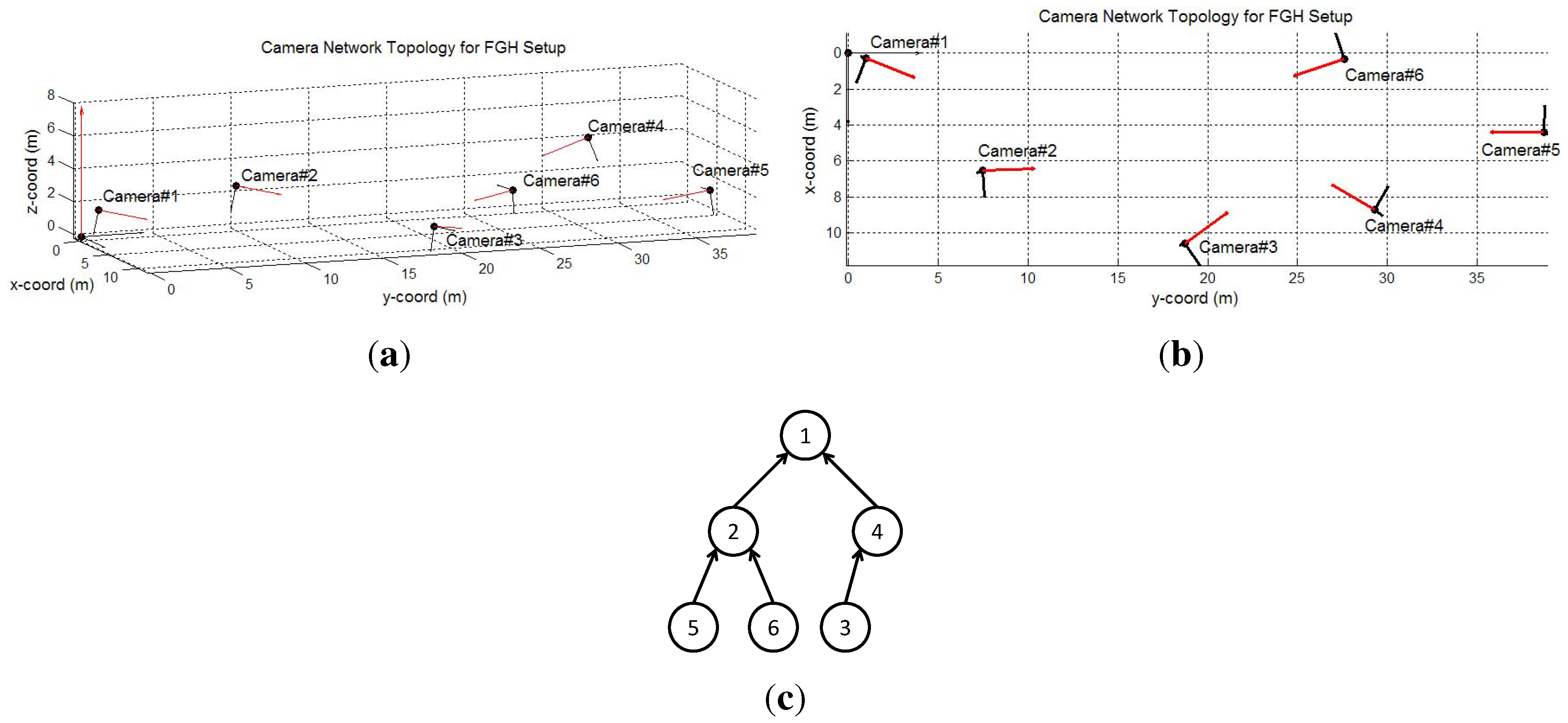


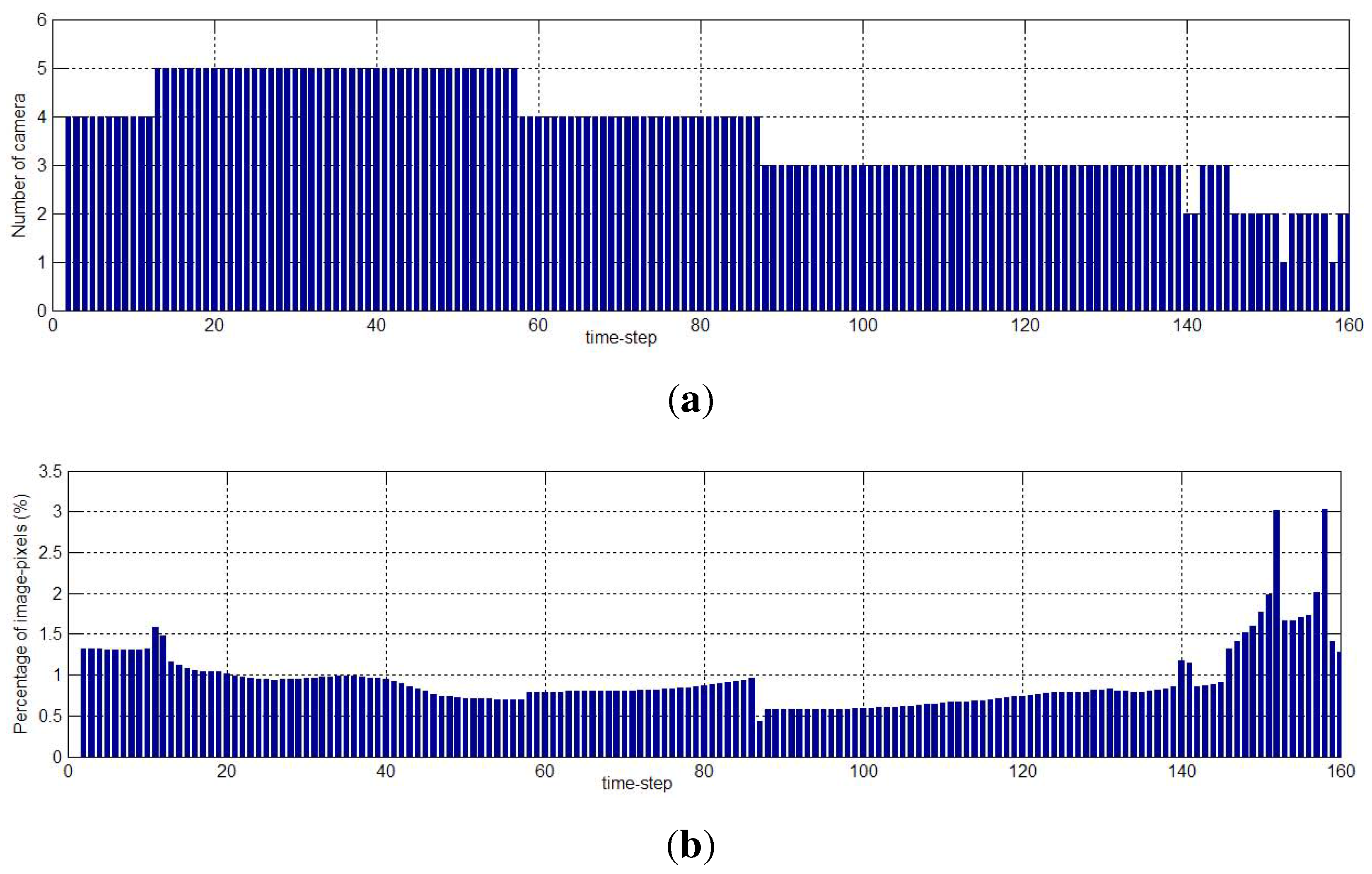
7. Conclusions
Acknowledgements
Conflict of Interest
References
- Rinner, B.; Winkler, T.; Schriebl, W.; Quaritsch, M.; Wolf, W. The Evolution from Single to Pervasive Smart Cameras. In Proceedings of the ACM/IEEE International Conference on Distributed Smart Cameras (ICDSC), Stanford, CA, USA, 7–11 September 2008.
- Tyagi, A.; Keck, M.; Davis, J.; Potamianos, G. Kernel-Based 3D Tracking. In Proceedings of IEEE Workshop on Visual Surveillance, CVPR’07, Minneapolis, MN, USA, 22 June 2007.
- Fleck, S.; Busch, F.; Straßer, W. Adaptive probabilistic tracking embedded in smart cameras for distributed surveillance in a 3D model. EURASIP J. Embedded Syst. 2007, 24. [Google Scholar]
- Hu, W.; Tan, T.; Wang, L.; Maybank, S. A survey on visual surveillance of object motion and behaviors. Trans. Sys. Man Cyber Part C 2004, 34, 334–352. [Google Scholar]
- Yilmaz, A.; Javed, O.; Shah, M. Object tracking: A survey. ACM Comput. Surv. 2006, 38. [Google Scholar] [CrossRef]
- Toyama, K.; Krumm, J.; Brumitt, B.; Meyers, B. Wallflower: Principles and Practice of Background Maintenance. In Proceedings of the IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999.
- Ohba, K.; Ikeuchi, K.; Sato, Y. Appearance-based visual learning and object recognition with illumination invariance. Mach. Vision Appl. 2000, 12, 189–196. [Google Scholar]
- Triesch, J.; von Der Malsburg, C. Democratic integration: Self-organized integration of adaptive cues. Neural Comput. 2001, 13, 2049–2074. [Google Scholar] [PubMed]
- Hayman, E.; Eklundh, J.O. Probabilistic and Voting Approaches to Cue Integration for Figure-Ground Segmentation. In Proceedings of the 7th European Conference on Computer Vision-Part III, ECCV’02, Copenhagen, Denmark, 27 May–2 June 2002; pp. 469–486.
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [PubMed]
- Moravec, H. Visual Mapping by a Robot Rover. In Proceedings of the 6th International Joint Conference on Artificial Intelligence, Tokyo, Japan, 20–23 August 1979; pp. 599–601.
- Harris, C.; Stephens, M. A Combined Corner and Edge Detection. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, September 1988; pp. 147–151.
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N. A tutorial on particle filters for on-line non-linear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Bar-Shalom, Y. Tracking and Data Association; Academic Press Professional, Inc.: San Diego, CA, USA, 1987. [Google Scholar]
- Reid, D. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Birchfield, S. Elliptical Head Tracking Using Intensity Gradients and Color Histograms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 23–25 June 1998; pp. 232–237.
- Comaniciu, D.; Meer, P.; Member, S. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Comaniciu, D.; Ramesh, V.; Meer, P. Kernel-based object tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 564–577. [Google Scholar] [CrossRef]
- Tao, H.; Sawhney, H.; Kumar, R. Object tracking with Bayesian estimation of dynamic layer representations. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 75–89. [Google Scholar] [CrossRef]
- Isard, M.; MacCormick, J. BraMBLe: A Bayesian Multiple-blob Tracker. In Proceedings of Eighth IEEE International Conference on the Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 34–41.
- Pérez, P.; Hue, C.; Vermaak, J.; Gangnet, M. Color-Based Probabilistic Tracking. In Proceedings of the 7th European Conference on Computer Vision, ECCV’02, Copenhagen, Denmark, 28–31 May 2002.
- Quaritsch, M.; Kreuzthaler, M.; Rinner, B.; Bischof, H.; Strobl, B. Autonomous multicamera tracking on embedded smart cameras. EURASIP J. Embedded Syst. 2007, 2007, 35–35. [Google Scholar]
- Shirmohammadi, B.; Taylor, C.J. Distributed Target Tracking Using Self Localizing Smart Camera Networks. In Proceedings of the Fourth ACM/IEEE International Conference on Distributed Smart Cameras, Atlanta, GA, USA, September 2010; pp. 17–24.
- Focken, D.; Stiefelhagen, R. Towards Vision-Based 3-D People Tracking in a Smart Room. In Proceedings of the Fourth IEEE International Conference on Multimodal Interfaces, Pittsburgh, PA, USA, 14–16 October 2002.
- Mittal, A.; Davis, L.S. M2Tracker: A multi-view approach to segmenting and tracking people in a cluttered scene. Int. J. Comput. Vis. 2003, 51, 189–203. [Google Scholar] [CrossRef]
- Soto, C.; Song, B.; Chowdhury, A.K.R. Distributed Multi-Target Tracking in a Self-Configuring Camera Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1486–1493.
- Fleuret, F.; Berclaz, J.; Lengagne, R.; Fua, P. Multicamera people tracking with a probabilistic occupancy map. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 267–282. [Google Scholar] [CrossRef] [PubMed]
- Berclaz, J.; Shahrokni, A.; Fleuret, F.; Ferryman, J.; Fua, P. Evaluation of Probabilistic Occupancy Map People Detection for Surveillance Systems. In Proceedings of the IEEE International Workshop on Performance Evaluation of Tracking and Surveillance, Miami, FL, USA, 20–25 June 2009.
- Leibe, B.; Cornelis, N.; Cornelis, K.; van Gool, L. Dynamic 3D Scene Analysis from a Moving Vehicle. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR’07, Minneapolis, MN, USA, 17–22 June 2007.
- Gandhi, T.; Trivedi, M.M. Person tracking and reidentification: Introducing Panoramic Appearance Map (PAM) for feature representation. Mach. Vision Appl. 2007, 18, 207–220. [Google Scholar] [CrossRef]
- Gandhi, T.; Trivedi, M.M. Panoramic Appearance Map (PAM) for Multi-Camera Based Person Re-Identification. In Proceedings of the IEEE Conference on Advanced Video and Signal Based Surveillance, Sydney, NSW, Australia, 22–24 November 2006.
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Tron, R.; Vidal, R.; Terzis, A. Distributed Pose Averaging in Camera Networks via Consensus on SE(3). In Proceedings of the Second ACM/IEEE International Conference on Distributed Smart Cameras, ICDSC 2008, Stanford, CA, USA, 7–11 September 2008.
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering with Matlab Exercises and Solutions; John Wiley & Sons: Hoboken, NJ, USA, 1996; Chapter 8. [Google Scholar]
- Bilmes, J. A Gentle Tutorial of the EM Algorithm and Its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models; Technical Report TR-97-021; International Computer Science Institute: Berkeley, CA, USA, April 1998. [Google Scholar]
- Kushwaha, M. Feature-Level Information Fusion Methods for Urban Surveillance Using Heterogeneous Sensor Networks. Ph.D. Thesis, Vanderbilt University, Nashville, TN, USA, 2010. [Google Scholar]
- Kushwaha, M.; Koutsoukos, X. 3D Target Tracking in Distributed Smart Camera Networks with In-Network Aggregation. In Proceedings of the Fourth ACM/IEEE International Conference on Distributed Smart Cameras, Atlanta, GA, USA, September 2010; pp. 25–32.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kushwaha, M.; Koutsoukos, X. Collaborative 3D Target Tracking in Distributed Smart Camera Networks for Wide-Area Surveillance. J. Sens. Actuator Netw. 2013, 2, 316-353. https://doi.org/10.3390/jsan2020316
Kushwaha M, Koutsoukos X. Collaborative 3D Target Tracking in Distributed Smart Camera Networks for Wide-Area Surveillance. Journal of Sensor and Actuator Networks. 2013; 2(2):316-353. https://doi.org/10.3390/jsan2020316
Chicago/Turabian StyleKushwaha, Manish, and Xenofon Koutsoukos. 2013. "Collaborative 3D Target Tracking in Distributed Smart Camera Networks for Wide-Area Surveillance" Journal of Sensor and Actuator Networks 2, no. 2: 316-353. https://doi.org/10.3390/jsan2020316




