Channel Allocation in Wireless Networks with Directional Antennas
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
- We study the channel allocation in general DIR networks. In particular, we try to answer the question: how many channels are needed to ensure collision-free communications in a DIR network.
- We formulate the channel allocation problem as a graph coloring problem. We derive the upper bounds on the number of channels to ensure collision-free communications in a DIR network. It is shown that the upper bounds on the number of channels heavily depend on the node density and the interference ratio.
- We compare our derived upper bounds with the results derived from OMN networks. We also investigate the tightness of our derived upper bounds by constructing several scenarios.
- We also take the side-lobes and back-lobes of a directional antenna as well as the physical channel characteristics (e.g., the signal path loss) into account. Specifically, our results show that when the beamwidth of a directional antenna is quite narrow, the effect of the side-lobes and back-lobes is so small that they can often be ignored.
- Our results are also useful in practice. In particular, our results can be used to roughly estimate the number of channels needed in the given configuration of a wireless network (e.g., a WSN with directional antennas). On the other hand, when the number of available channels is limited, our results can be used to suggest the proper network setting.
2. Models and Problem Formulation
2.1. Models
2.1.1. Antenna Model
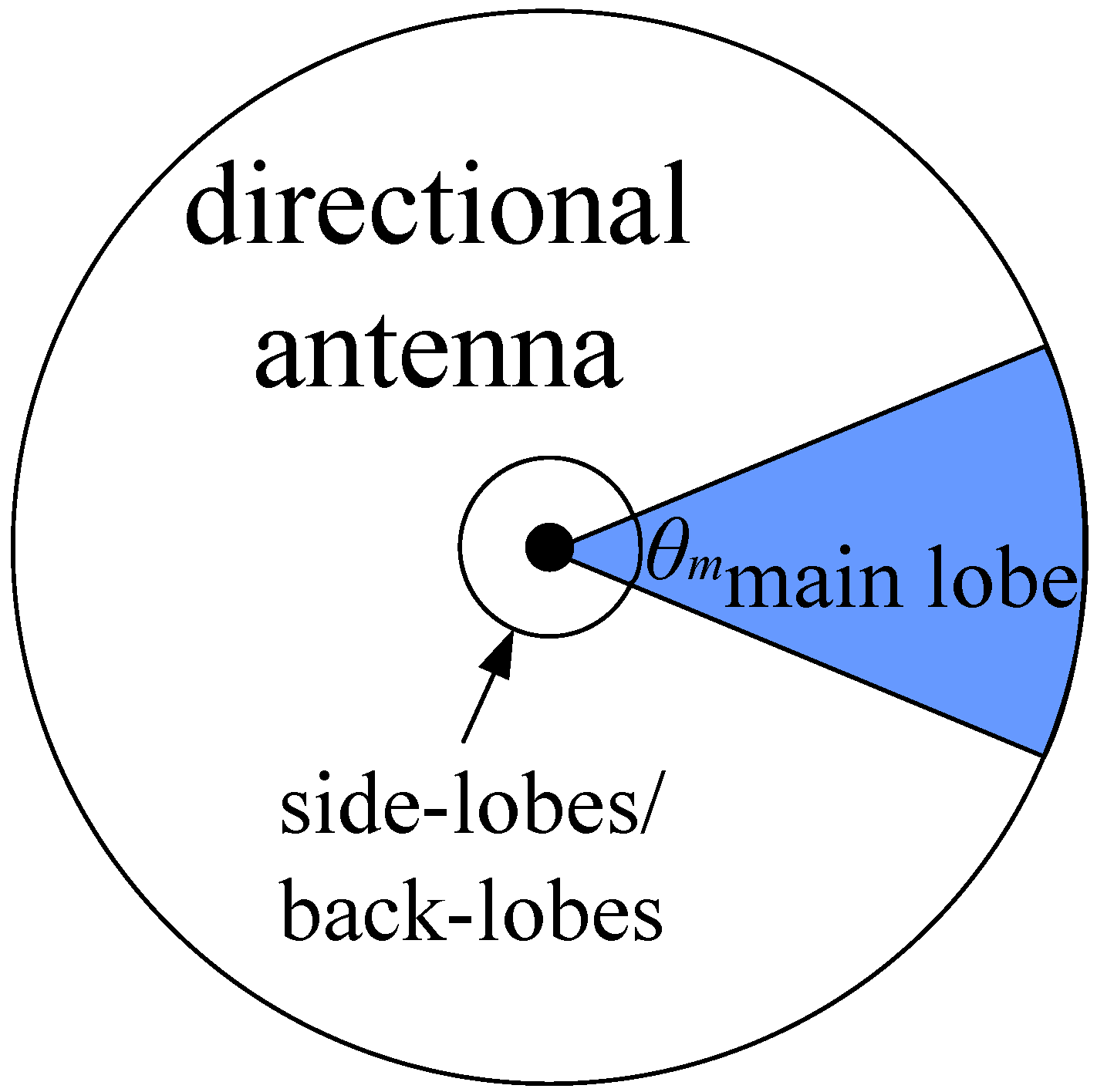
2.1.2. Interference Model
- (1)
- is within the transmission range of and is within the transmission range of .
- (2)
- is covered by the antenna beam of . Similarly, is also covered by the antenna beam of .
- (3)
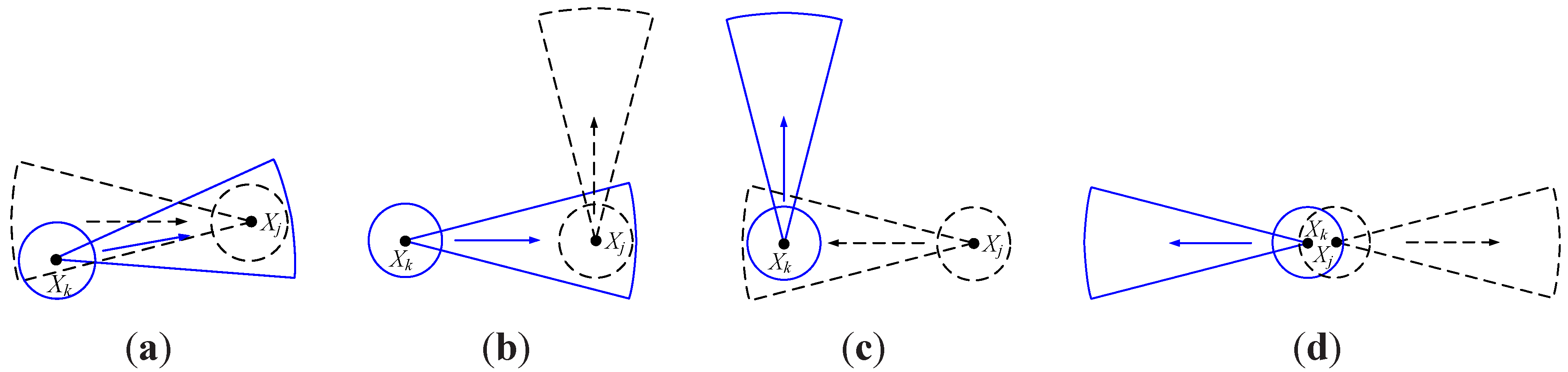
- No other node within the interference range(the interference range is used to denote the maximum distance within which a node can be interfered by an interfering signal) is simultaneously transmitting over the same channel and in the same direction toward .
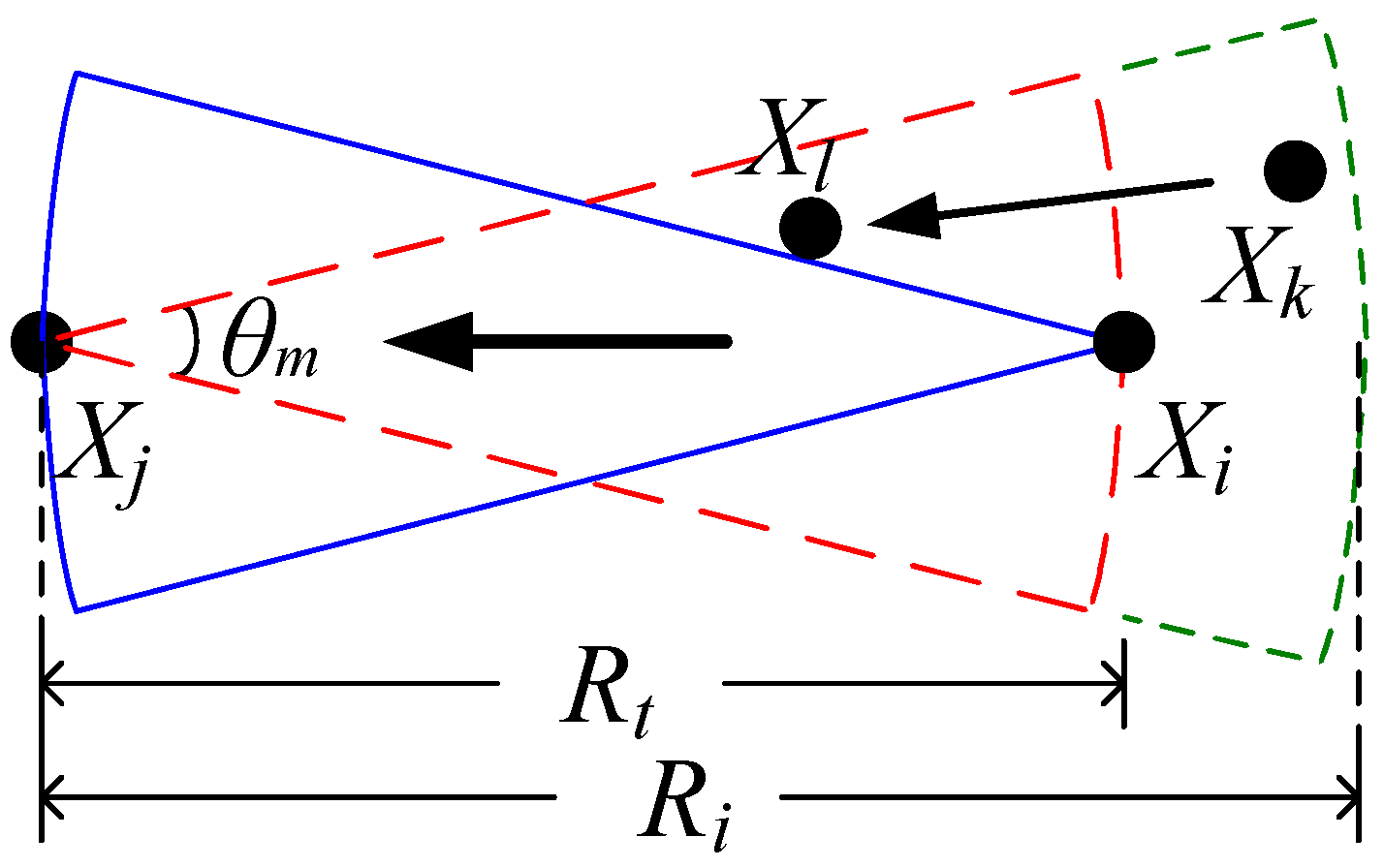
2.2. Definitions and Problem Formulation
2.3. Conflict Graph
3. Upper Bounds on the Number of Channels
3.1. Background Results
3.2. Upper Bounds on the Number of Channels
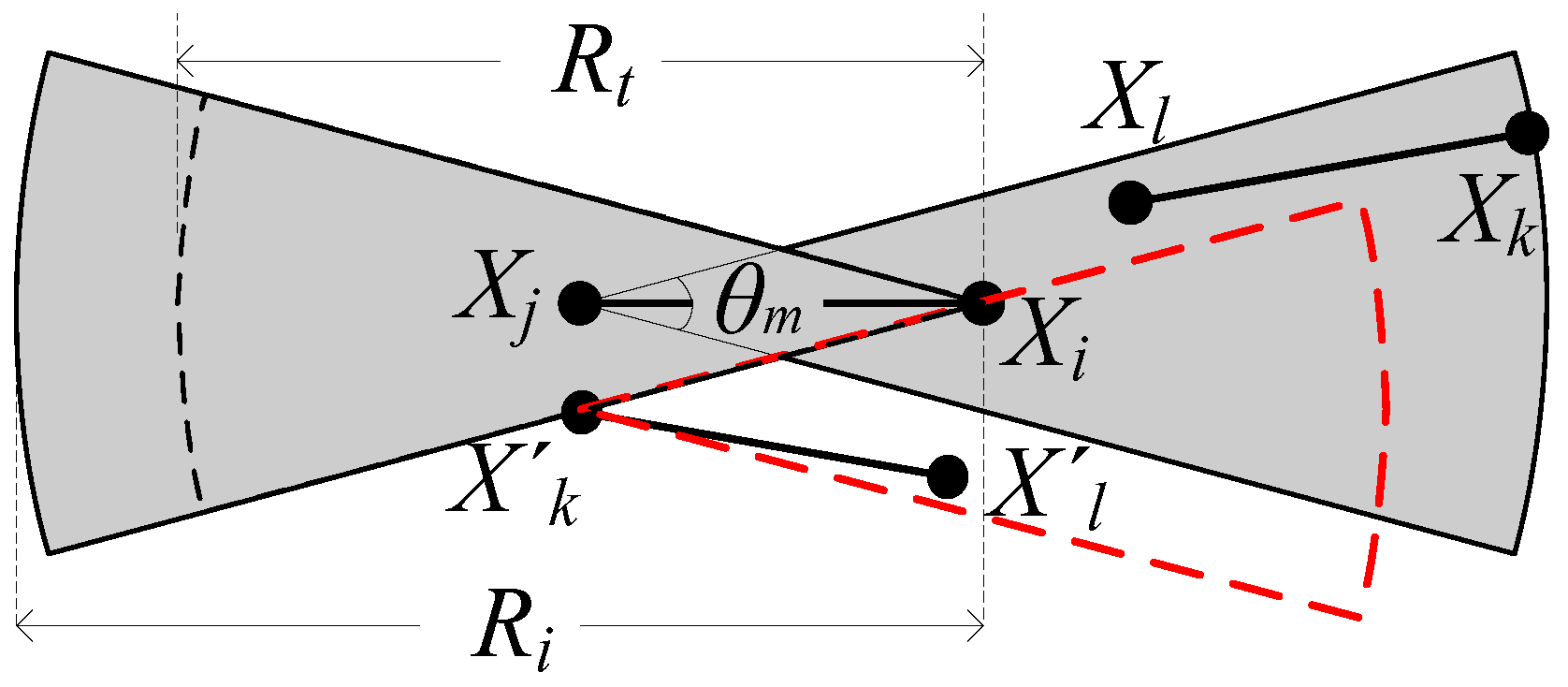
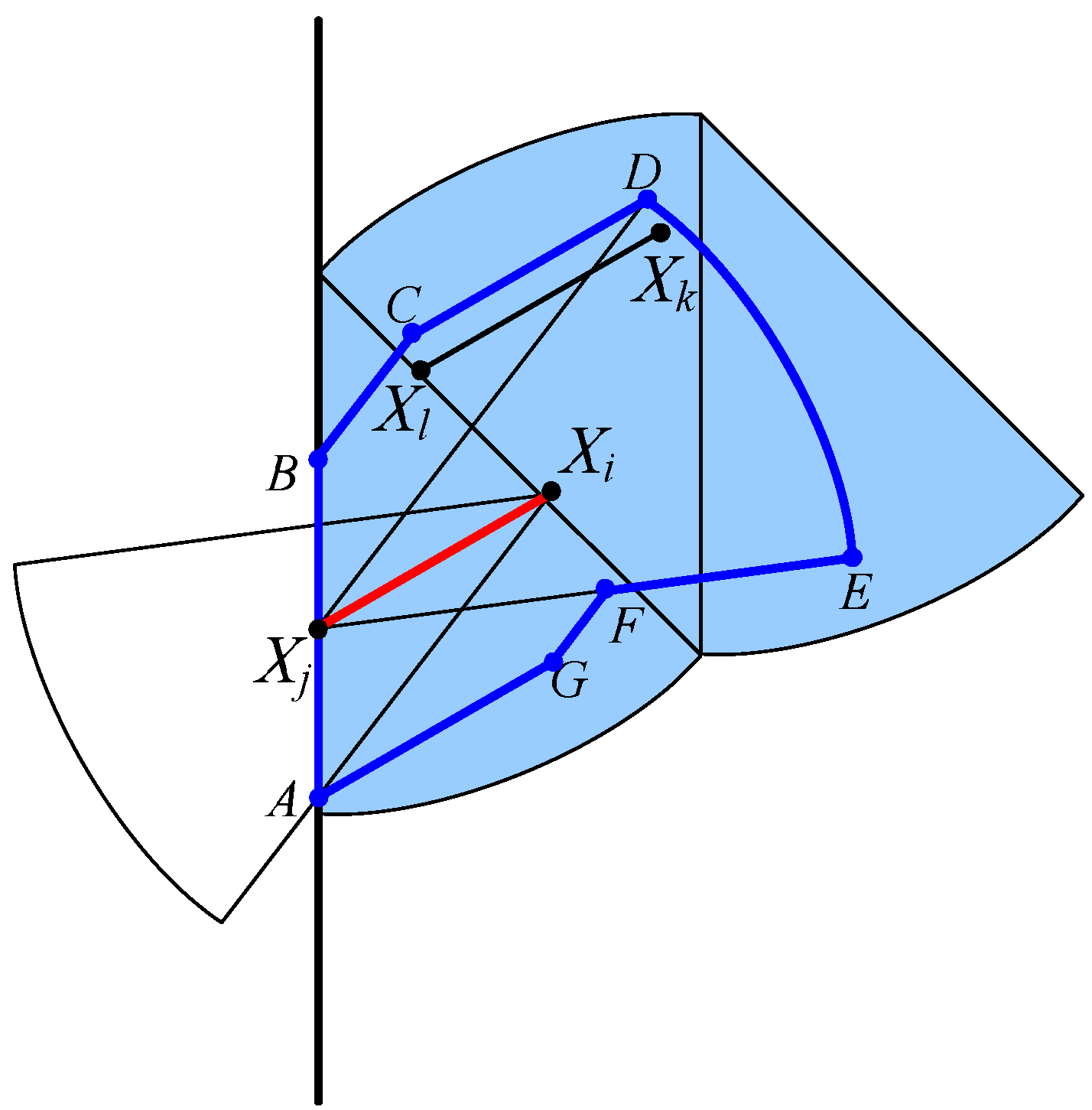
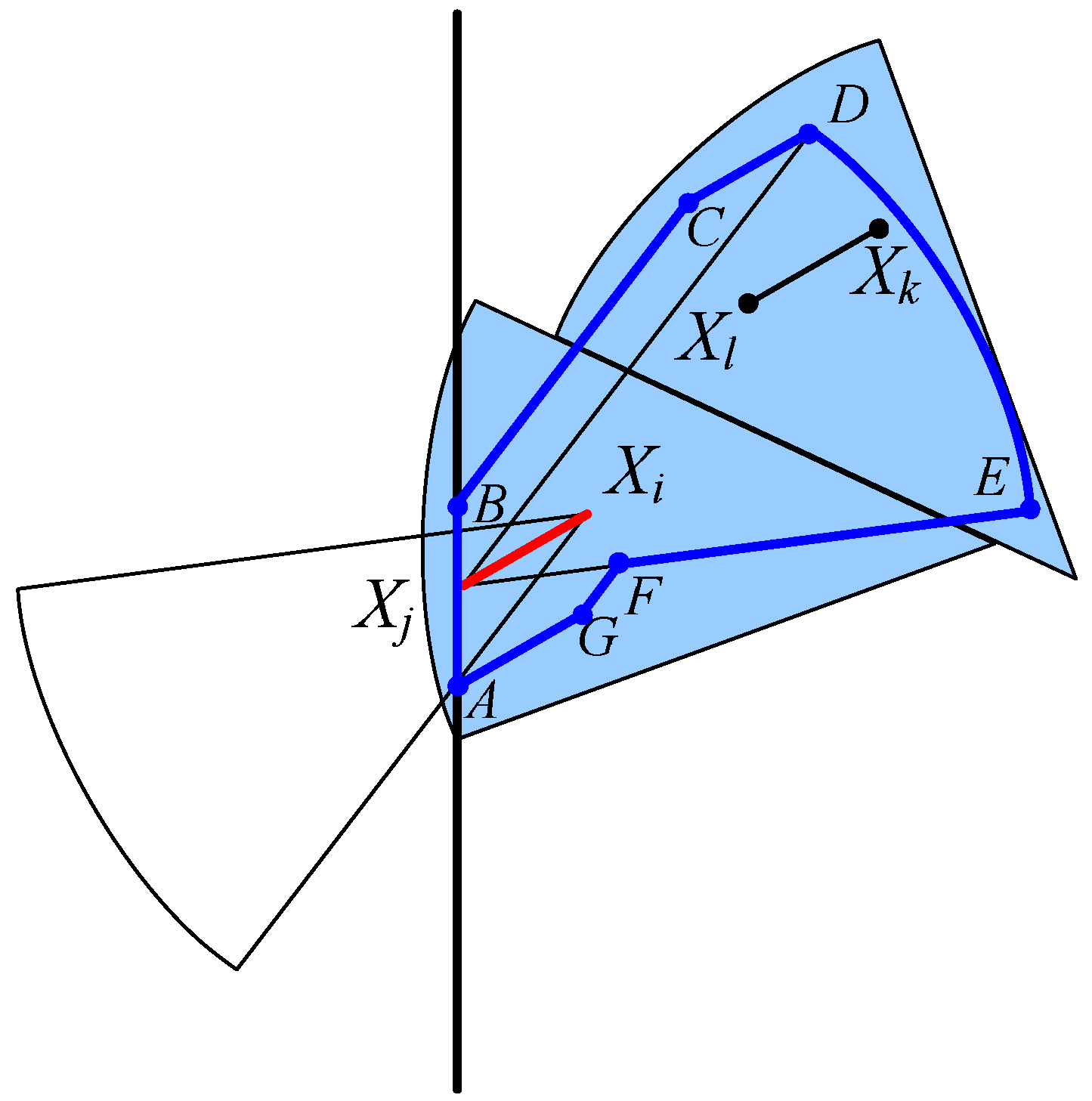
4. Tightness of the Upper Bounds
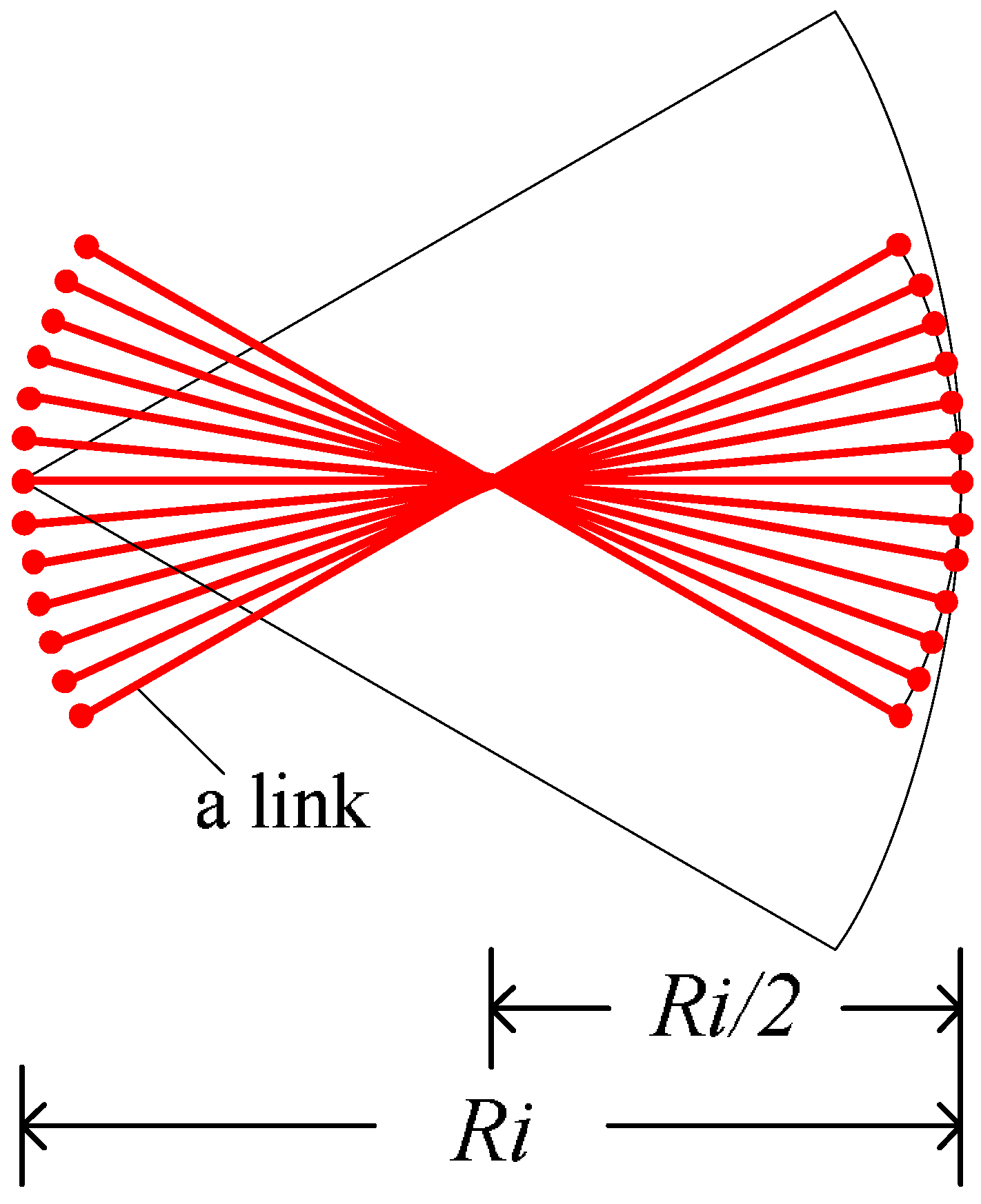

5. Discussions and Implications
| OMN Networks [12] | DIR Networks | |||
|---|---|---|---|---|
| r | Upper bounds | Lower constraints | Upper bounds | Lower constraints |
| 1 | ||||
| 2 | ||||
| 4 | D | |||
| ∞ | 1 | |||
6. Extension with Side-Lobes/Back-Lobes as Well as the Path Loss Effect
6.1. Antenna Model with Side-Lobes and Back-Lobes

6.1.1. Omni-Directional Antenna
6.1.2. Directional Antenna
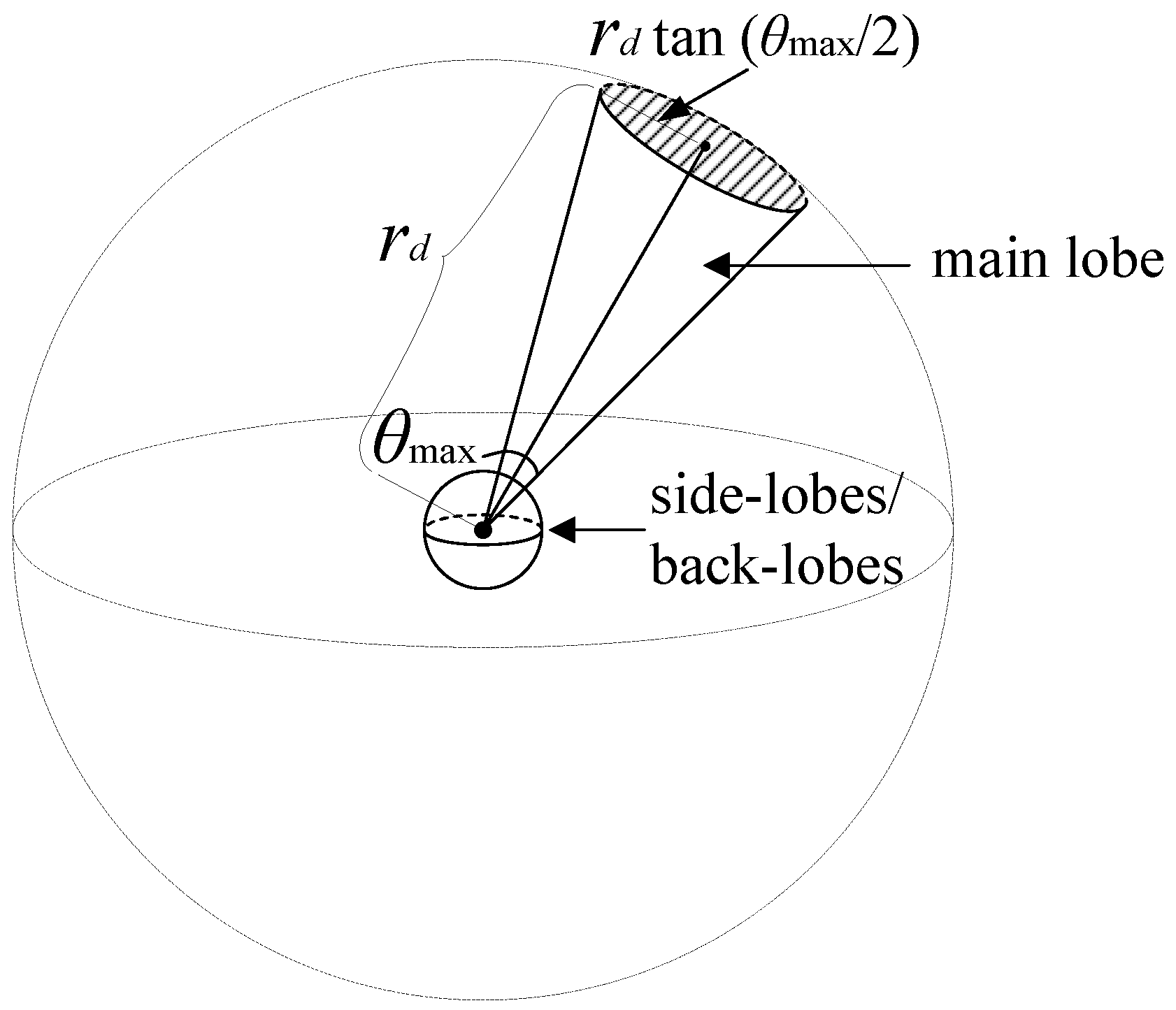
| Main Beamwidth | Main Beam Gain | Side-Lobe and Back-Lobe Gain |
|---|---|---|
| 10 (10 ) | (−7.4 ) | |
| 25.12 (14 ) | (−7.6 ) | |
| 100 (20 ) | (−6.5 ) | |
| 398 (26 ) | (−4.0 ) |
6.2. Physical Channel Model
| Scenarios | Interfering Node | Interfered Node | Interference Range |
|---|---|---|---|
| I | Main beam | Main beam | |
| II | Main beam | Side-lobes and back-lobes | |
| III | Side-lobes and back-lobes | Main beam | |
| IV | Side-lobes and back-lobes | Side-lobes and back-lobes |

7. Conclusions
Acknowledgements
References
- Zhang, J.; Jia, X.; Zhou, Y. Analysis of capacity improvement by directional antennas in wireless sensor networks. ACM Trans. Sensor Netw. 2012, 9, 1–3. [Google Scholar] [CrossRef]
- Dai, H.N. Throughput and Delay in Wireless Sensor Networks Using Directional Antennas. In Proceedings of the Fifth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Melbourne, Australia, 7–10 December 2009.
- Raniwala, A.; Chiueh, T. Architecture and Algorithms for an IEEE 802.11-Based Multi-Channel Wireless Mesh Network. In Proceedings of International Conference on Computer Communications (INFOCOM), Miami, FL, USA, 13–17 March 2005.
- So, J.; Vaidya, N.H. Multi-Channel MAC for Ad Hoc Networks: Handling Multi-Channel Hidden Terminals Using a Single Transceiver. In Proceedings of ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Tokyo, Japan, 24–26 May 2004.
- Kyasanur, P.; Vaidya, N.H. Routing and Interface Assignment in Multi-Channel Multi-Interface Wireless Networks. In Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 13–17 March 2005.
- Nasipuri, A.; Zhuang, J.; Das, S. A Multichannel CSMA MAC Protocol for Multihop Wireless Networks. In Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 21–24 September 1999.
- Bahl, P.; Chandra, R.; Dunagan, J. SSCH: Slotted Seeded Channel Hopping for Capacity Improvement in IEEE 802.11 Ad-Hoc Wireless Networks. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), Philadelphia, PA, USA, 26 September–1 October 2004.
- Draves, R.; Padhye, J.; Zill, B. Routing in Multi-Radio, Multi-Hop Wireless Mesh Networks. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), Philadelphia, PA, USA, 26 September–1October 2004.
- Kyasanur, P.; Vaidya, N.H. Capacity of MultiChannel Wireless Networks: Impact of Number of Channels and Interfaces. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), Cologne, Germany, 28 August–2 September 2005.
- S Kodialam, M.; Nandagopal, T. Characterizing the Capacity Region in Multi-Radio Multi-Channel Wireless Mesh Networks. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), Cologne, Germany, 28 August–2 September 2005.
- Jain, K.; Padhye, J.; Padmanabhan, V.N.; Qiu, L. Impact of Interference on Multi-Hop Wireless Network Performance. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), San Diego, CA, USA, 14–19 September 2003.
- Cao, L.; Wu, M.Y. Upper Bound of the Number of Channels for Conflict-free Communication in Multi-Channel Wireless Networks. In Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), Hong Kong, China, 11—15 March 2007.
- Li, W.W.L.; Zhang, Y.J.; So, A.M.C.; Win, M.Z. Slow adaptive OFDMA systems through chance constrained programming. IEEE Trans. Signal Proccess. 2010, 58, 3858–3869. [Google Scholar] [CrossRef]
- Yi, S.; Pei, Y.; Kalyanaraman, S. On the Capacity Improvement of Ad Hoc Wireless Networks Using Directional Antennas. In Proceedings of ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Annapolis, MD, USA, 1–3 June 2003.
- Ramanathan, R. On the Performance of Ad Hoc Networks with Beamforming Antennas. In Proceedings of ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Long Beach, CA, USA, 4–5 October 2001.
- Takai, M.; Martin, J.; Bagrodia, R.; Ren, A. Directional Virtual Carrier Sensing for Directional Antennas in Mobile Ad Hoc Networks. In Proceedings of ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Lausanne, Switzerland, 9–11 June 2002.
- Choudhury, R.R.; Yang, X.; Vaidya, N.H.; Ramanathan, R. Using Directional Antennas for Medium Access Control in Ad Hoc Networks. In Proceedings of ACM International Conference on Mobile Computing and Networking (MobiCom), Atlanta, GA, USA, 23–28 September 2002.
- Korakis, T.; Jakllari, G.; Tassiulas, L. A MAC Protocol for Full Exploitation of Directional Antennas in Ad-Hoc Wireless Networks. In Proceedings of ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Annapolis, MD, USA, 1–3 June 2003.
- Zhang, Z. Pure Directional Transmission and Reception Algorithms in Wireless Ad Hoc Networks with Directional Antennas. In Proceedings of IEEE Internationl Conference on Communications, Seoul, Korea, 16–20 May 2005.
- Ramanathan, R.; Redi, J.; Santivanez, C.; Wiggins, D.; Polit, S. Ad Hoc Networking with Directional Antennas: A Complete System Solution. IEEE JSAC 2005, 23, 496–506. [Google Scholar] [CrossRef]
- Dai, H.N.; Ng, K.W.; Wu, M.Y. A Busy-Tone based MAC Scheme for Wireless Ad Hoc Networks Using Directional Antennas. In Proceedings of IEEE Globecom, Washington, DC, USA, 26–30 November 2007.
- Dai, H.N.; Ng, K.W.; Wong, R.C.W.; Wu, M.Y. On the Capacity of Multi-Channel Wireless Networks Using Directional Antennas. In Proceedings of International Conference on Computer Communications (INFOCOM), Phoenix, AZ, USA, 13—18 April 2008.
- Raman, B. Channel Allocation in 802.11-Based Mesh Networks. In Proceedings of International Conference on Computer Communications (INFOCOM), Barcelona, Spain, 23–29 April 2006.
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Panconesi, A.; Rizzi, R. Some simple distributed algorithms for sparse networks. Distrib. Comput. 2001, 14, 97–100. [Google Scholar] [CrossRef]
- Szekeres, G.; Wilf, H.S. An inequality for the chromatic number of a graph. J. Comb. Theory 1968, 4, 1–3. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
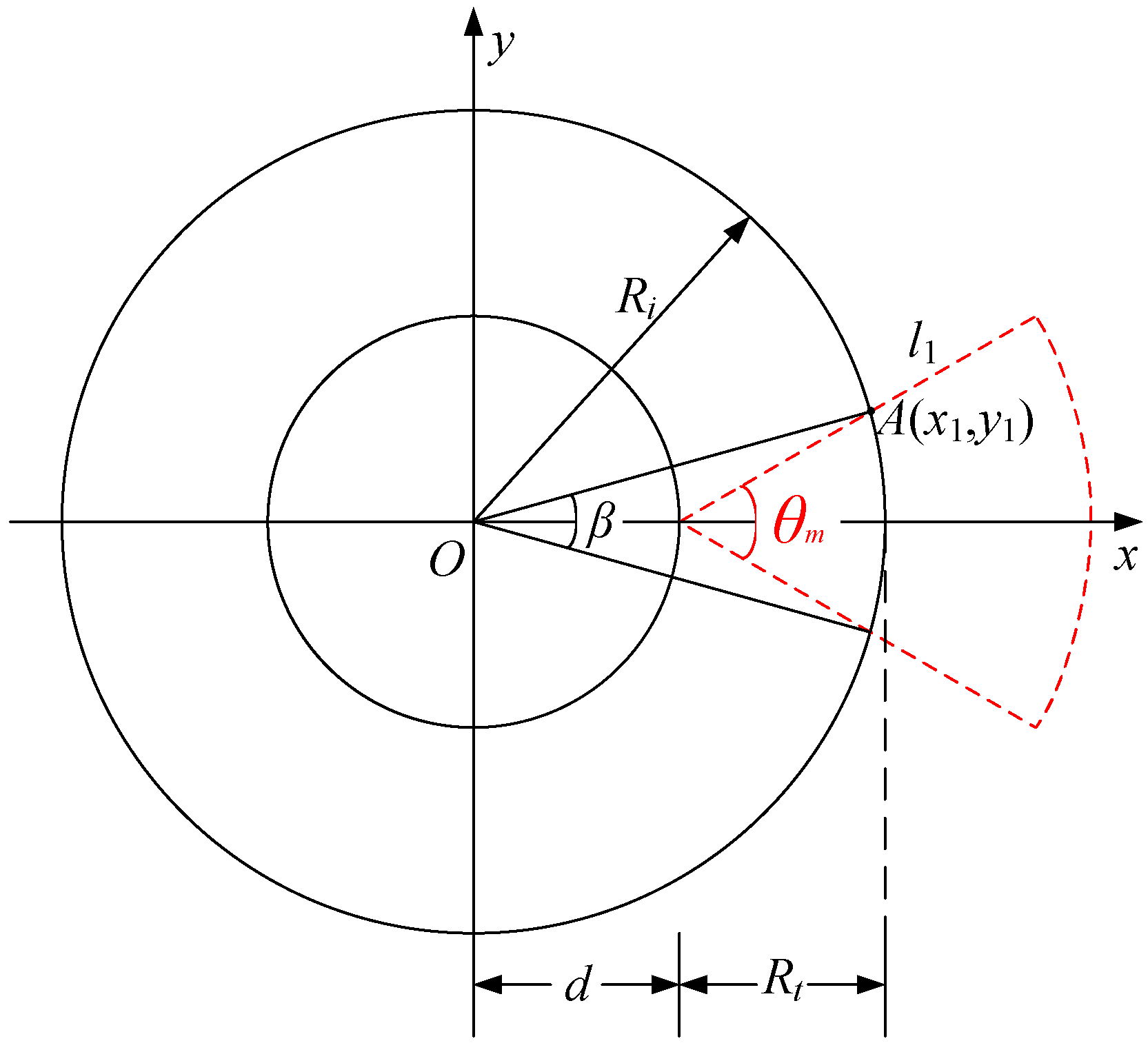
A. Appendix 1. Calculation of the Coverage Angle β
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dai, H.-N.; Ng, K.-W.; Wu, M.-Y. Channel Allocation in Wireless Networks with Directional Antennas. J. Sens. Actuator Netw. 2013, 2, 213-234. https://doi.org/10.3390/jsan2020213
Dai H-N, Ng K-W, Wu M-Y. Channel Allocation in Wireless Networks with Directional Antennas. Journal of Sensor and Actuator Networks. 2013; 2(2):213-234. https://doi.org/10.3390/jsan2020213
Chicago/Turabian StyleDai, Hong-Ning, Kam-Wing Ng, and Min-You Wu. 2013. "Channel Allocation in Wireless Networks with Directional Antennas" Journal of Sensor and Actuator Networks 2, no. 2: 213-234. https://doi.org/10.3390/jsan2020213
APA StyleDai, H.-N., Ng, K.-W., & Wu, M.-Y. (2013). Channel Allocation in Wireless Networks with Directional Antennas. Journal of Sensor and Actuator Networks, 2(2), 213-234. https://doi.org/10.3390/jsan2020213






