Category Attribute-Oriented Heterogeneous Resource Allocation and Task Offloading for SAGIN Edge Computing

Abstract

Space-Air-Ground Integrated Network (SAGIN), which is considered a network architecture with great development potential, exhibits significant cross-domain collaboration characteristics at present. However, most of the existing works ignore the matching and adaptability of differential tasks and heterogeneous resources, resulting in significantly inefficient task execution and undesirable network performance. As a consequence, we formulate a category attribute-oriented resource allocation and task offloading optimization problem with the aim of minimizing the overall scheduling cost. We first introduce a task–resource matching matrix to facilitate optimal task offloading policies with computation resources. In addition, virtual queues are constructed to take the impacts of randomized task arrival into account. To solve the optimization objective which jointly considers bandwidth allocation, transmission power control and task offloading decision effectively, we proposed a deep reinforcement learning (DRL) algorithm framework considering type matching. Simulation experiments demonstrate the effectiveness of our proposed algorithm as well as superior performance compared to others.

1. Introduction

Mobile edge computing (MEC) enables Internet of Things (IoT) devices with limited resources, such as computing power and energy, by providing network services at the edge of networks (i.e., on the user’s side) [1]. Thus, it has received extensive attention and produced many works in recent years [2,3]. However, traditional edge computing based on terrestrial networks is unable to provide network services to users in remote areas (e.g., oceans, deserts, and forests), which occupy most of the Earth’s surface area [4,5]. This severely limits the realization of ubiquitous computing. Thanks to the high bandwidth and seamless coverage of low earth orbit (LEO) satellites, providing edge computing solutions to devices in remote areas via LEO satellites has become a promising proposal and research focus over the last few years [6,7]. Furthermore, Space-Air-Ground Integrated Network (SAGIN) integrates multi-domain network resources to enhance service capabilities and extend the range of network coverage significantly via LEO satellites. It also utilises Unmanned Aerial Vehicles (UAVs) to overcome complex terrain and provide supplementary network resources, making it a desirable architecture for providing efficient, ubiquitous network services to IoT devices in remote areas [8,9,10].

Although the SAGIN architecture has the potential to provide full-area, seamless network coverage, it still faces challenges such as highly dynamic topologies and highly heterogeneous resources [11]. Furthermore, the direct-to-cell trend means that the massive scale of IoT devices and tasks will make efficient decision-making even more challenging [12]. This conflicts with the requirements of a space-based task offloading environment, which necessitates fast, high-performance decision-making. Traditional iteration-based heuristic algorithms cannot meet the requirements of fast responses or high-performance decision-making in constrained space-based environments. Therefore, deep reinforcement learning (DRL)-based approaches are currently demonstrating unique advantages, as they can continuously optimize decision-making strategies. By continuously engaging with environmental dynamics and monitoring system state fluctuations in real time, deep reinforcement learning can leverage its autonomous learning and policy optimization capabilities to gain a technological advantage in dynamic and uncertain edge computing environments [13,14].

Inspired by task offloading using deep reinforcement learning, Tang and Wong proposed a DRL-based MEC system that enables mobile devices to autonomously decide on task offloading in order to minimize long-term costs [15]. Tang et al. presented a three-layer hierarchical computing model that integrates cloud and edge computing within a hybrid LEO satellite framework. This design enables ground users to offload tasks with the aim of reducing overall energy consumption while taking into account satellite access latency and processing resource constraints [16]. Furthermore, to improve communication efficiency in MEC systems, Li et al. designed a resource allocation scheme that leverages DRL to jointly optimize bandwidth and transmission power [17]. By integrating UAVs into air–ground MEC networks, Shang and Liu proposed an architecture that provides computational resources through joint optimization of user association and radio resource allocation, thereby reducing user energy consumption under stringent latency requirements [18]. Nevertheless, these studies did not consider task queue management, which is critical to handling dynamic user demands and ensuring efficient utilization of resources. To address this, Wang et al. designed a DRL-based, drone-assisted IoT offloading strategy that optimizes bandwidth, power, and task queues under dynamic loads [19].

The motivation for this work stems from a key limitation in existing DRL-based task offloading approaches for SAGIN systems. The relationship between task categories and resource attributes is rarely considered. Tasks with distinct processing requirements are often treated uniformly, which leads to inefficient resource utilization and increased system scheduling costs in dynamic, heterogeneous SAGIN environments. To address such an issue, we propose a DRL-based optimization framework that integrates category-attribute matching to guide intelligent task offloading decisions and minimize overall scheduling costs. Specifically, we utilise a matrix of coefficients to quantify the degree of matching between task categories and heterogeneous resources, thereby establishing explicit task–resource correlations through mathematical modelling. Virtual queues are introduced to model queue backlogs and waiting times, reflecting the impact of dynamic task arrivals. The DRL agent continuously interacts with the environment, adjusting offloading strategies based on feedback to improve adaptability and matching accuracy across diverse resource domains. Furthermore, we consider practical constraints such as limited satellite coverage duration, UAV mobility and IoT device limitations. Then, we jointly optimise bandwidth allocation, transmission power control, task queues and offloading decisions to achieve efficient, system-wide coordination. The significance of this work lies in addressing the mismatch between diverse task requirements and heterogeneous resource capabilities in SAGIN-MEC systems. By incorporating task-category and resource-attribute matching into the DRL framework, the proposed method enables more efficient offloading decisions. Combined with virtual queue modeling and joint resource control, it improves system-level adaptability and task scheduling performance under dynamic and heterogeneous conditions. Extensive experimentation demonstrates the many advantages of the proposed approach in various dynamic SAGIN scenarios.

The primary contributions of this paper can be outlined as follows:

• We formulate a joint optimisation problem that incorporates the dynamic evolution of long-term task queues and the nodes’ transmission power, task-offloading strategies, and the type matching of tasks and resources. This formalization represents the relationships between these factors to improve task offload efficiency and resource utilization.
• We incorporate a task–resource type matching matrix into reinforcement learning, fully utilizing the matching coefficients to reflect the compatibility between task categories and resource characteristics. This enables more optimized decision-making during task offloading, improving resource utilization and overall system performance.
• We integrate a penalty mechanism into the task queue model using reinforcement learning to improve resource utilization and task scheduling efficiency. This mechanism mitigates excessive queue backlogs in dynamic SAGIN, which can lead to resource overload, high latency, and task loss. By embedding the queue length into the reward function, we dynamically guide the optimization of offloading strategies to enhance overall system performance.

The paper is set out like this: Section 2 outlines the SAGIN-MEC system and formalizes the associated task offloading and resource allocation challenge. Section 3 presents the algorithmic framework. Section 4 discusses the experimental evaluation, and Section 5 concludes the paper.

2. System Model and Problem Formulation

This section first introduces the SAGIN framework and then formulates the problem.

2.1. Space-Air-Ground Integrated Network

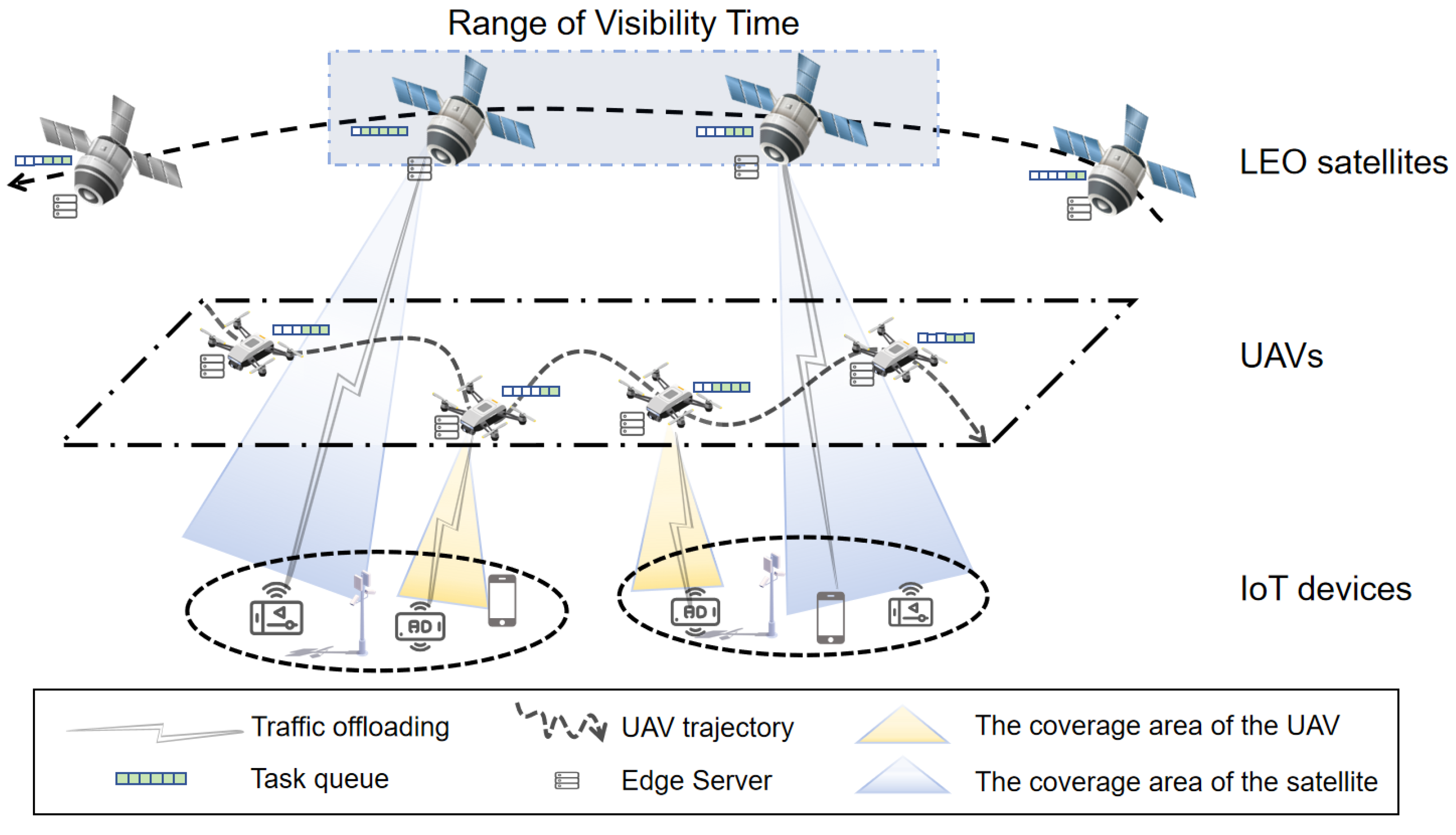
We introduce the SAGIN framework as shown in Figure 1. The system comprises L LEO satellites, U UAVs, and I IoT devices. Let $\mathcal{L}=\{1,2,\dots ,L\}$ represent the set of LEO satellites, $\mathcal{U}=\{1,2,\dots ,U\}$ denote the set of UAVs, and $\mathcal{I}=\{1,2,\dots ,I\}$ denote the set of IoT devices acting as ground user equipment that generates computational tasks. Here, $l\in \mathcal{L}$, $u\in \mathcal{U}$, and $i\in \mathcal{I}$ represent the l-th satellite, the u-th UAV, and the i-th IoT device. Each IoT device, equipped with multiple transceivers, can offload tasks to a UAV or an LEO satellite via reinforcement learning–based decision-making, but only one connection is active at any time. IoT devices transmit computational tasks, while a reinforcement learning mechanism determines whether to offload them to UAVs or satellites for processing. As shown in Figure 1, both UAVs and LEO satellites are equipped with edge servers and maintain task queues for processing offloaded computation. Satellites provide broader but time-limited coverage. The shaded regions in Figure 1 indicate the respective coverage areas.

2.2. Task Model

To clearly describe the dynamically changing network scenario due to the random arrival of tasks, the system can be modeled by discretizing time into slots. These time slots are collectively referred to as set $\mathcal{T}=\{1,2,\dots ,T\}$. At each time interval $t\in \mathcal{T}$, a task ${\mathcal{O}}_t^i=(D_t^i,C_t^i,{\Theta }_t^i)$ arrives at the i-th IoT device, where $D_t^i$ represents the size of the task in bits, $C_t^i$ indicates the number of CPU cycles required per bit, and ${\Theta }_t^i$ indicates the task categories.   Task categories are defined as a set ${\mathcal{T}}_{\mathrm{type}}=\{{\Theta }_1,{\Theta }_2,\dots ,{\Theta }_K\}$. Each ${\Theta }_k$ represents a distinct category of tasks characterized by QoS requirements, computational properties, and resource preferences. The offloading decision for device i in time slot t is $a_t^i$, which is either 0 or 1, where $a_t^i=0$ indicates assigning the task to a UAV and $a_t^i=1$ denotes assigning to a satellite.

Offloaded tasks accumulate in task queues $Q_{n,t}$ at UAVs and satellites. Let $n\in \mathcal{N}$ denote a node, where $\mathcal{N}=\mathcal{U}\cup \mathcal{L}$, with $\mathcal{U}$ representing UAVs and $\mathcal{L}$ representing satellites. Each node device $n\in \mathcal{N}$ maintains a task queue $Q_{n,t}$ indicating pending tasks at time slot t. The evolution of the task queue is influenced by tasks originating from IoT devices, with ${\lambda }_{i,n,t}$ denoting the task volume offloaded from device i to node n. The variable ${\lambda }_{n,t}$ quantifies the number of new tasks assigned to node n at time t, which can be calculated as follows:

$${\lambda }_{n,t}=\sum _{i\in {\mathcal{I}}_n}{\lambda }_{i,n,t}$$

(1)

where $i\in {\mathcal{I}}_n$ represents the group of IoT devices that offload tasks to node n. The task queue dynamics for a single node n are defined as follows:

$$Q_{n,t+1}=max\{Q_{n,t}-{\mu }_{n,t}+{\lambda }_{n,t},0\},\mathrm{for}n\in \mathcal{N}$$

(2)

where ${\mu }_{n,t}$ refers to the number of tasks executed by node n at time t, as determined by the node’s processing power. The aggregated task queue represents the total workload of UAVs and satellites. It is defined as the sum of individual task queues across all nodes of the same type as follows:

$$Q_{\mathcal{N},t}=\sum _{n\in \mathcal{N}}{Q}_{n,t}$$

(3)

The dynamic updates for the aggregated task queues can be formulated as follows [20]:

$$Q_{\mathcal{N},t+1}=\sum _{n\in \mathcal{N}}max\{Q_{n,t}-{\mu }_{n,t}+{\lambda }_{n,t},0\}$$

(4)

$Q_{\mathcal{N},t}$ provides a system-level view of the task load across all UAVs and satellites, enabling efficient resource allocation and load balancing decisions.

2.3. Communication Model

In SAGIN, IoT devices communicate with UAVs and satellites through wireless channels. The quality of communication is determined by the channel performance, which varies depending on the node capabilities and environmental factors. This section outlines the channel gain models for ground-to-UAV and ground-to-satellite links.

2.3.1. UAV Communication Link

We consider air–ground communication channels in the Ultra High Frequency (UHF) band. Let $d_{i,u,t}$ represent the distance from the IoT device i to the UAV u at time t as follows [21]:

$$d_{i,u,t}=\sqrt{H_u^2+{\parallel w_{u,t}-w_i\parallel }^2}$$

(5)

We define $H_u$ as the UAV’s altitude and $w_{u,t}$ as its horizontal location at time t. The variable $w_i$ corresponds to the horizontal coordinates of the IoT device i, where i is drawn from the set $\mathcal{I}$ of all devices. The large-scale fading component ${\delta }_{i,u,t}$ caused by path loss is expressed as [22,23]:

$${\delta }_{i,u,t}={\beta }_0{d}_{i,u,t}^{-ϵ}$$

(6)

where ${\beta }_0$ denotes the channel coefficient measured at a reference distance $d_0=1\mathrm{m}$, and $ϵ$ characterizes the signal attenuation rate over distance. To account for multipath effects, the fine-grained fading variable H is characterized using a Rician distribution [24]:

$$H=\sqrt{{\displaystyle \frac{\partial }{\partial +1}}}{H}_0+\sqrt{{\displaystyle \frac{1}{\partial +1}}}{H}_{\Delta }$$

(7)

Here, ∂ stands for the Rician K-factor, indicating the ratio of dominant to scattered signal power. $H_0$ captures the deterministic Line-of-Sight (LoS) contribution, while $H_{\Delta }$ reflects the Non-Line-of-Sight (NLoS) component modeled as a Rayleigh random variable. At time slot t, the channel gain $h_{i,u,t}$ for the wireless connection between UAV u and ground IoT device i is described as [25]:

$$h_{i,u,t}={\delta }_{i,u,t}H$$

(8)

The uplink data rate for IoT devices offloading tasks to a UAV at time t is formulated as follows [26]:

$${\varphi }_{i,u,t}=u_u\left(i\right)B_u{log}_2\left(1+{\displaystyle \frac{p_i^t{h}_{i,u}^t}{{\sum }_{j=1,j\ne i}^I{p}_j^t{h}_{j,u}^t+{\sigma }^2}}\right)$$

(9)

Here, $u_u\left(i\right)$ denotes the portion of bandwidth assigned to IoT device i, while $B_u$ indicates the total bandwidth resource available at the UAV. The term $p_{i,u}^t$ represents the transmit power for device i, and ${\sigma }^2$ corresponds to the background noise power. ${\sum }_{j=1,j\ne i}^N{p}_{j,u}^t{h}_{j,u}^t$ represents interference from other devices and noise.

2.3.2. Satellite Communication Link

In terrestrial IoT devices, the dimensions of the antennas can considerably influence the achievable wireless transmission rates. Because antenna size is typically inversely proportional to operating frequency, higher-frequency systems often require smaller antennas. Therefore, in satellite communication, the Ku and Ka bands are commonly used for communication between terrestrial IoT devices and satellites [27]. The path loss $L_p(f_l,d_{i,l,t})$ in free-space conditions is expressed as follows [28]:

$$L_p(f_l,d_{i,l}^t)=\zeta +20log\left(d_{i,l}^t\right)+20log\left(f_l\right)+A_{\mathrm{env}}$$

(10)

where $f_l$ denotes the satellite operating frequency in MHz, and $d_{i,l}^t$ represents the link distance between IoT device i and satellite l at time t. The constant $\zeta =32.44$ represents the free-space path loss offset in MHz and kilometers. Environmental attenuation $A_{\mathrm{env}}$ accounts for factors such as rain fade and atmospheric absorption, which significantly affect channel gain, especially at higher frequencies. For simplicity, $A_{\mathrm{env}}$ can be modeled as a constant $A_{\mathrm{env}}=F_{\mathrm{rain}}$, where $F_{\mathrm{rain}}$ represents the average attenuation due to rain fade. The channel gain $h_{i,l,t}$ for the communication link at time t is modeled as [29]:

$$h_{i,l}^t=G_l-L_p(f_l,d_{i,l}^t)-A_{\mathrm{env}}$$

(11)

Let $G_l$ be the transmit gain of the satellite. At time t, the uplink throughput achieved by IoT devices communicating with it is computed as follows:

$${\varphi }_{i,l,t}=u_l\left(i\right)B_l{log}_2\left(1+{\displaystyle \frac{p_{i,l}^t{h}_{i,l}^t}{{\sum }_{j=1,j\ne i}^I{p}_{j,l}^t{h}_{j,l}^t+{\sigma }^2}}\right)$$

(12)

In this equation, $u_l\left(i\right)$ denotes the bandwidth allocated to IoT device i, $B_l$ denotes total available bandwidth of satellite l, $p_{i,l}^t$ represents transmission power allocated to device i, and ${\sigma }^2$ indicates noise power. The term ${\sum }_{j=1,j\ne i}^N{p}_{j,s}^t{h}_{j,s}^t$ denotes interference from other devices and noise.

2.4. Computation Model

In heterogeneous edge computing environments, tasks ${\mathcal{O}}_t^i$ arriving at the i-th IoT device at time t are characterized by their task categories ${\Theta }_{i,t}\in {\mathcal{T}}_{\mathrm{type}}=\{{\Theta }_1,{\Theta }_2,\dots ,{\Theta }_K\}$. The task categories vector is defined as follows:

$${\Theta }_{i,t}={\left[\begin{array}{cccc}{\Theta }_{i,t}^{\left(1\right)}& {\Theta }_{i,t}^{\left(2\right)}& \dots & {\Theta }_{i,t}^{\left(K\right)}\end{array}\right]}^{\top }$$

(13)

where K is the number of predefined task categories, such as computation-intensive, parallel computing, or real-time signal processing types.

Each UAV or satellite node consists of multiple heterogeneous computing devices, such as a Central Processing Unit (CPU), Graphics Processing Unit (GPU), Field Programmable Gate Array (FPGA), and other specialized processors. Let the set of all computing resource characteristics supported by these heterogeneous devices be denoted as follows $\mathcal{X}$:

$$\mathcal{X}=\{x_1,x_2,\dots ,x_z\}$$

(14)

where each $x_z$ represents a distinct type of computing resource, and z denotes the total number of computing resource characteristics in the system.

To represent the availability of each resource characteristic at different nodes, we define a binary resource characteristics indicator matrix $\mathbf{C}\left(t\right)\in {\{0,1\}}^{n\times z}$, where n is the total number of nodes that include UAVs and satellites. The nodes indexed from 1 to j correspond to UAVs, while the nodes indexed from $j+1$ to n correspond to satellites. The i-th row of the matrix corresponds to node i, and the z-th column corresponds to the type of computing resources $x_z$.

The matrix is formally defined as:

$$\mathbf{C}(t)=\left[\begin{array}{cccc}{c}_1^{x_1}& c_1^{x_2}& \dots & c_1^{x_z}\\ c_2^{x_1}& c_2^{x_2}& \dots & c_2^{x_z}\\ ⋮& ⋮& \ddots & ⋮\\ c_j^{x_1}& c_j^{x_2}& \dots & c_j^{x_z}\\ c_{j+1}^{x_1}& c_{j+1}^{x_2}& \dots & c_{j+1}^{x_z}\\ ⋮& ⋮& \ddots & ⋮\\ c_n^{x_1}& c_n^{x_2}& \dots & c_n^{x_z}\end{array}\right]$$

Each element $c_n^{x_z}\left(t\right)$ in the matrix represents a binary indicator of whether node n supports the type of computation resource $x_z$ at time t. Specifically, $c_n^{x_z}\left(t\right)=1$ indicates that node n is equipped with resource characteristics $x_z$, enabling it to execute tasks that rely on this type of hardware. In contrast, $c_n^{x_z}\left(t\right)=0$ implies that the node lacks this resource.

The UAV and satellite nodes consist of multiple individual devices. Each node n that can represent a UAV or a satellite has a corresponding resource vector $c_n$, which characterizes its computational, memory, and communication capabilities. For the n-th node, the resource vector is as follows:

$$c_n={\left[\begin{array}{cccc}{c}_n^{\left(1\right)}& c_n^{\left(2\right)}& \dots & c_n^{\left(k\right)}\end{array}\right]}^{\top }$$

(15)

where k represents the number of resource characteristics, and each $c_n^{\left(q\right)}$, $q\in \{1,2,\dots ,k\}$, describes a specific resource characteristic of the corresponding node.

To evaluate the compatibility between a task $R_{i,t}$ and the computational resources of a specific node n, we define a compatibility coefficient ${\psi }_{i,n,t}$, which quantifies the suitability of offloading the task to the node device n. The coefficient is calculated as follows:

$${\psi }_{i,n,t}={\alpha }_{i,t}^{\top }M{c}_n$$

(16)

where ${\alpha }_{i,t}$ represents the task categories vector, $c_n$ denotes the resource vector of node device n, and $M\in {\mathbb{R}}^{m\times k}$ is a weight matrix. The weight matrix M adjusts the relative importance of different task categories and resource characteristics, ensuring that the compatibility calculation aligns with the specific requirements of the application scenario.

The transmission delay $T_{i,n,t}^{\mathrm{trans}}$ for node device n is calculated using the transmission rate as follows:

$$T_{i,n,t}^{\mathrm{trans}}={\displaystyle \frac{D_{i,t}}{{\varphi }_{i,n,t}}}$$

(17)

where $D_{i,t}$ is the data size of task $R_{i,t}$, and $R_{i,n,t}$ is the transmission rate between IoT device i and node n.

The computation delay $T_{i,n,t}^{\mathrm{comp}}$ for node device n is adjusted by the adaptability coefficient ${\psi }_{i,n,t}$ as follows:

$$T_{i,n,t}^{\mathrm{comp}}={\displaystyle \frac{1}{{\psi }_{i,n,t}}}{\displaystyle \frac{D_{i,t}·C_{i,t}}{f_n}}$$

(18)

where $C_{i,t}$ denotes the computation intensity of the task, and $f_n$ denotes the computational capacity of node device n.

The total time delay $T_{i,n,t}$ for node n consists of transmission and computation components as follows:

$$T_{i,n,t}=T_{i,n,t}^{\mathrm{trans}}+T_{i,n,t}^{\mathrm{comp}}$$

(19)

The energy utilization of IoT device i comprises transmission, computation, and idle energy consumption. The amount of energy consumed during data transmission to node n is calculated as follows:

$$E_{i,n,t}^{\mathrm{trans}}=P_{i,n,t}^{\mathrm{trans}}·T_{i,n,t}^{\mathrm{trans}}$$

(20)

where $P_{i,n,t}^{\mathrm{trans}}$ refers to the transmit power of device i when communicating with node n.

The computation related energy for device i is given by the following:

$$E_{i,n,t}^{\mathrm{comp}}=P_n^{\mathrm{comp}}·T_{i,n,t}^{\mathrm{comp}}$$

(21)

where $P_n^{\mathrm{comp}}$ is the processing power of node n.

The idle energy consumption is computed as follows:

$$E_{i,t}^{\mathrm{idle}}=P_i^{\mathrm{idle}}·T_{i,t}^{\mathrm{idle}}$$

(22)

where $P_i^{\mathrm{idle}}$ refers to the standby power of device i, and $T_{i,t}^{\mathrm{idle}}$ denotes the duration for which device i remains inactive. The total energy expenditure of device i in interaction with node n is as follows:

$$E_{i,n,t}=E_{i,n,t}^{\mathrm{trans}}+E_{i,n,t}^{\mathrm{comp}}+E_{i,t}^{\mathrm{idle}}$$

(23)

2.5. Problem Formulation

We construct an optimization task $\mathcal{P}$ aiming to lower scheduling costs in SAGIN by accounting for the following three main criteria: latency, energy, and queue size. The weights ${\omega }_t$, ${\omega }_e$, and ${\omega }_q$ determine their relative impact. The formulation of $\mathcal{P}$ is presented as follows:

$$\begin{array}{cc}\hfill \mathcal{P}:& min\sum _{i\in \mathcal{I}}\sum _{n\in \mathcal{N}}\sum _{t\in \mathcal{T}}\left[({\omega }_t{T}_{i,n,t}+{\omega }_e{E}_{i,n,t}+{\omega }_q{Q}_{n,t}\right]\hfill \\ \hfill \mathrm{subject}\mathrm{to}:\\ \hfill C_1:& a_t^i\in \{0,1\},\forall i\in \mathcal{I},t\in \mathcal{T},\hfill \\ \hfill C_2:& \sum _{i\in \mathcal{I}}(1-a_t^i)B_u+a_t^i{B}_s\le B_{\max },\forall n\in \mathcal{N},t\in \mathcal{T},\hfill \\ \hfill C_3:& \sum _{i\in \mathcal{I}}{a}_t^i{T}_{i,n,t}\le T_{n,t}^{\mathrm{vis}},\forall n\in \mathcal{N},t\in \mathcal{T},\hfill \\ \hfill C_4:& \sum _{i\in \mathcal{I}}\sum _{n\in \mathcal{N}}\sum _{t\in \mathcal{T}}{E}_i^{\max }-T_{i,n,t}^{\mathrm{trans}}{P}_{i,n,t}^{\mathrm{trans}}-E_{i,t}^{\mathrm{idle}}=E_i^{\mathrm{rem}}\ge 0,\hfill \\ \hfill C_5:& Q_{n,t}\le Q_{n,t}^{\max }\forall n\in \mathcal{N},t\in \mathcal{T}.\hfill \end{array}$$

The objective is the average cost across all tasks, nodes, and time slots. Constraint $C_1$ ensures that the offloading decision $a_t^i$ is binary, indicating the task is executed locally or offloaded. Constraint $C_2$ limits bandwidth usage to the maximum available bandwidth. Constraint $C_3$ restricts task completion time to the node’s available processing time. Constraint $C_4$ ensures energy consumption does not exceed the device’s maximum capacity. Constraint $C_5$ limits the queue length to avoid excessive backlog at each node. These constraints regulate delay, resource usage, and system balance under heterogeneous network conditions.

It is important to clarify the nature of the proposed optimization problem $\mathcal{P}$ in terms of convexity and computational complexity. The problem involves discrete decision variables $a_t^i\in \{0,1\}$, which represent binary offloading choices. Due to the presence of such integer variables, problem $\mathcal{P}$ falls into the category of Mixed-Integer Linear Programming (MILP). MILP problems are known to be non-convex and NP-hard, meaning that they cannot, in general, be solved efficiently to global optimality using conventional convex optimization techniques [30,31]. This non-convexity arises not from the objective function or constraint linearity, but from the discrete nature of the decision space introduced by integer variables. To address this challenge, we propose a DRL-based solution framework in Section 3. This framework is specifically designed to efficiently handle the high-dimensional and discrete decision space of MILP-type problems, such as ours, and reduce the computational burden associated with classical optimization solvers.

3. Algorithm Design

3.1. Markov Transformation

Considering the optimization problem $\mathcal{P}$, the long-term objectives need to be integrated and treated in a multi-step decision-making framework. We can transform it into a Markov decision process (MDP) problem, which is typically defined by a four-tuple (S, A, P, R) [32]. The elements of (S, A, P, R) are defined as follows:

State: At time t, the system state $s_t\in \mathcal{S}$ comprises various elements that reflect the system’s condition as follows: $s_t^i=\left[D_t^i,C_t^i,{\Theta }_t^i,E_{i,t}^{\mathrm{rem}},E_{u,t}^{\mathrm{rem}},h_{i,u,t},h_{i,l,t},T_{l,t}^{\mathrm{vis}},Q_{u,t},Q_{l,t}\right].$

Action: The control input $a_t\in A$ at slot t includes the following: $a_t=\{a_t^i,B_{i,t},P_{i,n,t}\mid i\in \mathcal{I},n\in \mathcal{N}\}$.

State Transition: Given the current state $s_t$ and action $a_t$, the system’s evolution to the next state $s_{t+1}$ occurs with the following probability: $P(s_{t+1}\mid s_t,a_t)$

Reward: To reduce the cumulative cost in the SAGIN architecture, the immediate reward at time t is expressed as follows: $r(s_t,a_t)=-{\sum }_{i\in \mathcal{I}}{\sum }_{n\in \mathcal{N}}{\sum }_{t\in \mathcal{T}}\left[{\omega }_t{T}_{i,n,t}+{\omega }_e{E}_{i,n,t}+{\omega }_q{Q}_{n,t}\right]$.

3.2. TM-DDPG Based Offloading Algorithm

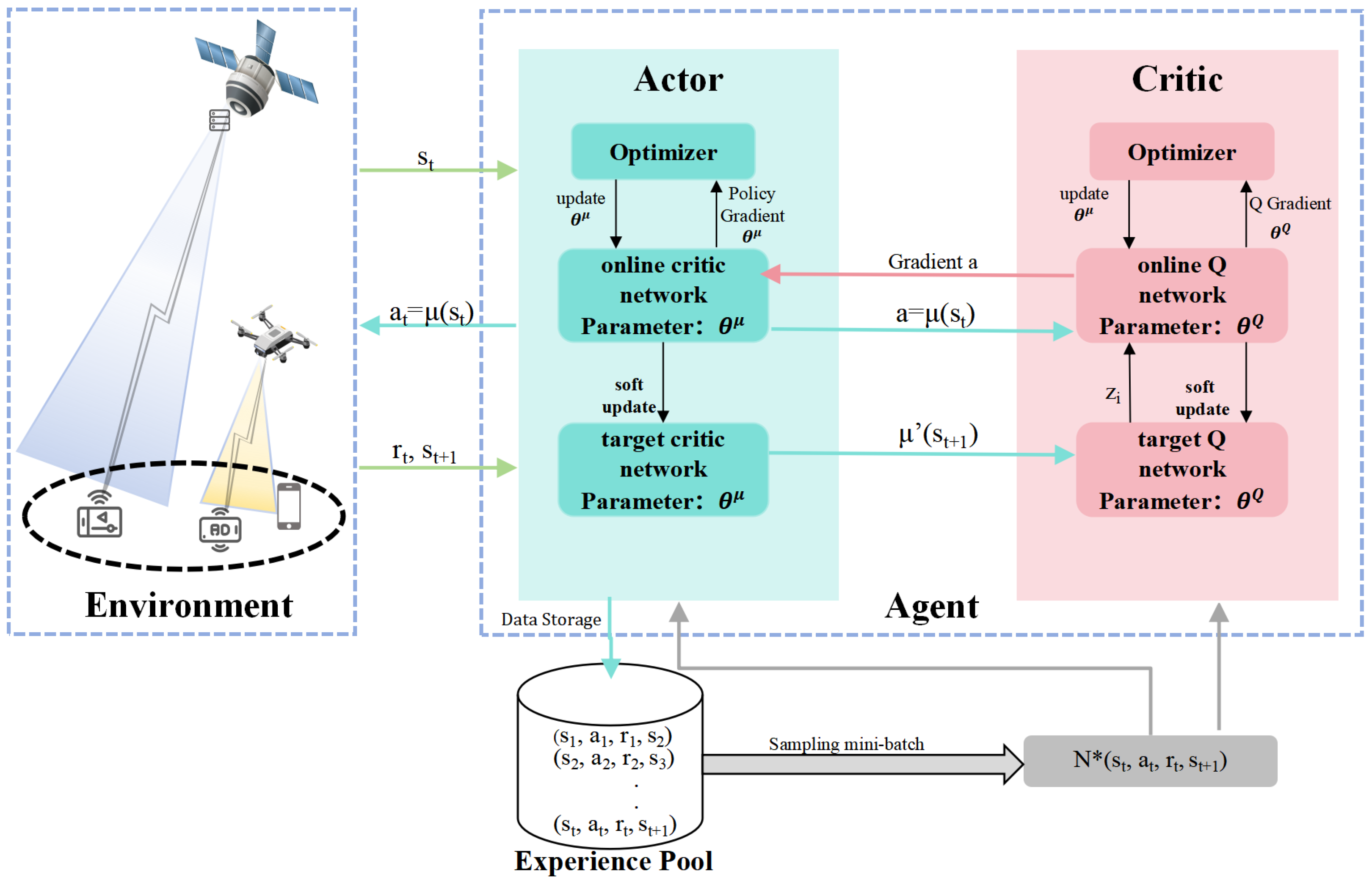
As shown in Figure 2, the agent in the type matching enhanced deep deterministic policy gradient (TM-DDPG) algorithm comprises the following two neural networks: an actor and a critic, parameterized by ${\theta }^a$ and ${\theta }^c$, respectively. The actor network interaction with the SAGIN environment results in the current state, $S_{i,k}$ being obtained. Based on this state, an appropriate action, $a_{i,k}$, is selected. The selected action then generates the next state $S_{i,k+1}$. The reward received by the agent R is recorded in the experience replay buffer to facilitate subsequent learning and optimization. The actor network’s parameter set, denoted by the symbol ${\theta }^a$, is iteratively optimized based on the collected experiences through the process of gradient updating.

Meanwhile, the actor network’s target network selects the corresponding action $a_{i,k+1}$ based on the next state $S_{i,k+1}$ output by the current network and updates the target network’s parameter set ${\theta }^{a^{\prime }}$ accordingly. To evaluate the effectiveness of the policy, the critic network calculates the Q-value for the given state and action combination (S, A). Then it updates the parameter set of the current network ${\theta }^{c^{\prime }}$, based on this Q-value. Using the current state and action, the critic target network derives the target Q-value and correspondingly refines its parameters ${\theta }^{c^{\prime }}$. The Q-value represents the total expected return that the agent will receive by performing a specific action in a particular state. It depends not only on the immediate reward, but also on the expectation of rewards in the future.

The Q-value update follows the principle of the Bellman equation, expressed as follows:

$$Q(S,A)=R+\gamma maxQ(S^{\prime },A^{\prime })$$

(24)

Here, $maxQ(S^{\prime },A^{\prime })$ refers to the highest estimated Q-value following action $A^{\prime }$ in state $S^{\prime }$, while $Q(S,A)$ indicates the present value estimate for the current state-action pair. The critic network is gradually refined by reducing the discrepancy between this estimate and the target Q-value. The TM-DDPG algorithm guides the actor network toward an optimal policy for maximizing long-term returns. To this end, the parameters ${\theta }^a$ are optimized by maximizing the corresponding policy objective function, as follows:

$$J\left(\theta \right)=-{\displaystyle \frac{1}{N}}\sum _{j=1}^{N}Q(S_j,A_j;{\theta }^a)$$

(25)

Here, N denotes the total number of data samples. The critic network’s goal is to train an optimal value function by reducing the loss function to update the current network parameters ${\theta }^c$. The loss function is defined as follows: Where $\tau$ is the update coefficient. The TM-DDPG algorithm demonstrates significant advantages in the task offloading problem within the SAGIN edge computing environment. It can handle complex continuous action spaces and dynamically adjust policies to cope with time-varying network environments. It demonstrates significant advantages in latency optimization and energy consumption reduction. TM-DDPG optimizes the policy (actor) and the value function (critic) through the agent–critic structure of the agent network. This structure improves learning efficiency and enables agents to adapt quickly to dynamic network environments. TM-DDPG optimizes the immediate reward at each time step and considers the long-term task offloading returns, thereby improving the system’s overall performance. Therefore, when addressing the task offloading problem in the SAGIN environment, TM-DDPG can achieve efficient, flexible, and intelligent offloading decisions while meeting the optimization objectives.

$$L\left({\theta }^{\prime }\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(Q(S,A)-Q(S^{\prime },A^{\prime })\right)}^2$$

(26)

where $Q(S^{\prime },A^{\prime })$ is the target Q-value, and $Q(S,A)$ is the current Q-value. The agent updates the target network parameter set using a soft update method. This method smoothly adjusts the target network parameters towards the current ones, preventing sudden changes and ensuring stable training as follows:

$${\theta }_i^{a^{\prime }}\leftarrow \tau {\theta }_i^a+(1-\tau ){\theta }_i^{a^{\prime }}{\theta }_i^{c^{\prime }}\leftarrow \tau {\theta }_i^c+(1-\tau ){\theta }_i^{c^{\prime }}$$

(27)

To evaluate the computational overhead of the TM-DDPG algorithm, we analyze the complexity of its core learning components—the actor and critic networks, as described in Algorithm 1. These networks take the global state vector $s_t\in \mathcal{S}$ as input, which is formed by concatenating the local observations from all IoT devices. Each per-device state $s_t^i\in {\mathbb{R}}^{d_s}$, where $d_s=9+K$ denotes the state dimension and K is the number of predefined task categories. Given I IoT devices, the total input dimension becomes $I\times d_s$. We denote by $L_h$ the number of hidden layers in each neural network and by H the number of neurons per hidden layer. Suppose the training is performed using a batch size of J. Then, the computational complexity of a single training iteration is approximately $\mathcal{O}\left(J{L}_{h}H{\left(I{d}_s\right)}^2\right)$. Let Z denote the total number of training episodes. Then the overall time complexity of TM-DDPG is $\mathcal{O}\left(ZJ{L}_{h}H{\left(I{d}_s\right)}^2\right)$ [33].

Algorithm 1 M-DDPG algorithm in the SAGIN scenario

1: Initialize experience replay buffer and network parameters for the user terminal agent: ${\theta }^a$, ${\theta }^c$, ${\theta }^{c^{\prime }}$, ${\theta }^{a^{\prime }}$; 2: for$episode=1$ to M do 3:     Initialize SAGIN environment parameters and construct an integrated space-air-ground task offloading network; 4:     Initialize the agent’s state $S_0$; 5:     for $t=1$ to T do 6:         Derive action $A_t$ from state $S_t$ using the policy output of the Actor network; 7:         Perform $A_t$ to transition to $S_{t+1}$ and receive instantaneous reward $R_t$; 8:         Save the tuple $(S_t,A_t,R_t,S_{t+1})$ into the experience memory; 9:         if t thenhe experience buffer is not full 10:            Continue interactions; 11:         else 12:            Randomly sample $(S_t,A_t,R_t,S_{t+1})$ from the experience buffer; 13:            Compute the target value; 14:            Compute the critic network loss function and update the critic network parameters ${\theta }^c$; 15:            Update the actor network parameters ${\theta }^a$ to maximise the policy objective function; 16:         end if 17:     end for 18:     Soft update the target network parameters ${\theta }^{c^{\prime }}$ and ${\theta }^{a^{\prime }}$; 19: end for

In addition to time complexity, we also analyze the space complexity of the TM-DDPG algorithm. The primary contributor to memory consumption is the experience replay buffer used to store transitions $(s_t,a_t,r_t,s_{t+1})$ for training. Each transition takes up $\mathcal{O}\left(I{d}_s\right)$ space. Therefore, the overall memory complexity of the replay buffer is $\mathcal{O}\left(\mathrm{W}I{d}_s\right)$, where W denotes the buffer size. Additionally, the actor and critic networks require memory for storing their parameters. Each network has approximately $\mathcal{O}(L_h{H}^2+HI{d}_s)$ parameters. Since both actor and critic (along with their target networks) are maintained, the total parameter memory cost becomes $\mathcal{O}\left(4(L_h{H}^2+HI{d}_s)\right)$. Combining both parts, the total space complexity is $\mathcal{O}(\mathrm{W}I{d}_s+L_h{H}^2+HI{d}_s)$, where the replay buffer typically dominates.

4. Performance Evaluation

In this section, we extend the analysis by introducing three additional reinforcement learning variants for comparison. Non-DDPG refers to the original Deep Deterministic Policy Gradient algorithm without type-matching. TM-TD3 denotes the type-matching-enhanced Twin Delayed Deep Deterministic Policy Gradient (TD3). Non-TD3 represents the standard TD3 algorithm without the type-matching mechanism. These variants are included to assess the generalization capability of the type-matching design across different algorithmic frameworks and to evaluate its contribution beyond DDPG-based methods.

The algorithms in this paper are implemented in a Python 3.11 environment and run on a Windows 10 system equipped with an NVIDIA RTX 4090Ti GPU and 16GB RAM. Additionally, the deep reinforcement learning environment is based on Pytorch 2.2.2 and Numpy 1.26.4.

Table 1. Simulation parameters.

Symbol	Value	Description
$f_l$	20 GHz	IoT device with satellite communication frequency
$B_l$	50 MHz	IoT device with satellite bandwidth
$F_{\mathrm{rain}}$	12.2 dB	Rain attenuation
$f_{\mathrm{UAV}}$	400 MHz	IoT device with UAV communication frequency
$B_u$	10 MHz	IoT device bandwidth
∂	6	Rician fading factor
$E_{u,\max }$	100 kJ	Maximum energy of UAV
${\sigma }^2$	–70 dBm	Communication noise
$D_t^{\left(i\right)}$	[100 Kb, 2 Mb]	Task data size of the i-th IoT device
$p_{i,\max }$	6.3 W	Maximum transmitting power of IoT device
$E_{i,\max }$	30 J	Maximum energy of IoT device
$v_{\mathrm{UAV}}$	[0, 50] m/s	UAV moving speed

summarizes the primary simulation parameters employed in the SAGIN-MEC scenario, which involves communications among satellites, UAVs, and IoT devices. The parameters include communication frequencies and bandwidths for both satellite and UAV links, energy and transmission power constraints of IoT devices and UAVs, channel characteristics such as rain attenuation and fading factors, task data sizes, and the velocity range of UAVs. These settings define the network conditions under which the proposed framework is evaluated. Some representative parameter configurations for the SAGIN-MEC environment are listed in the table below [34].

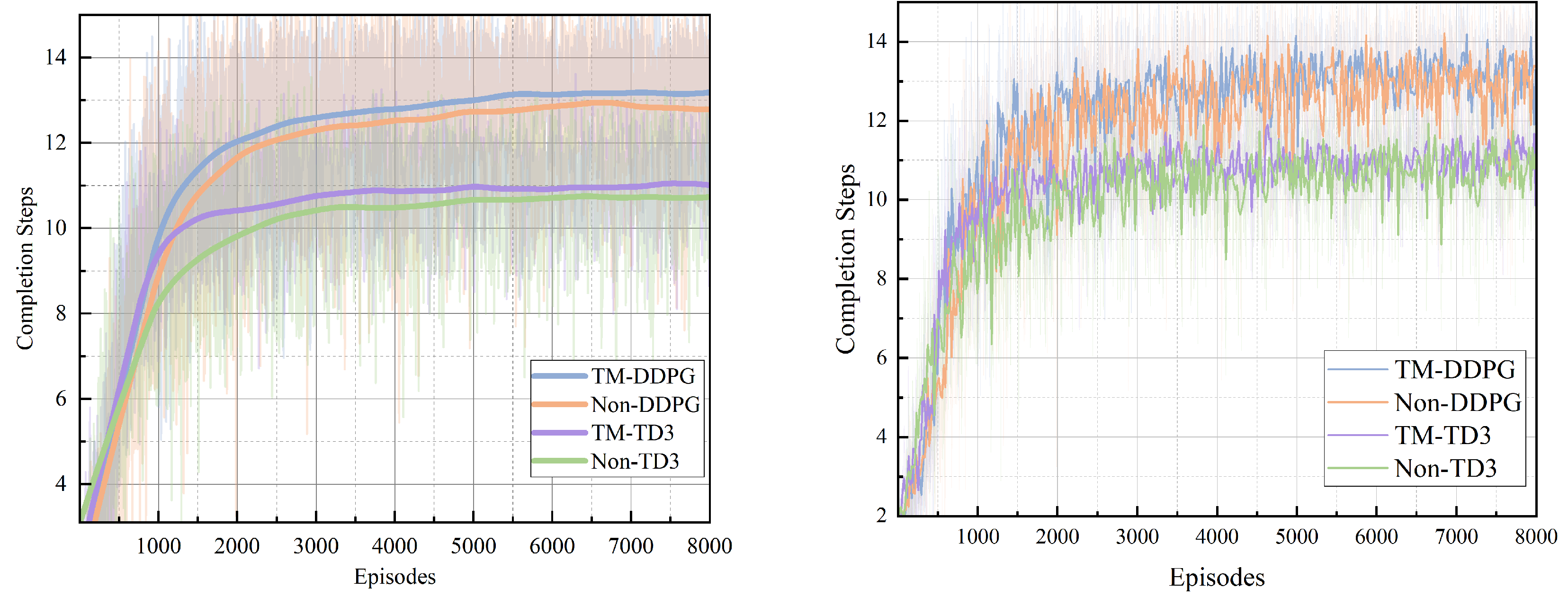
Figure 3 illustrates the learning performance of four reinforcement learning algorithms over 8000 training episodes, where the x-axis represents the number of episodes and the y-axis denotes the average task completion steps per episode. Higher values indicate more efficient task execution under the learned policy. The figure compares TM-DDPG, Non-DDPG, TM-TD3, and Non-TD3 to evaluate the effectiveness of the proposed TM enhancement. TM-DDPG demonstrates the most rapid convergence, achieving stable performance above 13 steps after approximately 2000 episodes. This indicates that the TM mechanism enables the agent to quickly adapt to environment dynamics and effectively learn optimal offloading strategies. TM-TD3 also benefits from the enhancement, converging more slowly but maintaining a clear performance margin over Non-TD3 throughout training. Non-DDPG exhibits relatively stable convergence and performs competitively, but consistently lags behind TM-DDPG in both convergence speed and final task completion steps. Non-TD3 shows the slowest learning progress and the lowest asymptotic performance, with significant variance across episodes. TM-TD3 achieves modest improvement, confirming that TM contributes positively across different algorithmic frameworks. The shaded regions around each curve represent the variance over repeated runs, reflecting learning stability. TM-based approaches not only improve mean performance but also reduce fluctuation during training, which is crucial in dynamic environments. Overall, the results validate that task–resource matching significantly enhances both learning efficiency and policy robustness, particularly within the DDPG framework. To provide a clearer view of training stability and short-term variance, we additionally present the right subfigure in Figure 3, which depicts the same metric using a sliding window of 20 episodes. The shaded areas represent variability during training. Compared to Non-TM variants, TM-based algorithms not only demonstrate improved average performance but also significantly reduce variance, which is crucial in dynamic environments. These results confirm that task–resource matching enhancement contributes to both learning efficiency and robustness across different DRL frameworks.

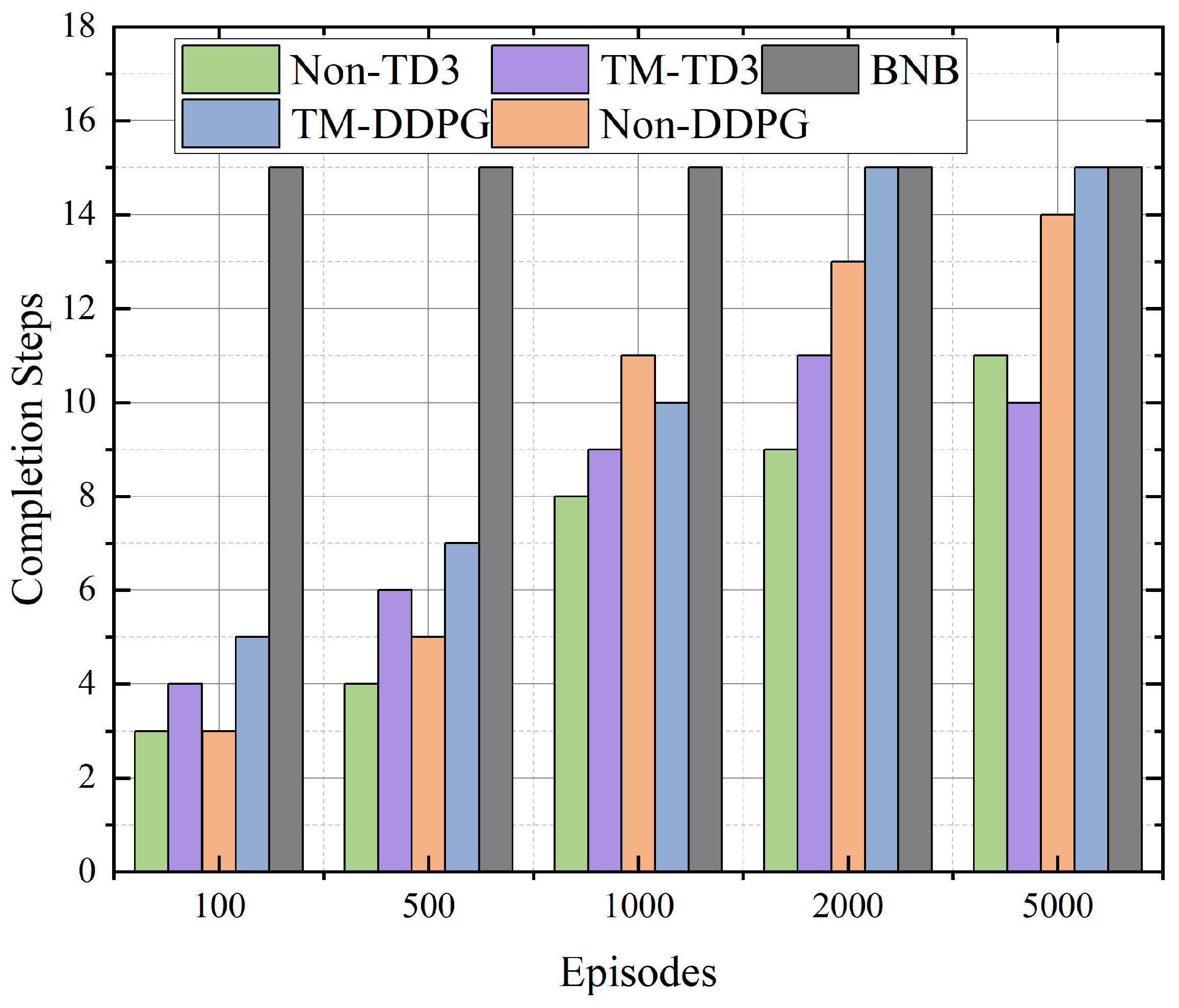
Figure 4 presents the task completion steps of different methods over training episodes, while learning-based approaches improve over time, the Branch-and-Bound (BNB) method achieves the highest number of completion steps. However, BNB is a deterministic optimization algorithm with exponential time complexity. Its performance comes at the cost of substantial computational overhead, making it unsuitable for large-scale or time-constrained environments. In contrast, the proposed TM-DDPG offers a favorable trade-off between performance and efficiency, enabling practical deployment in dynamic offloading scenarios.

Figure 5 shows the training reward curves of TM-DDPG, Non-DDPG, TM-TD3, and Non-TD3 over 8000 episodes. The reward is computed as a weighted combination of task latency, energy consumption, and queue length, reflecting the quality of each offloading decision. Higher reward values indicate more efficient and balanced task execution. TM-DDPG achieves the highest reward and exhibits rapid convergence within the first 1500 episodes, followed by stable performance with low variance. TM-TD3 also shows continuous improvement and maintains a moderate advantage over Non-TD3 throughout training, though it converges more slowly and reaches a slightly lower peak than TM-DDPG. Non-DDPG gradually increases but plateaus at a lower level, indicating less efficient policy learning. Non-TD3 demonstrates high fluctuation and limited reward gain, suggesting instability and poorer decision-making capability. The shaded regions around each curve represent the variance across multiple runs, indicating learning stability. TM-enhanced algorithms not only reach higher reward levels but also reduce variance, which is critical in dynamic environments. These results validate the effectiveness of the task–resource matching mechanism in improving policy quality and training stability, with particularly significant gains observed under the DDPG framework.

Figure 6 presents the reward distributions of TM-DDPG, Non-DDPG, TM-TD3, and Non-TD3 during the first 100 training episodes. Each boxplot illustrates the distribution of episode rewards using the interquartile range, with whiskers indicating the minimum and maximum observed values. Higher median rewards and narrower boxes indicate better and more consistent performance. TM-DDPG achieves a significantly higher median reward and a tighter distribution than Non-DDPG, suggesting that the task–resource matching (TM) mechanism enables faster policy adaptation and more effective early-stage decision-making. In contrast, TM-TD3 shows a lower median and wider spread than Non-TD3, indicating unstable learning and greater variability. This may result from the interaction between TD3’s delayed policy updates and the TM mechanism, which could disrupt learning in the early phase. Overall, the TM mechanism enhances early performance in DDPG but introduces instability when combined with TD3.

Figure 7 shows the reward distributions over the final 100 episodes after training convergence. TM-DDPG consistently outperforms all other variants, achieving the highest median reward with minimal variance, reflecting robust policy stability and superior decision quality. Non-DDPG follows with slightly lower rewards and a wider spread. TM-TD3 achieves a modest improvement over Non-TD3 in both median and variability, but the gap between the two is smaller compared to the DDPG variants. Both TD3-based algorithms exhibit greater variance than DDPG-based ones, indicating less stable convergence behavior. These results demonstrate that the TM mechanism significantly improves long-term performance in DDPG, while its effect on TD3 is limited and less reliable.

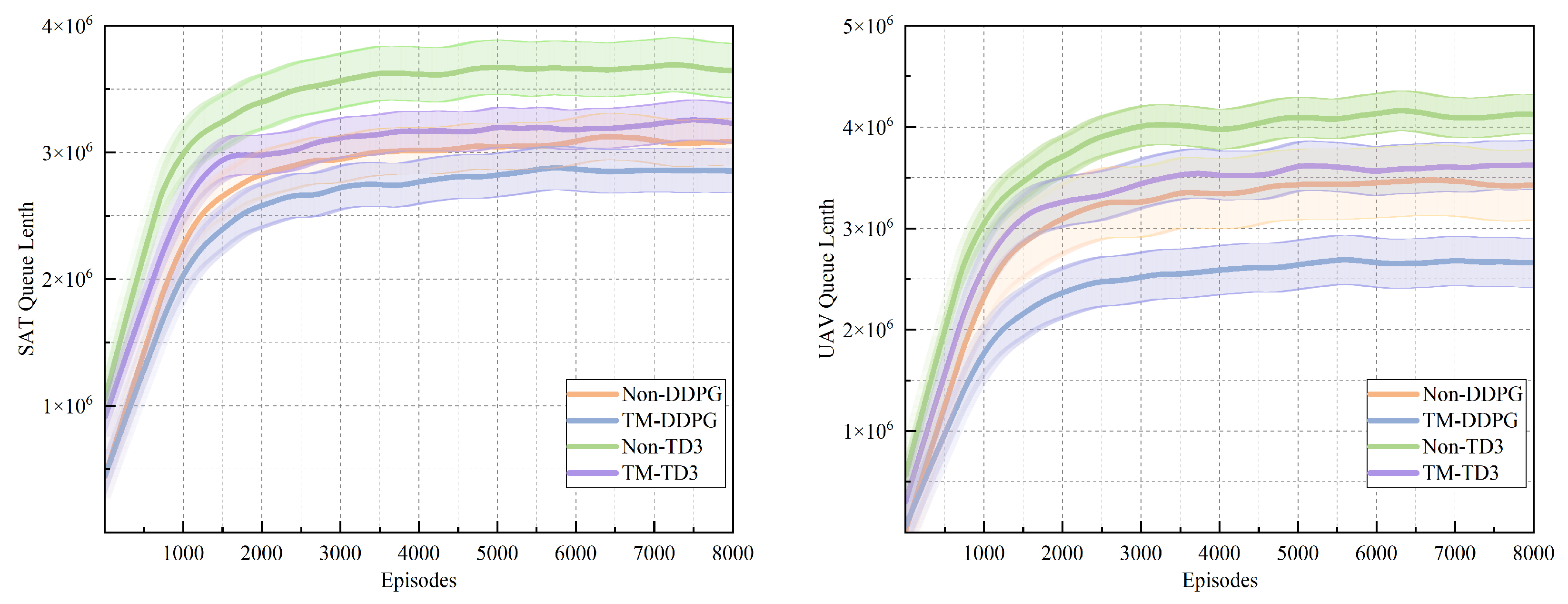
Figure 8 compares the task queue lengths of TM-DDPG, Non-DDPG, TM-TD3, and Non-TD3 on satellite and UAV nodes over 8000 training episodes. The left subfigure shows the queue length on satellite (SAT) nodes, while the right subfigure presents the same metric on UAV nodes. Queue length reflects the degree of task accumulation at each node, which is directly related to system load, latency, and congestion. All algorithms exhibit a sharp increase in queue length during the early training phase, followed by gradual stabilization as their policies converge. TM-DDPG consistently maintains the lowest queue length on both satellite and UAV nodes, indicating more effective task distribution and faster convergence. In contrast, Non-TD3 results in the highest queue length throughout training, suggesting inefficient offloading behavior and greater system pressure. TM-TD3 performs slightly better than Non-DDPG on satellites but worse on UAVs, reflecting mixed effectiveness of the task–resource matching (TM) mechanism in the TD3 framework. The variance bands surrounding each curve represent performance variability across independent runs. TM-DDPG shows both lower queue length and reduced variance, indicating more stable and balanced learning. Overall, the TM mechanism significantly improves load balancing and reduces node congestion, especially when combined with DDPG. This leads to improved system responsiveness and supports more efficient learning of offloading policies.

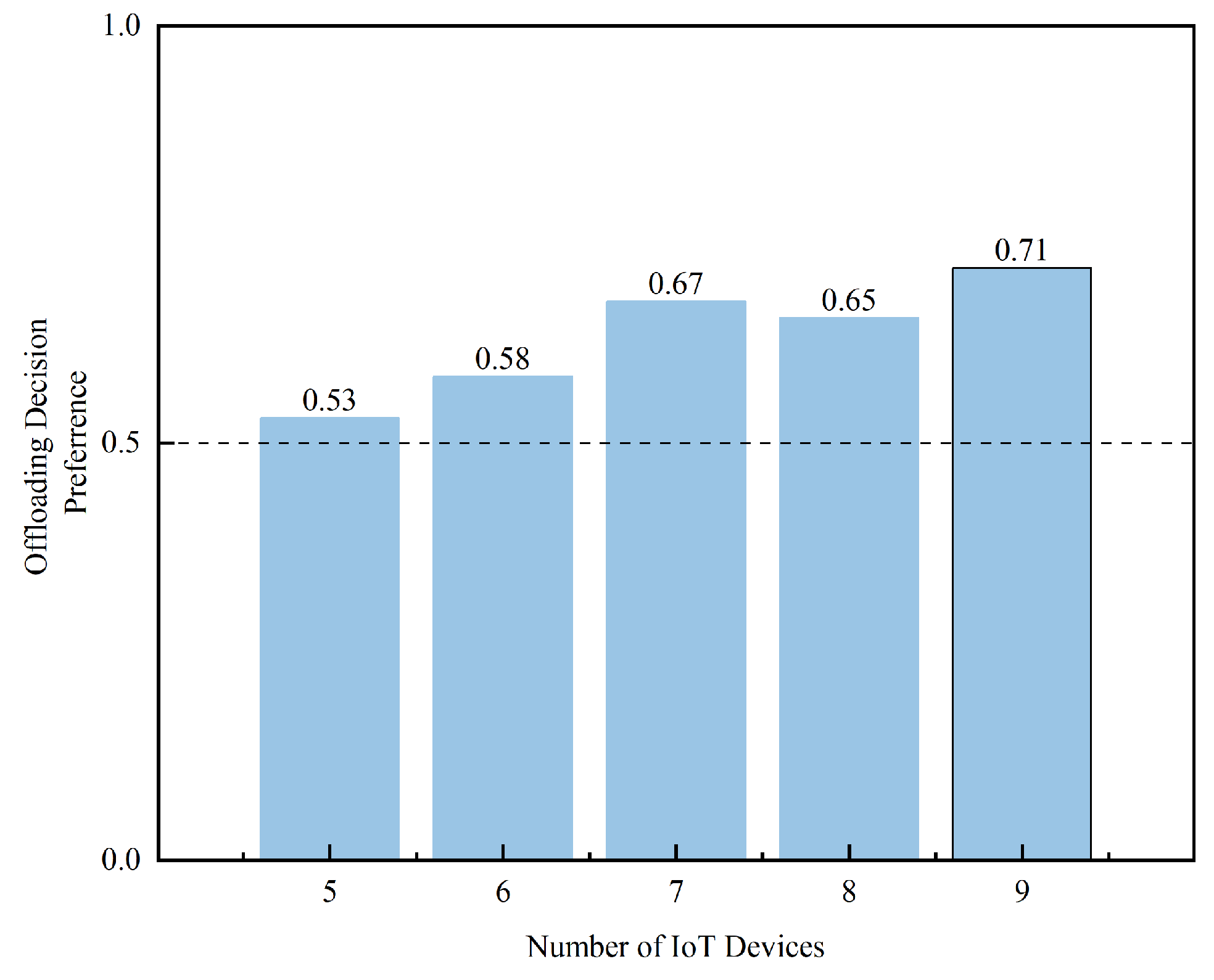
Figure 9 presents the offloading preference learned by TM-DDPG under different numbers of IoT devices, ranging from 5 to 9. The y-axis represents the proportion of offloading decisions directed toward satellite nodes, where a value above 0.5 indicates a preference for satellite over UAV offloading. As the number of IoT devices increases, the preference shifts upward from 0.53 to 0.71. This trend suggests that under higher system load, TM-DDPG increasingly favors satellite nodes due to their stronger processing capacity and higher bandwidth. Satellite links can accommodate more concurrent offloading requests and provide stable performance under traffic pressure. Importantly, the preference never reaches 1.0, indicating that UAVs are still actively selected. Their inclusion is based on real-time environmental factors such as queue length, latency, and transmission cost. TM-DDPG adapts its policy to leverage both UAV and satellite resources, achieving dynamic and balanced load distribution. The resulting strategy reflects a resource-aware and task-sensitive offloading behavior suited to heterogeneous edge environments.

Figure 10 illustrates the average task latency under varying numbers of IoT devices for three different offloading strategies. The latency values are computed as the average of each node device’s local processing delay and task transmission delay, aggregated over multiple episodes after the training process has converged.The Random strategy produces the highest latency across all settings. Its delay increases rapidly as the number of devices grows and peaks at device count eight. The results suggest a lack of effective task allocation. Non-DDPG performs better than Random and keeps lower latency overall. However, its average delay continues to rise with more devices, indicating limited scalability under high load. TM-DDPG achieves the lowest latency across all tested scenarios. Its performance remains stable with minimal fluctuations. The zoomed view shows that TM-DDPG maintains low latency even as the system becomes more congested. This indicates that its offloading policy adapts well to load variations and uses available resources more efficiently.

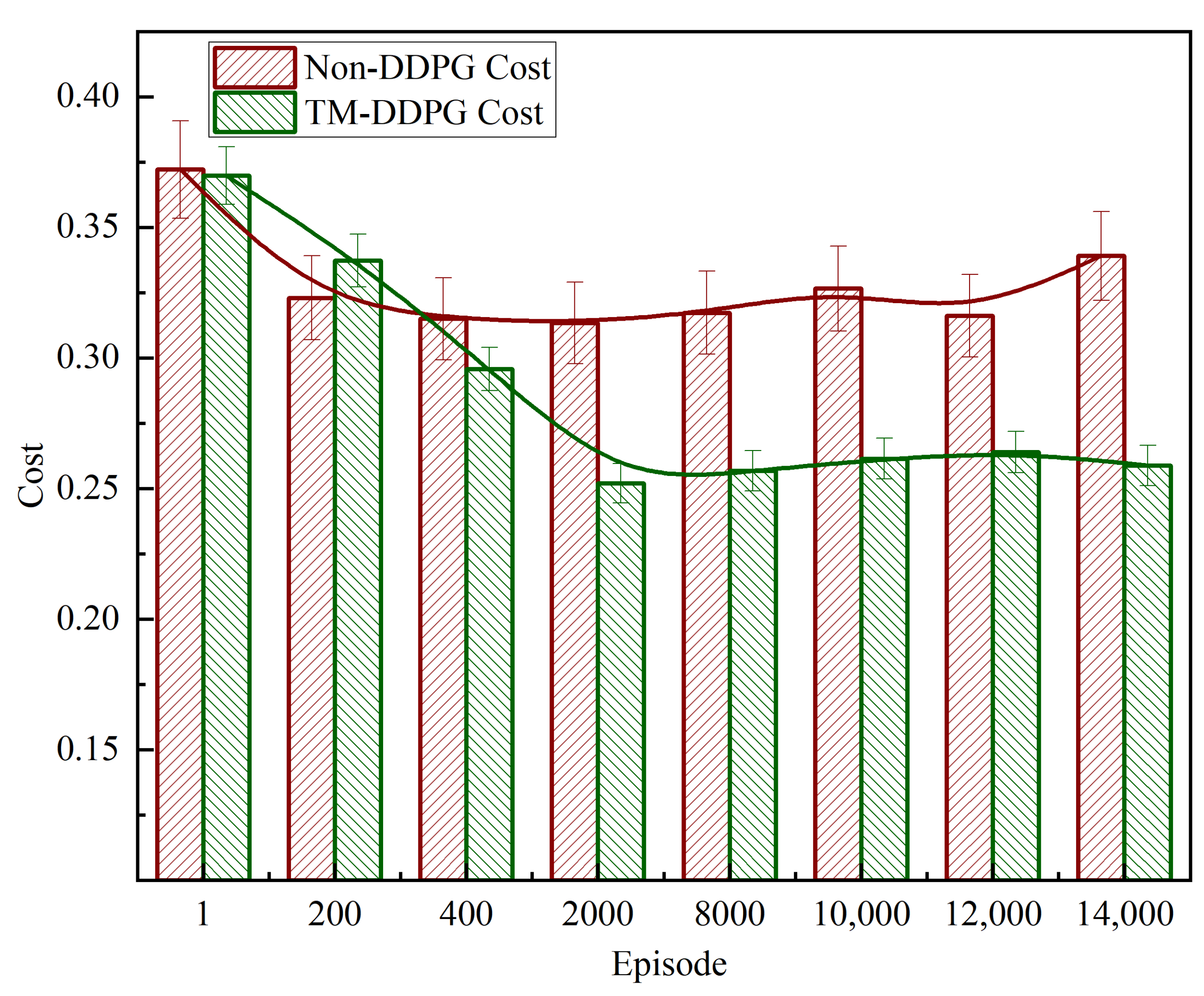
Figure 11 illustrates the cost evolution of TM-DDPG and Non-DDPG across selected training episodes. The y-axis represents the average offloading cost, which combines factors such as energy consumption, transmission delay, and task queuing time. Each bar denotes the average cost at a given episode, and the error bars represent a fixed margin added for visual comparison. The green bars correspond to TM-DDPG, while the red bars represent Non-DDPG. Additionally, smoothed trend lines are superimposed for both algorithms to highlight long-term behavior. In the early training phase (Episode 1–1000), both algorithms begin with similarly high cost levels. TM-DDPG then shows a steady downward trend, indicating effective policy learning and faster convergence. By contrast, Non-DDPG achieves partial cost reduction but fluctuates more significantly and stabilizes at a higher cost level. In the later stages (Episode 8000 onward), TM-DDPG maintains consistently lower cost values with minimal variation, demonstrating improved robustness and stable long-term performance. These results confirm that the task–resource matching enhancement enables TM-DDPG to better adapt to system dynamics and achieve superior cost-efficiency during and after convergence.

5. Conclusions

In this paper, we present a task offloading and resource allocation formulation framework tailored for dynamic and heterogeneous SAGIN environments. The framework integrates a task–resource matching matrix and reinforcement learning to optimize bandwidth, transmission power, and task queue management. The key features of the framework include a matching mechanism that matches task categories with resource characteristics, efficient dynamic queue modeling and a TM-DDPG algorithm that enables real-time optimization. Experimental results show that the proposed framework significantly outperforms existing approaches by reducing system cost, decreasing latency, and improving resource utilization. These results validate the effectiveness of the framework in addressing the challenges of task offloading in heterogeneous SAGIN.

Although this study has demonstrated favorable performance in task offloading and resource allocation, several limitations remain. The current framework does not consider UAV path planning, which is critical for practical deployment in dynamic airspace environments. Moreover, the proposed model is based on a single-agent architecture and does not account for coordination or conflict resolution among multiple agents. Realistic scenarios often involve multiple UAVs, satellites, and ground nodes, introducing more complex interactions and resource competition. Future work will consider integrating path planning into the reinforcement learning framework to enable adaptive trajectory control. Additionally, multi-agent cooperation strategies will be explored to support efficient task allocation and resource management across SAGIN, thereby enhancing the scalability and applicability of the proposed method in real-world heterogeneous environments.