Environmental Factors in Structural Health Monitoring—Analysis and Removal of Effects from Resonance Frequencies
Abstract
1. Introduction
2. Damage Detection Methodology
2.1. Effect of Environmental Factors on the Resonant Frequencies
2.2. Removal of Effect of Environmental Factors
2.3. Selection of Damage-Sensitive Features
2.4. Mahalanobis Distance in Structural Damage Detection
3. Results and Discussion
3.1. The Monitored Object
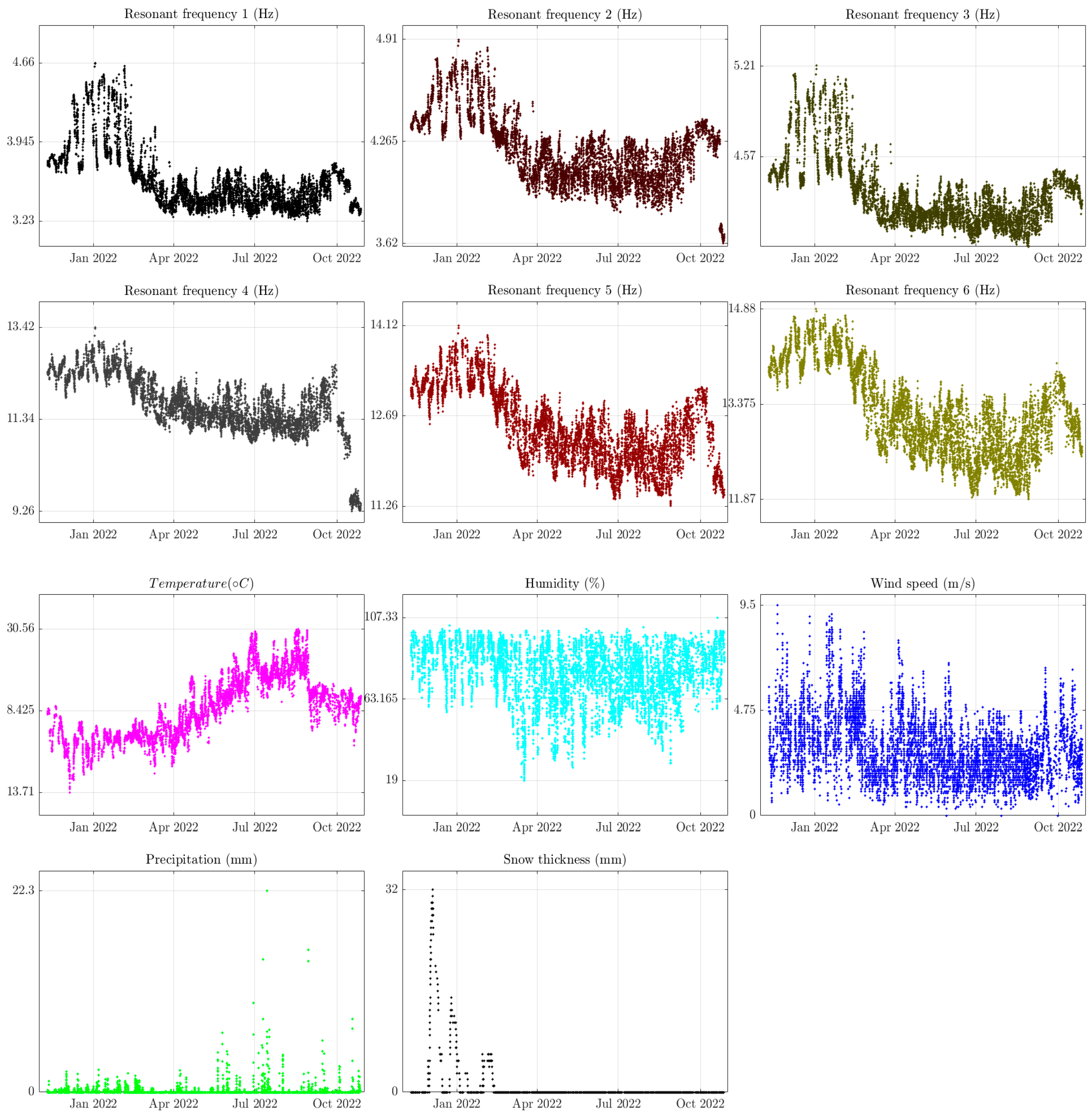
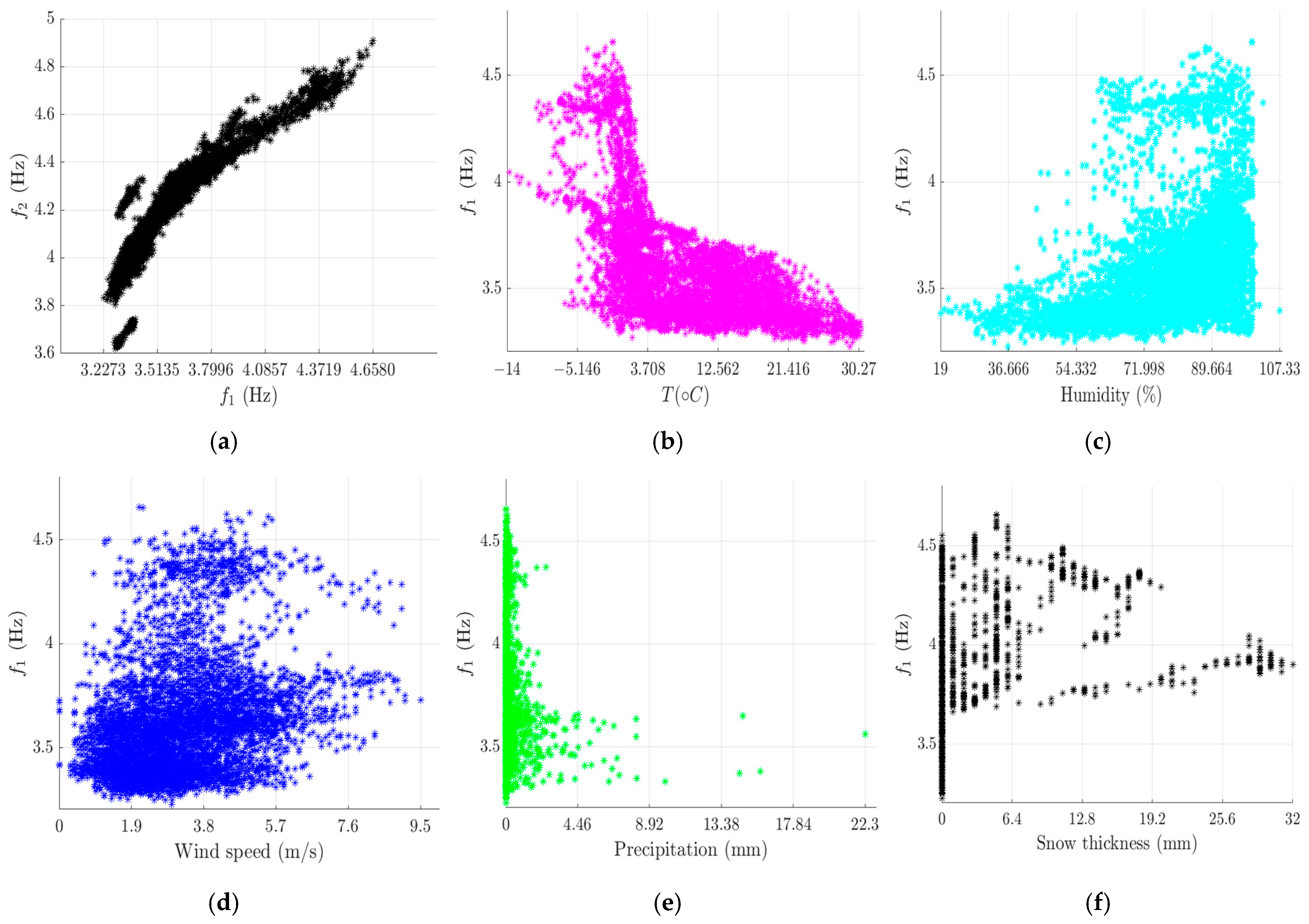
3.2. Exploration of Resonant Frequencies
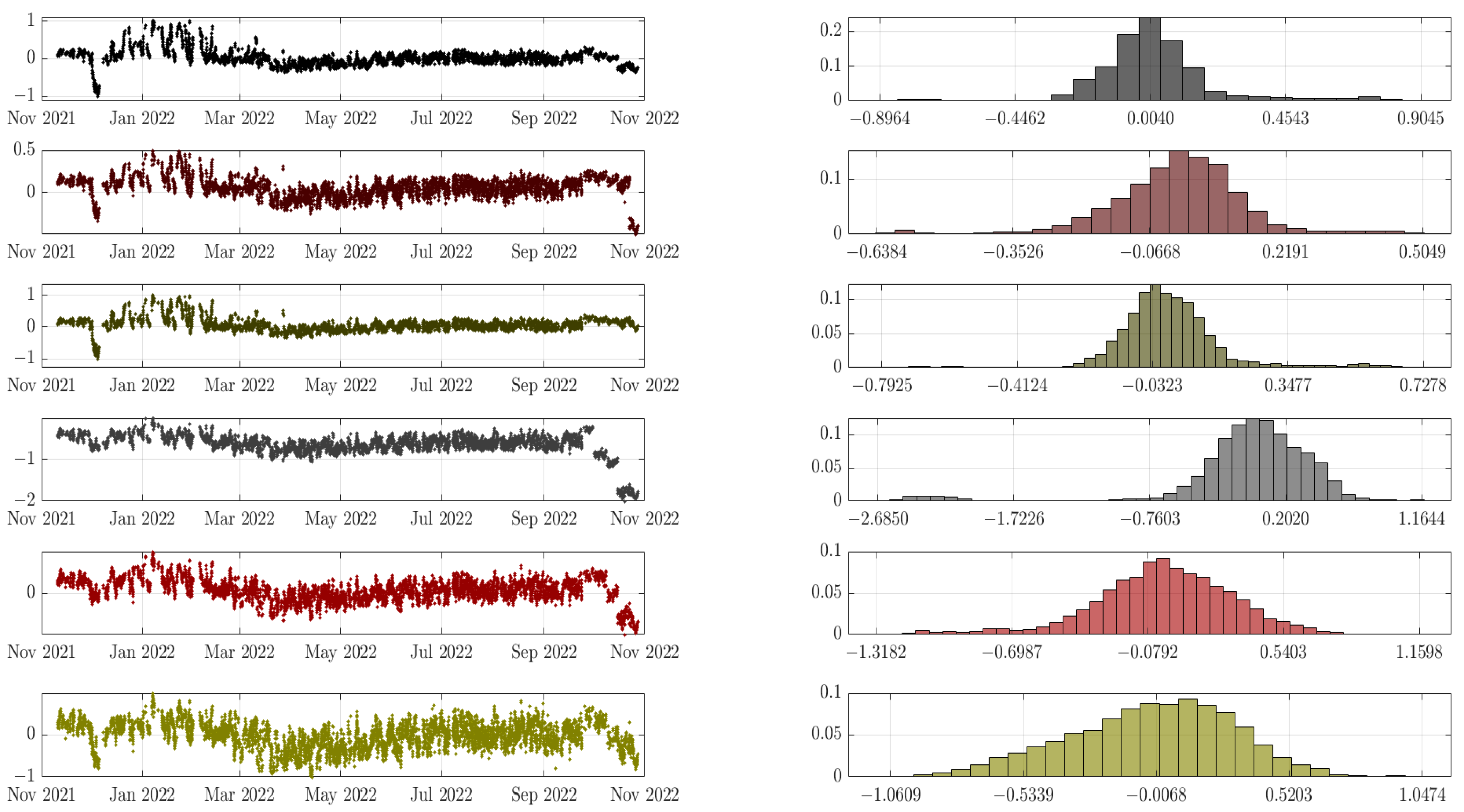
3.2.1. Time Series
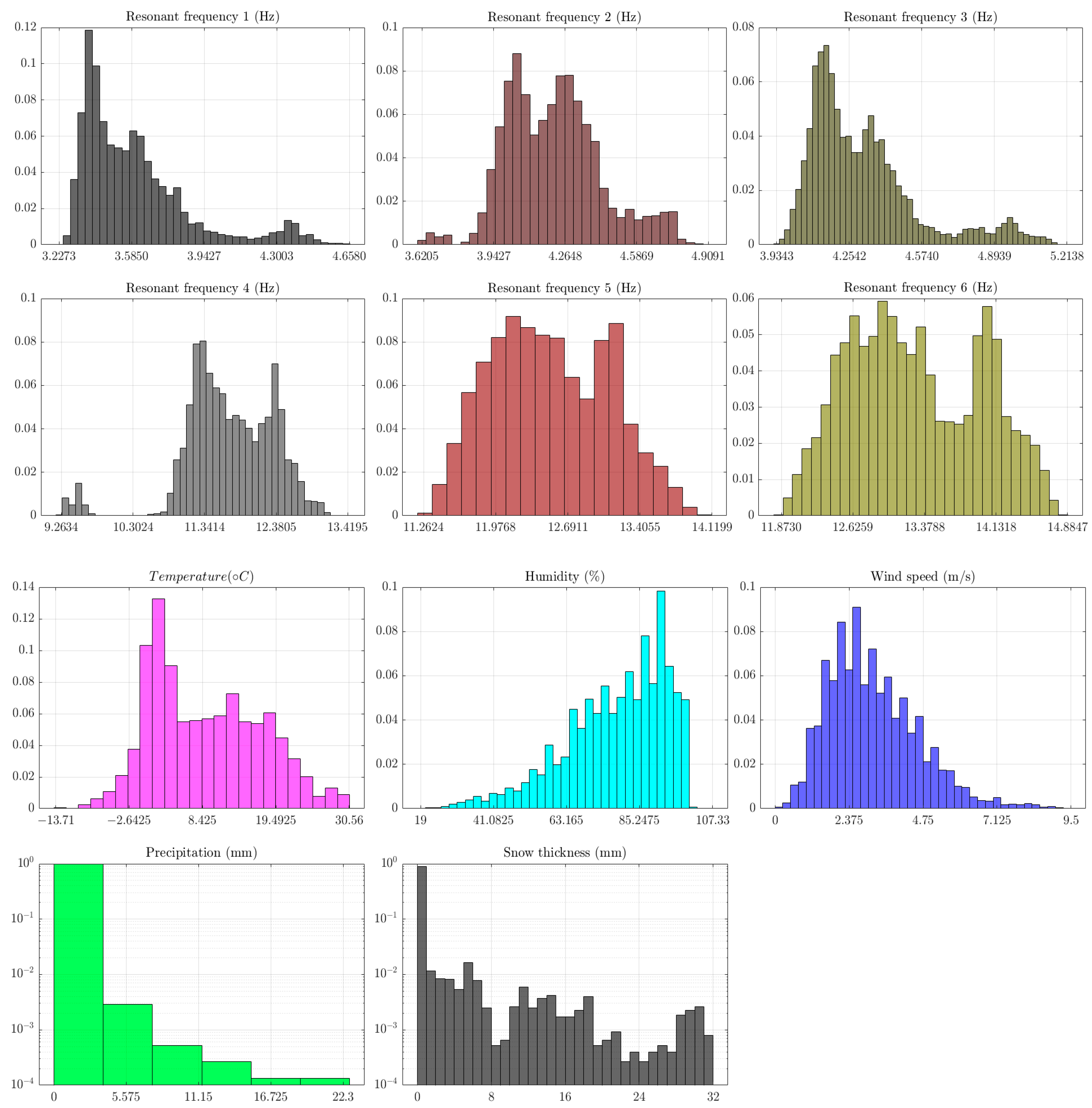
3.2.2. Probability Density Function Estimates
- If the mean value is equal (or very close) to the median and the skewness is equal (or close) to zero. This property holds for symmetric distributions, which is also the case of a normal distribution.
- It is known that the kurtosis of a normal distribution is three. Hence, an excess kurtosis or a difference between the kurtosis of the distribution in question and that of a normal variable (3) is usually calculated. If the excess kurtosis is equal (or very close) to zero, the distribution is close to normal.
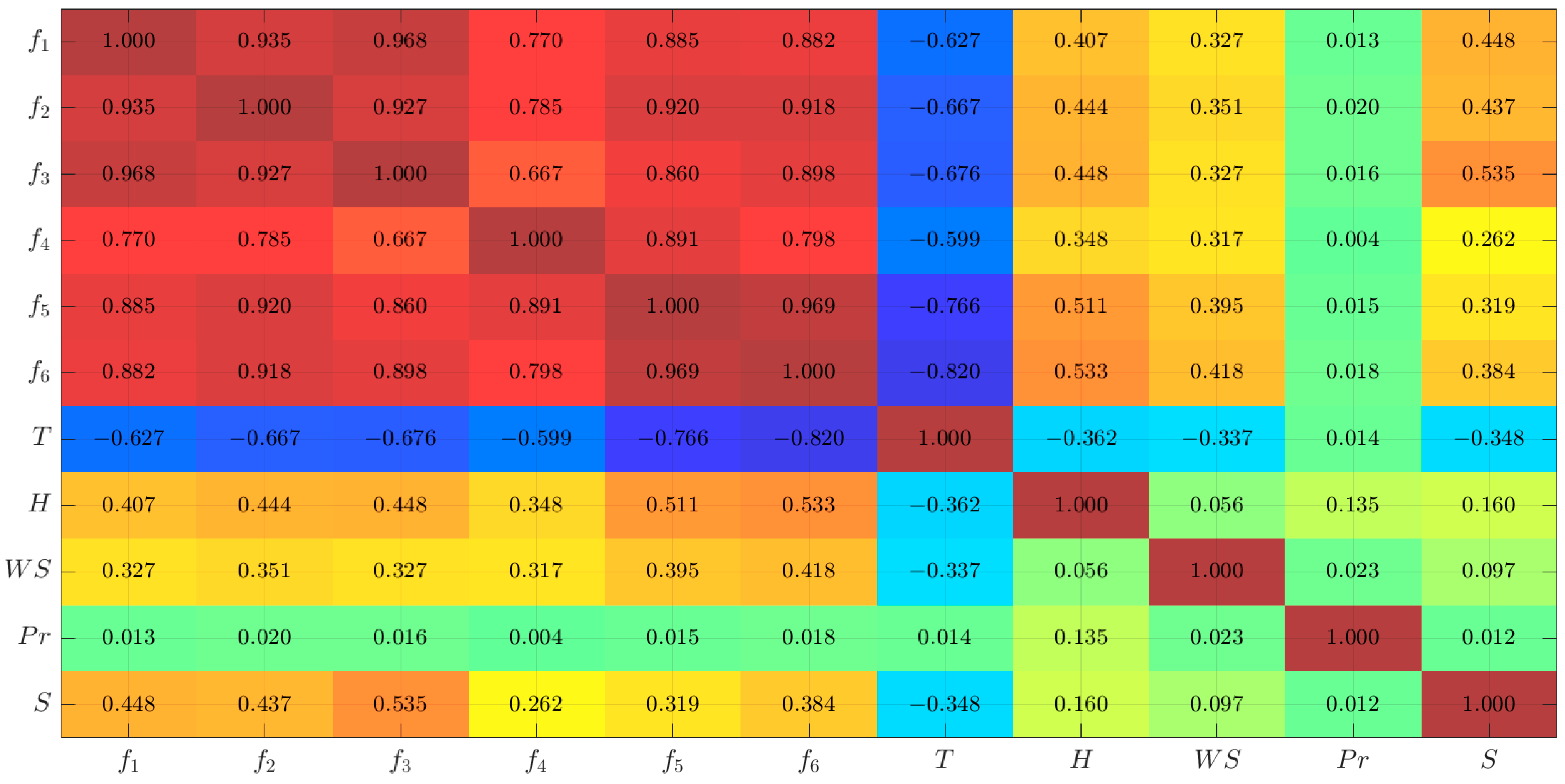
3.2.3. Mutual Correlation
3.3. Feature Analysis
3.3.1. Hyperparameter Optimization
3.3.2. Residual Analysis
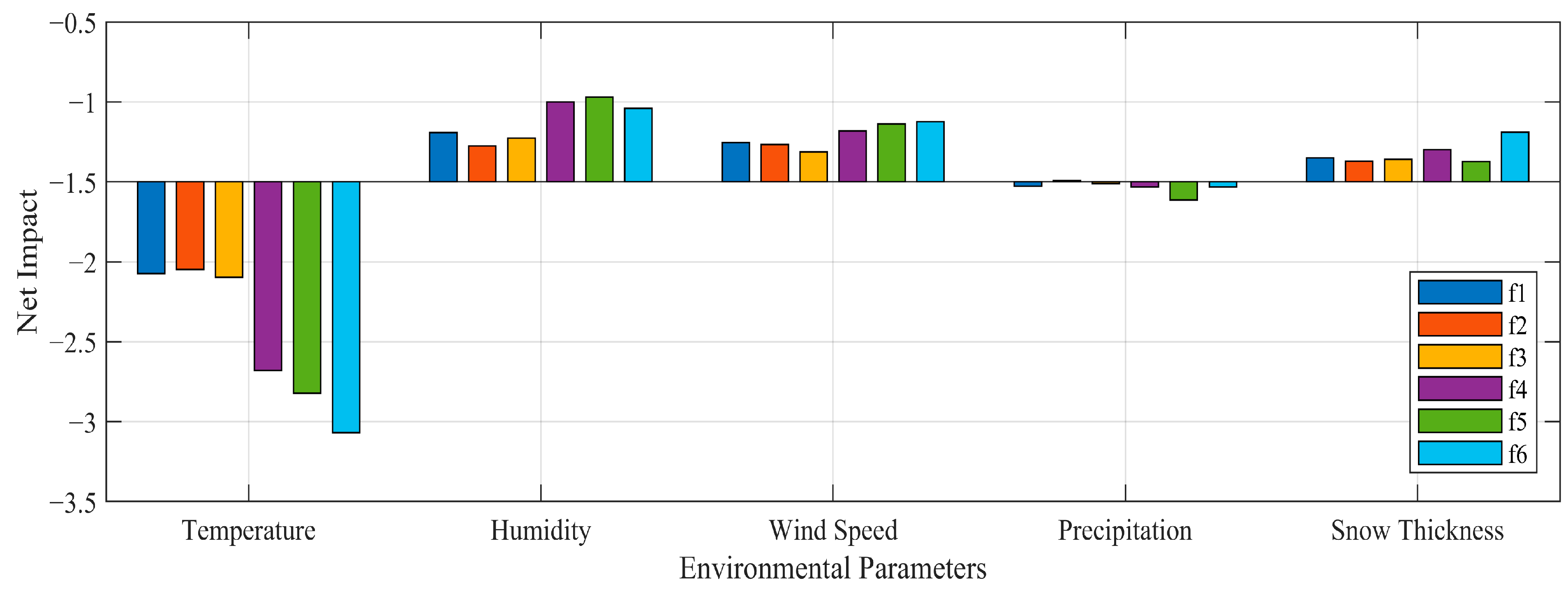
3.3.3. Impact of Environmental Factors on Resonant Frequencies
3.4. Classification of Structural Integrity
- (1)
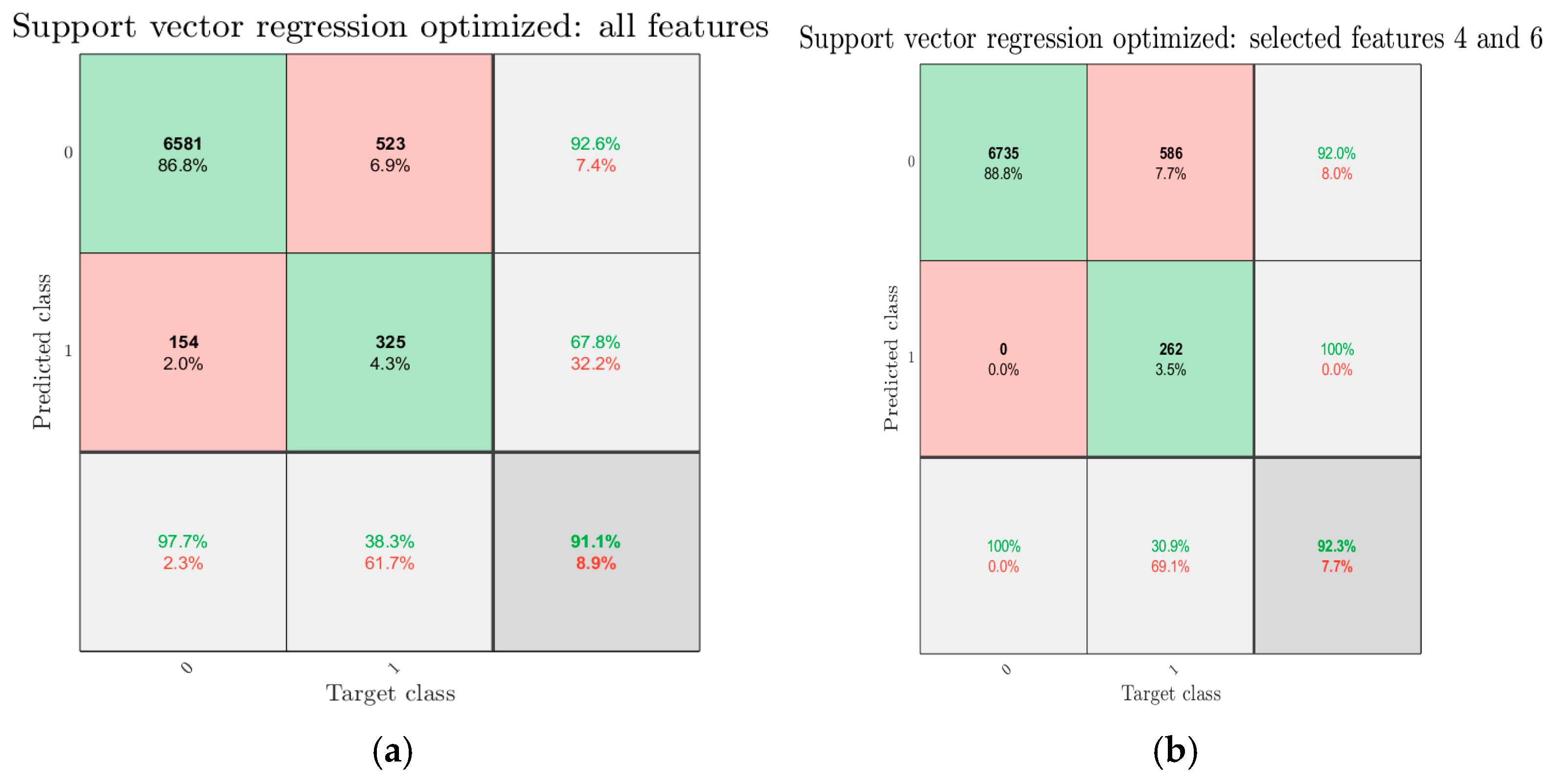
- Residuals of all resonance frequencies are used. Here, , .
- (2)
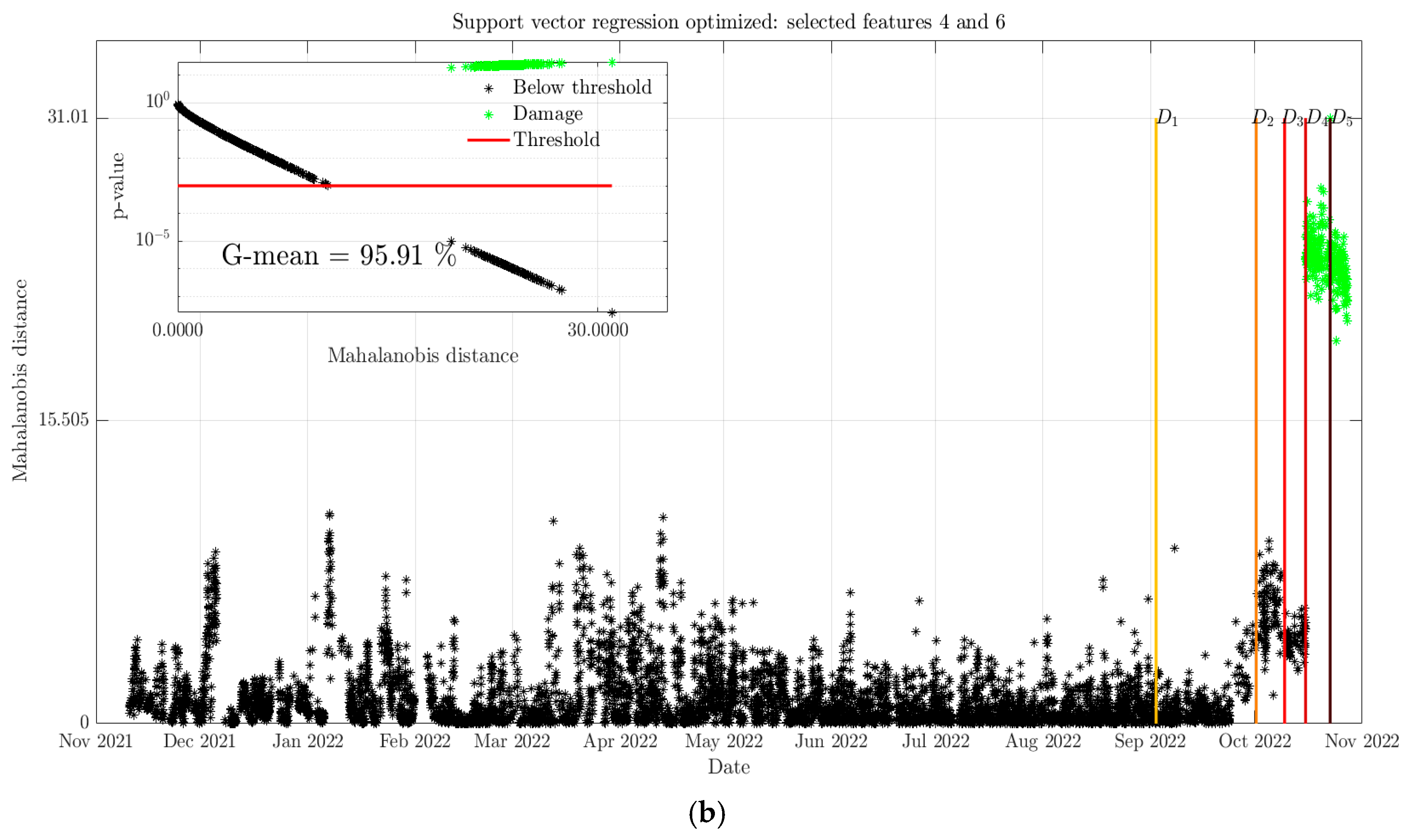
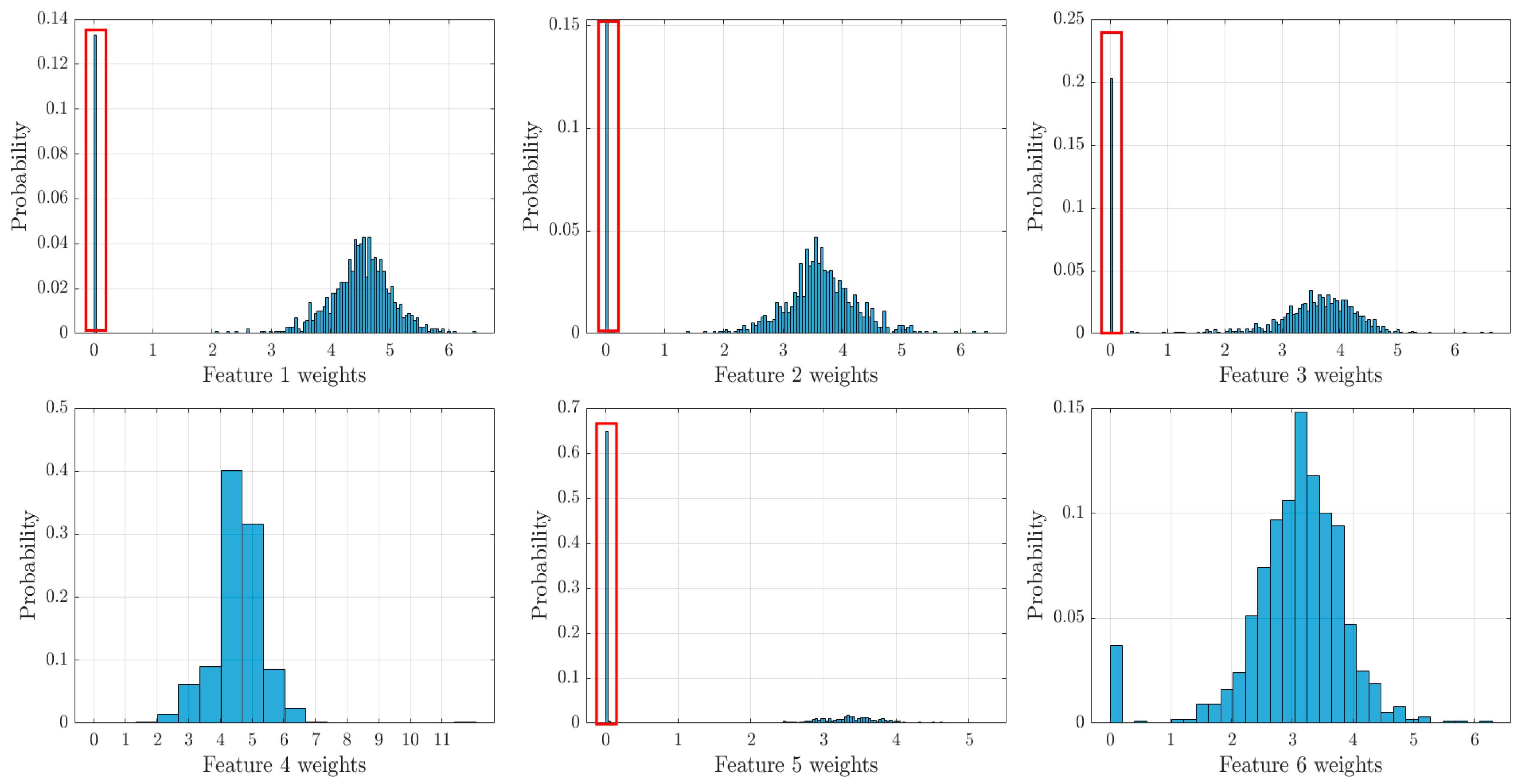
- Only the most informative residuals are selected. The employment of the NCA algorithm results in using only two features with the largest importance weights—resonance frequencies no. 4 and 6, as shown in Figure 10. Thus, for this scenario . Then, and . A total of 1000 NCA algorithm runs are performed, since the outcome of the procedure is not fully deterministic. In Figure 11, histograms of feature weights normalized to probability for residuals of each frequency are plotted. Bin number is optimized according to the procedure described earlier. As can be seen, large probabilities of very small feature weights are obtained for features (residuals) no. 1, 2, 3, and 5. These probabilities are, respectively, 0.133, 0.153, 0.203, and 0.649. Thus, these features do not contribute significantly due to small weights and are dismissed. On the other hand, features (residuals) no. 4 and 6 are retained.
4. Summary and Conclusions
- No visible indications of damage could be seen from the measured acceleration signals. On the other hand, the use of the MD statistical indicator revealed the progression of damage.
- Analysis of the Pearson correlation coefficients revealed that the resonance frequencies exhibited a strong positive mutual linear correlation. However, a visual inspection of scatterplots between variables suggested that the relationship between the resonant frequencies and all environmental factors was nonlinear.
- Estimation of impacts of environmental factors on the resonant frequencies showed that temperature had a dominant effect on all resonance frequencies overall and this effect was to decrease the frequency values. The second most important variable was humidity and also wind speed, which both increased the values of all resonant frequencies. Precipitation was a negligible factor, while snow thickness was moderately important.
- The residuals of resonance frequencies obtained through the support vector regression were not normally distributed. This may have been related to the partial mitigation of environmental effects on resonant frequencies, especially the significant fluctuations occurring during the winter period.
- The detection of damage was formulated as a classification task and classification performance was assessed via the geometric mean (G-mean), which is suitable for imbalanced datasets. In general, the classification performance was about 79% and 96% for the scenarios of using all features and selecting only the most informative features, respectively. In both scenarios, bolt tightening was not detected as damage, since the associated MD values were below the threshold. It may have been that the induced resonance frequency changes were not significant enough. For this purpose, other damage-sensitive features, for example, autoregressive coefficients derived from the measured signals, may prove to be more effective. Such an approach was used in [41,42,43]. Other types of damage were successfully detected, even though a single case of the removal of a structural element was not detected. This may have been due to the location of this element relative to the position of accelerometers.
- The largest proportion of false alarms was observed in the winter months, where the resonance frequencies had the largest deviations from the mean value. This stemmed from the non-normality of the residuals (see point 4) and implied that the removal of the temperature effect was not entirely complete. The selection of features resulted in significant reduction in false alarms, but also increased the masking of damage. Here, there was a trade-off between both types of errors—missed damage detections and false alarms. In the case when structural collapse could lead to a loss of human lives, it is preferable to minimize the possibility of missed damage detections, since each occurrence of damage may be catastrophic (depending on the structural exploitation conditions). False alarms can only cause inconvenience. From this point of view, feature selection actually worsened the performance of the model, even though the overall performance indicator (the G-mean) was higher.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHM | Structural health monitoring |
| MD | Mahalanobis distance |
| DSF | Damage-sensitive features |
| OMA | Operational modal analysis |
| SVR | Support vector regression |
| NCA | Neighborhood component analysis |
| G-mean | Geometric mean |
References
- William, C.; Salawu, O.S. Damping as a damage indication parameter. In Proceedings of the 15th International Modal Analysis Conference, Tokyo, Japan, 1–4 September 1997; pp. 1531–1536. [Google Scholar]
- Chang, K.C.; Kim, C.W. Modal parameter identification and vibration-based damage detection of a damaged steel trussed bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Janeliukstis, R.; McGugan, M. Control of damage-sensitive features for early failure prediction of wind turbine blades. Struct. Control Health Monit. 2022, 29, e2852. [Google Scholar] [CrossRef]
- Song, M.; Mehr, N.P.; Moaveni, B.; Hines, E.; Ebrahimian, H.; Bajric, A. One year monitoring of an offshore wind turbine: Variability of modal parameters to ambient and operational conditions. Eng. Struct. 2023, 297, 117022. [Google Scholar]
- Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572. [Google Scholar] [CrossRef]
- Weijtjens, W.; Verbelen, T.; Sitter, G.D.; Devriendt, C. Foundation structural health monitoring of an offshore wind turbine a full-scale case study. Struct. Health Monit. 2016, 15, 389–402. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Pr. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Figueiredo, E.; Peres, N.; Moldovan, I.; Nasr, A. Impact of climate change on long-term damage detection for structural health monitoring of bridges. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Rodrigues, M.; Miguéis, V.L.; Felix, C.; Rodrigues, C. Machine learning and cointegration for structural health monitoring of a model under environmental effects. Expert. Syst. Appl. 2024, 238, 121739. [Google Scholar] [CrossRef]
- Leibniz University Hannover; Kahrger, B.; Möller, S.K.; Jonscher, C.; Grießmann, T.; Rolfes, R. Detectability of structural damage to a lattice tower using eigenfrequencies and Gaussian Process Regression. Res. Rev. J. Nondestruct. Test. 2024, 2, 1–12. [Google Scholar] [CrossRef]
- Cava, C.R.D.G.; Avendaño-Valencia, L. Addressing practicalities in multivariate nonlinear regression for mitigating environmental and operational variations. Struct. Health Monit. 2023, 22, 1237–1255. [Google Scholar]
- Gaile, L.; Amador, S.; Brincker, R. Initial results from the continuous monitoring campaign of a wooden frame specimen. In Proceedings of the 9th International Modal Analysis Conference, Vancouver, BC, Canada, 3–6 July 2022. [Google Scholar]
- Ubertini, F.; Comanducci, G.; Cavalagli, N.; Pisello, A.L.; Materazzi, A.L.; Cotana, F. Environmental effects on natural frequencies of the San Pietro bell tower in Perugia, Italy, and their removal for structural performance assessment. Mech. Syst. Signal Pr. 2017, 82, 307–322. [Google Scholar] [CrossRef]
- Avendaño-Valencia, L.D.; Chatzi, E.N. Sensitivity driven robust vibration-based damage diagnosis under uncertainty through hierarchical bayes time-series representations. Procedia Eng. 2017, 199, 1852–1857. [Google Scholar]
- Zhang, H.; Guo, J.; Xie, X.; Bie, R.; Sun, Y. Environmental effect removal based structural health monitoring in the internet of things. In Proceedings of the Seventh International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Taichung, Taiwan, 3–5 July 2013; pp. 512–517. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Worden, K. A comparison of linear approaches to filter out environmental effects in structural health monitoring. Mech. Syst. Signal Pr. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Giglioni, V.; García-Macías, E.; Venanzi, I.; Ierimonti, L.; Ubertini, F. The use of receiver operating characteristic curves and precision-versus-recall curves as performance metrics in unsupervised structural damage classification under changing environment. Eng. Struct. 2021, 246, 113029. [Google Scholar] [CrossRef]
- Cieri, L.; De Corso, A.; Fabbrocino, G.; Rainieri, C. Analysis of environmental effects on the natural frequencies of the Civitacampomarano’s belfry. In Proceedings of the International Conference on Operational Modal Analysis (IOMAC 2024), Naples, Italy, 22–24 May 2024; pp. 166–176. [Google Scholar]
- De Corso, A.; Rainieri, C. Extreme value statistics for alarm threshold setting in data-driven damage detection. In Proceedings of the International Conference on Operational Modal Analysis (IOMAC 2024), Naples, Italy, 22–24 May 2024; pp. 3–14. [Google Scholar]
- Sarmadi, H.; Yuen, K.V. Structural health monitoring by a novel probabilistic machine learning method based on extreme value theory and mixture quantile modeling. Mech. Syst. Signal Pr. 2022, 173, 109049. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; De Michele, C. Non-parametric empirical machine learning for short-term and long-term structural health monitoring. Struct. Health Monit. 2022, 21, 2700–2718. [Google Scholar] [CrossRef]
- Amer, A.; Kopsaftopoulos, F. Gaussian process regression for active sensing probabilistic structural health monitoring: Experimental assessment across multiple damage and loading scenarios. Struct. Health Monit. 2023, 22, 1105–1139. [Google Scholar] [CrossRef]
- Dia, A.; Makhoul, N. Comparison of modal parametric and nonparametric vibration-based techniques. In Proceedings of the 12th International Conference on Bridge Maintenance, Safety and Management (IABMAS), Copenhagen, Denmark, 24–28 June 2024; pp. 769–776. [Google Scholar]
- Kuok, S.C.; Yuen, K.V.; Roberts, S.; Girolami, M.A. Propagative broad learning for nonparametric modeling of ambient effects on structural health indicators. Struct. Health Monit. 2021, 20, 1409–1427. [Google Scholar]
- Helbing, G.; Ritter, M. Deep learning for fault detection in wind turbines. Renew. Sust. Energ. Rev. 2018, 98, 189–198. [Google Scholar]
- Bangalore, P.; Patriksson, M. Analysis of SCADA data for early fault detection, with application to the maintenance management of wind turbines. Renew. Energ. 2018, 115, 521e532. [Google Scholar] [CrossRef]
- Garcia, D.; Tcherniak, D.; Trendafilova, I. Damage assessment for wind turbine blades based on a multivariate statistical approach. J. Phys. Conf. Ser. 2015, 628, 012086. [Google Scholar]
- Sarmadi, H.; Karamodin, A. A novel anomaly detection method based on adaptive Mahalanobis-squared distance and one-class kNN rule for structural health monitoring under environmental effects. Mech. Syst. Signal Pr. 2020, 140, 106495. [Google Scholar]
- Mousavi, M.; Gandomi, A.H. Structural health monitoring under environmental and operational variations using MCD prediction error. J. Sound. Vib. 2021, 512, 116370. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Newry, UK, 2012. [Google Scholar]
- Agrawal, A.K.; Chakraborty, G. Neighborhood component analysis to leverage the class label information during feature selection to enhance the damage classification performance. Structures 2023, 57, 105174. [Google Scholar]
- Janeliukstis, R.; Mironovs, D.; Safonovs, A. Statistical structural integrity control of composite structures based on an automatic operational modal analysis—A review. Mech. Compos. Mater. 2022, 58, 181–208. [Google Scholar]
- Sohn, H.; Farrar, C.R.; Hunter, N.F.; Worden, K. Structural health monitoring using statistical pattern recognition techniques. J. Dyn. Syst-T ASME 2011, 123, 706–711. [Google Scholar]
- Colone, L.; Hovgaard, M.K.; Glavind, L.; Brincker, R. Mass detection, localization and estimation for wind turbine blades based on statistical pattern recognition. Mech. Syst. Signal Pr. 2018, 107, 266–277. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 5th ed.; Pearson/Allyn Bacon: Boston, MA, USA, 2007. [Google Scholar]
- Janeliukstis, R.; Rucevskis, S.; Chate, A. Condition monitoring with defect localisation in a two-dimensional structure based on linear discriminant and nearest neighbour classification of strain features. Nondestruct. Test. Eva 2020, 35, 48–72. [Google Scholar]
- Janeliukstis, R.; Mironovs, D. Wavelet-based output-only damage detection of composite structures. Sensors 2023, 23, 6121. [Google Scholar] [CrossRef]
- Wah, W.S.L.; Chen, Y.T.; Elamin, A.; Roberts, G.W. Damage detection under temperature conditions using PCA—An application to the Z24 Bridge. Proc. Inst. Civ. Eng. Struct. Build. 2020, 175, 1–13. [Google Scholar]
- Mosavi, A.A.; Dickey, D.A.; Seracino, R.; Rizkalla, S. Identifying damage locations under ambient vibrations utilizing vector autoregressive models and Mahalanobis distances. Mech. Syst. Signal Pr. 2012, 26, 254–267. [Google Scholar]
- Nandan, H.; Abrahamson, E.; Wang, X.; Brinkmann, C. Time series based damage detection and localization in an offshore platform using wireless sensor networks. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE14), San-Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Siddiqui, M.A.; Zonzini, F.; Quqa, S.; Palermo, A.; Landucci, M. A damage detection strategy based on autoregressive parameters. In Proceedings of the International Conference on Operational Modal Analysis (IOMAC 2024), Naples, Italy, 22–24 May 2024; pp. 3–14. [Google Scholar]

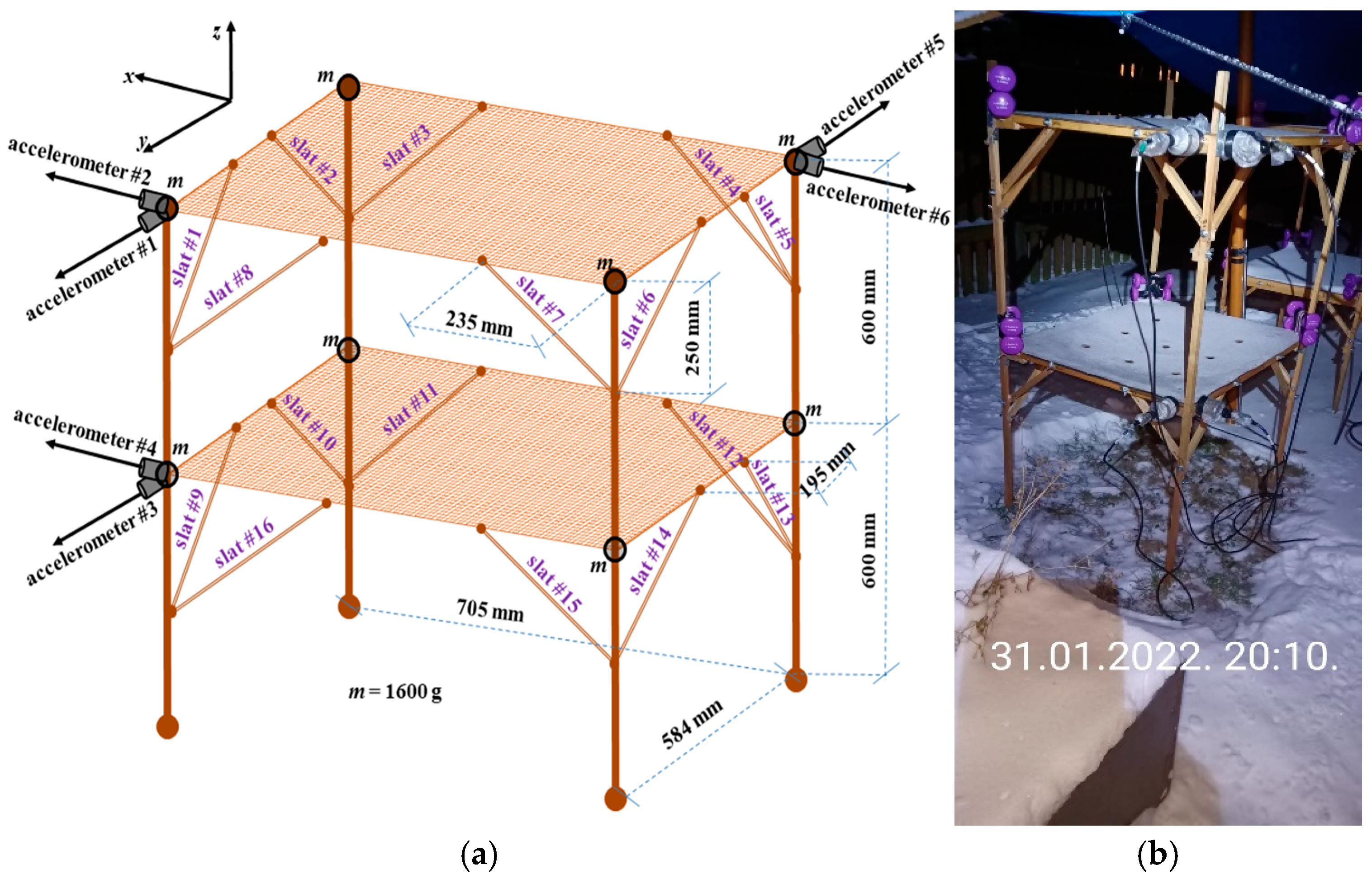


| Date | Modification | Damage Case | ||||
| 24 September 2022 13:56:25 | All bolts tightened | D1 | D2 | D3 | D4 | D5 |
| 1 October 2022 11:03:10 | Slat #1 removed | |||||
| 9 October 2022 15:20:50 | Slats #1 + #2 removed | |||||
| 15 October 2022 15:57:17 | Slats #1 + #2 + #3 + #4 removed | |||||
| 22 October 2022 18:11:24 | Slats #1 + #2 + #3 + #4 + #5 removed | |||||
| Variable | Mean | Median | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|
| 3.60 | 3.53 | 0.07 | 1.51 | 5.00 | |
| 4.21 | 4.21 | 0.05 | 0.42 | 3.18 | |
| 4.31 | 4.25 | 0.06 | 1.38 | 4.58 | |
| 11.69 | 11.65 | 0.45 | −0.91 | 5.09 | |
| 12.52 | 12.48 | 0.33 | 0.16 | 2.13 | |
| 13.29 | 13.20 | 0.47 | 0.18 | 1.97 | |
| 8.87 | 7.76 | 70.25 | 0.36 | 2.25 | |
| 78 | 81 | 234 | −0.83 | 3.25 | |
| 3.12 | 2.90 | 2.1 | 0.82 | 3.78 | |
| 0.1 | 0 | 0.4 | 17.25 | 449.63 | |
| 0.9 | 0 | 14.5 | 5.22 | 33.02 |
| Frequency | ||||||
|---|---|---|---|---|---|---|
| Box constraint | 2.0999 | 2.44823 | 2.35821 | 4.78081 | 4.51604 | 18.0755 |
| Epsilon | 0.00176763 | 0.00315976 | 0.001926 | 0.00221852 | 0.00272066 | 0.00694395 |
| Kernel scale | 0.661571 | 0.893224 | 0.707201 | 0.787161 | 1.11835 | 1.35609 |
| AD Test | ||||||
|---|---|---|---|---|---|---|
| p-value | 3.7 × 10−24 | 3.7 × 10−24 | 3.7 × 10−24 | 3.7 × 10−24 | 3.7 × 10−24 | 3.7 × 10−24 |
| reject | reject | reject | reject | reject | reject |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janeliukstis, R.; Ratnika, L.; Gaile, L.; Rucevskis, S. Environmental Factors in Structural Health Monitoring—Analysis and Removal of Effects from Resonance Frequencies. J. Sens. Actuator Netw. 2025, 14, 33. https://doi.org/10.3390/jsan14020033
Janeliukstis R, Ratnika L, Gaile L, Rucevskis S. Environmental Factors in Structural Health Monitoring—Analysis and Removal of Effects from Resonance Frequencies. Journal of Sensor and Actuator Networks. 2025; 14(2):33. https://doi.org/10.3390/jsan14020033
Chicago/Turabian StyleJaneliukstis, Rims, Lasma Ratnika, Liga Gaile, and Sandris Rucevskis. 2025. "Environmental Factors in Structural Health Monitoring—Analysis and Removal of Effects from Resonance Frequencies" Journal of Sensor and Actuator Networks 14, no. 2: 33. https://doi.org/10.3390/jsan14020033
APA StyleJaneliukstis, R., Ratnika, L., Gaile, L., & Rucevskis, S. (2025). Environmental Factors in Structural Health Monitoring—Analysis and Removal of Effects from Resonance Frequencies. Journal of Sensor and Actuator Networks, 14(2), 33. https://doi.org/10.3390/jsan14020033






