Abstract
The Single-Source Shortest Paths (SSSP) graph problem is a fundamental computation. This study attempted to characterize concretely the energy behaviors of the two primary methods to solve it, the Bellman–Ford and Dijkstra algorithms. The very different interactions of the algorithms with the hardware may have significant implications for energy. The study was motivated by the multidisciplinary nature of the problem. Gaining better insights should help vital applications in many domains. The work used reliable embedded sensors in an HPC-class CPU to collect empirical data for a wide range of sizes for two graph cases: complete as an upper-bound case and moderately dense. The findings confirmed that Dijkstra’s algorithm is drastically more energy efficient, as expected from its decisive time complexity advantage. In terms of power draw, however, Bellman–Ford had an advantage for sizes that fit in the upper parts of the memory hierarchy (up to 2.36 W on average), with a region of near parity in both power draw and total energy budgets. This result correlated with the interaction of lighter logic and graph footprint in memory with the Level 2 cache. It should be significant for applications that rely on solving a lot of small instances since Bellman–Ford is more general and is easier to implement. It also suggests implications for the design and parallelization of the algorithms when efficiency in power draw is in mind.
1. Introduction
One of the main issues with the latest generation of high-performance computing (HPC), developed mainly to surpass the performance of its predecessor, is power consumption. Due to the increased computation rates of the new systems, some problems may demand more care than others in terms of power draw, i.e., the rates at which they consume energy. In those settings, even a slight power advantage, when accumulated efficiently, may result in substantial savings due to the massive workload capacities. Previous studies along that line of thinking [1,2] encouraged a renewed look into classic HPC problems based on their energy behaviors. This work focuses on the Bellman–Ford and Dijkstra algorithms, two well-known methods for solving the single-source shortest paths (SSSP) problem.
The usual choices of algorithms based on time efficiency may not always be the best if aiming for a lower power footprint. For example, quicksort and mergesort are in the same average time complexity class. However, quicksort is invariably preferred since it runs faster. Work reported in [1,2] showed different versions of mergesort to be more power-efficient than quicksort. The first study examined bitonic mergesort, optimized for the GPU, while the second looked into the unoptimized natural version on a conventional CPU. In particular, the second one showed the natural mergesort to consume less power than a classically optimized 3-way fast quicksort, which the authors of that study interpreted as evidence pointing to mergesort having, perhaps, a natural algorithmic advantage. In [3], the study found that the faster 3-way version of the binary search consumed more power than the classic 2-way one in some practical scenarios. The savings in power, in some cases, may not have been impressive enough at face value. However, even little differences may cause consequential system-wide effects if a computation is a significant fraction of typical workloads, especially in huge systems with massive ones. The SSSP problem is a crucial component of some valuable high-performance workloads.
The SSSP problem is an extensively studied fundamental problem in graph theory with practical applications in diverse domains. Some of the most obvious can be found in navigation (e.g., Google Maps), goods distribution (e.g., warehouse to sales outlets), and telecommunication and computer networks (e.g., packet routing and broadcasting). Other prominent ones include optimizing communication and data movement in parallel systems [4], games [5], and path planning in self-driving cars [6]. Recent application areas include drones and smart cities. In the emerging field of cognitive computing, SSSP was proposed as a basis for a situationally adaptive scheduler for workloads in that domain [7]. Applications of shortest path problems, including the basic single-source version, may be found in networks where costs are associated with junctions also, such as waiting times or delays or some other node penalty [8]. Some networks of sensors and actuator nodes have applications that require efficient routing and propagation of signals [9] to help meet certain operational or quality of service needs. For example, in [10], Disjkstra’s algorithm was used as a blueprint for an energy-aware multicast routing for sensor actuator networks over wireless links using localized shortest path trees. It also served in [11] as the basis of the underlying routing topology while dealing with node placement, a fundamental problem for wireless sensor networks (WSNs). A good scheme could simplify routing and improve performance as a result. Dijkstra provided the shortest paths with the fewest hops between the signal source and sink nodes. Generally, sensor and actuator networks offer an array of potential applications for the SSSP problem and variants in diverse areas, such as production, healthcare, and automatic control [10].
In concept, consideration of SSSP is critical in optimizing routes and minimizing travel costs along links. The graph may be directed or undirected, and the edge weights may be positive or negative. The problem involves finding the shortest paths, in terms of total edge weights, from a given source vertex to all other vertices in a weighted graph. Technically, the solution is a family of paths that compose a singly rooted spanning tree. The weights of the shortest paths are unique but may be satisfied by different trees. Dijkstra’s algorithm [12] and the older Bellman–Ford [13,14] are the primary methods to solve the SSSP problem. Their approaches greatly vary, yielding strikingly different operational efficiency. Dijkstra uses a greedy approach based on a priority queue to solve in minimal steps [5]. It favors solutions with paths with fewer edges since it uses a breadth-first search (BFS) as a front end for vertex exploration. Its main advantage is reaching its destinations without traversing unnecessary nodes, but the edge weights may only be non-negative. The resulting time complexity is linearithmic if the queue uses a binary heap with the minimum key at the root and the graph is represented by its adjacency lists. A Fibonacci heap offers constant time queue insert operations [15] vs. logarithmic in a binary heap, leading to a better upper bound on the run time growth of Dijkstra under some conditions (see p. 585 in [16]). Bellman–Ford employs dynamic programming. It can navigate graphs to detect negative weight cycles [5]. It is more versatile than Dijkstra at the expense of quadratic time complexity. Programming these algorithms is not a trivial task. Achieving linearithmic efficiency in Dijkstra requires a properly implemented priority queue.
The preceding should highlight the foundational nature of the SSSP problem and its multidisciplinary role. Work reported in [7] was particularly interesting to the authors of this study. It sits at a crossroads of two main application areas: managing large high-performance workloads and cognitive computing. Hence, it is perhaps important to gain as much insight into the energy behaviors of its main algorithms as possible. The ongoing ubiquity of the SSSP computation and the power concerns of the new large systems motivated a new look into an old problem through a fresh approach. It may inspire, at least in some cases, a revisiting of old choices based on time complexity alone.
This research investigated the energy behaviors of the two principal algorithms for solving the SSSP problem. The algorithms, particularly Dijkstra’s, were optimized extensively. This study, however, focused on the most basic forms to identify which of the pair offered some natural advantage, perhaps due to the fundamentally different way it solved the problem or how its logic interacted with the hardware. It is reasonable to assume that this approach could provide a better platform for further efforts. The energy behaviors were explored empirically using recently established techniques. The study aims to quantify and analyze those behaviors. Power, the energy time rate, was examined as a separate concern. The main contribution of this work is a step towards a thorough review, based on a concrete real-world assessment, of the power and energy characteristics of the main methodical approaches behind the computation of the SSSP. It hopes to offer insights and recommendations, with power and energy as primary concerns, usable in the numerous applications from diverse areas that rely in various ways of solving the problem. For example, the insights gained about power draw may help design better solutions for sensor and actuator networks that depend on limited power sources, such as batteries. A reduced power footprint should also help cases where the network operates in an environment prone to thermal failures. Networks deployed in smart city and municipal settings are examples. The work also supports, for energy concerns, a need to look beyond classic time analysis.
In the context of this paper, the terms energy and power are not interchangeable. They are used here in their proper physical sense, where power is strictly the time rate of energy expenditure in watts. The phrase “energy behaviors” refers to all energy concerns generically. Algorithms are colored consistently across the figures, with edge density indicated by tone of color. The paper is structured as follows: Section 2 reviews selected past research. Section 3 outlines the methodology and details the procedures and materials used for this research. The findings are presented and discussed in Section 4. Section 5 closes with suggestions for future work after some final thoughts and concluding remarks.
2. Literature Review
As mentioned earlier, the SSSP problem has been the subject of broad interest in the past 60–70 years since the Bellman–Ford algorithm was published separately by R. Bellman, L. Ford, and E. Moore [17] (hence, it is also referred to as Bellman–Ford–Moore), leading to a large body of published work. Previous work tended to focus on speed in various hardware or application environments. The energy studies, for the most part, relied on complex modeling or simulation under such conditions. There was a lack of realistic data on the essential energy interactions with the machines. In this section, the authors attempt to sample the ongoing work on the two algorithms in the past decade to address either energy or other classic optimization concerns, such as running time or efficiency for some valuable special conditions or application areas. The review is in chronological order. Table 1 summarizes the reviewed works with their methods and contributions in contrast with the present work.

Table 1.
Summary of the papers reviewed in this section.
Kalpana and Thambidurai [18] introduced COAB, a method for optimizing shortest path queries through a blend of arc flags and bidirectional search. Executed on an AMD Athlon X2 Dual Core CPU paired with 4 GB of RAM and Ubuntu 9.04, using LEDA, COAB significantly enhanced the runtime and vertex visit count of Dijkstra’s algorithm, particularly on real-world graphs. However, the paper lacked a discussion on COAB limitations, such as scalability issues or performance variations on different graph types. Future work suggested, chiefly, was to explore combining the bidirectional arc flag vector with additional speedup techniques and parallelizing other preprocessing phases.
Zhang et al. [19] conducted an experimental evaluation to compare Dijkstra’s, Bellman–Ford, and the Shortest Path Faster Algorithm (SPFA) on random and grid maps. The key finding was an enhanced Bellman–Ford exceptional efficiency on grid maps, reducing processing time by two-thirds compared to SPFA. However, the improved version faced limitations. It was less efficient when the graph size was generated randomly, taking longer than the others. Additionally, it encountered challenges with depth problems, requiring excessive iterations in specific cases to find the shortest path.
Hajela and Pandey [20] proposed a hybrid implementation of the Bellman–Ford algorithm for solving shortest path problems using OpenCL. They divided the work between the CPU and GPU in a 1:3 ratio, which was the most efficient based on testing different ratios. The authors obtained a 2.88x acceleration compared to the parallel GPU implementation in solving SSSP problems and a 3.3x enhancement for All-Pairs Shortest Paths (APSP) problems. However, a limitation was that results were only from graphs with edge weights between and 10. The authors suggested that future work could focus on partitioning the algorithm for hybrid implementation rather than dividing the vertices.
Abousleiman and Rawashdeh [21] presented a novel approach to energy-efficient routing for electric vehicles via the Bellman–Ford algorithm. The authors proposed a modified version of the algorithm that considered some factors to optimize energy consumption during a journey, such as road gradient and traffic conditions. The methodology involves using real-world data and simulation to verify the efficacy of the proposed method. However, the paper acknowledged limitations in the accuracy of energy consumption models and the need for extensive computational resources for large-scale implementation. Further research was suggested to address these challenges and improve the practical applicability of the proposed method.
Busato and Bombieri [22] introduced a streamlined Bellman–Ford algorithm implementation tailored for Kepler GPU structures. The authors utilized the parallel processing capabilities of GPUs to significantly speed up the execution of the Bellman–Ford algorithm, which is traditionally computationally intensive. They optimized the use of shared memory and reduced thread divergence to achieve the increase. However, the paper acknowledges that the proposed implementation may not be as effective on non-Kepler architectures due to differences in hardware design. Furthermore, the paper does not address how the algorithm would perform with larger datasets that exceed the memory capacity of the GPU.
Mishra and Khare [23] investigated the efficacy of the Dijkstra algorithm on actual GPU hardware, delving into power, energy, and performance analysis. They employed Dynamic Voltage Frequency Scaling (DVFS) for energy conservation. They analyzed the algorithm at various frequency pairs and identified the optimum frequency pair for achieving either energy or performance gain. However, the paper did not address how the algorithm would perform with larger datasets that exceed the memory capacity of the GPU. Further research is needed to extend this methodology to a broader range of data sizes.
Cheng [24] introduced an extended version of the Dijkstra and Moore-Bellman–Ford algorithms to address the general SSSP problem (GSSSP). They presented novel ideas, such as order-preserving within the path function last road (OPLR). The author developed an extended Moore–Bellman–Ford algorithm (EMBFA) and an extended Dijkstra’s algorithm (EDA) tailored to specific conditions for GSSSP. Key findings included proof of efficiency, solving the problem in time for EDA and time for EMBFA, with n as vertices, m as edges, and as the time to obtain the path function value. However, the effectiveness of the algorithms depends on specific conditions, and their time complexity may be high for large graphs.
Schambers et al. [25] presented a novel approach to energy-efficient route planning for electric vehicles. The authors suggested a parallel adaptation of the Bellman–Ford algorithm for an embedded GPU system. This system can process negative edge weights, a functionality absent in conventional algorithms like Dijkstra’s or A*. Such an approach enabled the generation of routes with significantly lower energy consumption, all while upholding the performance standards of standard route planning software. However, the increased computational complexity of the Bellman–Ford algorithm and the need for reasonable processing speeds were acknowledged as limitations, leading to the suggestion of further research to address these challenges and improve the practical applicability of the proposed method.
Abderrahim et al. [26] introduced an energy-efficient multi-hop transmission method tailored for Wireless Sensor Networks (WSNs), utilizing the Dijkstra algorithm. The approach encompasses clustering sensor nodes, appointing cluster heads, and categorizing nodes into active and dormant states. Additionally, it selects a set of dependable relays to transmit data with minimal power consumption. This advancement builds upon earlier research by significantly mitigating power usage, surpassing the efficiency of prior transmission techniques. Nonetheless, the study overlooked assessing the performance with larger datasets beyond the network’s capacity.
Weber et al. [27] gave a generalized Bellman–Ford algorithm for symbolic optimal control. The algorithm was designed to handle cost functions that can take arbitrary values, including negative ones, and allowed for parallel execution. The authors demonstrated effectiveness through a detailed four-dimensional numerical example of aerial firefighting with UAVs (unmanned aerial vehicles). The key findings included the ability to handle negative cost values and efficient parallel execution. However, the performance depended on the dimensionality of problems, with challenges when the state-space dimension was high. The algorithm also required defining the cost functions in a specific way, which may limit its applicability in some scenarios.
Rai [28] conducted a comparative study on the Bellman–Ford and Dijkstra algorithms for shortest paths detection in Global Positioning Systems (GPSs). The author implemented both algorithms on a graph and analyzed their results. The key findings suggest that while both algorithms can effectively find the shortest path, the Bellman–Ford algorithm is more versatile as it can handle negative weights and visit a vertex more than once, thus providing an optimal path. However, the time complexity of Bellman–Ford was not better than Dijkstra, which could be a limitation for large networks. The author suggests that future research could focus on developing new algorithms based on Bellman–Ford for use in GPS systems.
3. Methods, Tools, and Procedures
This section starts by outlining the methodology used for the research, highlighting its main features, and proceeds to describe the experimental work in the following subsections. These detail the test datasets and the process used to generate them, the tools and materials used to obtain the code and the measurements, and the test environment and the measures employed to ensure credible results.
3.1. Methodology
The objective of the investigation is to gauge power consumption that may be attributed credibly to the computational characteristics of the algorithms. An algorithm, of course, is an abstract object. It may manifest its characteristics through compiled code, a run environment, and a physical machine with certain hardware assets and organizations. Each of the previous may contribute to an attempted measurement. Those additions obscure the desired behaviors. They are unwelcome and may be considered noise. Therefore, a methodology to ensure a reliable estimation by eliminating as much of that noise as reasonable is crucial. The researchers chose one based on ideas first developed in [2] and later refined and used in [29,30] on different CPU platforms. Three key features form the basis of the methodology:
- Eliminate as much of the effects due to the process used to generate the code. In particular, compilers use optimizations that may reduce the resemblance of the code to the original method. Moreover, they implement them differently. So they must be turned off as much as possible.
- Eliminate as many sources of power consumption from the run environment as possible. Modern operating systems multitask, constantly trying to do all sorts of things besides running user code. Of particular concern as noise are those that are heavy on energy.
- Use reliable, on-chip instrumentation to measure the targeted energy behaviors after eliminating hardware features that optimize or alter the natural power consumption. This empirical approach black-boxes complex behaviors and removes the need for involved modeling or complex simulations. Those methods require detailed knowledge of the processor and the memory and may not capture the whole behavior as faithfully.
Therefore, in a nutshell, the methodology calls for measures that turn off CPU features that alter power consumption, reduce OS activity not focused on the test code, and avoid compiler optimizations that shape the code in ways that make it behave in ways that differ from the algorithm significantly. Other environmental factors should also be addressed, such as thermal noise due to ambient and cross effects. The rest of this discussion highlights other notable features and the rationale.
Readings were averaged over 300 runs for a sound convergence as recommended by [2] based on experimentation in a similar setting. The CPU was allowed to cool down between trials. The input datasets were statically embedded into the code to eliminate factors, such as disk or network loading, that could impact timing or power consumption. These measures help control and reduce variability due to OS and other environmental factors. Collecting timing data is recommended to ensure correct programming and check for the complexity expected from the theory.
3.2. Dataset Generation
The selection of the input datasets is essential to generate the full extent of behaviors that allow reasonable insights into consumption patterns. Carefully chosen ones ensure the experiment’s validity. Before going for random graphs, available datasets on the Stanford Large Network Dataset Collection [31] were explored. Although this repository offers a wide range of graph datasets, none met the specific requirements of the experiment, which required graphs with randomly assigned edge weights within a specified range and a controlled probability of edge existence.
Randomization was employed to determine the edge weights to introduce variability in the input data. It involved assigning a random weight value to each edge in the graph, representing the distance associated with traversing that edge. The randomization ensured that each edge had a randomly chosen weight. The range should approximate practical scenarios. While the distances between vertices in a graph may vary widely depending on the application, a broad range of values allows for versatility in simulating the different scenarios. The range should be wide enough for comprehensive testing. The experiment utilized the Erdős–Rényi model [32], a foundational framework in network theory used to create random graphs characterized by a probability p for edge formation between n vertices, where , are sets of vertices and edges, and . This model is known for its simplicity and effectiveness. It enables the understanding of fundamental behaviors in random graphs. The model proved to be highly beneficial for the experiment. It was instrumental in providing a wide range of random graphs. It allowed the exploration of various graph structures by controlling the probability of edge formation between nodes. Different graph densities could be represented simply by adjusting its parameters.
The function directed_gnp_random_graph [33] in the rustworkx library, an open source package for network algorithms [34] used in this research, generates a random directed graph based on the Erdős–Rényi model. Values of p as low as 0.2 yielded fairly dense graphs, i.e., . Two input datasets were created with different edge densities and a range of vertices from 10 to 2000 with random integer weight values in 1–99,999,999. The sets represent two cases of edge density as follows:
- Fully dense, i.e., complete graphs, where every pair of vertices is connected, generated by setting the probability p to 1. The number of distinct edges is for a complete graph, but twice that must be created in the adjacency list of the digraph.
- Moderately dense graphs, generated by setting .
It is reasonable to expect energy behaviors to escalate as the number of edges increases since most graph algorithms must work harder. Therefore, the first case will be an upper bound on energy and power consumption, while the second provides a comparison point for variability in edge density.
3.3. Tools and Materials
Correct programming is vital for the experiment, especially for the relatively intricate Dijkstra algorithm. In addition, the implementation must comply with the purposes of the research. For example, a priority queue based on a sequential data structure or optimized versions of the algorithms will give correct answers but is inappropriate for the investigation. For those reasons, the authors decided to use well-known published code. The experiment’s programs were written in C++ with algorithm code from [35]. The program set up the code to run on a single thread with affinity to core 0 via the CPU_SET and sched_setaffinity functions from the GNU C library. These functions implement the Linux kernel interfaces for controlling the threads’ core affinity. The graph resided in adjacency lists of sink vertices and corresponding weights whose values randomized 27 bits of the 4-byte words used to store them. Priority queue operations relied on the C++ standard library container std::priority_queue. This queue implementation provides constant time access to the top priority element with logarithmic inserts and retrieves [36]. It includes an option for a min-heap, which allows for the efficient extraction of the minimum element for the distance checks. The gcc compiler produced the executables with the optimization option -O0. It only involves optimizations focused on reducing the cost of compilation and having a standard debugging experience [37], i.e., the statements are left independent, which works with the objectives of this research. Higher optimization levels tamper with the code to reduce its size or speed, which is undesirable in this context.
The Linux command perf [38] was used to acquire energy consumption data, run time, and other processor metrics. It is a robust command-line performance profiler available within the OS kernel. It works with RAPL (running average power limit), a hardware feature from Intel. The tool implements the RAPL interface to provide reliable readings from the CPU sensors. The researchers set up shell scripts to automatically execute binaries from specified directories, monitor temperatures, enforce delays, and systematically record the results. The Linux command sensors was used to monitor the CPU temperature. The -C option restricted perf to collecting data on core 0 to minimize its footprint. Some testing was initially conducted with LIKWID [39], the other notable instrumentation tool, but perf was preferred since it had better support and enjoys widespread use.
3.4. Experimental Environment and Procedures
Table 2 details the features of the machine used for the experiments. The main component is the HPC-class Haswell-EP CPU. The processor circa 2014 may seem at first to be a bit outdated. It is arguably still a suitable platform for the line of research conducted here for the following reasons. First, the relevant characteristics of this CPU platform are well documented in studies, such as [40]. Second, it features fully integrated voltage regulators (FIVR), i.e., on the CPU die, for finer control and reporting for different regions (CPU domains) of the chip package. Therefore, it can control the frequency and power states of cores efficiently and enable readings at a higher resolution as follows: Fairly accurate power readings for a core are possible if the rest were idle. In a realistic situation, those readings should still be credible as long as activity on the other cores is sufficiently low. Third, [41] showed that estimates reported by RAPL in the Haswell architecture matched plug power readings well. Thus, this well-known CPU part with reliable power numbers remains a reasonable test bed for probing the algorithmic behaviors.

Table 2.
Specifications of the experimental environment (powered by a Haswell-EP CPU). Most notably, the tiny, split Level 1 (L1) core caches and the relatively large, high-associativity L3 cache.
Aljabri et al. [2], based on the same CPU, recommended a list of measures to reduce the effects of factors that may act as noise. A light OS further reduces the noise related to the OS environment. Lubuntu is an official release of Ubuntu that features a lighter runtime environment. In addition, the following are the measures implemented for this study:
- Open system case conditions while keeping the ambient temperature consistent under moderate air conditioning and the CPU fan turned on at a constant speed.
- Turn off hyper-threading features as it results in a more intricate power model since the extra threads consume disproportionately less power by design.
- Deactivate Turbo Boost power management to maintain the CPU’s base frequency so the results are less affected by unpredictable patterns of internal thermal variation between runs.
- Terminate unnecessary operating system processes and services to run the system with minimal resource usage.
- Introduce a cool-off period between test case trials to allow the CPU to return to a consistent initial temperature of 40 °C as reported by the system sensors tool.
- Assign core 0 to execute the experimental code and allocate other processes to cores 2, 3, 4, and 5 to prevent costly context switching. Core 1 was left idle to limit temperature effects from neighboring cores.
4. Results and Discussion
This section first presents and discusses energy behaviors based on the data obtained from the experiment, then examines the resulting cache miss data to make sense of those behaviors. Table 3 displays the main results of the experiment. The energy numbers were based on readings reported by the profiler, whereas the corresponding power numbers were calculated from the run times reported by the tool. The numbers in the table were obtained from averages over 300 trials, as detailed in the previous section. They were rounded to enhance presentation. Shaded lines highlight cases where the power consumption for both algorithms was close, to the extent that they seem to perform similarly, more or less.

Table 3.
Average energy and power consumption and the percent difference in drawn power relative to Dijkstra (negative means better performance). Highlighted lines indicate a region where power performance seems to be about the same, within 5%.
4.1. Energy Behaviors
Even a cursory glance at the main results table shows that Dijkstra’s algorithm consumed much less energy than Bellman–Ford at both edge densities for most cases. For the smaller graphs, however, Bellman–Ford was more energy efficient (not by much, though, at an average of 86 and 75 mJ, corresponding to 28.5% and 41.1%, less for the fully and moderately dense cases, respectively). Figure 1 plots the energy data to reveal more. The steeper slope of the Bellman–Ford indicates that it increases at a higher rate as the vertex count increases. The rate seems higher for the greater edge density (see Figure 1a). The shaded region highlights the most intriguing feature, marking the change of trend where energy efficiency shifts towards Dijkstra. The averaged readings indicate that the inflection point occurred at 90–100 in the fully dense graphs and a little later, perhaps at 100–150, in the moderately dense ones.
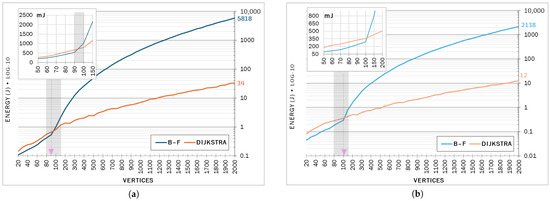
Figure 1.
Average energy consumption (in logarithmic scale), with a view on small cases (linear scale). A region where the trend reverses is highlighted. (a) Fully dense (complete) graphs; (b) Moderately dense graphs.
The substantial energy efficiency advantage seen in Dijkstra as the graphs grew in size and edge density should not be surprising. Figure 2 shows that the energy trend tracked the run time behavior (the regions of interest identified from the energy plots are marked). The shape of the curves suggests that the energy consumption pattern is perhaps similar to the time complexity of the algorithms, which explains the energy findings for the graph instances where Dijkstra was more energy-efficient. Bellman–Ford was slightly faster for the small cases, particularly at lower edge density, at an average of 13% and 30%, perhaps due to overheads of the priority queue in Dijkstra or due to a better fit in local memories. The timing data alone do not fully explain those cases (gains in energy were much higher at 29%, 41% than in time). Energy, after all, is the product of time and power.
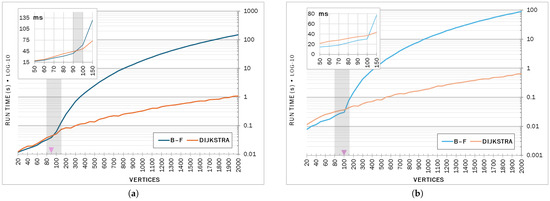
Figure 2.
Average execution time (logarithmic), with a linear scale view on small cases. Regions identified from the energy figures are highlighted. (a) Fully dense (complete) graphs; (b) Moderately dense graphs.
Energy behaviors are closely tied to the physical hardware, not just the frequency of operations, like in classic time analysis of algorithms. Power consumption takes both time and the hardware used into account. For example, addition and multiplication are often the most frequent operations of an algorithm whose rates of growth of their time costs or counts are the basis for quoting time efficiency. Multiplication hardware is, of course, more expensive and, therefore, expected to be less energy efficient. Flowing instructions efficiently through processors demands multiplication to respond in fewer clock cycles, preferably 1–2, like addition. It leads to more complex circuitry that must consume energy at high rates, i.e., power levels. Even if the energy budget is the same, the tighter timing necessitates higher power consumption. Examining the power may help better explain the energy behaviors. Higher rates could reflect dependence on an over-achieving energy-intensive functional unit or a poor fit in power-efficient local memories. An algorithm may fix both of those factors at the root. It may trade expensive operations for cheaper ones or try to improve the locality.
The power consumption in Figure 3 confirms a significant event in the region of interest identified earlier. The first observation was that while very clearly Dijkstra was considerably more efficient as the graphs grew both in size and complexity, the differences were not as pronounced as they were for the energy figures—in the low tens of watts in both cases. It is notable that while the energy consumption of Bellman–Ford was much higher, by up to two orders of magnitude, its rate of consumption was not that far behind Dijkstra’s. The second salient observation is the instance size region where Bellman–Ford was more power-efficient. The relative power advantage of Bellman–Ford in the small datasets was an average of 22.5% and 22.4% for the fully and moderately dense groups, respectively, resulting in 2.36 and 1.31 watts on average. One may add sizes that yielded negligible difference to extend the range where Bellman–Ford is competitive energy-wise. For example, the highlighted rows in Table 3 can be regarded as a region of performance parity, within a 5% difference in wattage, to extend the Bellman–Ford range to 200 vertices. Both algorithms consumed energy at an increasing rate as the graphs grew in size and density. Also, while the slope of the curve seems to not change for Dijkstra for all size instances in both density cases, Bellman–Ford noticeably changed after the power event. Therefore, energy consumption patterns may not be attributed only to time efficiency.
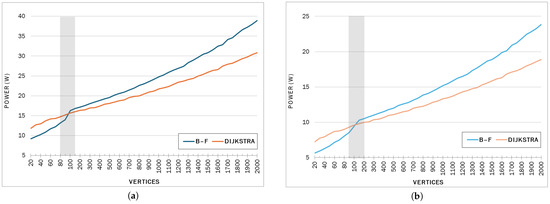
Figure 3.
Average power consumption in watts. (a) Fully dense (complete graph) cases; (b) Moderately dense cases.
The early power advantage of Bellman–Ford seems to point towards behaviors related to memory interactions. The graph data structure grows quadratically, reflecting sizes in regardless of implementation. Figure 4 shows a sampling of the memory footprints expected of the random graphs used in the experiment (the odd growth pattern is due to the design of the underlying C++ data structure). It indicates that one may expect some memory event to occur within the cache memory range where the energy behavior changes. The cache also stores instructions and other data items, but the graph data structure should dominate, especially for small sizes. In Dijkstra, it competes with the priority queue for space in the cache. The SRAM-based cache in modern CPUs tends to be on the same chip as the cores (as in the Haswell unit used here) in the same power-efficient CMOS technology. As a result, it has significant energy advantages over the off-chip DRAM-based main memory due to the physical proximity [42] and technology. Table 4 lists the memory access delays for the Haswell CPU, reflecting the proximity expected to have an energy impact. Therefore, a closer look at the cache activity is necessary to make sense of the energy behaviors. The next part of this section examines the cache miss data.
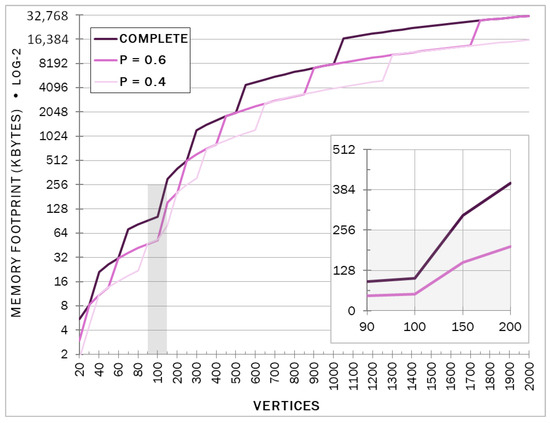
Figure 4.
Graph data structure size (KiB) in memory of a sample of random graphs (base-2 logarithmic). Shaded areas mark the cases that fit in the 256 KiB L2 cache. The inner view (in linear scale) focuses on cases that fit in 512 KiB for perspective.

Table 4.
Memory access latencies (from [40]).
4.2. Cache Analysis
Table 5 lists cache miss counts for Level 2 (L2) and Level 3 (L3) caches as reported by the profiler. The Level 1 (L1) caches are typically split, with data and instructions stored separately, and are too small to hold complete computations except for the tiniest ones. Any computation small enough to fit in L1 will have very little run time, which will pose challenges to profiling. In this experiment, the 32 KiB L1 caches generated thousands of misses immediately with the smallest test datasets (3248/4265 and 1410/2534 for the fully and moderately dense cases; the higher number was by Dijkstra). Therefore, the following analysis will lump the L1 cache with L2. The latency numbers in Table 4 justify the decision.

Table 5.
Average cache miss data.
Since the profiler reports miss counts, the cache miss events are evident in the table. However, plotting the numbers elucidates the effects visually. The discussion will initially focus on the fully dense case to uncover the trends at the worst case for graph complexity. Figure 5 shows the two main cache miss events in L2 and L3 caches at 90–100 and 250–350, respectively. After 350, both algorithms worked from the DRAM. The computation spilling from the L2 to L3 cache seems to be behind the region of interest from the energy and power curves where the trends reversed in favor of Dijkstra, i.e., its operational efficiency started to show in terms of energy behaviors. The effects of the second spill event, marking a shift to the less power-efficient DRAM, seem more subtle. The shaded parts in Table 5 highlight the two spill events in the fully dense case.
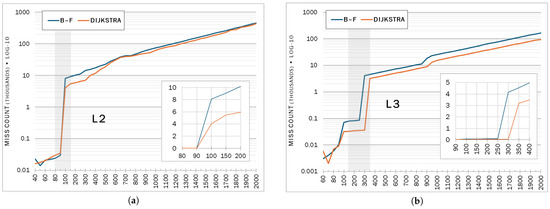
Figure 5.
Average cache misses by the fully dense (complete) graphs. In (b), the first apparent jump is insignificant and was exaggerated by the logarithmic scale. (a) Level 2 cache miss counts; (b) Level 3 cache miss counts.
Both algorithms were evicted from L2 at the same computation size. However, from Figure 5b, Dijkstra stayed in L3 longer than Bellman–Ford. Moreover, checking the highlighted values in the shaded parts in Table 5 under L3 reveals that once the computations settle in L3, Dijkstra generates fewer misses. The effect may also be observed in L2 data (compare the highlighted values under L2: about 10K at 350 vertices vs. 200 for Bellman–Ford). Bellman–Ford initially had the best locality with the smaller caches, but Dijkstra demonstrated a better fit in local memories once it moved to L3. The initial power efficiency of Bellman–Ford was probably due to fitting well with L1/L2 local memories relatively better than Dijkstra there. The increase in energy consumption rates seems to be due to increased reliance on the DRAM as computation sizes increase. However, Dijkstra seemed to exhibit better locality when the computation was in the DRAM, with L3 effectively operating as its power-efficient local memory, as evidenced by its lower miss counts as computation size increased. Hence, the better power efficiency, with a widening gap.
Comparing L2 miss data from the moderately dense case in Figure 6a, the previously described patterns seem to hold for the less complex graphs. However, they seem to have stayed in L2 slightly longer (evicted at 100–150 vs. 90–100), generating fewer misses. Having a lower edge density, it seems, resulted in a better locality. Figure 6b displays this effect on the power consumption patterns. It is tempting to infer from the plots that the relative advantage of Dijkstra increases with edge density, but a look back at Table 3 quickly confirms that is not the case according to the data.
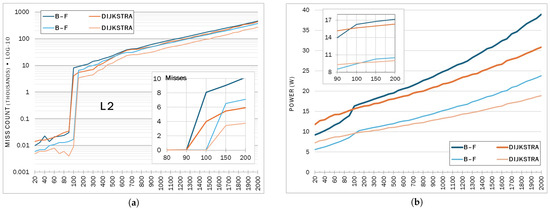
Figure 6.
Moderately dense graphs (in lighter color) compared against fully dense ones. (a) L2 cache miss behavior; (b) power consumption patterns.
In closing, from the viewpoint of the computations, there seem to have been two energy consumption patterns. One may say that they experienced two different power environments depending on the hardware involved in the work. The first was power-efficient low-latency cache-dominated, and the other was influenced predominantly by the less efficient DRAM. Dijkstra displayed better locality in the second environment, with fewer edges and better so. In addition to the edge density, the memory footprint of the graph depends on the data structure. It is, therefore, beneficial, from an energy viewpoint, to reduce the bytes used to store the graph to a bare minimum, which depends on the application. Both algorithms would see a benefit. Bellman–Ford would extend its advantageous power environment, and Dijkstra would reduce the competition with the priority queue in both power environments.
5. Conclusions
This research demonstrated that the Bellman–Ford algorithm outperformed Dijkstra’s algorithm in power efficiency when dealing with datasets small enough to fit in the upper layers of the memory hierarchy. The advantage correlated with the interaction of the memory footprint of the graph with the L2 cache in particular. Otherwise, for all cases from mid-size graphs onwards, the energy advantage was decisively in favor of Dijkstra, in line with its runtime behavior. The energy result should be unsurprising due to the massive time efficiency gap. Therefore, the corresponding gap in energy should follow in like fashion as graph sizes grow. As expected, more edges lead to more power and energy consumption. The findings were consistent, to an extent, with those reported in [23] from a GPU implementation, which is worth noting, considering the vast architectural differences between the processing environments. That GPU study, however, was limited, so more investigation may be needed before one can draw solid conclusions there.
The findings suggest that the graph size and processor setup (e.g., cache configuration) may play crucial roles when choosing between Dijkstra and Bellman–Ford with energy or power concerns in mind. The most obvious conclusion is that Bellman–Ford seems to be a better choice when processing a lot of small graphs. In particular, a power-sensitive massive high-performance system, where this computation is a significant fraction, should be expected to see notable benefits with Bellman–Ford. Moreover, the findings encourage when implementing Dijkstra to switch to Bellman–Ford when the remaining graph is small enough or maybe the overheads of the priority queue are no longer worth it. In parallel versions, they favor finer-grained partitioning for Bellman–Ford and the opposite for Dijkstra, tuned to the sizes of the inner cache levels in both cases.
The other major conclusion is about the edge density. Many practical applications, such as social and collaboration networks or web-page link structures, rely on sparse graphs. In those cases, a massive number of vertices remains relatively stable. Meanwhile, the edge counts, in addition to being relatively low, are expected to be more variable. The density findings suggest that one should expect those applications to enjoy some relative power and energy efficiency naturally. More importantly, the energy behavior of graph algorithms that share the efficiency of Dijkstra, such as Prim’s algorithm, should also scale steadily there, effectively linearly, with the edge count. From an energy behaviors perspective, those algorithms may benefit from monitoring and actively culling those edges, likely from dead/broken relations, to keep consumption in check.
The findings, in total, underscore the significance of factoring in power and energy consumption alongside the usual time and space performance metrics when designing the algorithms. This concern is critical in HPC settings where energy behavior is vital in terms of both cost and, ultimately, performance. The exceedingly low energy figures reported for Dijkstra in the highest test cases may be deceptive (see the last line in Table 3). They hide relatively high energy consumption rates at about 19–31 watts, almost comparable to Bellman–Ford. Interestingly, an Intel Haswell still powered 11 systems in the renowned TOP500.ORG lineup as of June 2024 [43]. Therefore, these high numbers may be considered fair representations of the power draw to expect in some contemporary HPC environments, which is remarkable. To put those figures in perspective, the SSSP computation consumed as much as the rated TDP (thermal design power) for some consumer ultraportable devices in 2023–24. It highlights the importance of looking at power and energy as separate concerns. A final insight from this research is, perhaps, the need to go beyond the classic time analysis for a nuanced understanding of energy behaviors. Carefully mapping basic algorithmic behaviors to energy-significant hardware is fruitful. While time is a rigidly enforced physical quantity, we have choices with energy. We can choose operations and functional units and tune behaviors to influence energy budgets and how fast we spend those budgets.
Looking ahead to future research, the preceding part of this section has perhaps already alluded to some directions. In particular, a comprehensive study in a GPU setting would be interesting. Corroborating the power finding may support a notion of algorithmic origins for that trend. A hybrid that merges features from both algorithms in some way to strike a good balance between power and time efficiency may be attractive. Moreover, one may want to explore an algorithm with active edge management for sparse graph applications, such as those described above. In particular, it would be interesting to have an AI-based “oracle” that dynamically suggests likely dead or less relevant edges to ignore temporarily to help keep the power draw within desired power envelopes. As a final suggestion, it seems from the cache miss data that a larger L2 cache, e.g., 512 KiB as in the AMD Epyc 7003 (Milan) Series, likely extends the range of instance sizes that can enjoy the power advantage of Bellman–Ford beyond the 90–100 vertex marks reported here. More work is needed to confirm that, including looking into other valuable workloads to check for the effect. It could lend more support for increasing the size of that cache in HPC-class processors.
Author Contributions
Conceptualization, O.A. and M.A.-H.; methodology, M.A.-H.; software, O.A.; validation, O.A. and M.A.-H.; formal analysis, M.A.-H.; investigation, O.A.; resources, M.A.-H.; data curation, O.A.; writing—original draft preparation, M.A.-H. and O.A.; writing—review and editing, M.A.-H.; visualization, M.A.-H. and O.A.; supervision, M.A.-H.; project administration, O.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SSSP | Single-Source Shortest Paths |
| HPC | High-Performance Computing |
| B–F | Bellman–Ford [Algorithm] |
| RAPL | Running Average Power Limit |
| FIVR | Fully Integrated Voltage Regulator |
References
- Abulnaja, O.A.; Ikram, M.J.; Al-Hashimi, M.A.; Saleh, M.E. Analyzing power and energy efficiency of bitonic mergesort based on performance evaluation. IEEE Access 2018, 6, 42757–42774. [Google Scholar] [CrossRef]
- Aljabri, N.; Al-Hashimi, M.; Saleh, M.; Abulnaja, O. Investigating power efficiency of mergesort. J. Supercomput. 2019, 75, 6277–6302. [Google Scholar] [CrossRef]
- Al-Hashimi, M.; Aljabri, N. Exploring Power Advantage of Binary Search: An Experimental Study. Int. J. Adv. Comput. Sci. Appl. 2022, 13. [Google Scholar] [CrossRef]
- Padua, D. (Ed.) Parallel Communication Models. In Encyclopedia of Parallel Computing; Springer: Berlin/Heidelberg, Germany, 2011; p. 1409. [Google Scholar]
- AbuSalim, S.W.; Ibrahim, R.; Saringat, M.Z.; Jamel, S.; Wahab, J.A. Comparative Analysis between Dijkstra and Bellman-Ford Algorithms in Shortest Path Optimization. IOP Conf. Ser. Mater. Sci. Eng. 2020, 917, 012077. [Google Scholar] [CrossRef]
- Delling, D.; Goldberg, A.V.; Nowatzyk, A.; Werneck, R.F. PHAST: Hardware-accelerated shortest path trees. J. Parallel Distrib. Comput. 2013, 73, 940–952. [Google Scholar] [CrossRef]
- Ahmad, M.; Michael, C.J.; Khan, O. A Case for a Situationally Adaptive Many-core Execution Model for Cognitive Computing Workloads. In Proceedings of the ASPLOS 2016 International Workshop on Cognitive Architectures, (CogArch), Atlanta, GA, USA, 2 April 2016. [Google Scholar]
- Lewis, R. Algorithms for Finding Shortest Paths in Networks with Vertex Transfer Penalties. Algorithms 2020, 13, 269. [Google Scholar] [CrossRef]
- Inga, E.; Inga, J.; Ortega, A. Novel Approach Sizing and Routing of Wireless Sensor Networks for Applications in Smart Cities. Sensors 2021, 21, 4692. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Ruiz, P.M.; Stojmenovic, I. Energy-efficient geographic multicast routing for Sensor and Actuator Networks. Comput. Commun. 2007, 30, 2519–2531. [Google Scholar] [CrossRef]
- Schmitt, J.; Bondorf, S.; Poe, W.Y. The Sensor Network Calculus as Key to the Design of Wireless Sensor Networks with Predictable Performance. J. Sens. Actuator Netw. 2017, 6, 21. [Google Scholar] [CrossRef]
- Dljkstra, E. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 50, 269–271. [Google Scholar] [CrossRef]
- Ford, L.R. Network Flow Theory; RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Sedgewick, R.; Wayne, K. Algorithms, 4th ed.; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Introduction to Algorithms, 4th ed.; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Moore, E. The Shortest Path through a Maze. In Proceedings of the International Symposium on the Theory of Switching; Springer: Berlin/Heidelberg, Germany, 1959; pp. 285–292. [Google Scholar]
- Kalpana, R.; Thambidurai, P. Optimizing shortest path queries with parallelized arc flags. In Proceedings of the 2011 International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 3–5 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 601–606. [Google Scholar]
- Zhang, W.; Chen, H.; Jiang, C.; Zhu, L. Improvement and experimental evaluation bellman-ford algorithm. In Proceedings of the 2013 International Conference on Advanced ICT and Education (ICAICTE-13), Hainan, China, 20–22 September 2013; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 138–141. [Google Scholar]
- Hajela, G.; Pandey, M. A Fine Tuned Hybrid Implementation for Solving Shortest Path Problems Using Bellman Ford. Int. J. Comput. Appl. 2014, 99, 29–33. [Google Scholar] [CrossRef]
- Abousleiman, R.; Rawashdeh, O. A Bellman-Ford approach to energy efficient routing of electric vehicles. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Chennai, India, 27–29 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Busato, F.; Bombieri, N. An efficient implementation of the Bellman-Ford algorithm for Kepler GPU architectures. IEEE Trans. Parallel Distrib. Syst. 2015, 27, 2222–2233. [Google Scholar] [CrossRef]
- Mishra, A.; Khare, N. Power and Performance Characterization of the Dijkstra’s Graph algorithm on GPU. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 858. [Google Scholar]
- Cheng, C.D. Extended Dijkstra algorithm and Moore-Bellman-Ford algorithm. arXiv 2017, arXiv:1708.04541. [Google Scholar]
- Schambers, A.; Eavis-O’Quinn, M.; Roberge, V.; Tarbouchi, M. Route planning for electric vehicle efficiency using the Bellman-Ford algorithm on an embedded GPU. In Proceedings of the 2018 4th International Conference on Optimization and Applications (ICOA), Mohammedia, Morocco, 26–27 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Abderrahim, M.; Hakim, H.; Boujemaa, H.; Touati, F. Energy-Efficient Transmission Technique based on Dijkstra Algorithm for decreasing energy consumption in WSNs. In Proceedings of the 2019 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 599–604. [Google Scholar]
- Weber, A.; Kreuzer, M.; Knoll, A. A generalized Bellman-Ford algorithm for application in symbolic optimal control. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2007–2014. [Google Scholar]
- Rai, A. A Study on Bellman Ford Algorithm for Shortest Path Detection in Global Positioning System. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 2118–2126. [Google Scholar] [CrossRef]
- Alqurashi, F.S.; Al-Hashimi, M. An Experimental Approach to Estimation of the Energy Cost of Dynamic Branch Prediction in an Intel High-Performance Processor. Computers 2023, 12, 139. [Google Scholar] [CrossRef]
- Alsari, S.; Al-Hashimi, M. Investigation of Energy and Power Characteristics of Various Matrix Multiplication Algorithms. Energies 2024, 17, 2225. [Google Scholar] [CrossRef]
- Leskovec, J.; Krevl, A. Stanford Large Network Dataset Collection. 2014. Available online: https://snap.stanford.edu/data/ (accessed on 16 May 2024).
- Erdös, P.; Rényi, A. On random graphs I. Publ. Math. Debr. 1959, 6, 290–297. [Google Scholar] [CrossRef]
- rustworkx.directed_gnp_random_graph—rustworkx 0.14.2—rustworkx.org. Available online: https://www.rustworkx.org/apiref/rustworkx.directed_gnp_random_graph.html (accessed on 19 April 2024).
- Treinish, M.; Carvalho, I.; Tsilimigkounakis, G.; Sá, N. rustworkx: A High-Performance Graph Library for Python. J. Open Source Softw. 2022, 7, 3968. [Google Scholar] [CrossRef]
- Halim, S.; Halim, F. Competitive Programming 3: The New Lower Bound of Programming Contests (Handbook for ACM ICPC and IOI Contestants), 3rd ed.; Lulu: Morrisville, NC, USA, 2013; Available online: https://www.lulu.com/shop/steven-halim/competitive-programming-3/paperback/product-21059906.html?srsltid=AfmBOorJsTa4w9IgGZY55WuEr31nMr0pAoiUc2H62IFIXLNYeawPcofb&page=1&pageSize=4 (accessed on 9 October 2024).
- C++ Containers Library: std::priority_queue. Available online: https://en.cppreference.com/w/cpp/container/priority_queue (accessed on 20 June 2024).
- Free Software Foundation. A GNU Manual (3.10 Options That Control Optimization). 2017. Available online: https://gcc.gnu.org/onlinedocs/gcc-7.5.0/gcc/Optimize-Options.html (accessed on 26 April 2024).
- Perf Wiki—perf.wiki.kernel.org. Available online: https://perf.wiki.kernel.org/ (accessed on 4 December 2023).
- Gruber, T.; Eitzinger, J.; Hager, G.; Wellein, G. Likwid. Version V5 2022, 2, 20. [Google Scholar]
- Saini, S.; Hood, R.; Chang, J.; Baron, J. Performance evaluation of an Intel Haswell-and Ivy Bridge-based supercomputer using scientific and engineering applications. In Proceedings of the 2016 IEEE 18th International Conference on High Performance Computing and Communications; IEEE 14th International Conference on Smart City; IEEE 2nd International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Sydney, NSW, Australia, 12–14 December 2016; IEEE: Sydney, NSW, Australia, 2016; pp. 1196–1203. [Google Scholar]
- Khan, K.N.; Hirki, M.; Niemi, T.; Nurminen, J.K.; Ou, Z. RAPL in Action: Experiences in Using RAPL for Power measurements. ACM Trans. Model. Perform. Eval. Comput. Syst. (TOMPECS) 2018, 3, 1–26. [Google Scholar] [CrossRef]
- Theis, T.N.; Wong, H.S.P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 2017, 19, 41–50. [Google Scholar] [CrossRef]
- TOP500: The List Highlights—June 2024. Available online: https://top500.org/lists/top500/2024/06/highs/ (accessed on 20 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).