Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure
Abstract
1. Introduction
1.1. Relevance of the Research
1.2. State-of-the-Art
- Development of a mathematical model to determine the helicopter TE sensor network output signal in a sensor failure case.
- Development of a neural network and its training algorithm to model helicopter TE parameters in a sensor network failure event.
- Development of a test bench for the helicopter TE parameters in a sensor network for the semi-naturalistic modeling implementation of a sensor failure event.
- Conduct a computational experiment consisting of model helicopter TE parameters during a gas-generator rotor speed sensor failure under various temperature conditions.
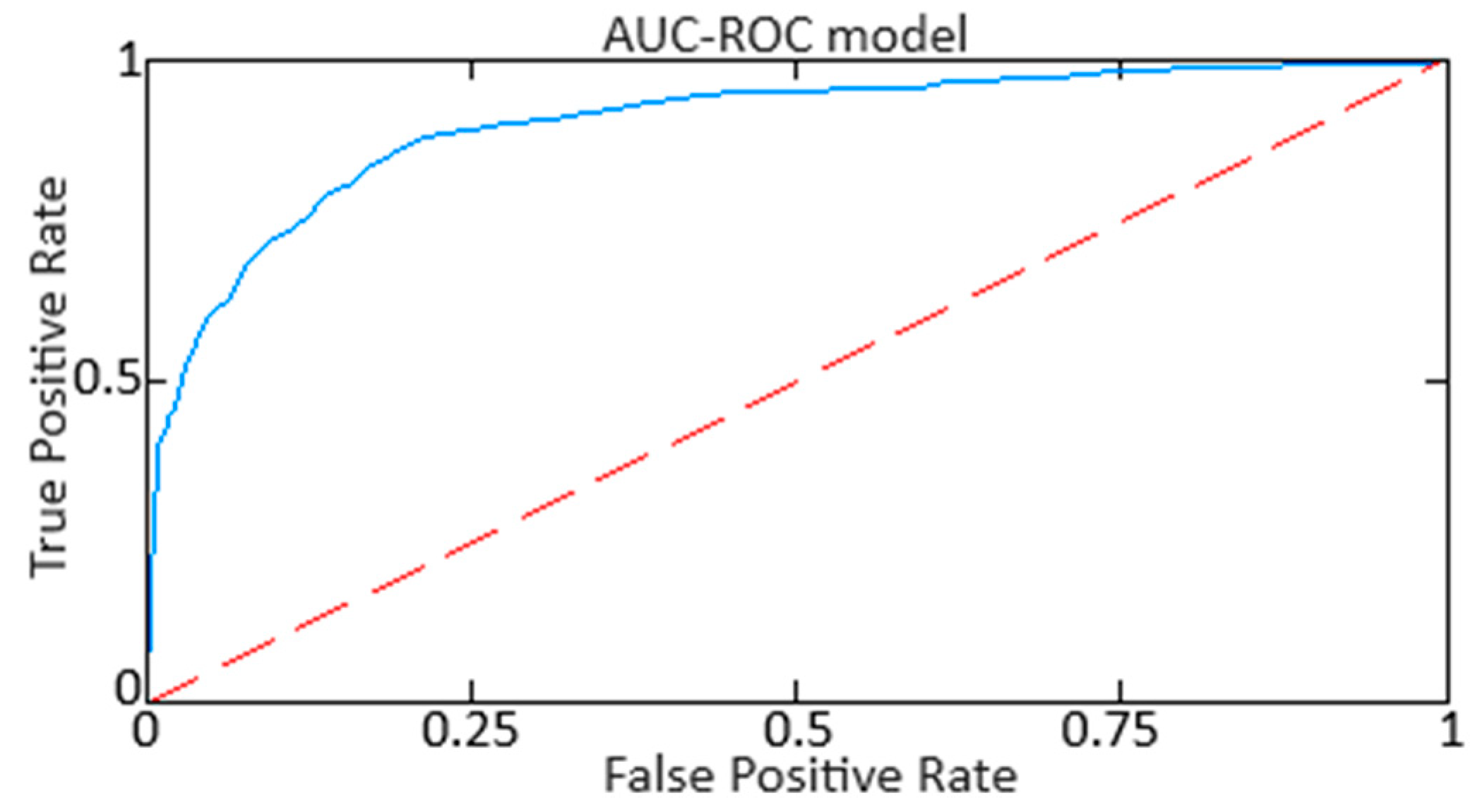
- Assess the results obtained for quality using traditional metrics.
1.3. Paper Organization
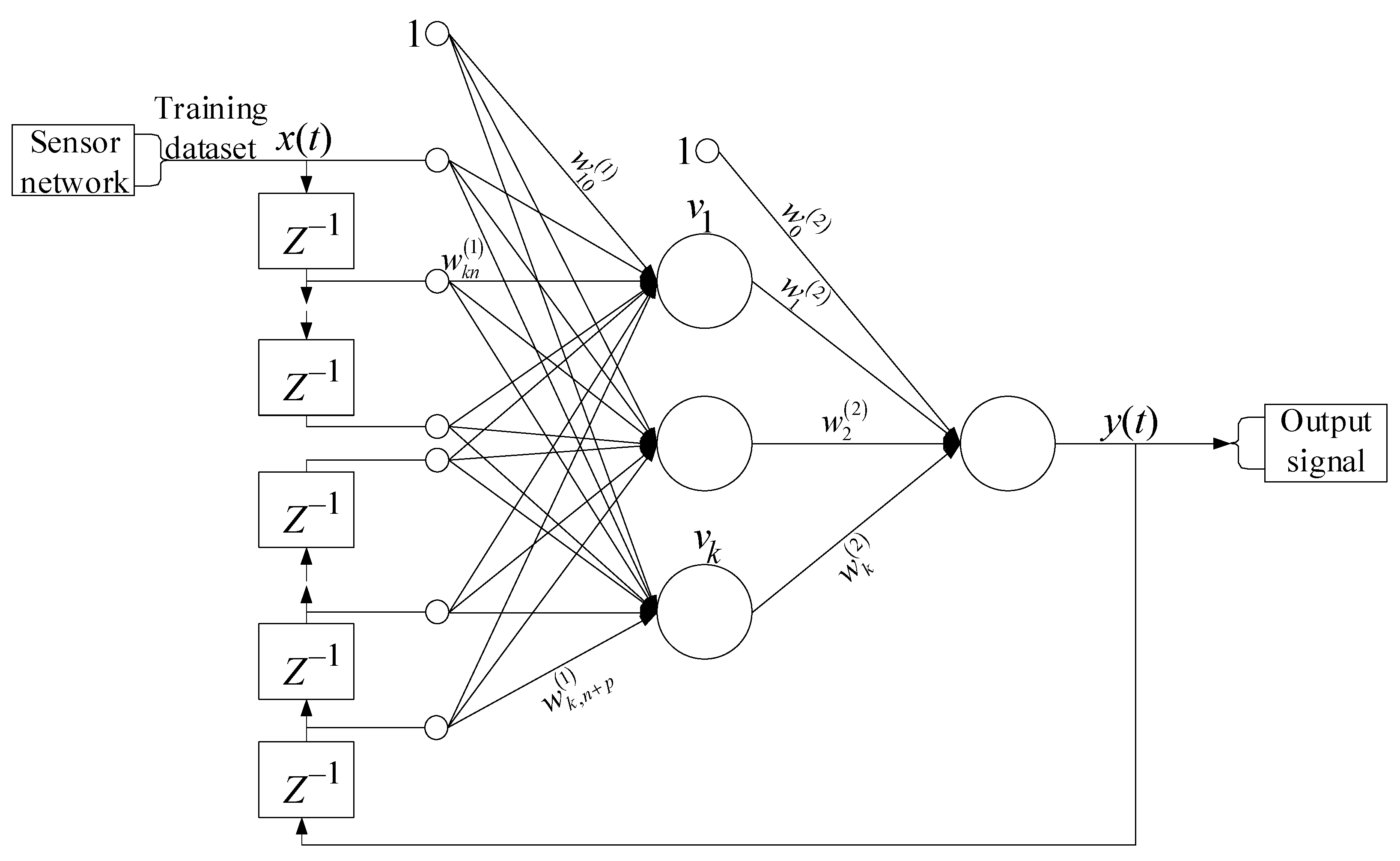
2. Materials and Methods
| Algorithm 1: The pseudocode of the NARX neural network training (author’s research). |
| initialize_weights(); learning_rate = 0.01; epochs = 1000; N = length_of_training_data; d_in = input_delay; d_out = output_delay; for epoch in range(epochs): total_error = 0; for i in range(d_in, N): x = get_input_sequence(i, d_in); y_true = get_true_output(i); y_pred = forward_pass(x); error = y_true − y_pred; total_error += error ** 2; gradients = backward_pass(error, x); update_weights(gradients, learning_rate); print(f“Epoch {epoch + 1}, Total Error: {total_error}”); if total_error < threshold: break. |
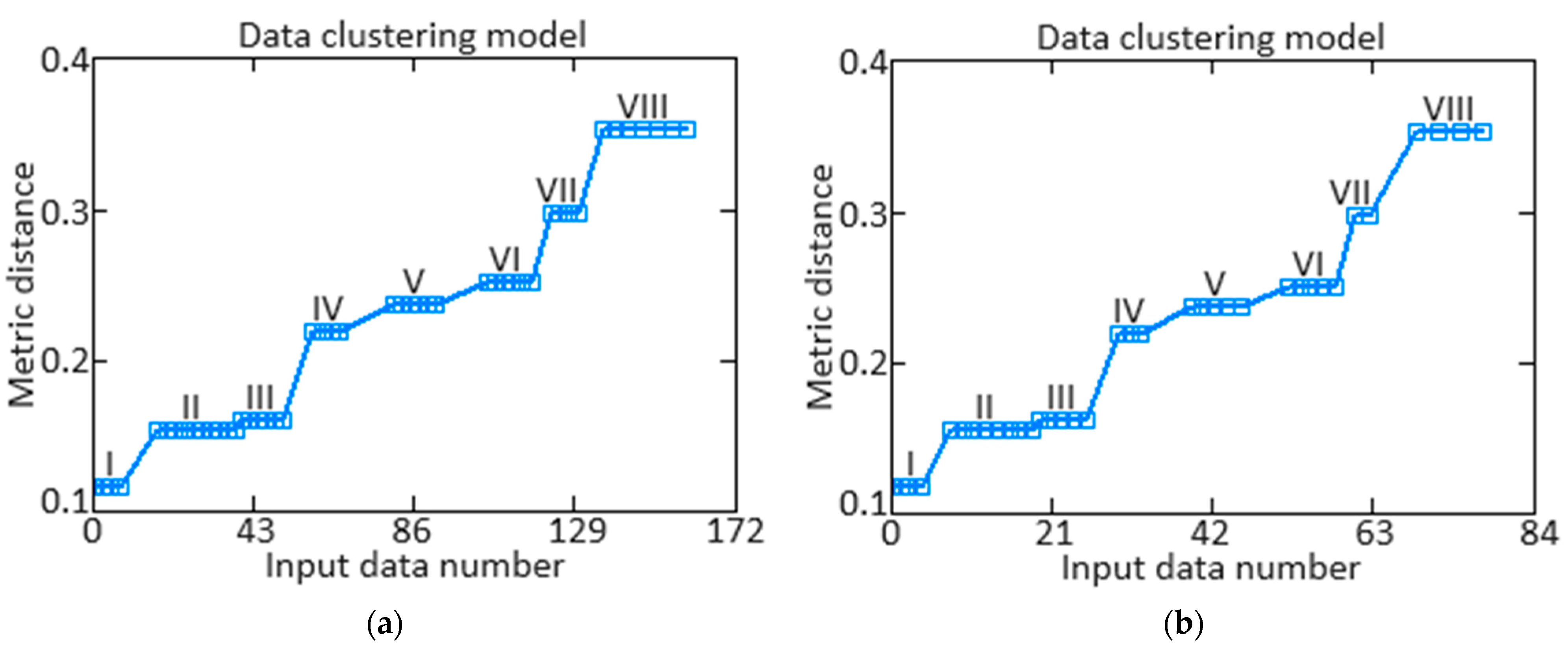
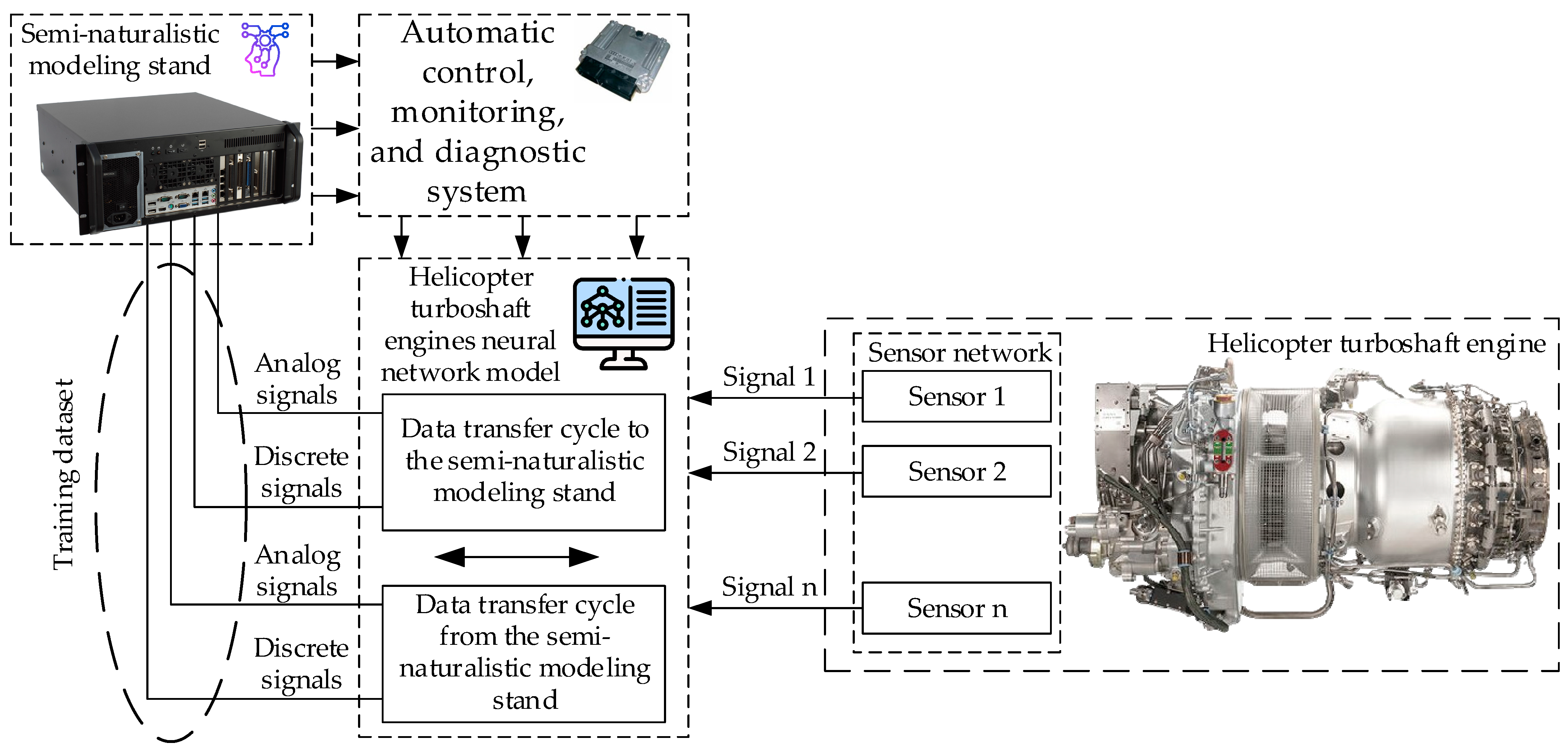
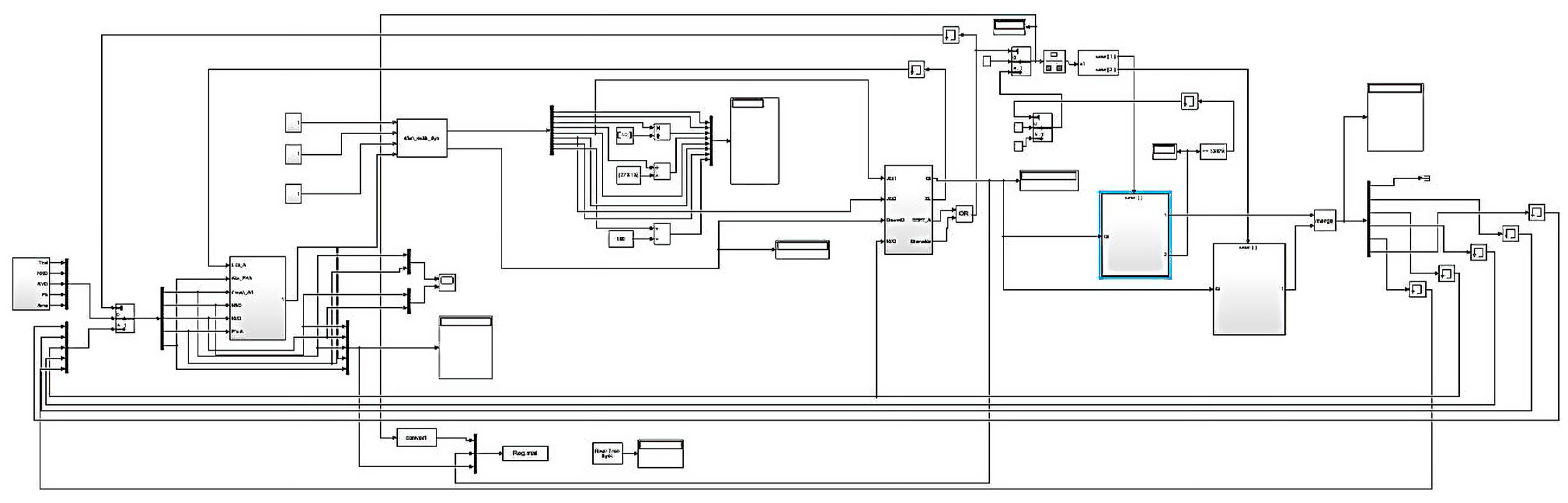
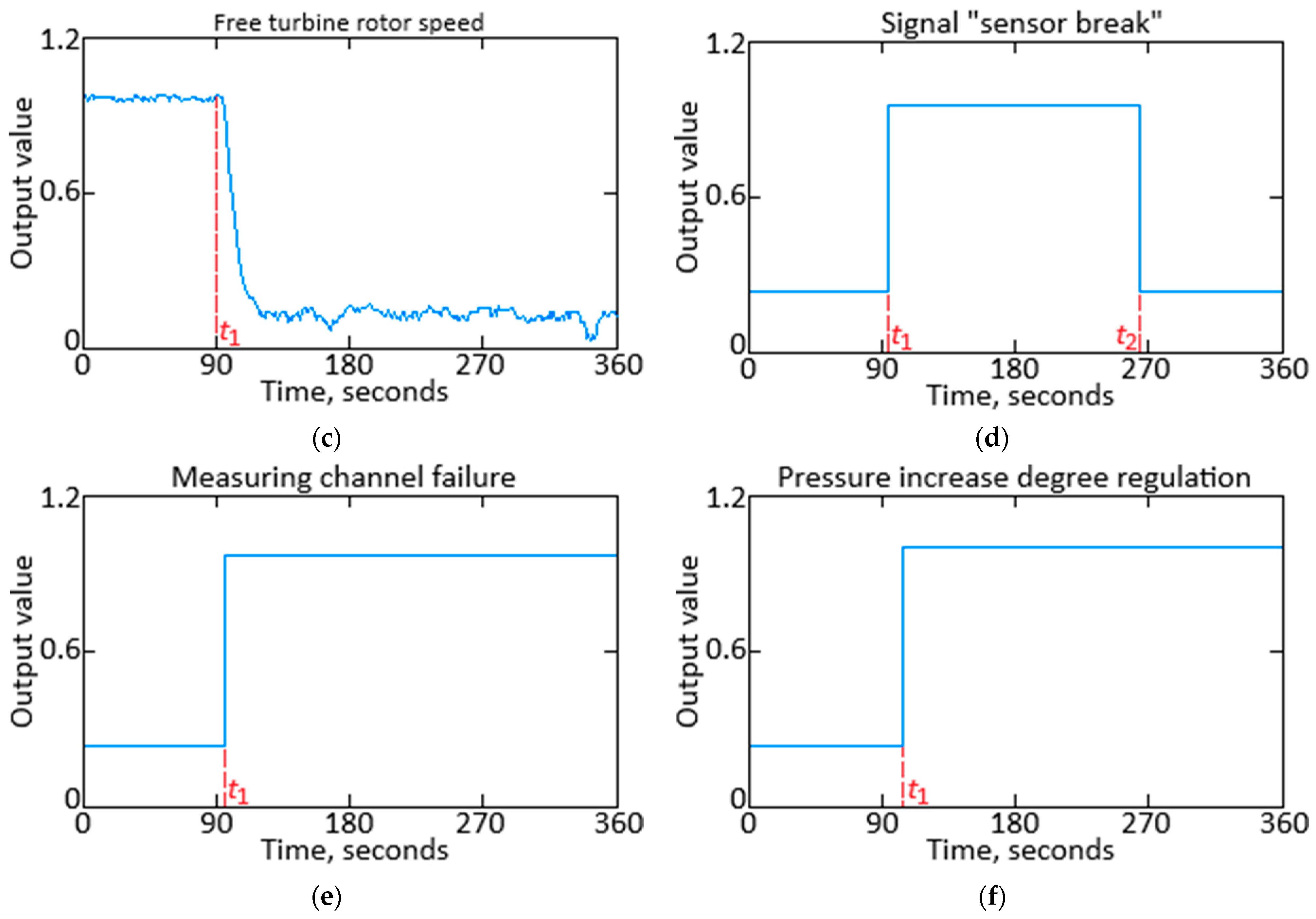
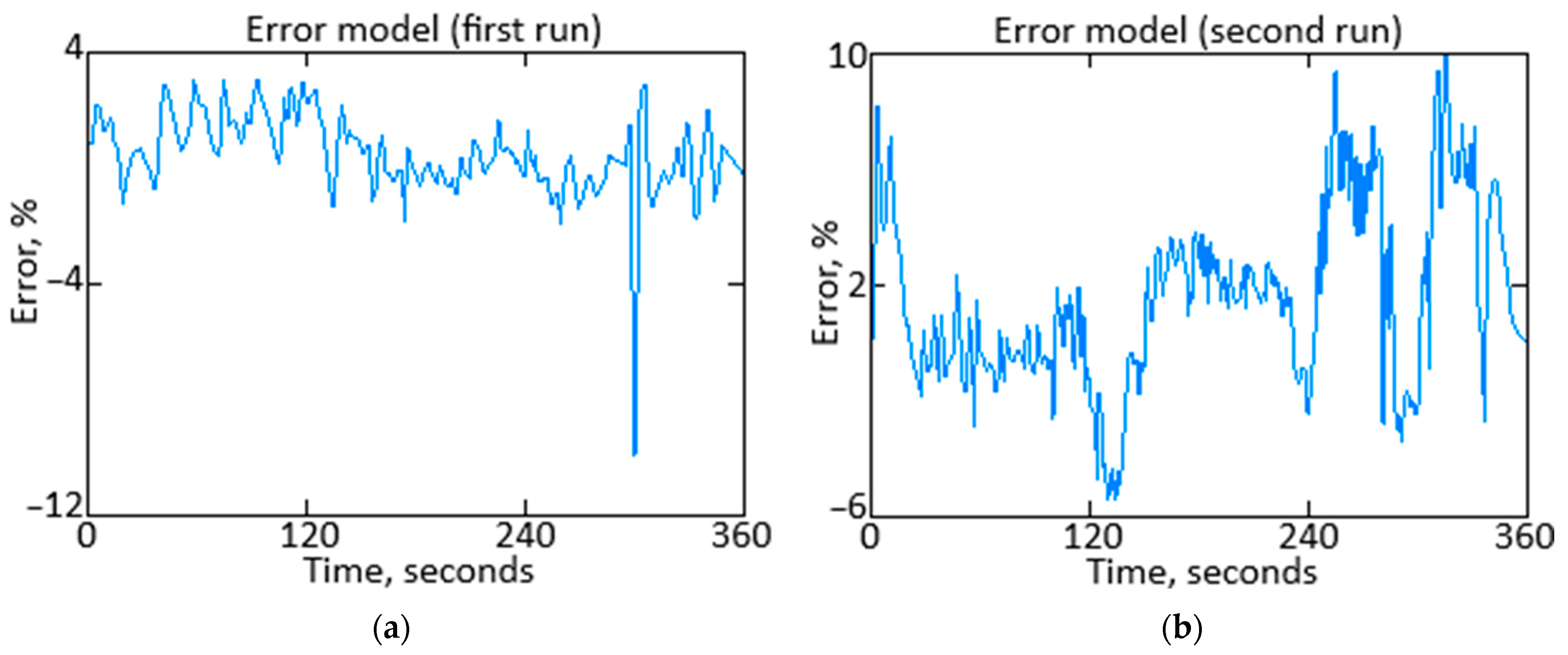
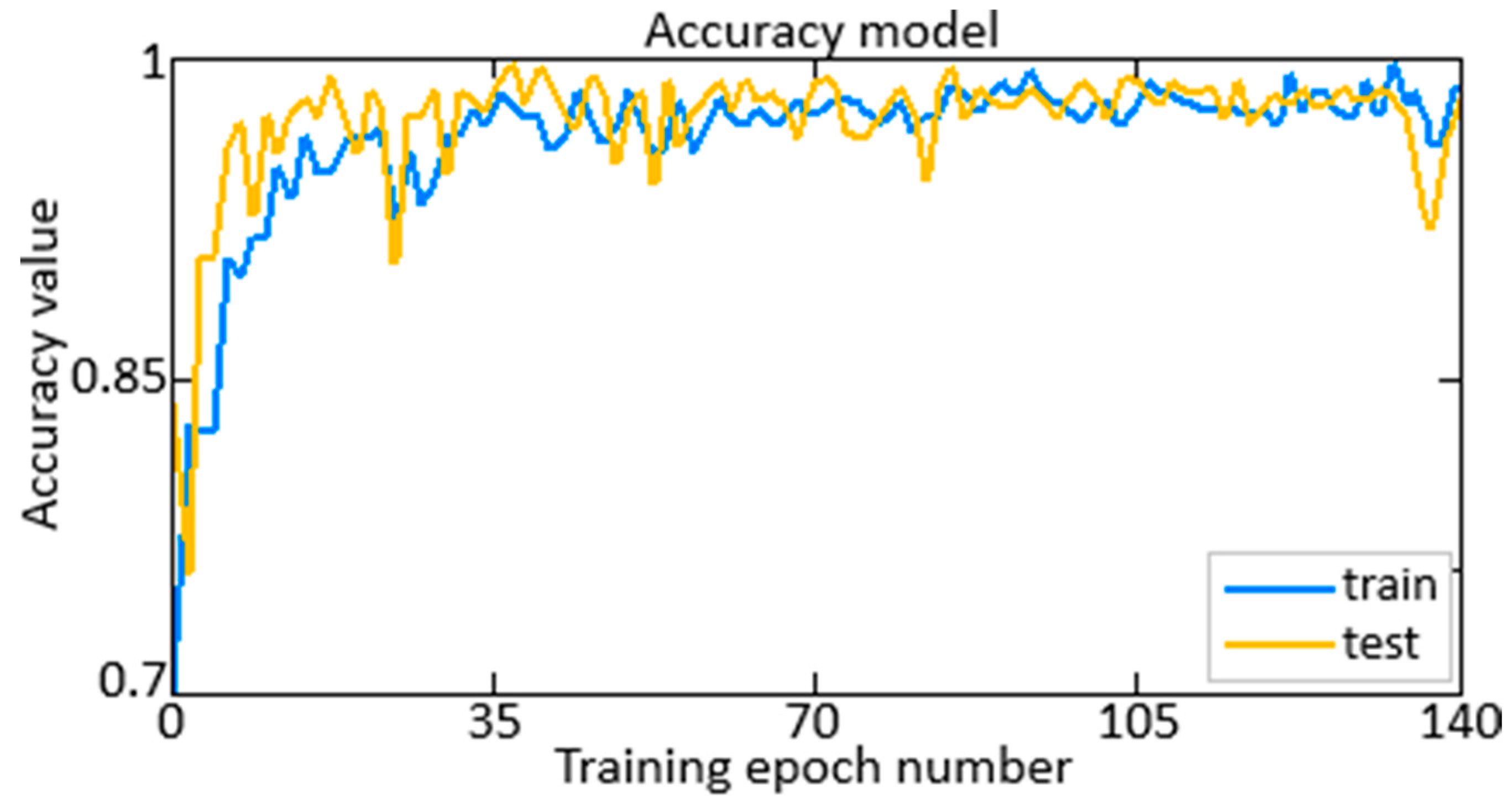
3. Case Study
| Algorithm 2: The pseudocode describing how the sample sizes for the training and test datasets were obtained (author’s research). |
| sensor_data = get_sensor_data(); length = len(sensor_data); sample_size = 256; def get_training_sample(sensor_data, sample_size): if length < sample_size: raise ValueError(“Data are insufficient to obtain a dataset”); training_sample = []; for i in range(sample_size): index = select_index(length); training_sample.append(sensor_data[index]); return training_sample; training_sample = get_training_sample(sensor_data, sample_size); normalized_sample = normalize(training_sample); train_model(normalized_sample). |
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lan, J.; Patton, R.J.; Punta, E. Fault-Tolerant Tracking Control for A 3-DOF Helicopter with Actuator Faults and Saturation. IFAC-PapersOnLine 2017, 50, 5250–5255. [Google Scholar] [CrossRef]
- Pérez-Ventura, U.; Fridman, L.; Capello, E.; Punta, E. Fault Tolerant Control Based on Continuous Twisting Algorithms of a 3-DoF Helicopter Prototype. Control Eng. Pract. 2020, 101, 104486. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, K.; Jiang, B. Practical Prescribed-Time Active Fault-Tolerant Control for Mixed-Order Heterogeneous Multiagent Systems: A Fully Actuated System Approach. Automatica 2024, 166, 111721. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Vysotska, V.; Nazarkevych, M.; Lytvyn, V. The Method of Restoring Lost Information from Sensors Based on Auto-Associative Neural Networks. Appl. Syst. Innov. 2024, 7, 53. [Google Scholar] [CrossRef]
- Zhu, X.; Li, D. Robust Fault Estimation for a 3-DOF Helicopter Considering Actuator Saturation. Mech. Syst. Signal Process. 2021, 155, 107624. [Google Scholar] [CrossRef]
- Kumar, S.R.; Devakumar, J. Recurrent Neural Network Based Sensor Fault Detection and Isolation for Nonlinear Systems: Application in PWR. Prog. Nucl. Energy 2023, 163, 104836. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, Y.; Yang, X.; Zhang, K.; Liu, F. An Intelligent Online Fault Diagnosis System for Gas Turbine Sensors Based on Unsupervised Learning Method LOF and KELM. Sens. Actuators A Phys. 2024, 365, 114872. [Google Scholar] [CrossRef]
- Shen, Y.; Khorasani, K. Hybrid Multi-Mode Machine Learning-Based Fault Diagnosis Strategies with Application to Aircraft Gas Turbine Engines. Neural Netw. 2020, 130, 126–142. [Google Scholar] [CrossRef]
- Shuai, M.; Yafeng, W.; Hua, Z.; Linfeng, G. Parameter Modelling of Fleet Gas Turbine Engines Using Gated Recurrent Neural Networks. J. Phys. Conf. Ser. 2023, 2472, 012012. [Google Scholar] [CrossRef]
- Khattak, W.R.; Salman, A.; Ghafoor, S.; Latif, S. Multi-Modal LSTM Network for Anomaly Prediction in Piston Engine Aircraft. Heliyon 2024, 2024 10, e25120. [Google Scholar] [CrossRef]
- Boujamza, A.; Lissane Elhaq, S. Attention-Based LSTM for Remaining Useful Life Estimation of Aircraft Engines. IFAC-PapersOnLine 2022, 55, 450–455. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Nosal, O. Highly Sensitive Methods for Vibration Diagnostics of Fatigue Damage in Structural Elements of Aircraft Gas Turbine Engines. Procedia Struct. Integr. 2022, 35, 74–81. [Google Scholar] [CrossRef]
- Wei, X.; Yingqing, G. Aircraft Engine Sensor Fault Diagnostics Based on Estimation of Engine’s Health Degradation. Chin. J. Aeronaut. 2009, 22, 18–21. [Google Scholar] [CrossRef]
- Szrama, S.; Lodygowski, T. Aircraft Engine Remaining Useful Life Prediction Using Neural Networks and Real-Life Engine Operational Data. Adv. Eng. Softw. 2024, 192, 103645. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.-G.; Sampath, S. A Hierarchical Structure Built on Physical and Data-Based Information for Intelligent Aero-Engine Gas Path Diagnostics. Appl. Energy 2023, 332, 120520. [Google Scholar] [CrossRef]
- Weiser, C.; Ossmann, D. Fault-Tolerant Control for a High Altitude Long Endurance Aircraft. IFAC-PapersOnLine 2022, 55, 724–729. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, Y.; Chen, Z.; Zhang, N.; Xue, X.; Zhou, J. Measurement of Health Evolution Tendency for Aircraft Engine Using a Data-Driven Method Based on Multi-Scale Series Reconstruction and Adaptive Hybrid Model. Measurement 2022, 199, 111502. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.-P.; Chen, Y.-B. Unilateral Alignment Transfer Neural Network for Fault Diagnosis of Aircraft Engine. Aerosp. Sci. Technol. 2021, 118, 107031. [Google Scholar] [CrossRef]
- Skarka, W.; Nalepa, R.; Musik, R. Integrated Aircraft Design System Based on Generative Modelling. Aerospace 2023, 10, 677. [Google Scholar] [CrossRef]
- Baláž, M.; Kováčiková, K.; Novák, A.; Vaculík, J. The Application of Internet of Things in Air Transport. Transp. Res. Procedia 2023, 75, 60–67. [Google Scholar] [CrossRef]
- Bouzidi, Z.; Terrissa, L.S.; Zerhouni, N.; Ayad, S. An Efficient Cloud Prognostic Approach for Aircraft Engines Fleet Trending. Int. J. Comput. Appl. 2018, 42, 514–529. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J.; Stushchanskyi, Y. Neural Network Modeling of Helicopters Turboshaft Engines at Flight Modes Using an Approach Based on “Black Box” Models. CEUR Workshop Proc. 2024, 3624, 116–135. [Google Scholar]
- Vysotska, V.; Vladov, S.; Yakovliev, R.; Yurko, A. Hybrid Neural Network Identifying Complex Dynamic Objects: Comprehensive Modelling and Training Method Modification. CEUR Workshop Proc. 2024, 3702, 124–143. [Google Scholar]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Modified Searchless Method for Identification of Helicopters Turboshaft Engines at Flight Modes Using Neural Networks. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 257–262. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, S.; Jafari, S.; Nikolaidis, T. Gas Turbine Aero-Engines Real Time on-Board Modelling: A Review, Research Challenges, and Exploring the Future. Prog. Aerosp. Sci. 2020, 121, 100693. [Google Scholar] [CrossRef]
- Yang, Q.; Tang, B.; Li, Q.; Liu, X.; Bao, L. Dual-Frequency Enhanced Attention Network for Aircraft Engine Remaining Useful Life Prediction. ISA Trans. 2023, 141, 167–183. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Harrison, R.F.; Mills, A.R.; Fleming, P.J. Bayesian Hierarchical Models for Aerospace Gas Turbine Engine Prognostics. Expert Syst. Appl. 2015, 42, 539–553. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, V.S.; Butt, M.M.; Sheikh, N.A.; Khan, S.A.; Afzal, A. Thermo-Mechanical Analysis and Estimation of Turbine Blade Tip Clearance of a Small Gas Turbine Engine under Transient Operating Conditions. Appl. Therm. Eng. 2020, 179, 115700. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, D.; Zhang, H.; Yang, J. Periodic Analysis on Gas Path Fault Diagnosis of Gas Turbines. ISA Trans. 2022, 129, 429–441. [Google Scholar] [CrossRef]
- Zhu, P.; Yu, L.; Zeng, J. Prescribed Performance Control for Nonlinear Parameter-Varying Systems with an Application to Turbofan Engine. J. Frankl. Inst. 2023, 360, 7722–7738. [Google Scholar] [CrossRef]
- Vladov, S.; Kovtun, V.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. The Helicopter Turboshaft Engine’s Reconfigured Dynamic Model for Functional Safety Estimation. Electronics 2024, 13, 3477. [Google Scholar] [CrossRef]
- Ibrahem, I.M.A.; Akhrif, O.; Moustapha, H.; Staniszewski, M. Nonlinear Generalized Predictive Controller Based on Ensemble of NARX Models for Industrial Gas Turbine Engine. Energy 2021, 230, 120700. [Google Scholar] [CrossRef]
- Amirkhani, S.; Tootchi, A.; Chaibakhsh, A. Fault Detection and Isolation of Gas Turbine Using Series–Parallel NARX Model. ISA Trans. 2022, 120, 205–221. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Liu, B.; Xu, M.; Li, M.; Song, Z. Model-Based Deduction Learning Control: A Novel Method for Optimizing Gas Turbine Engine Afterburner Transient. Energy 2024, 292, 130512. [Google Scholar] [CrossRef]
- Fedorov, E.; Dikova, Y. Development of the method of prediction of content of explosive gases in mines. Sci. Pap. Donetsk Natl. Tech. Univ. Ser. Inform. Cybern. Comput. Sci. 2015, 1, 97–104. [Google Scholar]
- Vladov, S.; Yakovliev, R.; Bulakh, M.; Vysotska, V. Neural Network Approximation of Helicopter Turboshaft Engine Parameters for Improved Efficiency. Energies 2024, 17, 2233. [Google Scholar] [CrossRef]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signal Integration from Thermogas-Dynamic Parameter Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M. Neural Network Method for Parametric Adaptation Helicopters Turboshaft Engines On-Board Automatic Control System Parameters. CEUR Workshop Proc. 2023, 3403, 179–195. [Google Scholar]
- Kim, H.-Y. Statistical Notes for Clinical Researchers: Chi-Squared Test and Fisher’s Exact Test. Restor. Dent. Endod. 2017, 42, 152. [Google Scholar] [CrossRef]
- Stefanovic, C.M.; Armada, A.G.; Costa-Perez, X. Second Order Statistics of -Fisher-Snedecor Distribution and Their Application to Burst Error Rate Analysis of Multi-Hop Communications. IEEE Open J. Commun. Soc. 2022, 3, 2407–2424. [Google Scholar] [CrossRef]
- Babichev, S.; Krejci, J.; Bicanek, J.; Lytvynenko, V. Gene expression sequences clustering based on the internal and external clustering quality criteria. In Proceedings of the 2017 12th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 5–8 September 2017. [Google Scholar] [CrossRef]
- Hu, Z.; Kashyap, E.; Tyshchenko, O.K. GEOCLUS: A Fuzzy-Based Learning Algorithm for Clustering Expression Datasets. Lect. Notes Data Eng. Commun. Technol. 2022, 134, 337–349. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Makaryants, G.M. Micro Gas Turbine Engine Imitation Model. Aerosp. Mech. Eng. 2017, 16, 65–74. [Google Scholar] [CrossRef]
- Denisova, E.V.; Chernikova, M.A. Development of semi-naturalistic modeling stands for studying the gas turbine engines automatic control systems. Mod. High Technol. 2019, 7, 122–131. [Google Scholar]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Optimization of Helicopters Aircraft Engine Working Process Using Neural Networks Technologies. CEUR Workshop Proc. 2022, 3171, 1639–1656. [Google Scholar]
- Kilic, U.; Yalin, G.; Cam, O. Digital Twin for Electronic Centralized Aircraft Monitoring by Machine Learning Algorithms. Energy 2023, 283, 129118. [Google Scholar] [CrossRef]
- Barthorpe, R.J.; Worden, K. Emerging Trends in Optimal Structural Health Monitoring System Design: From Sensor Placement to System Evaluation. J. Sens. Actuator Netw. 2020, 9, 31. [Google Scholar] [CrossRef]
- Shubyn, B.; Maksymyuk, T.; Gazda, J.; Rusyn, B.; Mrozek, D. Federated Learning: A Solution for Improving Anomaly Detection Accuracy of Autonomous Guided Vehicles in Smart Manufacturing. Lect. Notes Electr. Eng. 2024, 1198, 746–761. [Google Scholar] [CrossRef]
- Rusyn, B.; Lutsyk, O.; Kosarevych, R.; Obukh, Y. Application Peculiarities of Deep Learning Methods in the Problem of Big Datasets Classification. Lect. Notes Electr. Eng. 2021, 831, 493–506. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Zhang, H. Research on Adaptive Feedforward Control Method for Tiltrotor Aircraft/Turboshaft Engine System Based on Radial Basis Function Neural Network. Aerosp. Sci. Technol. 2024, 150, 109180. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Zhao, Y.-P. A Novel Inter-Domain Attention-Based Adversarial Network for Aero-Engine Partial Unsupervised Cross-Domain Fault Diagnosis. Eng. Appl. Artif. Intell. 2023, 123, 106486. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, C.; Xi, Z.; Zhang, H.; Zhao, Q. An Adaptive Matching Control Method of Multiple Turboshaft Engines. Eng. Appl. Artif. Intell. 2023, 123, 106496. [Google Scholar] [CrossRef]
- Pasieka, M.; Grzesik, N.; Kuźma, K. Simulation modeling of fuzzy logic controller for aircraft engines. Int. J. Comput. 2017, 16, 27–33. [Google Scholar] [CrossRef]
- Andriushchenko, K.; Rudyk, V.; Riabchenko, O.; Kachynska, M.; Marynenko, N.; Shergina, L.; Kovtun, V.; Tepliuk, M.; Zhemba, A.; Kuchai, O. Processes of managing information infrastructure of a digital enterprise in the framework of the «Industry 4.0» concept. East. Eur. J. Enterp. Technol. 2019, 1, 60–72. [Google Scholar] [CrossRef]
- Cherrat, E.M.; Alaoui, R.; Bouzahir, H. Score fusion of finger vein and face for human recognition based on convolutional neural network model. Int. J. Comput. 2020, 19, 11–19. [Google Scholar] [CrossRef]
- Hu, Z.; Dychka, I.; Potapova, K.; Meliukh, V. Augmenting Sentiment Analysis Prediction in Binary Text Classification through Advanced Natural Language Processing Models and Classifiers. Int. J. Inf. Technol. Comput. Sci. 2024, 16, 16–31. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J. Neuro-Fuzzy System for Detection Fuel Consumption of Helicopters Turboshaft Engines. CEUR Workshop Proc. 2023, 3628, 628–647. [Google Scholar]
- Kovtun, V.; Altameem, T.; Al-Maitah, M.; Kempa, W. Entropy-Metric Estimation of the Small Data Models with Stochastic Parameters. Heliyon 2024, 10, e24708. [Google Scholar] [CrossRef]
- Kovtun, V.; Grochla, K.; Połys, K. Investigation of the Information Interaction of the Sensor Network End IoT Device and the Hub at the Transport Protocol Level. Electronics 2023, 12, 4662. [Google Scholar] [CrossRef]
- Xu, Z.; Pei, J.; Ding, S.; Chen, L.; Zhao, S.; Shen, X.; Zhu, K.; Shao, L.; Zhong, Z.; Yan, H.; et al. Gas Exchange Optimization in Aircraft Engines Using Sustainable Aviation Fuel: A Design of Experiment and Genetic Algorithm Approach. Energy AI 2024, 17, 100396. [Google Scholar] [CrossRef]
- Feng, X.; Zhu, X.; Zhao, W.; Yan, C. Coupling Mechanical Model and Failure of Aeroengine Ceramic Matrix Composite Based on Genetic Algorithm. Meas. Sens. 2024, 33, 101226. [Google Scholar] [CrossRef]
- Aygun, H.; Turan, O. Application of Genetic Algorithm in Exergy and Sustainability: A Case of Aero-Gas Turbine Engine at Cruise Phase. Energy 2022, 238, 121644. [Google Scholar] [CrossRef]
- Jafari, S.; Nikolaidis, T. Meta-Heuristic Global Optimization Algorithms for Aircraft Engines Modelling and Controller Design; A Review, Research Challenges, and Exploring the Future. Prog. Aerosp. Sci. 2019, 104, 40–53. [Google Scholar] [CrossRef]
- Khan, N.; Abdi, S.A.A.; Khan, T.A.; Rizvi, S.S.A. Minimization of High Maintenance Cost and Hazard Emissions Related to Aviation Engines: An Implementation of Functions Optimizations by Using Genetic Algorithm for Better Performance. Eng. Proc. 2023, 46, 11. [Google Scholar] [CrossRef]
- Iuspa, L.; Scaramuzzino, F.; Petrenga, P. Optimal Design of an Aircraft Engine Mount via Bit-Masking Oriented Genetic Algorithms. Adv. Eng. Softw. 2003, 34, 707–720. [Google Scholar] [CrossRef]
- Rusyn, B.; Lutsyk, O.; Kosarevych, R.; Kapshii, O.; Karpin, O.; Maksymyuk, T.; Gazda, J. Rethinking Deep CNN Training: A Novel Approach for Quality-Aware Dataset Optimization. IEEE Access 2024, 12, 137427–137438. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M.; Drozdova, S. Neural Network Method for Helicopters Turboshaft Engines Working Process Parameters Identification at Flight Modes. In Proceedings of the 2022 IEEE 4th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 20–22 October 2022. [Google Scholar] [CrossRef]
- Vlasenko, D.; Inkarbaieva, O.; Peretiatko, M.; Kovalchuk, D.; Sereda, O. Helicopter Radio System for Low Altitudes and Flight Speed Measuring with Pulsed Ultra-Wideband Stochastic Sounding Signals and Artificial Intelligence Elements. Radioelectron. Comput. Syst. 2023, 3, 48–59. [Google Scholar] [CrossRef]
- de Voogt, A.; Nero, K. Technical Failures in Helicopters: Non-Powerplant-Related Accidents. Safety 2023, 9, 10. [Google Scholar] [CrossRef]
- de Voogt, A.; St. Amour, E. Safety of Twin-Engine Helicopters: Risks and Operational Specificity. Saf. Sci. 2021, 136, 105169. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, R.; Yuan, Y.; Wang, L. Influence of Engine Dynamic Characteristics on Helicopter Handling Quality in Hover and Low-Speed Forward Flight. Aerospace 2023, 11, 34. [Google Scholar] [CrossRef]
- Bisikalo, O.; Danylchuk, O.; Kovtun, V.; Kovtun, O.; Nikitenko, O.; Vysotska, V. Modeling of Operation of Information System for Critical Use in the Conditions of Influence of a Complex Certain Negative Factor. Int. J. Control Autom. Syst. 2022, 20, 1904–1913. [Google Scholar] [CrossRef]
- Turchenko, V.; Chalmers, E.; Luczak, A. A deep convolutional auto-encoder with pooling–Unpooling layers in caffe. Int. J. Comput. 2019, 1, 8–31. [Google Scholar] [CrossRef]
- Altameem, A.; Al-Ma’aitah, M.; Kovtun, V.; Altameem, T. A Computationally Efficient Method for Assessing the Impact of an Active Viral Cyber Threat on a High-Availability Cluster. Egypt. Inform. J. 2023, 24, 61–69. [Google Scholar] [CrossRef]
- Xia, H. Modeling and Control Strategy of Small Unmanned Helicopter Rotation Based on Deep Learning. Syst. Soft Comput. 2024, 6, 200146. [Google Scholar] [CrossRef]

| Failure Type\Impact Aspect | Measurement Accuracy | System Reliability | Operation under Extreme Conditions | Response Time | Economic Impact | Safety |
|---|---|---|---|---|---|---|
| Instantaneous failure | High | Reduced | Not relevant | Immediate disruption | High costs | High risk |
| Intermittent failure | Medium | Unstable | May be hindered | Delays | Potential additional costs | Medium risk |
| Partial failure | Accuracy degradation | Partial | Depends on the situation | Possible delays | Additional costs for correction | Medium risk |
| Multiple failure | Very high error | Critical | Critical | Significant delays | Significant economic losses | Critical risk |
| Drift failure | Gradual degradation | Gradual degradation | May be problematic | Delays | Gradual additional costs | Medium risk |
| Systematic failure | Constant degradation | Constant degradation | May be hindered | Stable slowdown | High economic losses | Medium risk |
| Random failure | Unpredictable impact | Unpredictable impact | May be problematic | Uncertain | Unpredictable costs | Medium risk |
| Material degradation failure | Gradual degradation | Gradual degradation | May be problematic | Delays | Gradual additional costs | Medium risk |
| Thermal failure | Accuracy degradation | Temporary or permanent | Critical | Slowdown | High replacement costs | High risk |
| Vibration failure | Unpredictable impact | Unpredictable | Critical | Possible delays | Potential additional costs | High risk |
| Moisture failure | Gradual degradation | Gradual degradation | Critical | Slowdown | High repair costs | Medium risk |
| Electromagnetic interference failure | Accuracy degradation | Possible issues | May be hindered | Possible delays | Additional shielding costs | Medium risk |
| Software failure | Unpredictable impact | Unpredictable | May be problematic | Slowdown | High software correction costs | Medium risk |
| Leakage current failure | Accuracy degradation | Temporary or permanent | Not relevant | Slowdown | High replacement costs | High risk |
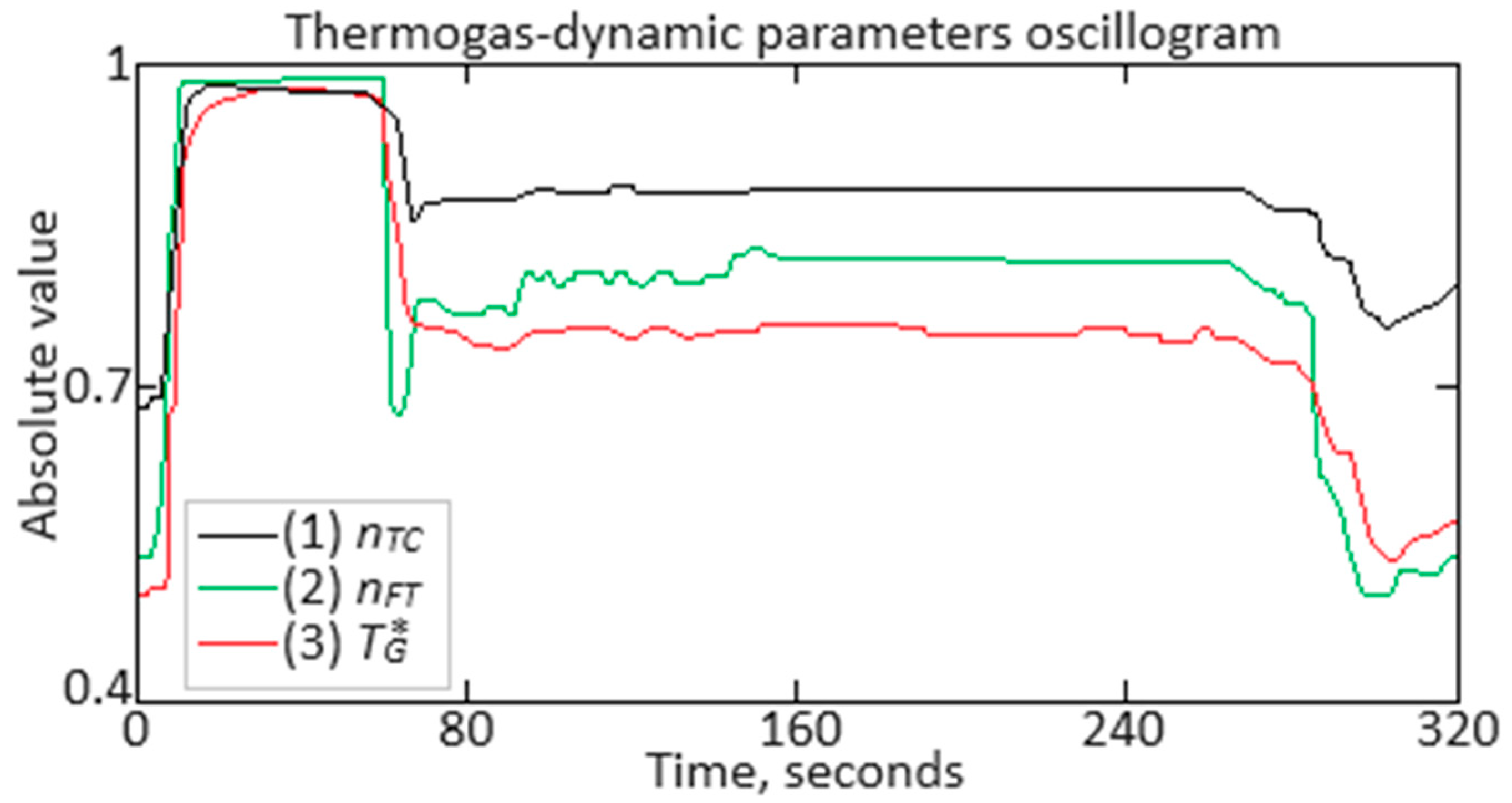
| Value | 1 | … | 43 | … | 96 | … | 160 | … | 211 | … | 235 | … | 256 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nTC | 0.686 | … | 0.972 | … | 0.903 | … | 0.904 | … | 0.912 | … | 0.741 | … | 0.824 |
| nFT | 0.532 | … | 0.987 | … | 0.746 | … | 0.753 | … | 0.762 | … | 0.455 | … | 0.506 |
| 0.488 | … | 0.980 | … | 0.712 | … | 0.722 | … | 0.724 | … | 0.519 | … | 0.522 |
| Actual\Predicted | Failure | Normal | Description |
|---|---|---|---|
| Failure | TP | FN | TP (True Positives) is the cases number where the model correctly predicted a failure FP (False Positives) is the cases number where the model incorrectly predicted a failure, although no failure was present TN (True Negatives) is the cases number where the model correctly predicted no failure FN (False Negatives) is the cases number where the model failed to detect a real failure |
| Normal | FP | TN |
| Genetic Algorithm Operators | Genetic Algorithm Types | ||
|---|---|---|---|
| Type 1 | Type 2 | Type 3 | |
| Reproduction | Equiprobable selection | Linearly ordered selection | The equiprobable and linearly combination ordered selection |
| Crossing over | Equally probable, individuals’ selection is the best individuals with the worst crossing | Equally probable, individuals’ selection is the best individuals with the best crossing | Equally probable, selection of individuals is the crossing the best individuals with the worst and the best individuals with the best combination |
| Mutation | Homogeneous with high probability | Homogeneous with low probability | Heterogeneous |
| Reduction | Equiprobable scheme | Selection scheme | The equiprobability and selection scheme combination |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Sachenko, A.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. J. Sens. Actuator Netw. 2024, 13, 66. https://doi.org/10.3390/jsan13050066
Vladov S, Sachenko A, Sokurenko V, Muzychuk O, Vysotska V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. Journal of Sensor and Actuator Networks. 2024; 13(5):66. https://doi.org/10.3390/jsan13050066
Chicago/Turabian StyleVladov, Serhii, Anatoliy Sachenko, Valerii Sokurenko, Oleksandr Muzychuk, and Victoria Vysotska. 2024. "Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure" Journal of Sensor and Actuator Networks 13, no. 5: 66. https://doi.org/10.3390/jsan13050066
APA StyleVladov, S., Sachenko, A., Sokurenko, V., Muzychuk, O., & Vysotska, V. (2024). Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. Journal of Sensor and Actuator Networks, 13(5), 66. https://doi.org/10.3390/jsan13050066








