Abstract
The optimal functionality and dependability of mechanical systems are important for the sustained productivity and operational reliability of industrial machinery, and have a direct impact on its longevity and profitability. Therefore, the failure of a mechanical system or any of its components would be detrimental to production continuity and availability. Consequently, this study proposes a robust diagnostic framework for analyzing the blade conditions of shot blast industrial machinery. The framework explores the spectral characteristics of the vibration signals generated by the industrial shot blast for discriminative feature excitement. Furthermore, a peak detection algorithm is introduced to identify and extract the unique features present in the peak magnitudes of each signal spectrum. A feature importance algorithm is then deployed as the feature selection tool, and these selected features are fed into ten machine learning classifiers (MLCs), with extreme gradient boosting (XGBoost (version 2.1.1)) as the core classifier. The results show that the XGBoost classifier achieved the best accuracy of 98.05%, with a cost-efficient computational cost of 0.83 s. Other global assessment metrics were also implemented in the study to further validate the model.
1. Introduction
Over the years, research and development studies concerning prognostics and health management (PHM) have shown a significantly impressive spark in intensity across industries and academia, cutting across various disciplines, namely physics, mathematics, computer science, engineering, and so on. PHM, in simple terms, implies a computational framework that involves a balanced integration of information, physical knowledge, and in-depth information about the performance, operation, and maintenance of systems, components, and structures [1,2].
Since the onset of Industry 4.0, which introduced artificial intelligence, interaction between humans and machines has positively evolved. This transformation involves the integration of human intelligence with the Internet of Things (IoT), cyber-physical systems, and machine learning (ML). These advancements enhance efficiency and productivity, fostering seamless collaboration between humans and intelligent systems [2,3,4,5]. The synergy between AI, IoT, and ML has led to smarter, more responsive technologies, revolutionizing industries and improving overall human–machine interactions. Consequently, researchers have employed these advanced methodologies—AI, ML, and deep learning (DL)—to explore and extend the useful life of industrial machinery [6,7]. These advanced methodologies achieve this by exploiting the unique features inherent in the generated data signals, such as vibration signals, thermal signals, current signals, and acoustic signals, via sensors. These signals are utilized by these advanced technologies, either individually or collectively, for pattern recognition, aiding in prognostics, classification, prediction, diagnostics, and more. This is often termed a data-driven approach in research studies, and in most cases, its optimal performance is heavily reliant on the quality and quantity of the generated dataset and, most importantly, the signal-processing tools and the quality of the features extracted, especially in ML fault diagnostics and isolation (FDI) scenarios [8,9].
Over the decades, Fourier analysis has been one of the renowned techniques for analyzing current signals and vibration signals due to the simplicity of its implementation and also its unique ability to decompose a given signal into its constituent sinusoidal components [10,11]. In FDI instances, the Fourier transform has been successfully implemented to develop robust and efficient platforms and models. Nevertheless, it has certain limitations, which include computational inefficiencies when handling large datasets and also its tendency to provide an average view of the frequency spectrum. This implies that it does not bear additional information about how the different frequency components change over time [11,12].
To address these drawbacks, the fast Fourier transform (FFT) offers faster computational speed, while the short-time Fourier transform (STFT) provides the added advantage of transforming a signal into both its frequency and time domains. The compatibility of Fourier analysis with vibration signals is well documented in the literature [11,12,13,14]. In addition, the performance of an ML-based model is highly dependent on the nature of the features fed to the machine learning classifier. Feature extraction and selection techniques are known to help extract and select useful features, which optimize the performance of an MLC model [15].
Although DL-based algorithms are often considered more powerful than traditional ML-based models, due to their computation strength and versatility—especially in instances of large and complex datasets—traditional MLCs are often preferred in instances of small- or medium-sized datasets where efficiency in terms of computational cost is paramount. Furthermore, a traditional MLC like XGBoost provides high efficiency in terms of accuracy and efficient computational cost requirements, which are often challenging for most MLC models [16].
2. Motivation and Literature Review
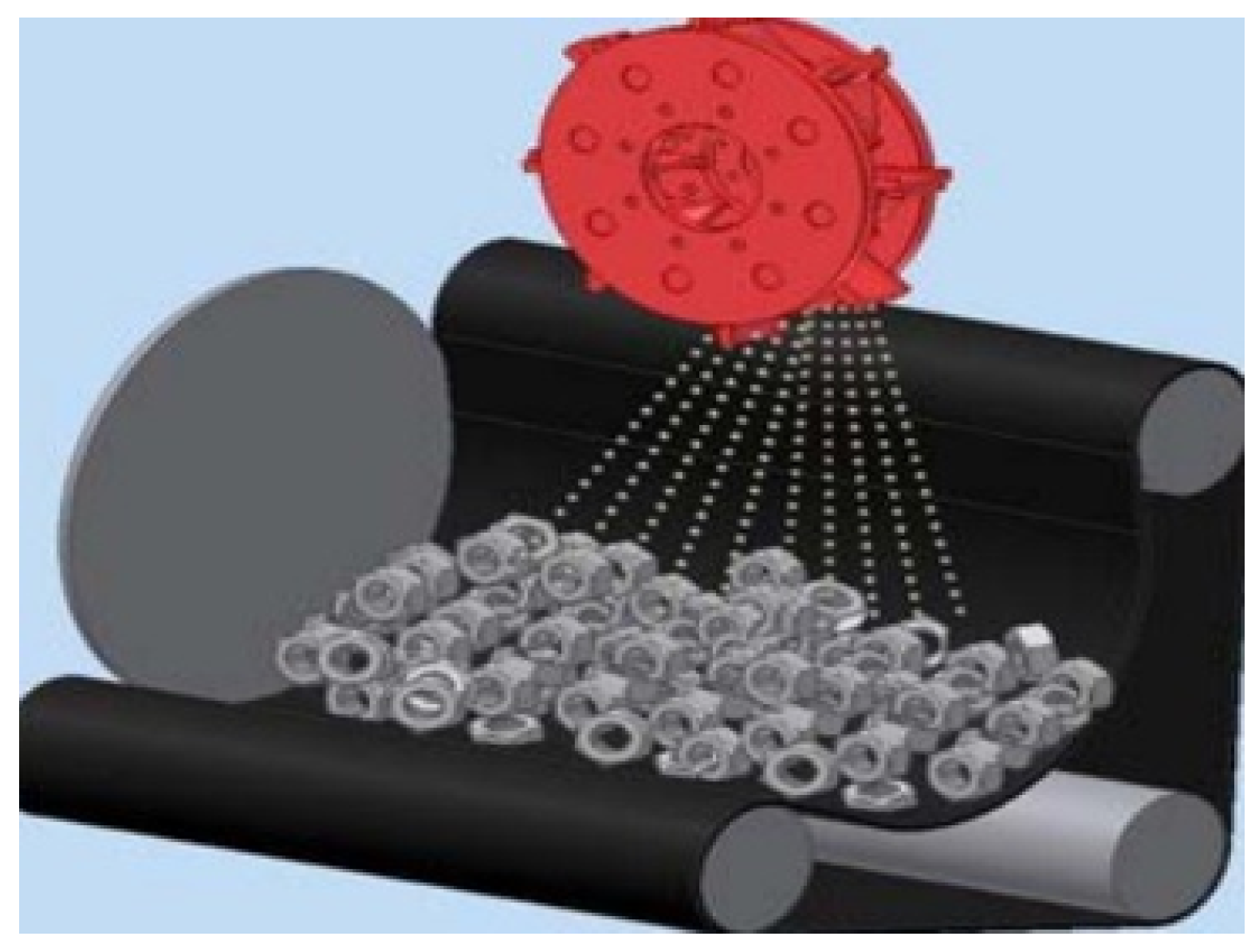
The importance of PHM has grown over the years as researchers have devised numerous models to enhance the productivity and lifespan of industrial machinery. In this study, an FDI model is implemented for fault classification in the blades of a shot blast machine. A shot blast machine is an industrial machine used for polishing, cleaning, and strengthening metallic surfaces using fine particles called shot balls. Its working mechanism, which is shown in Figure 1, involves forcibly thrusting abrasive materials (shot balls) by its blades in a rotary motion against a given surface at a very high velocity.
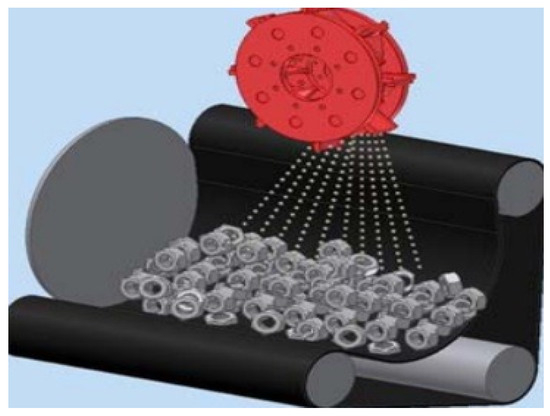
Figure 1.
Shot Blast Working Mechanism.
Failures encountered in shot blast machinery cut across wheel bearing failure, blade failure, mechanical failure, motor failure, belt failure, and worn out parts due to the abrasiveness of the shot balls, incorrect angling by the blade—thereby directing the shot balls to the wrong spots—dust accumulation leading to wear and tear, and other failures due to human error [17]. According to this study [18], the most commonly encountered failure is blade failure due to the abrasive nature of the shot balls and the high shooting velocity. Blade failure is often caused by four major types of failures, which include the following:
- Fine shots: The abrasive nature of the shot balls wears the blades over time, which is one of the major causes of blade failure.
- Sand presence: Sand particles wear down the blade faster than fine shot balls, causing irregularities on the blades. These sand particles often travel along the edge of the blade, wearing them down and causing shot balls to drop from one blade to another, hence causing further irregularities.
- Presence of chips and flakes: Similar to sand, chips and flakes wear down the blade more quickly. Often, the flakes and chips are introduced into the fine shot balls via a torn sieve from air separators.
- Casting defects: This is a manufacturing issue that leads to the rapid deterioration of the blade, causing it to wear down faster than usual.
The presence of these failures often lead to downtime, loss of revenue, and increased power consumption. Hence, there is need for an FDI framework to ensure that these faults are mitigated or detected early. For an efficient FDI, it is important that all the necessary techniques required for the desired outcome are adequately deployed. However, the drawbacks of FFT such as spectral leakage, interpretation complexity, noise sensitivity, and poor performance with non-stationary signals have been highlighted in literature. For instance, in [19], the authors exploited the underlying frequencies in the vibration signal of a bearing for fault detection and analysis. They conducted an online bearing vibration defect analysis using an enhanced FFT algorithm. However, they concluded that more sophisticated signal analysis tools were needed to achieve better results. This was also highlighted in a study by Altobi et al. [20], where they implemented a model for fault classification in five centrifugal pump operating conditions using frequency-domain analysis. They deployed an FFT algorithm to identify faults generated from both stationary and non-stationary centrifugal pump vibration signals. In their findings, they emphasized the need to improve or augment the FFT with other methods, particularly for non-stationary signals.
To solve these underlying challenges of FFT, superior alternative signal-processing tools such as Hilbert transform (HT), STFT, wavelet transform (WT), etc., as well as sensor fusion methodologies, and unique ideologies have been implemented in various studies. The authors, Tan and Uddin, highlighted in their study [21] that, due to the low-frequency output of FFT on their dataset, HT, which is not restricted by frequency resolution, was used as a substitute for bridge fault detection. Similarly, in [22], Fang et al. employed a multi-signal fusion strategy, integrating the vibration and acoustic signals with FFT, which significantly enhanced the diagnostic accuracy. Again, in this study [23], the author deployed a simple feature extraction technique that, according to their findings, aided in optimizing their model by enhancing the FFT-transformed signals. In their methodology, they applied FFT to the raw signal vibration signals of an induction motor as the signal-processing tool to excite the frequency components of the signals as well as their amplitudes. They then divided the frequency spectrum obtained from the FFT into segments, and the energy coefficients for each segment were calculated as the sum of the FFT amplitudes. These coefficients were used as features, which were then trained using a ML algorithm. The efficiency of their model was validated, achieving 99.7% model precision. Additionally, the nature of the feature extraction and selection techniques employed in a model significantly influences the efficiency of a given diagnostic model. This was demonstrated in this study [24], the authors highlighted the importance of feature extraction and selection in the VSA using time and frequency domain features for diagnosing the defects in various rolling bearing components. In their analysis, they deployed time and frequency statistical feature extraction methods and further integrated the Fisher score (FS) and the genetic algorithm (GA) into their feature selection methodology, which achieved remarkable accuracies when fed to the support vector classifier.
Generally, an MLC model is incomplete without a MLC algorithm. Every ML classifier algorithm has its strong points and pitfalls. However, in terms of performance, some tree algorithms and boosting algorithms stand out from other classifiers. XGBoost, being an enhanced version of the gradient boosting algorithm, offers high performance at a very efficient computational cost. Shukla, Kankar, and Pachori, in their study [25], compared various autonomous methods for condition monitoring using ensemble learning and ML methods for fault classification in bearings. They evaluated the performances of the decision tree (DT), support vector machine (SVM), and XGBoost. Their result revealed that the XGBoost outperformed the other classifiers, validating its unique performance capability, even in instances of small datasets. Additionally, another performance analysis was conducted in this study [26], focusing on the exploitation of ensemble learning methods, which are known to be a high-performing ML algorithm. The authors compared the accuracy performances of random forest (RF), AdaBoost, and XGBoost. Their experiment demonstrated that the scalable XGBoost outperformed other models and also showed an improved predictive accuracy compared to the original PFA algorithm.
Despite these advancements, existing methods often require complex combinations of multiple techniques, which can increase computational costs and model complexity. In contrast, our proposed peak detection approach simplifies the feature extraction process by directly detecting the relevant frequency peaks from FFT using a threshold technique to extract the most important peaks. This method significantly filters out noise and unwanted signals, allowing for more precise fault classification with reduced computational overhead. Moreover, our study emphasizes feature importance methods for selecting the most relevant features, unlike previous works that rely on more general selection techniques. By focusing on XGBoost as the core classifier, our approach not only improves the diagnostic accuracy but also ensures computational efficiency, making it a robust alternative to more complicated models. Furthermore, the core motivation for this lies in [10], where the authors concatenated the peak extracts from the FFT, power spectral density, and high auto-correlation features for their diagnostic model using current signals from the various operating conditions of an induction motor. Their model achieved an accuracy of 79.25%, which did not meet expectations.
With the intention of representing a robust framework that would mitigate some of the setbacks that deter the accuracy of vibration analytical models that embrace FFT as the signal-processing tool, this study makes the following contributions:
- A proposed framework for fault VSA-based diagnosis in the blade of a shot blast machine using peak detection approach. The proposed peak detection approach served as a discriminative feature extraction technique, which also addresses the limitation of FFT by exploiting the amplitude of that raw signal’s FFT using a threshold technique. The threshold technique is applied to filter out unwanted signals, enhancing the signal, and ensuring the detection of relevant peaks that correspond to potential faults.
- The implementation of a robust and efficient feature selection technique—the feature importance method which selected the most relevant feature for an adequate fDI.
- An extensive comparison and analysis of various MLC algorithms, including XGBoost, which was the core classifier algorithm.
- A computational cost evaluation of the MLC algorithm to ensure that the model presents an efficient yet computationally inexpensive model.
The remaining sections are structured in this manner: Section 3 talks about the theoretical background of the core backbone of the study; Section 4 discusses the experimental model and the model’s technicality; Section 5 presents the experimental setup and the visualizations; Section 6 discusses the results of the study and future works; and Section 7 concludes the study.
3. Theoretical Background
3.1. Vibration Signal Analysis
VSA is one of the most popular methods for fault detection in mechanical systems, due to the nature of vibration signals, which contain a rich spectral content of mechanical systems, especially in faulty states. VSA exploits these generated signals to extract and analyze their characteristics. In fault detection, these signal characteristics often contain the signal’s unique signatures, which are harnessed in VSA to utilize their individual discriminative features to develop an FDI model. These signatures inherent in vibration signals differ significantly between healthy and faulty states, as faulty signals tend to generate faulty harmonics that become more visible when signal-processing tools are deployed. However, vibration signals are often laced with noise, typically Gaussian noise and white noise, which can envelop the original signal. FFT, DFT, STFT, HT, discrete wavelet transform (DWT), continuous wavelet transform (CWT), etc., have been deployed in various studies to reveal the signal for the spectral constituents of mechanical systems in VSA, aiding in the development of robust diagnostic models [1,27,28,29,30]. Amongst these, Fourier analysis has been one of the most widely used techniques, with DFT and FFT serving as the bedrock for many advanced signal-processing tools [10], as they segment signals by representing them through their constituent sinusoidal components. However, the inherent pitfall of FFT, such as its sensitivity to noise, limited time–frequency resolution, and the assumption of signal stationarity, etc., led to the introduction and utilization of STFT. STFT provides time–frequency components for the signals, addressing some of the limitations with FFT, as documented in research studies [12].
On the other hand, wavelet transform is also a powerful tool that has been employed in research studies with great efficiency, as it analyzes signals at different scales and resolutions using wavelet series. Unlike FT, WT dissects signals into square integrable wavelets, providing the signal’s transient time and frequency characteristics [28,29,30]. However, its complexity in implementation, especially in selecting an appropriate mother wavelet, remains a concern [30]. These challenges with traditional signal-processing tools often inspire the development of new methods, as research aims to present alternatives that offer a variety of choices. For instance, HT, Hilbert–Huang transform, variation mode decomposition, etc., have been developed to address most of these issues, particularly noise sensitivity [27,29,31].
Generally, the VSA implementation depends on the nature of the data, the choice of the signal-processing tool, and the adaptability of classifier algorithms to discriminative features, especially in the context of a diagnostic model.
3.2. Extreme Gradient Boosting (XGBoost)
XGBoost employs the gradient boosting machine (GBM) structure, which is a subset of an ensemble learning tree technique [32]. It represents a unique class of gradient boosting algorithms that can be effectively applied to both classification and regression modeling. Generally, GBM classifier or regressor models are known for their high efficiency and often outperform most ML algorithms, as documented in numerous studies [25,26]. XGBoost, however, introduces several structural improvements to address the limitations and errors found in traditional ensemble learning methods such as GBM and AdaBoost [25,26,32]. One of the core drawbacks of most ensemble learning classifiers, expensive computational demands, makes the XGBoost a unique model as it presents a relatively faster model [32]. On a broader level, the robust structure of XGBoost can be attributed to its integration of three key gradient boosting techniques: regularized boosting, stochastic boosting, and gradient boosting. These techniques, combined with regularization parameter tuning, make XGBoost particularly effective. Its mechanism involves applying decision tree algorithms to classify a given dataset [32,33].
For instance, when XGBoost makes a prediction based on a training dataset—such as in the case of a linear model—the prediction is typically a weighted sum of the input features. The weights, which represent the model’s parameters, are learned from the training data. These predictions are then used to solve tasks such as regression, classification, or ranking. The primary objective is to optimize these parameters to minimize the objective function, thereby ensuring model efficiency [33]. However, the effectiveness of the model can vary depending on the selected parameters. To enhance performance by reducing the risk of overfitting, XGBoost employs regularization techniques like Lasso (L1) and Ridge (L2) regularization. Lasso regularization adds a penalty proportional to the absolute values of the parameters, which encourages sparsity by driving some parameters to zero. On the other hand, Ridge regularization adds a penalty proportional to the squares of the parameters, discouraging large parameter values and thereby reducing model complexity [32,33,34].
The influence of the XGBoost algorithm has been widely recognized and reported in studies such as those concerned with ML data mining challenges, and it has been commonly employed amongst Kaggle’s competitors as well as by data scientists in this particular field [26,34].
To dig deeper into the structural architecture of the boosting algorithm for an in-depth understanding, assume that, for a given set, , with m pairs and n features. Subsequently, can be defined as the prediction value of the given model and is shown in Equation (1) [26]:
where represents the predicted valued generated by the Kth tree of the ith sample. At every given iteration of the gradient boosting, the residuals are tuned to correct the errors on the initial predictors to optimize the loss function. The introduction of the XGBoost enhances the function by minimizing the objective function as shown below:
with
where l represents the loss function which is a measure of the difference between the predicted value and the target value . stands for the regularization term which in this context is a factor utilized to measure the tree complexity, and present the degrees of regularization. and T stand for the vector and numbers of leaves assigned to each tree, respectively.
To obtain the value of that minimizes the loss function, there is need for optimization. To easily accommodate different loss functions, the second-order derivation of Equation (2) is determined as shown below [25,26]:
where and are the first- and second-order gradient statistics on the loss function:
Removing the constant terms to expand , an approximated version of the equation is obtained and is shown in Equation (5) below [26]:
This instance of leaf j is denoted in the equation by . For a given fixed tree structure p, the optimal weight value of each leaf j can be calculated, thus, . Substituting the into the objective function—Equation (5)—a simplified optimal objective value of the objective function is generated as shown in Equation (6):
where and are and , respectively.
In reality, it is quite unattainable to illustrate all the functionality of all the leaves in the tree structure p. A greed algorithm from a single leaf and that iteratively adds branches to the tree is implemented instead. The decision to further add a split to a given tree is implemented by the function below:
and represent the instance sets of the right and left nodes after the splitting.
4. Experimental Model
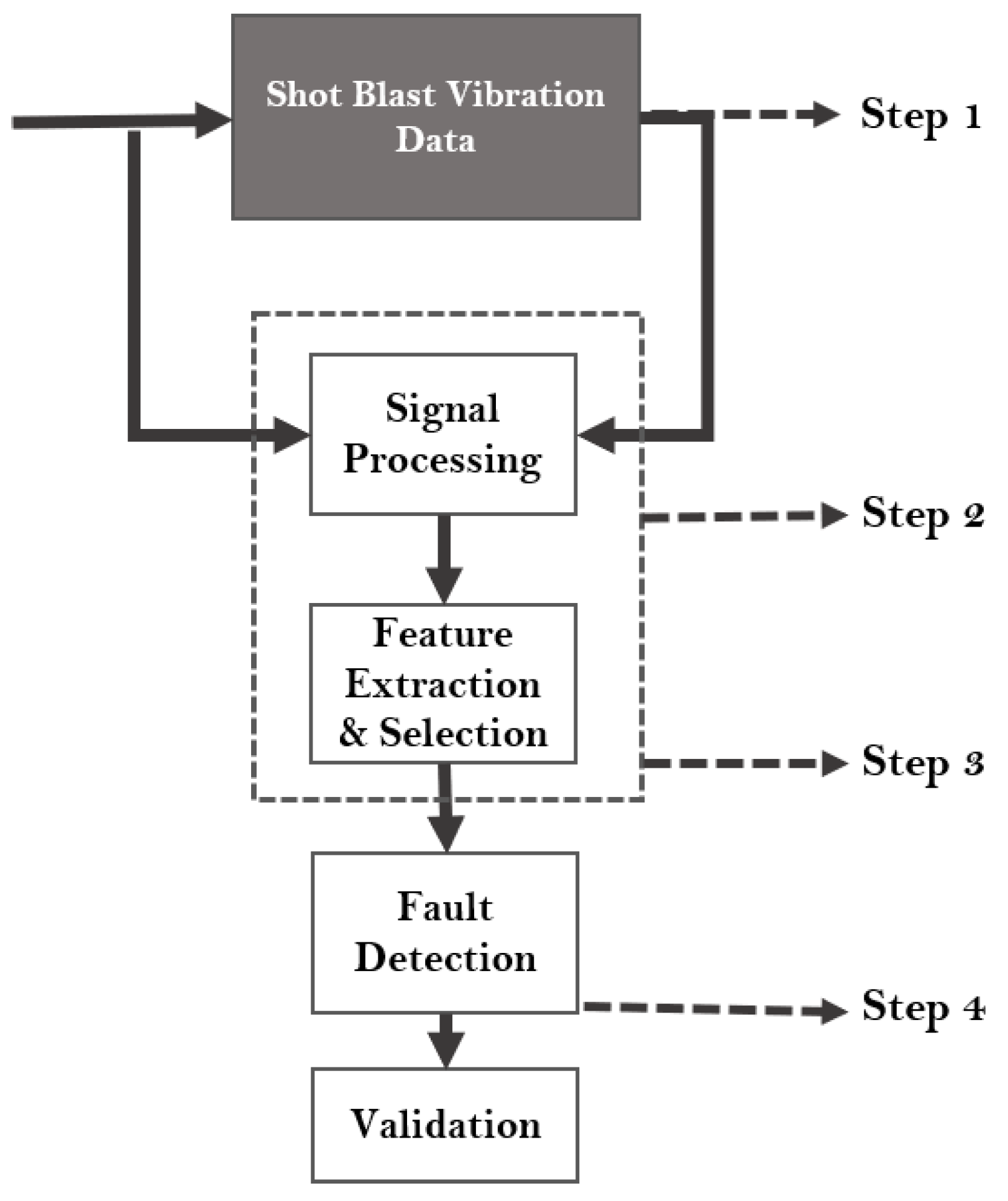
The proposed diagnostic flowchart, illustrated in Figure 2, highlights the critical importance of subjecting signals (in our case, vibration signals) to unique signal-processing techniques to facilitate the development of a robust diagnostic model. This model primarily consists of four (4) steps. The first step involves the data collection stage, which entails gathering raw vibration data signals from the shot blast industrial machine, encompassing both healthy and fault datasets. The second step involves the implementation of signal-processing techniques, where the collected signals are subjected to spectral transformations aimed at unveiling their detailed components. This transformation enhances the interpretability of the signals by the diagnostic algorithms. Subsequently, in the third step (feature extraction and selection stage), useful characteristics are extracted from the signals, serving as the operating conditions features. The model employs a robust feature extraction technique to ensure the optimal feature representation of each class. To further optimize the computational cost of the model’s training process; a feature importance methodology is implemented as the feature selection tool to identify the most important features and reduce the features to the desired number. The fourth step involves training the selected features using various MLCs for fault detection. This enables the model to accurately distinguish and classify the fault and healthy signals. To validate our model’s efficiency, the performance assessment metrics are introduced to ensure high precision and accuracy in predictions.
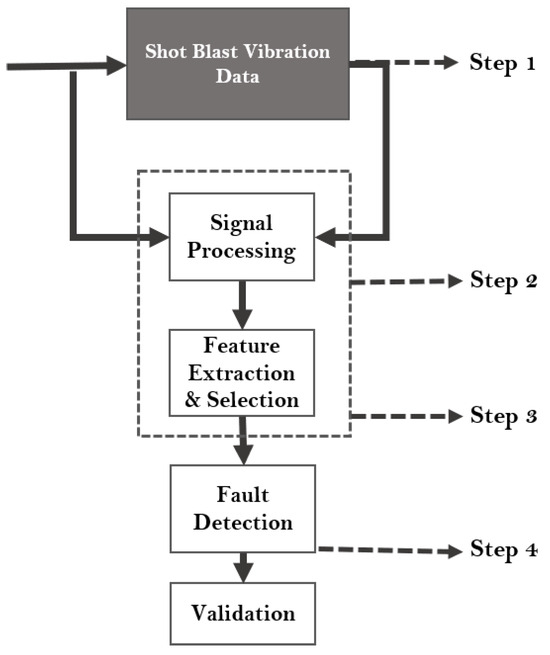
Figure 2.
The proposed diagnostic flowchart.
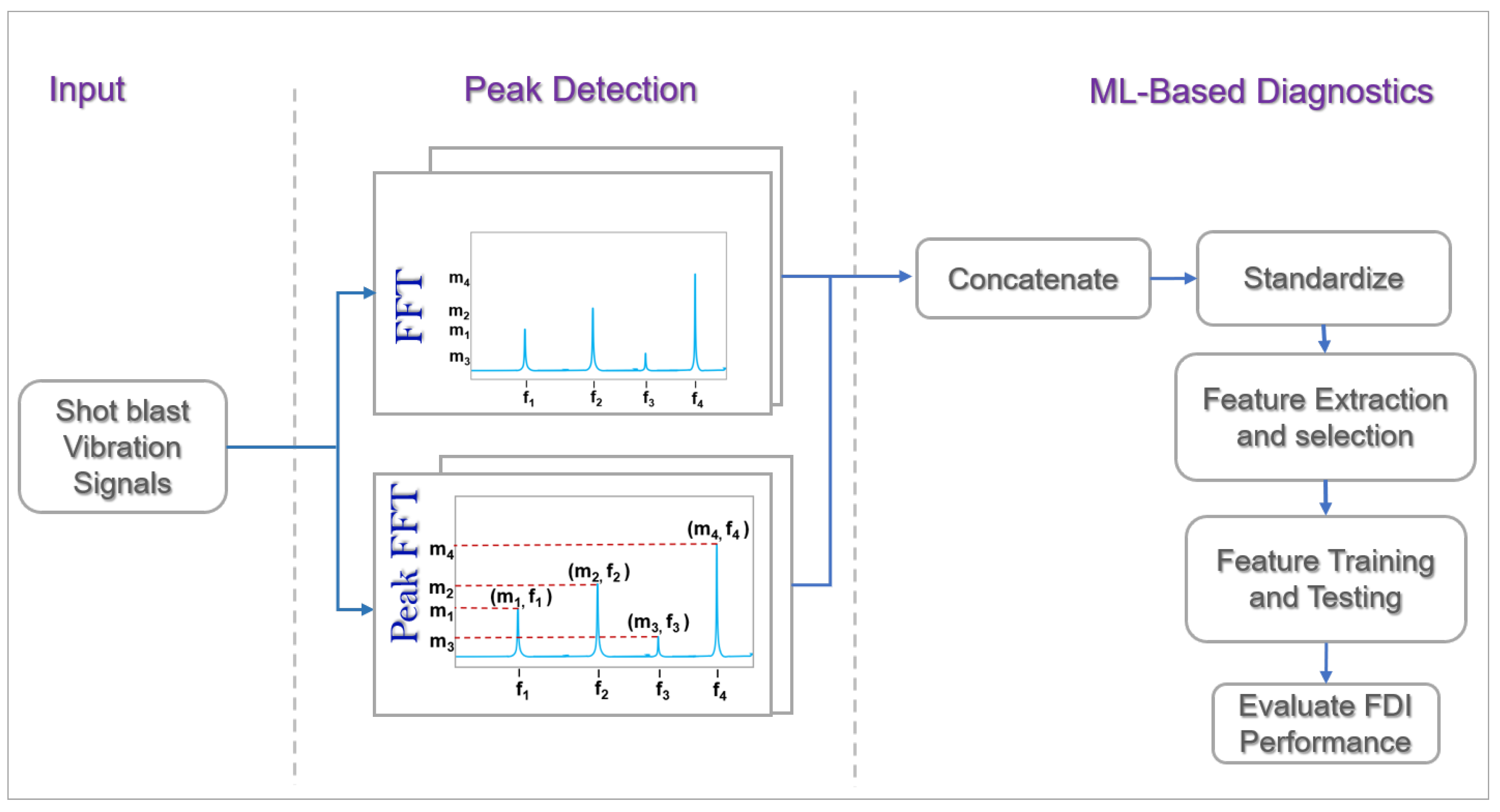
This multi-stage approach, as shown in Figure 3, ensures that the diagnostic model is not only robust but also capable of delivering a reliable and precise fault detection model, thus enhancing the overall efficacy of the diagnostic process. Due to the nature of our dataset being vibration data, the spectral transform of the signals is determined using the FFT signal-processing technique. A peak detection algorithm is implemented to serve as the feature extraction technique. The mechanism of the core constituents of the techniques implemented in our study are broken down as follows.
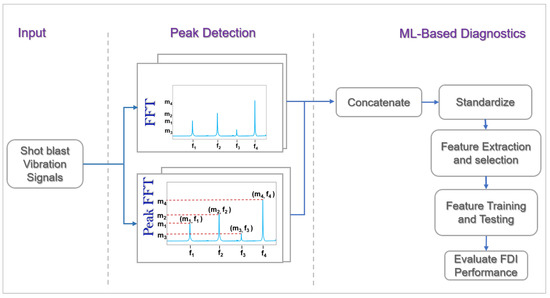
Figure 3.
Detailed diagnostic model.
4.1. The Spectral Peak Detection Technique for Feature Characteristics Extraction
Vibration signal analysis has long been a dependable methodology for condition monitoring in PHM. In the case of a shot blast machine’s blade vibration signals, owing to the nature of its operation, the signals are assumed to be composed of varying periodic signals which are a reflection of its operational changes. Despite their complexity and non-stationary characteristics, which often do not conform to the regular sine and cosine wave functions, these signals can still be effectively analyzed using the FFT technique. By leveraging the varying magnitudes of alternating spectral peaks observed in the FFT of raw signals under different operating conditions, we utilized these spectral peaks and their corresponding frequencies as distinctive features for our fault diagnostics framework. To mitigate the pitfalls often experienced when implementing FFT with non-stationary signals, a peak detection threshold was implemented to ensure that the relevant peak amplitudes were accurately extracted.
Mathematically, given that the raw one-dimension vibration signal from the shot blast industrial machine is , then the FFT of this signal denoted by can be derived using Equation (7):
where is the n-th sample of the vibration signal, N is the total number of the signal samples, k is the index of the frequency ranging from 0 to , and is the frequency domain output.
To achieve peak detection extraction, the magnitude spectrum, which represents the strength of the frequency components present in the FFT signal, is first derived. Equation (8) illustrates the mathematical procedure of the magnitude spectrum derivation:
where and are the real and imaginary components of the Fourier coefficient .
Hence, the peak detection algorithm, which identifies frequency components in the magnitude spectrum possessing the highest amplitude, is implemented to signify the dominant frequency signal in the given signal. The mathematical representation for a peak at an index is shown as follows:
Practically, to filter insignificant peaks and noise, conditions like thresholds are implemented. In this study, we implemented a peak threshold of 0.0001 m/s2.
4.2. Feature Selection Technique
The importance of feature selection cannot be overstated due to its indispensable role in a diagnostic setup; if the wrong feature selection technique is implemented, the performance of a model can be greatly altered. The XGBoost library provides an option that computes feature importance based on different metrics. The feature importance technique is a tree-based algorithm model which is a type of embedding feature selection method; however, the default method used by the XGBoost for feature importance is weight, also known as frequency, whose principle involves counting the times a given feature is utilized in splitting the data across all trees in a model. Other methods used by the XGBoost include gain and cover; the gain method uses the average gain of a feature across all trees in a given model, which is often considered the most accurate, and the cover method uses the average coverage of data points affected and/or impacted whenever a feature is used to make a decision. XGBoost utilizes the F-score to measure a feature’s performance across all trees in the feature selection process. In this study, the feature selection is set up using the frequency method which was more suitable for our dataset. Mathematically, for a given feature f, the feature importance I using the frequency methodology can be computed using Equation (10):
T is the set of all nodes in all trees.
is the feature used at node t.
is an indicator function that shows 1 when feature j is used at node t, and 0 otherwise.
4.3. Model Performance Evaluation Criteria
Model evaluation is a prerequisite in setting up a model to ensure its efficacy. Architecturally, ML models vary and differ in structure, making their performance unique across different datasets with diagnostic scenarios at a given instance. Therefore, these standards ensure that the performance of a ML algorithm is thoroughly assessed and verified, regardless of its performance compared across other similar models.
The core purpose of the global standard metrics is to ensure that the most suitable ML algorithm is selected for a given model to consummate its robustness. Some of these global metrics employed in this study include accuracy (), precision (), F1-score, sensitivity (), specificity (), and false alarm rate (). Mathematically, these global standards can be defined as shown in Equations (11)–(16):
where TP, FP, TN, and FN represent the true positive, false positive, true negative, and false negative, respectively. In the context of classification, TP indicates the correctly predicted classes by a model at a given instance. FP stands for the number of instances in which a model predicts a class to be positive while it is negative; this is also known as a false alarm. When a model correctly predicts a class as negative, it is known as TN. FN indicates the instances where a model incorrectly predicts a class to be negative. Additionally, other evaluation metrics are also introduced to ensure that the models are thoroughly evaluated to give the desired output. Such metrics include computational cost, complexity, and the confusion matrix. The prowess of the confusion matrix lies in the ability to showcase individual performance in classification algorithms. It summarizes the outputs of a given model’s prediction, providing a detailed breakdown of TP, FP, TN, and FN. It aids in giving an in-depth analysis of the performance of a classification model, for both binary and multi-class classification issues.
5. Experimental Setup and Visualization
This study proposes a peak detection vibration analysis diagnostic framework for the condition-based monitoring of a shot blast industrial machine, which was set up at TSR, a company located in Gumi-si, Republic of Korea. Whilst its headquarters are in Gumi, Gyeongsangbuk-do, Republic of Korea, TSR also manages additional mass production at the TSR Mexico Plant. TSR is an automobile part manufacturing company known for meeting the needs of the global automobile market through world-class product development and continuous technological advancement. The setup was conducted on a shot blast industrial machine at TSR. Given the machine’s size and its status as an industrial machine rather than a prototype, all necessary safety precautions were observed.
Figure 4 shows the machine setup and sensor placement at the TSR industrial complex. The major components of the shot blast machine include the belt, motor, and the shot balls. The rotary motion of the shot blast blades is provided by the induction motor, which is transferred to the blade via the belt. Figure 5 illustrates the functionality (input and output) of the shot blast machine, Figure 5a shows the condition of a sample cylinder before undergoing the shot blasting process, while Figure 5b shows the cylinder after it has undergone a shot blasting process.

Figure 4.
Data collection setup.

Figure 5.
Shot blast product finishing: (a) Raw input; and (b) Finished product.
To effectively collect data signals from the shot blast machine, an accelerometer was attached at the most appropriate position with the aid of a TENMARS ST140D vibration meter. A unidirectional PCB Piezotronics accelerometer was employed for the purpose of data collection and generated at a sampling rate of 60 samples per second and an NI 9234 DAQ was employed to convert the generated analog into digital signals for data analysis.
Due to the inherent complexities of the shot blast machine’s operation and the experiment being conducted using running industrial machinery, an extensive long-range monitoring process of the shot blast machine was conducted to observe potential failure occurrences. The major fault observed during this period was the shot blast blade deterioration, which is one of its most frequently occurring faults. Figure 6 shows a visual representation of the healthy blades and the deteriorated blades as used in the experiment, providing a comprehensive perception of the observed and monitored healthy and deteriorated states of the shot blast blades. Table 1 details the operational conditions involved in the study.

Figure 6.
Blade conditions: (a) Healthy blade; and (b) Faulty blade.

Table 1.
Operating conditions used in the study.
The operational functionality of the shot blast primarily centered around the removal of scale, rust, and debris from products by rotating and shooting fine tiny metallic and non-metallic particles, known as shots or grits. The operational specifications of the shot blast blades are predominantly determined by the dimensions and types of motor, pulley, and belt powering the shot blades. In this study, the shot blast blade operated at an approximate speed of 2000 rpm, propelling the shot balls at a high velocity ranging from 60 to 100 m per second (m/s). This substantial high blasting velocity often results in the deterioration of the shot blades, transitioning from HSBB-1 to DSBB-2.
5.1. Signal Processing for Feature Engineering
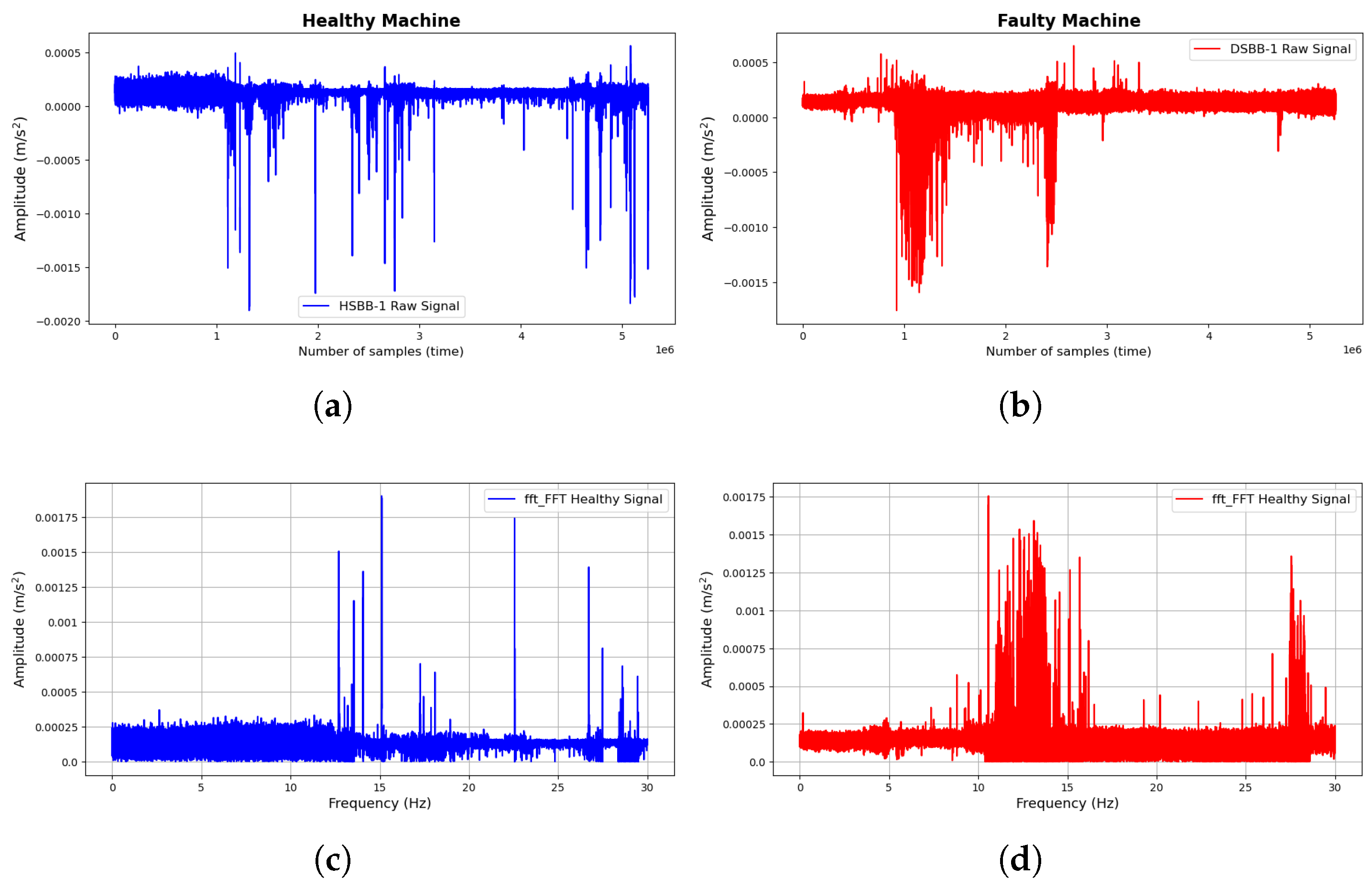
Vibration data were collected from the shot blast industrial machine at just two operating conditions: HSBB-1 and DSBB-1. Figure 7a,b show the visual representation of the vibration signals as collected from the shot blast industrial machine at both operating conditions, with blue representing HSBB-1 and red representing DSBB-2.
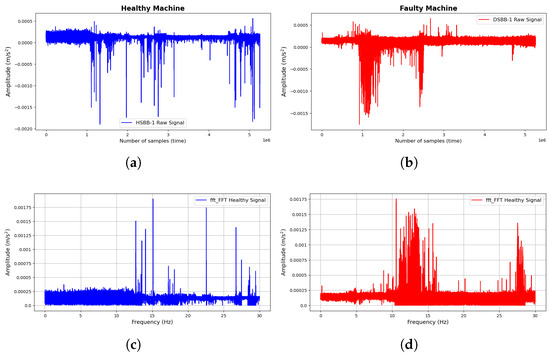
Figure 7.
Current signals collected from the shot blast machine: (a) Raw healthy signal; (b) Raw faulty signal; (c) FFT of the healthy signal; and (d) FFT of the faulty signal.
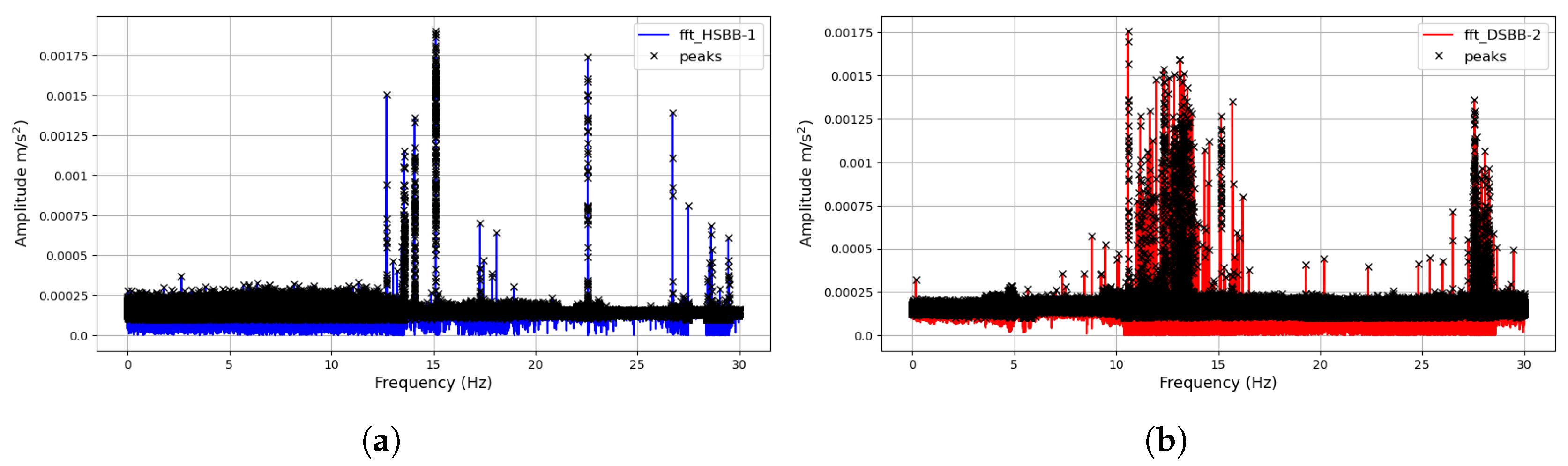
The visualization reveals the dissimilarity between the operating conditions of both signals generated by the shot blast machine. Analytically, the signals appear similar at the onset; however, significant differences in spikes and amplitudes emerge as the number of data samples increases. The data collection scheme employed in the experiment involved collecting an extensive dataset over a prolonged period. The data collection were halted after blade maintenance was conducted, and the collected data signals were visualized to observe their variations over time. This process enables the extraction of fault data signals from the entire dataset, highlighting the core differences in operating conditions and labeled. Next, the signals were subjected to an FFT signal-processing for feature extraction using the technique discussed in Section 4 and shown in Figure 7c,d. In most fault diagnostic models, analyzing signals in the frequency domain often helps reveal the relevant characteristics of the signal, which would help in discriminative feature extraction, especially in the detection and diagnosis of mechanical systems [35]. As highlighted in the previous section, a peak detection approach was implemented for feature extraction. Through engineered mathematical procedures, thirty (30) features were generated from the peak frequencies and standardized. These efficiently characterize both operational conditions and serve as their unique and distinguishing attributes. Figure 8 represents the FFTs and their corresponding peak detection initialization for feature extraction.
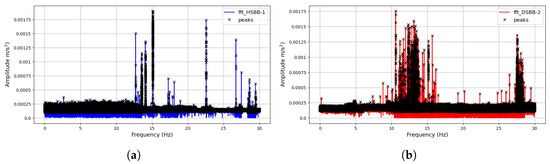
Figure 8.
Peak detection feature extraction: (a) Peak detection extract from healthy signal’s FFT; (b) Peak detection extract from faulty signal’s FFT.
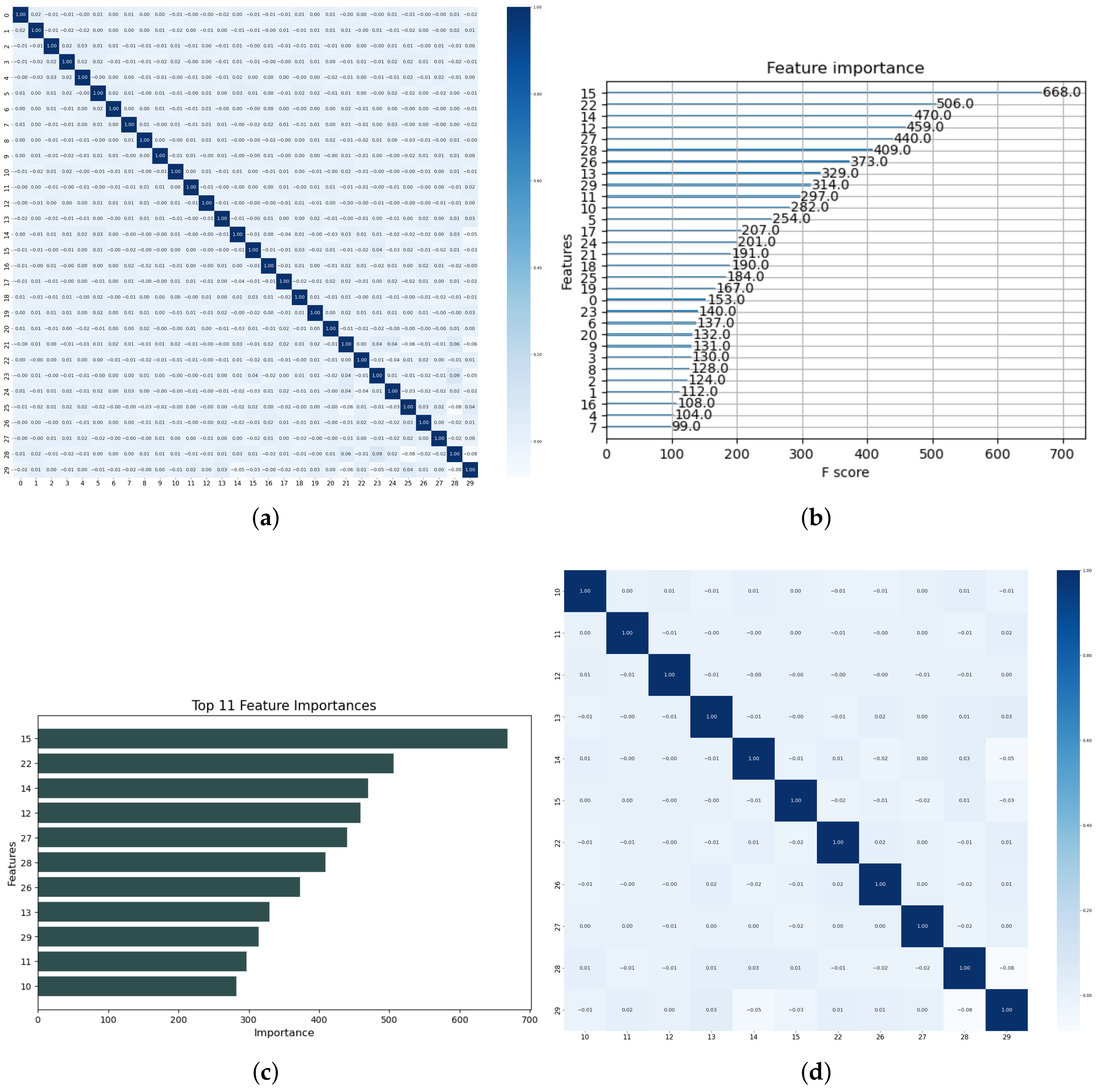
Furthermore, a feature importance technique is implemented for feature selection, which is vital in removing redundant features and also maintaining a healthy computational cost, especially in cases where the data are extensive. Figure 9 outlines the procedures involved in implementing the feature selection technique. Firstly, a correlation plot of the features is presented to determine the most suitable feature selection technique for our model. The correlation plot of all 30 features, as shown in Figure 9a. The features showed no correlation, which suggests that a correlation-filter feature selection approach might not give the desired output instance. Consequently, a more suitable and robust ’feature importance’ technique is adopted in this study.
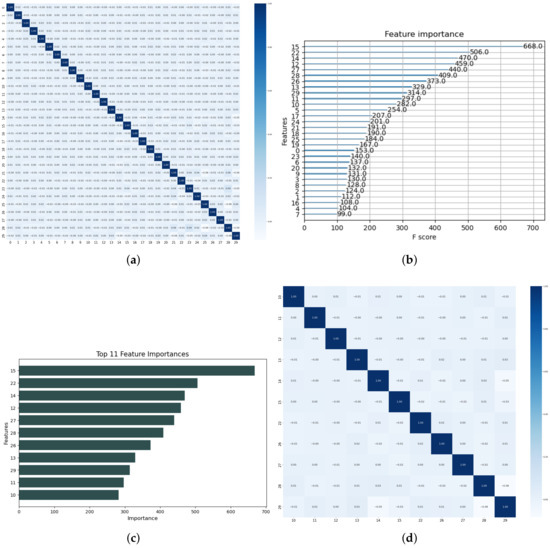
Figure 9.
Signal processing: (a) Correlation plot of all extracted features; (b) Feature importance plot of all extracted features; (c) Selected feature plot; and (d) Correlation plot of the selected features.
Secondly, the feature importance scores are determined, and Figure 9b illustrates the visualization of each feature’s performance of the 30 features. The F-score displays the individual performance of each feature across all XGBoost trees during the feature selection process. The final step, which heavily relies on the expertise and experimentation of the researcher, involves selecting features that are deemed less important based on their F-scores. In our approach, we implemented a benchmark F-score of 275 for feature selection. Using this yardstick, we retained 11 features and eliminated 19 features. Figure 9c,d shows the 11 selected features and their correlation plots, respectively.
5.2. Feature Evaluation
Theoretically, the performance of a traditional ML model is heavily dependent on the discriminative strength of its training features. In our study, the implementation of the Spearman correlation filter for discriminative feature selection was not feasible because the extracted features were already highly discriminative, as illustrated in Figure 9a. Over the years, various techniques have been employed in selecting discriminative features, which are crucial for a successful diagnostic model. These techniques include the filter method, wrapper method, embedded method, and more. Due to the inherently discriminative nature of our features, methods like the correlation-filter-based method were ruled out. Figure 9a shows Spearman’s correlation heatmap of the 30 peak features extracted from the shot blast machine signal, which were mostly uncorrelated with a mean correlation score of the features below zero. This indicates that the features are not correlated and can be efficiently employed for a diagnostic model. However, our study aimed to present a cost-efficient model. Therefore, we focused on reducing the number of features by removing redundant ones while retaining the important features using their feature importance scores as a means of selection. Figure 9d shows the visualization of the correlation heatmap of 11 selected features, confirming that they are discriminative enough for our diagnostic modeling.
5.3. Machine Learning Algorithm-Based Diagnosis
Practically, the success of a traditional MLC algorithm for a diagnostics model is heavily reliant on the success of the feature extraction and selection techniques in a given model. Furthermore, the architectural structure and learning technique of an ML model also play a vital role in the performance of a given model; hence, the need to employ a wide range of ML classifier to ascertain their performance, ensuring that the best ML classifier that is most suitable for a model is affixed to the model. Accordingly, in our study, we deployed 10 popular and robust ML classifiers in feature training and classification for fault diagnosis. Table 2 presents the summary of the individual parameters of the ML classifiers deployed in our modeling, which were selected based on their hyper-parameter tuning performance.

Table 2.
Classifiers and their respective architecture.
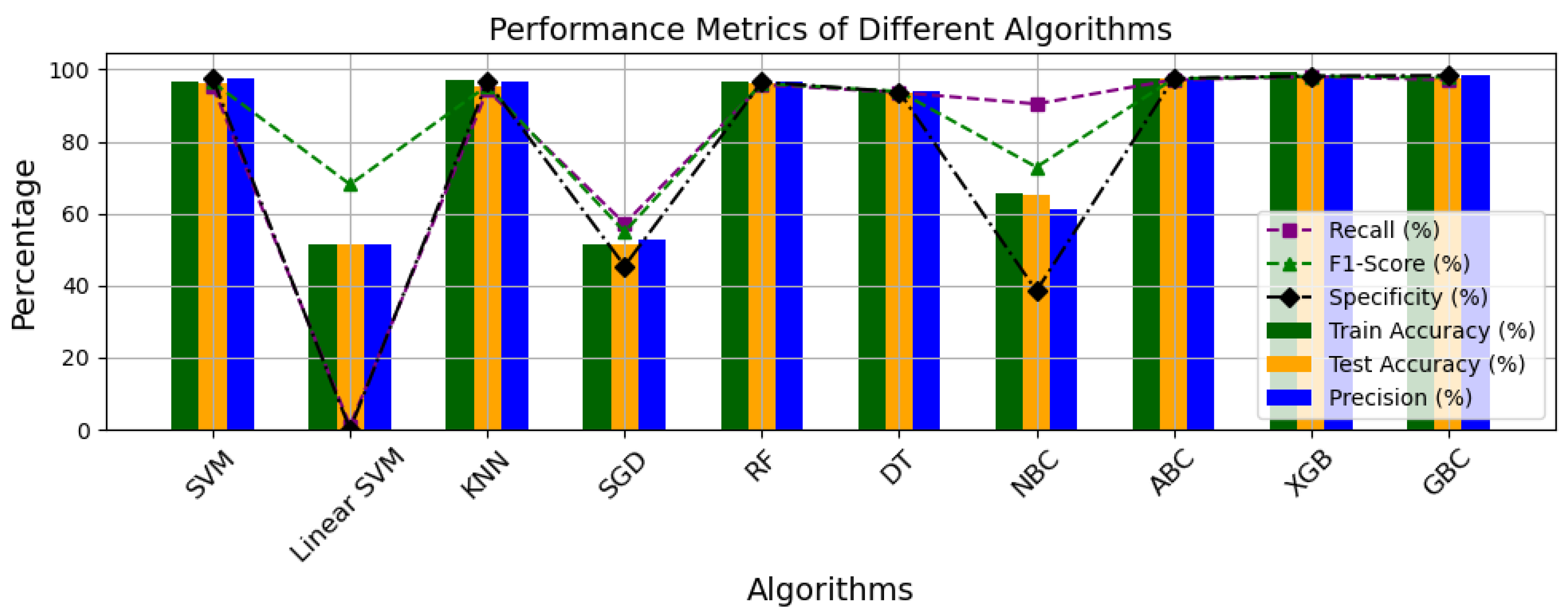
For the optimal efficiency of ML classifiers, adequate parameter optimization is deployed to ensure that the best desired results are achieved for the most efficiency. As highlighted earlier, the computation cost of the model was also deployed as a means of ML classifier validation and assessment alongside other global performance metrics. Table 3 and Figure 10 show the breakdown of the individual performance of the ML model using the evaluation metrics deployed in our study.

Table 3.
Classifiers and their respective performance matrix results.
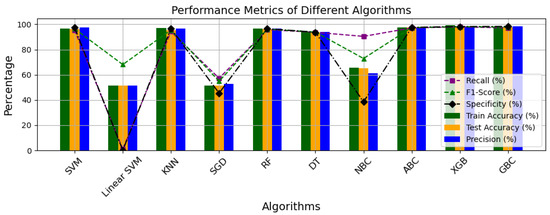
Figure 10.
Performance metrics plot of all ML classifier models.
Generally, the performance of an ML classifier model is often based on its accuracy score, especially its test accuracy, because this shows the ability of the model to perform as intended. In addition to the accuracy scores, the precision, recall, F1-score, and specificity of these models were determined for thorough evaluation. Out of the 10 models, 7 performed perfectly well with regard to their test scores. Among all of these, the XGBoost had the best accuracy with GBC coming next with less than 2.0% difference, SGD and linear SVM had the lowest test accuracy scores of 51.50% and 51.58%, respectively, which indicates that the model did not adequately adapt to the features.
Given that the accuracies of most models are relatively high and fairly similar, it becomes necessary to evaluate their performances using other metrics. The precision score, defined as the ratio of true positives to the total predicted positives, indicates that the GBC has the highest score at 98.3906%, closely followed by the XGBoost model at 98.2730%, with a difference of less than 0.2%. In contrast, the recall metric, which measures the ratio of true positives to the total actual positives, reveals that the linear SVM, despite its overall poor performance, achieved a perfect score of 100%. This indicates that the linear SVM correctly predicted the positive class more accurately than any other model. Furthermore, evaluations of the F1-score, which is the harmonic mean of precision and recall, and specificity, which is the ratio of true negatives to total actual negatives, show that XGBoost scored the highest F1-score at 98.1101%, while GBC achieved the highest specificity at 98.3075%, respectively. Overall, the XGBoost and GBC models significantly outperformed the other models across all global evaluation metrics. This highlights the importance of employing additional evaluation criteria to comprehensively assess and select the optimal ML classifier algorithm for our model.
The best-performing ML classifier algorithms, XGBoost and GBC, as shown in Table 4, took 0.83 s and 188 s, respectively, to achieve their results. The cost efficiency of the XGBoost can be attributed to its advanced techniques, which include tree pruning, regularization, and parallelization, making it an optimized version of GBC. In contrast, GBC involves training multiple trees sequentially, which often makes it computationally expensive. Technically, linear SVM is expected to be computationally less expensive than RBF-SVM. However, this is not the case in this study, where RBF-SVM took 96.22 s, while linear SVM took 477.22 s. This discrepancy can be attributed to factors such as data size, data complexity, and the inefficiencies of the parameters implemented. Overall, the classifier models are computationally fair, except for linear SVM and RF, which exhibited high computational costs of 477.55 and 276.73 s, respectively, in their execution processes. Although NBC displayed the lowest computational cost, its poor accuracy limits it from being our ideal classifier model. The high computational cost of RF can be attributed to its ensemble nature and the complexity of training many trees. Therefore, this assessment indicates that the XGBoost is the best ML classifier algorithm for our model, as it provides the best accuracy with minimal computational expense.

Table 4.
Computational costs of the training and testing process.
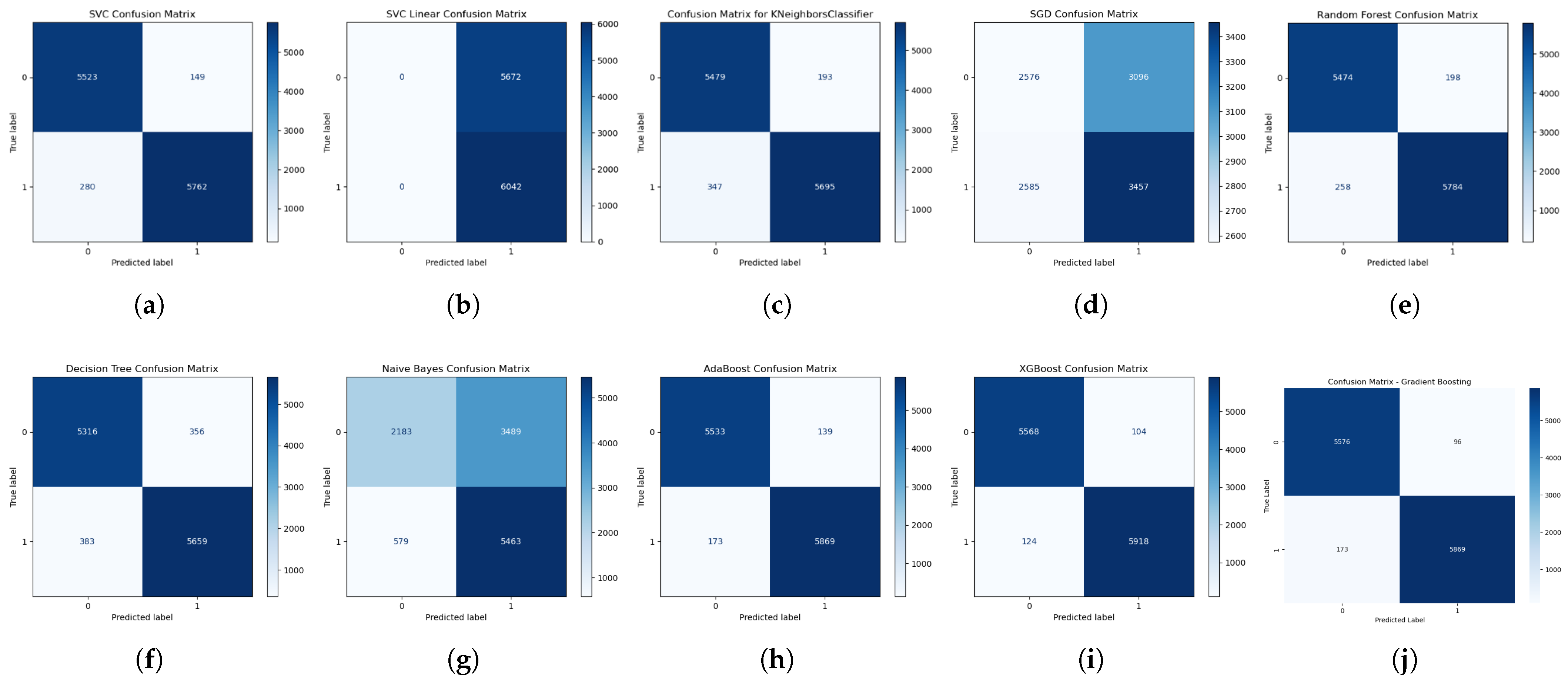
Upon examining the confusion matrix, we conducted a final assessment by evaluating each algorithm’s performance in each class using confusion matrix visualization. This revealed the exact predictions and mispredictions of each class, i.e., operating conditions, by each ML classifier algorithm. Figure 11 shows the confusion matrix resulting from a 5-fold cross-validation of each algorithm based on the test data. Surprisingly, the linear SVM returned the highest true positive rate (TP); however, it also returned the highest false positive rate (FP) while having zero predictions in both true negative (TN) and false negative (FN) instances. This suggests that the linear SVM classifier predicted all features to be of one class, which resulted in 100% recall. This means that its specificity and false alarm rate are 0% and 100%, respectively. The stochastic gradient descent (SGD) classifier returned the highest FN, while GBC and XGBoost returned the highest TN. Focusing on the best-performing classifier algorithms, XGBoost and GBC, XGBoost returned a higher TP with 5918 samples (97.9477%) compared to GBC’s 5869 samples (97.1367%), a difference of 0.811%, which corresponds to their recall difference. Conversely, GBC returned a slightly higher TN with 5576 samples (98.3075%) compared to XGBoost’s 5568 samples (98.1664%), a difference of 0.1411%, which corresponds to their specificity difference.
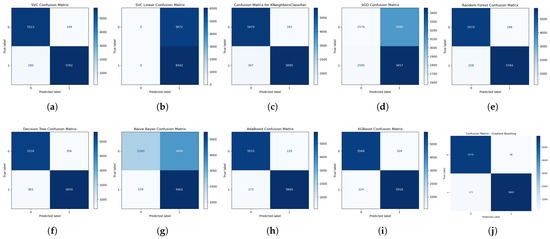
Figure 11.
Test data confusion matrix of all ML classifier algorithms: (a) RBF SVM; (b) Linear SVM; (c) KNN; (d) SGD; (e) RF; (f) DT; (g) NBC; (h) ABC; (i) XGBoost; and (j) GBC.
Analytically, it is clear that the slightly higher accuracy of XGBoost over GBC lies in its higher prediction of the positive class.
6. Discussion and Future Works
Shot blast machines are indispensable in various industries, especially in construction, aerospace, ship construction, manufacturing, recycling, re-furbishing, and automobile sectors, where high-quality finishing is required for optimal product performance and durability. This highlights the importance of a robust diagnostic framework to minimize breakdowns and avoid unnecessary downtime. This study aimed to develop a computationally cost-effective and highly efficient diagnostic model to ensure the adequate condition monitoring of the shot blast blades. Overall, the study’s goals were achieved, with the XGBoost achieving a test accuracy of 98.0536% at a computation cost of 0.83 s. This performance validates the efficiency of the XGBoost as a diagnostic tool and also validates our model. XGBoost’s prowess is attributed to its advanced architecture and optimization techniques, including tree pruning, regularization, and parallel processing, making it one of the most powerful ML algorithms, particularly for complex datasets.
XGBoost’s ability to handle complex data efficiently incorporates regularization to prevent overfitting, and parallel computational execution significantly enhances its execution speed and accuracy. Additionally, XGBoost’s flexibility in handling various data types and supporting custom objective functions further solidifies its robustness and adaptability. The model’s success in this study further demonstrates XGBoost’s suitability and adaptions in real-time condition monitoring, in this case, shot blast blades, ensuring continued and reliable operating conditions in critical industrial applications. However, being an ML classifier algorithm, its success is highly dependent on the discriminative rate of the input features deployed for diagnosis. In this study, the combination of a peak detection feature extract and a feature importance feature selection approach presented features that enable the XGBoost to give the desired output.
For future work, there is the potential to test our model on different industrial machinery to ensure its robustness and adaptability to various data types. The current study conducted a diagnostic assessment using only two classes, which may suffice for multi-class scenarios. Therefore, further studies should explore different stages of blade degradation to verify the model’s classification efficiency. However, the nature of the industrial shot blast machine might limit data generation across various shot blast blade degradation stages. Thus, while our initial results are promising, expanding the model’s application and testing it under more complex conditions is crucial for validating its effectiveness in diverse settings.
Furthermore, the primary goal of this study was to develop a model that outperforms the one presented in [10]. Our proposed model demonstrated superior results in terms of accuracy and computational efficiency. Specifically, our model achieved a fault detection accuracy of 98.05% at a computational cost of 0.83 s, which is significantly higher than the 79.25% accuracy and the 3.66 s computational expense reported in the other study, which used a concatenation of peak feature values from three signal-processing techniques: FFT, power spectral density, and auto-correlation. On a deeper level, not only is our model more efficient, but it also presents a simpler and faster approach. This results in a unique model that is not only effective but also less complex, making it computationally efficient and easier to implement.
The implications of these findings are substantial, as they indicate that our model can be effectively implemented for industrial applications. Its simplicity does not compromise the uniqueness of the model; rather, it ensures a less complex and more computationally efficient solution that is both effective and easy to implement. This makes it particularly suitable for real-time industrial applications where quick and accurate fault detection is paramount to prevent downtime, and in situations where computational resources might be limited. This suggests that our model could make a valuable contribution to the field of industrial fault diagnosis and condition-based monitoring.
7. Conclusions
This project presented a peak-detection-based approach for highly discriminative feature extraction, focusing on the FFT peak coordinates from the vibration signal of shot blast industrial machinery to extract 30 discriminative features. A feature selection technique using feature importance was implemented to select the 11 most important features using the XGBoost library. These highly discriminative features were fed to 10 ML-based classifiers, and their classification accuracies are summarized in this study.
An extensive comparison of ML-based diagnostic classifier models was conducted, providing a generalization blueprint for shot blast blade fault diagnosis. The results demonstrated that XGBoost exhibited high speed and accuracy, achieving the best test accuracy of 98.0536% with a computational cost of 0.83 s, which was the second lowest. The model with the lowest computational cost was naive Bayes at 0.09 s; however, its accuracy was one of the poorest, making it inadequate for adaptation as our model’s classifier. Gradient boosting classifier (GBC) displayed a very good accuracy of 97.7036%, but its computational cost was very high, making it unsuitable for the goal of the study, which aimed for a cost-efficient model.
Overall, the study highlights the effectiveness of XGBoost as a robust and efficient model for fault diagnosis in shot blast machinery, balancing high accuracy and a reasonable computational cost.
Author Contributions
Conceptualization, J.-H.L. and C.N.O.; methodology, C.N.O.; software, J.-H.L. and C.N.O.; formal analysis, C.N.O.; investigation, J.-H.L., C.N.O. and B.C.S.; resources, J.-H.L., C.N.O., B.C.S. and J.-W.H.; data curation, J.-H.L.; writing—original draft, J.-H.L. and C.N.O.; writing—review and editing, C.N.O.; visualization, J.-H.L. and C.N.O.; supervision, B.C.S. and J.-W.H.; project administration, J.-W.H.; funding acquisition, J.-W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2024-RS-2024-00438430) supervised by the IITP (Institute for Information and communications Technology Planning and Evaluation).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to laboratory regulations.
Conflicts of Interest
All authors declare no conflicts of interest.
References
- Hu, Y.; Miao, X.; Si, Y.; Pan, E.; Zio, E. Prognostics and health management: A review from the perspectives of design, development and decision. Reliab. Eng. Syst. Saf. 2022, 217, 108063. [Google Scholar] [CrossRef]
- Lee, J.-H.; Okwuosa, C.N.; Hur, J.-W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, P.; Zymbler, M. Internet of Things is a revolutionary approach for future technology enhancement: A review. J. Big Data 2019, 6, 111. [Google Scholar] [CrossRef]
- Zhou, I.; Makhdoom, I.; Shariati, N.; Raza, M.A.; Keshavarz, R.; Lipman, J.; Abolhasan, M.; Jamalipour, A. Internet of Things 2.0: Concepts, Applications, and Future Directions. IEEE Access 2021, 9, 70961–71012. [Google Scholar] [CrossRef]
- Do, J.S.; Kareem, A.B.; Hur, J.-W. LSTM-Autoencoder for Vibration Anomaly Detection in Vertical Carousel Storage and Retrieval System (VCSRS). Sensors 2023, 23, 1009. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, W.; Du, W.; Li, N.; Wang, J. Data-driven fault diagnosis method based on the conversion of erosion operation signals into images and convolutional neural network. Process Safety Environ. Prot. 2021, 149, 591–601. [Google Scholar] [CrossRef]
- Yang, H.; Meng, C. Data-Driven Feature Extraction for Analog Circuit Fault Diagnosis Using 1-D Convolutional Neural Network. IEEE Access 2020, 8, 18305–18315. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Akpudo, U.E.; Hur, J.-W. A Cost-Efficient MCSA-Based Fault Diagnostic Framework for SCIM at Low-Load Conditions. Algorithms 2022, 15, 212. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Stanković, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
- Akan, A.; Cura, O.K. Time–frequency signal processing: Today and future. Digit. Signal Process. 2021, 119, 103216. [Google Scholar] [CrossRef]
- Boudinar, A.H.; Aimer, A.F.; Khodja, M.E.A.; Benouzza, N. Induction Motor’s Bearing Fault Diagnosis Using an Improved Short Time Fourier Transform. In Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2019; pp. 411–426. [Google Scholar] [CrossRef]
- Yoo, Y.J. Fault Detection of Induction Motor Using Fast Fourier Transform with Feature Selection via Principal Component Analysis. Int. J. Precis. Eng. Manuf. 2019, 20, 1543–1552. [Google Scholar] [CrossRef]
- Theng, D.; Bhoyar, K.K. Feature selection techniques for machine learning: A survey of more than two decades of research. Knowl. Inf. Syst. 2024, 66, 1575–1637. [Google Scholar] [CrossRef]
- Li, K.; Yao, S.; Zhang, Z.; Cao, B.; Wilson, C.M.; Kalos, D.; Kuan, P.F.; Zhu, R.; Wang, X. Efficient gradient boosting for prognostic biomarker discovery. Bioinformatics 2022, 38, 1631–1638. [Google Scholar] [CrossRef]
- Wrona, R.; Zyzak, P.; Zioikowskia, E.; Brzezinskia, M. Methodology of Testing Shot Blasting Machines in Industrial Conditions. Arch. Foundry Eng. 2012, 12, 1897–3310. [Google Scholar] [CrossRef]
- Pandurang, K.A.; Varpe, R.S. Factors. In National Conference on Emerging Trends in Engineering & Technology (NCETET-2023); Bharati Vidyapeeth’s College of Engineering: Kolhapur, India, 2023; ISBN 978-93-91535-44-5. Available online: http://proceeding.conferenceworld.in/NCETET-2023/Preface.pdf (accessed on 5 October 2024).
- Lin, H.-C.; Ye, Y.-C.; Huang, B.-J.; Su, J.-L. Bearing vibration detection and analysis using enhanced fast Fourier transform algorithm. Adv. Mech. Eng. 2016, 8, 1687814016675080. [Google Scholar] [CrossRef]
- ALTobi, M.A.S.; Bevan, G.; Wallace, P.; Harrison, D.; Ramachandran, K.P. Centrifugal Pump Condition Monitoring and Diagnosis Using Frequency Domain Analysis. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations. CMMNO 2018. Applied Condition Monitoring; Fernandez Del Rincon, A., Viadero Rueda, F., Chaari, F., Zimroz, R., Haddar, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 15, pp. 1631–1638. [Google Scholar] [CrossRef]
- Tan, C.; Uddin, N. Hilbert Transform Based Approach to Improve Extraction of “Drive-by” Bridge Frequency. Smart Struct. Syst. 2020, 25, 265–279. [Google Scholar] [CrossRef]
- Fang, X.; Zheng, J.; Jiang, B. A rolling bearing fault diagnosis method based on vibro-acoustic data fusion and fast Fourier transform (FFT). Int. J. Data Sci. Anal. 2024. [Google Scholar] [CrossRef]
- Duc Nguyen, V.; Zwanenburg, E.; Limmer, S.; Luijben, W.; Back, T.; Olhofer, M. A Combination of Fourier Transform and Machine Learning for Fault Detection and Diagnosis of Induction Motors. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China, 5–6 August 2021; pp. 344–351. [Google Scholar] [CrossRef]
- Kumar, R.; Anand, R.S. Bearing fault diagnosis using multiple feature selection algorithms with SVM. Prog. Artif. Intell. 2024, 13, 119–133. [Google Scholar] [CrossRef]
- Shukla, R.; Kankar, P.K.; Pachori, R.B. Automated bearing fault classification based on discrete wavelet transform method. Life Cycle Reliab. Saf. Eng. 2021, 10, 99–111. [Google Scholar] [CrossRef]
- Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interact. Learn. Environ. 2021, 31, 3360–3379. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Hur, J.-W. An Intelligent Hybrid Feature Selection Approach for SCIM Inter-Turn Fault Classification at Minor Load Conditions Using Supervised Learning. IEEE Access 2023, 11, 89907–89920. [Google Scholar] [CrossRef]
- Yuan, W. Study on Noise Elimination of Mechanical Vibration Signal Based on Improved Wavelet. In Proceedings of the 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 141–143. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Wavelet Denoising for the Vibration Signals of Wind Turbines Based on Variational Mode Decomposition and Multiscale Permutation Entropy. IEEE Access 2020, 8, 40347–40356. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.-W. An Automated Sensor Fusion Approach for the RUL Prediction of Electromagnetic Pumps. IEEE Sens. J. 2021, 9, 38920–38933. [Google Scholar] [CrossRef]
- Chaitanya, B.K.; Yadav, A.; Pazoki, M.; Abdelaziz, A.Y. Chapter 8—A comprehensive review of islanding detection methods. In Uncertainties in Modern Power Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 1664–1674. [Google Scholar] [CrossRef]
- Demir, S.; Sahin, E.K. An investigation of feature selection methods for soil liquefaction prediction based on tree-based ensemble algorithms using AdaBoost, gradient boosting, and XGBoost. Neural Comput. Appl. 2023, 35, 3173–3190. [Google Scholar] [CrossRef]
- Dhaliwal, S.S.; Nahid, A.-A.; Abbas, R. Effective Intrusion Detection System Using XGBoost. Information 2018, 9, 149. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Y. The Comparison of LightGBM and XGBoost Coupling Factor Analysis and Prediagnosis of Acute Liver Failure. IEEE Access 2020, 8, 220990–221003. [Google Scholar] [CrossRef]
- Randall, R.B. Basic Signal Processing Techniques. In Vibration-Based Condition Monitoring; Springer: Dordrecht, The Netherlands, 2011; pp. 63–141. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).