A Learning-Based Energy-Efficient Device Grouping Mechanism for Massive Machine-Type Communication in the Context of Beyond 5G Networks

Abstract

With the increasing demand for high data rates, low delay, and extended battery life, managing massive machine-type communication (mMTC) in the beyond 5G (B5G) context is challenging. MMTC devices, which play a role in developing the Internet of Things (IoT) and smart cities, need to transmit short amounts of data periodically within a specific time frame. Although blockchain technology is utilized for secure data storage and transfer while digital twin technology provides real-time monitoring and management of the devices, issues such as constrained time delays and network congestion persist. Without a proper data transmission strategy, most devices would fail to transmit in time, thus defying their relevance and purpose. This work investigates the problem of massive random access channel (RACH) attempts while emphasizing the energy efficiency and access latency for mMTC devices with critical missions in B5G networks. Using machine learning techniques, we propose an attention-based reinforcement learning model that orchestrates the device grouping strategy to optimize device placement. Thus, the model guarantees a higher probability of success for the devices during data transmission access, eventually leading to more efficient energy consumption. Through thorough quantitative simulations, we demonstrate that the proposed learning-based approach significantly outperforms the other baseline grouping methods.

1. Introduction

Massive machine-type communication (mMTC), estimated to support around ${10}^6$ devices per km², is a crucial enabler for a wide range of heterogeneous and ubiquitous applications in 5G and future beyond 5G (B5G) wireless networks [1].

The massive deployment of battery-powered devices (or machines) is expected to serve Internet of Things (IoT) applications.

In the massive machine-type communication (mMTC) scenario, a high connection density is needed to support many devices in a network that may transmit only occasionally, at a low bit rate, and with zero/very low mobility. Due to their size constraints and distributed nature (mainly remotely located), mMTC devices’ battery size and replacement possibilities are also constrained. Therefore, their battery life is expected to be more than 10 years.

Providing guaranteed network access to these devices represents a challenge for the network operators, as the network will suffer from high MAC signaling overhead affecting the mMTC devices’ characteristic energy efficiency [2]. The high number of collisions in contention-based random access procedures leads to a waste of energy and a failure of mission-critical services, such as environmental monitoring alarms, automated traffic control and driving, and eHealth services. In summary, current MTC load control solutions are based on inflexible grouping criteria and simplified application execution models. However, an IoT application may require a group of sensors to work together, and each sensor may have a different capability, i.e., each sensor could perform different tasks. In that regard, the random access procedure also impacts the energy consumption of the devices, which, if not regulated, may lead to a complete blackout as most of these devices are primarily powered by batteries.

Although significant efforts have been made to address the issue of network congestion and access delay [3], the matter of energy efficiency in this context has not received sufficient attention. We have taken a different approach, recognizing that the sustainability of battery-powered sensors located remotely depends heavily on their constant availability. While previous approaches have led to significant progress in achieving satisfactory quality of service (QoS), robustness, and scalability, a more comprehensive understanding of the mMTC architecture is necessary to achieve these goals.

In our previous work, we formulated the grouping decision as a combinatorial optimization problem and used a bin packing-based heuristic algorithm to solve the problem [4]. This has shown promising results compared to other grouping strategies, such as location-based and feature-based strategies. Now, in the context of the B5G network with massive MTC device deployments, we leverage the relationship between the energy consumed and the random access of each device to propose an efficient grouping mechanism capable of guaranteeing the successful and timely transmission of the sensors while guaranteeing efficient energy utilization. Our approach considers the application-to-device relationship while grouping the devices. We propose a grouping strategy that transforms applications into task execution frameworks and initiates sequential device triggering. This approach is designed to minimize signaling overload by providing exclusive resource access to each group member.

As the field of artificial intelligence (AI) is evolving, academics and industry leaders are using machine learning (ML) methodologies to help solve multiple problems in wireless communication networks [5]. From network optimization to resource allocation and other theme-specific enhancements, ML algorithms, such as reinforcement learning, federated learning, echo state networks (ESNs), adversarial machine learning (AML), and distributed reinforcement learning, are widely implemented to enhance wireless communications in B5G scenarios. Such ML applications in wireless network management enhance efficiency and pave the way for more adaptive and intelligent wireless network infrastructures and strategies. In [6], Shi highlights the learning-to-optimize techniques in 6G networks, covering various ML frameworks and their applications in solving complex optimization problems in wireless networks.

To address the massive MTC scenario with network congestion problems, the authors in [7] proposed a random access scheme as a partially observable Markov decision process (POMDP) framework to guarantee a short access delay requirement for high-priority UEs without any additional energy consumption of low-priority UEs during the access procedure. In [8], Sejan proposes a temporal convolutional network (TCN)-based model for RIS-based wireless communication, demonstrating its effectiveness through simulation results in terms of bit error rate and symbol error rate. In a more recent research, Tamim presents a machine learning (ML)-based traffic steering (TS) scheme for open RAN (O-RAN) to predict network congestion and proactively steer traffic to reduce expected queuing delay, focusing on enhancing the performance and reliability of RAN access for massive IoT networks [9].

Many researchers, including [10,11], have focused on reducing the time complexity of heuristic models. However, due to the inherent computational complexity of these models, a decrease in performance is likely as the number of devices increases. We anticipate this decrease in performance by proposing to integrate machine learning techniques to enhance the grouping strategy with energy efficiency and low latency access in mind. In other words, our grouping strategy aims to reduce the collision rate and the devices’ energy consumption. This goal is critical in B5G network scenarios with more deployed mMTC devices, diverse applications, and complex and ubiquitous scenarios. It requires a deeper sense of efficiency and scalability. Therefore, a multi-aspect efficiency grouping strategy targeting energy consumption, access delay, and the miss rate is worth considering.

This work proposes a learning-based energy-efficient device grouping mechanism for massive MTC in a (B5G) network capable of reducing the miss rate, energy consumption, and access delay. The reinforcement learning technique is applied to optimize the grouping decision and the intra-group device access scheduling based on the application’s arrival time and time constraints. Powered by reinforcement learning, it offers a trifold approach that simultaneously addresses access delay, energy consumption, and the success rate of mMTC devices within the contention-based RACH framework of B5G networks.

To the best of our knowledge, this is the first mMTC grouping strategy considering the scalability factor and device heterogeneity in the context of massive deployment in the B5G network. The main contributions of this paper can be listed as follows:

• We formulate a group number minimization problem to efficiently coordinate each device’s access to the network and propose a machine learning-powered energy-efficient mechanism, prompting devices to join a group to minimize the overall energy within delay constraints. Our model can interact with the dynamic environment without increasing the model’s complexity.
• We present the implementation of the grouping strategy as a Markov decision process (MDP)-based constrained optimization with a policy gradient. Constraints such as group condition, devices, application arrival, and time constraints are considered the state with the Lagrange relaxation technique. The action to group each device is based on the constraints mentioned above.
• We investigate the impact of massive access attempts on energy consumption and access delay in the proposed model. Given the heterogeneity of the applications in the real world, we show that certain delay-tolerant applications can afford the miss rate, so the non-tolerant ones can be completed before the expiration of the time constraint.

The simulations conducted in this study compare a neural network to multiple baseline grouping strategies. They were carried out under a realistic scenario where many IoT devices were deployed [12].

The results show that, regardless of the model used, the risk of collision increases as more devices try to access the network. This highlights the criticality of the proposed dynamic algorithm selection method, which has a miss rate of less than 4% in the worst-case scenario. Furthermore, the simulations also indicate that the proposed machine learning-based grouping mechanism outperforms the baseline models considering collision percentage, energy efficiency, and delay. This underscores the effectiveness of the proposed method in improving the performance of IoT networks.

The rest of this paper is organized as follows: Section 2 describes the related research works. Section 3 introduces the system model. The signaling overload problem is presented in Section 4. Section 5 presents the proposed solutions. The simulation results for various performance metrics are presented in Section 6. Finally, conclusions are drawn in Section 8.

2. Related Works

2.1. Reinforcement Learning

Reinforcement learning is a subfield of machine learning that focuses on how an agent interacts with its environment by taking actions based on a Markov decision process (MDP). After taking an action, the agent receives feedback as a reward, indicating whether the decision was good or bad. By observing the environment’s state at each step, the agent strategically chooses actions to maximize its cumulative reward.

Many scholars have been using both subsets of RL to address some problems in the wireless network. In [13], Ohtsuki explores the various possibilities of using machine learning techniques to enhance communication in 5G and beyond. In [14], the authors categorize the different 6G ultra-reliable low-latency communication (URLLC) enablers while investigating a few promising ML solutions to achieve intelligent connectivity for the 6G URLLC services, such as massive URLLC. In [15], Tan and colleagues propose a DRL-based mechanism to expedite the resource allocation for multiple and diversified MTC services in the context of the massive deployment of MTC devices (MTDs). In [16], the authors use the well-known Q-learning technique to propose an intelligent duty cycle control for machine-to-machine communication (M2M). Hameed and colleagues in [17] address the problem of network congestion by proposing a random access channel scheme based on the Q-learning method.

2.2. Network Congestion and Signaling Overload in Wireless Network

One of the first proposed mechanisms was described in 3GPP as the access class barring (ABC). It proposes grouping devices, with each group presented as a class. The base station transmits a barring factor to each class, specifying the probability of any device belonging to a specific group launching the random access procedure. By doing so, the barring factor’s randomness reduces the number of simultaneous attempts at the random access procedure. In [18], Alves et al. address the issue of massive access in NOMA-based mMTC. In [19], the authors propose a random preamble selection time, preventing the devices from starting their process simultaneously. They also propose implementing an exponential-decrease back-off window for the successful re-transmission of devices that fail to access the network due to collision. In [20], the authors first provide an overview of 3GPP MTC, including random access and radio resource management procedures. Then, the authors propose a grouping-based resource management scheme, taking device requirements as the clustering criteria. Both traffic congestion and processing complexity were alleviated. In [21], devices that share a resource within a granted time interval are grouped according to their cell association. A group-based communication scheme was proposed by Lee et al. [22], where transmissions from closely located devices were aggregated to improve efficiency and fixed numbers and sizes of groups were considered. In [23], Taleb and Ksentini proposed a set of messaging procedures to enable the bulk signaling and dynamic grouping of MTC devices with common subscription features. Tseng et al. [24] proposed an ID-sharing mechanism to reduce the signaling load and achieve power savings. Social features can also be adapted for grouping, as shown in [25]. Ito et al., in [26], proposed to assign the same international mobile subscriber identity (IMSI) to multiple IoT devices. In [27], the authors surveyed the current issues in an ultra-dense network while considering some possible machine learning-assisted solutions. Coleman and colleagues, in [28], highlight some physical- and medium-access techniques to address the problem of massive access attempts from mMTC devices in the B5G network.

2.3. Energy Consumption Minimization for MTC

In the B5G network, most researchers focus on congestion control for MTC devices, with few targeting battery lifespan extension. A specific model was proposed in [29], to optimize the energy consumption of periodical data collection in a self-powered IoT network with non-orthogonal multiple access (NOMA). In our previous work [30], we surveyed the NB-IoT technical aspects. Singh in [31] presents an extensive analysis of IoT devices’ energy consumption for low-power wide-area network (LPWAN) technologies. Fovios quantifies the impact of some NB-IoT parameters on the devices’ energy consumption. They also explain how network configurations can affect the devices’ battery lifespan [32]. Osama highlights the importance of optimized energy efficiency and latency reduction for IoT devices in B5G and 6G networks. The study shows that algorithms achieving high energy efficiency will also achieve low latency with repetitions [33].

For contention-based preamble collision probability in [34], Chang and Lin propose a predictive algorithm that effectively minimizes random contention collisions and delays.

3. System Model and Symbol Definitions

3.1. RACH Procedure Scenario

This study considers the contention-based random access procedure of N mMTC devices (MTDs) in one cell of a B5G network environment. Based on the traffic pattern of the MTC devices, we can divide them into three groups: periodical, on-demand, and event-driven.

$$N=N_P+N_O+N_E$$

(1)

$N_P$, $N_O$, and $N_E$ represent periodical, on-demand, and event-driven types of MTD, respectively.

Each device must follow a contention-based network access procedure to obtain authorization and resources for data transmission. Due to their diversity, these devices may be accessed at any time. Hence, there is the possibility of having a massive number of devices trying to access the network simultaneously. Given the very small number of available preambles in each random access opportunity (RAO), which is $W=54$, the set of preambles is then presented as $\mathcal{P}a=\{\mathcal{P}{a}_0,\dots ,\mathcal{P}{a}_{w-1},\mathcal{P}{a}_l\}$

3.1.1. RACH Messaging Structure

Two random access (RA) procedures are supported: a four-step RA type with MSG1 and a two-step RA type with MSGA. Both types of RA procedures support contention-based random access (CBRA) and contention-free random access (CFRA) [35]. The MSG1 of the four-step RA type consists of a preamble on the physical random access channel (PRACH). The MSGA of the two-step RA type includes a preamble on PRACH and a payload on the physical uplink shared channel (PUSCH). Depending on the active messaging type, after the initial message’s (MSG1 or MSGA) transmission, the UE monitors for a response from the network within a configured window.

If the RA procedure with a two-step RA type is not completed after several MSGA transmissions, the UE can switch to CBRA with a four-step RA type [36].

3.1.2. Success and Collision Probability

In the 5G scenario with massive MTDs, we assume many MTDs will select the same preamble, causing the collision [5]. The NR base station will refuse access to the contenting devices, creating a massive signal overload. The failed devices will still try to re-transmit after a predefined back-off window [37]. The success of an attempt exists if and only if one device utilizes the $w$^th preamble. Accordingly, the three probabilities are defined as follows:

• With the maximum preamble $W=54$, the probability that the $w-th$ preamble is unclaimed is given by

  $$\mathbb{P}\left(a\right)=\left(\genfrac{}{}{0pt}{}{N}{0}\right){\left(\frac{1}{W_{\mathcal{P}a}}\right)}^0{\left(1-\frac{1}{W_{\mathcal{P}a}}\right)}^N$$

  (2)

  where $\left(\genfrac{}{}{0pt}{}{N}{0}\right)$ is the binomial coefficient.
• The probability that only one device claimed the $w^{th}$ preamble is

  $$\mathbb{P}\left(b\right)=\left(\genfrac{}{}{0pt}{}{N}{1}\right){\left(\frac{1}{W_{\mathcal{P}a}}\right)}^1{\left(1-\frac{1}{W_{\mathcal{P}a}}\right)}^{N-1}$$

  (3)
• The probability that two or more devices are contending for the l-th preamble and colliding is

  $$\mathbb{P}\left(c\right)=1-\left(\mathbb{P}\left(a\right)+\mathbb{P}\left(b\right)\right)$$

  (4)

Considering the system model, we can summarize the scenario as a massive number of devices concurring to a select few numbers of available preambles and ever-increasing transmission attempts from previously failed devices wasting energy to perform the transmission without any guarantee of success. Given this situation and the delay-intolerant characteristics of some MTDs, exploring an intelligent way to guarantee the successful access and data transmission of the MTC devices according to the latency characteristics of the applications requesting them is critical.

3.2. mMTC Architecture

The 3rd Generation Partnership Project (3GPP) proposes a system architecture for MTC over the LTE network [38]. The MTC applications are hosted by application servers (MTC ASs) for task management and connected to the core network (CN) through the service capability server (SCS). Applications come with a set of required tasks to be executed by devices before the time expires. The actions of MTC devices are triggered by a message from MTC AS. After authorization checking, the MTC interworking function (MTC-IWF) relays triggering messages from SCS to MTC devices. When the cellular IoT (CIoT) device receives the triggering request message, it checks the ability to complete the requested tasks. If an MTC device has the ability, a packet data network (PDN) connection with the CN is created to perform the desired transmissions, and the tasks are executed by the MTC device during the scheduled period. Each device triggered by an MTC server is followed by several signaling messages exchanged on the network.

The MTC applications are hosted by application servers (MTC ASs) for task management and scheduling and are connected to the core network (CN) through the service capability server (SCS). After authorization checking, the MTC interworking function (MTC-IWF) relays trigger requests from SCS to MTC devices. If an MTC device can execute the requested tasks, a packet data network (PDN) connection with the CN is created to perform the desired transmissions. Each application comes with a set of requirements, and the corresponding tasks have to be executed before the time expires [38].

Therefore, the main high-level MTC operation players are applications, tasks, and devices. For massive deployment, recurring MTC applications are one of the main types. In addition, energy efficiency is one of the problems in the massive access scheme. Reducing signaling and saving energy are the two main topics of this paper. We adopt the grouping mechanism, sharing the same ID in a group, to reduce the signaling overhead and use the power-saving mode (PSM) to reduce power consumption.

3.3. mMTC Energy Consumption

The PSM and discontinuous reception (DRX) are two important energy-saving methods used for MTC devices. In our scheme, we chose the PSM rather than DRX because, with the PSM, the RF modules are turned off, with the result that the device becomes unreachable (i.e., no response to paging messages). With DRX, even during that period of unavailability, there is no need to re-establish the connection when it is time to wake up because the device remains registered to the network throughout the entire PSM time. Thus, it is more suitable for our scheme. Without loss of generality, the PSM is represented as a semi-markov model with three modes and four states:

• PSM: $S_1$
• Connected mode: $S_2,S_3$
• Idle mode: $S_4$

The overall energy consumption of a device j is equal to the sum of energy consumed during each state, as follows:

$$E_j=\sum _{k\in PSM,act,Idle}{E}_{k_j}$$

(5)

$$E_{PS{M}_j}=PS{M}_j·t_{PS{M}_j}$$

(6)

$$E_{Idl{e}_j}=Idl{e}_j·t_{idl{e}_j}$$

(7)

$$E_{ac{t}_j}=E_{rac{h}_j}·\sum _{q=0}^{R_{max}}{y}_{j,q}+E_{tr{x}_j}$$

(8)

$$y_{j,q}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{device}j\mathrm{collided}\mathrm{on}\mathrm{attempt}q\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(9)

where $E_{PS{M}_j},E_{ac{t}_j}$, and $E_{Idl{e}_j}$ define the energy consumed by device j during the sleep, active, and idle modes, respectively, while $R_{max}$ represents the maximum re-transmission [39]. Equation (8) details the energy consumption components during the active mode for MTC devices, encompassing RACH procedures and data transmission.

In the PSM scheme, after the MME receives the grouping result from the AS, the MME needs to trigger the devices during their scheduled period and send a message about the next active time to the devices in a group. Only one device can transmit the data in a group on the mobile network. The other devices use the PSM to save energy and wait for the active time to connect to the mobile network [26].

The overall average consumed energy is

$$E_{MT{C}_{ave}}=\frac{1}{N}\sum _{j=1}^N{E}_j$$

(10)

3.4. mMTC Signaling Overload

Signaling overload and battery lifetime are two of the leading IoT problems. The application server needs to trigger the device by the control messages, but the proportion of the control messages and the transmitted data is inefficient. The EPC is not affordable when it transmits a large number of messages at the peak time. The traffic model combines the payload size and protocol header overhead. When the devices are triggered, the signaling considers the total header, so we ignore the payload size. The protocol stack includes the Constrained Application Protocol (CoAP), Datagram Transport Layer Security (DTLS), User Datagram Protocol (UDP), and Internet Protocol (IP).

With the massive and ever-growing number of MTC devices, reducing the signaling message is more important than ever. This will solve the server congestion problem and reduce the energy consumption of MTC devices in the B5G network. The mMTC devices are put on the mobile network and respond to the server’s request automatically. The packet size varies between 4 and 21 bytes. The energy-saving mechanism can extend the life of device batteries by reducing the frequency of replacements.

3.5. mMTC Access Delay

In a contention-based scenario, the minimum latency for the RACH procedure is at least 15 ms, excluding step 1, waiting time [40]. In this section, we further explore the latency details to analyze the impact of collisions on the overall latency.

As mentioned above, the possibility of collision exists in a contention-based RACH. When it happens, it impacts the overall latency of the device’s transmission operation. The overall latency of a device is mathematically represented as follows:

$$D_{MT{C}_{j\left(init\right)}}=D_{rach-1}\left(\right(1+R_{max})\times x_j)+R_{max}(T_{Back}\times x_j)$$

(11)

$$D_{MT{C}_{j\left(final\right)}}=D_{rach-2}+D_{trx}$$

(12)

$$D_{MT{C}_j}=D_{MT{C}_{j\left(init\right)}}+D_{MT{C}_{j\left(final\right)}}$$

(13)

$$x_j=\left\{\begin{array}{cc}1\hfill & \text{if device}j\mathrm{collided}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(14)

Thus, the operation delay of a device accessing the network is relative to its initial access attempts. At the same time, its re-transmission is conditioned on its failure to successfully process MSg3, and the back-off time facing it is conditioned to wait before the next attempt for the maximum defined re-transmission attempts. Thus, $D_{MT{C}_{j\left(init\right)}}$ and $D_{MT{C}_{j\left(final\right)}}$ define the initial and the final RACH attempts, respectively. $T_{Back}$ is the back-off time. The average access delay defines the average time an mMTC device takes to access the network. This is mathematically described as the ratio of the total delay of each device over the total number of devices.

$$D_{MT{C}_{ave}}=\frac{\sum D_{MT{C}_j}}{N}$$

(15)

4. Problem Formulation

4.1. The Execution Model for IoT Applications

To analyze the execution of recurring MTC applications, one of the main types of massive access, we propose a graph-based model representing the relation between three key entities, applications, tasks, and devices, as shown in  Figure 1. Applications, tasks, and devices are linked to the encapsulated underlying network components. Let $\mathcal{M}=\{1,2,\dots ,M\}$, $\mathcal{K}=\{1,2,\dots ,K\}$, and $\mathcal{N}=\{1,2,\dots ,N\}$ denote a set of applications, a set of tasks, and a set of devices, respectively. For example, in  Figure 1, Application 1 executes Task 3, which requires reactions from Device 2 and N to be performed.

Matrices can be defined from the graph for analysis in the later sections. Two predetermined matrices before performing grouping are the application to task matrix $A={\left[a_{i,j}\right]}_{M\times K}$ and the task to device matrix $S={\left[s_{i,j}\right]}_{K\times N}$. Also, the per-device task execution time is a combination of data transmission and on-device processing duration, which is denoted as a column vector $t={(t_1,t_2,\dots ,t_K)}^{\mathsf{T}}$.

In this work, we have considered the ubiquitous aspect of IoT devices and the heterogeneous aspects of IoT applications. The applications include different tasks, and the devices supporting them are triggered to report or finish them. For example, if the reporting tasks are triggered for a smart meter, all devices supporting these tasks must upload the mobile autonomous reporting (MAR) periodic reports to the server. In addition, if the network command tasks are triggered, the devices complete the tasks without the uploading process. The smart meter application needs to record each device’s water, gas, and electricity load every 4 h and at midnight. In addition, smart meter applications need to read the setup parameters and configuration management and restrict the resource supply at peak times. The related application needs to record each device’s water, gas, and electricity load every four hours and at midnight. In addition, smart meter applications need to read the setup parameters and configuration management and restrict the resource supply at the peak time.

4.2. The Group Number Minimization Problem

In a massive MTC scenario, the devices transmit data or act after the applications’ trigger devices. Without using the energy-saving mechanism, the devices need to switch on the antenna to wait for the triggering message. The devices in PSM can turn off the antenna when they are idle. When applications trigger the devices to finish the task or control the devices entering an active state, the signaling messages are transmitted.

The objective is to reduce the signaling messages subject to execution time constraints. Reducing signaling messages means reducing the number of active devices. Devices that are active at the same time can form groups, and only one device can enter the active state in each group.

The active device minimization problem can be transformed into a group number minimization problem, representing each device j as a group i of one item. Devices can be grouped into a subset of candidate groups, $\mathcal{P}=\{1,2,\dots ,P\}$. When groups are assigned, a group to device mapping matrix $\mathbf{G}={\left[g_{i,j}\right]}_{P\times N}$ can be determined as grouping results. A sub-graph from the application point of view is required to formulate the problem with latency constraint ${\tau }_m$ per application. The task of device mapping for a specific application m is a masked version of $\mathbf{U}$:

$${\mathbf{U}}_m={\left[u_{i,j}^m\right]}_{K\times N}={[u_{i,j}·a_{m,i}]}_{K\times N}.$$

(16)

The matrix multiplication $\mathbf{G}{\mathbf{U}}_m^{\mathsf{T}}$ in dimension $P\times K$ then refers to the number of individual task runs of application m in each group.

To minimize the number of groups created, the problem is therefore formulated as follows:

$$min\sum _{i\in \mathcal{P}}{y}_i$$

(17)

subject to

$$\mathbf{G}{\mathbf{U}}_m^{\mathsf{T}}\mathbf{t}+{\mathbf{w}}_m\left(\mathbf{G}\right)\le {\tau }_m·\mathbf{y},\forall m\in \mathcal{M}$$

(18)

$$\sum _{i\in \mathcal{P}}{g}_{i,j}=1,\forall j\in \mathcal{N}$$

(19)

$$z_i=\left\{\begin{array}{cc}1\hfill & {\displaystyle \mathrm{if}\sum _{j\in \mathcal{N}}{g}_{i,j}\ge 1}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\forall i\in \mathcal{P}\right.$$

(20)

$$g_{i,j}=\left\{\begin{array}{cc}1\hfill & \text{if device}j\text{is assigned to group}i\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(21)

The objective of (17) is to minimize the number of assigned groups. In (18), the total task execution time plus waiting time has to be less than the constraint ${\tau }_m$ for each application m. $\mathbf{G}{\mathbf{U}}_m^{\mathsf{T}}\mathbf{t}$ is the required task execution time for each group with dimension $P\times 1$. The waiting time between task executions ${\mathbf{w}}_m\left(\mathbf{G}\right)$ is the outcome of task scheduling given grouping results. Due to the exclusive access opportunities of devices in a group, a task may need to wait for other tasks to be finished based on the scheduled order. Also, in (19), a device can be assigned to only one group. The binary indicator $z_i$ in (20) indicates whether or not at least one device exists in the group. In (21), the variable $g_{i,j}$ indicates that device j is assigned to group i. The formulation is a variation of the bin packing problem. Devices and groups are analogies to objects and bins; latency constraints of applications reflect bin sizes. There are several obstacles to optimally solving the problem. First, the problem is NP-hard [4]. Second, the bin-size-equivalent time constraint depends on group members and is dynamic. Third, the waiting time function is scheduling algorithm-dependent and non-linear. Fourth, frequent re-grouping needs to be avoided for practical usage.

4.3. Grouping and Task Execution

In a massive MTC scenario, the execution of each application consists of a set of tasks, which may be triggered at different times. Some specific devices must execute those tasks within a specific time frame called their time constraint, which is denoted as a column vector $\tau ={({\tau }_1,{\tau }_2,...,{\tau }_m)}^T$. From an application perspective, it is essential to note that the urgency of an application is not dictated by the number of tasks it performs. For instance, consider application m, a smart meter tasked with the daily reporting of electricity usage within 24 h, as depicted in Figure 2.

Typically, the tasks associated with an application can be handled by a single device. However, specific applications may necessitate the activation of multiple devices/sensors to complete their tasks. Some devices can perform one task while others can perform multiple, which explains the possibility of an application triggering one or multiple devices to execute its task. For example, in Figure 3, consider a patient-reported outcome application measuring a patient’s vitals via an eHealth system that engages various sensors, such as ECG, blood pressure (BP), and body temperature monitors, to gather comprehensive health data. Each device has exclusive access to the network while other group members are disconnected or in sleep mode. In environments where groups contain numerous devices, there is an inherent risk that some tasks may not meet their designated time constraints. These are referred to as missed tasks, as illustrated in Figure 3.

These perspectives are critical as they help us to strategically integrate tasks with lower delay tolerance within some empty spots in the groups, optimizing the utilization of group resources.

5. Proposed mMTC Device Grouping Algorithms

Considering the traffic diversity of mMTC devices and the network’s requirements, a sustainable and valuable grouping solution must consider all constraints during the grouping process.

The problem is further formulated as a combinatorial optimization. It is an NP-hard problem. In our previous work, we proposed using a heuristic-based combinatorial method to group the device optimally. Consequently, the number of groups will be reduced while the successful connection of each device will be guaranteed. This is opposed to the popular idea of electing a cluster head for data transmission in each group [41]. In our previously proposed algorithm, the intra-group activity is more dynamic as devices take turns transmitting while others are in sleep mode. This will further reduce the total energy spent from a group perspective.

5.1. Previously Proposed Algorithms

This section covers the two algorithms we proposed in our earlier works. They both targeted the same objective: to optimize group creation and successful device access to the network. This section also highlights the application process of different strategies under different considerations.

5.1.1. Best Fit Decreasing Solution with Dynamic Bin Size

In the classic bin packing problems, the bin sizes are fixed. By mapping the grouping problem to a variation of bin packing, a modified version of the well-known best fit decreasing algorithm was proposed to effectively group mMTC devices with individual application latency requirements [4,42]. The number of bins corresponds to the number of groups created, while the bin size is a combination of grouped applications’ time constraints. The application time constraint is critical in the grouping and scheduling strategy. Thus, the devices were not only grouped to reduce the number of simultaneous RACH attempts but also scheduled based on a priority-based criterion involving the application’s time constraint requiring services from these devices. This solution is designed to be practical and avoid frequent re-grouping. Doing so guarantees that the most urgent devices will access the network earlier in a group.

The solution is designed to be practical to perform and can avoid frequent re-grouping. This strategy matches a more realistic scenario, as any re-grouping will affect the execution sequence of tasks in groups. A situation with the tightest time constraints is considered when applying the algorithm, and a relaxing factor $\gamma \ge 1$ is introduced to control the extension of the final bin sizes. Applications are assumed to begin concurrently when grouping, and the time constraint in (18) becomes $\gamma ·{\tau }_m$ for adjustment. In the long run, applications may start at different times, so less-saturated task requests are generally expected. The formed groups can remain unchanged and still meet latency requirements. Furthermore, when packing a device into a group, the expected per-device task execution time $T_n$, equivalent to the object size, is defined with an application Poisson arrival rate of ${\lambda }_m$. For example, referring to  Figure 1, device N can run tasks 1 and 3, which can be triggered by application M or 1. So, the weighted duration of device N is

$$T_N=\frac{{\lambda }_1{t}_3+{\lambda }_M{t}_1}{{\lambda }_1+{\lambda }_M}.$$

(22)

The grouping problem shares the same objective with bin packing: optimizing group devices while minimizing the number of groups created. The BFD bin packing algorithm and the earliest deadline for the first scheduling are adopted. Devices are first sorted following the descending order of $T_n$ and assigned to a group one by one. The device-linked tasks in a group are then scheduled in the order of corresponding application time constraints so that a task related to an application with the latest deadline can be executed first. The algorithm evaluates the device-dependent space of each group for all related applications. A device joins a group that has space to accommodate it with minimum remaining space. A new group is created automatically if no group fits the device. The process continues iteratively until no un-grouped device is left.

According to the concept of exclusive access, only one device can connect to the network at a time in each group. The MTC device can use the Group ID instead of its ID to connect to the network. This alleviates the MTC identifier shortage (using the Group IMSI) and leads to a better resource management strategy [43]. The other benefit is the reduction in energy consumption, as other devices remain detached when one is attached. The BFD algorithm has a computational complexity of $O(nlogn)$ and a packing performance of $(11/9)·(\mathrm{optimal}\mathrm{number}\mathrm{of}\mathrm{bins})+1$[4].

5.1.2. MILP Solution with Fixed Time Constraints

Because of the quick and ever-growing expansion of the number of mMTC devices in the IoT environment, a strict constraint-based algorithm will lose its effectiveness over time. With the same idea, we tried to gain more control over group creation by adding a packing vector $(\Gamma )$. This packing factor helped us control the number of devices per group.

The problem was further relaxed and presented as a mixed integer linear programming problem (MILP) by converting the time constraints from applications to group points of view. We define the row vector ${\mathbf{g}}_i$ as the i-th row of $\mathbf{G}$, indicating devices in a group i. Referring to Figure 2, from a group point of view, tasks can be scheduled to run consecutively, and the waiting time is therefore eliminated when saturated. If we replace the application-dependent time constraint with a group-specific ${\tau }_G$, the constraint becomes fixed and linear. The relaxed group-based condition is

$${\mathbf{g}}_i{\left(\sum _{m\in \mathcal{M}}{\mathbf{S}}_m\right)}^{\mathsf{T}}\mathbf{t}\le {\tau }_G·y_i,\forall i\in \mathcal{P}.$$

(23)

The constraint (18) in the original problem is replaced by (23) to form an MILP problem.

The MILP problem can be solved by mixed-integer optimizers such as MOSEK [44]. MOSEK applies the linear programming-based algorithm to solve the MILP optimization problem.

In the previous solution, solving the MILP problem required predetermined device and group sizes. However, it is not practical to define and set a constant value for the total device time and the group size. Because of this, we used a method that solves the MILP problem after the best fit decreasing (BFD) solution. Aided by the result of the BFD model, we use the obtained values to determine the group size and the device size in the MILP solution. At the end of the process, the algorithm minimizes the total number of groups created, denoted ${\sum }_{i\in \mathcal{P}}{\mathit{y}}_i$.

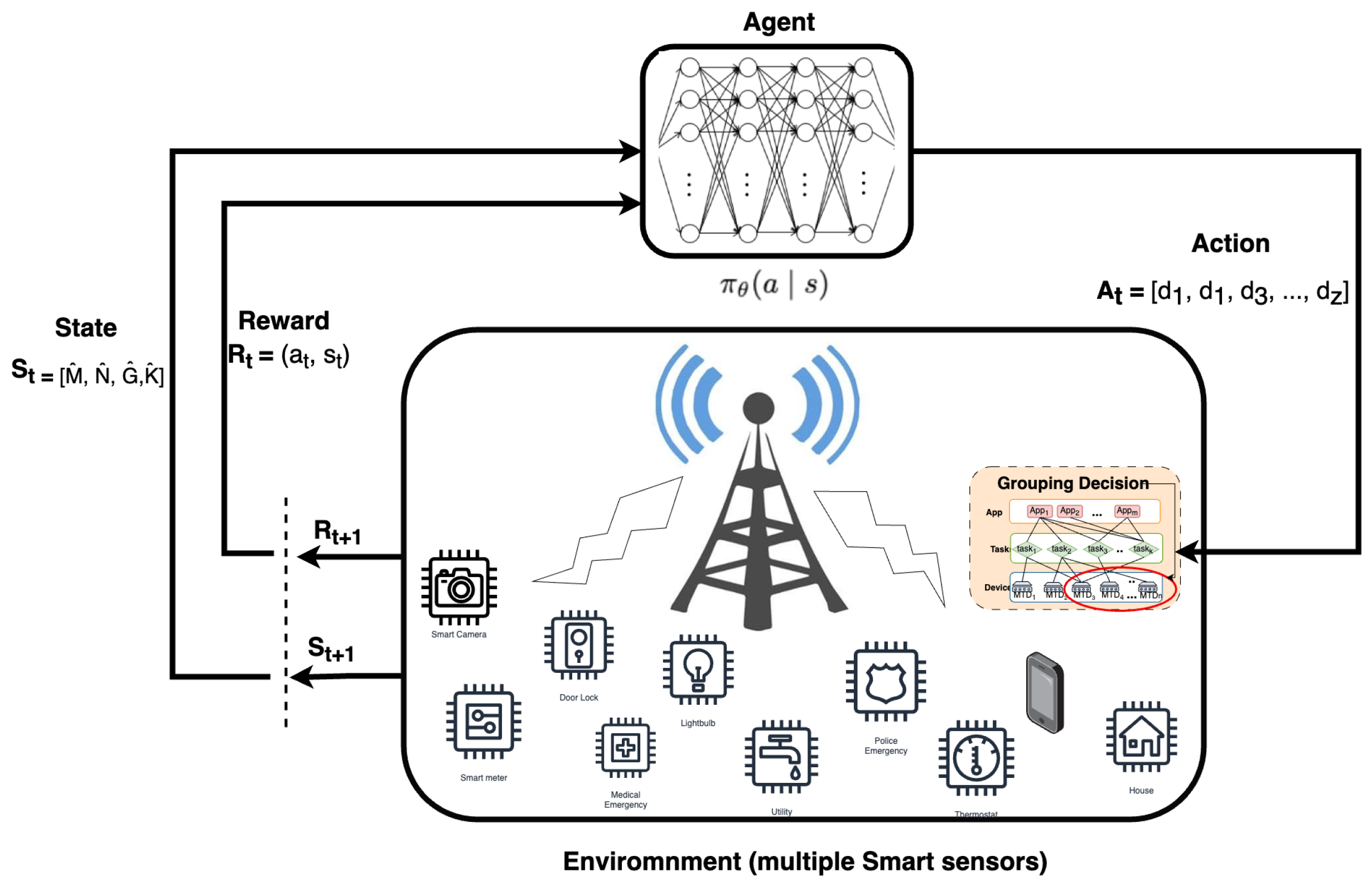
5.2. Reinforcement Learning-Based Device Grouping Algorithm

In the context of the B5G network, with mMTC as one of the key enablers, it is increasingly evident that the proliferation of smart devices will be exponential. Given this observation, we concluded that any proposed model should be scalable. Although our two previously proposed methods showed impressive results, their performance will decrease as the number of devices grows due to the computational complexity, as the time complexity of BFD is $0\left(nlogn\right)$ [10,11].

This work addresses the problems using a reinforcement learning (RL) model, leveraging its well-documented efficacy in tackling a broad spectrum of combinatorial optimization problems. Studies such as those by [45,46,47], along with earlier works by [48], underscore RL’s ability to deliver outstanding outcomes in diverse combinatorial optimization settings. We reformulate our problem as a constrained Markov decision process (MDP) and introduce an attention-based RL model that not only adapts to complex, dynamic environments but also offers a more sustainable grouping strategy compared to previous models. RL’s inherent flexibility and adaptability allow it to interact seamlessly with dynamic environments, optimizing decisions to maximize long-term benefits without adding complexity to the model.

The problem has been mathematically reformulated as a sequential decision-making problem in recent research studies [49,50]. In this reformulation, the agent is a recurring neural network (RNN) that performs actions to group MTC devices based on a specific policy $\pi \left(s\right)$. The agent receives feedback called a “Reward” for its actions. Considering the time constraint of the application and the weight of the device, the agent’s primary objective is to find the optimal policy $\pi (\ast )$ that guides the device grouping actions, minimizing the number of groups created and maximizing the overall reward R.

5.2.1. Constrained Optimization with Policy Gradients

The Reinforcement Learning Framework

As previously mentioned, the problem is reformulated as a constrained Markov decision process (MDP), where the interaction between the agent and the environment is defined as follows:

Environment: This represents the network configuration with the total number of devices, their specific features, and their weight (how many tasks they have to perform and what these tasks are). It also holds the device’s status (previously grouped devices) and the “yet to be grouped” devices. These devices can perform an RACH if no grouping action is intended. So, each MTD behaves independently during the initial time, and no group exists.

Agent: For each instance t until the time horizon H, it generates the corresponding grouping vector (action), indicating in which group G the device n should be placed. The environment then evaluates the grouping decision and, using (1), computes the quality of the action (reward). The whole process proceeds iteratively until all possible combinations are explored. The overall reward value determines the best grouping strategy. The time frame is defined as a set of time steps t with t ∈ [1, H].

State: The state contains the status of the MTDs, applications, and groups, such as the grouping status of a device $\widehat{\mathbf{N}}$, the situation of the groups $\widehat{\mathbf{G}}$, the specific situation of an application $\widehat{\mathbf{M}}$ (arrival time, time constraints), the task status for each application $\widehat{{\mathbf{K}}_{\mathbf{M}}}$, the task status for each device $\widehat{{\mathbf{K}}_N}$, and the application status for each device $\widehat{{\mathbf{M}}_{\mathbf{N}}}$. $S_t$ represents the MTD/group conditions at time step t.

$${\mathbf{s}}_t=[\widehat{\mathbf{N}},\widehat{\mathbf{G}},\widehat{\mathbf{M}},\widehat{{\mathbf{K}}_{\mathbf{M}}},\widehat{{\mathbf{K}}_{\mathbf{N}}},\widehat{{\mathbf{M}}_{\mathbf{N}}}].$$

(24)

In summary, the expression $s_t=[\widehat{N},\widehat{G},\widehat{M},\widehat{K_M},\widehat{K_N},\widehat{M_N}]$ represents a sequence of elements within the state vector $s_t$ of the model. Each element in the sequence corresponds to a specific variable or parameter within the state vector, defining the relation between the elements.

Action: As seen in Figure 4, the action set At is defined as the set grouping decision in which an MTD is assigned to a group. Hence, it determines the assignment action of MTD n to group G at time step t. During eachstate, a grouping action is feasible if one or more groups have enough space to fit. Now, the decision d involves choosing among all the possibilities to decide which group to assign the device to because each device may have different task/application features and different space/size requirements. Keep in mind that our goal is to optimize the device placement decision. Accordingly, the action at time t involves a set of grouping decisions with z as the total number of possibilities:

$${\mathbf{a}}_t=[d_1,d_t,d_3,...,d_z].$$

(25)

Reward: The reward set $R_t$ determines the set of feedbacks following the actions $A_t$. It aims to incentivize a good action. Hence, $rt$ is the incentive awarded to the agent for performing the action that consists of assigning the $MT{D}_n$ to a group G in the best possible way [51] with less free space in the group, as per our objective).

RNN Architecture

The proposed neural architecture is a sequence-to-sequence (seq2seq) model based on an encoder–decoder structure. The decoder is built as an attention-based LTSM model, which outputs the group to which the device considered as an encoder input will be assigned.

The model trains a multi-stacked LSTM cell to act as a recurrent neural network (RNN) agent capable of embedding information from the environment and variable-length sequences batched from the entire combination’s input space. The rewards are used to optimize the parameter for future grouping actions using a stochastic gradient descent policy.

5.2.2. Lagrange Relaxation

Considering the environment’s constraints, it is essential to prompt the agent to achieve feasible solutions during the MTC device grouping decision. We apply the Lagrange relaxation mechanism to reduce the complexity further. The proposed RL algorithm aims to implement a reward signal for constraint satisfaction and, inversely, a penalty signal for constraint dissatisfaction [52,53].

As per the goal of our initial problem formulation, the objective of the proposed RL model is to maximize the reward for each constraint-satisfied device grouping decision, and it is given by

$$\begin{array}{cc}\hfill \mathrm{Maximize}& \sum _{t=0}^{T}R(s_t,a_t)\hfill \\ \hfill \mathrm{Subject}\mathrm{to}& s_{t+1}=f(s_t,a_t)\forall t,\hfill \end{array}$$

where $R(s_t,a_t)$ denotes the reward function, $s_t$ represents the state at time t, $a_t$ is the action taken at time t, and f is the state transition function. The constraints, as mentioned earlier, on the states, such as application time constraints and actions, are denoted by $C(s_t,a_t)\le 0$. The Lagrange relaxation introduces a Lagrange multiplier $\lambda$ and modifies the objective function to include the product of these multipliers and the constraints. The relaxed problem is formulated as follows:

$$\begin{array}{cc}\hfill \mathrm{Maximize}& L=\sum _{t=0}^T\left[R(s_t,a_t)+{\lambda }_{t}C(s_t,a_t)\right]\hfill \\ \hfill \mathrm{Subject}\mathrm{to}& s_{t+1}=f(s_t,a_t)\forall t,\hfill \end{array}$$

(26)

where ${\lambda }_t$ represents the Lagrange multiplier associated with the constraint at time t. Here, the term ${\lambda }_{t}C(s_t,a_t)$ acts as a penalty for violating the constraints but is integrated into the objective function to facilitate solving the dual problem, optimizing over both primal variables (states and actions) and dual variables (Lagrange multipliers).

The augmented objective function in the context of policy gradients with Lagrange relaxation is given by

$$J(\theta ,\lambda )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^{T}R(s_t,a_t)+\lambda C(s_t,a_t)\right]$$

(27)

where

• $J(\theta ,\lambda )$ is the augmented objective function, depending on policy parameters $\theta$ and Lagrange multipliers $\lambda$.
• ${\mathbb{E}}_{\tau \sim {\pi }_{\theta }}$ denotes the expectation over trajectories $\tau$ generated by following policy $\pi$ parameterized by $\theta$.
• $R(s_t,a_t)$ is the reward received after executing action $a_t$ in state $s_t$.
• $C(s_t,a_t)$ represents the constraint function, which should ideally be non-positive for all states and actions. Positive values indicate constraint violations.
• $\lambda$ is the Lagrange multiplier associated with the constraint.

Policy Gradient Update

The policy parameters $\theta$ are updated using gradients of the augmented objective function:

$${\theta }_{new}={\theta }_{old}+\alpha {\nabla }_{\theta }J(\theta ,\lambda )$$

(28)

where $\alpha$ is the learning rate.

In summary, our model contains two phases, which are described as follows:

• The grouping phase: As detailed in the Algorithm 1, in this phase, the agent generated a grouping vector to point out in which bin the device should be placed. This is performed according to some policies regulating the group size and the obligation of assigning the device to the group that has the least remaining space after the assignment.
• The evaluation phase: In the evaluation phase, the grouping action is evaluated, and the rewards are generated based on whether or not the assignment is correct given the policies mentioned above and the environmental state during the grouping phase.

Algorithm 1 Lagrangian RL for Device Grouping
1:	Inputs:
2:	$S=\{s_1,s_2,\dots ,s_k\}$: State set representing device characteristics
3:	A: Action set for device grouping
4:	$\pi$: Policy function mapping S to A
5:	$C(s,a)\le 0$: Constraints on states and actions
6:	$\lambda$: Lagrange multiplier
7:	Initialize RL model parameters $\theta$, policy $\pi$, state set S, action set A, and $\lambda$.
8:	for each device in the network do
9:	Observe state $s\in S$.
10:	Determine action $a^{\ast }={\pi }_{\theta }\left(s\right)$ for device grouping.
11:	Execute $a^{\ast }$, grouping the device accordingly.
12:	Update S with new device groupings.
13:	end for
14:	for each action $a^{\ast }$ during grouping do
15:	Evaluate grouping effectiveness and constraint satisfaction.
16:	Calculate reward $R(s,a)$ and penalty $\lambda C(s,a)$.
17:	Update $\theta$ using the gradient of $R(s,a)+\lambda C(s,a)$.
18:	Adjust $\lambda$ based on constraint violations.
19:	end for
20:	Output: Optimized device groupings with minimal unallocated space, adhering to constraints.

6. Performance Analysis

6.1. Simulation Setup and Environmental Parameters

The following subsections outline the configuration settings, simulation environment details, and key parameters in the experimental simulations. They describe the setup of the simulation scenarios, including the number of devices, tasks, applications, and other relevant factors.

6.1.1. Neural Network Configuration Parameters

As shown in

Table 1. Neural network parameters.

Parameter Description	Value
Neural Network Configuration	LSTM-based RL model
LSTM Layers	3 stacks with 64 hidden layers each
Batch Size	64
Epoch	50
Optimizer	Adam
Activation Function	ReLu
Learning Rate	10−3

, the neural network was configured with specific parameters for the study. The neural network was trained on an ASUS Gaming Computer equipped with a 3.60 GHz CPU and a GeForce T1088i GPU with 32 G of RAM. Our program was written in Python 3.6, and the neural network was built using TensorFlow 1.18. The neural network comprised three stacks of LSTM, with 64 hidden layers each. The batch size was set to 64. We used an Adam optimizer to train our models [54]. A learning rate of 10⁻³ was initially used during training.

The parameters in Table 1 were optimized using the Optuna framework. The tuning process incorporated a comprehensive range of potential configurations, focusing primarily on optimizing learning rates, the number of LSTM layers, and the units in each layer to ensure robust learning capabilities. For pre-training, the network utilized policy-gradient methods on a large dataset to effectively initialize LSTM weights. This technique optimizes cumulative rewards, aligning the network’s outputs with long-term goals and expediting convergence during subsequent training phases.

6.1.2. Dataset

To ensure a fair and consistent comparison across the algorithms, the parameters utilized to generate the dataset for the other algorithms (best fit decreasing and modified best fit decreasing) are identical to those used in training the neural network for this study [55]. Other scholars [56,57] have used well-known parameters, such as application inter-arrival time and IoT network traffic pattern. These are listed in

Table 2. Simulation parameters.

Parameter	Description	Value
N	Number of devices	1000 to 5000
K	Number of different tasks	10 and 40
w	Number of preambles	54
-	Tasks per application run	1 to 5, uniform distribution
-	Tasks per device support	1, 3, 5, uniform distribution
M	Number of applications	20
${\tau }_m$	Time constraint of an application	2% of inter-arrival time
$\frac{1}{{\lambda }_m}$	Mean of application inter-arrival time	30 min (5%), 1 h (15%), 2 h (40%), 24 h (40%)
t	Device task execution time	uniform (0.1, 0.2) s
-	Targeted simulation time frame	1 RAO
$R_{max}$	Maximum re-transmission	10
$T_{back}$	Back-off time	20 ms
C	Energy consumption per RACH attempt	264 $\mu$J [58]

. This approach ensures that any observed differences in model performance can be attributed directly to the models’ inherent characteristics rather than discrepancies in the experimental setup.

6.2. Performance Metrics

For a proper evaluation of the proposed methods, three commonly used performance metrics are used:

• Miss rate probability: This metric is the ratio between the number of failed devices or devices exceeding the maximum re-transmission limit or time constraint and the total number of devices N attempting to access the network via a RACH procedure.
• Total energy consumption: This metric is the total energy consumed for N devices performing a two-step RACH mechanism attempt.
• Overall RACH access delay: This metric is the average time for N successful data packet receptions started by the first RACH attempt. We consider the maximum re-transmission to be 20 and the back-off time to be 20 ms.

6.3. Comparing Algorithms

Similar to the metrics, the comparative algorithms are as follows:

• Feature-based grouping: Groups devices based on specific features such as device type, data requirements, or application.
• Location-based grouping: Groups devices based on their geographical proximity to leverage the spatial correlation of channel conditions. It provides the foundation for group-based services [22,59].
• Best fit decreasing (BFD): A heuristic algorithm that groups devices based on their task load and the application’s time constraint to minimize the number of failed RACH attempts. This algorithm also aims at minimizing the number of groups created [24].
• MILP grouping: Formulates the device grouping problem as a mixed-integer linear programming problem, including a relaxed version of BFD for reduced computational complexity [55].

6.4. Numerical Results

The following subsections present the outcomes and findings obtained from the simulations and analyses conducted in the study. They thoroughly examine the performance metrics, statistical data, and key observations from the experimental simulations.

6.4.1. The Impact of Massive Access on the RACH Success Probability

Figure 5a,b confirm and demonstrate the theoretical analysis of the impact of increasing the number of devices in a network where the number of preambles is limited. Applying Equations (2)–(4), it is observed in Figure 5a that, regardless of the number of devices, the success probability of the devices accessing the network increases when the number of preambles increases. Figure 2 shows that, during the re-transmission attempts of devices, the probability of collision is almost 50% when only 30 preambles are available because the collided devices will remain in the system, waiting for the expiration of their back-off time to re-transmit. The re-transmitting devices will join the group of newly arrived devices, resulting in a more congested network and exponentially increasing the probability of collision.

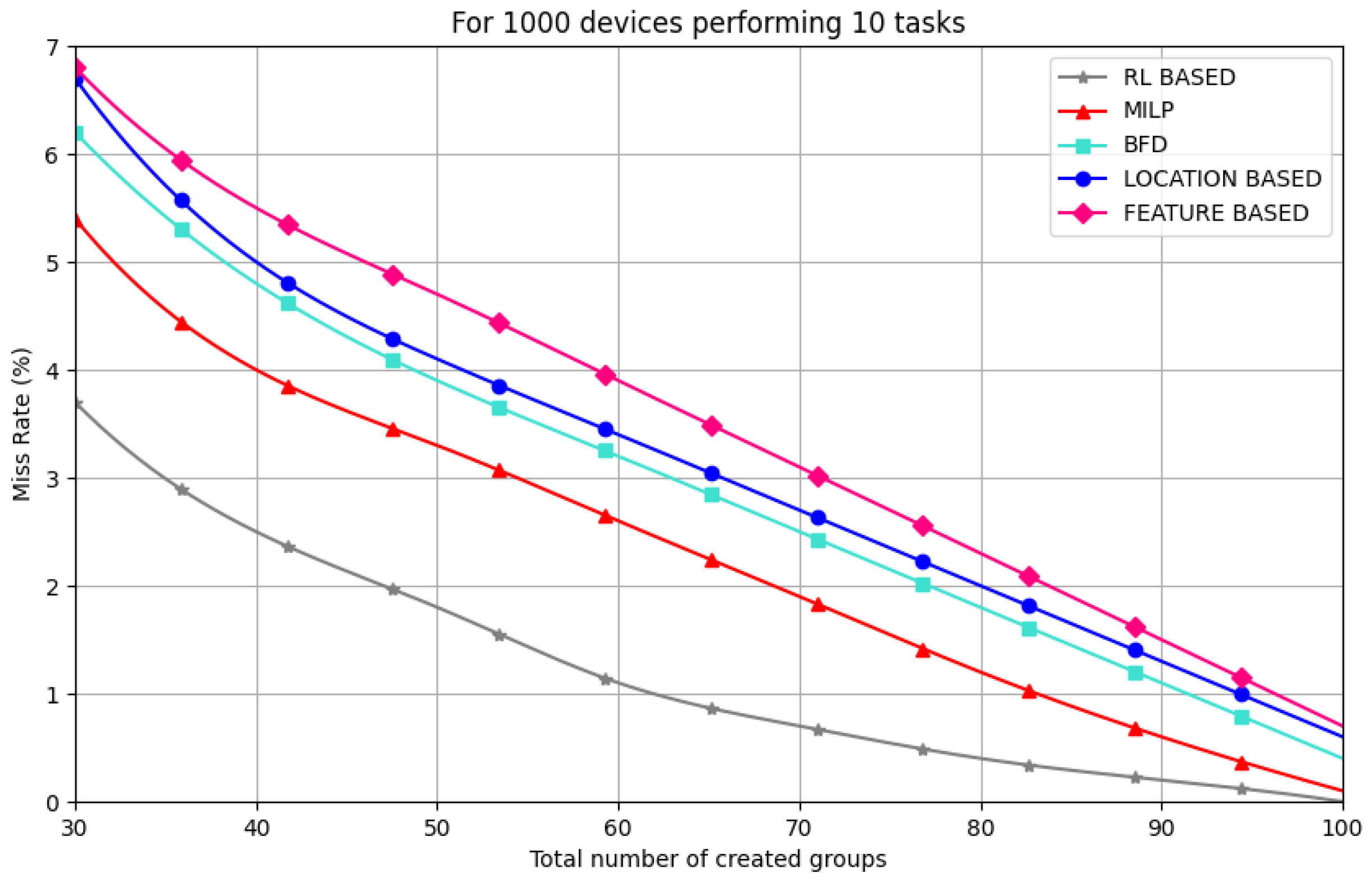
6.4.2. Loading and Miss Rate Analysis

All three of our proposed models effectively reduce the number of simultaneous attempts. It is also observed that the RL-based model (purple) performs better in all scenarios (device number). We observed that the BFD model, which targets strict task completion, keeps the number of devices per group at around 10; this is because of the time constraint. The MILP-based model (R-BFD) offers a more relaxed strategy where more devices can join the groups. It is reflected in Figure 6 that, as the $\gamma$ factor increases, almost 30 devices joined the group instead of 15 when using the BFD model. Although this surely impacts the reduction in the number of groups, it may also increase the miss rate ratio. Even if the goal is to have fewer possible groups, it is worth mentioning that having overly crowded groups is not ideal, as each device in a group will have to wait for its turn to be active and transmit. This creates a trade-off between the traditional RACH procedure, where all attempts are simultaneous, causing massive collisions, and having crowded groups by reducing simultaneous attempts; the consequence of the latter will be the transmission latency of the devices, which will indeed cause some devices to miss their transmission timeline.

To set a balance in this trade-off, we consider the heterogeneity of MTC devices, as each category has a specific time constraint (delay-tolerant vs. delay-non-tolerant). With this in mind, we can afford a small percentage of miss rate, especially on non-urgent reports (e.g., smart meters).

It is shown in Figure 6 that the RL-based model outperforms the other models with a less than $4\%$ miss rate in the worst-case scenario, where we have fewer groups and more “in-group” devices. Both MILP and BFD outperform the feature-based and location-based models. As the paper targets a massive MTC scenario, the RL-based model shows that scalability is needed to group devices. The primary goal is to reduce the number of groups created and guarantee punctual transmission for devices with a miss rate margin of 4%, which is affordable for delay-tolerant devices.

6.4.3. Impact of Efficient Grouping on the Overall mMTC Energy Consumption

In this subsection, it is essential to consider energy consumption because the mMTC devices are mainly powered by batteries. Hence, we analyze the impact of collisions on the energy consumed by the devices. We consider the total energy consumed for a two-step RACH mechanism as 264 $\mu$J [58]. Without loss of generality, we run the simulations for 1000 devices performing 10 tasks. As observed in Figure 7, when the collision rate is high, the energy consumption increases exponentially. The increase is the consequence of collision because the collided devices need to re-transmit with no guarantee of success in the following attempts. We can also observe that the RL-based model offers better energy efficiency than other grouping mechanisms, mainly because we took advantage of the devices’ and applications’ specific completion time constraints to implement an optimized scheduling mechanism. Hence, the flow ratio of attempts can be relaxed over time while guaranteeing that those with low latency requirements can be prioritized, improving the QoS.

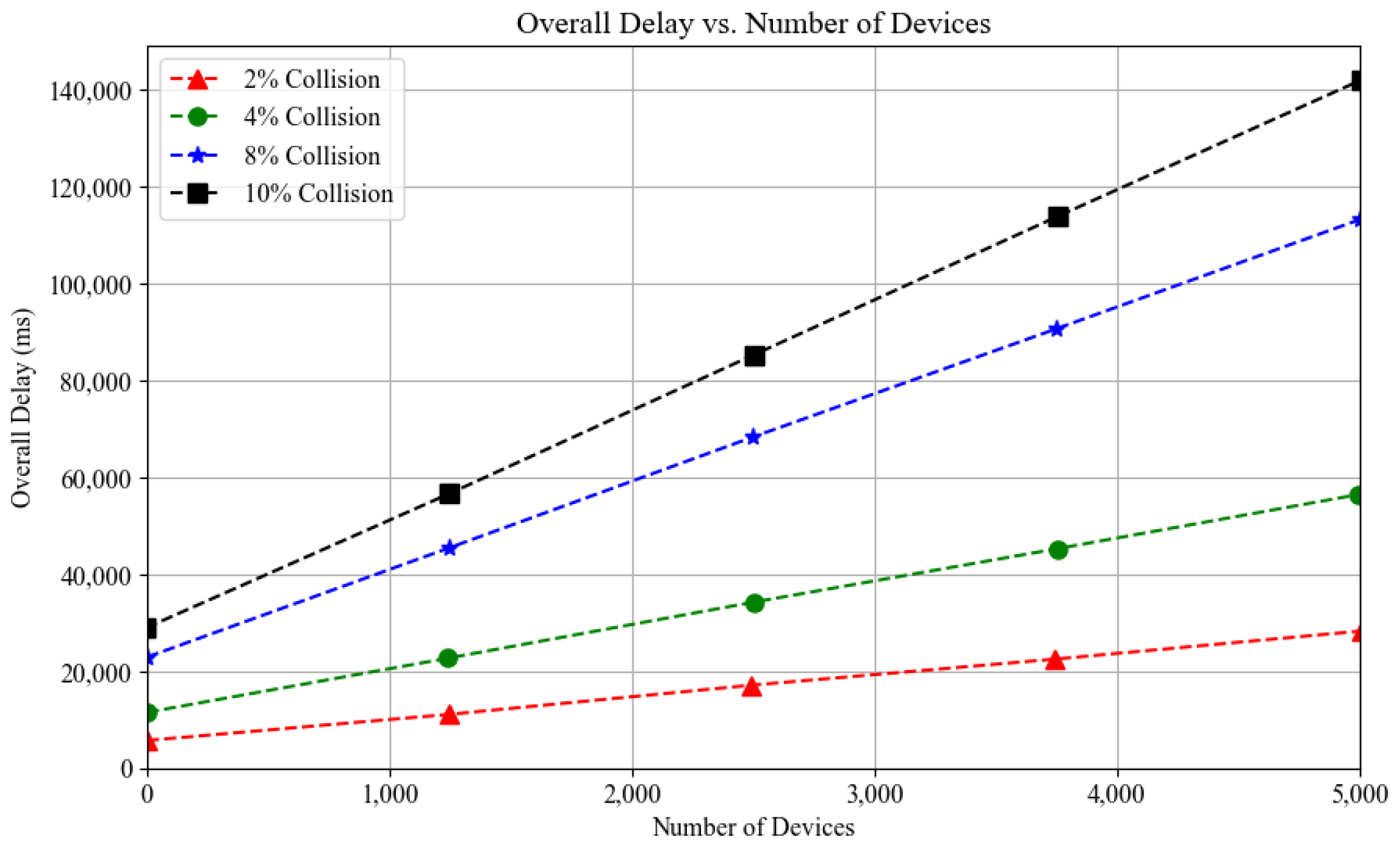
6.4.4. Impact of Efficient Grouping on the Overall mMTC Transmission Delay

The transmission delay is the average time for successful data packet reception. As for the energy consumption, Figure 8 shows the access delays as the traffic load increases exponentially as the collision percentage increases from 2% to 10%. Every time a device fails the RACH due to collisions, it enters the waiting period set by the back-off timer while new devices keep arriving. Consequently, collided devices in the back-off mode are joined by new devices, further increasing the congestion. As a result, more devices will be forced to enter the back-off mode, increasing the delay.

Figure 9 shows the probability density function (PDF) of the latency for each method across a wide range of different grouping scenarios (30, 50, 60, 70, 90, 100/group). It is demonstrated that the proposed mechanism outperforms the other methods with reduced latency in terms of access delay. The area under the curve gives the probability of the variable falling within the interval of 58,000 ms to 63,000 ms, while other methods exceed 66,000 ms. The peak in the plot shows the high likelihood of our method’s latency being around 60,000 ms. This is mainly because our method leverages the information related to the device’s time constraint during the grouping, which results in fewer failed attempts and, hence, a lower access delay.

7. Discussion

The results of this study shed light on the effectiveness of the proposed learning-based energy-efficient device grouping mechanism for massive machine-type communications (mMTCs) in beyond 5G (B5G) networks. By leveraging reinforcement learning techniques, the algorithm optimizes device grouping decisions and intra-group access scheduling, aiming to reduce miss rates, energy consumption, and access delays in contention-based random access channel (RACH) frameworks.

Our analysis revealed that the RL-based model successfully improved energy efficiency, reduced access delays, and enhanced the success rate of mMTC devices within B5G networks. Considering key factors such as application arrival times, time constraints, and device heterogeneity, the algorithm provided a comprehensive solution for optimizing device grouping in large-scale MTC deployments, mirroring a real-world scenario. Comparisons with existing strategies demonstrated the algorithm’s superiority in addressing key challenges in mMTC environments.

However, it is essential to acknowledge the computational complexity associated with the reinforcement learning model, which may pose implementation challenges in highly dynamic network settings. Additionally, the algorithm’s generalizability across diverse network configurations and communication scenarios requires further investigation to ensure robust performance in varied environments. Future research efforts should mitigate these limitations and enhance the algorithm’s adaptability to evolving network conditions.

8. Conclusions

This paper highlights the relevance of massive access attempts in B5G networks. Along with the previously proposed grouping mechanisms, we adopted a learning-based model that guarantees excellent performance even when the number of devices increases. The simulation results show the performance of the learning-based method, which offers better performance considering the case of massive access. We analyzed the impact of a collision on the device’s energy consumption and transmission delay. Considering device heterogeneity, we show that the RL-based model offers better results. The experimental results clearly illustrate the grouping performance of our proposed attention-based reinforcement learning model. Time complexity can be measured with better parameters to further describe the advantages of our proposed reinforcement learning-based grouping strategy.