Abstract
The robust stabilization of doubly fed induction generators in wind turbines against external disturbances is considered in this study. It is assumed that the angular speeds of wind turbines can only be measured and sent to the controller in a discrete-time fashion over a network. To generate the sampling times, three different triggering schemes were developed: time-triggering, static event-triggering, and dynamic event-triggering mechanisms; moreover, performance comparisons were conducted between such approaches. The design methodology is based on emulation, such that the plant is first stabilized in continuous-time where a robust feedback law is constructed based on the linear quadratic Gaussian regulator (LQG) approach. Then, the impact of the network is taken into account, and an event-triggering mechanism is built so that closed-loop stability is maintained and the Zeno phenomenon is avoided by using temporal regularization. The necessary stability constraints are framed as a linear matrix inequality, and the whole system is modeled as a hybrid dynamical system. A numerical simulation is used to demonstrate the effectiveness of the control strategy. The results show that the event-triggering mechanisms achieve a significant reduction of around 50% in transmissions compared to periodic sampling. Moreover, numerical comparisons with existing approaches show that the proposed approach provides better performance in terms of the stability guarantee and number of transmissions.
1. Introduction
Due to the increasing electricity demand, the diminishing reserves of fossil fuels, and growing concerns over climate change, there has been much interest in integrating renewable energy sources (RES) with conventional electric grids in recent years. Wind farms, which use either fixed-speed or variable-speed wind turbines (WTs), offer one of the most promising avenues for supplying the grid with electricity. Induction generators, particularly doubly fed induction generators (DFIGs), are popular forms of AC generators used in variable-speed wind turbines. A rotor-side converter and a grid-side converter are used to connect the rotor winding in a DFIG to the grid in a back-to-back architecture. The stator winding in a DFIG is directly connected to the grid. When compared to other types of induction generators, the DFIG has several advantages in terms of resilience and stable functioning against external disturbances, see, e.g., [,,].
The fundamental task of wind turbine controllers is to ensure proper supply–demand matching between the local grid and the wind farm. Controlling the wind turbine generator’s speed of rotation is a common way to accomplish this power balance. In the literature, several continuous-time control systems for DFIG-based wind turbines have been proposed, e.g., [,,,,,,,,,], as well as discrete-time systems, e.g., [,,,,]. In reality, common for the controller to be a digital platform while the plant output is evaluated by analog sensors. In some circumstances, the plant and the controller must communicate via a common digital channel, which requires networked control systems. This creates network-induced errors and increases the difficulty of the control design [,,]. The sampling effect, in particular, is a problem brought on by digital implementation and can seriously impair system performance or possibly cause instability. Traditionally, time-triggering approaches have been used to treat the sampling impact. The stabilizing sample frequency in these systems is selected based on the worst-case scenario, which in practice may be conservative. A different approach, known as the event-triggered control, has been established in the literature. In this approach, the output-dependent rule is used to produce the transmission sequence, depending on the desired stability attributes and the present state of the system. In contrast to periodic sampling, the number of transmissions can be drastically decreased in this approach [,,]. The triggering conditions must preclude Zeno behavior (infinite transmissions in a finite amount of time) in order to be practical. When the plant can only be measured for output and is prone to perturbations, the problem becomes more difficult. Two ETC schemes are developed in this paper for the DFIG wind turbine. The first ETC mechanism is based on the static triggering threshold, which has been considered in several works in the literature, e.g., [,]. The main drawback of this technique is that the generated inter-transmission times can occasionally become periodic. To avoid this behavior, the dynamic ETC mechanism is also developed in this study, where the triggering threshold involves an additional dynamic variable; see [,].
By utilizing the LQG feedback law, we explore the robust stabilization issue of a DFIG-based wind turbine. We make the assumption that the controller can only receive measurements of the wind turbine shaft’s angular speed through a digital network at discrete points in time. The closed-loop system’s stability is then maintained while avoiding the Zeno behavior by creating an output feedback event-triggering mechanism. By enforcing a positive constant on the inter-transmission intervals, a process known as temporal regularization, the latter attribute is attained. Due to the network sampling-induced errors, the closed-loop system exhibits both continuous-time dynamics and discrete changes. We formulate the total system as a hybrid dynamical system to handle such mixed dynamics []. The necessary requirements are framed as a linear matrix inequality (LMI), facilitating a methodical design approach. The developed approach ensures stability for the closed-loop system. The numerical simulation is used to show the efficiency of the approach.
The contribution of this paper is summarized as follows:
- An observer-based event-triggering mechanism is developed for a DFIG wind turbine.
- To capture the sampled data characteristic of the control system, the closed-loop system is described as a hybrid system.
- The produced sampling times of the proposed approach are less than the traditional periodic time-triggered controllers.
- The developed ETC approach provides better performance compared to the existing results in terms of the stability guarantee and number of triggering instants.
A preliminary version of this paper was published in [], where only the pitch angle control problem under static event-triggered control was explored. Compared to [], in this paper, we extend the analysis to three implementation scenarios:
- Time-triggered control, where an upper bound on the maximally allowable transmission interval is derived for periodic sampling implementation. Also, the corresponding hybrid model and the guaranteed stability property are presented in this case. This was not provided in [].
- Static ETC, as in []; in this version, we provide the complete analysis and stability proof, which are not provided in [] due to space limitations.
- Dynamic ETC, where the performance of the static ETC in [] is elevated by introducing a new triggering rule based on a dynamic threshold to allow for a further reduction in transmissions. This case is a novel contribution compared to [].
Moreover, compared to [], the performance comparisons between the three triggering schemes previously mentioned were conducted in terms of the number of transmissions and the state responses to illustrate the advantages of the developed dynamic ETC. In addition, in this version we provide a numerical comparison with relevant techniques of the literature to further support the advantages of the proposed approach.
The rest of this paper is structured as follows. Related works are presented in Section 2. The adopted notation and preliminaries are presented in Section 3. In Section 4, the description of the implementation scenario is presented and the problem is formally stated. We present the hybrid dynamical model of the networked control system in Section 6 to capture the mixed dynamics. In Section 7, the considered triggering implementations are explored, where we include the design of periodic time-triggered controllers and synthesize the static and dynamic event-triggering mechanisms. Numerical simulations are provided in Section 8, where the performances of the considered triggering mechanisms are examined. Our conclusion is summarized in Section 9.
2. Related Work
To our knowledge, the application of ETC to DFIG-based wind turbines has only been examined in a few works [,,,,]. The authors of [] developed an ETC for damping the sub-synchronous resonance of DFIG wind turbines based on the sliding mode control (SMC). The constructed ETC in [] and the triggering threshold involve constant parameters to prevent Zeno behavior. However, such constant parameters in the ETC rule can only guarantee practical stabilization of the state in the neighborhood of the origin, even in the absence of disturbances. In [], the issue of active power-sharing DFIG wind turbines has been studied under ETC implementation. To that end, a consensus-based approach has been developed in a fully distributed manner to achieve the balance between power supply and load demand. The ETC mechanism in [] is based on a time-dependent threshold to achieve the trade-off between the number of transmissions and the desired convergence rate. Hence, the implementation setup and the control objective in [] are different from the considered problem in this study. The approach in [] is concerned with the direct power control of DFIG wind turbines under the ETC and is based on the SMC. Moreover, the extended state observer has been designed to cope with external disturbances. To cope with Zeno, the triggering threshold consists of a static ETC term and a positive constant, which can only ensure practical stability even when disturbances vanish. In [], an asynchronous ETC mechanism was synthesized for LTI systems subject to external disturbances. The proposed ETC approach in [] is based on static cost functions and involves a fixed positive parameter to rule out Zeno. The technique was applied to a linearized model of a DFIG wind turbine, demonstrating a significant reduction in transmission times compared to periodic sampling. The authors of [] proposed an ETC mechanism based on dynamic memory for tracking the frequency variations in a multi-area wind power system. The overall model was described as a continuous-time LTI system and the closed-loop stability was studied using Lyapunov–Krasovskii functions. We note that the stability analyses in [,,,,] were carried out in continuous time; this does not accurately represent the hybrid dynamical nature of NCS. In contrast to the aforementioned findings, in this research, we investigate the situation where the wind turbine is subject to external disturbances, such as variations in wind speed and changes in power demand, but only the wind turbine shaft speed is accessible for measurement. Additionally, the stabilizing control method, the resulting robustness property, and the event-triggering mechanism are distinct from those created in the results described earlier. Furthermore, the total system is designed as a hybrid system to describe such networked control systems with a more accurate model, in contrast to [,,,,].
Table 1 illustrates the main contributions of the developed ETC approaches compared to the relevant results, which consist of the following main points:

Table 1.
Novelty of the proposed approach w.r.t. the existing results.
- The overall system is modeled as a hybrid dynamical system to account for both continuous-time and discrete-time dynamics, in contrast to [,,,].
- The developed ETC approaches are ensured to provide better performance than conventional time-triggered controllers in terms of reduced transmission, thanks to the structure of the proposed ETC mechanism. Such an advantage cannot be guaranteed by the existing techniques used in [,,,].
- Furthermore, a simulation comparison with closely related work [] shows that the constructed ETC in this study outperforms the ETC mechanism presented in [] in terms of transmission.
3. Preliminaries
A standard notation is adopted in this paper. denotes the set of real numbers, denotes the set of real positive numbers, and denotes the set of integer numbers.
Based on the framework in [], we consider the following hybrid systems:
where is the state, is the external disturbance, is the flow set, F is the flow map, is the jump set, and G is the jump map.
Definition 1
([]). System (1) is said to achieve -gain stability from the input w to the output if the following holds:
where , , and the achieved gain is less than or equal to ϑ.
4. System Model
The considered wind power system mainly involves a wind turbine, the customer loads, the auxiliary diesel generator, and some dispatchable loads, as shown in Figure 1.
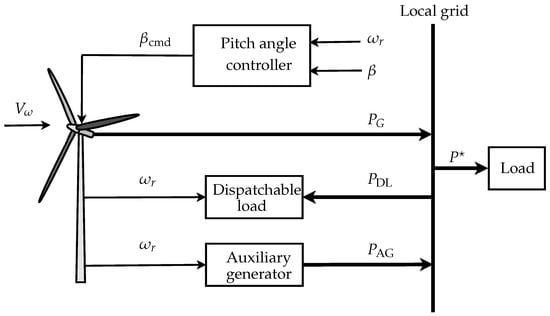
Figure 1.
Layout of DFIG-based wind turbine control.
The power demand from the grid, denoted by , is assumed to be delivered by extracted power from the WT. The objective of the controller is to regulate the pitch angle of the WT to adjust the output power to meet the change in power demand. The diesel generator compensates for the defect in the output power in case . On the other hand, when , the excess power is dissipated by means of dispatchable loads, such as the resistor bank or irrigation system [].
The linearized model of the considered system is given by []
where and are the pitch angle and the shaft angular speed of the wind turbine, respectively, is the command signal from the controller (to adjust the pitch angle), and and are the variations in power demand and wind speed, respectively. The parameters , J denote the time constant of the wind turbine blade and the moment of inertia, respectively, is the load power demand, and refers to the moment of inertia J at the angular speed linearization . The coefficients are functions of the constant parameters of the wind turbine; their expressions can be found in []. We assume that only the angular speed can be measured. Hence, the state space model of DFIG is given by
where is the state vector, is the control signal, gathers the external disturbances, and y is the measured output. The dimensions of are , , , and . The matrices are given by
We assume that the sensors and the controller are not co-located and the feedback measurement is sent to the controller over a shared digital network, as shown in Figure 2. As such, the out measurement is only accessible to the controller at discrete sampling times . Moreover, the control input is kept constant between two sampling times using ZOH implementation. We assume that the communication network is noiseless and delay-free. This assumption ensures that the transmitted output measurement from the sensors and the received information at the controller at any triggering instant are matched.
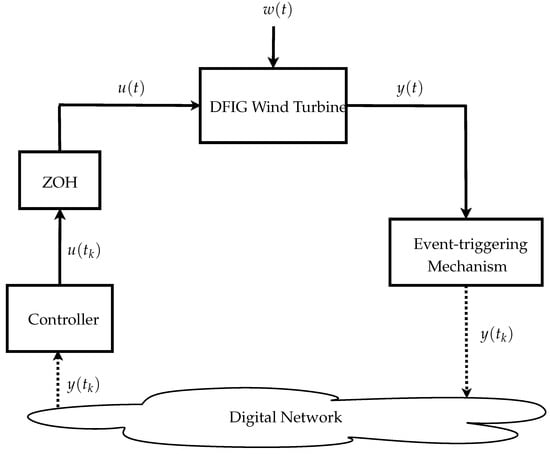
Figure 2.
Networked control schematic of the DFIG wind turbine system.
In NCS, the network is often used by multiple feedback loops and applications. Hence, in such control schemes, it is important to reduce the data transmission over the channel as much as possible to avoid network congestion. To that end, we employ an ETC mechanism to orchestrate the sampling instants, where the output should be submitted according to the system stability/performance status. The constructed ETC has to preserve the closed-loop stability and prevent the accumulation of sampling times due to hardware constraints. Hence, the control design problem can be formally stated as follows:
Problem statement. We design a stabilizing feedback law and an event-triggering mechanism, where the system stability is ensured in an appropriate sense and the Zeno behavior is prevented in the presence of external disturbances.
5. Control Design
We stabilize the system using an observer-based controller of the following type, since only the output (y) is accessible for measurements rather than the complete state (x):
where denotes the estimated state and are the observer and controller gain matrices, respectively. It was shown in [] that pair is controllable, and pair is observable for any DFIG parameter.
The control input u is updated only at discrete time instants since the output measurement y is supposed to be transmitted over a digital channel, while the controller is directly fed to the plant. We investigate the case where the sequence of transmission instants is generated by an output feedback event-triggering condition in order to decrease the number of transmissions. A ZOH is used to keep the transmitted output measurement constant between two transmission instants. As a result, in view of (4)–(6), the closed-loop system can be described by
Obviously, the sampled-data system contains interactions between continuous- and discrete-time behaviors and it is, therefore, a hybrid dynamical system by nature. Hence, in order to deal with the system in an appropriate manner, we need to take into account the combined dynamics.
By first stabilizing the plant without taking the communication network into account, and then accounting for the sampling-induced error, we develop the event-triggered controller, in accordance with the emulation approach. The closed-loop stability is then maintained by an event-triggering rule that we derive.
First, let us assume that the full state x is measured, i.e., . Then, we can design an LQR controller to strike a balance between the state response and the control effort by using the following quadratic cost function:
where are symmetric positive definite diagonal matrices. Then, by solving the algebraic Riccati equation (ARE)
the optimal state feedback law is given by , with
We take into account that only an output (y), not the entire state, is monitored. The state is then estimated using the state observer in (6). We use the Kalman filter to design the observer gain F by resolving the following algebraic Riccati equation since the wind turbine is impacted by outside disturbances.
where are symmetric positive definite diagonal matrices. Consequently, the observer gain (Kalman gain) F is given by
6. Hybrid Dynamical Model
Due to the ZOH implementation and the fact that the last transmitted measurement is kept constant between two consecutive sampling times, a sampling error is induced until is updated at the next transmission instant. We define the sampling-induced error of the output measurement as follows:
It should be noted that at each transmission, the sampling error is reset to zero, updating the previous value to the true value . Thus, we have
Define with , then
By means of the framework [], we define the closed-loop system as a hybrid dynamical system, where the terms flow dynamics and jump dynamics refer to the system’s continuous-time behavior and discrete-time changes, respectively. Additionally, the flow set and the jump set, respectively, describe the conditions under which the system operates in continuous-time or discrete-time.
To facilitate the derivation of the hybrid mode, we introduce an auxiliary time variable with the following dynamics:
The variable keeps track of the amount of time that has passed between the transmission instant and the subsequent sampling time , at which is reset to zero, as described in (17).
Let . Then, the hybrid dynamical system is
where and . We designed the flow set and the jump set based on the triggering rule, as will be presented in the next section.
In the following sections, we discuss different event-triggering schemes to maintain closed-loop stability in the presence of sampling. We start with the conventional time-triggered control to derive the maximal allowable sampling period. Then, we explain two different ETC rules based on static and dynamic triggering thresholds.
7. Design of the Triggering Rules
In this section, we explore the design of the triggering rules, where the stability of the closed-loop system is maintained. We start with the traditional time-triggered control and we derive an upper bound on the periodic sampling period. Next, we construct a static ETC mechanism based on the available output information. Then, we enhance the performance of the ETC by enriching the triggering threshold with a dynamic variable to enlarge the inter-transmission times.
7.1. Time-Triggered Control
Conventional periodic time-triggered control is based on the principle that the intervals between transmissions are separated by a fixed constant time, . In other words, the TTC mechanism is given by
which leads to sets in (18) to be
In this context, it is often necessary to derive the so-called maximally allowable transmission interval (MATI) boundary, under which closed-loop stability is guaranteed. A popular approach to compute this MATI is via the technique presented in [], which provides an explicit expression of the MATI bound based on the system parameters. Let us define , then it holds that
where and . The following Lemma adapts the results presented in [] to LTI hybrid systems (18) for robust stabilization.
Lemma 1.
Proof of Lemma 1.
Let .
Consequently, it holds for all and almost all .
Consequently, it holds that, for all and almost all
By post- and pre-multiplying LMI (22), respectively, by the state vector and its transpose, we obtain
implying that
and the conclusion of Lemma 1 holds. □
Lemma 1 establishes an -gain stability property for the system from to ; see []. Then, according to [], the MATI bound is given by
with and from Lemma 1. To provide some intuition about the bound in [], we define a dynamic variable as follows:
where , comes from Lemma 1 and L, as defined in (21). As such, the upper bound is computed as the time it takes for to decrease from to .
The derivation of the sampling period T is often based on the worst-case scenario, which is conservative. For instance, when the desired stability or performance measure is achieved and no more disturbances affect the plant, it is unnecessary to keep updating the control law with the same sampling frequency as in the stage of transient response. This motivates the event-triggered control idea, where the sampling instants are only generated when needed, according to the system state.
7.2. Static Event-Triggering
Here, we provide an outline of how to create an output feedback event-triggering scenario that preserves the sampled data system’s stability. Preventing the occurrence of the Zeno behavior is one of the primary difficulties dealt with in the design of an ETC, which is particularly difficult when just the output y is measured and the plant is influenced by external disturbances. An effective solution for this problem is to enforce a positive dwell time T on the inter-sampling times; see [,]. In this way, the ETC condition takes the following form:
where are design parameters to be specified later. According to (29), a new transmission instant is only permitted after the passage of time T from the previous triggering instant , such that is satisfied. Consequently, (18) becomes
The enforced minimum time T is as in (27), and the same conditions as in Lemma 1 are required. Then, in view of (25), if we enforce
then it holds that
which ensures that the closed-loop system is -stable. Hence, sets in (30) are defined with and . We have the following results.
Theorem 1.
Proof of Theorem 1.
We consider the following Lyapunov function for all ,
with and , as defined in (25) and (21). We study the continuous- and discrete-time dynamics of .
Let and define ; in view of (18) and the fact that , we obtain
Let , and suppose that , which implies that . Hence, in view of (30) since . Consequently,
where .
When and , we have . As above, in view of Lemma 1 and (28), we obtain
Using the fact that , we obtain
7.3. Dynamic Event-Triggering
The developed ETC in the previous section belongs to the static event-triggering class since the triggering threshold is not a dynamic system. The problem with this static ETC is that it can result in a conservative number of transmissions. To improve the transmission performance, the ETC can be modified to the following dynamic form:
where is a dynamic variable with the following dynamics; see [,]
with functions and given by
with parameters and with for any small . In this case, we need to include the dynamics of in the hybrid model (18). Hence, with a slight abuse of notation, we redefine . Then, the hybrid dynamical system becomes
and the flow and jump sets are modified, based on (39) to
We obtain the following results.
Theorem 2.
Proof of Theorem 2.
Similar to [,], we consider the following Lyapunov function for all
where for with P comes from Lemma 1.
Let . In view of (42) and (43), and because and , we have that
As a result, we deduce that, for all , .
Dynamics of R during flows. We consider two cases.
By using the fact that and since in view of (41), for all and , we have that
Case 2: Let and and, thus, . Then it holds that since for . Hence, in view of (44), for this case, we obtain that . By following similar lines as before, in view of (41), and by using the fact that , we obtain (47). Thus, property (47) holds for all and the -gain stability is guaranteed.
□
8. Results and Discussion
We verify the theoretical results discussed in the previous section by simulating system (4) with the parameters in Table 2 [].

Table 2.
Parameters of DFIG [].
As a result, the following state space matrices are obtained
Then, we apply the developed ETC approaches by following the procedure in Algorithm 1 below.
| Algorithm 1: Guidelines on how to apply the ETC approaches |
| Start |
| 1: Define the wind turbine parameters and compute the matrices in (5) |
| 2: Check controllability and observability |
| If the system is controllable and observable, do: |
| 1: Choose , and compute the controller gain K |
| 2: Choose , and compute the observer gain L |
| 3: Construct the matrices for the hybrid model (18) |
| 4: Check the feasibility of LMI (22) |
| If LMI is feasible, do: |
| 1: Find and compute |
| 2: Set the initial condition and start the simulation |
| End |
We design the controller and the observer gains with , and , and we obtain and . Then, by using the MATLAB environment with the YALMIP toolbox and the SeDuMi solver [], the following values are then obtained from the solution of the LMI condition (22): , , , which leads to , and the MATI bound in (27) was found to be s. Thus, all of the ETC parameters have been established. Then, by using the hybrid equation (HyEQ) toolbox for MATLAB [], simulations of system (18) execute the initial condition for 10 s, with random external disturbances satisfying . The closed-loop response is presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
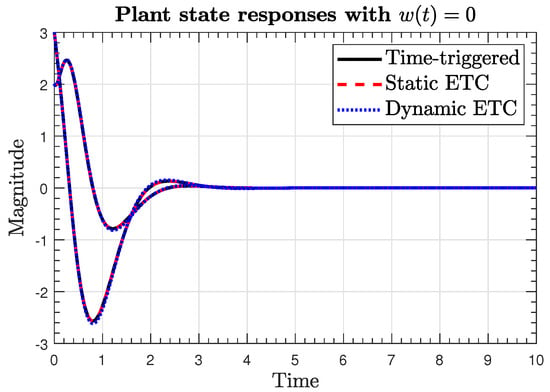
Figure 3.
Plant and observer state trajectories in the absence of disturbances.
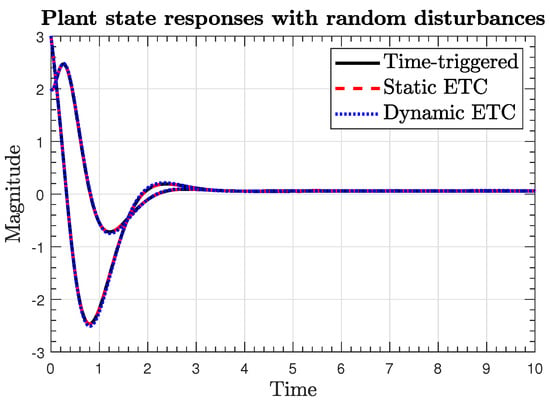
Figure 4.
Plant and observer state trajectories with random disturbances.
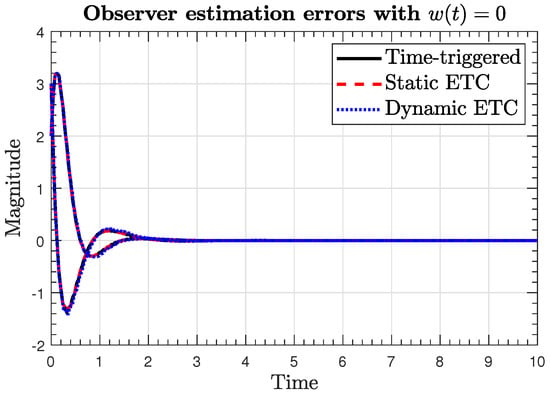
Figure 5.
Trajectories of the estimation errors in the absence of disturbances.
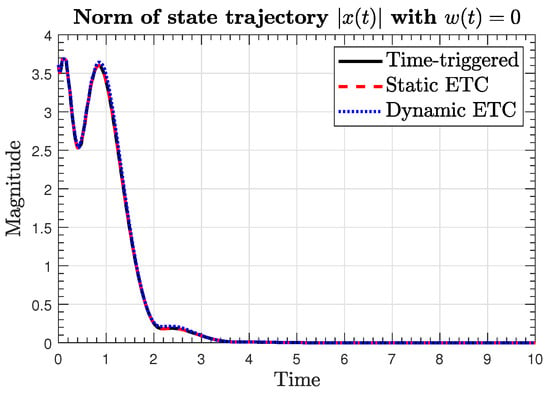
Figure 6.
Norm of the state trajectories in the absence of disturbances.
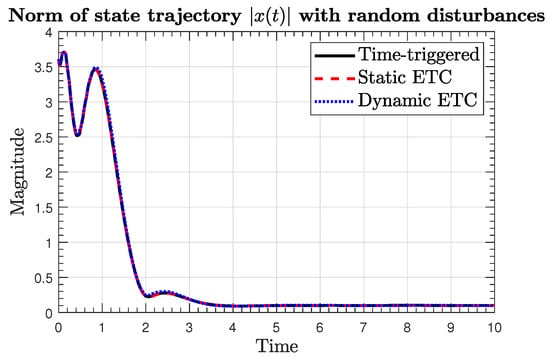
Figure 7.
Norm of the state trajectories in the presence of disturbances.
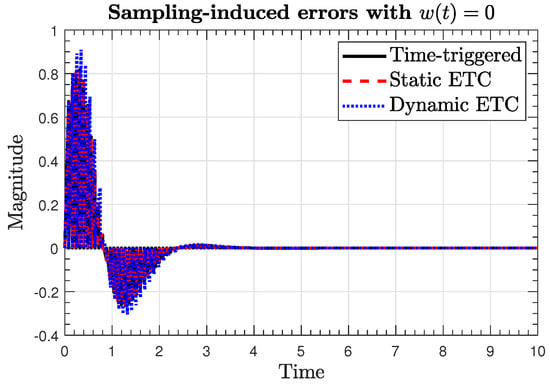
Figure 8.
Sampling-induced errors in the absence of disturbances.
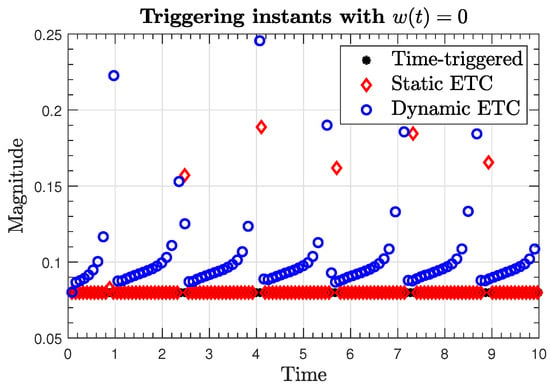
Figure 9.
Inter-transmission times in the absence of disturbances.
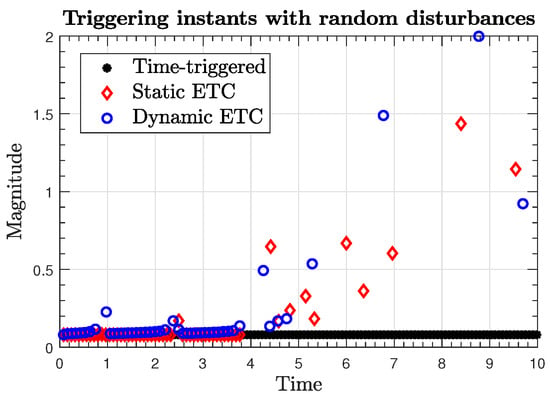
Figure 10.
Inter-transmission times with random disturbances.
Figure 3 and Figure 4 show the plant responses in the absence and presence of external disturbances, respectively, for the three implementation scenarios in Section 7.1, Section 7.2 and Section 7.3. We note that the state responses in the event-triggered implementations (29), (39) are almost identical to the state response in the time-triggered control (19) in terms of the peak overshoot and settling time, implying that the ETC implementation maintains the closed-loop response quality, even with fewer transmissions. We also note that the plant trajectories exhibit large overshoot in the three cases, indicating that the feedback law can be further modified or constructed by other design methods to mitigate such behavior.
Figure 5 presents the estimation error trajectories of the designed observer, which converge to the origin at less than 3 s. This implies that the estimated states approach the actual plant states in a short time.
The norms of the state trajectories in the three implementation scenarios are shown in Figure 6, where we can see that asymptotically converges to the origin, i.e., the global asymptotic stability is achieved when no external disturbances are affecting the plant. On the other hand, when the plant is affected by external disturbances, we can see in Figure 7 that converges to a neighborhood to the origin, as stated by Theorems 1 and 2, i.e., the stability is guaranteed.
Figure 8 shows the sampling-induced errors in the three implementation scenarios, where it can be noted that the sampling errors are reset to zero at any transmission instant, as explained in (14).
The generated sampling times are presented in Figure 9 for the case of , where it can be seen that the generated number of transmissions by the ETC mechanisms (29) and (39) is much less than with the time-triggered control (19). In fact, the simulation results showed that a reduction of more than 50% in the number of transmissions was achieved. Moreover, Figure 9 shows that the dynamic ETC (39) has performs better than the static ETC (29) in terms of reduced transmissions. A similar conclusion can be stated for the generated transmission times in the presence of disturbances, as shown in Figure 10.
Figure 11 reveals the trade-off between the guaranteed gain , the triggering threshold (upper plot), and the enforced minimum sampling period T (lower plot). We see that when the is enlarged, the triggering threshold is increased, which can lead to larger inter-transmission intervals and vice versa; see (30). Hence, this provides a tuning guide for the user according to the desired implementation properties.
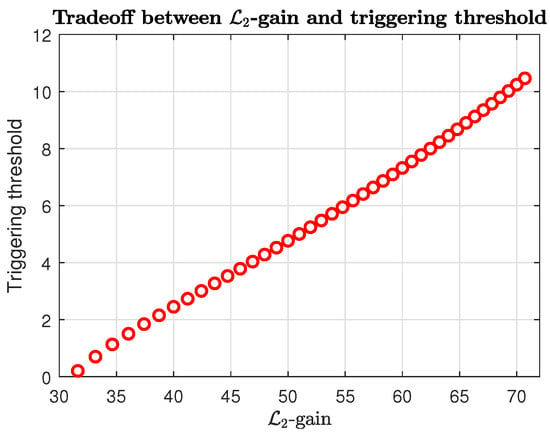
Figure 11.
Trade-off between the gain and the parameters of the ETC mechanism.
To further illustrate the advantage of the proposed approach, a simulation comparison was carried out with [] on the same plant model and with the same plant parameters, as shown in Table 3. The first column of Table 3 shows the number of transmission instants under the time-triggered control, as developed in Section 7.1. Moreover, for static and dynamic ETCs, the proposed approach generates much fewer transmissions than the ETC technique presented in [], which highlights the benefits of the proposed methods.

Table 3.
Comparison with [] on the number of triggering times.
We only performed simulation comparison with [] since a similar DFIG wind turbine model and similar observer-based controllers were studied [], which makes the ETC comparison relevant. In contrast, the approaches presented in [,] considered SMC controllers, and the approach presented in [] considers power regulation controllers based on the multi-agent system method. As such, due to the different control structures and different DFIG wind turbine models in these works, the ETC comparison is not relevant since different feedback laws will result in different transmission performances of the ETC, even with a typical plant model. To further clarify this point, we note that the feedback law directly affects the structure of the closed-loop matrices, , in view of (16). Consequently, this affects the obtained values of the ETC parameters from the feasibility of LMI (22). As a result, the ETC performance will vary with different control structures.
To conclude our discussion, the simulation results in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 demonstrate that the event-triggering strategies (29), (39) produce a closed-loop response comparable to that of periodic time-triggering, while significantly reducing the number of transmissions; this allows for the efficient use of communication resources and highlights the benefits of the developed approaches.
9. Conclusions
In this paper, we examined robust control design for the pitch angle of DFIG ET under ETC implementation. The created method only uses output feedback, guarantees the closed-loop system’s asymptotic stability, and guards against the emergence of Zeno behavior. In order to account for both continuous-time dynamics and discrete transitions, the entire system is described as a hybrid dynamical system. Simulations support the technique’s effectiveness. The outcomes demonstrate that by significantly lowering the number of transmissions, the ETC mechanism outperforms the time-triggered control.
In this paper, we concentrate on output feedback stabilization. In practice, several practical control applications necessitate set point reference tracking for system state/output using common methods, such as PID control, which is an intriguing research area to consider. Future developments of this work might also consider quantization and packet dropouts that arise with digital implementation.
The implementation scenario in this study assumes that only the plant is affected by external disturbances similar to []. The inclusion of measurement noise and transmission delays is important in practice; however, those phenomena induce technical challenges on the stability analysis and require thorough investigation, which will be an interesting extension to this work.
Author Contributions
Conceptualization, M.A.; methodology, M.A.; formal analysis, D.A.; investigation, D.A.; Simulation, M.A.; writing—original draft preparation, M.A.; writing—review and editing, D.A.. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Prince Sultan University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Acronyms | |
| ARE | algebraic Riccati equation |
| ETC | event-triggered control |
| ETM | event-triggering mechanism |
| DFIG | doubly fed induction generator |
| LMI | linear matrix inequality |
| LTI | linear time-invariant |
| LQR | linear quadratic regulator |
| MATI | maximal allowable transmission interval |
| NCS | networked control system |
| RES | renewable energy sources |
| SDC | sampled-data control |
| SMC | sliding mode control |
| WT | wind turbine |
| ZOH | zero-order hold |
| List of Symbols | |
| pitch angle of WT | |
| angular speed of WT | |
| pitch angle command | |
| variation in power demand | |
| variation in wind speed | |
| time constant of WT blade | |
| J | moment of inertia of WT blade |
| load power demand | |
| inertia J at | |
| functions of WT parameters | |
| state vector of WT | |
| control input | |
| external disturbances on WT | |
| measured output of WT | |
| constant matrices of WT model | |
| sampling error | |
| triggering instant | |
| updated values of at | |
| estimated state by observer | |
| threshold constant for static ETC | |
| K | controller gain matrix |
| F | observer gain matrix |
| controllability matrix | |
| observability matrix | |
| J | quadratic cost function |
| controller LQR matrices | |
| observer LQR matrices | |
| dimension of plant state | |
| auxiliary time variable | |
| concatenated state vector | |
| flow set of the hybrid model | |
| jump set of the hybrid model | |
| T | periodic sampling interval |
| MATI bound | |
| dynamic variable to compute | |
| function of the sampling error | |
| Lyapunov function candidates | |
| dynamic ETC variable | |
| , | dynamic ETC functions |
References
- Abulizi, M.; Zhang, C.; Xie, L. Research of current control strategies for doubly-fed wind power generation system. In Proceedings of the 2023 IEEE 6th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 24–26 February 2023; Volume 6, pp. 55–59. [Google Scholar] [CrossRef]
- Ntuli, W.K.; Sharma, G.; Kabeya, M. Development of Grid–Connected Renewable Generation Control Techniques. In Proceedings of the 2022 IEEE PES/IAS PowerAfrica, Kigali, Rwanda, 22–26 August 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Badal, F.; Das, P.; Sarker, S.; Das, S. A survey on control issues in renewable energy integration and microgrid. Prot. Control Mod. Power Syst. 2019, 4, 8. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; El Ouanjli, N.; Mossa, M.A.; Bhaskar, M.S.; Lan, N.K.; Quynh, N.V. A New Robust Direct Torque Control Based on a Genetic Algorithm for a Doubly-Fed Induction Motor: Experimental Validation. Energies 2022, 15, 5384. [Google Scholar] [CrossRef]
- Nadour, M.; Essadki, A.; Nasser, T. Comparative analysis between PI & backstepping control strategies of DFIG driven by wind turbine. Int. J. Renew. Energy Res. 2017, 7, 1307–1316. [Google Scholar]
- Hosseini, E.; Behzadfar, N.; Hashemi, M.; Moazzami, M.; Dehghani, M. Control of Pitch Angle in Wind Turbine Based on Doubly Fed Induction Generator Using Fuzzy Logic Method. J. Renew. Energy Environ. 2022, 9, 1–7. [Google Scholar]
- Abdelmalek, S.; Azar, A.T.; Dib, D. Fuzzy fault-tolerant control for doubly fed induction generator in wind energy conversion system. Int. J. Adv. Intell. Paradig. 2021, 20, 38–57. [Google Scholar] [CrossRef]
- Colombo, L.; Corradini, M.; Ippoliti, G.; Orlando, G. Pitch angle control of a wind turbine operating above the rated wind speed: A sliding mode control approach. ISA Trans. 2020, 96, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Surinkaew, T.; Ngamroo, I. Robust power oscillation damper design for DFIG-based wind turbine based on specified structure mixed H2H∞ control. Renew. Energy 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P.; Abbaszadeh, M.; Wira, P. Nonlinear optimal control for wind power generators comprising a multi-mass drivetrain and a DFIG. J. Frankl. Inst. 2019, 356, 2582–2605. [Google Scholar] [CrossRef]
- Bouchemha, A.; Azar, A.T.; Laatra, Y.; Souaidia, C.; Dib, D. Sensor and sensorless speed control of doubly-fed induction machine. Int. J. Adv. Intell. Paradig. 2021, 19, 194–215. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J. A Super Twisting Fractional Order Terminal Sliding Mode Control for DFIG-Based Wind Energy Conversion System. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ullah, N.; Ro, J. Sensorless fractional order composite sliding mode control design for wind generation system. ISA Trans. 2021, 111, 275–289. [Google Scholar] [CrossRef] [PubMed]
- Torchani, B.; Sellami, A.; Garcia, G. Variable speed wind turbine control by discrete-time sliding mode approach. ISA Trans. 2016, 62, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Djilali, L.; Sanchez, E.N.; Belkheiri, M. Discrete-Time Neural Input Output Feedback Linearization Control for a DFIG based Wind Turbine. In Proceedings of the 2017 6th International Conference on Systems and Control (ICSC), Batna, Algeria, 7–9 May 2017; pp. 57–62. [Google Scholar]
- Ruiz-Cruz, R.; Sanchez, E.N.; Ornelas-Tellez, F.; Loukianov, A.G.; Harley, R.G. Particle Swarm Optimization for Discrete-Time Inverse Optimal Control of a Doubly Fed Induction Generator. IEEE Trans. Cybern. 2013, 43, 1698–1709. [Google Scholar] [CrossRef]
- Solís-Chaves, J.S.; Rodrigues, L.L.; Rocha-Osorio, C.M.; Filho, A.J.S. A long-range generalized predictive control algorithm for a DFIG based wind energy system. IEEE/CAA J. Autom. Sin. 2019, 6, 1209–1219. [Google Scholar] [CrossRef]
- Tohidi, A.; Hajieghrary, H.; Hsieh, M. Adaptive Disturbance Rejection Control Scheme for DFIG-Based Wind Turbine: Theory and Experiments. IEEE Trans. Ind. Appl. 2016, 52, 2006–2015. [Google Scholar] [CrossRef]
- Baillieul, J.; Antsaklis, P. Control and communication challenges in networked real-time systems. Proc. IEEE 2007, 95, 9–28. [Google Scholar] [CrossRef]
- Cloosterman, M.; Hetel, L.; van de Wouw, N.; Heemels, W.; Daafouz, J.; Nijmeijer, H. Controller synthesis for networked control systems. Automatica 2010, 46, 1584–1594. [Google Scholar] [CrossRef]
- Heemels, W.; Teel, A.; van de Wouw, N.; Nešić, D. Networked Control Systems with Communication Constraints: Tradeoffs between Transmission Intervals, Delays and Performance. IEEE Trans. Autom. Control 2010, 55, 1781–1796. [Google Scholar] [CrossRef]
- Forni, F.; Galeani, S.; Nešić, D.; Zaccarian, L. Event-triggered transmission for linear control over communication channels. Automatica 2014, 50, 490–498. [Google Scholar] [CrossRef]
- Abdelrahim, M.; Postoyan, R.; Daafouz, J.; Nešić, D. Event-triggered dynamic feedback controllers for nonlinear systems with asynchronous transmissions. In Proceedings of the 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 5494–5499. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B.; Cucuzzella, M.; Ferrara, A.; Yu, X. A Survey on Event-Triggered Sliding Mode Control. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 206–217. [Google Scholar] [CrossRef]
- Fu, A.; Mazo, M., Jr. Decentralized periodic event-triggered control with quantization and asynchronous communication. Automatica 2018, 94, 294–299. [Google Scholar] [CrossRef]
- Li, F.; Fu, J.; Du, D. An improved event-triggered communication mechanism and control co-design for network control systems. Inf. Sci. 2016, 370-371, 743–762. [Google Scholar] [CrossRef]
- Dolk, V.; Abdelrahim, M.; Heemels, W. Event-triggered Consensus Seeking under Non-uniform Time-Varying Delays. IFAC-PapersOnLine 2017, 50, 10096–10101. [Google Scholar] [CrossRef]
- Dolk, V.; Borgers, D.; Heemels, W. Dynamic Event-triggered Control: Tradeoffs Between Transmission Intervals and Performance. In Proceedings of the IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2764–2769. [Google Scholar]
- Goebel, R.; Sanfelice, R.; Teel, A. Hybrid Dynamical Systems: Modeling, Stability, and Robustness; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Abdelrahim, M.; Cucuzzella, M.; Almakhles, D. Output Feedback Event-triggered Control of Doubly Fed Induction Generators For Wind Turbines. In Proceedings of the 11th International Conference on Smart Grid (icSmartGrid 2023), Paris, France, 5–7 June 2023. [Google Scholar] [CrossRef]
- Nafiz Musarrat, M.; Fekih, A. Event-Triggered robust control scheme for sub-synchronous resonance mitigation in DFIG-based WECS. Int. J. Electr. Power Energy Syst. 2023, 148, 109006. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Z.; Dong, Y.; Jiang, S.; Ding, Z. Fully-Distributed Deloading Operation of DFIG-Based Wind Farm for Load Sharing. IEEE Trans. Sustain. Energy 2021, 12, 430–440. [Google Scholar] [CrossRef]
- Xiong, L.; Li, J.; Li, P.; Huang, S.; Wang, Z.; Wang, J. Event-triggered prescribed time convergence sliding mode control of DFIG with disturbance rejection capability. Int. J. Electr. Power Energy Syst. 2021, 131, 106970. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Memon, A. Asynchronous sampled-data approach for event-triggered systems. Int. J. Control 2017, 90, 2508–2516. [Google Scholar] [CrossRef]
- Li, B.; Hu, S.; Zhong, Q.; Shi, K.; Zhong, S. Dynamic memory event-triggered proportional-integral-based H∞ load frequency control for multi-area wind power systems. Appl. Math. Comput. 2023, 453, 128070. [Google Scholar] [CrossRef]
- Fazeli, M.; Asher, G.; Klumpner, C.; Yao, L. Novel integration of DFIG-based wind generators within microgrids. IEEE Trans. Energy Convers. 2011, 26, 840–850. [Google Scholar] [CrossRef]
- Nešić, D.; Teel, A.; Carnevale, D. Explicit Computation of the Sampling Period in Emulation of Controllers for Nonlinear Sampled-Data Systems. IEEE Trans. Autom. Control 2009, 54, 619–624. [Google Scholar] [CrossRef]
- Carnevale, D.; Teel, A.; Nešić, D. A Lyapunov proof of an improved maximum allowable transfer interval for networked control systems. IEEE Trans. Autom. Control 2007, 52, 892–897. [Google Scholar] [CrossRef]
- Abdelrahim, M.; Postoyan, R.; Daafouz, J. Event-triggered control of nonlinear singularly perturbed systems based only on the slow dynamics. In Proceedings of the IFAC Symposium on Nonlinear Control Systems, Toulouse, France, 4–6 September 2013; pp. 347–352. [Google Scholar] [CrossRef]
- Abdelrahim, M.; Dolk, V.; Heemels, W. Input-to-state stabilizing event-triggered control for linear systems with output quantization. In Proceedings of the 55th IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 2016; pp. 483–488. [Google Scholar] [CrossRef]
- Dolk, V.; Borgers, D.; Heemels, W. Output-based and decentralized dynamic event-triggered control with guaranteed -gain performance and Zeno-freeness. IEEE Trans. Autom. Control 2017, 62, 34–49. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar] [CrossRef]
- Sanfelice, R.G.; Copp, D.; Nanez, P. A toolbox for simulation of hybrid systems in MATLAB/SIMULINK: Hybrid equations (HyEQ) toolbox (HSCC). In Proceedings of the 16th international conference on Hybrid systems: Computation and Control, Philadelphia, PA, USA, 8–11 April 2013; pp. 101–106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).