Abstract
There are many different fields in which wireless sensor networks (WSNs) can be used such as environmental monitoring, healthcare, military, and security. Due to the vulnerability of WSNs, reliability is a critical concern. Evaluation of a WSN’s reliability is essential during the design process and when evaluating WSNs’ performance. Current research uses the reliability block diagram (RBD) technique, based on component functioning or failure state, to evaluate reliability. In this study, a new methodology-based RBD, to calculate the energy reliability of various proposed chain models in WSNs, is presented. A new method called D-Chain is proposed, to form the chain starting from the nearest node to the base station (BS) and to choose the chain head based on the minimum distance D, and Q-Chain is proposed, to form the chain starting from the farthest node from the BS and select the head based on the maximum weight, Q. Each chain has three different arrangements: single chain/single-hop, multi-chain/single-hop, and multi-chain/multi-hop. Moreover, we applied dynamic leader nodes to all of the models mentioned. The simulation results indicate that the multi Q-Chain/single-hop has the best performance, while the single D-Chain has the least reliability in all situations. In the grid scenario, multi Q-Chain/single-hop achieved better average reliability, 11.12 times greater than multi D-Chain/single-hop. On the other hand, multi Q-Chain/single-hop achieved 6.38 times better average reliability than multi D-Chain/single-hop, in a random scenario.
1. Introduction
Multiple sensor nodes make up a wireless sensor network (WSN), where these nodes can sense, measure, gather, and transmit information from the environment via radio. In a wide range of applications, such as healthcare, industrial control, public security, commercial, military, and environmental monitoring, WSNs are widely used [1,2,3]. A WSN has limited storage, battery, and processing capacity, which affects the network lifetime, quality of service, and cost [4,5]. Furthermore, data collection and transmission in WSNs may be affected by attacks or interference in harsh environments. Therefore, a WSN’s reliability is an important issue, to be sure that the WSN works properly. It is essential to calculate WSN reliability, to minimize the cost, minimize the node power consumption, and maximize the network lifetime, as unreliable WSNs may fail to accomplish the tasks, resulting in inefficient use of sensor resources [6]. The reliability of the WSN can be evaluated using various methods such as Markov chain theory, universal generating function (UGF), a Monte Carlo (MC) simulation approach, a reliability block diagram (RBD), fault tree (FT) [7], and a signal strength and trust model [8].
The routing issue in transferring data from the source node to the target node is one of the most significant challenges facing WSNs. Existing routing protocols can be classified into single-hop and multi-hop, where in single-hop, the data is directly sent from the node to the base station (BS), while the data is sent to the BS through several nodes in multi-hop [5]. Multi-hop routing protocols fall into two main categories based on the network structure: hierarchical and flat [9,10,11]. In the flat routing protocol, all nodes perform the same task and function. Whereas in hierarchical routing protocols, different tasks and functions are assigned to the nodes [10,12,13,14]. The three main types of the flat routing protocol are: proactive (table-driven), reactive (source-initiated), and hybrid [10]. RPL, Hydro, CPT, and Zigbee are the most popular proactive routing protocols [15,16]. LOAD, LOADng, AODVbis, and Tiny AODV are some examples of reactive routing protocols [15,16,17]. Moreover, zone routing is an example of hybrid routing protocols. Figure 1 illustrates the three main types of hierarchical routing protocols: cluster-based, tree-based, and chain-based [2,5,9,13,18].
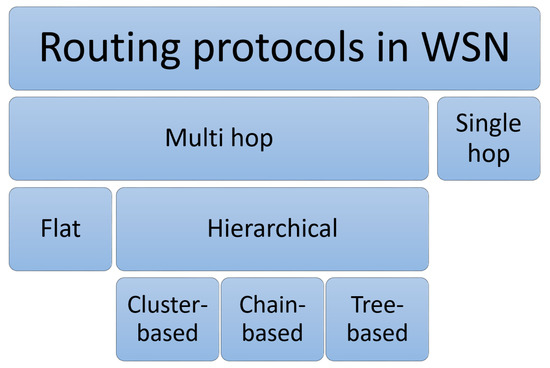
Figure 1.
Routing protocols in WSN.
In cluster-based routing [19,20,21,22], each cluster has at most one cluster head (CH) that manages the cluster, while other nodes are called cluster members (CMs), as illustrated in Figure 2, where the CMs send the collected data to the CH and do not directly communicate with the BS. In the WSN, the BS serves as both the central data-collecting node and the common destination for data gathered from the nodes. There are usually no power restrictions on the BS, which acts as a bridge between WSN and the end user (via communication). The most popular cluster-based routing protocol is the low-energy adaptive clustering hierarchy (LEACH) [13].
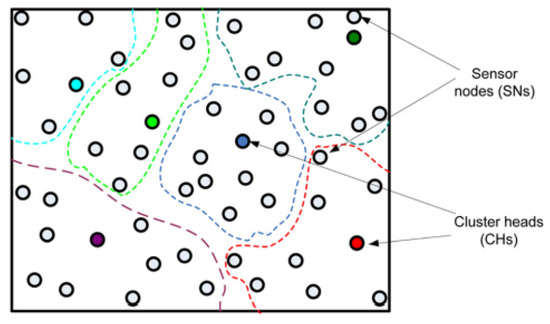
Figure 2.
Cluster-based WSN (each cluster is depicted in a distinct color).
As shown in Figure 3, the tree-based topology deploys nodes in a logical tree configuration, with all sensor data being transferred from leaf nodes (children) to their respective parents [12,18].
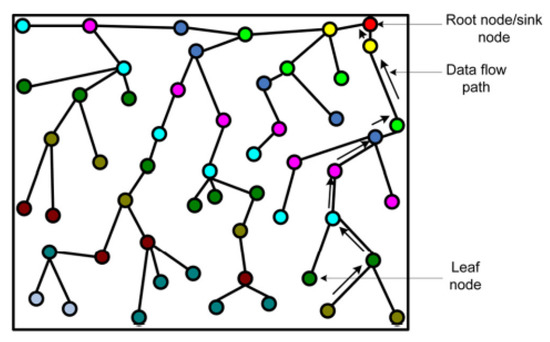
Figure 3.
Tree-based WSN (distinct colors are used to represent each tree level).
An appropriate neighbor node is selected as the parent node for every node in a tree-based approach. A routing tree is constructed with a sink node that acts as a root node, and all nodes are connected to the root through the most energy-saving path [23]. The sensor node’s data is transmitted along the tree towards the root node (sink) and is fused between nodes. There are different tree-based routing protocols such as energy-aware data aggregation tree (EADAT), balanced aggregation tree routing (BATR), power-efficient data gathering and aggregation protocol (PEDAP), and enhanced tree routing (ETR) [18].
On the other hand, chain-based topology arranges nodes to form and construct chains, where each chain has a chain leader and sensor nodes, as shown in Figure 4 [9]. In WSN, a chain can be built either by the nodes themselves, using a greedy strategy, or by the BS, which will calculate and broadcast the chain to all nodes. Single chains or multi-chains can be constructed in chain-based routing. Chain-based routing is simpler to configure and maintain than cluster-based routing [13,18]. Furthermore, local communication conserves energy compared to cluster-based routing, since nodes only transmit data to nearby nodes (i.e., their next nearest neighbor nodes) [12,18,24]. There are various protocols and algorithms that can be implemented based on chain routing, such as power efficient gathering in sensor information systems (PEGASIS), concentric clustering scheme (CCS), balanced chain-based routing protocol (BCBRP), and rotation PEGASIS-based (RPB) [2,13,18]. However, the most popular protocol is PEGASIS, where a chain is constructed from the farthest node from the BS, followed by the closest not-connected neighbor node, and so on [13]. The chain head is responsible for data aggregation and data processing. Therefore, a new chain head can be selected randomly in the event that the current chain head fails.
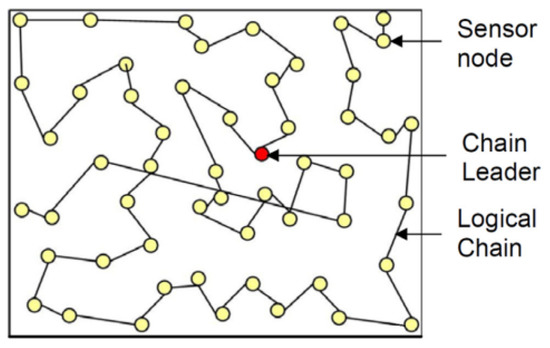
Figure 4.
Chain-based WSN (the color yellow is used to represent sensor nodes, whereas the color red is used to represent the chain leader).
In this paper, we focus on hierarchical routing protocols that are categorized according to the network structure, particularly chain-based routing protocols. There are a number of applications that benefit from chain-based topology, including monitoring coal mine gas, periodic monitoring of building conditions, wind power, parking management systems, IoT-WSN-based smart agricultural environments, and underwater smart things. Furthermore, a chain-based topology can be applied as part of a fog-supported WSN, along with other topologies [9,25]. This work proposes various chain configurations and evaluates the system reliability of different proposed chain-based routing models, based on the proposed RBD in WSN. The power consumption for each node is the main factor that is considered to evaluate the system’s reliability. The main contributions of this work are summarized below:
- Various chain-based routing models are considered and discussed.
- Chain head selection approaches that are based on weight Q, or distance D, are investigated and evaluated.
- We propose a new RBD-based methodology, to evaluate the reliability of different chain-based routing models in cases of fixed and dynamic chain head settings, where the node reliability is evaluated based on energy.
The work in this paper is presented as follows: Section 2 presents the related work. The background of the reliability block diagram is illustrated in Section 3. The proposed model is presented in Section 4. Section 5 discusses the experimental setup and results, and Section 6 gives the conclusions of our proposed work.
2. Related Work
This section demonstrates the previous studies regarding evaluating the system reliability of WSNs. The different techniques for evaluating WSN reliability are discussed. Moreover, analyzing and calculating WSN reliability-based RBD is illustrated.
Studies, evaluations, and analyses of WSNs’ reliability have been previously carried out in several studies [26,27]. Evaluation of the reliability of a WSN can be conducted utilizing different techniques, of which the most well-known are a universal generating function [28], a Markov model [29], a fault tree [30], and a Monte Carlo simulation [31], where the authors utilized an ordered binary decision diagram (OBDD) beside a Monte Carlo simulation, to evaluate the WSN’s reliability. The authors of [32] proposed a Monte Carlo Markov chain simulation method to evaluate the reliability, regarding data capacity and coverage area, of mobile WSNs with multi-state nodes, but the power consumption was not taken into account. A Markov model was proposed in [33], to address the reliability of sensor nodes in a WSN-based monitoring strategy, but power consumption was not considered. A modified sum of disjoint products approach was proposed in [34], for evaluating the reliability of WSN with multi-state nodes, where the reliability was evaluated based on the network’s dynamic state only. The reliability evaluation of WSNs and compromised node identification was described in [8], where an enhanced way of evaluating reliable nodes was proposed to protect the entire WSN from compromised nodes. A new efficient algorithm-based OBDD was proposed in [6], to evaluate WSN reliability, where the proposed approach executed the recursive construction of OBDD once. A new sum of disjoint products technique (SDP) was proposed in [35] to generate disjoint products and calculate the network reliability. Moreover, probabilistic analysis was utilized to evaluate the network transmission reliability in [36], where the required retransmission was decreased and the transmission reliability was improved.
The reliability block diagram paradigm (RBD), is one of the most useful techniques to calculate reliability [37,38]. The reliability was evaluated via RBD in the following studies: RBD was applied in [37], to analyze the reliability of a mesh network that consisted of different tree and star networks and was classified as a series–parallel system. The authors of [39] evaluated the reliability of star and cluster WSNs with dynamic dependent nodes based on dynamic RBD (DRBD), where it overcame the Markov model’s limitations because it considered nonlinear discharge processes. Furthermore, the author in [40] calculated the reliability of star, cluster, and mesh WSNs, with sleep/wake-up interfering nodes-based DRBD and Petri nets, which overcame the Markov model’s limitations according to nonlinear processes. Since RBD overcomes the limits of the Markov model, RBD is utilized to evaluate WSNs’ reliability in [5], considering the DIRECT, FLOODING, and LEACH routing algorithms and battery level. In [41], the reliability of a mesh WSN was analyzed and evaluated, based on RBD and fault tree analysis. Moreover, the authors studied the effects of way redundancy and node arrangements on reliability. The authors in [42] analyzed the reliability of WSN data transport protocols based on RBD and the higher-order logic theorem prover.
Reliability is an important factor to consider when evaluating the performance of WSNs since it can be evaluated according to network power, where a dead sensor node is unable to transmit data and affects the entire system. The reliability of different network topologies in WSN-based RBD has been evaluated in a range of studies, except for chain routing, which has not been examined in any studies. All published works have assumed the same concept of probability, where probability is 1 for a working node and 0 for a failure node. However, in our proposed RBD, the probability of each node is evaluated based on the ratio between the residual energy and the initial energy of the node. Moreover, all the previous research assumes that the system fails in series configuration if any node fails, while our proposed RBD continues the reliability evaluation until the chain head dies, in the case of a stationary chain head, or till the network dies, in the case of a dynamic chain head.
3. Reliability Block Diagram (RBD)
RBD is a technique for evaluating the reliability of a whole system. All the components of a system are represented graphically, and their reliability determines the overall system’s reliability. A block indicates whether a component is working or not, so the reliability depends on the configurations of the components [41]. A series configuration, a parallel configuration, and a combined (hybrid) configuration are the most commonly used configuration types, as shown in Figure 5, Figure 6 and Figure 7, respectively [5]. Whenever a component fails in a series configuration, the entire system fails. Thus, the least reliable component is the one that has the most impact on the overall reliability. Therefore, the reliability of a system in series is lower than the reliability of the least reliable component.

Figure 5.
RBD organized in series.
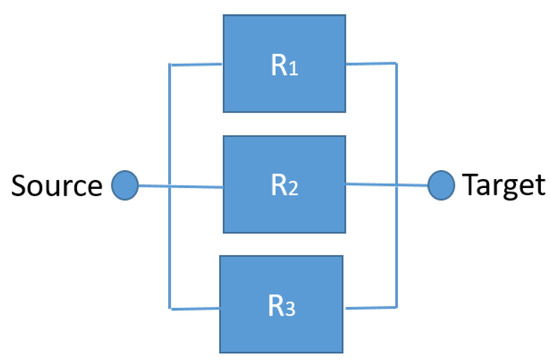
Figure 6.
RBD organized in parallel.
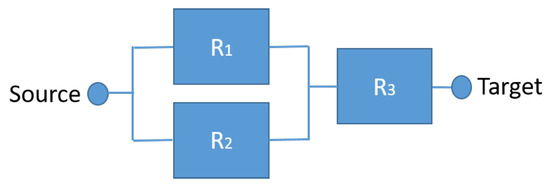
Figure 7.
RBD organized in a hybrid configuration.
In a series system, reliability is defined as the product of the reliability of the components that make it up (series reliability = R1 × R2 × R3), where R1, R2, and R3 represent the working reliability of components 1, 2, and 3, respectively [43]. For a parallel system to function properly, at least one unit must function.
In a parallel configuration, the system reliability is largely affected by the item characterized by the highest reliability trend, where the system reliability is derived from the complement of the product of the reliability of each component (parallel reliability = 1 − ((1 − R1) × (1 − R2) × (1 − R3))) [43].
In a hybrid configuration, combining blocks creates other formats: series–parallel, parallel–series, bridge, and k-out-of-n. In order to solve the reliability problem, the parallel blocks must first be solved, and then the series blocks (hybrid reliability = R3 × (1 − ((1 − R1) × (1 − R2)))).
4. Proposed Algorithm for Reliability Computing of Chain Routing Protocols in WSN
In this section, we present the radio energy model, simulation parameters, reliability evaluation based RBD, chain head selection, chain formation, and reliability calculation methods used in our work.
4.1. Radio Energy Model
We employ a first-order radio model to calculate energy consumption in data transmission, by sensors with the parameters shown in Table 1. Based on the distance between the transmitter and receiver , attenuation is used if d is less than a specific threshold distance , and attenuation is used if d is greater than . The dissipated power can be calculated as follows:
where, and are the powers consumed by the transmitter and receiver, respectively [44,45]. According to the first-order radio model, nJ/bit is consumed by the radio to run the transmitter or receiver circuitry, and J, pJ/bit/m, pJ/bit/m, and are required for the transmitter amplifier, where, k is the number of bits and d is the distance in meters. Transmitter circuitry also consumes nJ/bit, to aggregate the data received by the child nodes. Each sensor compresses the received bits by a data aggregation () factor of 0.6, using distributed compressive sampling.

Table 1.
Parameter settings.
4.2. Reliability Evaluation Based RBD
RBD evaluates the system reliability, where a block indicates whether the node is functioning or not. In our proposed RBD, the chain excludes the failed node and continues the system reliability evaluation until the network dies, in the case of a mobile leader node system, or until the leader node dies, in the case of a stationary leader node system. The energy of each node is considered the key to the energy system reliability evaluation, since R1, R2, and R3, discussed previously, do not indicate a working or failure node in our proposed technique, but they indicate the energy of each working node with respect to the initial energy. The series reliability can be evaluated through the product of each working node’s energy,
while the parallel reliability can be evaluated by the complement of the product of the energy reliability of each working node,
where R represents the reliability, i is the iteration, n indicates the node, refers to the number of nodes in the chain, and , where indicates the node energy. In a hybrid architecture, the system reliability can be evaluated by calculating the parallel reliability followed by the series reliability.
4.3. Chain Head Selection
- Chain head selection based on weight Q: In single-chain formation, the BS chooses the chain head (CH) based on the weight Q assigned to each node (Q-Chain). Each node computes its weight Q, by dividing its residual energy by its distance from the BS, as described in Equation (5). The BS compares the weights of all the nodes in the chain and judges the node with the highest weight as a CH. Each node i, is transferring the data to parent nodes, and then the CH sends the collected data to the sink. In multi-chain single-hop routing, the BS selects one CH for each chain, and the CHs send the collected data to the BS. On the contrary, in multi-chain multi-hop routing, the leader node (LN) is selected from the CHs based on the highest Q. The CHs send the collected data to the LN, and the LN sends the data to the BS.where, E denotes the residual energy of sensor node i, while indicates the distance between sensor node i and the sink.
- Chain head selection based on distance D: In single-chain formation, the BS chooses the CH based on distance D (D-Chain), where each node computes its distance from the BS. The BS compares the distances of all the nodes in the chain and the node that has the lowest distance is assigned as a CH. Each node i, transfers the data to parent nodes, then the CH sends the collected data to the BS. In multi-chain single-hop routing, the BS selects one CH for each chain, and the CHs send the collected data to the BS. While in multi-chain multi-hop routing, the LN is selected from the CHs based on the lowest D. The CHs send the collected data to the LN, and then the LN sends the data to the sink.
4.4. Chain Formation
- Q-Chain formation: The distance between each node and the BS is calculated. The last node in the chain is selected as the farthest node from the BS. To select the previous node, the distances of all nodes to the last node are evaluated, and the nearest node to the last node is chosen as the previous node in the chain formation, and so on.
- D-Chain formation: The distance to the BS for each node is calculated. The first node in the chain is selected based on the node’s nearest distance, which will be the CH. To select the next node in the chain, the distances of all nodes to the first node are evaluated, and the nearest node to the first node is chosen as the next node in the chain formation, and so on.
The chain excludes any failure node and rearranges the parents and children of the previous node and the next node of the failure node in the chain, as illustrated in Figure 8. For more clarification, assume node C is the failure node, then, the parent of node C (node B) becomes the parent of node D and the children of node C (node D) become children of node B. Figure 9 illustrates different suggested models. The models under consideration are illustrated below:
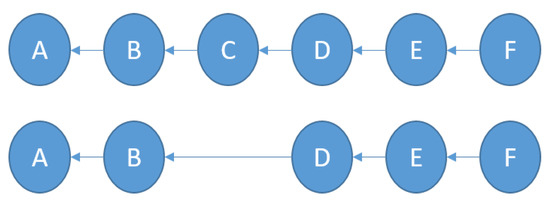
Figure 8.
Chain formation.
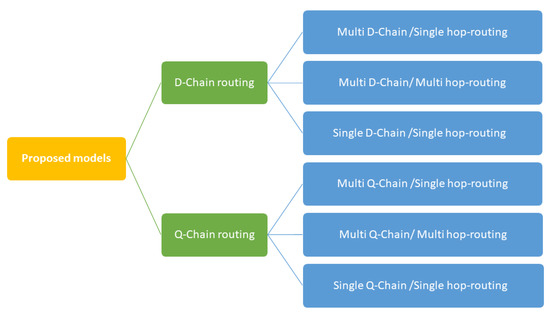
Figure 9.
Proposed models.
- -
- Single D-Chain routing (SD-Chain): series configuration, where both the CH and sensor nodes are placed in series, as illustrated in Figure 10, where the red node is the CH and the blue nodes are the chain members (CM).
 Figure 10. SD-Chain formation.
Figure 10. SD-Chain formation. - -
- Single Q-Chain routing (SQ-Chain): hybrid configuration, where the CH is placed in series with two subsystems of sensor nodes that are placed in parallel, as presented in Figure 11.
 Figure 11. SQ-Chain formation.
Figure 11. SQ-Chain formation. - -
- Multi D-Chain single-hop routing (MD-Chain-SH): hybrid configuration, where the CHs of chains are placed in parallel to each other, while sensor nodes are placed in series with their CH, as shown in Figure 12.
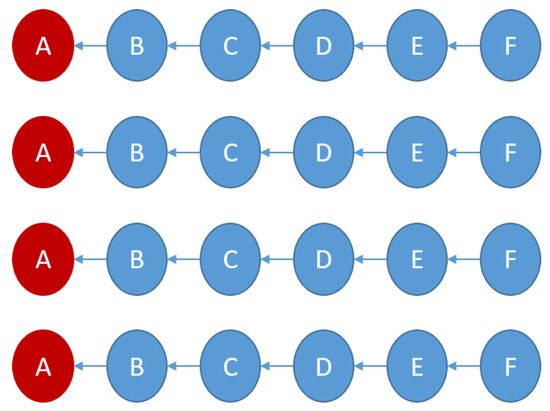 Figure 12. MD-Chain-SH formation.
Figure 12. MD-Chain-SH formation. - -
- Multi Q-Chain single-hop routing (MQ-Chain-SH): Figure 13 presents a hybrid configuration, where the CHs of the chains are placed in parallel to each other, while the CH is placed in series with two subsystems of sensor nodes that are placed in parallel.
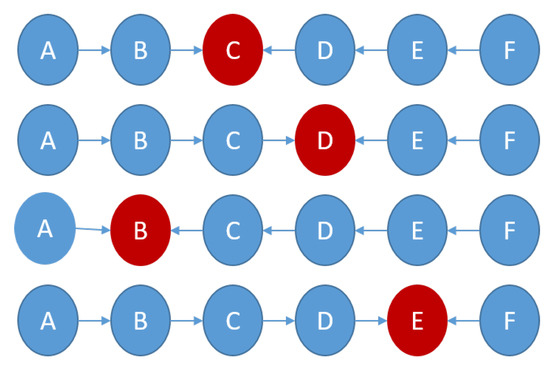 Figure 13. MQ-Chain-SH formation.
Figure 13. MQ-Chain-SH formation. - -
- Multi D-Chain multi-hop routing (MD-Chain-MH): hybrid configuration, where the LN is placed in series with its sensor nodes and the CHs, that are placed in parallel; it is illustrated in Figure 14, where the LN is the green node. Moreover, each CH and its sensor nodes are placed in series.
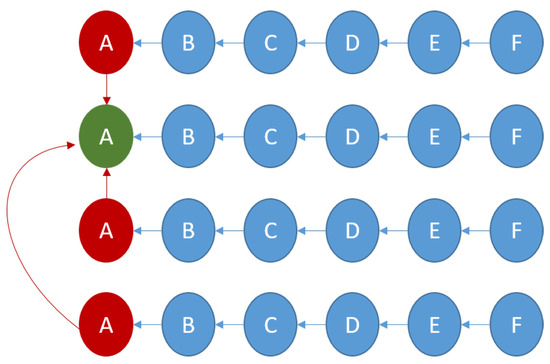 Figure 14. MD-Chain-MH formation.
Figure 14. MD-Chain-MH formation. - -
- Multi Q-Chain multi-hop routing (MQ-Chain-MH): hybrid configuration, where the LN is placed in series with its sensor nodes and the CHs, that are placed in parallel. Moreover, each CH and its sensor nodes are placed in series, while the two subsystems of sensor nodes are placed in parallel, as shown in Figure 15.
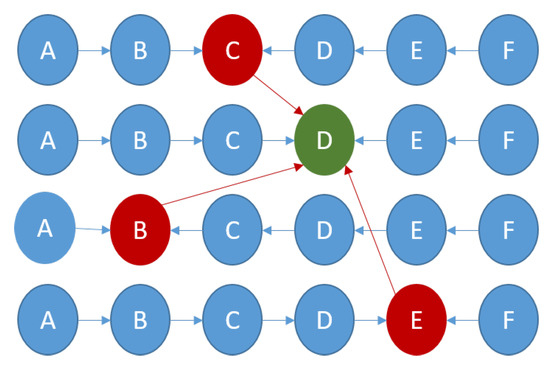 Figure 15. MQ-Chain-MH formation.
Figure 15. MQ-Chain-MH formation.
4.5. Proposed Reliability Calculation
This section explains the calculation of the RBD for the various proposed models that are illustrated previously in Section 4.4. The reliability of these models, based on stationary or mobile CHs, is calculated as follows:
- -
- SD-Chain: in this configuration, the chain members are connected to each other serially and the reliability calculation relies on the series reliability that is explained in Section 4.2. Moreover, the reliability calculation depends on the CH energy; while the CH or the network is alive, continue the reliability calculation, as illustrated in Algorithm 1.
- -
- SQ-Chain: in this model, the CH could be anywhere through the chain, since it is selected based on Q. The chain may divide into two serial chains, where each chain ends at the CH. While the chain member does not reach the alive CH, calculate the reliability for both chains serially. Both chains are parallel, so calculate the parallel reliability, then the series with the CH, as shown in Algorithm 2.
- -
- MD-Chain-SH: the SD-Chain is divided into multiple serial chains, and the nodes of each chain are arranged serially with their CH. Each chain calculates the series reliability with the CH, then calculates the parallel reliability for all chains that are parallel to each other, as clarified in Algorithm 3.
- -
- MQ-Chain-SH: the MQ-Chain has the same node arrangement as the SQ-Chain discussed above, but for multi-chains instead of a single chain. However, calculating the reliability for MQ-Chain-SH has the same steps as calculating the reliability of SQ-Chain, in addition to one more step that calculates the parallel reliability for all multi-chains, as explained in Algorithm 4.
- -
- MD-Chain-MH: this model has multiple D-Chains, while each chain has one CH that collects the data from its chain members, the whole chain has one LN that collects the data from the CHs. Algorithm 5 clarifies the reliability calculation for MD-Chain-MH. Each chain calculates the reliability serially for the chain nodes and then calculates the series reliability for the chain with the CH, if the CH is not the LN. Calculate the parallel reliability for all chains, then calculate the reliability serially with LN.
- -
- MQ-Chain-MH: in this configuration, each chain has a CH, and the whole network has an LN. This model has multiple Q-Chains, where the reliability for each chain is calculated in series and then parallel until it arrives at the CH. If the CH is not the LN, then calculate the reliability of the chain serially with the CH. Finally, calculate the parallel reliability of whole chains and then series reliability with the LN, as described in Algorithm 6.
| Algorithm 1 Calculate reliability of SD-Chain. |
|
| Algorithm 2 Calculate reliability of SQ-Chain. |
|
| Algorithm 3 Calculate reliability of MD-Chain-SH. |
|
| Algorithm 4 Calculate reliability of MQ-Chain-SH. |
|
| Algorithm 5 Calculate reliability of MD-Chain-MH. |
|
| Algorithm 6 Calculate reliability of MQ-Chain-MH. |
|
5. Experimental Setup and Results
The simulation of the chain reliability-based RBD proposed, is conducted utilizing MATLAB R2022a software, on an Intel(R) Xeon(R) W-2145 CPU @3.70 GHz 3.70 GHz computer processor. In this section, we present the simulation results for our proposed work, in order to determine its performance by considering the average reliability of 20 runs. In this section, two types of chain-based stationary CH and mobile CH are evaluated. Single-chain, multi-chain/single-hop, and multi-chain/multi-hop models are evaluated, for both CH cases and both chain models (Q-Chain and D-Chain). Chain formation of 100 nodes, based on Q and D for a single chain, is presented in Figure 16, while chain formation of 100 nodes and 4 chains, based on Q and D for a multi-chain/single-hop and a multi-chain/multi-hop, are presented in Figure 17 and Figure 18, respectively.
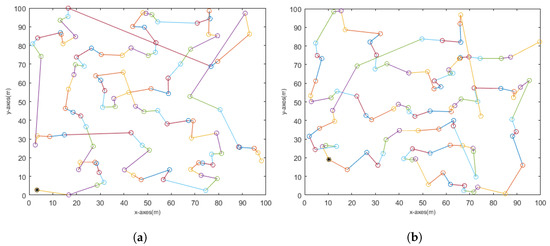
Figure 16.
Single-chain formation: (nodes are represented using various colors, while ❋ is used to represent the CH) (a) D-Chain, (b) Q-Chain.
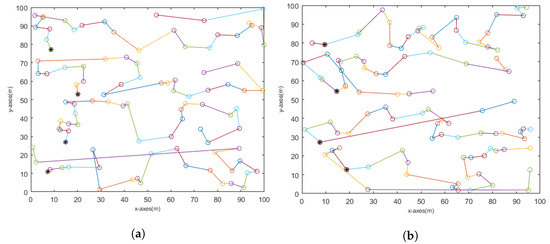
Figure 17.
Multi-chain single-hop formation: (nodes are represented using different colors, while ❋ represents the CH). (a) D-Chain, (b) Q-Chain.
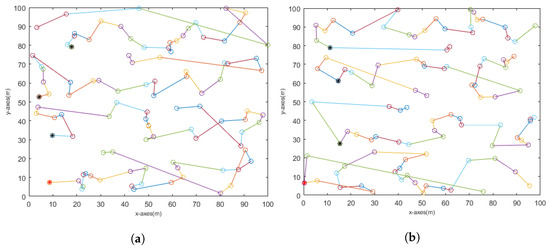
Figure 18.
Multi-chain multi-hop formation: (nodes are depicted using a range of colors, whereas the CH is symbolized by ❋ and the LN is symbolized by ❋). (a) D-Chain, (b) Q-Chain.
5.1. Experimental Parameters
We consider a 100 m × 100 m area for a WSN with 100 sensor nodes and a BS placed at . Single chain and multi-chain are the two assumed different configurations, where a single chain has 100 nodes and a multi-chain has 4 chains with 25 nodes in each. We propose two scenarios for arranging the nodes as follows:
- Grid scenario: the area is divided equally into four areas, where the nodes are randomly distributed in 100 m × 25 m, in a chain. For more clarification, nodes in the region are randomly distributed in the ranges 0–25, 26–50, 51–75, and 76–100 in the y-axis, among regions 1, 2, 3, and 4, respectively.
- Random scenario: the nodes are randomly distributed among 100 m × 100 m, regardless of the chain configuration.
5.2. Simulation Results
The reliability evaluations of D-Chain and Q-Chain, in the case of stationary CH for the proposed models, are illustrated in Figure 19, Figure 20 and Figure 21. It is apparent across all models, that the D-Chain exhibits the poorest reliability performance, which utilizes distance as the sole criterion for selecting the CH and LN. Furthermore, this distance-centric approach overlooks the consideration of remaining energy levels, leading to low reliability. Conversely, the Q-Chain outperforms the D-Chain, due to its incorporation of both distance and energy as parameters in the CH selection process, resulting in superior reliability performance.
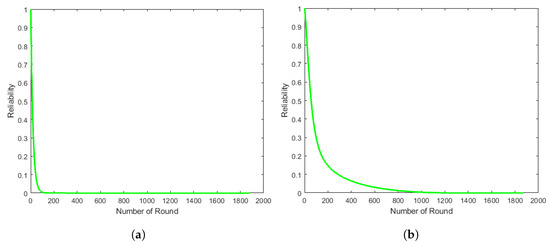
Figure 19.
Single-chain stationary CH energy reliability-based proposed RBD: (a) D-Chain, (b) Q-Chain.
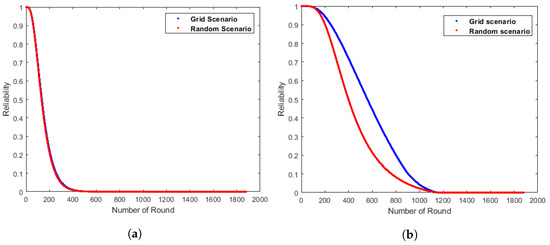
Figure 20.
Multi-chain single-hop stationary CHs energy reliability-based proposed RBD: yellow (a) D-Chain, (b) Q-Chain.
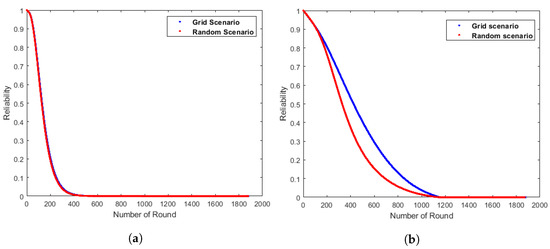
Figure 21.
Multi-chain multi-hop stationary CHs energy reliability-based proposed RBD: yellow (a) D-Chain, (b) Q-Chain.
Figure 19a, Figure 20a and Figure 21a demonstrate that the SD-Chain model displays the lowest reliability, due to its construction process that employs a greedy approach, using only distance as a parameter for selecting the next connection. This results in long-distance connections between nodes, causing some nodes to deplete their energy quickly. Additionally, relying solely on the distance to choose the next hop connection, without considering the remaining energy, can lead to weak points in the chain, potentially disconnecting some nodes. On the contrary, the MD-Chain model boasts the highest reliability among the D-Chain models. MD-Chain has a shorter chain length than SD-Chain, leading to less energy consumption, as more than one CH receives the data and sends it to the BS.
Table 2 makes it abundantly clear that the SD-Chain exhibits the lowest level of reliability among all the models. In both scenarios, random and grid, the MD-Chain-SH demonstrates 1.1 times higher average reliability than MD-Chain-MH, when comparing the average reliability of the D-Chain over iterations 100–500.

Table 2.
Comparison of D-Chain models.
Figure 19b, Figure 20b and Figure 21b illustrate that the MQ-Chain-SH model performs the best among the Q-Chain models, whereas the SQ-Chain model exhibits the lowest reliability. The performance of MQ-Chain in the grid and random scenarios can be compared by referring to Figure 20b and Figure 21b. It can be observed that, in the MQ-Chain/single-hop model, the reliability is better in the grid scenario than in the random scenario. Moreover, an MQ-Chain-MH-based grid scenario has better reliability than an MQ-Chain-MH-based random scenario.
Table 3 illustrates that MQ-Chain-SH in a grid scenario has better average reliability, 7.6 times and 1.3 times, than SQ-Chain and MQ-Chain-MH, respectively, through the iterations 200 to 1000. In addition, MQ-Chain-MH has 5.6 times better average reliability than SQ-Chain. In a random scenario, MQ-Chain-SH has 4.4 times and 1.4 times better average reliability than SQ-Chain and MQ-Chain-MH, respectively. Moreover, MQ-Chain-MH has 3.3 times better average reliability than SQ-Chain. MQ-Chain-SH and MQ-Chain-MH-based grids are 1.8 times and 1.9 times better than random. In the grid scenario, MQ-Chain-SH has 11.12 times better average reliability than MD-Chain-SH. Additionally, MQ-Chain-SH has 6.38 times better average reliability than MD-Chain-SH, in a random scenario.

Table 3.
Comparison of Q-Chain models.
- In both D-Chain and Q-Chain cases, as the number of iterations increases, the reliability decreases, due to the gradual loss of energy in the nodes over time. However, it is worth noting that the rate of energy loss is more significant in D-Chain than in Q-Chain. This is because, in D-Chain, the choice of CH depends on distance, while the available energy of the nodes to perform their tasks is disregarded.
- The performance of the grid case is superior to that of the random case, possibly because the number of nodes in the grid is nearly equal, leading to a lower rate of energy loss compared to the random scenario.
- In both D-Chain and Q-Chain cases, the multi-chain single-hop exhibits better performance than the multi-chain multi-hop. This is due to the fact that, in the multi-hop case, the nodes carry an extra load, resulting in increased energy loss, that ultimately impacts performance.
In the case of mobile CH, the reliability of D-Chain and Q-Chain are presented in Figure 22, Figure 23 and Figure 24. Obviously, Q-Chain performs better than D-Chain in terms of energy reliability. MD-Chain has better reliability than SD-Chain, although D-Chain reliability fluctuates in all models, as illustrated in Figure 22a, Figure 23a and Figure 24a. This is due to the fact that the CH and LN are selected based on the distance (nearest node to the BS), which implies that the CH remains constant during rounds until it fails, at which point a new CH is selected. Furthermore, the reliability of a mobile CH is assessed continuously during each CH selection, unlike in a static CH scenario, where reliability is only evaluated until the CH dies. This assessment takes into account that the new CH has energy, while the previous one has depleted its energy. In addition, the CH experiences a significant energy loss because it is responsible for transferring all the received data to the BS. Moreover, the failed nodes are removed from the chain and the chain is rearranged, without taking into account the presence of the failed nodes. The Q-Chain models for mobile CH are illustrated in Figure 22b, Figure 23b and Figure 24b. MQ-Chain outperforms SQ-Chain reliability. Moreover, MQ-Chain-SH has better performance than MQ-Chain-MH.
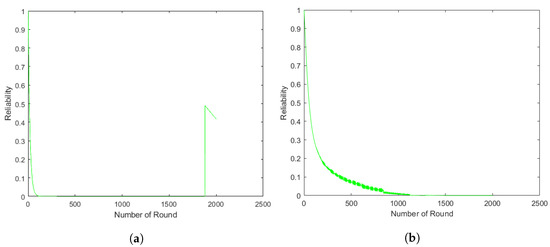
Figure 22.
Single-chain mobile CH energy reliability-based proposed RBD: (a) D-Chain, (b) Q-Chain.
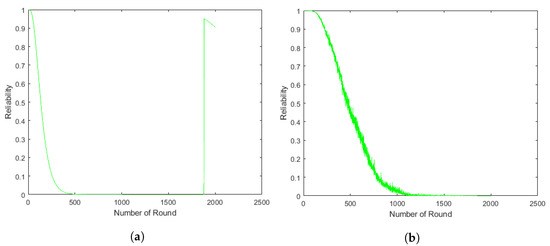
Figure 23.
Multi-chain single-hop mobile CHs energy reliability-based proposed RBD: yellow (a) D-Chain, (b) Q-Chain.
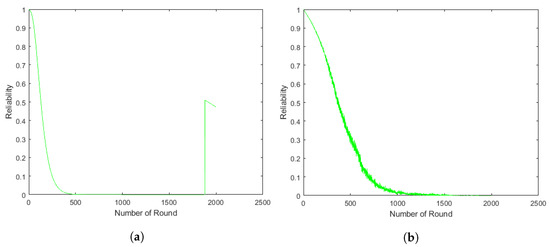
Figure 24.
Multi-chain multi-hop mobile CHs energy reliability-based proposed RBD: yellow (a) D-Chain, (b) Q-Chain.
6. Conclusions
Wireless sensor networks (WSNs) are susceptible to attacks and interference in harsh environments, making reliability a crucial and essential issue. The reliability block diagram (RBD) technique has been used in various research related to WSNs and other different situations to evaluate reliability; however, all of these studies utilize RBD based on the component state of either working (1) or failing (0). Additionally, the reliability-based RBD technique assumes that the system fails if any component fails, however, the parallel system functions when at least one component is functioning. Our proposed RBD can calculate the system reliability based on the node energy, where the reliability is evaluated for different types of chains and various models of chain structures. A D-Chain is a chain that starts formation based on the nearest node to the BS and selects the chain head (CH) regarding the minimum distance of the node to the BS. On the other hand, a Q-Chain starts chain formation based on the farthest node from the BS and selects the CH based on the maximum weight. Each chain has three different models: a single-chain, a multi-chain/single-hop, and a multi-chain/multi-hop. The system reliability is calculated for all these models based on a stationary chain head (CH) and mobile CH. Our results show that Q-Chain reliability outperforms D-Chain reliability in all cases, models, and situations. A single chain is less reliable than a multi-chain for both D-Chain and Q-Chain, regardless of whether the CH is stationary or mobile. In addition, multi Q-Chain/single-hop outperforms all models in both cases, stationary CH or mobile CH. This work can be extended to calculate the system reliability-based throughput using the same concept as the proposed RBD technique, evaluating the system reliability for different chain models and various network configurations.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khedr, A.M.; Osamy, W. Minimum connected cover of a query region in heterogeneous wireless sensor networks. Inf. Sci. 2013, 223, 153–163. [Google Scholar] [CrossRef]
- Marhoon, H.A.; Mahmuddin, M.; Awang Nor, S. Chain-based routing protocols in wireless sensor networks: A survey. ARPN J. Eng. Appl. Sci. 2015, 10, 1389–1398. [Google Scholar]
- Osamy, W.; Khedr, A.M.; Salim, A.; AlAli, A.I.; El-Sawy, A.A. Recent studies utilizing artificial intelligence techniques for solving data collection, aggregation and dissemination challenges in wireless sensor networks: A review. Electronics 2022, 11, 313. [Google Scholar] [CrossRef]
- Shrestha, A.; Xing, L.; Liu, H. Modeling and evaluating the reliability of wireless sensor networks. In Proceedings of the 2007 Annual Reliability and Maintainability Symposium, Orlando, FL, USA, 22–25 January 2007; pp. 186–191. [Google Scholar]
- Dâmaso, A.; Rosa, N.; Maciel, P. Reliability of wireless sensor networks. Sensors 2014, 14, 15760–15785. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Li, X.; Li, Y.; Chen, S. Evaluate reliability of wireless sensor networks with OBDD. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar]
- Xu, X.; Tang, J.; Xiang, H. Data Transmission Reliability Analysis of Wireless Sensor Networks for Social Network Optimization. J. Sens. 2022, 2022, 3842722. [Google Scholar] [CrossRef]
- Nidhya, M.; Chinnaiyan, R. Reliability Evaluation of Wireless Sensor Networks Using EERN Algorithm. In Proceedings of the International Conference on Computer Networks and Communication Technologies, Coimbatore, India, 23–24 May 2019; Springer: Singapore, 2019; pp. 849–856. [Google Scholar]
- Khedr, A.M.; Aziz, A.; Osamy, W. Successors of PEGASIS protocol: A comprehensive survey. Comput. Sci. Rev. 2021, 39, 100368. [Google Scholar] [CrossRef]
- Pantazis, N.A.; Nikolidakis, S.A.; Vergados, D.D. Energy-efficient routing protocols in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2012, 15, 551–591. [Google Scholar] [CrossRef]
- Priyadharshini, S.; Chakrapani, A. Survey on Energy Efficient Hierarchical Routing Protocols. J. Adv. Res. Dyn. Control. Syst. 2017, 15, 626–632. [Google Scholar]
- Mishra, S.; Kumar, U.; Sharma, N.; Upadhyay, U. Wireless sensor network-a literature survey based on merits & demerits of various routing protocols. In Proceedings of the 2020 Fourth International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 8–10 January 2020; pp. 939–945. [Google Scholar]
- Singh, H.; Singh, D. Taxonomy of routing protocols in wireless sensor networks: A survey. In Proceedings of the 2016 2nd International Conference on Contemporary Computing and Informatics (IC3I), Noida, India, 14–17 December 2016; pp. 822–830. [Google Scholar]
- Aziz, A.; Osamy, W.; Khedr, A.M.; El-Sawy, A.A.; Singh, K. Grey Wolf based compressive sensing scheme for data gathering in IoT based heterogeneous WSNs. Wirel. Netw. 2020, 26, 3395–3418. [Google Scholar] [CrossRef]
- Rani, S.; Kumar, A.; Bagchi, A.; Yadav, S.; Kumar, S. RPL based routing protocols for load balancing in IoT network. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1950, p. 012073. [Google Scholar]
- Hassani, A.E.; Sahel, A.; Badri, A. Assessment of a proactive routing protocol RPL in Ipv6 based wireless sensor networks. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakech, Morocco, 28–30 October 2019; pp. 1–7. [Google Scholar]
- Clausen, T.; Yi, J.; Bas, A.; Herberg, U. A Depth First Forwarding (DFF) Extension for the LOADng Routing Protocol. In Proceedings of the 2013 First International Symposium on Computing and Networking, Matsuyama, Japan, 4–6 December 2013; pp. 404–408. [Google Scholar] [CrossRef]
- Liu, X. Atypical hierarchical routing protocols for wireless sensor networks: A review. IEEE Sens. J. 2015, 15, 5372–5383. [Google Scholar] [CrossRef]
- Osamy, W.; Khedr, A.M. FACS: Fairness aware clustering scheme for monitoring applications of internet of things based wireless sensor networks. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 3615–3629. [Google Scholar] [CrossRef]
- Osamy, W.; El-Sawy, A.A.; Salim, A. CSOCA: Chicken Swarm Optimization Based Clustering Algorithm for Wireless Sensor Networks. IEEE Access 2020, 8, 60676–60688. [Google Scholar] [CrossRef]
- Osamy, W.; Khedr, A.M.; El-Sawy, A.A.; Salim, A.; Vijayan, D. IPDCA: Intelligent proficient data collection approach for IoT-enabled wireless sensor networks in smart environments. Electronics 2021, 10, 997. [Google Scholar] [CrossRef]
- Salim, A.; Osamy, W.; Khedr, A.M. IBLEACH: Intra-balanced LEACH protocol for wireless sensor networks. Wirel. Netw. 2014, 20, 1515–1525. [Google Scholar] [CrossRef]
- Hamouid, K.; Othmen, S.; Barkat, A. LSTR: Lightweight and secure tree-based routing for wireless sensor networks. Wirel. Pers. Commun. 2020, 112, 1479–1501. [Google Scholar] [CrossRef]
- Mamun, Q. A qualitative comparison of different logical topologies for wireless sensor networks. Sensors 2012, 12, 14887–14913. [Google Scholar] [CrossRef]
- Borujeni, E.M.; Rahbari, D.; Nickray, M. Fog-based energy-efficient routing protocol for wireless sensor networks. J. Supercomput. 2018, 74, 6831–6858. [Google Scholar] [CrossRef]
- Sun, N.; Xu, J.; Wei, H.; Miao, H.; Wang, J. A network state based reliability evaluation model for WSNs. In Proceedings of the 2017 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Kanazawa, Japan, 26–28 June 2017; pp. 303–308. [Google Scholar] [CrossRef]
- Wategaonkar, D.N.; Deshpande, V.S. Characterization of reliability in WSN. In Proceedings of the 2012 World Congress on Information and Communication Technologies, Trivandrum, India, 30 October–2 November 2012; pp. 970–975. [Google Scholar] [CrossRef]
- Liu, Q.; Yin, X.; Yang, X.; Ma, Y. Reliability evaluation for wireless sensor networks with chain structures using the universal generating function. Qual. Reliab. Eng. Int. 2017, 33, 2685–2698. [Google Scholar] [CrossRef]
- Kumar, V.; Patel, R.B.; Singh, M.; Vaid, R. Reliability analysis in wireless sensor networks. Int. J. Eng. Technol. 2011, 3, 74–79. [Google Scholar]
- Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Reliability and availability evaluation of wireless sensor networks for industrial applications. Sensors 2012, 12, 806–838. [Google Scholar] [CrossRef]
- Chowdhury, C.; Aslam, N.; Ahmed, G.; Chattapadhyay, S.; Neogy, S.; Zhang, L. Novel algorithms for reliability evaluation of remotely deployed wireless sensor networks. Wirel. Pers. Commun. 2018, 98, 1331–1360. [Google Scholar] [CrossRef]
- Chakraborty, S.; Goyal, N.K.; Mahapatra, S.; Soh, S. A Monte-Carlo Markov chain approach for coverage-area reliability of mobile wireless sensor networks with multistate nodes. Reliab. Eng. Syst. Saf. 2020, 193, 106662. [Google Scholar] [CrossRef]
- Kabashkin, I.; Kundler, J. Reliability of sensor nodes in wireless sensor networks of cyber physical systems. Procedia Comput. Sci. 2017, 104, 380–384. [Google Scholar] [CrossRef]
- Chakraborty, S.; Goyal, N.K.; Mahapatra, S.; Soh, S. Minimal path-based reliability model for wireless sensor networks with multistate nodes. IEEE Trans. Reliab. 2019, 69, 382–400. [Google Scholar] [CrossRef]
- Yeh, W.C. An improved sum-of-disjoint-products technique for the symbolic network reliability analysis with known minimal paths. Reliab. Eng. Syst. Saf. 2007, 92, 260–268. [Google Scholar] [CrossRef]
- Tan, J.; Liu, W.; Wang, T.; Xiong, N.N.; Song, H.; Liu, A.; Zeng, Z. An adaptive collection scheme-based matrix completion for data gathering in energy-harvesting wireless sensor networks. IEEE Access 2019, 7, 6703–6723. [Google Scholar] [CrossRef]
- Lin, C.M.; Teng, H.K.; Yang, C.C.; Weng, H.L.; Chung, M.C.; Chung, C.C. A mesh network reliability analysis using reliability block diagram. In Proceedings of the 2010 8th IEEE International Conference on Industrial Informatics, Osaka, Japan, 13–16 July 2010; pp. 975–979. [Google Scholar]
- Sahinoglu, M.; Ramamoorthy, C.V. RBD tools using compression, decompression, hybrid techniques to code, decode, and compute reliability in simple and complex embedded systems. IEEE Trans. Instrum. Meas. 2005, 54, 1789–1799. [Google Scholar] [CrossRef]
- Distefano, S. Reliability evaluation of WSN with dynamic-dependent nodes. Int. J. Reliab. Qual. Saf. Eng. 2011, 18, 515–530. [Google Scholar] [CrossRef]
- Distefano, S. Evaluating reliability of WSN with sleep/wake-up interfering nodes. Int. J. Syst. Sci. 2013, 44, 1793–1806. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Bartolini, A.; Del Rio, C.; Guidi, G.; Patrizi, G. Reliability Analysis of Wireless Sensor Network for Smart Farming Applications. Sensors 2021, 21, 7683. [Google Scholar] [CrossRef]
- Ahmed, W.; Hasan, O.; Tahar, S. Formal reliability analysis of wireless sensor network data transport protocols using HOL. In Proceedings of the 2015 IEEE 11th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Abu Dhabi, United Arab Emirates, 19–21 October 2015; pp. 217–224. [Google Scholar]
- Dâmaso, A.; Rosa, N.; Maciel, P. Integrated evaluation of reliability and power consumption of wireless sensor networks. Sensors 2017, 17, 2547. [Google Scholar] [CrossRef] [PubMed]
- Liu, F. Majority Decision Aggregation with Binarized Data in Wireless Sensor Networks. Symmetry 2021, 13, 1671. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd annual Hawaii international conference on system sciences, Maui, HI, USA, 7 January 2000; p. 10. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).