An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things
Abstract
1. Introduction
- We propose a certificateless, forward-secure HECC-based digital signature scheme that provides privacy, gets rid of the key escrow problem, and ensures its forward security.
- A comprehensive security analysis is conducted to demonstrate that the proposed scheme is secure against various types of cyber-attacks.
- Finally, the efficiency of the proposed scheme is evaluated by comparing it to other existing schemes in terms of its computation and communication costs. The results reveal that the proposed scheme is more efficient.
2. Literature Review
3. Preliminaries
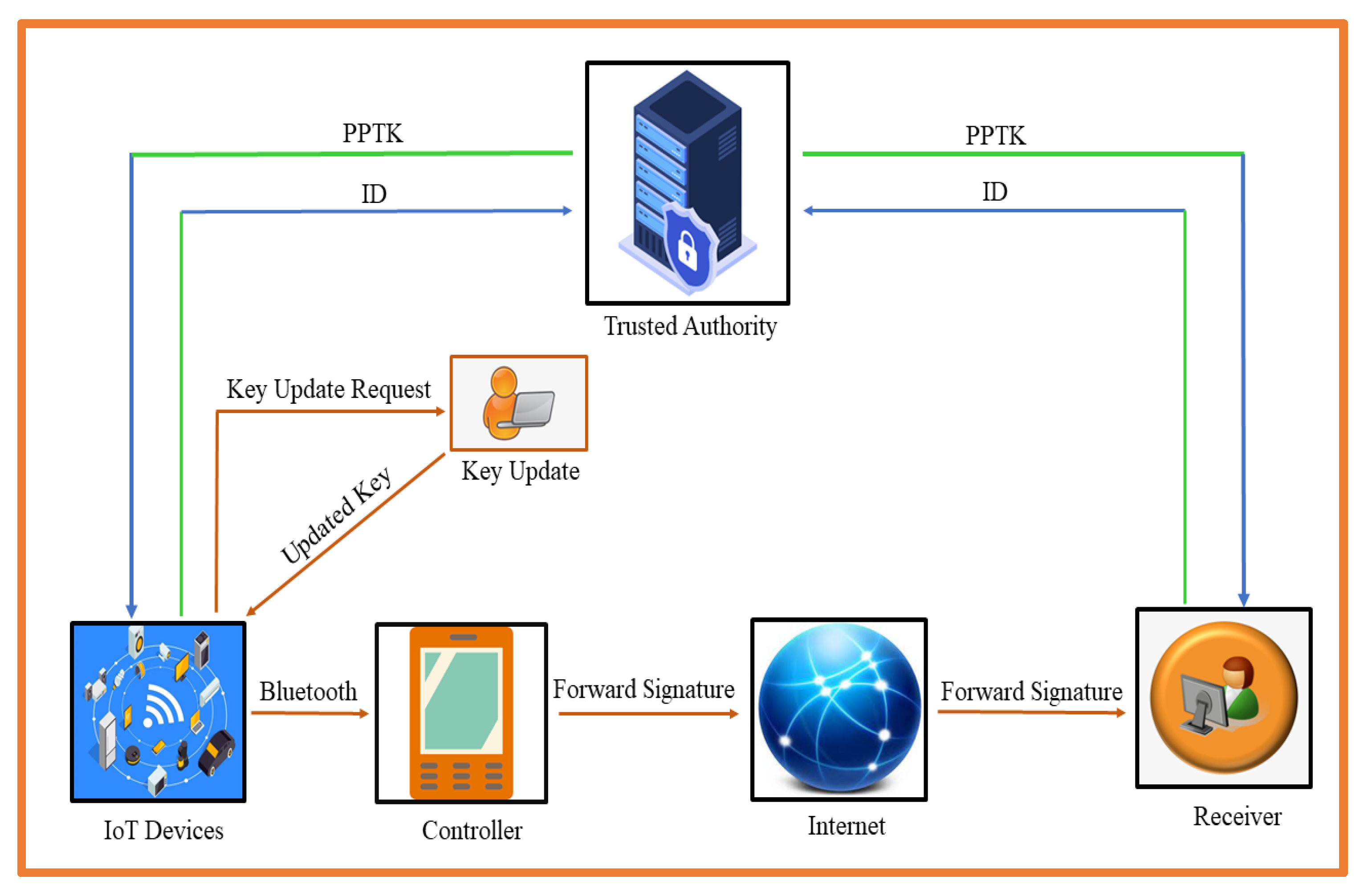
3.1. Network Model
3.2. Syntax of Certificateless Forward Signature
- Initialization: The trusted authority (TA) generates public parameter param, his private key (), and public key () by taking as input the security parameter of hyperelliptic curve.
- Generate Private Number: Given the security parameter and param, the user () selects as his private number.
- Generate Partial Private Key: Given user identity (), public key of TA (), and public parameter param, TA generates the tuple (, ) as a partial private key for user with identity ().
- Generate Private Key: Given a private number () and the tuple (, ), a ser () sets () as his private key.
- Key Update: In this phase, it renews the signature key pair by replacing () on , before signature generations and also renews the verification public key as ,.
- Generate Public Key: Given a private number () and the tuple (, ), the user () sets () as his public key, where .
- Generate Forward Signature: Given a message , the updated signature key pair ,, param, signer identity (), and , generate and send the signature tuple () to the verifier.
- Forward Signature Verification: Given a message , the public key pair , param, signer identity (), and (), the verifier verifies the received signature tuple.
3.3. Hyperelliptic Curve Discrete Logarithm Problem (HECDLP)
4. Certificateless Forward-Secure Signature Scheme
- Initialization: Here, the trusted authority performs the following mathematical computations:
- Select hyper elliptic curve () with genus 2.
- Suggest the finite field () of order , where its range is not more than 80 bits.
- Suggest the devisor of , where its range is not more than 80 bits.
- Suggest three irreversible, one-way, and collision-resistant hash functions () from the SHA family.
- TA computes the public key , where is the randomly selected private key from.
- TA publishes the public parameter set {,,}.
- Generate Private Number: User () selects from as a private number.
- Generate Partial Private Key: Upon the request of with identity , TA selects from and computes , , and .
- Generate Private Key: The User () sets () as his private key.
- Key Update: In this phase, it renews the signature key pair by replacing () on , before signature generations and also renews the verification public key as ,.
- Generate Public Key: The user () sets () as his public key, where .
- Generate Forward Signature: Given a message , the updated signature key pair ,, {,,}, signer identity (), and , the signer performs the following computations:
- Signer selects from and computes .
- Compute and .
- Compute and send () to verifier.
- Forward Signature Verification: Given a message , the public key pair , {,,}, signer identity (), and (), the verifier performs the following computations:
5. Correctness
6. Security Analysis
- Query: When submits the query with , the challenger () combs in and returns , if it was available previously. Otherwise, it chooses from and sends it to.
- Query: When submits the query with , the challenger () combs in and returns , if it was available previously. Otherwise, it chooses from and sends it to.
- Query: When submits the query with , the challenger () combs in and returns , if it was available previously. Otherwise, it chooses from and sends it to.
- User Creation Query: When submits query with, the challenger () combs in and returns , and (), if they exist. Otherwise, it goes for the following conditions:
- If , three variables are chosen by , which computes , and .
- If , three variables are chosen by , which computes , , and sets . Then, it returns () and renews , to and updates .
- Replace Public Key Query: When submits a query with, the challenger () replaces , and , and returns them to .
- Private Number Query: When submits a query with, the challenger () combs in and returns , if it exists. Otherwise, it goes for the following conditions:
- If , three variables are chosen by , which computes and .
- If , three variables are chosen by , which computes , , and sets . Then, it renews , and returns to and updates .
- Partial Private Key Query: When submits a query with, the challenger () checks if , and then it combs in and returns , if it exists. Otherwise, it stops the further executions.
- Generate Forward Signature Query: When submits a query with, the challenger () combs in , and for the record of ,,,, ,,, and . If or , randomly chooses and and sends them to . Otherwise, three variables are chosen by , which computes and returns to .
- If there exists no collision during the user creation query, its probability is .
- When is not called for the partial private key query on , its probability is .
- can send forward a signature if , and its probability is .
- can find the valid value from , and its probability is .
- can find the valid value from , and its probability is ().
- The combined probability will be what follows:().
- Query: This query is performed as in Theorem 1.
- Query: This query is performed as in Theorem 1.
- Query: This query is performed as in Theorem 1.
- User Creation Query: When submits a query with, the challenger () combs in and returns , and (), if they exist. Otherwise, it goes for the followed conditions:
- If , three variables are chosen by , which computes and .
- If , three variables are chosen by , which computes , , and sets . Then, it returns () and renews , to and updates .
- Private Number Query: Here, is not allowed to access on , and will not stop further executions if Otherwise, the challenger () combs in and returns if it exists.
- Partial Private Key Query: When submits a query with, the challenger () combs in and returns if it exists.
- Generate Forward Signature Query: When submits a query with, the challenger () combs in , and for the record of ,,,, ,,, and . If or , randomly chooses and , and sends them to . Otherwise, three variables are chosen by , which computes , and returns to .
- If there exists no collision during the user creation query, its probability is .
- When is not called for the partial private key query on , its probability is .
- can send forward a signature if , and its probability is .
- can find the valid value from , and its probability is .
- can find the valid value from , and its probability is ().
- The combined probability will be what follows:().
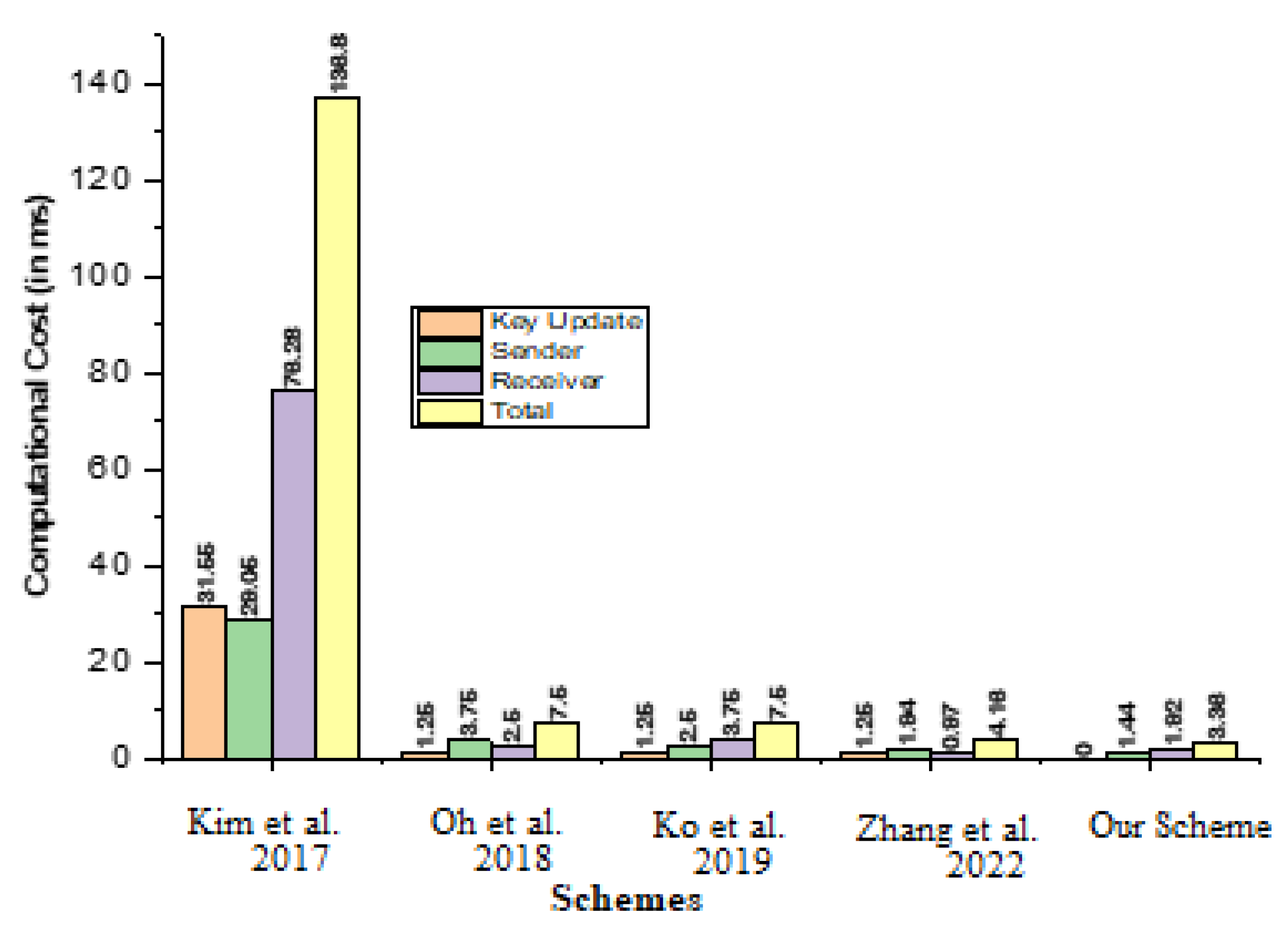
7. Computational Cost
- Computational cost reduction process between the newly proposed scheme and Kim et al. [21], which is represented and processed as .
- Computational cost reduction process between the newly proposed scheme and Oh et al. [22], which is represented and processed as .
- Computational cost reduction process between the newly proposed scheme and Ko et al. [23], which is represented and processed as .
- Computational cost reduction process between the newly proposed scheme and Ping et al. [26], which is represented and processed as .
8. Communication Overhead
- Communication overheads reduction process between the newly proposed scheme and Kim et al. [21], which is represented and processed as .
- Communication overheads reduction process between the newly proposed scheme and Oh et al. [22], which is represented and processed as .
- Communication overheads reduction process between the newly proposed scheme and Ko et al. [23], which is represented and processed as .
- Communication overheads reduction process between the newly proposed scheme and Zhang et al. [26], which is represented and processed as .
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fazeldehkordi, E.; Grønli, T.-M. A Survey of Security Architectures for Edge Computing-Based IoT. IoT 2022, 3, 332–365. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Williams, P.; Dutta, I.K.; Daoud, H.; Bayoumi, M. A Survey on Security in Internet of Things with a Focus on the Impact of Emerging Technologies. Internet Things 2022, 19, 100564. [Google Scholar] [CrossRef]
- Villa-Henriksen, A.; Edwards, G.T.C.; Pesonen, L.A.; Green, O.; Sørensen, C.A.G. Internet of Things in Arable Farming: Implementation, Applications, Challenges and Potential. Biosyst. Eng. 2020, 191, 60–84. [Google Scholar] [CrossRef]
- Khan, M.A.; Kumar, N.; Mohsan, S.A.H.; Khan, W.U.; Nasralla, M.M.; Alsharif, M.H.; Zywiolek, J.; Ullah, I. Swarm of UAVs for Network Management in 6G: A Technical Review. IEEE Trans. Netw. Serv. Manag. 2022. [Google Scholar] [CrossRef]
- Ullah, I.; Alkhalifah, A.; Althobaiti, M.M.; Al-Wesabi, F.N.; Hilal, A.M.; Khan, M.A.; Ming-Tai Wu, J. Certificate-Based Signature Scheme for Industrial Internet of Things Using Hyperelliptic Curve Cryptography. Wirel. Commun. Mob. Comput. 2022, 2022, 7336279. [Google Scholar] [CrossRef]
- Majeed, R.; Abdullah, N.A.; Mushtaq, M.F.; Kazmi, R. Drone Security: Issues and Challenges. Int. J. Adv. Comput. Sci. Appl. 2021, 12. [Google Scholar] [CrossRef]
- Xiang, D.; Li, X.; Gao, J.; Zhang, X. A Secure and Efficient Certificateless Signature Scheme for Internet of Things. Ad. Hoc. Netw. 2022, 124, 102702. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, S.; Chen, X.; He, Y.; Jiang, S. A Forward-Secure and Efficient Authentication Protocol through Lattice-Based Group Signature in VANETs Scenarios. Comput. Netw. 2022, 214, 109149. [Google Scholar] [CrossRef]
- Yadav, V.K.; Andola, N.; Verma, S.; Venkatesan, S. PSCLS: Provably Secure Certificateless Signature Scheme for IoT Device on Cloud. J. Supercomput. 2022. [Google Scholar] [CrossRef]
- Ullah, I.; Khan, M.A.; Abdullah, A.M.; Mohsan, S.A.H.; Noor, F.; Algarni, F.; Innab, N. A Conditional Privacy Preserving Generalized Ring Signcryption Scheme for Micro Aerial Vehicles. Micromachines 2022, 13, 1926. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Khan, M.A.; Kumar, N.; Abdullah, A.M.; AlSanad, A.A.; Noor, F. A Conditional Privacy Preserving Heterogeneous Signcryption Scheme for Internet of Vehicles. IEEE Trans. Veh. Technol. 2022, 1–10. [Google Scholar] [CrossRef]
- Malkin, T.; Micciancio, D.; Miner, S. Composition and Efficiency Tradeoffs for Forward-Secure Digital Signatures. Cryptol. Eprint Arch. 2001. Available online: https://eprint.iacr.org/2001/034 (accessed on 13 November 2022).
- Itkis, G.; Reyzin, L. Forward-Secure Signatures with Optimal Signing and Verifying. Adv. Cryptol. CRYPTO 2001, 2001, 332–354. [Google Scholar] [CrossRef]
- Kozlov, A.; Reyzin, L. Forward-Secure Signatures with Fast Key Update. Secur. Commun. Netw. 2003, 2576, 241–256. [Google Scholar] [CrossRef]
- McCullagh, N.; Barreto, P.S.L.M. Efficient and Forward-Secure Identity-Based Signcryption. Cryptol. Eprint Arch. 2004. Available online: https://eprint.iacr.org/ (accessed on 13 November 2022).
- Boyen, X.; Shacham, H.; Shen, E.; Waters, B. Forward-Secure Signatures with Untrusted Update. In Proceedings of the 13th ACM conference on Computer and Communications Security CCS ’06 2006, Alexandria, VI, USA, 30 October–3 November 2006. [Google Scholar] [CrossRef]
- Liu, J.K.; Wong, D.S. Solutions to Key Exposure Problem in Ring Signature. Cryptol. Eprint Arch. 2005. Available online: https://eprint.iacr.org/2005/427 (accessed on 13 November 2022).
- Das, A.K.; Sharma, P.; Chatterjee, S.; Sing, J.K. A Dynamic Password-Based User Authentication Scheme for Hierarchical Wireless Sensor Networks. J. Netw. Comput. Appl. 2012, 35, 1646–1656. [Google Scholar] [CrossRef]
- Qian, X.; Chengxiang, T.; Jun, F.; Zhijie, F.; Wenye, Z. Lattice-Based Forward Secure and Certificateless Signature Scheme. J. Comput. Res. Dev. 2017, 54, 1510. [Google Scholar] [CrossRef]
- Kim, J.; Oh, H. Forward-Secure Digital Signature Schemes with Optimal Computation and Storage of Signers. ICT Syst. Secur. Priv. Prot. 2017, 502, 523–537. [Google Scholar] [CrossRef]
- Oh, H.; Kim, J.; Shin, J.S. Forward-Secure ID Based Digital Signature Scheme with Forward-Secure Private Key Generator. Inf. Sci. 2018, 454–455, 96–109. [Google Scholar] [CrossRef]
- Ko, H.; Jeong, G.; Kim, J.; Kim, J.; Oh, H. Forward Secure Identity-Based Signature Scheme with RSA. ICT Syst. Secur. Priv. Prot. 2019, 562, 314–327. [Google Scholar] [CrossRef]
- Du, H.; Wen, Q.; Zhang, S.; Gao, M. A New Provably Secure Certificateless Signature Scheme for Internet of Things. Ad. Hoc. Netw. 2020, 100, 102074. [Google Scholar] [CrossRef]
- Saqib, M.; Jasra, B.; Moon, A.H. A Lightweight Three Factor Authentication Framework for IoT Based Critical Applications. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 6925–6937. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Y.; Liu, M.; Shang, Y.; Fu, Z. An ECC-Based Digital Signature Scheme for Privacy Protection in Wireless Communication Network. Wirel. Commun. Mob. Comput. 2022, 2022, 1977798. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, D.; Obaidat, M.S.; Vijayakumar, P. Edge-Assisted Intelligent Device Authentication in Cyber-Physical Systems. IEEE Internet Things J. 2022, 1. [Google Scholar] [CrossRef]
- Ullah, I.; Khan, M.A.; Khan, F.; Jan, M.A.; Srinivasan, R.; Mastorakis, S.; Hussain, S.; Khattak, H. An Efficient and Secure Multi-Message and Multi-Receiver Signcryption Scheme for Edge Enabled Internet of Vehicles. IEEE Internet Things J. 2021, 9, 2688–2697. [Google Scholar] [CrossRef]
- Ullah, I.; Amin, N.U.; Khan, M.A.; Khattak, H.; Kumari, S. An Efficient and Provable Secure Certificate-Based Combined Signature, Encryption and Signcryption Scheme for Internet of Things (IoT) in Mobile Health (M-Health) System. J. Med. Syst. 2020, 45, 4. [Google Scholar] [CrossRef] [PubMed]

| No | Symbol | Description |
|---|---|---|
| 1 | Represents a hyper elliptic curve with genus 2 | |
| 2 | Represents a finite field of order p, where its range is not more than 80 bits | |
| 3 | Represents a devisor, where its range is not more then 80 bits | |
| 4 | Represent three irreversible, one-way, and collision-resistant hash functions from the SHA family | |
| 5 | The public key of TA, and it is made from the combination of secret key and devisor | |
| 6 | The secret key of TA, and it is randomly selected from Fp | |
| 7 | This symbol is used to indicate user | |
| 8 | These two symbols are used to indicate the private key of Ui | |
| 9 | This is used to represent the private number of Ui | |
| 10 | This is used to represent the identity of Ui | |
| 11 | This is used to represent the update private key pair of Ui | |
| 12 | This is used to represent the public key pair of Ui | |
| 13 | This is used to represent the update public key pair of Ui | |
| 14 | This is used to represent the signature pair generated by signer | |
| 15 | This is used to represent bilinear pairing-based multiplication | |
| 16 | Xⅇ | This is used to represent the exponential |
| 17 | This is used to represent elliptic curve multiplication | |
| 18 | This is used to represent hyperelliptic curve multiplication | |
| 19 | This is used to represent the bilinear pairing operation | |
| 20 | This is used to represent the challenger, which will support the adversary during security analysis | |
| 21 | This is used to represent the type 1 adversary | |
| 22 | This is used to represent the type 2 adversary | |
| 23 | This is used to represent the non-negligible probability type 1 and type 2 adversaries | |
| 24 | This is used to represent the query for Hl | |
| 25 | This is used to represent partial private key query | |
| 26 | This is used to represent user creation query | |
| 27 | This is used to denote the query for Hk | |
| 28 | This is used to denote the query for Hj |
| Schemes | Key Update | Sender | Receiver | Total |
|---|---|---|---|---|
| Kim et al. [21] | ||||
| Oh et al. [22] | ||||
| Ko et al. [23] | 1Xⅇ | 2Xⅇ | ||
| Zhang et al. [26] | ||||
| Our Scheme | - |
| Schemes | Key Update | Sender | Receiver | Total |
|---|---|---|---|---|
| Kim et al. [21] | 8 × 1.25 + 5 × 4.31 = 31.55 | 5 × 4.31 + 6 × 1.25 = 29.05 | 3 × 4.31 + 3 × 1.25 + 4 × 14.90 = 76.28 | 17 × 1.25 + 13 × 4.31 + 4 × 14.90 = 136.88 |
| Oh et al. [22] | 1 × 1.25 = 1.25 | 3 × 1.25 = 3.75 | 2 × 1.25 = 2.5 | 6 × 1.25 = 7.5 |
| Ko et al. [23] | 1 × 1.25 = 1.25 | 2 × 1.25 = 2.5 | 3 × 1.25 = 3.75 | 6 × 1.25 = 7.5 |
| Zhang et al. [26] | 1 × 1.25 = 1.25 | 2 × 0.97 = 1.94 | 1 × 0.97 = 0.97 | 1 × 1.25 + 3 × 0.97 = 4.16 |
| Our Scheme | - | 3 × 0.48 = 1.44 | 4 × 0.48 = 1.92 | 7 × 0.48 = 3.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, T.A.; Ullah, I.; Khan, M.A.; Lorenz, P.; Innab, N. An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things. J. Sens. Actuator Netw. 2023, 12, 10. https://doi.org/10.3390/jsan12010010
Shah TA, Ullah I, Khan MA, Lorenz P, Innab N. An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things. Journal of Sensor and Actuator Networks. 2023; 12(1):10. https://doi.org/10.3390/jsan12010010
Chicago/Turabian StyleShah, Tahir Ali, Insaf Ullah, Muhammad Asghar Khan, Pascal Lorenz, and Nisreen Innab. 2023. "An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things" Journal of Sensor and Actuator Networks 12, no. 1: 10. https://doi.org/10.3390/jsan12010010
APA StyleShah, T. A., Ullah, I., Khan, M. A., Lorenz, P., & Innab, N. (2023). An Efficient Certificateless Forward-Secure Signature Scheme for Secure Deployments of the Internet of Things. Journal of Sensor and Actuator Networks, 12(1), 10. https://doi.org/10.3390/jsan12010010








