Antenna Delay-Independent Simultaneous Ranging for UWB-Based RTLSs
Abstract
:1. Introduction
- A TWR session simultaneously measures the ranges between a mobile node and several anchor nodes,
- knowledge or measurement of UWB nodes’ antenna delay values are not required for the range estimations,
- relatively faster-ranging sessions with limited air-time occupancy, and
- clock synchronization is not required between any of the involved UWB nodes.
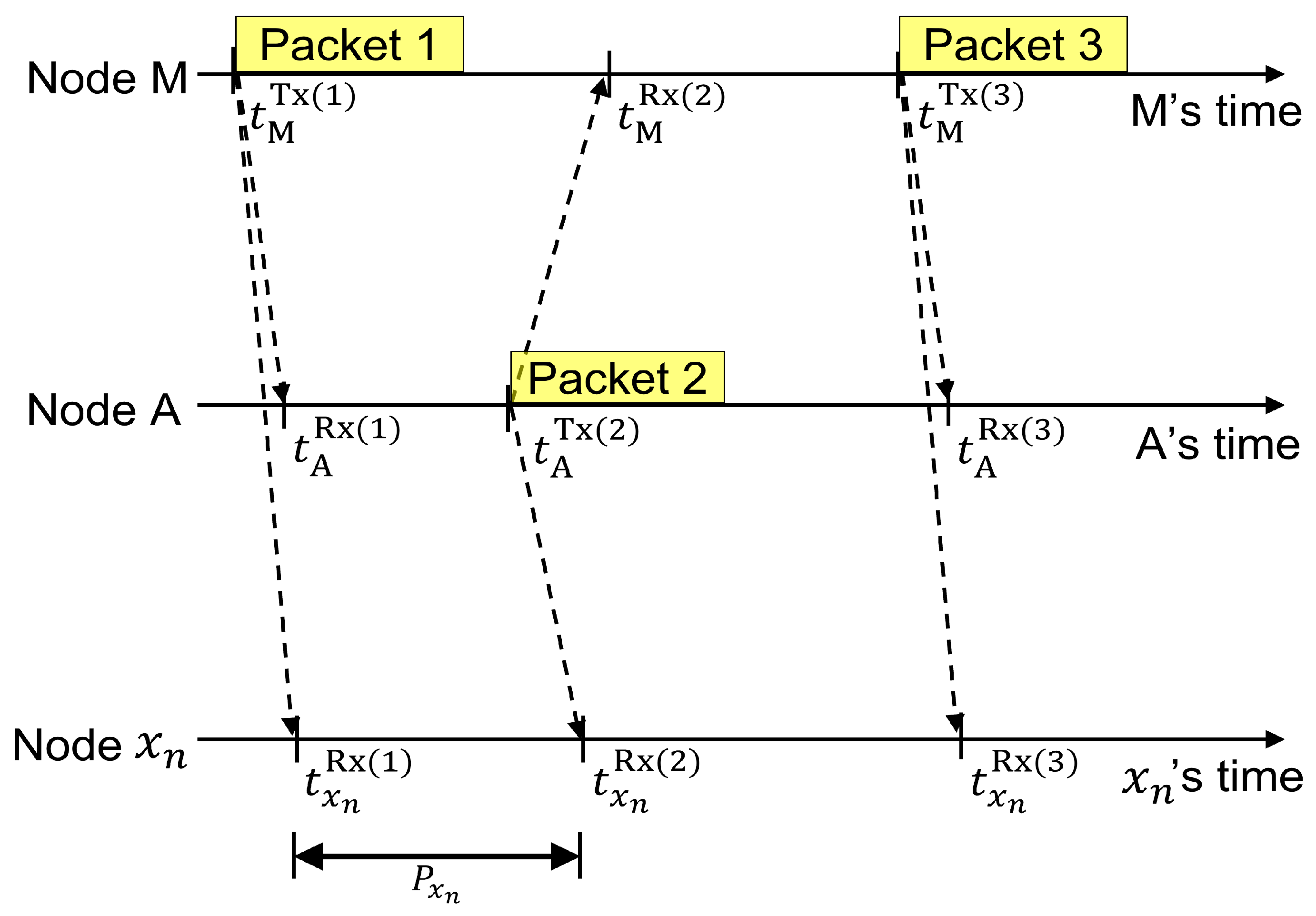
2. Antenna Delay-Independent Simultaneous Ranging
2.1. Mathematical Modeling
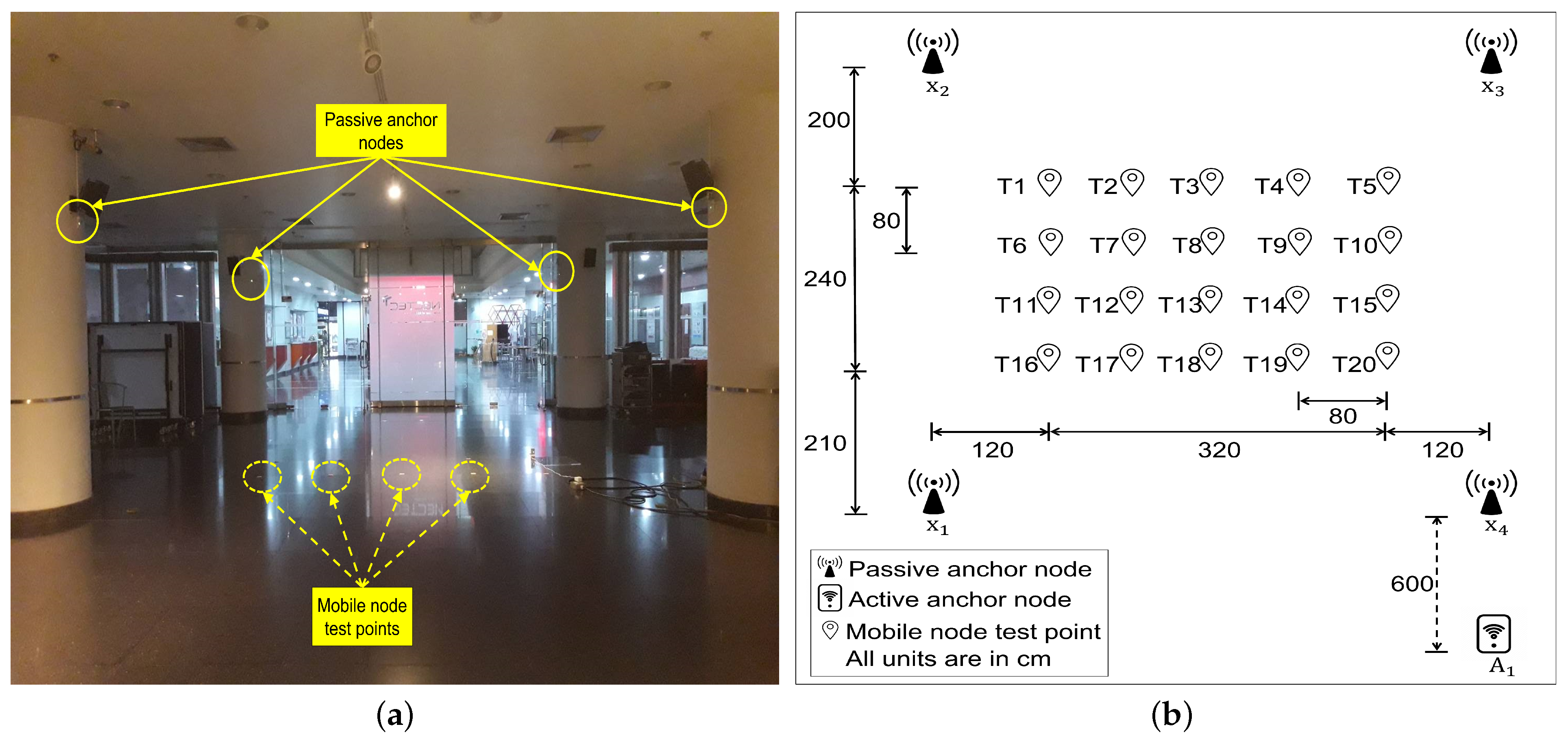
2.2. System Design and Implementation
- Step 1:
- Place each powered anchor node in its corresponding fixed, well-known position.
- Step 2:
- Identify an active anchor node, , and passive anchor nodes, , and measure the distances between them.
- Step 3:
- Place the powered mobile node, , in an arbitrary location.
- Step 4:
- Session-data collection.
- Step 4.1:
- Upon the PC’s request, the master node issues the command to begin a TWR session. It then assigns M to transmit the first and third sensing packets, A to transmit the second sensing packet, and to listen to the packets.
- Step 4.2:
- Upon completion of a TWR session, computes their corresponding reception time difference based on (8).
- Step 4.3:
- After a successful TWR session, the master node gathers and stores the session-data of respective nodes as a log file into the PC.
- Step 4.4:
- The Step 4.1 through Step 4.3 processes is continued for 1000 sets of log files.
- Step 5:
- The processing of the collected log files is performed at the PC, where the ranges between M and are simultaneously estimated by the least-squares method.
3. Numerical Results
3.1. Air-Time Occupancy
3.2. Experimental Evaluation
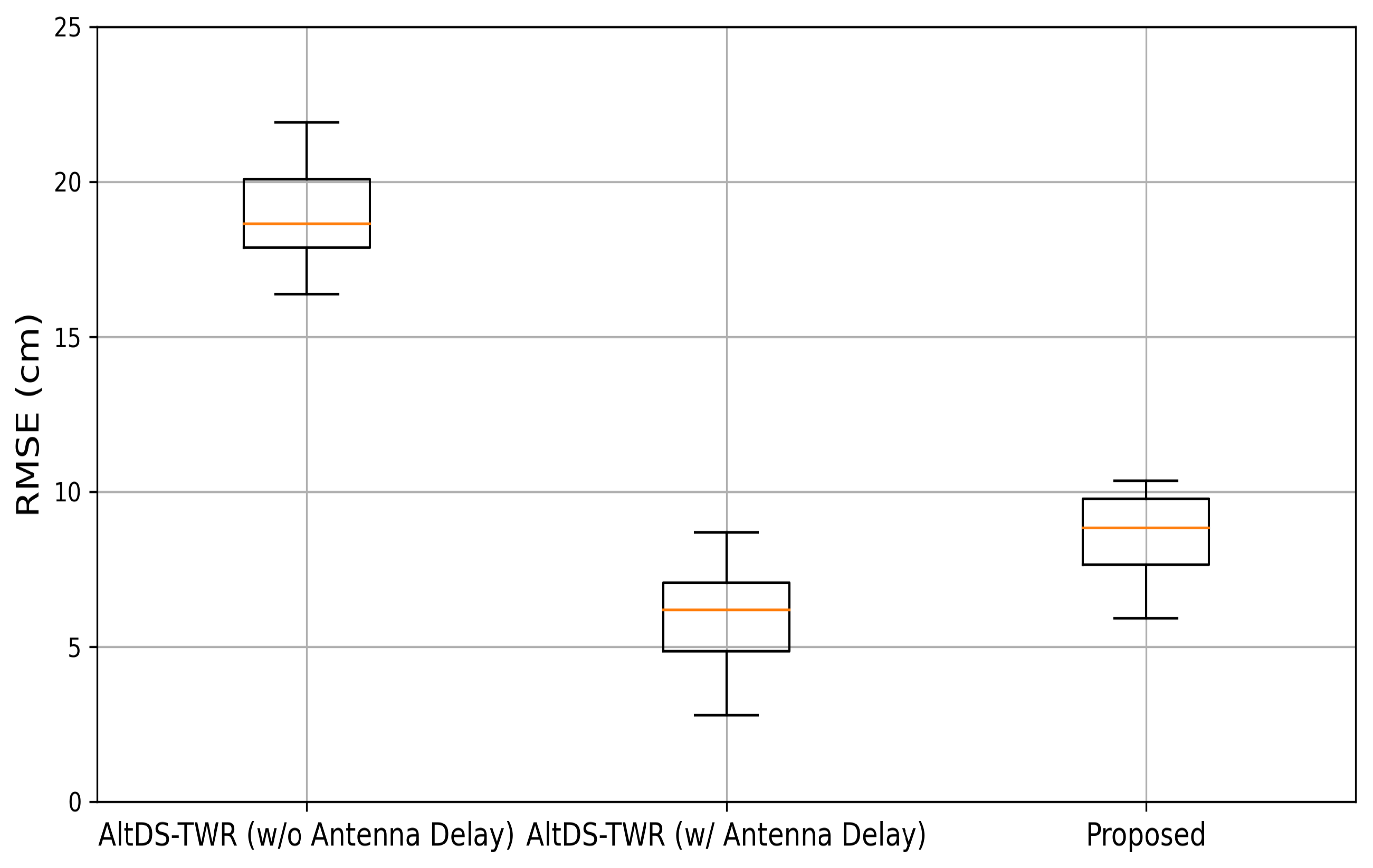
3.2.1. Range Estimation
3.2.2. Position Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, L.; Javali, A.; Nyamangoudar, R.; Priya, R.; Mishra, P.; Routray, S.K. An update on location based services: Current state and future prospects. In Proceedings of the 2017 International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 18–19 July 2017; pp. 220–224. [Google Scholar] [CrossRef]
- Usman, M.; Asghar, M.R.; Ansari, I.S.; Granelli, F.; Qaraqe, K.A. Technologies and Solutions for Location-Based Services in Smart Cities: Past, Present, and Future. IEEE Access 2018, 6, 22240–22248. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef] [Green Version]
- Mendoza-Silva, G.M.; Torres-Sospedra, J.; Huerta, J. A Meta-Review of Indoor Positioning Systems. Sensors 2019, 19, 4507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shum, L.C.; Faieghi, R.; Borsook, T.; Faruk, T.; Kassam, S.; Nabavi, H.; Spasojevic, S.; Tung, J.; Khan, S.S.; Iaboni, A. Indoor Location Data for Tracking Human Behaviours: A Scoping Review. Sensors 2022, 22, 1220. [Google Scholar] [CrossRef]
- Gandhi, G.M.; Rama, P. GPS based Multi-hop Communication with Localization in Subterranean Wireless Sensor Networks. Procedia Comput. Sci. 2015, 57, 1189–1198. [Google Scholar] [CrossRef] [Green Version]
- Du, H.; Zhang, C.; Ye, Q.; Xu, W.; Kibenge, P.L.; Yao, K. A hybrid outdoor localization scheme with high-position accuracy and low-power consumption. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 4. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, A.F.G.; Fernandes, D.M.A.; Catarino, A.P.; Monteiro, J.L. Localization and Positioning Systems for Emergency Responders: A Survey. IEEE Commun. Surv. Tutor. 2017, 19, 2836–2870. [Google Scholar] [CrossRef]
- Almansa, C.M.; Shule, W.; Queralta, J.P.; Westerlund, T. Autocalibration of a Mobile UWB Localization System for Ad-Hoc Multi-Robot Deployments in GNSS-Denied Environments. CoRR 2020. [Google Scholar] [CrossRef]
- Simon, T. Indoor Positioning and Navigation. Sensors 2021, 21, 4793. [Google Scholar] [CrossRef]
- IEEE 802.15.4a; IEEE Standard for Information Technology—Local and Metropolitan Area Networks—Specific Requirements—Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs): Amendment 1: Add Alternate PHYs. Technical Report; IEEE: Piscataway, NJ, USA, 2007.
- Karapistoli, E.; Pavlidou, F.; Gragopoulos, I.; Tsetsinas, I. An overview of the IEEE 802.15.4a Standard. IEEE Commun. Mag. 2010, 48, 47–53. [Google Scholar] [CrossRef]
- IEEE Std 802.15.4-2011 (Revision of IEEE Std 802.15.4-2006); IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs). IEEE: Piscataway, NJ, USA, 2011; pp. 1–314. [CrossRef]
- IEEE 802.15.4z-2020; IEEE 802.15.4z-2020—IEEE Standard for Low-Rate Wireless Networks–Amendment 1: Enhanced Ultra Wideband (UWB) Physical Layers (PHYs) and Associated Ranging Techniques. Technical Report; IEEE: Piscataway, NJ, USA, 2020.
- Yang, J.; Chen, Y. Indoor Localization Using Improved RSS-Based Lateration Methods. In Proceedings of the 2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Seco, F.; Jimenez, A.R.; Prieto, C.; Roa, J.; Koutsou, K. A survey of mathematical methods for indoor localization. In Proceedings of the 2009 IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 26–28 August 2009; pp. 9–14. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hach, R. Symmetric double side two way ranging. In Contribution to IEEE 802.15.4A, IEEE P802.15 Work. Group for Wireless Pers. Area Netw. (WPAN), Doc. IEEE P.802.15-05-0334-00-004a; Technical Report; IEEE Computer Society: Washington, DC, USA, 2005. [Google Scholar]
- Jiang, Y.; Leung, V.C.M. An Asymmetric Double Sided Two-Way Ranging for Crystal Offset. In Proceedings of the 2007 International Symposium on Signals, Systems and Electronics, Bremen, Germany, 30 July–2 August 2007; pp. 525–528. [Google Scholar] [CrossRef]
- Neirynck, D.; Luk, E.; McLaughlin, M. An alternative double-sided two-way ranging method. In Proceedings of the 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, Y.; Chaudhari, Q.; Serpedin, E. Clock Synchronization of Wireless Sensor Networks. IEEE Signal Process. Mag. 2011, 28, 124–138. [Google Scholar] [CrossRef]
- Lian Sang, C.; Adams, M.; Hörmann, T.; Hesse, M.; Porrmann, M. Numerical and Experimental Evaluation of Error Estimation for Two-Way Ranging Methods. Sensors 2019, 19, 616. [Google Scholar] [CrossRef] [Green Version]
- Shah, S.; Demeechai, T. Multiple Simultaneous Ranging in IR-UWB Networks. Sensors 2019, 19, 5415. [Google Scholar] [CrossRef] [Green Version]
- Laadung, T.; Ulp, S.; Alam, M.M.; Moullec, Y.L. Novel Active-Passive Two-Way Ranging Protocols for UWB Positioning Systems. IEEE Sens. J. 2022, 22, 5223–5237. [Google Scholar] [CrossRef]
- Decawave Limited. APS011 Application Note, Sources of Error in DW1000 Based Two-Way Ranging (TWR) Schemes; Decawave: Dublin, Ireland, 2014. [Google Scholar]
- Decawave Limited. APS014 Application Note, Antenna Delay Calibration of DW1000-Based Products and Systems; Decawave: Dublin, Ireland, 2018. [Google Scholar]
- Basiri, A.; Lohan, E.S.; Moore, T.; Winstanley, A.; Peltola, P.; Hill, C.; Amirian, P.; Figueiredo e Silva, P. Indoor location based services challenges, requirements and usability of current solutions. Comput. Sci. Rev. 2017, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Horváth, K.A.; Ill, G.; Milánkovich, Á. Calibration method of antenna delays for UWB-based localization systems. In Proceedings of the 2017 IEEE 17th International Conference on Ubiquitous Wireless Broadband (ICUWB), Salamanca, Spain, 12–15 September 2017; pp. 1–5. [Google Scholar]
- Gui, X.; Guo, S.; Chen, Q.; Han, L. A New Calibration Method of UWB Antenna Delay Based on the ADS-TWR. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7364–7369. [Google Scholar]
- Shah, S.; Chaiwong, K.; Kovavisaruch, L.O.; Kaemarungsi, K.; Demeechai, T. Antenna Delay Calibration of UWB Nodes. IEEE Access 2021, 9, 63294–63305. [Google Scholar] [CrossRef]
- Piavanini, M.; Barbieri, L.; Brambilla, M.; Cerutti, M.; Ercoli, S.; Agili, A.; Nicoli, M. A Calibration Method for Antenna Delay Estimation and Anchor Self-Localization in UWB Systems. In Proceedings of the 2022 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0&IoT), Trento, Italy, 7–9 June 2022; pp. 173–177. [Google Scholar] [CrossRef]
- Shah, S.; Kovavisaruch, L.o.; Kaemarungsi, K.; Demeechai, T. Node Calibration in UWB-Based RTLSs Using Multiple Simultaneous Ranging. Sensors 2022, 22, 864. [Google Scholar] [CrossRef]
- Decawave Limited. Decawave DWM1001 Datasheet; Decawave: Dublin, Ireland, 2017. [Google Scholar]
- Segger Microcontroller. Segger Embedded Studio. Available online: https://www.segger.com/products/development-tools/embedded-studio/ (accessed on 11 December 2022).
- Horváth, K.A.; Ill, G.; Milánkovich, Á. Passive extended double-sided two-way ranging with alternative calculation. In Proceedings of the 2017 IEEE 17th International Conference on Ubiquitous Wireless Broadband (ICUWB), Salamanca, Spain, 12–15 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A Novel NLOS Mitigation Algorithm for UWB Localization in Harsh Indoor Environments. IEEE Trans. Veh. Technol. 2019, 68, 686–699. [Google Scholar] [CrossRef]
- Sang, C.L.; Steinhagen, B.; Homburg, J.D.; Adams, M.; Hesse, M.; Ruckert, U. Identification of NLOS and Multi-Path Conditions in UWB Localization Using Machine Learning Methods. Appl. Sci. 2020, 10, 3980. [Google Scholar] [CrossRef]
- Park, J.; Nam, S.; Choi, H.; Ko, Y.; Ko, Y. Improving Deep Learning-Based UWB LOS/NLOS Identification with Transfer Learning: An Empirical Approach. Electronics 2020, 9, 1714. [Google Scholar] [CrossRef]

| Ranging Scheme | Air-Time Occupancy (Sensing Packets) | Required Number of Sensing Packets (for N = 4) |
|---|---|---|
| SS-TWR | 8 | |
| SDS-TWR | 12 | |
| AltDS-TWR | 12 | |
| AltDS-TWR&PR | 4 | 4 |
| Proposed | 3 | 3 |
| Test Point | RMSE (cm) | ||
|---|---|---|---|
| AltDS-TWR | AltDS-TWR | Proposed | |
| (w/o Antenna Delay) | (w/Antenna Delay) | ||
| T1 | 18.96 | 5.66 | 8.79 |
| T2 | 20.03 | 5.42 | 10.35 |
| T3 | 20.44 | 8.11 | 9.9 |
| T4 | 20.07 | 7.99 | 8.1 |
| T5 | 21.92 | 7.18 | 9.76 |
| T6 | 18.07 | 4.96 | 7.02 |
| T7 | 18.15 | 6.75 | 9.94 |
| T8 | 18.39 | 4.71 | 8.57 |
| T9 | 20.78 | 8.68 | 10.07 |
| T10 | 21.55 | 8.14 | 8.91 |
| T11 | 18.2 | 4.48 | 7.67 |
| T12 | 20.12 | 6.38 | 7.53 |
| T13 | 17.88 | 4.89 | 7.98 |
| T14 | 16.61 | 5.97 | 9.54 |
| T15 | 20.08 | 7.03 | 9.43 |
| T16 | 18.91 | 6.9 | 8.85 |
| T17 | 16.61 | 6.82 | 9.82 |
| T18 | 16.37 | 2.78 | 5.92 |
| T19 | 17.83 | 3.83 | 7.25 |
| T20 | 17.82 | 3.82 | 6.86 |
| Maximum | 21.92 | 8.68 | 10.35 |
| Minimum | 16.37 | 2.78 | 5.92 |
| Average | 18.93 | 6.03 | 8.61 |
| Test Point | RMSE (cm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AltDS-TWR | AltDS-TWR | Proposed | ||||||||||
| (w/o Antenna Delay) | (w/Antenna Delay) | |||||||||||
| Coordinates | Position | Coordinates | Position | Coordinates | Position | |||||||
| x- | y- | z- | x- | y- | z- | x- | y- | z- | ||||
| T1 | 6.83 | 14.95 | 20.15 | 26 | 4.98 | 5.11 | 6.41 | 9.59 | 6.38 | 10.63 | 8.37 | 14.96 |
| T2 | 15.24 | 17.99 | 13.28 | 27.06 | 3.68 | 8.59 | 7.4 | 11.92 | 7.14 | 1.96 | 10.08 | 12.51 |
| T3 | 17.87 | 12.37 | 14.61 | 26.19 | 4.86 | 6.57 | 7.34 | 10.98 | 9.68 | 7.64 | 9.6 | 15.63 |
| T4 | 12.68 | 10.37 | 20.87 | 26.53 | 7.17 | 7.18 | 5.33 | 11.46 | 9.73 | 6.6 | 8.97 | 14.79 |
| T5 | 17.27 | 9.25 | 15.59 | 25.04 | 9.39 | 5.71 | 4.32 | 11.81 | 10.08 | 5.93 | 10.39 | 15.64 |
| T6 | 3.41 | 19.83 | 18.46 | 27.31 | 2.37 | 7.07 | 6.71 | 10.03 | 10.27 | 9.91 | 7.5 | 16.12 |
| T7 | 6.12 | 8.32 | 23.6 | 25.76 | 6.94 | 0.28 | 5.53 | 8.88 | 12.4 | 6.68 | 8.01 | 16.20 |
| T8 | 2.05 | 4.47 | 10.83 | 11.89 | 3.05 | 6.14 | 6.67 | 9.57 | 14.6 | 3.17 | 3.88 | 15.44 |
| T9 | 10.43 | 9.24 | 20.03 | 24.4 | 0.91 | 6.61 | 11 | 12.87 | 8.04 | 8.63 | 7.04 | 13.74 |
| T10 | 14.35 | 8.42 | 19.69 | 25.78 | 6.68 | 8.48 | 6.83 | 12.77 | 7.31 | 4.47 | 9.97 | 13.15 |
| T11 | 14.68 | 8.82 | 14.3 | 22.31 | 11.24 | 2.3 | 5.25 | 12.62 | 5.46 | 8.51 | 11.63 | 15.41 |
| T12 | 12.27 | 3.55 | 20.92 | 24.51 | 8.5 | 6.84 | 2.26 | 11.14 | 9.44 | 8.61 | 6.93 | 14.54 |
| T13 | 9.5 | 4.41 | 19.07 | 21.76 | 1.96 | 7.16 | 9.22 | 11.84 | 8.74 | 4.67 | 8.44 | 13.02 |
| T14 | 9.79 | 2.9 | 17.5 | 20.26 | 3.62 | 5.83 | 5.9 | 9.05 | 6.7 | 6.13 | 9.22 | 12.94 |
| T15 | 13.14 | 5.59 | 22.53 | 26.67 | 5.57 | 8.34 | 3.76 | 10.71 | 9.39 | 8.51 | 6.64 | 14.31 |
| T16 | 18 | 10.68 | 12.39 | 24.32 | 8.22 | 4.08 | 6.97 | 11.52 | 4.1 | 10.84 | 8.44 | 14.34 |
| T17 | 4.81 | 10.4 | 10.95 | 15.85 | 8.13 | 4.23 | 0.35 | 9.17 | 3.08 | 7.85 | 4.89 | 9.75 |
| T18 | 3.04 | 4.85 | 11.28 | 12.65 | 2.85 | 4.79 | 4.46 | 7.14 | 1.98 | 9.37 | 7.19 | 11.98 |
| T19 | 16.76 | 10.6 | 18.29 | 26.98 | 6.4 | 5.7 | 7.11 | 11.14 | 8.07 | 4.8 | 9.14 | 13.1 |
| T20 | 17.48 | 7.69 | 19.57 | 27.34 | 3.02 | 5.19 | 8.5 | 10.41 | 7.12 | 4.55 | 10.94 | 13.82 |
| Maximum | 18 | 19.83 | 23.6 | 27.34 | 11.24 | 8.59 | 11 | 12.87 | 14.6 | 10.84 | 11.63 | 16.2 |
| Minimum | 2.05 | 2.9 | 10.83 | 11.89 | 0.91 | 0.28 | 0.35 | 7.14 | 1.98 | 1.96 | 3.88 | 9.75 |
| Average | 11.28 | 9.24 | 17.2 | 23.43 | 5.47 | 5.81 | 6.07 | 10.73 | 7.99 | 6.97 | 8.36 | 14.07 |
| Ranging Scheme | Clock Synchronization | Air Efficient | Simultaneous Ranging | Signaling Messages (Constrained Reply-Delay Time) | Antenna Delay Calibration |
|---|---|---|---|---|---|
| SS-TWR | Not required | No | No | No | Required |
| SDS-TWR | Not required | No | No | Yes | Required |
| AltDS-TWR | Not required | No | No | No | Required |
| AltDS-TWR&PR | Not required | Yes | Yes | No | Required |
| Proposed | Not required | Yes | Yes | No | Not required |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.; Chaudhary, S.; Ullah, R.; Parnianifard, A.; Siddiqi, M.Z.; Vanichchanunt, P.; Santipach, W.; Wuttisittikulkij, L. Antenna Delay-Independent Simultaneous Ranging for UWB-Based RTLSs. J. Sens. Actuator Netw. 2023, 12, 1. https://doi.org/10.3390/jsan12010001
Shah S, Chaudhary S, Ullah R, Parnianifard A, Siddiqi MZ, Vanichchanunt P, Santipach W, Wuttisittikulkij L. Antenna Delay-Independent Simultaneous Ranging for UWB-Based RTLSs. Journal of Sensor and Actuator Networks. 2023; 12(1):1. https://doi.org/10.3390/jsan12010001
Chicago/Turabian StyleShah, Shashi, Sushank Chaudhary, Rizwan Ullah, Amir Parnianifard, Muhammad Zain Siddiqi, Pisit Vanichchanunt, Wiroonsak Santipach, and Lunchakorn Wuttisittikulkij. 2023. "Antenna Delay-Independent Simultaneous Ranging for UWB-Based RTLSs" Journal of Sensor and Actuator Networks 12, no. 1: 1. https://doi.org/10.3390/jsan12010001
APA StyleShah, S., Chaudhary, S., Ullah, R., Parnianifard, A., Siddiqi, M. Z., Vanichchanunt, P., Santipach, W., & Wuttisittikulkij, L. (2023). Antenna Delay-Independent Simultaneous Ranging for UWB-Based RTLSs. Journal of Sensor and Actuator Networks, 12(1), 1. https://doi.org/10.3390/jsan12010001








