A Lightweight Hybrid Scheme for Hiding Text Messages in Colour Images Using LSB, Lah Transform and Chaotic Techniques
Abstract
1. Introduction
- Invisibility, which denotes that the stego-image resembles the original image;
- Payload/capacity, which indicates the quantity of hidden data that can be held private in the cover medium;
- Robustness against statistical assaults, represented by the peak signal-to-noise ratio (PSNR) and mean square error (MSE), fidelity measures used to assess robustness against statistical attacks;
- Computation complexity, which is a calculation of the cost of embedding and extracting a secret message.
2. Related Work
3. Basic Concepts
3.1. Chaotic Map
3.1.1. Tent Map
3.1.2. Ikeda Map
3.1.3. The Proposed Hyperchaotic Map
- Using Equations (1) and (2), generate N keys using the Tent map;
- Rather than using the Y values in equation 4, apply the Tent map sequences as input to the Ikeda map to create its series;
- Use a distribution of values in the interval [0, 1];
3.2. Lah Transform
3.3. Least Significant Bit (LSB)
3.4. Lucas Series
4. Proposed Algorithms
4.1. Suggested Vector Partition Algorithm
- Convert the input text file to a decimal representation before converting it to binary form, then store it as vector V.
- Determine the length of the input vector V; let this be L.
- Set the lowest length permitted to MinL = 9 and the maximum length allowed to MaxL = 32 (values determined experimentally, as described in Remark 5).
- Perform the following steps for each value of vector V:
- a.
- Calculate the value of c, which is equal to mod (L, MaxL).
- b.
- If the value of c is greater than nine or equal to zero, use the equation MaxL = MaxL + 1. Otherwise, store the initial split length in the vector labelled “Elem,” as Elem(i) = c, then remove the amount of the cut-off c from the whole length L such that L = L − c.
- c.
- Amend the maximum allowed length according to the following equation: MaxL = round ((MaxL/3) ×2).
- d.
- Return to step a.
- Advance to the next stage with the result vector “Elem”, which will contain the suggested lengths of the original vector V.
4.2. Text Encryption Algorithm Proposal
- Read the text from the .txt file offered as input.
- Convert the read value from the ASCII code to the binary representation for each symbol in the read file.
- Combine the values in their binary format to form a single vector (V).
- Call the Suggested vector partition algorithm and save the results in the Elem vector.
- To shuffle the values for each segment length contained in Elem, perform the following steps:
- a.
- Determine the length Li from the vector Elem, and then read the values from the original vector with length Li.
- b.
- Change the placements of the values in the vector at Li. Put the elements in the even places first, followed by the items in the odd positions.
- c.
- The main transition is performed by utilising the values produced in the Lucas series, which offers position indication for the values in the vector. Every two sequentially created values are thus swapped.
- d.
- Slip to the right by two locations to rotate the generated values in the final vector.
- Convert all eight bits from binary to decimal representation, and then convert these to ASCII code.
- Place the ciphertext generated by the encryption procedure in a new.txt file.
4.3. Suggested Hiding Algorithm
- Read the encrypted text file and transform it from ASCII format to decimal format, then save it in vector format.
- Convert each decimal value in the vector element to a binary representation and save each binary data point (0 or 1) in a unique location within the encrypted text file’s value vector.
- Read the pixels in the cover colour image, and split them into red, green, and blue channels.
- Create a series of random values with a length equal to the number of values included in each channel of the colour image by using a hyperchaotic map with a range of 1 to 255.
- Arrange the produced random values in ascending order and save each value’s index in a new result vector for later use.
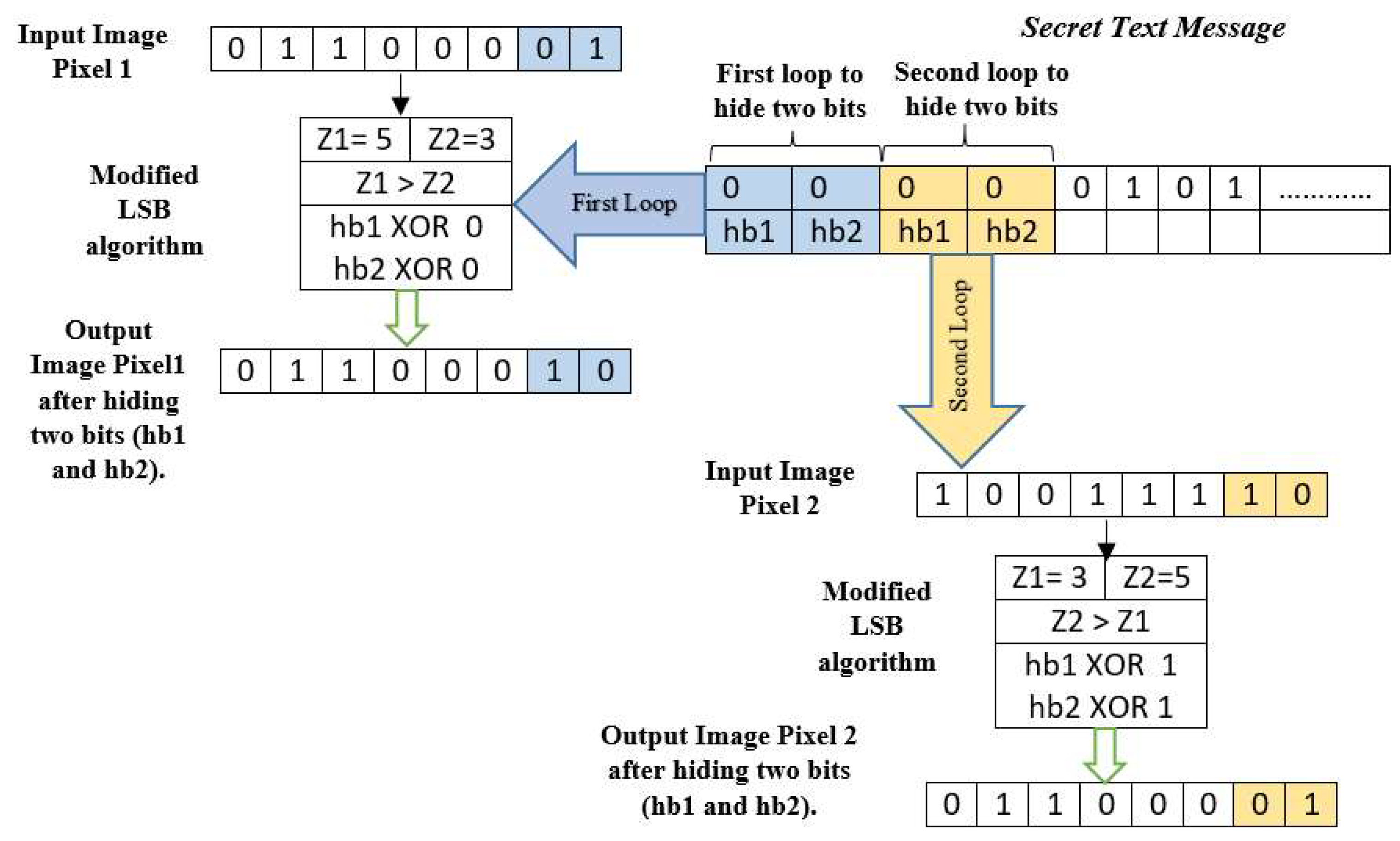
- For each of the three channels (red, green, and blue), complete the following steps (Figure 2 illustrates the modified LSB from step 6a to 6j):
- a.
- Choose two values from the bit vector to hide (hb1, hb2).
- b.
- Convert these values from a binary matrix to a one-dimensional vector.
- c.
- Select four values from the full vector of values, depending on the ascending vector of the indexes, and then apply the Lah transform.
- d.
- Convert each new value of the four output values of the Lah transformation from decimal to binary representation.
- e.
- Determine the number of zeros (Z1) and ones (Z2) in the binary representation, excluding the last two bits.
- f.
- If (Z1) is greater than (Z2), apply the following equations: X1 = XOR(hb1,0), X2 = XOR(hb2,0)
- g.
- Place the first new value, X1, in position 1 of the binary representation of the value, and the second new value, X2, in position 2 of the binary representation.
- h.
- If (Z2) is greater than or equal to (Z1), apply the following equations: X1 = XOR(hb1,1), X2 = XOR(hb2,1)
- i.
- Hide the first new value, X1, in position 1 of the binary representation of the value, and the second new value, X2, in position 2 of the binary representation.
- j.
- Return the updated value after concealment to a decimal representation
- k.
- To access these values, perform an inverse Lah transformation and store these to the same positions inside the overall image value pixel.
- l.
- Convert the resultant vector into a matrix.
- Combine the three resulting matrices into a single image that reflects the final image post steganography technique.
4.4. Recovery Procedure
- Read the pixels in the stego colour image, and split them into red, green, and blue channels.
- Arrange the resulting series of random values in ascending order and save each value’s index in a new result vector for later use.
- For each of the three channels (red, green, and blue), complete the following:
- a.
- Convert values from a binary matrix to a one-dimensional vector.
- b.
- Select four values from the full vector of values based on the ascending vector of the indexes, and then apply the Lah transform.
- c.
- Convert each new value of the four output values of the Lah transformation from decimal to binary representation.
- d.
- Determine the number of zeros (Z1) and ones (Z2) in the binary representation, except for the last two bits.
- 1-
- If (Z1) is greater than (Z2), perform the following steps: read the first value X1 in position 1 of the binary representation of the value and the second value X2 in position 2 of the binary representation to restore the hidden text bits (hb1, hb2) in the form hb1 = XOR(X1,0), hb2 = XOR(X2,0).
- 2-
- If (Z2) is larger than or equal to (Z1), then restore the first value X1 in position 1 of the binary representation of the value and the second value X2 in position 2 of the binary representation (hb1, hb2) as follows: hb1 = XOR(X1,0), hb2 = XOR(X2,0).
- 3-
- Arrange all restored binary values into the result vector until the text file’s requested length is reached.
- 4-
- Return the updated value after restoring it to a decimal representation.
- 5-
- To get the actual values, perform the inverse Lah transformation and store the results to the same positions inside the overall image value pixel.
- 6-
- Convert the resultant vector to a matrix.
- e.
- Transform the restored result vector from binary format to decimal format, then to ASCII format.
- f.
- Save the text vector in ASCII codes in the file as encrypted text.
- g.
- Combine the three resulting matrices into a single image that reflects the final image.
4.5. Suggested Decryption Mechanism
- Read the text from the .txt file input.
- Convert the read value from the ASCII code to a decimal representation and then to a binary representation for each symbol in the read file.
- Combine the values in their binary format to form a single vector (V).
- Call the suggested vector partition algorithm and save the results in the Elem vector.
- To shuffle the values for each segment length contained in the Elem, perform the following steps:
- a.
- Calculate Li (the length) from the vector Elem, and then extract the values from the original vector of length Li.
- b.
- To rotate the produced values in the final vector to their original locations, shift left two locations.
- c.
- The transition is carried out by employing the values generated by the Lucas series, which indicate the locations of the values in the vector. Every two values produced are thus consecutively swapped.
- d.
- Modify the values’ places in the vector at Li, placing the elements in the odd places first, followed by the items in the even places.
- Convert all eight bits from binary to decimal representation, and then to ASCII code.
- Place the deciphered text generated after the decryption procedure in a new .txt file.
5. Experimental Results
5.1. MSE and PSNR Measures
5.2. Structural Similarity Index (SSIM)
5.3. Normalised Cross Correlation (NCC)
5.4. Root Mean Square Error (RMSE)
5.5. Correlation Coefficient (CC)
5.6. Bias
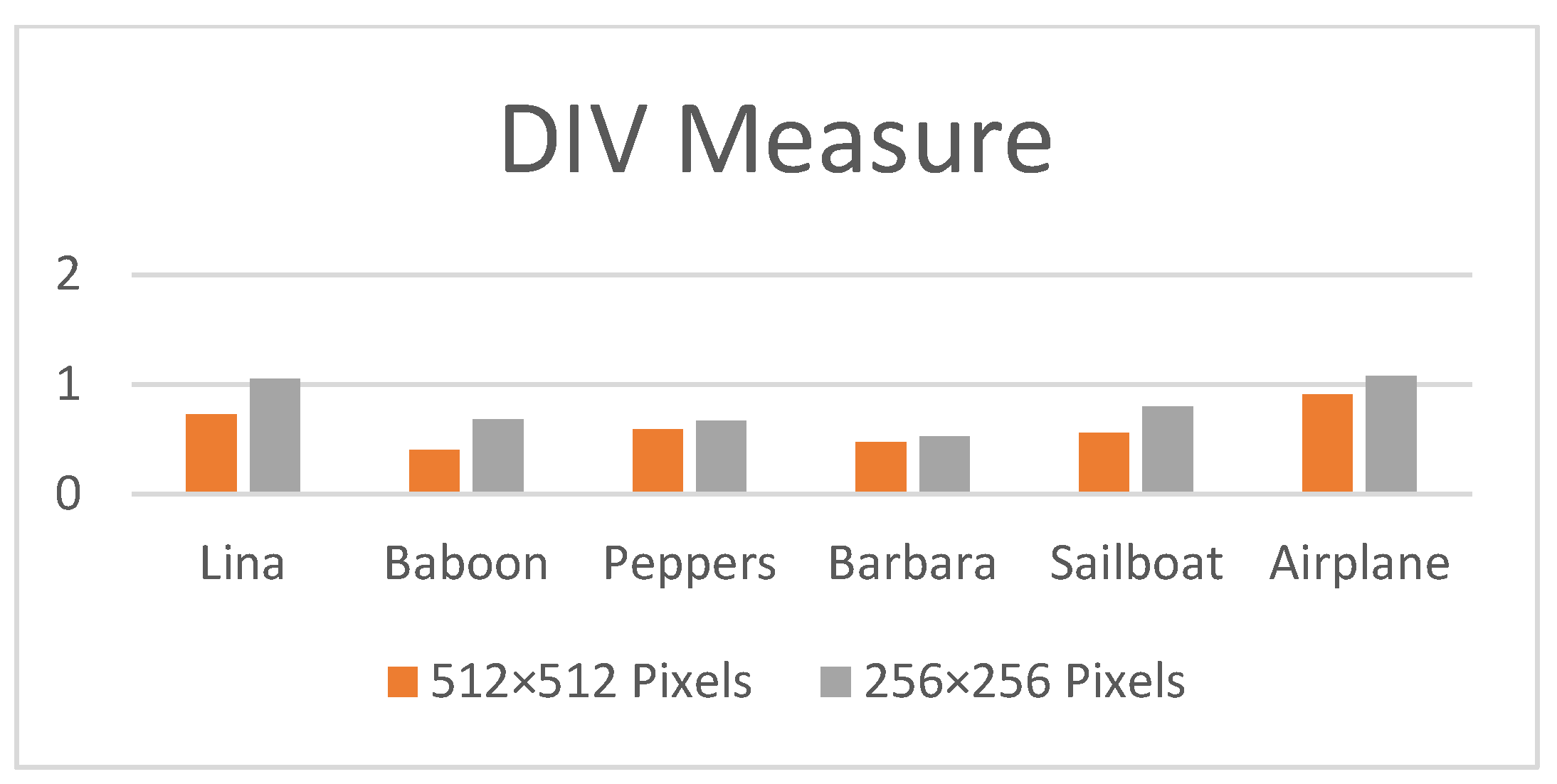
5.7. Difference in Variance (DIV)
5.8. Structural Contents (SC)
5.9. Entropy Differential
5.10. Local Quality Index (LQI)
5.11. Average Difference (AD)
5.12. Maximum Difference (MD)
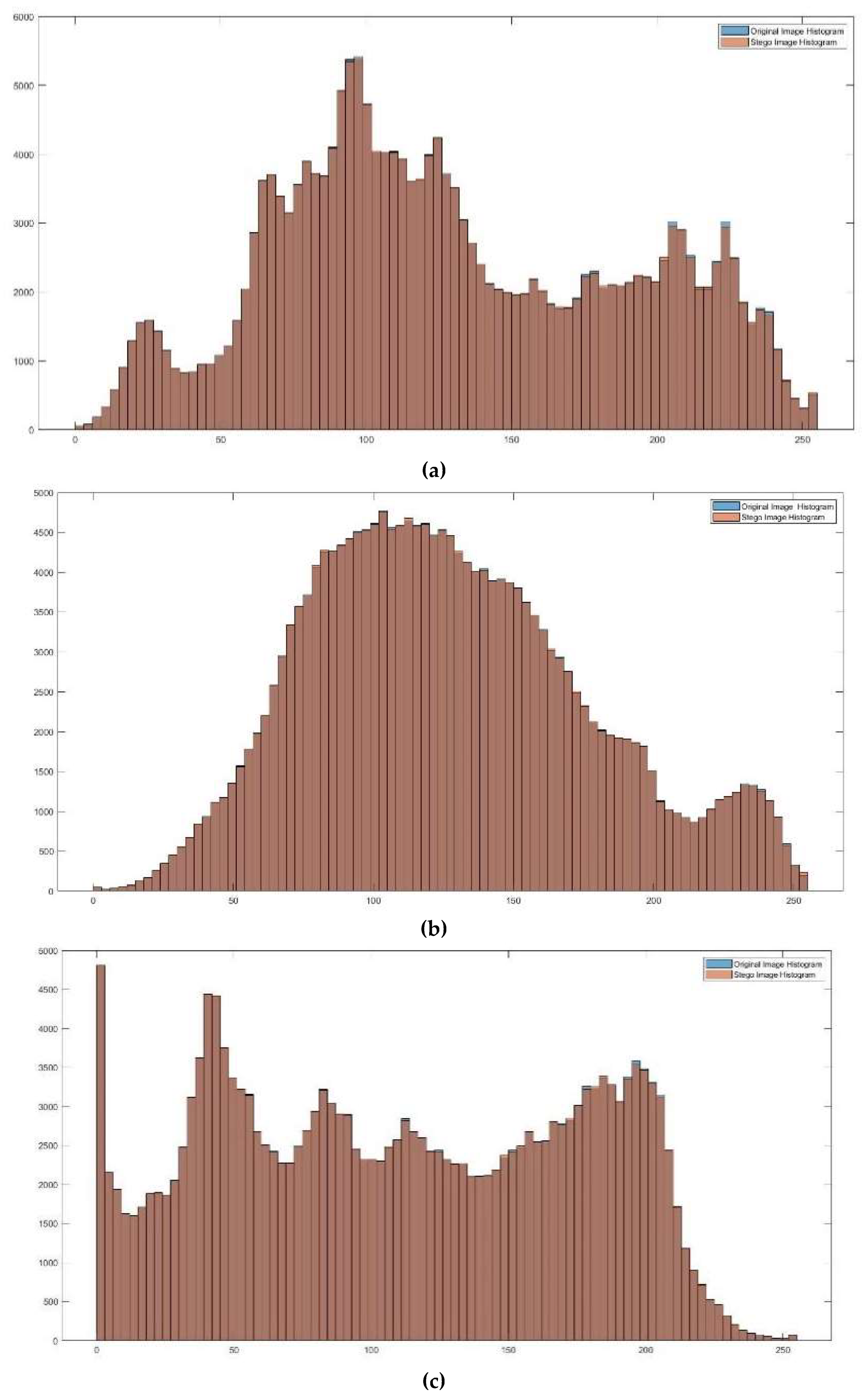
5.13. Histogram
5.14. Information Entropy
5.15. Implementation Time
5.16. Analysis of Data Steganography Method by Distance
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ambika; Biradar, R.L.; Burkpalli, V. Encryption-Based Steganography of Images by Multiobjective Whale Optimal Pixel Selection. Int. J. Comput. Appl. 2019, 1–10. [Google Scholar] [CrossRef]
- Al Sibahee, M.A.; Lu, S.; Abduljabbar, Z.A.; Liu, X.; Abdalla, H.B.; Hussain, M.A.; Hussien, Z.A.; Jassim Ghrabat, M.J. Lightweight Secure Message Delivery for E2E S2S Communication in the IoT-Cloud System. IEEE Access 2020, 8, 218331–218347. [Google Scholar] [CrossRef]
- Gulve, A.K.; Joshi, M.S. An Image Steganography Method Hiding Secret Data into Coefficients of Integer Wavelet Transform Using Pixel Value Differencing Approach. Math. Probl. Eng. 2015, 2015, 684824. [Google Scholar] [CrossRef]
- Fateh, M.; Rezvani, M.; Irani, Y. A New Method of Coding for Steganography Based on LSB Matching Revisited. Secur. Commun. Netw. 2021, 2021, 6610678. [Google Scholar] [CrossRef]
- Nagaraj, V.; Vijayalakshmi, V.; Zayaraz, G. Color Image Steganography Based on Pixel Value Modification Method Using Modulus Function. IERI Procedia 2013, 4, 17–24. [Google Scholar] [CrossRef]
- Sahu, A.K.; Sahu, M. Digital Image Steganography and Steganalysis: A Journey of the Past Three Decades. Open Comput. Sci. 2020, 10, 296–342. [Google Scholar] [CrossRef]
- Abdullah, S.M.; Abduljaleel, I.Q. Speech Encryption Technique Using S-Box Based on Multi Chaotic Maps. TEM J. 2021, 10, 1429–1434. [Google Scholar] [CrossRef]
- Islam, M.R.; Tanni, T.R.; Parvin, S.; Sultana, M.J.; Siddiqa, A. A Modified LSB Image Steganography Method Using Filtering Algorithm and Stream of Password. Inf. Secur. J. A Glob. Perspect. 2021, 30, 359–370. [Google Scholar] [CrossRef]
- El-Khamy, S.E.; Korany, N.O.; Mohamed, A.G. A New Fuzzy-DNA Image Encryption and Steganography Technique. IEEE Access 2020, 8, 148935–148951. [Google Scholar] [CrossRef]
- Priyadharshini, A.; Umamaheswari, R.; Jayapandian, N.; Priyananci, S. Securing Medical Images Using Encryption and LSB Steganography. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19 February 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Gedkhaw, E.; Soodtoetong, N.; Ketcham, M. The Performance of Cover Image Steganography for Hidden Information within Image File Using Least Significant Bit Algorithm. In Proceedings of the 2018 18th International Symposium on Communications and Information Technologies (ISCIT), Bangkok, Thailand, 26–29 September 2018; pp. 504–508. [Google Scholar] [CrossRef]
- Cemkasapbaşi, M.; Elmasry, W. New LSB-Based Colour Image Steganography Method to Enhance the Efficiency in Payload Capacity, Security and Integrity Check. Sādhanā 2018, 43, 68. [Google Scholar] [CrossRef]
- Kasapbasi, M.C. A New Chaotic Image Steganography Technique Based on Huffman Compression of Turkish Texts and Fractal Encryption with Post-Quantum Security. IEEE Access 2019, 7, 148495–148510. [Google Scholar] [CrossRef]
- Darbani, A.; AlyanNezhadi, M.M.; Forghani, M. A New Steganography Method for Embedding Message in JPEG Images. In Proceedings of the 2019 5th Conference on Knowledge Based Engineering and Innovation (KBEI), Tehran, Iran, 28 February–1 March 2019; pp. 617–621. [Google Scholar] [CrossRef]
- Joshi, K.; Gill, S.; Yadav, R. A New Method of Image Steganography Using 7th Bit of a Pixel as Indicator by Introducing the Successive Temporary Pixel in the Gray Scale Image. J. Comput. Netw. Commun. 2018, 2018, 9475142. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Jin, H.; Hussien, Z.A.; Yassin, A.A.; Hussain, M.A.; Abbdal, S.H.; Zou, D. Robust Image Document Authentication Code with Autonomous Biometrie Key Generation, Selection, and Updating in Cloud Environment. In Proceedings of the 2015 11th International Conference on Information Assurance and Security (IAS), Marrakech, Morocco, 14–16 December 2015; pp. 61–66. [Google Scholar] [CrossRef]
- Amakdouf, H.; Zouhri, A.; EL Mallahi, M.; Qjidaa, H. Color Image Analysis of Quaternion Discrete Radial Krawtchouk Moments. Multimed. Tools Appl. 2020, 79, 26571–26586. [Google Scholar] [CrossRef]
- Amakdouf, H.; Zouhri, A.; El Mallahi, M.; Tahiri, A.; Chenouni, D.; Qjidaa, H. Artificial Intelligent Classification of Biomedical Color Image Using Quaternion Discrete Radial Tchebichef Moments. Multimed. Tools Appl. 2021, 80, 3173–3192. [Google Scholar] [CrossRef]
- Saad, A.H.S.; Mohamed, M.S.; Hafez, E.H. Coverless Image Steganography Based on Optical Mark Recognition and Machine Learning. IEEE Access 2021, 9, 16522–16531. [Google Scholar] [CrossRef]
- Hashim, M.M.; Rahim, M.S.M. Image Steganography Based on Odd/Even Pixels Distribution Scheme and Two Parameters Random Function. J. Theor. Appl. Inf. Technol. 2017, 95, 5977–5986. [Google Scholar]
- Harahap, M.K.; Khairina, N. Dynamic Steganography Least Significant Bit with Stretch on Pixels Neighborhood. JISEBI 2020, 6, 151. [Google Scholar] [CrossRef]
- Hussein, H.L.; Abbass, A.A.; Naji, S.A.; Al-augby, S.; Lafta, J.H. Hiding Text in Gray Image Using Mapping Technique. J. Phys. Conf. Ser. 2018, 1003, 012032. [Google Scholar] [CrossRef]
- Almayyahi, A.A.; Sulaiman, R.; Qamar, F.; Essa, A. High-Security Image Steganography Technique Using XNOR Operation and Fibonacci Algorithm. IJACSA 2020, 11. [Google Scholar] [CrossRef]
- Ratnasari, D.; Aji, A.S. Text to Color Image Steganography Using LSB Technique and XOR Operations. Int. J. Appl. Bus. Inf. Syst. 2019, 3, 59–65. [Google Scholar]
- Madhu, D.; Vasuhi, S. Image Steganography: 2-Bit XOR Algorithm Used in YCbCr Color Model with Crypto-Algorithm. In Proceedings of the 2020 4th International Conference on Computer, Communication and Signal Processing (ICCCSP), Chennai, India, 28 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Nassif Jassim, K.; Khudhur Nsaif, A.; Kuder Nseaf, A.; Hazidar, A.H.; Priambodo, B.; Naf’an, E.; Masril, M.; Handriani, I.; Pratama Putra, Z. Hybrid Cryptography and Steganography Method to Embed Encrypted Text Message within Image. J. Phys. Conf. Ser. 2019, 1339, 012061. [Google Scholar] [CrossRef]
- Sulaiman, R.; Kirana, C.; Sugihartono, T.; Juniawan, F.P. RC4 Algorithm and Steganography to Double Secure Messages in Digital Image. In Proceedings of the 2020 8th International Conference on Cyber and IT Service Management (CITSM), Pangkal Pinang, Indonesia, 23–24 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Muhammad, K.; Ahmad, J.; Farman, H.; Zubair, M. A Novel Image Steganographic Approach for Hiding Text in Color Images Using HSI Color Model. arXiv 2015, arXiv:1503.00388. [Google Scholar]
- Ronaldo Cahyono, H.K.; Atika Sari, C.; Ignatius Moses Setiadi, D.R.; Hari Rachmawanto, E. Dual Protection on Message Transmission Based on Chinese Remainder Theorem and Rivest Cipher 4. In Proceedings of the 2019 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 24–25 July 2019; pp. 74–78. [Google Scholar] [CrossRef]
- Jaradat, A.; Taqieddin, E.; Mowafi, M. A High-Capacity Image Steganography Method Using Chaotic Particle Swarm Optimization. Secur. Commun. Netw. 2021, 2021, 6679284. [Google Scholar] [CrossRef]
- Vishwas, C.G.M.; Kunte, R.S. An Image Cryptosystem Based on Tent Map. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; pp. 1069–1073. [Google Scholar] [CrossRef]
- Zhu, C.; Sun, K. Cryptanalyzing and Improving a Novel Color Image Encryption Algorithm Using RT-Enhanced Chaotic Tent Maps. IEEE Access 2018, 6, 18759–18770. [Google Scholar] [CrossRef]
- Tayel, M.; Dawood, G.; Shawky, H. Block Cipher S-Box Modification Based on Fisher-Yates Shuffle and Ikeda Map. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 59–64. [Google Scholar] [CrossRef]
- Sekertekin, Y.; Atan, O. An Image Encryption Algorithm Using Ikeda and Henon Chaotic Maps. In Proceedings of the 2016 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Alanazi, A.S. A Dual Layer Secure Data Encryption and Hiding Scheme for Color Images Using the Three-Dimensional Chaotic Map and Lah Transformation. IEEE Access 2021, 9, 26583–26592. [Google Scholar] [CrossRef]
- Emad, E.; Safey, A.; Refaat, A.; Osama, Z.; Sayed, E.; Mohamed, E. A Secure Image Steganography Algorithm Based on Least Significant Bit and Integer Wavelet Transform. J. Syst. Eng. Electron. 2018, 29, 639. [Google Scholar] [CrossRef]
- Wazirali, R.; Alasmary, W.; Mahmoud, M.M.E.A.; Alhindi, A. An Optimized Steganography Hiding Capacity and Imperceptibly Using Genetic Algorithms. IEEE Access 2019, 7, 133496–133508. [Google Scholar] [CrossRef]
- Pund-Dange, S.; Desai, C.G. Data Hiding Technique Using Catalan-Lucas Number Sequence. Indian J. Sci. Technol. 2017, 10, 1–6. [Google Scholar] [CrossRef]
- Güney Duman, M.; Duman, M. Encryption and Decryption of the Data by Using the Terms of the Lucas Series. Duzce Univ. J. Sci. Technol. 2021, 9, 1–7. [Google Scholar] [CrossRef]
- El Hanouti, I.; El Fadili, H.; Zenkouar, K. Breaking an Image Encryption Scheme Based on Arnold Map and Lucas Series. Multimed. Tools Appl. 2021, 80, 4975–4997. [Google Scholar] [CrossRef]
- Ehsan Ali, U.A.M.; Ali, E.; Sohrawordi, M.; Sultan, M.N. A LSB Based Image Steganography Using Random Pixel and Bit Selection for High Payload. IJMSC 2021, 7, 24–31. [Google Scholar] [CrossRef]
- Kordov, K.; Zhelezov, S. Steganography in Color Images with Random Order of Pixel Selection and Encrypted Text Message Embedding. PeerJ Comput. Sci. 2021, 7, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Zouhri, A.; Amakdouf, H.; El Mallahi, M.; Tahiri, A.; Lakhliai, Z.; Chenouni, D.; Qjidaa, H. Invariant Gaussian–Hermite Moments Based Neural Networks for 3D Object Classification. Pattern Recognit. Image Anal. 2020, 30, 87–96. [Google Scholar] [CrossRef]
- El Mallahi, M.; Zouhri, A.; El Affar, A.; Tahiri, A.; Qjidaa, H. Radial Hahn Moment Invariants for 2D and 3D Image Recognition. Int. J. Autom. Comput. 2018, 15, 277–289. [Google Scholar] [CrossRef]
- Boukili, B.; Mallahi, M.E.; Amrani, A.; Zouhri, A.; Boumhidi, I.; Hmamed, A. A New Approach for H∞ Deconvolution Filtering of 2D Systems Described by the Fornasini–Marchesini and Discrete Moments. Pattern Anal. Appl. 2022, 25, 63–76. [Google Scholar] [CrossRef]
- Boukili, B.; Mallahi, M.E.; El-Amrani, A.; Hmamed, A.; Boumhidi, I. H∞ Deconvolution Filter for Two-dimensional Numerical Systems Using Orthogonal Moments. Optim. Control. Appl. Meth. 2021, 42, 1337–1348. [Google Scholar] [CrossRef]
- El Mallahi, M.; Boukili, B.; Zouhri, A.; Hmamed, A.; Qjidaa, H. Robust H∞ Deconvolution Filtering of 2-D Digital Systems of Orthogonal Local Descriptor. Multimed. Tools Appl. 2021, 80, 25965–25983. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Abduljaleel, I.Q.; Ma, J.; Sibahee, M.A.A.; Nyangaresi, V.O.; Honi, D.G.; Abdulsada, A.I.; Jiao, X. Provably Secure and Fast Color Image Encryption Algorithm Based on S-Boxes and Hyperchaotic Map. IEEE Access 2022, 10, 26257–26270. [Google Scholar] [CrossRef]
- Dhawan, S.; Chakraborty, C.; Frnda, J.; Gupta, R.; Rana, A.K.; Pani, S.K. SSII: Secured and High-Quality Steganography Using Intelligent Hybrid Optimization Algorithms for IoT. IEEE Access 2021, 9, 87563–87578. [Google Scholar] [CrossRef]
- Sugiarto, B.; Sari, C.A.; De Rosal, I.M.S.; Rachmawanto, E.H. Performance Analysis of LSB Color Image Steganography Based on Embedding Pattern of the RGB Channels. In Proceedings of the 2020 International Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 19 September 2020; pp. 73–78. [Google Scholar] [CrossRef]
- Giuclea, M.; Popescu, C.-C. On Geometric Mean and Cumulative Residual Entropy for Two Random Variables with Lindley Type Distribution. Mathematics 2022, 10, 1499. [Google Scholar] [CrossRef]
- Das, P.; Ray, S.; Das, A. An Efficient Embedding Technique in Image Steganography Using Lucas Sequence. IJIGSP 2017, 9, 51–58. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, A.; Ghosal, S.K.; Sarkar, R. LSB Based Steganography with OCR: An Intelligent Amalgamation. Multimed. Tools Appl. 2020, 79, 11747–11765. [Google Scholar] [CrossRef]








| Static Meters | Between cover Image and Stego Image (256 × 256 Pixels) | Between cover Image and Stego Image (512 × 512 Pixels) | Embedded (Byte) | Percentage Ratio used from Image File (256 × 256 Pixels) for Hiding Information | Percentage Ratio used from Image File (512 × 512 Pixels) for Hiding Information | ||||
|---|---|---|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | ||||
| PSNR | 44.9771 | INF | INF | 51.0322 | INF | INF | 2000 | 10.200% | 32.227% |
| 37.9191 | INF | INF | 43.9355 | INF | INF | 10,000 | 2.040% | 6.445% | |
| 35.7730 | 49.7083 | INF | 41.6130 | INF | INF | 17,000 | 1.200% | 3.791% | |
| MSE | 2.0671 | 0 | 0 | 0.5127 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 10.4995 | 0 | 0 | 2.6274 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 17.2100 | 0.6954 | 0 | 4.4852 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| RMSE | 1.2242 | 0 | 0 | 0.4356 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 3.1435 | 0 | 0 | 1.4198 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 4.0733 | 0.5076 | 0 | 1.9580 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| NCC | 1 | 1 | 1 | 1 | 1 | 1 | 2000 | 10.200% | 32.227% |
| 1 | 1 | 1 | 1 | 1 | 1 | 10,000 | 2.040% | 6.445% | |
| 1 | 1 | 1 | 1 | 1 | 1 | 17,000 | 1.200% | 3.791% | |
| SSIM | 0.9875 | 1 | 1 | 0.9991 | 1 | 1 | 2000 | 10.200% | 32.227% |
| 0.9394 | 1 | 1 | 0.9956 | 1 | 1 | 10,000 | 2.040% | 6.445% | |
| 0.9069 | 0.9959 | 1 | 0.9926 | 1 | 1 | 17,000 | 1.200% | 3.791% | |
| Bias | 0.0008 | 0 | 0 | 0.0003 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 0.0019 | 0 | 0 | 0.0009 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 0.0026 | 0.0008 | 0 | 0.0013 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| DIV | 0.3650 | 0 | 0 | 0.2209 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 0.7981 | 0 | 0 | 0.5798 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 1.0512 | 0.1316 | 0 | 0.7261 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| CC | 0.9996 | 1 | 1 | 0.9999 | 1 | 1 | 2000 | 10.200% | 32.227% |
| 0.9978 | 1 | 1 | 0.9995 | 1 | 1 | 10,000 | 2.040% | 6.445% | |
| 0.9965 | 0.9999 | 1 | 0.9991 | 1 | 1 | 17,000 | 1.200% | 3.791% | |
| SC | 1 | 1 | 1 | 1 | 1 | 1 | 2000 | 10.200% | 32.227% |
| 1 | 1 | 1 | 1 | 1 | 1 | 10,000 | 2.040% | 6.445% | |
| 1 | 0.9999 | 1 | 1 | 1 | 1 | 17,000 | 1.200% | 3.791% | |
| Entropy Diff | 0.0547 | 0 | 0 | 0.0248 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 0.1935 | 0 | 0 | 0.0939 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 0.2755 | 0.0209 | 0 | 0.1462 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| Local Quality Index | 0.9564 | 1 | 1 | 0.9740 | 1 | 1 | 2000 | 10.200% | 32.227% |
| 0.8484 | 1 | 1 | 0.8919 | 1 | 1 | 10,000 | 2.040% | 6.445% | |
| 0.8006 | 0.9856 | 1 | 0.8434 | 1 | 1 | 17,000 | 1.200% | 3.791% | |
| AD | 0.0041 | 0 | 0 | −0.0009 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 0.0322 | 0 | 0 | 0.0057 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 0.0570 | −0.0034 | 0 | 0.0079 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| MD | 25 | 0 | 0 | 26 | 0 | 0 | 2000 | 10.200% | 32.227% |
| 26 | 0 | 0 | 26 | 0 | 0 | 10,000 | 2.040% | 6.445% | |
| 26 | 26 | 0 | 26 | 0 | 0 | 17,000 | 1.200% | 3.791% | |
| Image Name | Algorithm | Embedded (Bytes) | Image Size in Pixel | PSNR | MSE | Bias | SSIM |
|---|---|---|---|---|---|---|---|
| Lina | Proposed Algorithm | 100 | 256 × 256 | 58.7705 | 0.0863 | 0.00006 | 0.9994 |
| Lina | Proposed Algorithm | 100 | 512 × 512 | 64.4197 | 0.0235 | 0.00001 | 1 |
| Lina | [39] | 100 | 128 × 128 | 50.95 | 0.52 | - | 0.9990 |
| Lina | [35] | Not Determined | 256 × 256 | - | - | 0.0004 | 0.9651 |
| Entropy Type | Measurement Equation | Notes |
|---|---|---|
| Shannon Entropy | Where Pr represent probability, X represent cover image, Y represent stego image. | |
| Joint Entropy | ||
| Mutual Entropy | ||
| Relative Entropy | ||
| Conditional Entropy |
| Entropy Types | Proposed Algorithm WhenImage Size (256 × 256 Pixels) | Proposed Algorithm When Image Size (512 × 512 Pixels) | Embedded (byte) | ||
|---|---|---|---|---|---|
| Shannon Entropy | 7.4467 | 7.4470 | 7.4440 | 7.4442 | 2000 |
| 7.4467 | 7.4494 | 7.4440 | 7.4448 | 10,000 | |
| 7.4467 | 7.4526 | 7.4440 | 7.4450 | 17,000 | |
| Joint Entropy | 7.7963 | 22.2293 | 2000 | ||
| 8.7536 | 23.6106 | 10,000 | |||
| 9.3451 | 24.5933 | 17,000 | |||
| Mutual Entropy | 7.0977 | 21.3240 | 2000 | ||
| 6.1453 | 19.9479 | 10,000 | |||
| 5.5600 | 18.9670 | 17,000 | |||
| Relative Entropy | 0.0006 | 0.0003 | 2000 | ||
| 0.0009 | 0.0007 | 10,000 | |||
| 0.0037 | 0.0021 | 17,000 | |||
| Conditional Entropy | 0.3496 | −13.8790 | 2000 | ||
| 1.3069 | −12.4977 | 10,000 | |||
| 1.8984 | −11.5150 | 17,000 | |||
| Entropy Types | Proposed Algorithm | [35] | ||
|---|---|---|---|---|
| Shannon Entropy | 7.4467 | 7.4526 | 7.7330 | 7.7348 |
| Joint Entropy | 9.3451 | 9.4260 | ||
| Mutual Entropy | 5.5600 | 6.0147 | ||
| Relative Entropy | 0.0037 | 0.0009 | ||
| Conditional Entropy | 1.8984 | 1.6912 | ||
| Time (Second) | Image Size (256 × 256 Pixels) | Image Size (512 × 512 Pixels) | Embedded (byte) |
|---|---|---|---|
| Hiding Time | 3.7092 | 9. 9262 | 2000 |
| 3.8942 | 9.8410 | 10,000 | |
| 3.8141 | 9.9572 | 17,000 | |
| Recovery Time | 3.9100 | 10.0100 | 2000 |
| 3.9921 | 10.4015 | 10,000 | |
| 3.9704 | 10.7510 | 17,000 |
| Distance Metric | Image Size (256 × 256 Pixels) | Image Size (512 × 512 Pixels) | Embedded (byte) |
|---|---|---|---|
| Euclidean Distance | 0.0123 | 0.0126 | 2000 |
| 0.0051 | 0.0055 | 10,000 | |
| 0.0040 | 0.0042 | 17,000 | |
| Mean Squared Euclidean Distance | 0 | 0 | 2000 |
| 0 | 0 | 10,000 | |
| 0 | 0 | 17,000 | |
| Squared Euclidean Distance | 0.00015251 | 0.00015838 | 2000 |
| 0.00002651 | 0.00002983 | 10,000 | |
| 0.00001609 | 0.00001765 | 17,000 | |
| Mean Euclidean Distance | 0 | 0 | 2000 |
| 0 | 0 | 10,000 | |
| 0 | 0 | 17,000 | |
| Manhattan Distance | 878 | 858 | 2000 |
| 2010 | 1950 | 10,000 | |
| 2628 | 2512 | 17,000 | |
| Cosine Distance | 0.000117 | 0.00000706 | 2000 |
| 0.000686 | 0.00003798 | 10,000 | |
| 0.0011 | 0.00006436 | 17,000 | |
| Correlation Distance | 0.00039434 | 0.00002105 | 2000 |
| 0.0019 | 0.00010865 | 10,000 | |
| 0.0030 | 0.00018696 | 17,000 | |
| Mean Pattern Intensity | 0.000072 | 0.00000092 | 2000 |
| 0.000317 | 0.00000803 | 10,000 | |
| 0.009320 | 0.00007749 | 17,000 | |
| Earth Mover Distance | 0.0112 | 0.0044 | 2000 |
| 0.0432 | 0.0155 | 10,000 | |
| 0.0519 | 0.0158 | 17,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abduljaleel, I.Q.; Abduljabbar, Z.A.; Al Sibahee, M.A.; Ghrabat, M.J.J.; Ma, J.; Nyangaresi, V.O. A Lightweight Hybrid Scheme for Hiding Text Messages in Colour Images Using LSB, Lah Transform and Chaotic Techniques. J. Sens. Actuator Netw. 2022, 11, 66. https://doi.org/10.3390/jsan11040066
Abduljaleel IQ, Abduljabbar ZA, Al Sibahee MA, Ghrabat MJJ, Ma J, Nyangaresi VO. A Lightweight Hybrid Scheme for Hiding Text Messages in Colour Images Using LSB, Lah Transform and Chaotic Techniques. Journal of Sensor and Actuator Networks. 2022; 11(4):66. https://doi.org/10.3390/jsan11040066
Chicago/Turabian StyleAbduljaleel, Iman Qays, Zaid Ameen Abduljabbar, Mustafa A. Al Sibahee, Mudhafar Jalil Jassim Ghrabat, Junchao Ma, and Vincent Omollo Nyangaresi. 2022. "A Lightweight Hybrid Scheme for Hiding Text Messages in Colour Images Using LSB, Lah Transform and Chaotic Techniques" Journal of Sensor and Actuator Networks 11, no. 4: 66. https://doi.org/10.3390/jsan11040066
APA StyleAbduljaleel, I. Q., Abduljabbar, Z. A., Al Sibahee, M. A., Ghrabat, M. J. J., Ma, J., & Nyangaresi, V. O. (2022). A Lightweight Hybrid Scheme for Hiding Text Messages in Colour Images Using LSB, Lah Transform and Chaotic Techniques. Journal of Sensor and Actuator Networks, 11(4), 66. https://doi.org/10.3390/jsan11040066






