Floral Complexity Traits as Predictors of Plant-Bee Interactions in a Mediterranean Pollination Web
Abstract
1. Introduction
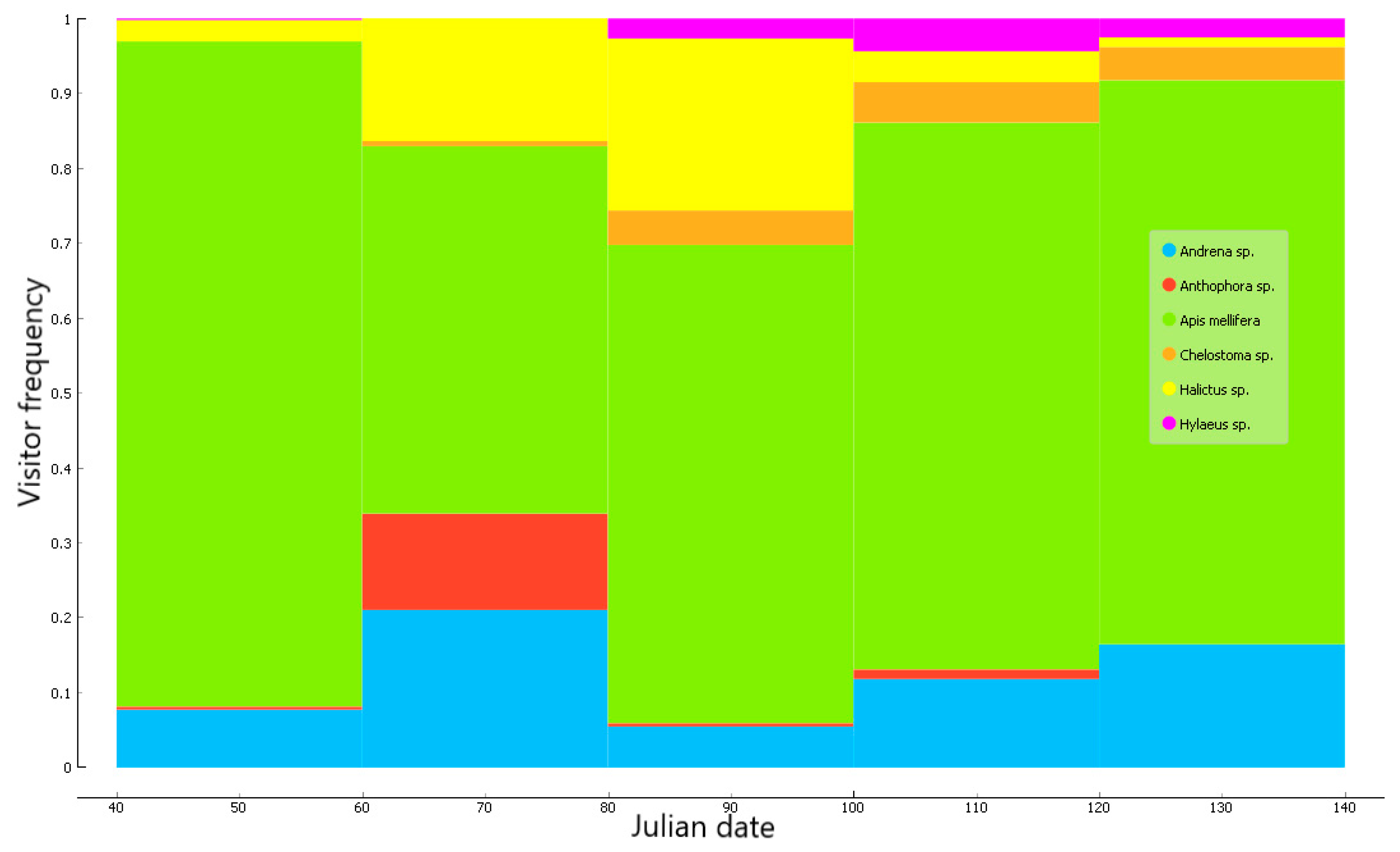
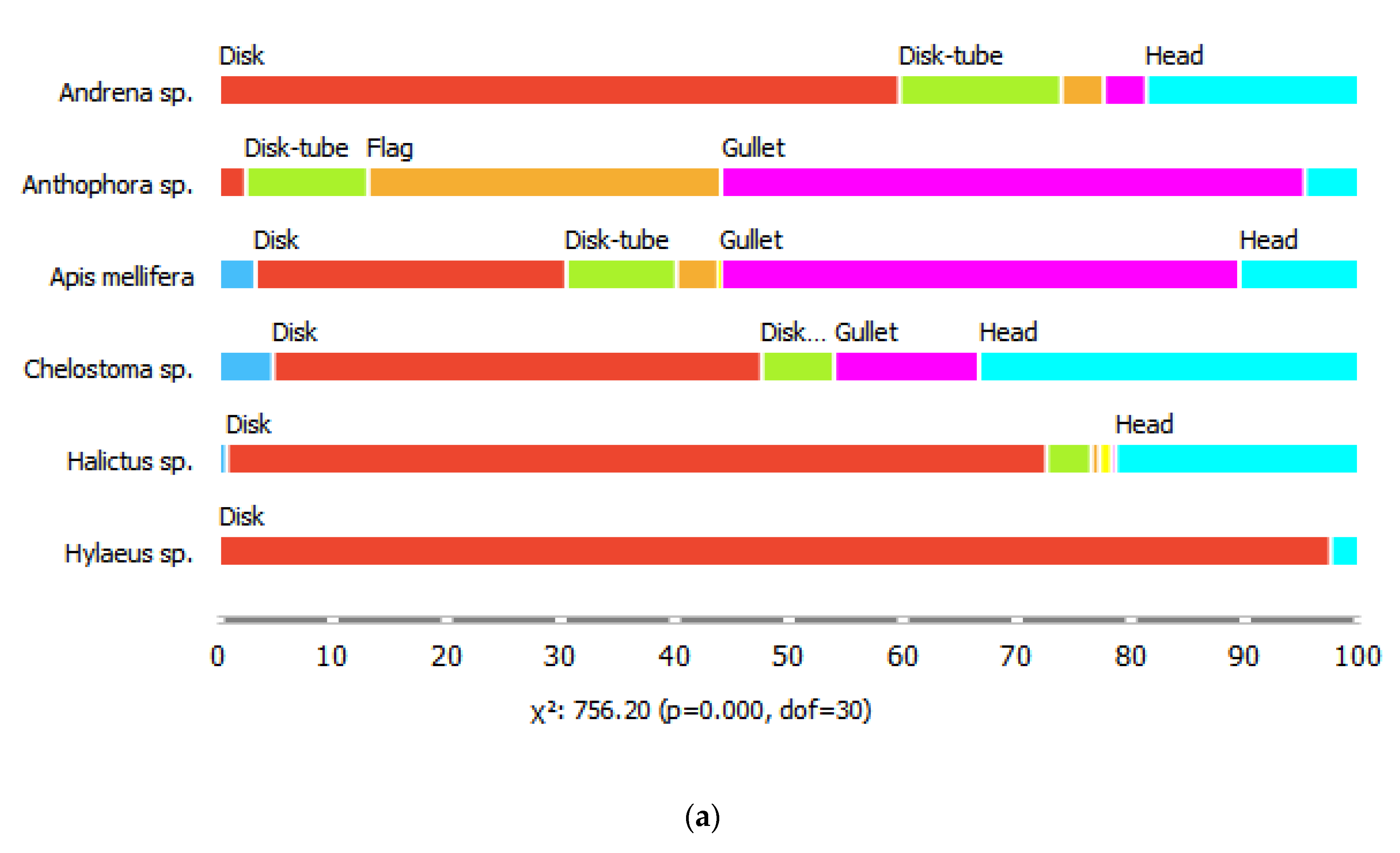
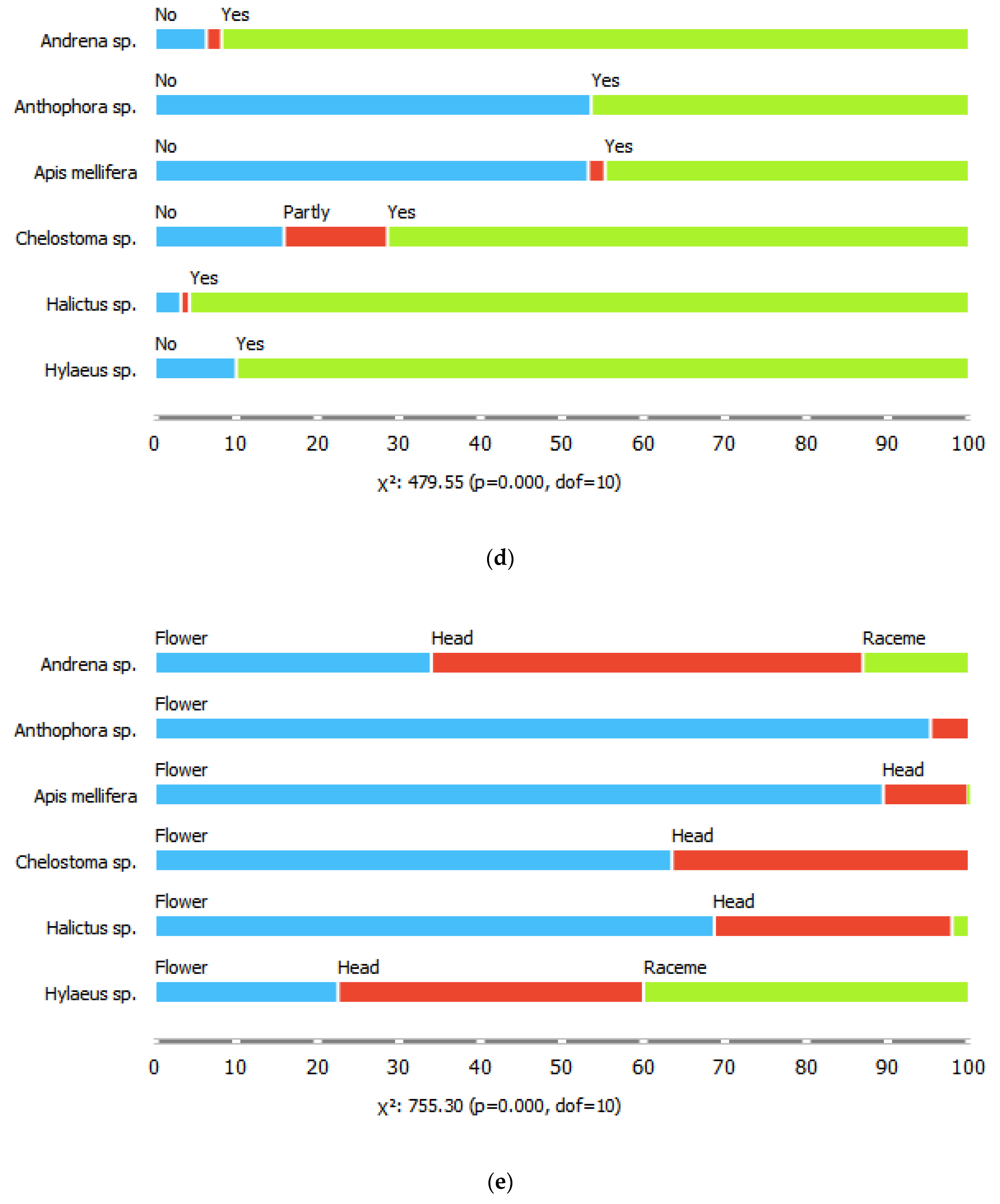
2. Results
3. Discussion
4. Materials and Methods
4.1. The Plant-Visitor Dataset
4.2. Flower Shape and Phenology Traits
4.3. Bees
4.4. Data Analysis
4.4.1. Predicting the Visitors
4.4.2. Ranking the Predictors
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarz, B.; Vázquez, D.P.; CaraDonna, P.J.; Knight, T.M.; Benadi, G.; Dormann, C.F.; Gauzens, B.; Motivans, E.; Resasco, J.; Blüthgen, N. Temporal scale-dependence of plant–pollinator networks. Oikos 2020, 129, 1289–1302. [Google Scholar] [CrossRef]
- Olito, C.; Fox, J.W. Species traits and abundances predict metrics of plant–pollinator network structure, but not pairwise interactions. Oikos 2015, 124, 428–436. [Google Scholar] [CrossRef]
- Vázquez, D.P.; Chacoff, N.P.; Cagnolo, L. Evaluating multiple determinants of the structure of plant–animal mutualistic networks. Ecology 2009, 90, 2039–2046. [Google Scholar] [CrossRef] [PubMed]
- Bascompte, J.; Jordano, P. Plant-animal mutualistic networks: The architecture of biodiversity. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 567–593. [Google Scholar] [CrossRef]
- Petanidou, T.; Kallimanis, A.S.; Tzanopoulos, J.; Sgardelis, S.P.; Pantis, J.D. Long-term observation of a pollination network: Fluctuation in species and interactions, relative invariance of network structure and implications for estimates of specialization. Ecol. Lett. 2008, 11, 564–575. [Google Scholar] [CrossRef]
- Mora, B.B.; Shin, E.; CaraDonna, P.J.; Stouffer, D.B. Untangling the seasonal dynamics of plant-pollinator communities. Nat. Commun. 2020, 11, 4086. [Google Scholar] [CrossRef]
- Stang, M.; Klinkhamer, P.G.; Van Der Meijden, E. Size constraints and flower abundance determine the number of interactions in a plant–flower visitor web. Oikos 2006, 112, 111–121. [Google Scholar] [CrossRef]
- Stang, M.; Klinkhamer, P.G.; Waser, N.M.; Stang, I.; van der Meijden, E. Size-specific interaction patterns and size matching in a plant–pollinator interaction web. Ann. Bot. 2009, 103, 1459–1469. [Google Scholar] [CrossRef]
- Klumpers, S.G.; Stang, M.; Klinkhamer, P.G. Foraging efficiency and size matching in a plant–pollinator community: The importance of sugar content and tongue length. Ecol. Lett. 2019, 22, 469–479. [Google Scholar] [CrossRef]
- Rosas-Guerrero, V.; Aguilar, R.; Martin-RodrÃiguez, S.; Ashworth, L.; Lopezaraiz-Mikel, M.; Bastida, J.; Quesada, M. A quantitative review of pollination syndromes: Do floral traits predict effective pollinators? Ecol. Lett. 2014, 17, 388–400. [Google Scholar] [CrossRef]
- Garibaldi, L.A.; Bartomeus, I.; Bommarco, R.; Klein, A.M.; Cunningham, S.A.; Aizen, M.A.; Boreux, V.; Garratt, M.P.; Carvalheiro, L.G.; Kremen, C. Editor’s Choice: Review: Trait matching of flower visitors and crops predicts fruit set better than trait diversity. J. Appl. Ecol. 2015, 52, 1436–1444. [Google Scholar] [CrossRef]
- Lázaro, A.; Jakobsson, A.; Totland, Ø. How do pollinator visitation rate and seed set relate to species’ floral traits and community context? Oecologia 2013, 173, 881–893. [Google Scholar] [CrossRef]
- McCall, C.; Primack, R.B. Influence of flower characteristics, weather, time of day, and season on insect visitation rates in three plant communities. Am. J. Bot 1992, 79, 434–442. [Google Scholar] [CrossRef]
- Fenster, C.B.; Armbruster, W.S.; Wilson, P.; Dudash, M.R.; Thomson, J.D. Pollination syndromes and floral specialization. Annu. Rev. Ecol. Evol. Syst. 2004, 35, 375–403. [Google Scholar] [CrossRef]
- Krishna, S.; Keasar, T. Morphological complexity as a floral signal: From perception by insect pollinators to co-evolutionary implications. Int. J. Mol. Sci. 2018, 19, 1681. [Google Scholar] [CrossRef]
- Keasar, T. Patterns of Flower Complexity in Plant Communities. In Annual Plant Reviews Online; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Stefanaki, A.; Kantsa, A.; Tscheulin, T.; Charitonidou, M.; Petanidou, T. Lessons from Red Data Books: Plant Vulnerability Increases with Floral Complexity. PLoS ONE 2015, 10, e0138414. [Google Scholar] [CrossRef]
- Lázaro, A.; Hegland, S.J.; Totland, Ø. The relationships between floral traits and specificity of pollination systems in three Scandinavian plant communities. Oecologia 2008, 157, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Olesen, J.M.; Bascompte, J.; Dupont, Y.L.; Elberling, H.; Rasmussen, C.; Jordano, P. Missing and forbidden links in mutualistic networks. Proc. R. Soc. B Biol. Sci. 2011, 278, 725–732. [Google Scholar] [CrossRef]
- Junker, R.R.; Blüthgen, N.; Brehm, T.; Binkenstein, J.; Paulus, J.; Martin Schaefer, H.; Stang, M. Specialization on traits as basis for the niche-breadth of flower visitors and as structuring mechanism of ecological networks. Funct. Ecol. 2013, 27, 329–341. [Google Scholar] [CrossRef]
- Morente-López, J.; Lara-Romero, C.; Ornosa, C.; Iriondo, J.M. Phenology drives species interactions and modularity in a plant-flower visitor network. Sci. Rep. 2018, 8, 9386. [Google Scholar] [CrossRef]
- Lázaro, A.; Gómez-Martínez, C.; Alomar, D.; González-Estévez, M.A.; Traveset, A. Linking species-level network metrics to flower traits and plant fitness. J. Ecol. 2020, 108, 1287–1298. [Google Scholar] [CrossRef]
- Peralta, G.; Vázquez, D.P.; Chacoff, N.P.; Lomáscolo, S.B.; Perry, G.L.; Tylianakis, J.M. Trait matching and phenological overlap increase the spatio-temporal stability and functionality of plant–pollinator interactions. Ecol. Lett. 2020. [Google Scholar] [CrossRef]
- Wolfe, L.M.; Sowell, D.R. Do pollination syndromes partition the pollinator community? A test using four sympatric morning glory species. Int. J. Plant Sci. 2006, 167, 1169–1175. [Google Scholar] [CrossRef]
- Urban-Mead, K.R. Predictability of bee community composition after floral removals differs by floral trait group. Biol. Lett. 2017, 13, 20170515. [Google Scholar] [CrossRef] [PubMed]
- Rumeu, B.; Sheath, D.J.; Hawes, J.E.; Ings, T.C. Zooming into plant-flower visitor networks: An individual trait-based approach. PeerJ 2018, 6, e5618. [Google Scholar] [CrossRef]
- Schleuning, M.; Neuschulz, E.L.; Albrecht, J.; Bender, I.M.; Bowler, D.E.; Dehling, D.M.; Fritz, S.A.; Hof, C.; Mueller, T.; Nowak, L. Trait-based assessments of climate-change impacts on interacting species. Trends Ecol. Evol. 2020, 35, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Pichler, M.; Boreux, V.; Klein, A.; Schleuning, M.; Hartig, F. Machine learning algorithms to infer trait-matching and predict species interactions in ecological networks. Methods Ecol. Evol. 2020, 11, 281–293. [Google Scholar] [CrossRef]
- Ornai, A.; Ne’eman, G.; Keasar, T. Management of forest fire buffer zones: Implications for flowering plants and bees. For. Ecol. Manag. 2020, 473, 118310. [Google Scholar] [CrossRef]
- Potts, S.G.; Vulliamy, B.; Dafni, A.; Ne’eman, G.; Willmer, P. Linking bees and flowers: How do floral communities structure pollinator communities? Ecology 2003, 84, 2628–2642. [Google Scholar] [CrossRef]
- Zohary, M. Vegetation of Israel and Adjacent Areas; Dr Ludwig Reichert Verlag: Wiesbaden, Germany, 1982. [Google Scholar]
- Demšar, J.; Curk, T.; Erjavec, A.; Gorup, Č.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A. Orange: Data mining toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]

| Predicted | ||||||||
|---|---|---|---|---|---|---|---|---|
| Andrena spp. | Anthophora spp. | Apis mellifera | Chelostoma spp. | Halictus spp. | Hylaeus spp. | ∑ | ||
| Actual | Andrena spp. | 71.6% | 0.0% | 21.0% | 0.0% | 7.4% | 0.0% | 81 |
| Anthophora spp. | 4.8% | 52.4% | 42.9% | 0.0% | 0.0% | 0.0% | 21 | |
| Apis mellifera | 0.4% | 0.2% | 97.6% | 0.2% | 1.5% | 0.0% | 460 | |
| Chelostoma spp. | 33.3% | 0.0% | 19.0% | 42.9% | 4.8% | 0.0% | 21 | |
| Halictus spp. | 3.4% | 0.0% | 24.7% | 0.0% | 71.9% | 0.0% | 89 | |
| Hylaeus spp. | 35.7% | 0.0% | 21.4% | 0.0% | 0.0% | 42.9% | 14 | |
| ∑ | 76 | 12 | 504 | 10 | 78 | 6 | 686 | |
| Predicted | ||||||||
|---|---|---|---|---|---|---|---|---|
| Andrena spp. | Anthophora spp. | Apis mellifera | Chelostoma spp. | Halictus spp. | Hylaeus spp. | ∑ | ||
| Actual | Andrena spp. | 59.3% | 0.0% | 34.6% | 0.0% | 2.5% | 3.7% | 81 |
| Anthophora spp. | 4.8% | 9.5% | 85.7% | 0.0% | 0.0% | 0.0% | 21 | |
| Apis mellifera | 0.4% | 0.0% | 98.3% | 0.0% | 1.3% | 0.0% | 460 | |
| Chelostoma spp. | 42.9% | 0.0% | 47.6% | 4.8% | 4.8% | 0.0% | 21 | |
| Halictus spp. | 12.4% | 0.0% | 70.8% | 0.0% | 16.9% | 0.0% | 89 | |
| Hylaeus spp. | 50.0% | 0.0% | 14.3% | 0.0% | 0.0% | 35.7% | 14 | |
| ∑ | 78 | 2 | 573 | 1 | 24 | 8 | 686 | |
| Predicted | ||||||||
|---|---|---|---|---|---|---|---|---|
| Andrena spp. | Anthophora spp. | Apis mellifera | Chelostoma spp. | Halictus spp. | Hylaeus spp. | ∑ | ||
| Actual | Andrena spp. | 22.2% | 0.0% | 69.1% | 1.2% | 7.4% | 0.0% | 81 |
| Anthophora spp. | 42.9% | 0.0% | 57.1% | 0.0% | 0.0% | 0.0% | 21 | |
| Apis mellifera | 3.7% | 0.0% | 89.3% | 0.9% | 6.1% | 0.0% | 460 | |
| Chelostoma spp. | 0.0% | 0.0% | 66.7% | 23.8% | 9.5% | 0.0% | 21 | |
| Halictus spp. | 1.1% | 0.0% | 53.9% | 0.0% | 44.9% | 0.0% | 89 | |
| Hylaeus spp. | 14.3% | 0.0% | 57.1% | 0.0% | 28.6% | 0.0% | 14 | |
| ∑ | 47 | 0 | 549 | 10 | 80 | 0 | 686 | |
| Factor | Full Model | Andrena | Anthophora Sp. | Apis mellifera | Chelostoma Sp. | Halictus Sp. | Hylaeus Sp. |
|---|---|---|---|---|---|---|---|
| Shape class | 0.054 | 10.109 | 11.374 | 6.762 | 21.001 | 3.507 | 0.854 |
| Reproductive Unit | 0.053 | 2.427 | 6.719 | 4.282 | 7.923 | 2.567 | 1.578 |
| Depth | 0.046 | 8.849 | 7.121 | 7.841 | 12.841 | 2.796 | 10.138 |
| Corolla Segmentation | 0.045 | 2.745 | 3.976 | 6.767 | 2.623 | 2.522 | 1.258 |
| Julian date | 0.031 | 0.227 | 0.922 | 0.191 | 0.616 | 0.418 | 0.814 |
| Year | 0.002 | 0.044 | 0.878 | 0.073 | 0.571 | 0.280 | 0.848 |
| Bee Genus | Number of Observations in the Visitation Dataset | Mean ± SE Proboscis Length (mm) | Mean ± SE Thorax Width (mm) |
|---|---|---|---|
| Hyaelus | 40 | 0.481 ± 0.041 | 1.523 ± 0.058 |
| Andrena | 268 | 0.997 ± 0.140 | 1.884 ± 0.072 |
| Halictus | 281 | 1.861 ± 0.251 | 2.213 ± 0.110 |
| Chelostoma | 63 | 2.002 ± 0.340 | 1.823 ± 0.103 |
| Anthophora | 84 | 3.868 ± 0.943 | 4.306 ± 0.143 |
| Apis | 1552 | 4.006 ± 0.154 | 4.376 ± 0.057 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ornai, A.; Keasar, T. Floral Complexity Traits as Predictors of Plant-Bee Interactions in a Mediterranean Pollination Web. Plants 2020, 9, 1432. https://doi.org/10.3390/plants9111432
Ornai A, Keasar T. Floral Complexity Traits as Predictors of Plant-Bee Interactions in a Mediterranean Pollination Web. Plants. 2020; 9(11):1432. https://doi.org/10.3390/plants9111432
Chicago/Turabian StyleOrnai, Alon, and Tamar Keasar. 2020. "Floral Complexity Traits as Predictors of Plant-Bee Interactions in a Mediterranean Pollination Web" Plants 9, no. 11: 1432. https://doi.org/10.3390/plants9111432
APA StyleOrnai, A., & Keasar, T. (2020). Floral Complexity Traits as Predictors of Plant-Bee Interactions in a Mediterranean Pollination Web. Plants, 9(11), 1432. https://doi.org/10.3390/plants9111432






