Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods: A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM)
Abstract
:1. Introduction
2. Results
2.1. Longitudinal Shrinkage and Swelling of the Tracheids Increases with CW Severity and Shows Hysteresis
2.2. Tangential and Radial Shrinkage of the Tracheids Decreases with CW Severity, with Tangential Shrinkage Greater than Radial Shrinkage
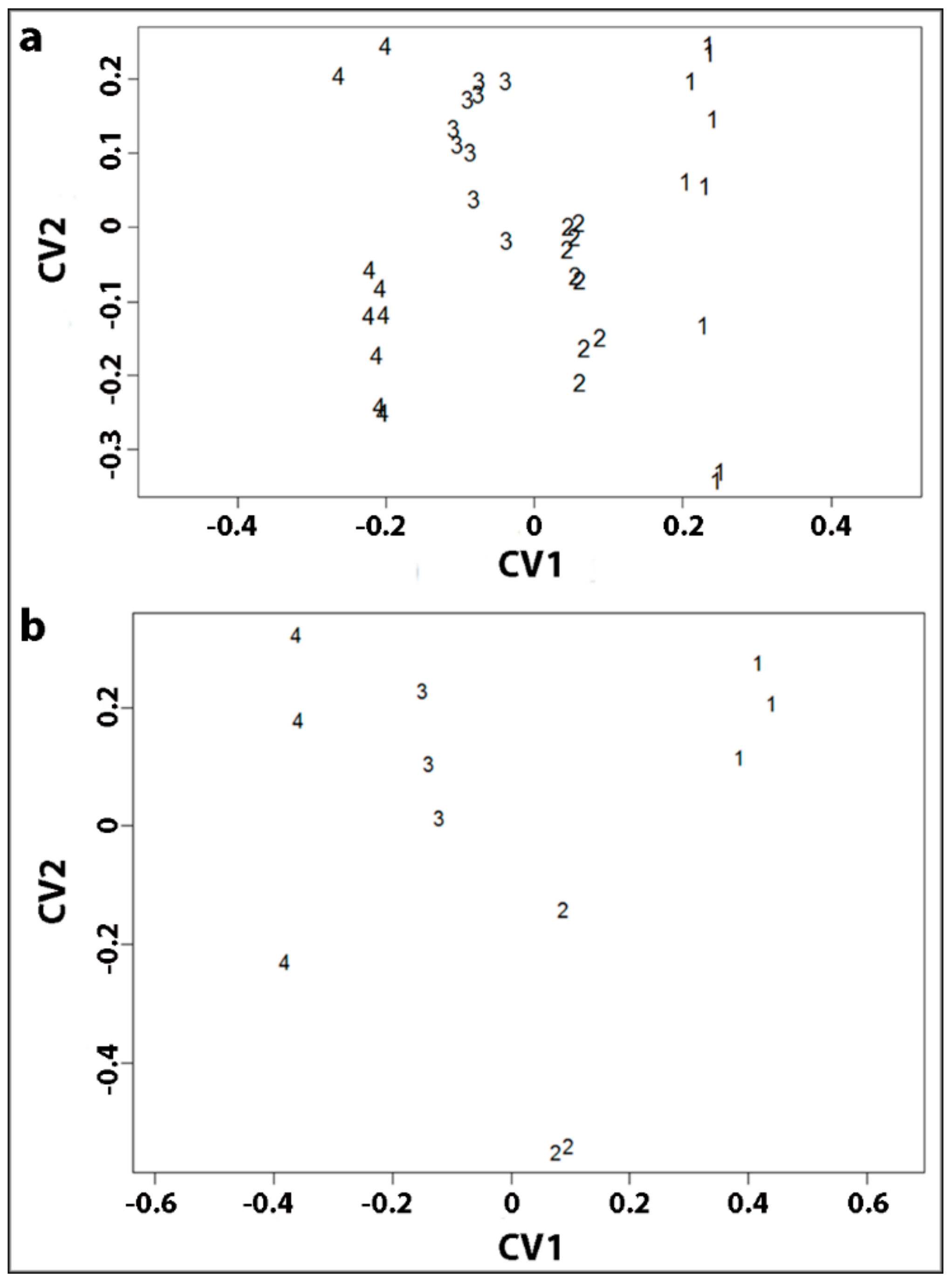
2.3. Statistical Analysis of Tracheid Shrinkage by Two-Way Factorial MANOVA Confirmed the Differences between Corewood Types
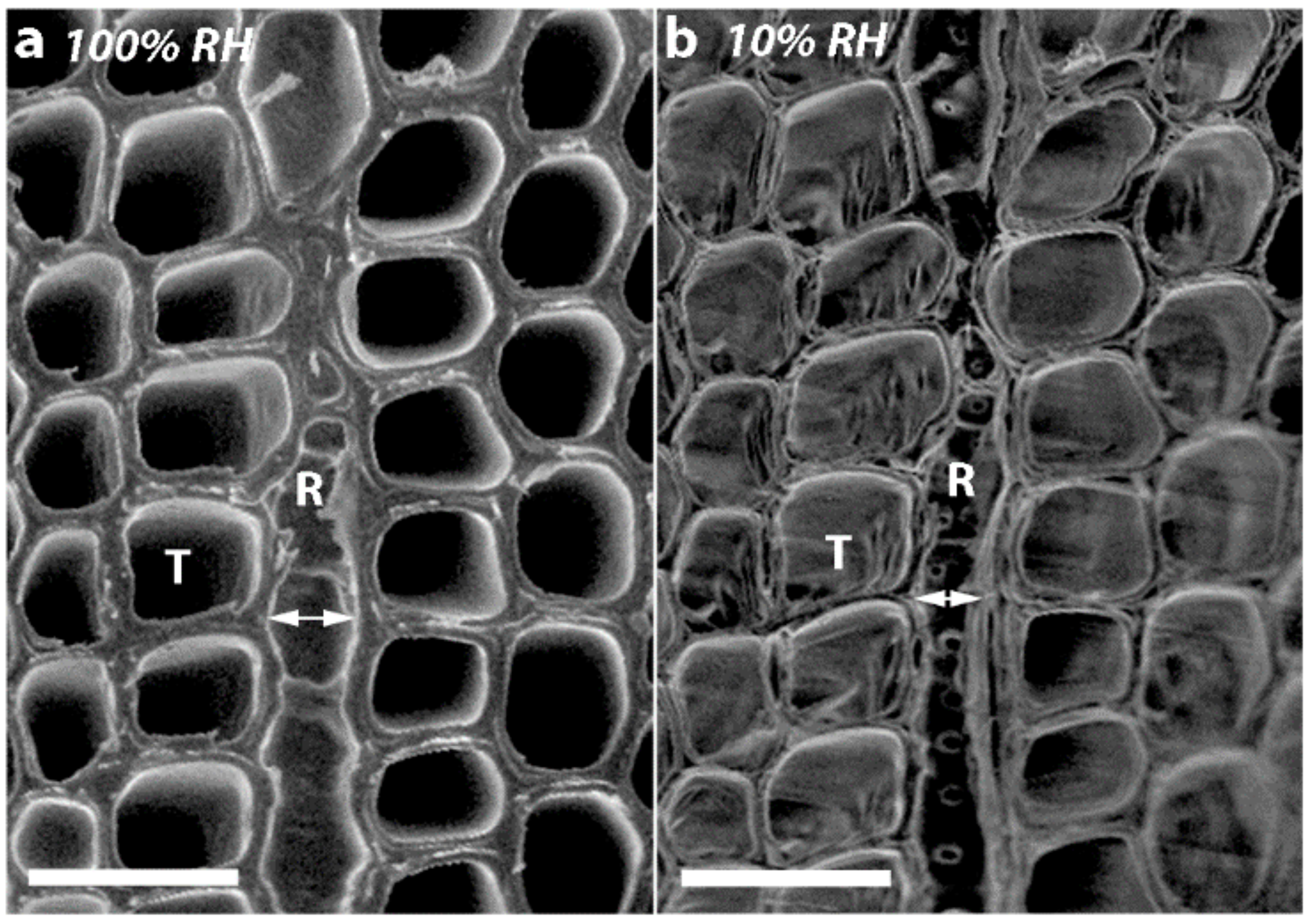
2.4. Micrographs of Transverse Surfaces Show that Tracheids Become Less Well Ordered, More Rounded and Their Walls Thicker with CW Severity
2.5. Transverse Wall Shrinkage Decreased with CW Severity and was Greater for Radial Walls than Tangential Tracheid Walls
2.6. Canonical Correlation Analysis Showed that Longitudinal Tracheid Shrinkage is Positively Correlated with Lignin Content and Galactose Percentage
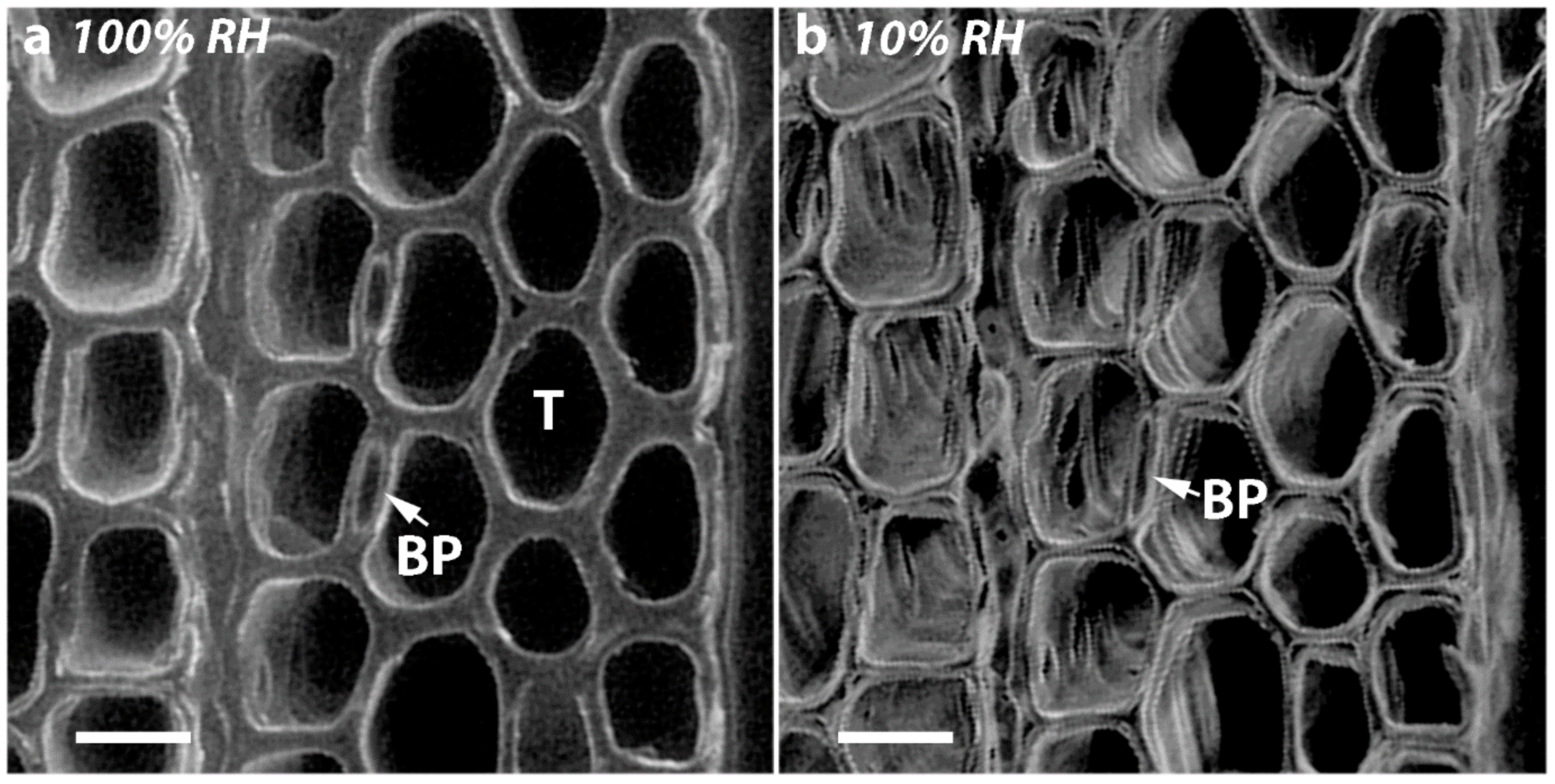
2.7. Diameters of Tracheid Bordered Pits Did Not Change Significantly on Drying but the Diameters of the Pit Apertures Decreased with Increasing CW Severity
3. Discussion
4. Materials and Methods
4.1. Tree Growth and Wood Samples
4.2. Variable-Pressure Scanning Electron Microscopy (VP-SEM)
4.3. Statistical Analysis
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Timell, T.E. Compression Wood in Gymnosperms; Springer: Berlin, Germany, 1986. [Google Scholar]
- Spear, M.; Walker, J.C.F. Dimensional instability in timber. In Primary Wood Processing. Principles and Practice; Walker, J.C.F., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 95–120. [Google Scholar]
- Glass, S.V.; Zelinka, S.L. Moisture relations and physical properties of wood. In Wood handbook: Wood as an Engineering Material; Ross, R.J., Ed.; US Dept. of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; pp. 4.1–4.19. [Google Scholar]
- Walker, J.C.F. Water in wood. In Primary Wood Processing. Principles and Practice; Walker, J.C.F., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 69–94. [Google Scholar]
- Evert, R.F. Esau’s Plant Anatomy: Meristems, Cells, and Tissues of the Plant Body: Their Structure, Function, and Development, 3rd ed.; Wiley: Hobohen, NJ, USA, 2006. [Google Scholar]
- Burdon, R.D.; Kibblewhite, R.P.; Walker, J.; Megraw, R.A.; Evans, R.; Cown, D.J. Juvenile versus mature wood: A new concept, orthogonal to corewood versus outerwood, with special reference to Pinus radiata and P. taeda. For. Sci. 2004, 50, 399–415. [Google Scholar]
- Meylan, B.A. Cause of high longitudinal shrinkage in wood. For. Prod. J. 1968, 18, 75–78. [Google Scholar]
- Brennan, M.; McLean, J.P.; Altaner, C.M.; Ralph, J.; Harris, P.J. Cellulose microfibril angles and cell-wall polymers in different wood types of Pinus radiata. Cellulose 2012, 19, 1385–1404. [Google Scholar] [CrossRef]
- Donaldson, L.A.; Grace, J.; Downes, G.M. Within-tree variation in anatomical properties of compression wood in radiata pine. IAWA J. 2004, 25, 253–271. [Google Scholar] [CrossRef]
- Yamamoto, H.; Sassus, F.; Ninomiya, M.; Gril, J. A model of anisotropic swelling and shrinking process of wood. Part 2. A simulation of shrinking wood. Wood Sci. Technol. 2001, 35, 167–181. [Google Scholar] [CrossRef]
- Harris, P.J.; Stone, B.A. Chemistry and molecular organization of plant cell walls. In Biomass Recalcitrance: Deconstructing of the Plant Cell Wall for Bioenergy; Himmel, M.E., Ed.; Blackwell: Oxford, UK, 2008; pp. 60–93. [Google Scholar]
- Zhang, M.; Chavan, R.R.; Smith, B.G.; McArdle, B.H.; Harris, P.J. Tracheid cell-wall structures and locations of (1→4)-β-d-galactans and (1→3)-β-d-glucans in compression woods of radiata pine (Pinus radiata D. Don). BMC Plant Biol. 2016, 16, 194–212. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Lapierre, C.; Nouxman, N.L.; Nieuwoudt, M.K.; Smith, B.G.; Chavan, R.R.; McArdle, B.H.; Harris, P.J. Location and characterization of lignin in tracheid cell walls of radiata pine (Pinus radiata D. Don) compression woods. Plant Physiol. Biochem. 2017, 118, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, L.A.; Singh, A.P. Formation and structure of compression wood. In Cellular Aspects of Wood Formation; Fromm, J., Ed.; Springer: Hamburg, Germany, 2013; pp. 225–256. [Google Scholar]
- Donaldson, L.A.; Singh, A.P. Reaction wood. In Secondary Xylem Biology. Origins, Functions, and Applications; Kim, Y.S., Funada, R., Singh, A.P., Eds.; Elsevier: London, UK, 2016; pp. 93–110. [Google Scholar]
- Donaldson, L.A.; Singh, A.P.; Yoshinaga, A.; Takabe, K. Lignin distribution in mild compression wood of Pinus radiata. Can. J. Bot. 1999, 77, 41–50. [Google Scholar]
- Donald, A.M. The use of environmental scanning electron microscopy for imaging wet and insulating materials. Nat. Mater. 2003, 2, 511–516. [Google Scholar] [CrossRef] [PubMed]
- Almeida, G.; Huber, F.; Perré, P. Free shrinkage of wood determined at the cellular level using an environmental scanning electron microscope. Maderas Ciencia y Tecnología 2014, 16, 187–198. [Google Scholar] [CrossRef]
- Manly, B.F.J. Multivariate Statistical Methods: A Primer; Chapman and Hall/CRC: Washington, DC, USA, 2004. [Google Scholar]
- Chauhan, S.S.; Sharma, M.; Thomas, J.; Apiolaza, L.A.; Collings, D.A.; Walker, J.C.F. Methods for the very early selection of Pinus radiata D. Don. for solid wood products. Ann. For. Sci. 2013, 70, 439–449. [Google Scholar] [CrossRef]
- Harris, J.M. Shrinkage and density of radiata pine compression wood in relation to its anatomy and mode of formation. N. Z. J. For. Sci. 1977, 7, 91–106. [Google Scholar]
- Xu, P.; Liu, H.; Evans, R.; Donaldson, L.A. Longitudinal shrinkage behaviour of compression wood in radiata pine. Wood Sci. Technol. 2009, 43, 423–439. [Google Scholar] [CrossRef]
- Floyd, S. Effect of hemicellulose on longitudinal shrinkage in wood. In The Hemicelluloses Workshop; Entwistle, K.M., Walker, J.C.F., Eds.; The Wood Technology Research Centre: University of Canterbury, Christchurch, New Zealand, 2005; pp. 115–120. [Google Scholar]
- Harris, P.J.; Smith, B.G. Plant cell walls and cell-wall polysaccharides: Structures, properties and uses in food products. Int. J. Food Sci. Technol. 2006, 41, 129–143. [Google Scholar] [CrossRef]
- Ryden, P.; MacDougall, A.J.; Tibbits, C.W.; Ring, S.G. Hydration of pectic polysaccharides. Biopolymers 2000, 54, 398–405. [Google Scholar] [CrossRef]
- Turnbull, C.M.; Baxter, A.L.; Johnson, S.K. Water-binding capacity and viscosity of Australian sweet lupin kernel fibre under in vitro conditions simulating the human upper gastrointestinal tract. Int. J. Food Sci. Nutr. 2005, 56, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Ralph, J.; Brunow, G.; Boerjan, W. Lignins. In Encyclopedia of Life Sciences; Wiley: Hoboken, NJ, USA, 2007; pp. 1–10. [Google Scholar]
- Chavan, R.R.; Fahey, L.M.; Harris, P.J. Quantification of (1→4)-β-d-galactans in compression wood using an immuno-dot assay. Plants 2015, 4, 29–43. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Ohnishi, J.; Yamasaki, Y.; Kaizu, S.; Koshijima, T. Binding-site analysis of the ether linkages between lignin and hemicelluloses in lignin–carbohydrate complexes by DDQ-oxidation. Agric. Biol. Chem. 1989, 53, 2233–2252. [Google Scholar]
- Piršelová, B.; Matušíková, I. Callose: The plant cell wall polysaccharide with multiple biological functions. Acta Physiol. Plant 2013, 35, 635–644. [Google Scholar] [CrossRef]
- Stone, B. Callose and related glucans. In Encyclopedia of Life Sciences; Wiley: Hoboken, NJ, USA, 2005; pp. 1–10. [Google Scholar]
- Vithanage, H.I.M.V.; Gleeson, P.A.; Clarke, A.E. The nature of callose produced during self-pollination in Secale cereale. Planta 1980, 148, 498–509. [Google Scholar] [CrossRef] [PubMed]
- Altaner, C.M.; Tokareva, E.N.; Jarvis, M.C.; Harris, P.J. Distribution of (1→4)-β-galactans, arabinogalactan proteins, xylans and (1→3)-β-glucans in tracheid cell walls of softwoods. Tree Physiol. 2010, 30, 782–793. [Google Scholar] [CrossRef] [PubMed]
- Thybring, E.E.; Thygesen, L.G.; Burgert, I. Hydroxyl accessibility in wood cell walls as affected by drying and re-wetting procedures. Cellulose 2017, 24, 2375–2384. [Google Scholar] [CrossRef]
- Derome, D.; Rafsanjani, A.; Patera, A.; Guyer, R.; Carmeliet, J. Hygromorphic behaviour of cellular material: Hysteretic swelling and shrinkage of wood probed by phase contrast X-ray tomography. Philos. Mag. 2012, 92, 3680–3698. [Google Scholar] [CrossRef]
- Barber, N.F.; Meylan, B.A. The anisotropic shrinkage of wood. A theoretical model. Holzforschung 1964, 18, 146–156. [Google Scholar] [CrossRef]
- Skaar, C. Wood-Water Relations; Springer: Berlin, Germany, 1988. [Google Scholar]
- Boutelje, J.B. The relationship of structure to transverse anisotropy in wood with reference to shrinkage and elasticity. Holzforschung 1962, 16, 33–46. [Google Scholar] [CrossRef]
- Messier, P.; Vitale, T. Cracking in albumen photographs: An ESEM investigation. Microsc. Res. Tech. 1993, 25, 374–383. [Google Scholar] [CrossRef] [PubMed]
- Hailwood, A.J.; Horrobin, S. Absorption of water by polymers: Analysis in terms of a simple model. Trans. Faraday Soc. 1946, 42, 84–92. [Google Scholar] [CrossRef]
- R Core Team. R: A Language with Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research; W.H. Freeman: New York, NY, USA, 2012. [Google Scholar]
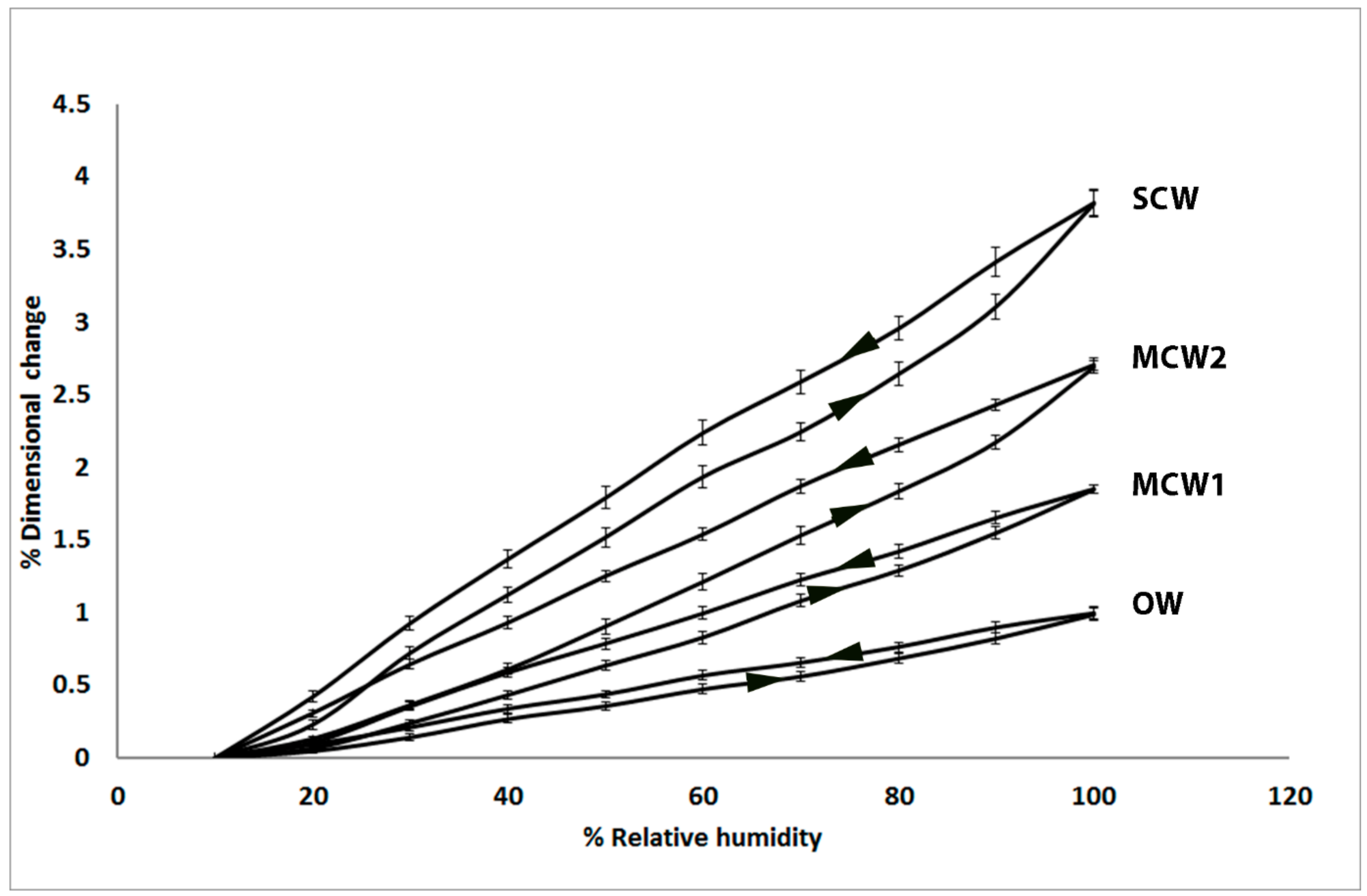



| Tree | Wood Types | Longitudinal Shrinkage % | Tangential Shrinkage % | Radial Shrinkage % |
|---|---|---|---|---|
| Tree 1 b | OW | 0.99 ± 0.03 | 6.48 ± 0.08 | 3.21 ± 0.02 |
| MCW1 | 1.85 ± 0.07 | 5.64 ± 0.05 | 2.94 ± 0.05 | |
| MCW2 | 2.71 ± 0.02 | 5.22 ± 0.03 | 2.23 ± 0.05 | |
| SCW | 3.82 ± 0.16 | 4.09 ± 0.04 | 2.08 ± 0.03 | |
| Tree 2 | OW | 0.89 ± 0.06 | 6.66 ± 0.07 | 3.09 ± 0.05 |
| MCW1 | 2.12 ± 0.05 | 5.81 ± 0.07 | 2.62 ± 0.04 | |
| MCW2 | 2.97 ± 0.07 | 5.18 ± 0.06 | 2.30 ± 0.06 | |
| SCW | 3.89 ± 0.08 | 4.24 ± 0.04 | 2.10 ± 0.03 | |
| Tree 3 | OW | 0.92 ± 0.07 | 6.76 ± 0.06 | 3.22 ± 0.05 |
| MCW1 | 1.93 ± 0.05 | 5.89 ± 0.05 | 2.89 ± 0.02 | |
| MCW2 | 2.78 ± 0.06 | 5.21 ± 0.04 | 2.51 ± 0.03 | |
| SCW | 3.72 ± 0.07 | 4.15 ± 0.04 | 2.16 ± 0.03 |
| CV1 | CV2 | |
|---|---|---|
| Tracheid shrinkage | ||
| a Longitudinal tracheid shrinkage (%) | 0.99 | 0.016 |
| Tangential tracheid shrinkage (%) | −0.99 | −0.148 |
| Radial tracheid shrinkage (%) | −0.97 | 0.213 |
| Tracheid wall shrinkage | ||
| a Longitudinal shrinkage (%) of tracheid walls | 1.00 | 0.028 |
| Transverse shrinkage (%) of tangential tracheid walls | −0.88 | 0.333 |
| Transverse shrinkage (%) of radial tracheid walls | −0.913 | −0.143 |
| CV1 | CV2 | CV3 | |
|---|---|---|---|
| Tracheid shrinkage variables | |||
| Longitudinal tracheid shrinkage % | −0.994 | −0.091 | 0.068 |
| Tangential tracheid shrinkage % | 0.992 | 0.045 | 0.119 |
| Radial tracheid shrinkage % | 0.969 | −0.189 | −0.159 |
| Chemical variables | |||
| AcBr-soluble lignin a | −0.985 | −0.043 | −0.134 |
| Arabinose b | 0.902 | 0.229 | −0.306 |
| Galactose b | −0.981 | −0.029 | 0.181 |
| Xylose b | 0.953 | 0.014 | −0.191 |
| Mannose b | 0.974 | −0.156 | −0.148 |
| Tracheid wall shrinkage variables | |||
| Longitudinal shrinkage (%) of tracheid walls | −0.992 | 0.046 | −0.121 |
| Transverse shrinkage (%) of tangential tracheid walls | 0.952 | −0.286 | −0.105 |
| Transverse shrinkage (%) of radial tracheid walls | 0.997 | 0.059 | −0.044 |
| Chemical variables | |||
| AcBr-soluble lignin a | −0.981 | 0.172 | −0.077 |
| Arabinose b | 0.955 | 0.226 | −0.133 |
| Galactose b | −0.990 | −0.067 | 0.074 |
| Xylose b | 0.974 | 0.021 | −0.190 |
| Mannose b | 0.975 | −0.049 | −0.103 |
| Wood Types | Diameters of Bordered Pits (μm) a | Width of Single Border b (μm) | Diameters of Apertures (μm) a | ||||
|---|---|---|---|---|---|---|---|
| 100% RH | 10% RH | Dimensional Changes % | 100% RH | 10% RH | Dimensional Changes % | ||
| OW | 10.87 ± 0.22 | 10.86 ± 0.22 | −0.10 ± 0.11 | 2.81 | 5.25 ± 0.10 | 5.17 ± 0.10 | −1.61 ± 0.15 |
| MCW 1 | 10.89 ± 0.12 | 10.87 ± 0.12 | −0.16 ± 0.14 | 2.81 | 5.28 ± 0.11 | 5.16 ± 0.11 | −2.41 ± 0.13 |
| MCW 2 | 10.17 ± 0.27 | 10.17 ± 0.27 | 0.01 ± 0.09 | 2.455 | 5.26 ± 0.11 | 5.11 ± 0.11 | −2.85 ± 0.13 |
| SCW | 8.72 ± 0.20 | 8.71 ± 0.21 | −0.10 ± 0.26 | 2.015 | 4.69 ± 0.13 | 4.47 ± 0.12 | −4.69 ± 0.21 |
| p Value of One-Way ANOVA | Post Hoc Contrasts by Duncan | ||||||
|---|---|---|---|---|---|---|---|
| OW-MCW1 | OW-MCW2 | MCW2-MCW1 | SCW-OW | SCW-MCW1 | SCW-MCW2 | ||
| Diameters of bordered pits | p < 0.001 *** | p > 0.1 | p < 0.05 * | p < 0.05 * | p < 0.001 *** | p < 0.001 *** | p < 0.001 *** |
| Change of bordered pit diameters on drying | p > 0.1 | p > 0.1 | p > 0.1 | p > 0.1 | p > 0.1 | p > 0.1 | p > 0.1 |
| Diameters of pit apertures | p < 0.001 *** | p > 0.1 | p > 0.1 | p > 0.1 | p < 0.001 *** | p < 0.001 *** | p < 0.001 *** |
| Change of pit aperture diameters on drying | p < 0.001 *** | p < 0.001 *** | p < 0.001 *** | p < 0.05 * | p < 0.001 *** | p < 0.001 *** | p < 0.001 *** |
| Steps | Water Vapour Pressure (Torr) | % Relative Humidity |
|---|---|---|
| 1 and 19 | 5.3 | 100 |
| 2 and 18 | 4.7 | 90 |
| 3 and 17 | 4.2 | 80 |
| 4 and 16 | 3.7 | 70 |
| 5 and 15 | 3.2 | 60 |
| 6 and 14 | 2.6 | 50 |
| 7 and 13 | 2.1 | 40 |
| 8 and 12 | 1.6 | 30 |
| 9 and 11 | 1.1 | 20 |
| 10 | 0.5 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Smith, B.G.; McArdle, B.H.; Chavan, R.R.; James, B.J.; Harris, P.J. Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods: A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM). Plants 2018, 7, 14. https://doi.org/10.3390/plants7010014
Zhang M, Smith BG, McArdle BH, Chavan RR, James BJ, Harris PJ. Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods: A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM). Plants. 2018; 7(1):14. https://doi.org/10.3390/plants7010014
Chicago/Turabian StyleZhang, Miao, Bronwen G. Smith, Brian H. McArdle, Ramesh R. Chavan, Bryony J. James, and Philip J. Harris. 2018. "Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods: A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM)" Plants 7, no. 1: 14. https://doi.org/10.3390/plants7010014
APA StyleZhang, M., Smith, B. G., McArdle, B. H., Chavan, R. R., James, B. J., & Harris, P. J. (2018). Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods: A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM). Plants, 7(1), 14. https://doi.org/10.3390/plants7010014





