Yield Sensitivity of Mungbean (Vigna radiata L.) Genotypes to Different Agrivoltaic Environments in Tropical Nigeria
Abstract
:1. Introduction
2. Results and Discussion
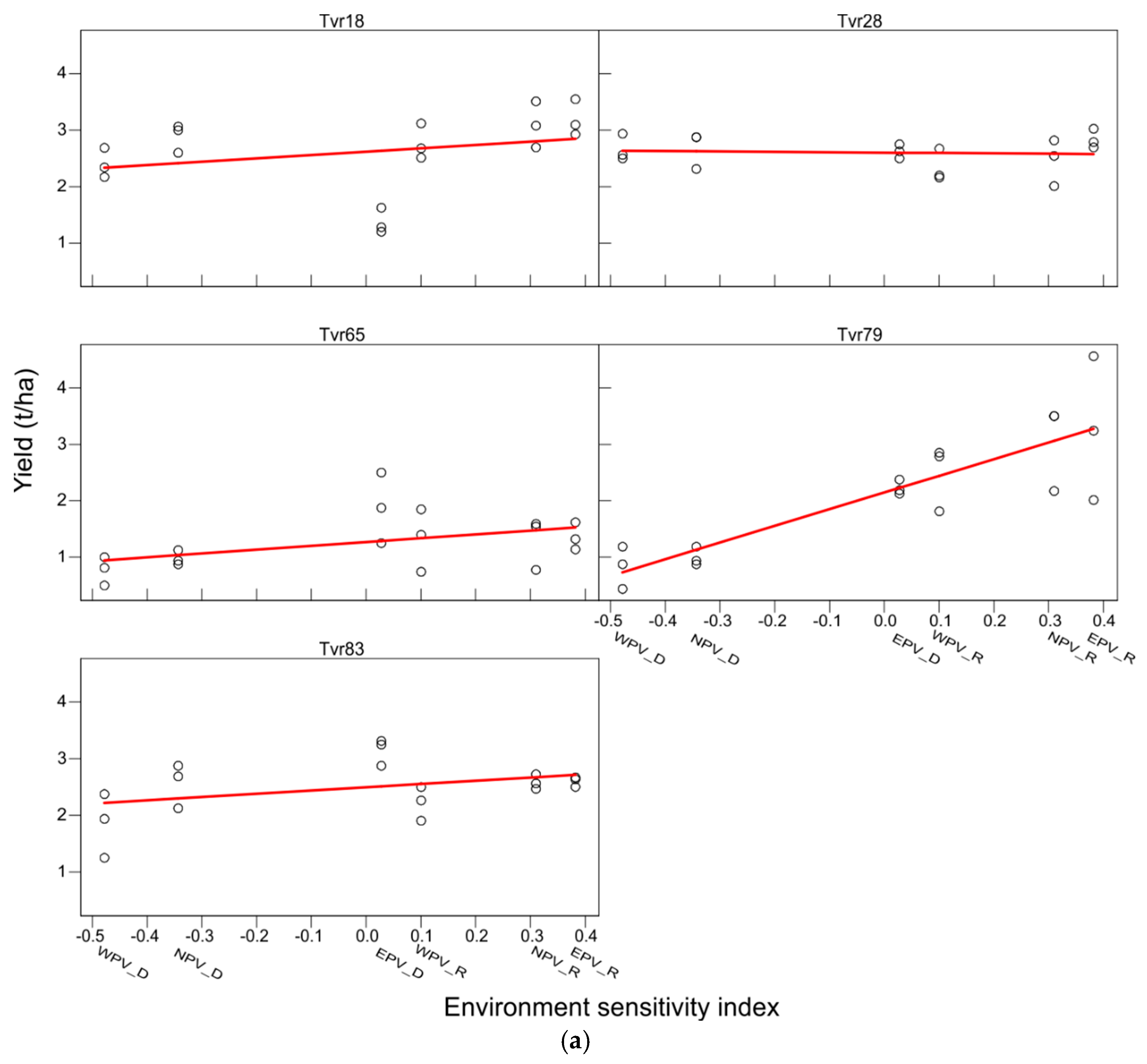
2.1. AMMI Analysis
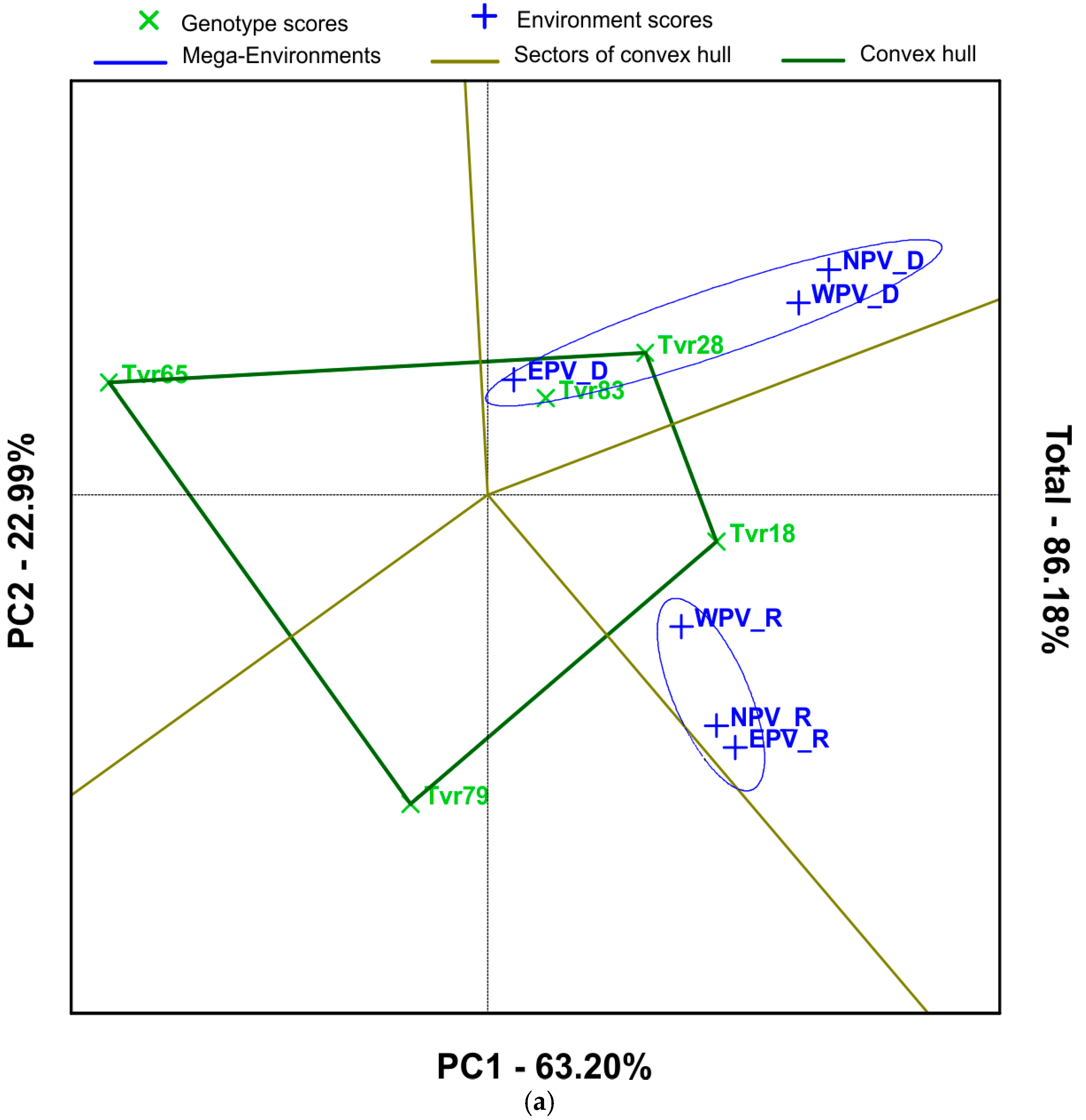
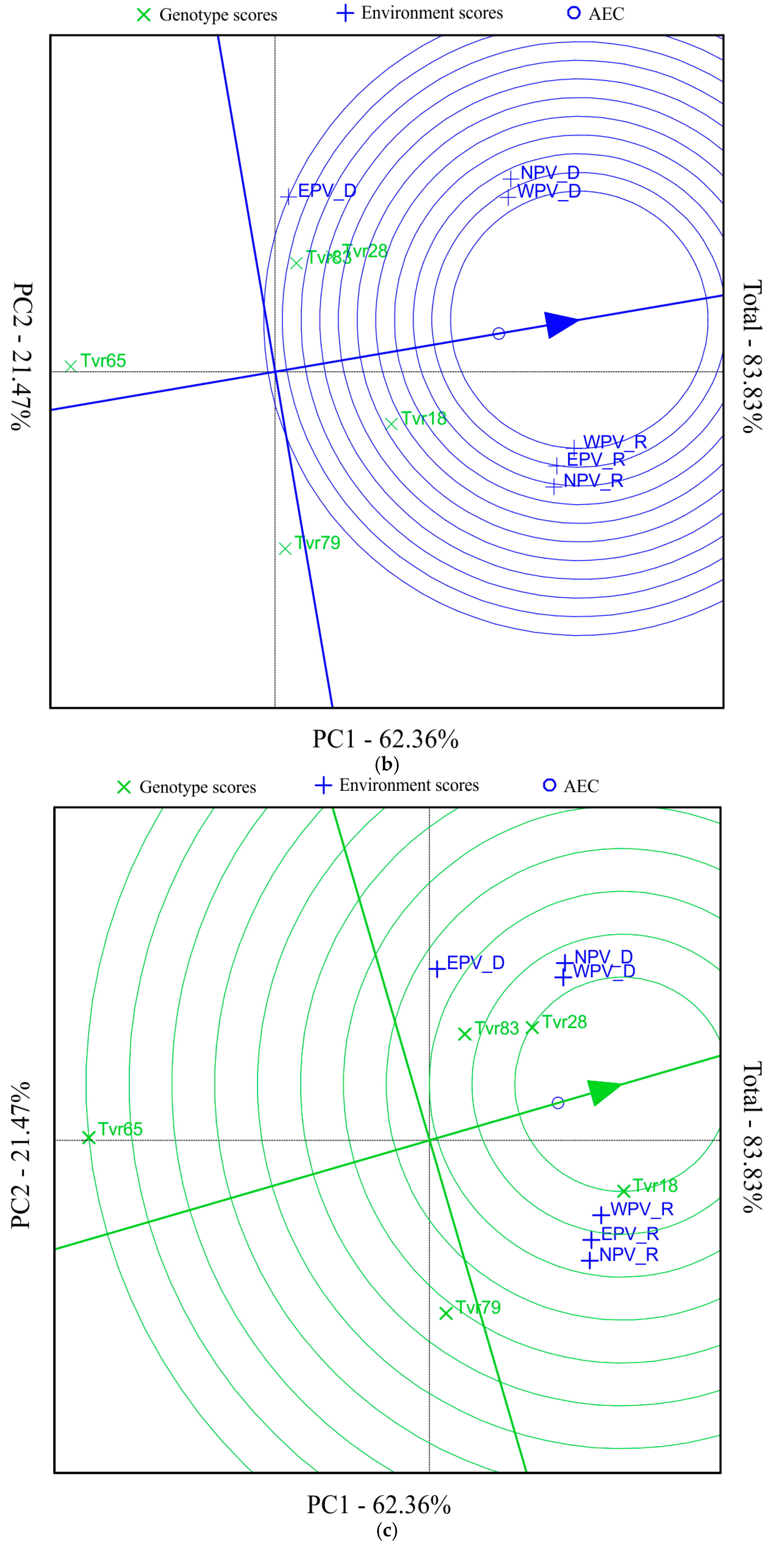
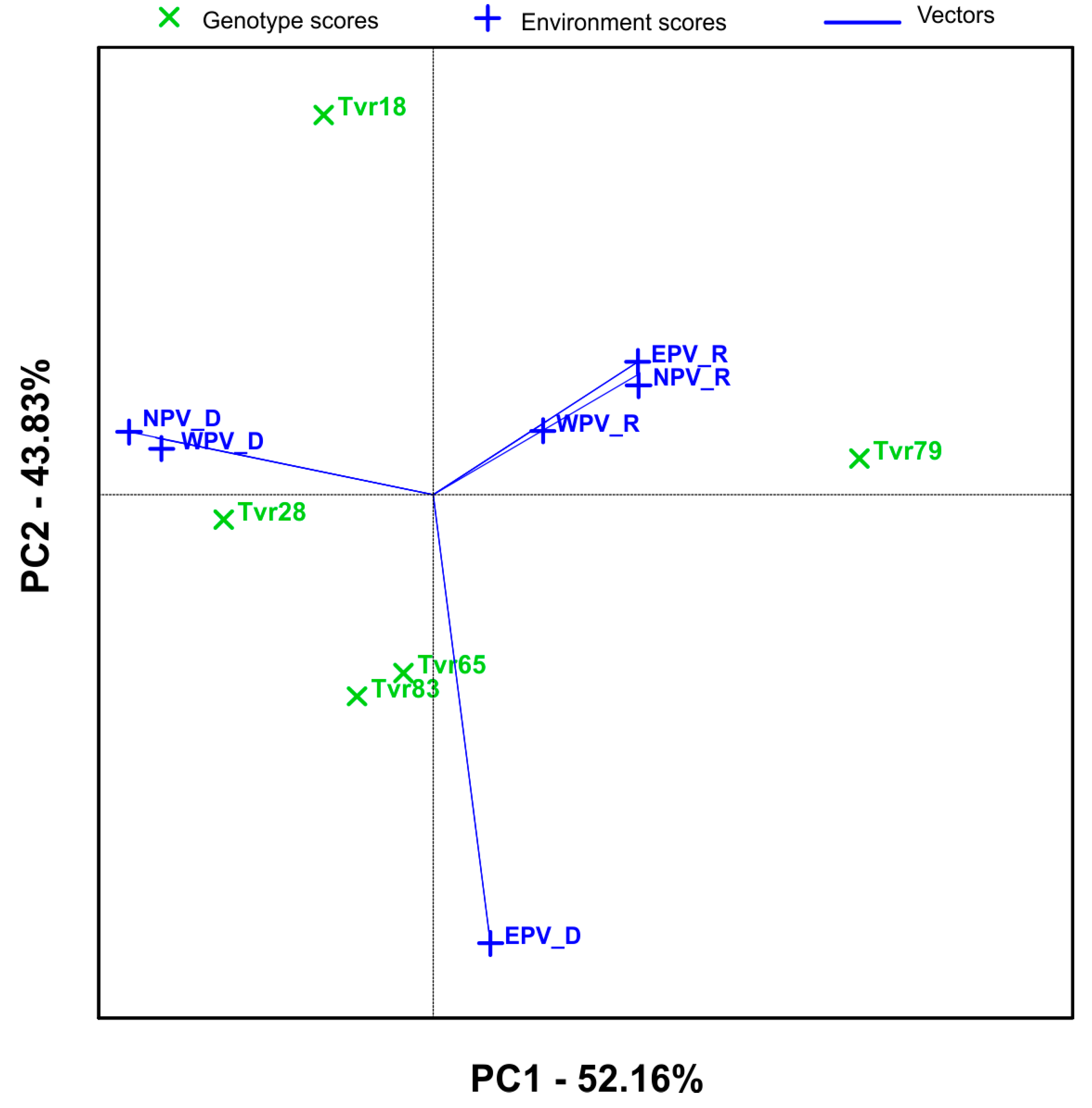
2.2. Mean Performance and Stability of Mungbean Genotypes and APV Environments by GGE Biplot
2.3. Conclusions
3. Materials and Methods
3.1. Experimental Site
3.2. Experimental Materials and Design
3.3. Crop Establishment
3.4. Microclimate Variability of the Six APV Environments
3.5. Data Collection and Statistical Analysis
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bavandpori, F.; Ahmadi, J.; Hossaini, S.M. Yield stability analysis of bread wheat lines using AMMI model. Agric. Commun. 2015, 3, 8–15. [Google Scholar]
- Kang, M.S.; Prabhakaran, V.T.; Mehra, R.B. Genotype-by-environment interaction in crop improvement. In Plant Breeding—Mendelian to Molecular Approaches; Jain, H.K., Kharkwal, M.C., Eds.; Narose Publishing House: New Delhi, India, 2004; pp. 536–572. [Google Scholar]
- Temesgen, B. The Role of Genotype by Environment Interaction in Plant Breeding. J. Nat. Sci. Res. 2020, 11, 9–17. [Google Scholar]
- Kienast, F.; Huber, N.; Hergert, R.; Bolliger, J.; Moran, L.S.; Hersperger, A.M. Conflicts between decentralized renewable electricity production and landscape services: A spatially explicit quantitative assessment for Switzerland. Renew. Sust. Energy Rev. 2017, 67, 397–407. [Google Scholar] [CrossRef]
- Farja, Y.; Maciejczak, M. Economic implications of agricultural land conversion to solar power production. Energies 2021, 14, 6063. [Google Scholar] [CrossRef]
- Havrysh, V.; Kalinichenko, A.; Szafranek, E.; Hruban, V. Agricultural land: Crop production or photovoltaic power plants. Sustainability 2022, 14, 5099. [Google Scholar] [CrossRef]
- Moscatelli, M.C.; Marabottini, R.; Massaccesi, L.; Marinari, S. Soil properties change after seven years of ground-mounted photovoltaic panels in Central Italy coastal area. Geoderma Reg. 2022, 29, e00500. [Google Scholar] [CrossRef]
- Ravishankar, E.; Charles, M.; Xiong, Y.; Henry, R.; Swift, J.; Rech, J.; Calero, J.; Cho, S.; Booth, R.E.; Kim, T.; et al. Balancing crop production and energy harvesting in organic solar-powered greenhouses. Cell Rep. Phys. Sci. 2021, 2, 100381. [Google Scholar] [CrossRef]
- Touil, S.; Ricga, A.; Fizir, M.; Bingwa, B. Shading effect of photovoltaic panels on horticulture crop production: A mini-review. Rev. Environ. Sci. Biotechnol. 2021, 20, 281–296. [Google Scholar] [CrossRef]
- Allardyce, C.S.; Fankhauser, C.; Zakeeruddin, S.M.; Grätzel, M.; Dyson, P.J. The influence of greenhouse-integrated photovoltaics on crop production. Sol. Energy 2017, 155, 517–522. [Google Scholar] [CrossRef]
- Dijk, M.V.; Morley, T.; Rau, M.L.; Saghai, Y. A meta-analysis of projected global food demand and population at risk of hunger for the period 2010–2050. Nat. Food 2021, 2, 494–501. [Google Scholar] [CrossRef]
- Ukwu, U.N.; Muller, O.; Meier-Grüll, M.; Uguru, M.I. Agrivoltaics shading enhanced the microclimate, photosynthesis, growth, and yields of Vigna radiata genotypes in tropical Nigeria. Sci. Rep. 2025, 15, 1190. [Google Scholar] [CrossRef] [PubMed]
- Ukwu, U.N.; Agbo, J.U.; Muller, O.; Schrey, S.; Nedbal, L.; Niu, Y.; Meier-Grüll, M.; Uguru, M. Effect of organic photovoltaic and red-foil transmittance on yield, growth and photosynthesis of two spinach genotypes under field and greenhouse conditions. Photosynth. Res. 2023, 157, 103–118. [Google Scholar] [CrossRef] [PubMed]
- Heuzé, V.; Tran, G.; Bastianelli, D.; Lebas, F. Mungbean (Vigna radiata). Feedipedia, a Programme by INRA, CIRAD, AFZ and FAO 2015. Available online: http://www.feedipedia.org/node/235 (accessed on 12 April 2023).
- Kim, D.K.; Jeong, S.C.; Gorinstein, S.; Chon, S.U. Total polyphenols, antioxidant and antiproliferative activities of different extracts in mungbean seeds and sprouts. Plant Food Human Nutr. 2012, 67, 71–74. [Google Scholar] [CrossRef]
- Sequeros, T.; Ochieng, J.; Schreinemachers, P.; Binagwa, P.H.; Huelgas, Z.M.; Hapsari, R.T.; Juma, M.O.; Kangile, J.R.; Karimi, R.; Khaririyatun, N.; et al. Mungbean in Southeast Asia and East Africa: Varieties, Practices and Constraints. Agric. Food Secur. 2021, 10, 2. [Google Scholar] [CrossRef]
- Mattos, P.H.C.; Oliveira, R.A.J.; Filho, C.B.; Daros, E.; Veríssimo, M.A.A. Evaluation of sugarcane genotypes and production environments in Paraná by GGE biplot and AMMI analysis. Crop. Breed. Appl. Biotechnol. 2013, 13, 83–90. [Google Scholar] [CrossRef]
- Regis, J.A.V.B.; Andrade, J.A.C.; Santos, A.; Moraes, A.; Trindade, R.W.R.; Henriques, H.J.R.; Polis, B.H.; Oliveira, L.C. Adaptability and phenotypic stability of sugarcane clones. Pesqui. Agropecu. Bras. 2018, 53, 42–52. [Google Scholar] [CrossRef]
- Kearsey, M.J.; Pooni, H.S. The Genet Ical Analysis Ofquantitative Traits; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Kamila, N.; Alina, L.; Wiesława, P.; Jan, B. Genotype by environment interaction for seed yield in rapeseed (Brassica napus L.) using additive main effects and multiplicative interaction model. Euphytica 2016, 208, 187–194. [Google Scholar]
- Finlay, K.W.; Wilkinson, G.N. The analys is of adaptation in a plant breeding programme. Aust. J. Agr. Res. 1963, 14, 742–754. [Google Scholar] [CrossRef]
- Yan, W.; Kang, M.S. GGE Biplot Analysis: A Graphical Tool for Breeders, Geneticists, and Agronomists; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Gauch, H.G. Statistical analysis of yield trials by AMMI and GGE. Crop. Sci. 2006, 46, 1488–1500. [Google Scholar] [CrossRef]
- Tena, E.; Goshu, F.; Mohamad, H.; Tesfa, M.; Tesfaye, D.; Seife, A. Genotype × environment interaction by AMMI and GGE-biplot analysis for sugar yield in three crop cycles of sugarcane (Saccharum officinarum L.) clones in Ethiopia. Cogent Food Agric. 2019, 5, 1651925. [Google Scholar] [CrossRef]
- Purchase, J.L.; Hatting, H.; Van Deventer, C.S. Genotype x environment interaction of winter wheat (T. aestivum) in South Africa: Stability analysis of yield performance. S. Afr. J. Plant Soil 2000, 17, 101–107. [Google Scholar] [CrossRef]
- Bhagwat, G.V.; Joseph, J.; Antony, R. Stability of advanced generation of intervarietal crosses in black gram (Vigna mungo L.) through AMMI analysis. Electron. J. Plant Breed. 2018, 9, 465–475. [Google Scholar] [CrossRef]
- Nath, D.; Dasgupta, T. Genotype × environment interaction and stability analysis in mungbean. IOSR JAVS 2013, 5, 62–70. [Google Scholar] [CrossRef]
- Crossa, J.; Gauch, H.G.; Zobel, R.W. Additive main effects and multiplicative interaction analysis of two international maize cultivar trials. Crop. Sci. 1990, 30, 493–500. [Google Scholar] [CrossRef]
- Yan, W.; Rajcan, I. Biplot analysis of test sites and trait relations of soybean in Ontario. Crop. Sci. 2002, 42, 11–20. [Google Scholar] [CrossRef]
- Ukwu, U.N.; Oburu, B.N.; Muojiama, S.O.; Osadebe, V.O.; Dauda, N.; Adewuyi, S.O. Morphology and agronomic evaluation of ten mungbean (Vigna radiata L.) accessions in derived savanna agroecology of southeast Nigeria. Asian J. Biol. Sci. 2023, 16, 110–120. [Google Scholar] [CrossRef]
- Ukwu, U.N.; Agbirionwu, A.C.; Dauda, N.; Adewuyi, S.O.; Osadebe, V.O.; Anozie, C.C. Response of mungbean (Vigna radiata L. Wilczek) genotypes to different spacing types in derived savannah agroecology of southeast Nigeria. Niger. J. Biotechnol. 2023, 40, 77–85. [Google Scholar] [CrossRef]
- Ukwu, U.N.; Oburu, B.N.; Udochukwu, D.P.; Adewuyi, S.O.; Muojiama, S.O.; Osadebe, V.O.; Ezeh, I.N.; Ishieze, P.U.; Dauda, N. Performance of mungbean (Vigna radiata L. Wilczek) accessions under intermittent water deficit stress in a tropical environment. J. Appl. Biol. Biotechnol. 2024, 12, 129–137. [Google Scholar] [CrossRef]
- Banik, B.R.; Khaldum, A.B.M.; Mondal, A.A.; Islam, A.; Rohman, M.M. Assessment of genotype-by-environment interaction using additive main effects and multiplicative interaction model (AMMI) in maize (Zea mays L.) hybrids. AJPS 2010, 3, 134–139. [Google Scholar]
- Falconer, D.S. Selection for large and small size in mice. J. Genet. 1952, 51, 470–501. [Google Scholar] [CrossRef]
- Lal, R.K.; Chanotiy, C.S.; Gupta, P.; Sarkar, S.; Singh, S.; Maurya, R.; Srivastva, S.; Chaudhar, P.K. Phenotypic stability, genotype × environmental interactions, and cultivar recommendations for essential oil yield in khus aromatic grass (Chrysopogon zizanioides). Ind. Crop. Prod. 2018, 111, 871–877. [Google Scholar] [CrossRef]
- Ukwu, U.N.; Muller, O.; Meier-Grüll, M.; Uguru, M.I. Genotype-environment interaction and yield stability of five Vigna radiata genotypes under contrasting agrivoltaics environments in a tropical dry season climate. CABI Agric. Biosci. 2025; in press. [Google Scholar] [CrossRef]
- Okoro, E.C.; Ugwu, E.B.; Onah, I.G.; Omeje, L.C. Rainfall and solar irradiance monitoring in Nsukka zone, Nigeria. Eur. J. Stat. Probab. 2021, 9, 1–10. [Google Scholar] [CrossRef]
- Ihejiofor, P.N.; Ukwu, U.N.; Adeoye, G. Determination of Kolgrace Bio-fertilizer Rate for Optimum Greengram (Vigna radiata L. Wilczek) Production in Ibadan, Southwest Nigeria. Agro-Science 2022, 21, 82–87. [Google Scholar] [CrossRef]
- Ihejiofor, P.N.; Ukwu, U.N.; Adeoye, G.O. Comparative Effects of Different Levels of Kolgrace Organic Fertilizer on the Growth and Yield Attributes of Greengram (Vigna radiata (L.) Wilczek) in the Screenhouse. Asian J. Res. Agric. For. 2020, 6, 1–7. [Google Scholar] [CrossRef]
- Duarte, J.B.; Venkovsky, R. Interaction of Genotypes x Environments: An Introduction to the AMMI Analysis; Series Monographs, n.9; Brazilian Society of Genetics: Ribeirão Preto, Brazil, 1999. [Google Scholar]
- Gauch, H.G. Statistical Analysis of Regional Yield Trials; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Purchase, J.L. Parametric Analysis to Describe G × E Interaction and Yield Stability in Winter Yield. Ph.D. Thesis, Faculty of Agriculture, University of Orange Free State, Bloemfontein, South Africa, 1997. [Google Scholar]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Yan, W.; Hunt, L.A.; Sheng, Q.; Szlavnics, Z. Cultivar evaluation and mega-environment investigation based on the GGE biplot. Crop. Sci. 2000, 40, 597–605. [Google Scholar] [CrossRef]
- Yan, W. GGE biplot: A Windows application for graphical analysis of multi-environment trial data and other types of two-way data. Agron. J. 2001, 93, 1111–1118. [Google Scholar] [CrossRef]



| Source | d.f. | s.s. | m.s. | %Total ss | %Treatment |
|---|---|---|---|---|---|
| Treatments | 29 | 51.18 | 1.77 *** | 82.5 | |
| Genotypes | 4 | 23.22 | 5.81 *** | 45.4 | |
| Environments | 5 | 8.55 | 1.71 *** | 16.7 | |
| Block | 12 | 1.39 | 0.12 | 2.2 | |
| G × E Interaction | 20 | 19.40 | 0.97 *** | 37.9 | |
| IPCA 1 | 8 | 10.12 | 1.27 *** | 19.8 | |
| IPCA 2 | 6 | 8.51 | 1.42 *** | 16.6 | |
| Residuals | 6 | 0.78 | 0.13 | ||
| Error | 48 | 9.48 | 0.20 | 15.3 | |
| Total | 89 | 62.05 | 0.70 |
| Genotype | EPV Dry | EPV Rainy | NPV Dry | NPV Rainy | WPV Dry | WPV Rainy | Mean | IPCA1 | IPCA2 | ASV |
|---|---|---|---|---|---|---|---|---|---|---|
| Tvr18 | 1.37 | 3.25 | 2.83 | 3.06 | 2.47 | 2.74 | 2.62 | 0.30 | 1.04 | 1.10 |
| Tvr28 | 2.62 | 2.70 | 2.85 | 2.55 | 2.49 | 2.42 | 2.60 | 0.58 | −0.07 | 0.69 |
| Tvr65 | 1.89 | 1.47 | 1.05 | 1.33 | 0.73 | 1.15 | 1.27 | 0.08 | −0.52 | 0.53 |
| Tvr79 | 2.23 | 3.23 | 1.03 | 3.08 | 0.79 | 2.52 | 2.15 | −1.17 | 0.10 | 1.39 |
| Tvr83 | 3.14 | 2.62 | 2.37 | 2.48 | 2.04 | 2.33 | 2.50 | 0.21 | −0.55 | 0.61 |
| Mean | 2.25 | 2.65 | 2.02 | 2.50 | 1.71 | 2.23 | 2.23 | |||
| IPCA1 | −0.15 | −0.53 | 0.79 | −0.54 | 0.72 | −0.30 | ||||
| IPCA2 | −1.17 | 0.35 | 0.16 | 0.32 | 0.15 | 0.20 |
| Source | d.f. | s.s. | m.s. | % of Total ss |
|---|---|---|---|---|
| Genotypes | 4 | 23.22 | 5.81 *** | 37.42 |
| Environments | 5 | 8.55 | 1.71 *** | 13.78 |
| Sensitivities | 4 | 9.20 | 2.30 *** | 14.83 |
| Residual | 76 | 21.07 | 0.28 | |
| Total | 89 | 62.05 | 0.70 |
| Treatment | Mean (t ha−1) | Sensitivity | Rank |
|---|---|---|---|
| Genotype | |||
| Tvr18 | 2.62 | 0.60 | 3 |
| Tvr28 | 2.60 | −0.07 | 1 |
| Tvr65 | 1.27 | 0.68 | 4 |
| Tvr79 | 2.15 | 2.95 | 5 |
| Tvr83 | 2.50 | 0.57 | 2 |
| Environment | |||
| EPV-D | 2.25 | 0.03 | 4 |
| EPV-R | 2.61 | 0.38 | 1 |
| NPV-D | 1.88 | −0.34 | 5 |
| NPV-R | 2.54 | 0.31 | 2 |
| WPV-D | 1.75 | −0.48 | 6 |
| WPV-R | 2.33 | 0.10 | 3 |
| Genotype | Growth Pattern | Hypo-Cotyl Color | Terminal Leaf Shape | Leaf Color | Petiole Color | Petiole Length | Seed Shape | Seed Luster |
|---|---|---|---|---|---|---|---|---|
| Tvr18 | Erect | Greenish purple | Cuneate | Green | GP | Long | Round | Dull |
| Tvr28 | Erect | Greenish Purple | Cuneate | Green | GP | Medium | Round | Dull |
| Tvr65 | Erect | Greenish purple | Cuneate | Green | GP | Medium | Round | Dull |
| Tvr79 | Semi- erect | Purple | Cuneate | Green | GP | Medium | Round | Dull |
| Tvr83 | Spreading | Green | Ovate | Dark-Green | Purple | Short | Oval | Shiny |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ukwu, U.N.; Muller, O.; Meier-Gruell, M.; Uguru, M.I. Yield Sensitivity of Mungbean (Vigna radiata L.) Genotypes to Different Agrivoltaic Environments in Tropical Nigeria. Plants 2025, 14, 1326. https://doi.org/10.3390/plants14091326
Ukwu UN, Muller O, Meier-Gruell M, Uguru MI. Yield Sensitivity of Mungbean (Vigna radiata L.) Genotypes to Different Agrivoltaic Environments in Tropical Nigeria. Plants. 2025; 14(9):1326. https://doi.org/10.3390/plants14091326
Chicago/Turabian StyleUkwu, Uchenna Noble, Onno Muller, Matthias Meier-Gruell, and Michael Ifeanyi Uguru. 2025. "Yield Sensitivity of Mungbean (Vigna radiata L.) Genotypes to Different Agrivoltaic Environments in Tropical Nigeria" Plants 14, no. 9: 1326. https://doi.org/10.3390/plants14091326
APA StyleUkwu, U. N., Muller, O., Meier-Gruell, M., & Uguru, M. I. (2025). Yield Sensitivity of Mungbean (Vigna radiata L.) Genotypes to Different Agrivoltaic Environments in Tropical Nigeria. Plants, 14(9), 1326. https://doi.org/10.3390/plants14091326








