Evapotranspiration Partitioning of the Populus euphratica Forest Ecosystem in the Drylands of Northwestern China
Abstract
1. Introduction
2. Results
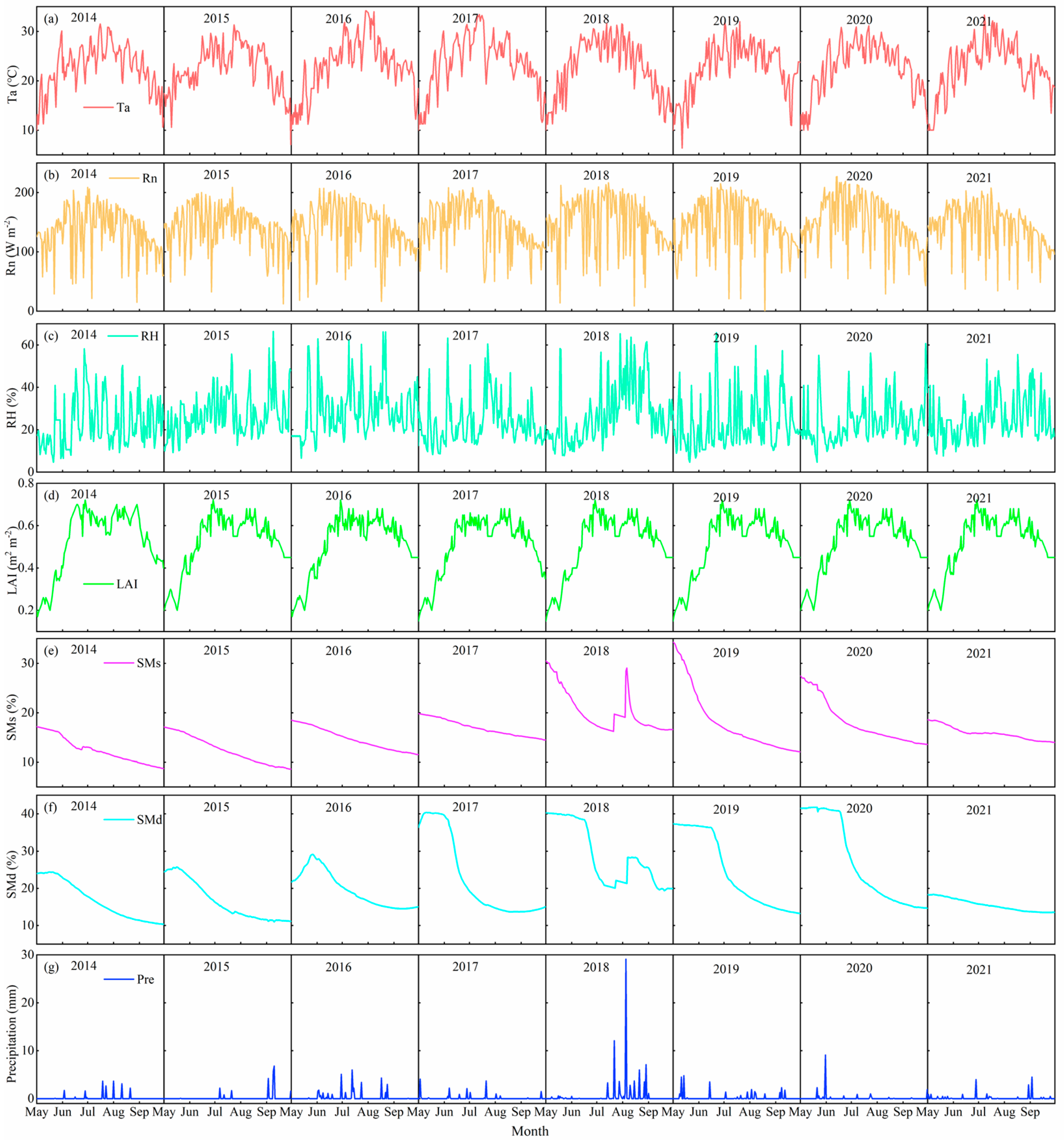
2.1. Environmental and Biological Factors
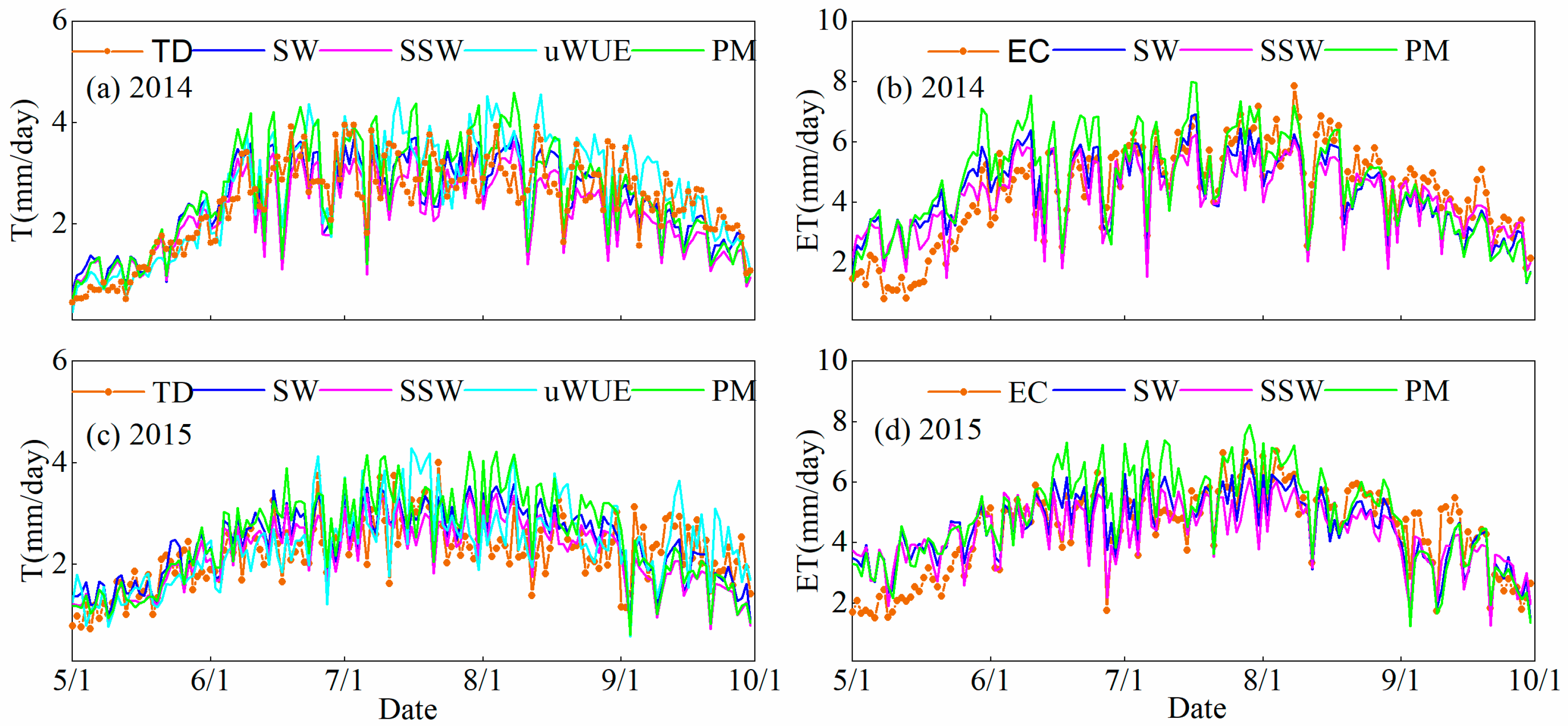
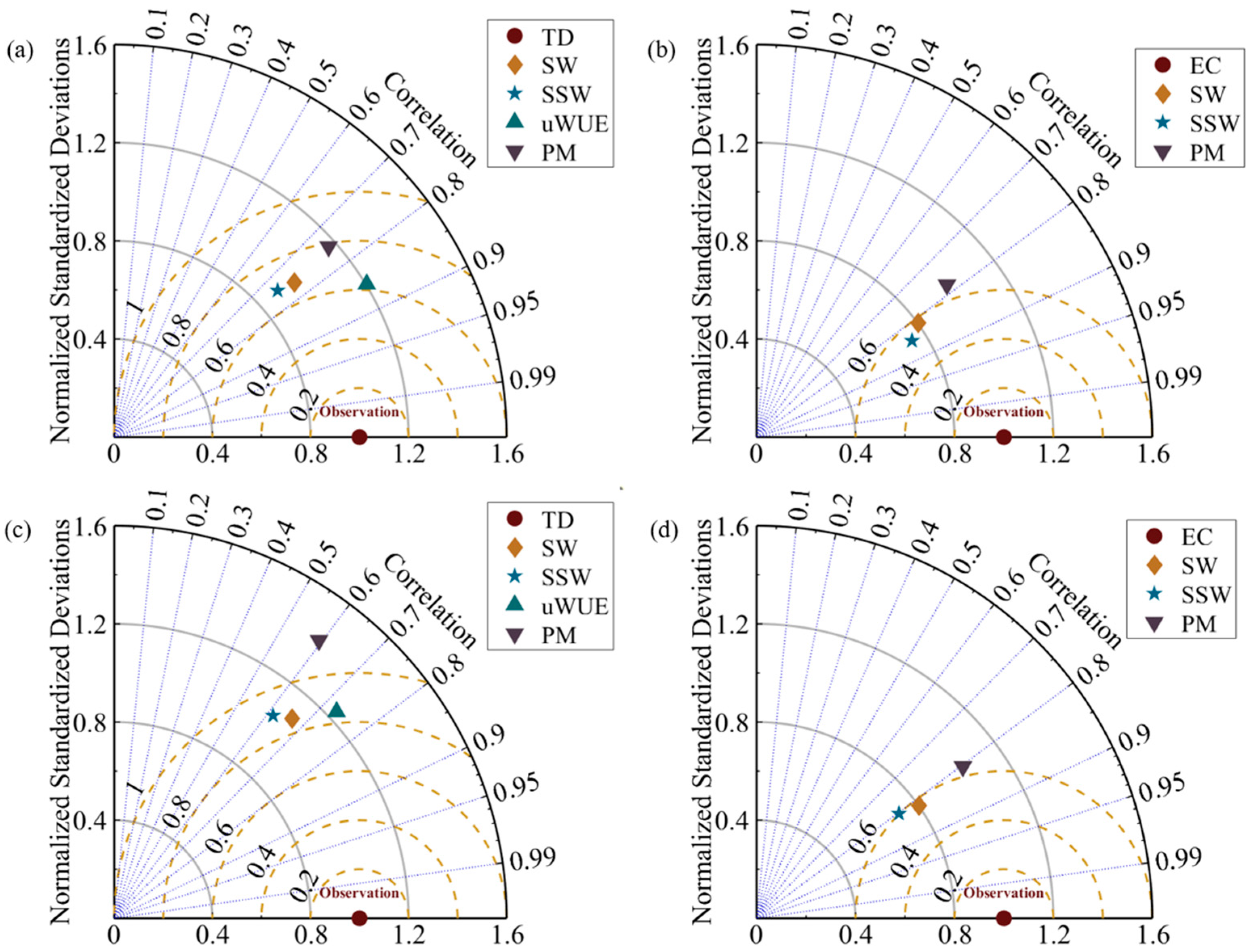
2.2. Comparison of the Methods for Partitioning ET
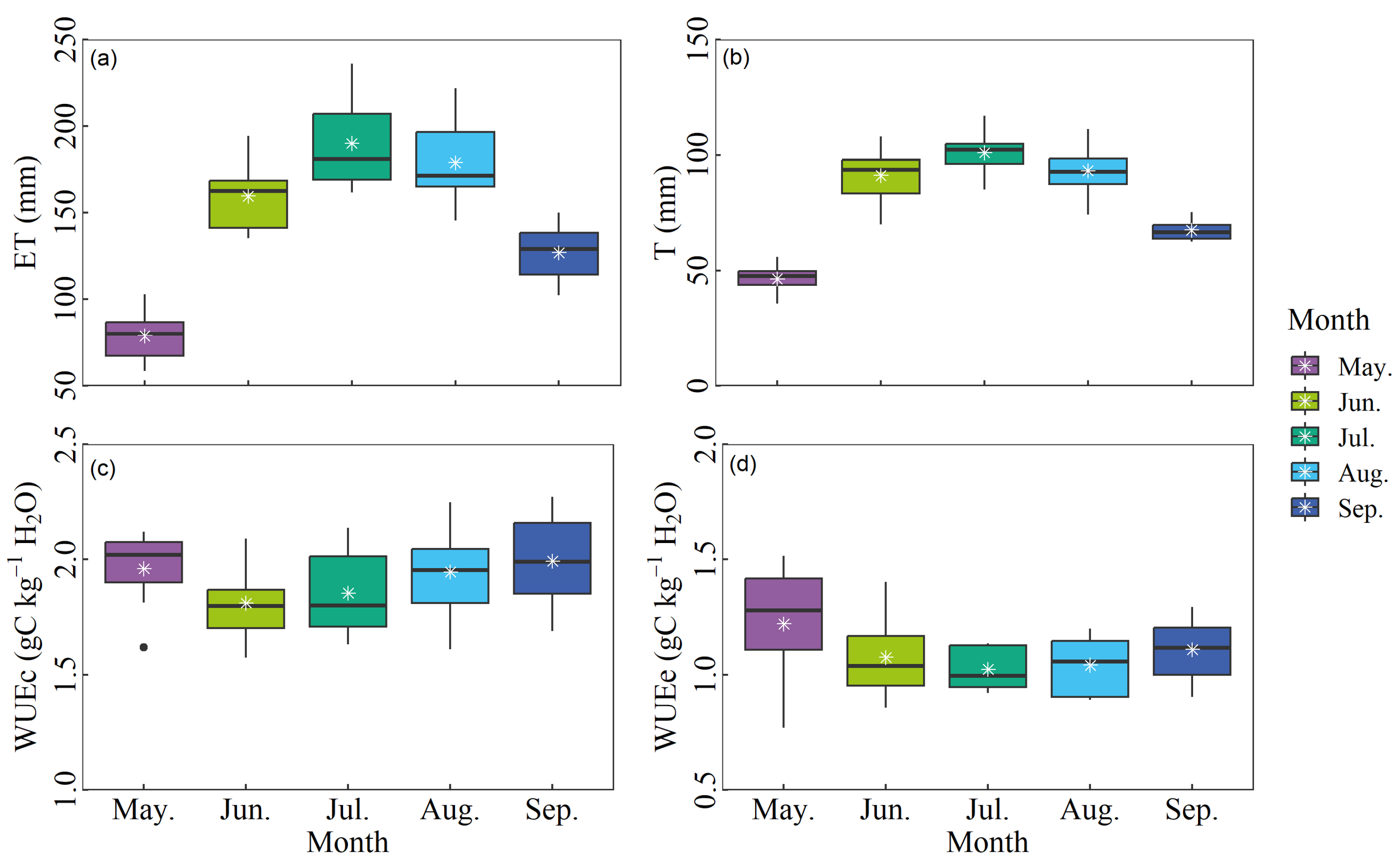
2.3. Seasonal Variations in ET, T, WUEc, and WUEe
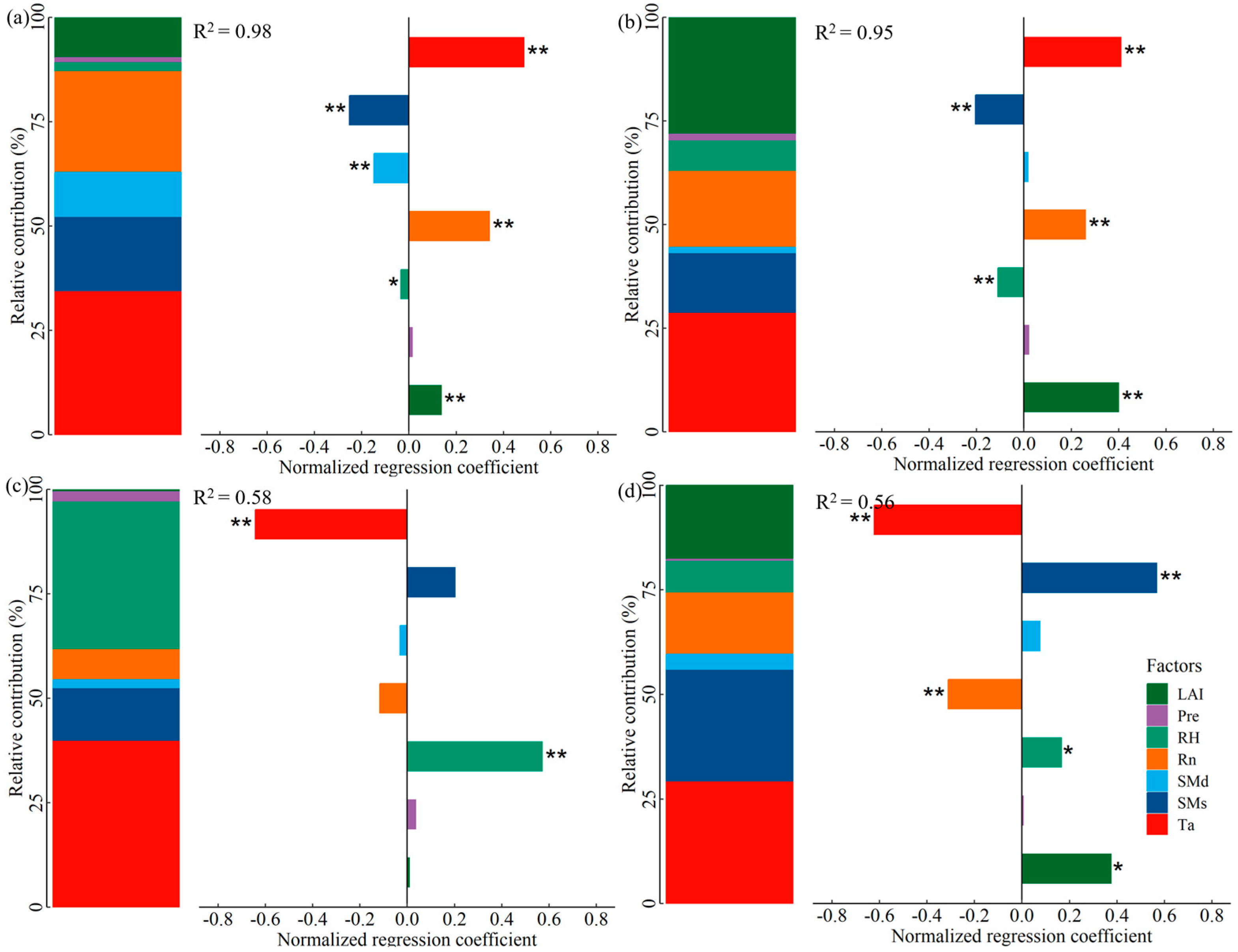
2.4. Responses of ET, T, WUEc, and WUEe to Influencing Factors
3. Discussion
3.1. Comparisons of the ET Partitioning Method
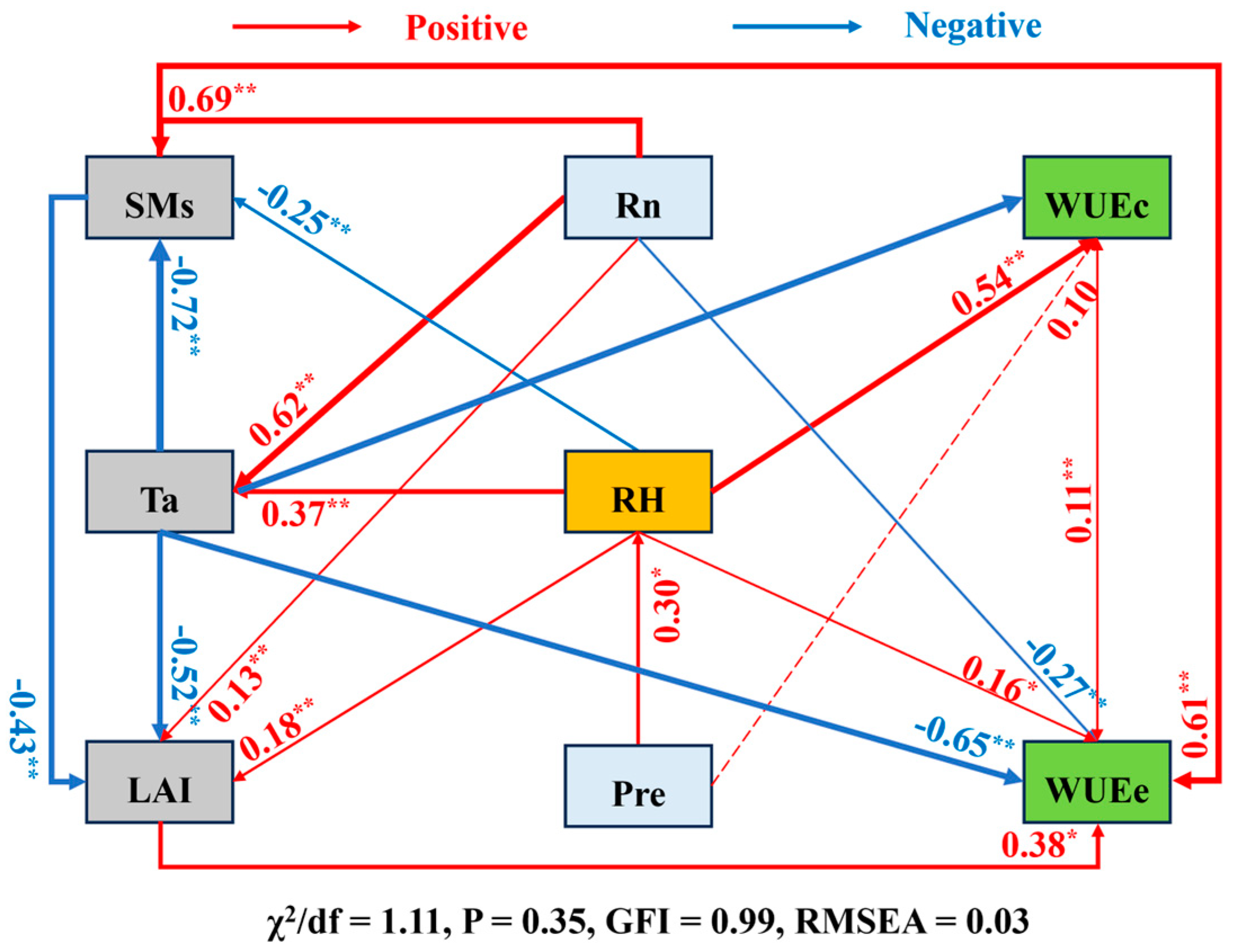
3.2. Effects of Environmental Factors on ET, T, WUEc, and WUEe
4. Materials and Methods
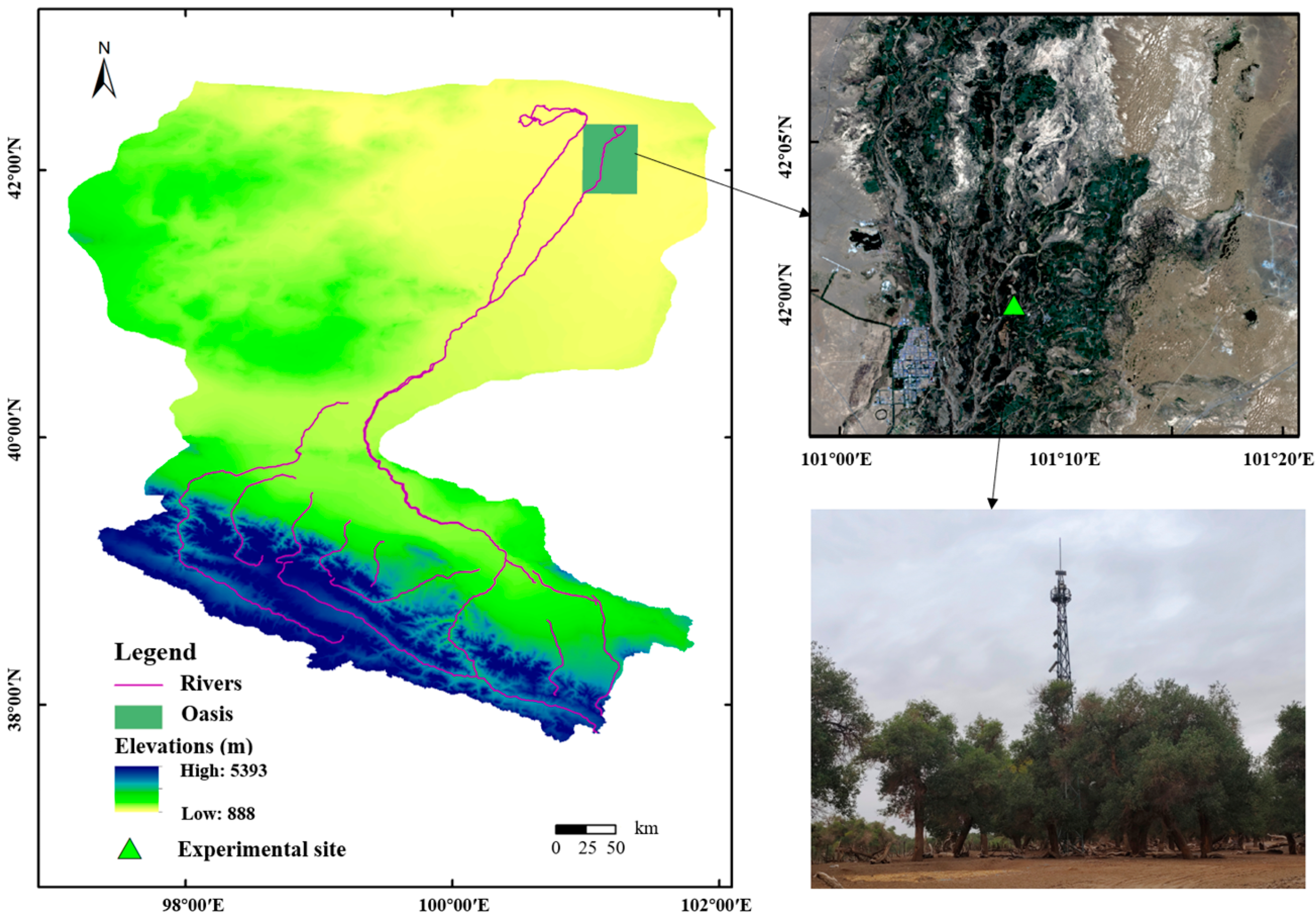
4.1. Study Site
4.2. Measurements and Data Processing
4.3. Methods for Partitioning ET
4.3.1. Underlying Water Use Efficiency (uWUE) Method
4.3.2. The Two-Source Shuttleworth and Wallace (SW) Model
4.3.3. The Improved Dual-Source (SSW) Model
4.3.4. The Two-Source Penman–Monteith (PM) Model
4.4. Methods for Calculating WUE
4.5. Statistical Analysis
4.6. Structural Equation Model (SEM)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ET | Evapotranspiration |
| T | Transpiration |
| E | Evaporation |
| WUE | Water use efficiency |
| uWUE | Underlying water use efficiency |
| WUEc | Canopy water use efficiency |
| WUEe | Ecosystem water use efficiency |
| Ta | Temperature |
| Rn | Radiation |
| LAI | Leaf area index |
| RH | Relative humidity |
| SMs | Shallow soil moisture content |
| SMd | Deep soil moisture content |
| Pre | Precipitation |
| SW | Shuttleworth and Wallace |
| SSW | Simplified Shuttleworth and Wallace |
| PM | Penman–Monteith |
| PT | Priestley–Taylor |
| EC | Eddy covariance |
| VPD | Vapor pressure deficit |
| GPP | Gross primary productivity |
References
- Bastin, J.F.; Berrahmouni, N.; Grainger, A.; Maniatis, D.; Mollicone, D.; Moore, R.; Castro, R. The extent of forest in dryland biomes. Science 2017, 356, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Zhao, W.; Daryanto, S.; Wang, L.; Fan, H.; Feng, Q.; Wang, Y. The spatial distribution and temporal variation of desert riparian forests and their influencing factors in the downstream Heihe River basin, China. Hydrol. Earth Syst. Sci. 2017, 21, 2405–2419. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Xiao, J.; Ma, M. Evapotranspiration components and water use efficiency from desert to alpine ecosystems in drylands. Agric. For. Meteorol. 2021, 298, 108283. [Google Scholar] [CrossRef]
- Sun, H.; Wang, P.; Chen, Q.; Zhang, D.; Xing, Y. Coupling the water use of Populus euphratica and Tamarix ramosissima and evapotranspiration partitioning in a desert riparian forest ecosystem. Agric. For. Meteorol. 2022, 323, 109064. [Google Scholar] [CrossRef]
- Deng, X.; Xu, H.; Ye, M.; Li, B.; Fu, J.; Yang, Z. Impact of long-term zero-flow and ecological water conveyance on the radial increment of Populus euphratica in the lower reaches of the Tarim River, Xinjiang, China. Reg. Environ. Change 2014, 15, 13–23. [Google Scholar] [CrossRef]
- Li, W.; Zhou, H.; Fu, A.; Chen, Y. Ecological response and hydrological mechanism of desert riparian forest in inland river, northwest of China. Ecohydrology 2013, 6, 949–955. [Google Scholar] [CrossRef]
- Katul, G.G.; Oren, R.; Manzoni, S.; Higgins, C.; Parlange, M.B. Evapotranspiration: A process driving mass transport and energy exchange in the soil–plant–atmosphere–climate system. Rev. Geophy. 2012, 50, 1209–8755. [Google Scholar] [CrossRef]
- Wang, P.; Yamanaka, T.; Li, X.; Wei, Z. Partitioning evapotranspiration in a temperate grassland ecosystem: Numerical modeling with isotopic tracers. Agric. For. Meteorol. 2015, 208, 16–31. [Google Scholar] [CrossRef]
- Guo, X.Y.; Cheng, G.D. Advances in the application of remote sensing to evapotranspiration research. Advances in Earth. Science 2004, 19, 107–114. [Google Scholar]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; Wood, E.F. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agr. Forest Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Gentine, P.; Zhang, Y.; Chen, J.; Chen, X. Recent increase in the observation−derived land evapotranspiration due to global warming. Environ. Res. Lett. 2022, 17, 024020. [Google Scholar] [CrossRef]
- Yan, H.; Yu, Q.; Zhu, Z.C.; Myneni, R.B.; Yan, H.M.; Wang, S.Q.; Shugart, H.H. Diagnostic analysis of interannual variation of global land evapotranspiration over 1982–2011: Assessing the impact of ENSO. J. Geophys. Res.-Atmos. 2013, 118, 8969–8983. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wires. Water 2016, 3, 834–853. [Google Scholar]
- Gentine, P.; Green, J.K.; Gu´erin, M.; Humphrey, V.; Seneviratne, S.I.; Zhang, Y.; Zhou, S. Coupling between the terrestrial carbon and water cycles—A review. Environ. Res. Lett. 2019, 14, 083003. [Google Scholar] [CrossRef]
- Green, J.K.; Seneviratne, S.I.; Berg, A.M.; Findell, K.L.; Hagemann, S.; Lawrence, D.M.; Gentine, P. Large influence of soil moisture on long-term terrestrial carbon uptake. Nature 2019, 565, 476–479. [Google Scholar] [CrossRef] [PubMed]
- Stoy, P.C.; El-Madany, T.S.; Fisher, J.B.; Gentine, P.; Good, S.P.; Wolf, S. Reviews and syntheses: Turning the challenges of partitioning ecosystem evaporation and transpiration into opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Cammalleri, C.; Rallo, G.; Agnese, C.; Ciraolo, G.; Minacapilli, M.; Provenzano, G. Combined use of eddy covariance and sap flow techniques for partition of ET fluxes and water stress assessment in an irrigated olive orchard. Agric. Water Manag. 2013, 120, 89–97. [Google Scholar] [CrossRef]
- Good, S.P.; Noone, D.; Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 2015, 349, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Welp, L.R.; Lee, X.H.; Kim, K.; Griffis, T.J.; Billmark, K.A.; Baker, J.M. δ18O of water vapour, evapotranspiration and the sites of leaf water evaporation in a soybean canopy. Plant Cell Environ. 2008, 31, 1214–1228. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.G.; Cable, W.; Hultine, K.; Hoedjes, J.C.B.; Yepez, E.A.; Simonneaux, V.; Timouk, F. Evapotranspiration components determined by stable isotope, sap flow and eddy covariance techniques. Agric. For. Meteorol. 2004, 125, 241–258. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Partitioning evapotranspiration based on the concept of underlying water use efficiency. Water Resour. Res. 2016, 52, 1160–1175. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops–an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Hu, Z.M.; Yu, G.R.; Zhou, Y.L.; Sun, X.M.; Li, Y.N. Partitioning of evapotranspiration and its controls in four grassland ecosystems: Application of a two–source model. Agric. For. Meteorol. 2009, 149, 1410–1420. [Google Scholar] [CrossRef]
- Kato, T.; Kimura, R.; Kamichika, M. Estimation of evapotranspiration, transpiration ratio and water–use efficiency from a sparse canopy using a compartment model. Agric. Water Manag. 2004, 65, 173–191. [Google Scholar] [CrossRef]
- Zhang, B.Z.; Kang, S.Z.; Li, F.S.; Zhang, L. Comparison of three evapotranspiration models to Bowen ratio–energy balance method for a vineyard in an and desert region of northwest China. Agric. For. Meteorol. 2008, 148, 1629–1640. [Google Scholar] [CrossRef]
- Li, X.; Yang, P.; Ren, S.; Li, Y.; Liu, H.; Du, J. Modeling cherry orchard evapotranspiration based on an improved dual-source model. Agric. For. Meteorol. 2010, 98, 12–18. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of the surface heat flux and evapotranspiration using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Song, Y.; Jin, L.; Zhu, G.; Ma, M. Parameter estimation for a simple two-source evapotranspiration model using Bayesian inference and its application to remotely sensed estimations of latent heat flux at the regional scale. Agric. For. Meteorol. 2016, 230, 20–32. [Google Scholar] [CrossRef]
- Wang, L.M.; Li, M.Y.; Wang, J.X.; Li, X.G.; Wang, L.C. An analytical reductionist framework to separate the effects of climate change and human activities on variation in water use efficiency. Sci. Total Environ. 2020, 727, 138306. [Google Scholar] [CrossRef]
- Hu, H.; Chen, L.; Liu, H.; Khan, M.Y.A.; Tian, F. Comparison of the vegetation effect on et partitioning based on eddy covariance method at five different sites of northern China. Remote Sens. 2018, 10, 1755. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, Z.; Liu, S.; Song, L.; Wang, X.; Zhou, S. Evapotranspiration partitioning for multiple ecosystems within a dryland watershed: Seasonal variations and controlling factors. J. Hydrol. 2021, 598, 126483. [Google Scholar] [CrossRef]
- Sun, J.Y.; Sun, X.Y.; Hu, Z.Y.; Wang, G.X. Exploring the influence of environmental factors in partitioning evapotranspiration along an elevation gradient on Mount Gongga, eastern edge of the Qinghai-Tibet Platea, China. J. Mt. Sci. 2020, 17, 384–396. [Google Scholar] [CrossRef]
- Jiao, L.; Lu, N.; Fu, B.; Wang, J.; Li, Z.; Fang, W.; Zhang, L. Evapotranspiration partitioning and its implications for plant water use strategy: Evidence from a black locust plantation in the semi-arid Loess Plateau, China. Forest Ecol. Manag. 2018, 424, 428–438. [Google Scholar] [CrossRef]
- Kochendorfer, J.P.; Ramírez, J.A. Ecohydrologic controls on vegetation density and evapotranspiration partitioning across the climatic gradients of the central United States. Hydrol. Earth Syst. Sci. 2008, 5, 649–700. [Google Scholar] [CrossRef]
- Wei, Z.; Yoshimura, K.; Wang, L.; Miralles, D.G.; Jasechko, S.; Lee, X. Revisiting the contribution of transpiration to global terrestrial evapotranspiration. Geophys. Res. Lett. 2017, 44, 2792–2801. [Google Scholar] [CrossRef]
- Du, X.Z.; Zhao, X.; Zhou, T.; Jiang, B.; Xu, P.P.; Wu, D.H.; Tang, B.J. Effects of climate factors and human activities on the ecosystem water use efficiency throughout northern China. Remote Sens. 2019, 11, 2766. [Google Scholar] [CrossRef]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 2013, 499, 324. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, X.; Yu, T.; Liu, B. Comparison of three evapotranspiration models with eddy covariance measurements for a Populus euphratica Oliv. forest in an arid region of northwestern China. J. Arid. Land 2016, 8, 146–156. [Google Scholar] [CrossRef][Green Version]
- Han, C.; Chen, R.; Liu, Z.; Yang, Y.; Liu, J.; Song, Y.; Wang, X. Cryospheric hydrometeorology observation in the Hulu catchment (CHOICE), Qilian Mountains, China. Vadose Zone J. 2018, 17, 1–18. [Google Scholar] [CrossRef]
- Niu, S.; Xing, X.; Zhang, Z.H.E.; Xia, J.; Zhou, X.; Song, B.; Li, L.; Wan, S. Water-use efficiency in response to climate change: From leaf to ecosystem in a temperate steppe. Glob. Chang. Biol. 2011, 17, 1073–1082. [Google Scholar] [CrossRef]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q. The Heihe Integrated Observatory Network: A basin-scale land surface processes observatory in China. Vadose Zone J. 2018, 17, 180072. [Google Scholar] [CrossRef]
- Qi, S.; Luo, F. Environmental degradation problems in the Heihe River Basin, northwest China. Water Environ. J. 2007, 21, 142–148. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X.; Zhou, S.; Yang, X.; Yu, K.; Wang, M. Quantifying plant transpiration and canopy conductance using eddy flux data: An underlying water use efficiency method. Agric. For. Meteorol. 2019, 271, 375–384. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Water use efficiency and evapotranspiration partitioning for three typical ecosystems in the Heihe River Basin, northwestern China. Agric. For. Meteorol. 2018, 253, 261–273. [Google Scholar] [CrossRef]
- Cao, R.; Huang, H.; Wu, G.; Han, D.; Jiang, Z.; Di, K.; Hu, Z. Spatiotemporal variations in the ratio of transpiration to evapotranspiration and its controlling factors across terrestrial biomes. Agric. For. Meteorol. 2022, 321, 108984. [Google Scholar] [CrossRef]
- Jiang, S.; Liang, C.; Cui, N.; Zhao, L.; Liu, C.; Feng, Y. Water use efficiency and its drivers in four typical agroecosystems based on flux tower measurements. Agric. For. Meteorol. 2020, 295, 108200. [Google Scholar] [CrossRef]
- Scott, R.L.; Knowles, J.F.; Nelson, J.A.; Gentine, P.; Li, X.; Barron-Gafford, G. Water availability impacts on evapotranspiration partitioning. Agric. For. Meteorol. 2021, 297, 108251. [Google Scholar] [CrossRef]
- Huang, S.; Yan, H.; Zhang, C.; Wang, G.; Acquah, S.J.; Yu, J. Modeling evapotranspiration for cucumber plants based on the Shuttleworth-Wallace model in a Venlo-type greenhouse. Agric. Water Manag. 2020, 228, 105861. [Google Scholar] [CrossRef]
- Lagos, L.O.; Martin, D.L.; Verma, S.B.; Irmak, S.; Irmak, A.; Eisenhauer, D.; Suyker, A. Surface energy balance model of transpiration from variable canopy cover and evaporation from residue-covered or bare soil systems: Model evaluation. Irrig. Sci. 2013, 31, 135–150. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Li, F.; Du, T.; Tong, L.; Kang, S. Comparison of dual crop coefficient method and Shuttleworth–Wallace model in evapotranspiration partitioning in a vineyard of northwest China. Agric. Water Manag. 2015, 160, 41–56. [Google Scholar] [CrossRef]
- Brisson, N.; Itier, B.; L’Hotel, J.C.; Lorendeau, J.Y. Parameterization of the Shuttleworth-Wallace model to estimate daily maximum transpiration for use in crop models. Ecol. Modell. 1998, 107, 159–169. [Google Scholar] [CrossRef]
- Lohammar, T.; Larsson, S.; Linder, S. FAST: Simulation models of gaseous exchange in Scots pine. Ecol. Bull. 1980, 32, 505–523. [Google Scholar]
- Choudhury, B.J.; Monteith, J. A four-layer model for the heat budget of homogeneous land surfaces. Q. J. R. Meteorol. Soc. 1988, 114, 373–398. [Google Scholar]
- Gao, G.; Zhang, X.; Yu, T. Evapotranspiration of a Populus euphratica forest during the growing season in an extremely arid region of northwest China using the Shuttleworth–Wallace model. J. For. Res (Harbin) 2015, 27, 879–887. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Y.; Chen, Y.; Friedman, J.; Hati, J.; Fang, G. Use of 2H and 18O stable isotopes to investigate water sources for different ages of Populus euphratica along the lower Heihe River. Ecol. Res. 2015, 30, 581–587. [Google Scholar] [CrossRef]
- Onyutha, C. Trends and variability of temperature and evaporation over the African continent: Relationships with precipitation. Atmósfera 2021, 34, 267–287. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Chen, Y.; Bai, Y.; Tong, Y.; Wang, P. Atmospheric water demand dominates daily variations in water use efficiency in alpine meadows, northeastern Tibetan Plateau. J. Geophys. 2019, 124, 2174–2185. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Yuan, G.; Luo, Y.; Shao, M.; Zhang, P.; Zhu, X. Evapotranspiration and its main controlling mechanism over the desert riparian forests in the lower Tarim River Basin. Sci. China Earth Sci. 2015, 58, 1032–1042. [Google Scholar] [CrossRef]
- Han, D.; Wang, G.; Liu, T. Hydroclimatic response of evapotranspiration partitioning to prolonged droughts in semiarid grassland. J. Hydrol. 2018, 563, 766–777. [Google Scholar] [CrossRef]
- Pan, H.; Ran, Q.; Hong, Y.; Wang, J.; Chen, X.; Ye, S. Long-term impacts of ecosystem restoration on saturated hydraulic conductivity in the Loess Plateau. J. Hydrol. 2023, 620, 129337. [Google Scholar] [CrossRef]
- Brummer, C.; Black, T.A.; Jassal, R.S.; Grant, N.J.; Spittlehouse, D. How climate and vegetation type influence evapotranspiration and water use efficiency in Canadian forest, peatland and grassland ecosystems. Agric. For. Meteorol. 2012, 153, 14–30. [Google Scholar] [CrossRef]
- Reichstein, M.; Tenhunen, J.D.; Roupsard, O.; Ourcival, J.M.; Rambal, S. Severe drought effects on ecosystem CO2 and H2O fluxes at three Mediterranean evergreen sites: Revision of current hypotheses? Glob. Chang. Biol. 2002, 8, 999–1017. [Google Scholar] [CrossRef]
- Quan, Q.; Zhang, F.; Tian, D.; Zhou, Q.; Wang, L.; Niu, S. Transpiration Dominates Ecosystem Water-Use Efficiency in Response to Warming in an Alpine Meadow. J. Geophys. 2018, 123, 453–462. [Google Scholar] [CrossRef]
- Avola, G.; Cavallaro, V.; Patanè, C.; Riggi, E. Gas exchange and photosynthetic water use efficiency in response to light, CO2 concentration, and temperature in Vicia faba. J. Plant Physiol. 2008, 165, 796–804. [Google Scholar] [CrossRef]
- Li, S.E.; Kang, S.; Zhang, L.; Du, T.; Tong, L. Ecosystem water use efficiency for a sparse vineyard in arid northwest China. Agric. Water Manag. 2015, 148, 24–33. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.; Jia, Q.; Yu, W. Water use efficiency of a rice paddy field in Liaohe Delta, Northeast China. Agric. Water Manag. 2017, 187, 222–231. [Google Scholar] [CrossRef]
- Beer, C.; Ciais, P.; Reichstein, M.; Baldocchi, D.; Law, B.E. Temporal and among-site variability of inherent water use efficiency at the ecosystem level. Glob. Biogeochem. Cycles 2009, 23, GB2018. [Google Scholar] [CrossRef]
- Li, Y.; Fan, J.; Hu, Z.; Shao, Q.; Harris, W. Comparison of evapotranspiration components and water-use efficiency among different land use patterns of temperate steppe in the Northern China pastoral-farming ecotone. Int. J. Biometeorol. 2016, 60, 827–841. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Jia, X.; Zha, T.; Bourque, C.P.A.; Tian, Y. Ecosystem water use efficiency in a young plantation in Northern China and its relationship to drought. Agric. For. Meteorol. 2019, 275, 1–10. [Google Scholar] [CrossRef]
- Zheng, H.; Lin, H.; Zhu, X.J.; Jin, Z.; Bao, H. Divergent spatial responses of plant and ecosystem water-use efficiency to climate and vegetation gradients in the Chinese Loess Plateau. Glob. Planet. Change 2019, 181, 102995. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, J.; Zheng, Y.; Li, S.; Zhou, Y. Increased carbon uptake and water use efficiency in global semi-arid ecosystems. Environ. Res. Lett. 2020, 15, 034022. [Google Scholar] [CrossRef]
- Li, Y.; Shi, H.; Zhou, L.; Earmus, D.; Huete, A. Disentangling Climate and LAI Effects on Seasonal Variability in Water Use Efficiency Across Terrestrial Ecosystems in China. J. Geophys. Res. Biogeosci. 2018, 123, 2429–2443. [Google Scholar] [CrossRef]
- Lei, H.; Gong, T.; Zhang, Y.; Yang, D. Biological factors dominate the interannual variability of evapotranspiration in an irrigated cropland in the North China Plain. Agric. For. Meteorol. 2018, 250, 262–276. [Google Scholar] [CrossRef]
- Su, Y.H.; Feng, Q.; Zhu, G.F.; Zhang, Q. Evaluating the different methods for estimating groundwater evapotranspiration using diurnal water table fluctuations. J. Hydrol. 2022, 607, 127508. [Google Scholar]
- Chen, Y.; Chen, Y.; Xu, C.; Ye, Z.; Li, Z.; Zhu, C.; Ma, X. Effects of ecological water conveyance on groundwater dynamics and riparian vegetation in the lower reaches of Tarim River, China. Hydrol. Process. 2010, 24, 170–177. [Google Scholar] [CrossRef]
- Hao, X.; Li, W. Impacts of ecological water conveyance on groundwater dynamics and vegetation recovery in the lower reaches of the Tarim River in northwest China. Environ. Monit. Assess. 2014, 186, 7605–7616. [Google Scholar] [CrossRef] [PubMed]
- Jiao, A.; Wang, W.; Ling, H.; Deng, X.; Yan, J.; Chen, F. Effect evaluation of ecological water conveyance in Tarim River Basin, China. Front. Environ. Sci. 2022, 10, 1019695. [Google Scholar] [CrossRef]
- Loreti, E.; van Veen, H.; Perata, P. Plant responses to flooding stress. Curr. Opin. Plant Biol. 2016, 33, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Yu, J.; Wang, P.; Zhang, Y.; Yu, Q. Interpreting the groundwater attributes influencing the distribution patterns of groundwater-dependent vegetation in NorthWestern China. Ecohydrology 2012, 5, 628–636. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Baldocchi, D.D. How eddy covariance flux measurements have contributed to our understanding of Global Change Biology. Global Change Biol. 2020, 26, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Wutzler, T.; Lucas-Moffat, A.; Migliavacca, M.; Knauer, J.; Sickel, K.; Šigut, L.; Menzer, O.; Reichstein, M. Basic and extensible post-processing of eddy covariance flux data with REddyProc. Biogeosciences 2018, 15, 5015–5030. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X. Energy balance closures in diverse ecosystems of an endorheic river basin. Agric. For. Meteorol. 2019, 274, 118–131. [Google Scholar] [CrossRef]
- Barr, A.G.; van der Kamp, G.; Black, T.A.; McCaughey, J.H.; Nesic, Z. Energy balance closure at the BERMS flux towers about the water balance of the White Gull Creek watershed 1999–2009. Agric. For. Meteorol. 2012, 153, 3–13. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Xu, Z. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Che, T.; Li, X.; Xu, T.R. A dataset of energy, water vapor, and carbon exchange observations in oasis–desert areas from 2012 to 2021 in a typical endorheic basin. Earth Syst. Sci. Data 2023, 15, 4959–4981. [Google Scholar] [CrossRef]
- Qiao, C.; Sun, R.; Xu, Z.; Zhang, L.; Liu, L.; Hao, L.; Jiang, G. A Study of Shelterbelt Transpiration and Cropland Evapotranspiration in an Irrigated Area in the Middle Reaches of the Heihe River in Northwestern China. IEEE Geosci. 2015, 12, 369–373. [Google Scholar]
- Ye, X.; Li, X.; Liu, J.; Xu, C.Y.; Zhang, Q. Variation of reference evapotranspiration and its contributing climatic factors in the Poyang Lake catchment, China. Hydrol. Process. 2014, 28, 6151–6162. [Google Scholar] [CrossRef]

| Evaluation Metrics | Chi-Square/df (χ2/df) | p Value | Comparative Fit Index (CFI) | Root-Mean-Square Error of Approximation (RMSEA) |
|---|---|---|---|---|
| Standard | <2 | >0.05 | >0.9 | <0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Feng, Q.; Su, Y.; Jian, C. Evapotranspiration Partitioning of the Populus euphratica Forest Ecosystem in the Drylands of Northwestern China. Plants 2025, 14, 680. https://doi.org/10.3390/plants14050680
Zhang Q, Feng Q, Su Y, Jian C. Evapotranspiration Partitioning of the Populus euphratica Forest Ecosystem in the Drylands of Northwestern China. Plants. 2025; 14(5):680. https://doi.org/10.3390/plants14050680
Chicago/Turabian StyleZhang, Qi, Qi Feng, Yonghong Su, and Cuo Jian. 2025. "Evapotranspiration Partitioning of the Populus euphratica Forest Ecosystem in the Drylands of Northwestern China" Plants 14, no. 5: 680. https://doi.org/10.3390/plants14050680
APA StyleZhang, Q., Feng, Q., Su, Y., & Jian, C. (2025). Evapotranspiration Partitioning of the Populus euphratica Forest Ecosystem in the Drylands of Northwestern China. Plants, 14(5), 680. https://doi.org/10.3390/plants14050680


.png)




