Hyperparameter Optimization for Tomato Leaf Disease Recognition Based on YOLOv11m
Abstract
1. Introduction
2. Materials and Methods
2.1. Improved Tomato Leaf Disease Dataset
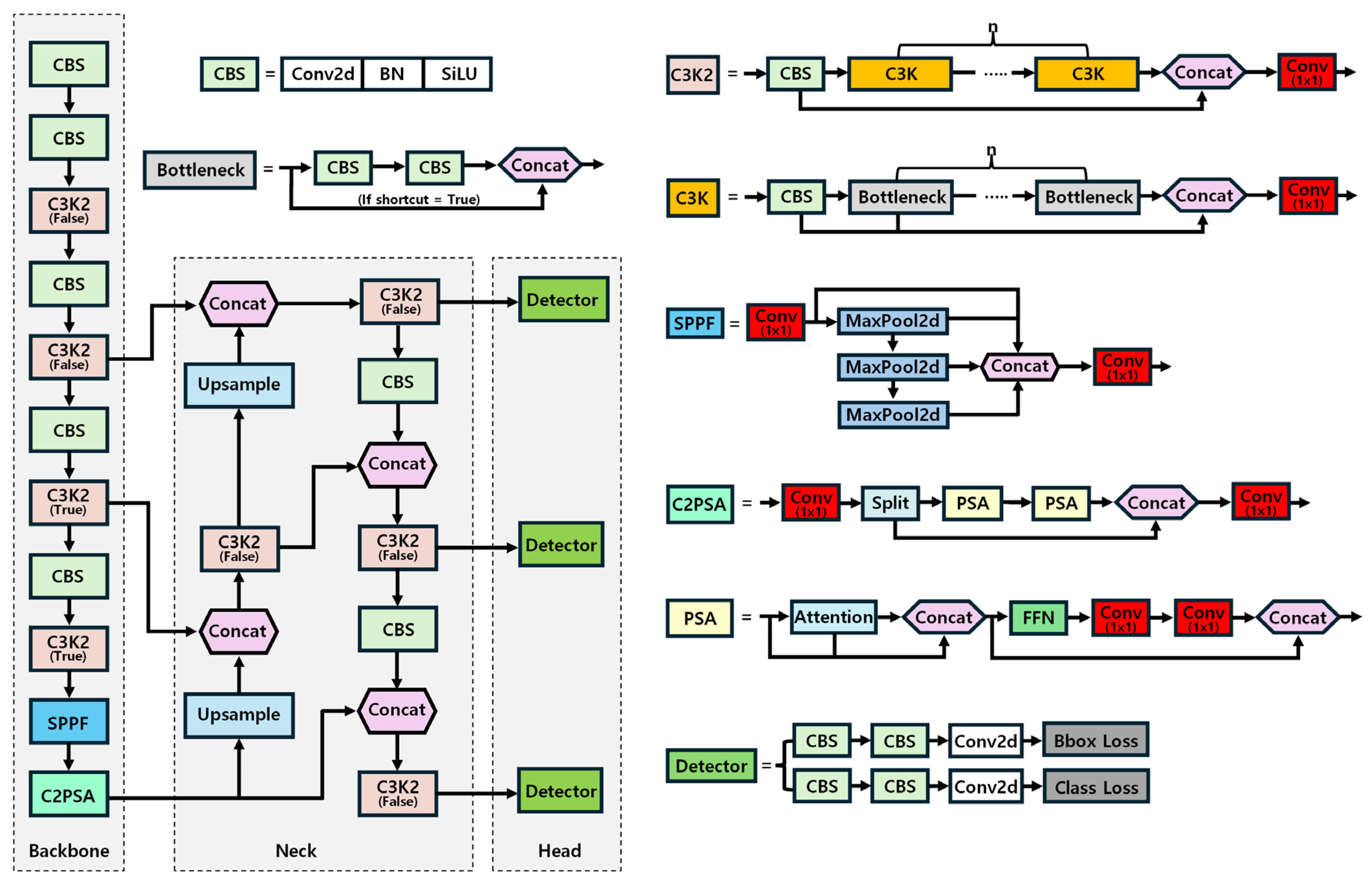
2.2. YOLOv11 Model
2.3. Evaluation Metrics
2.4. Workflow
2.4.1. Fine-Tuning
2.4.2. Hyperparameter Algorithms
2.4.3. Hyperparameters Analyzed
3. Results and Discussions
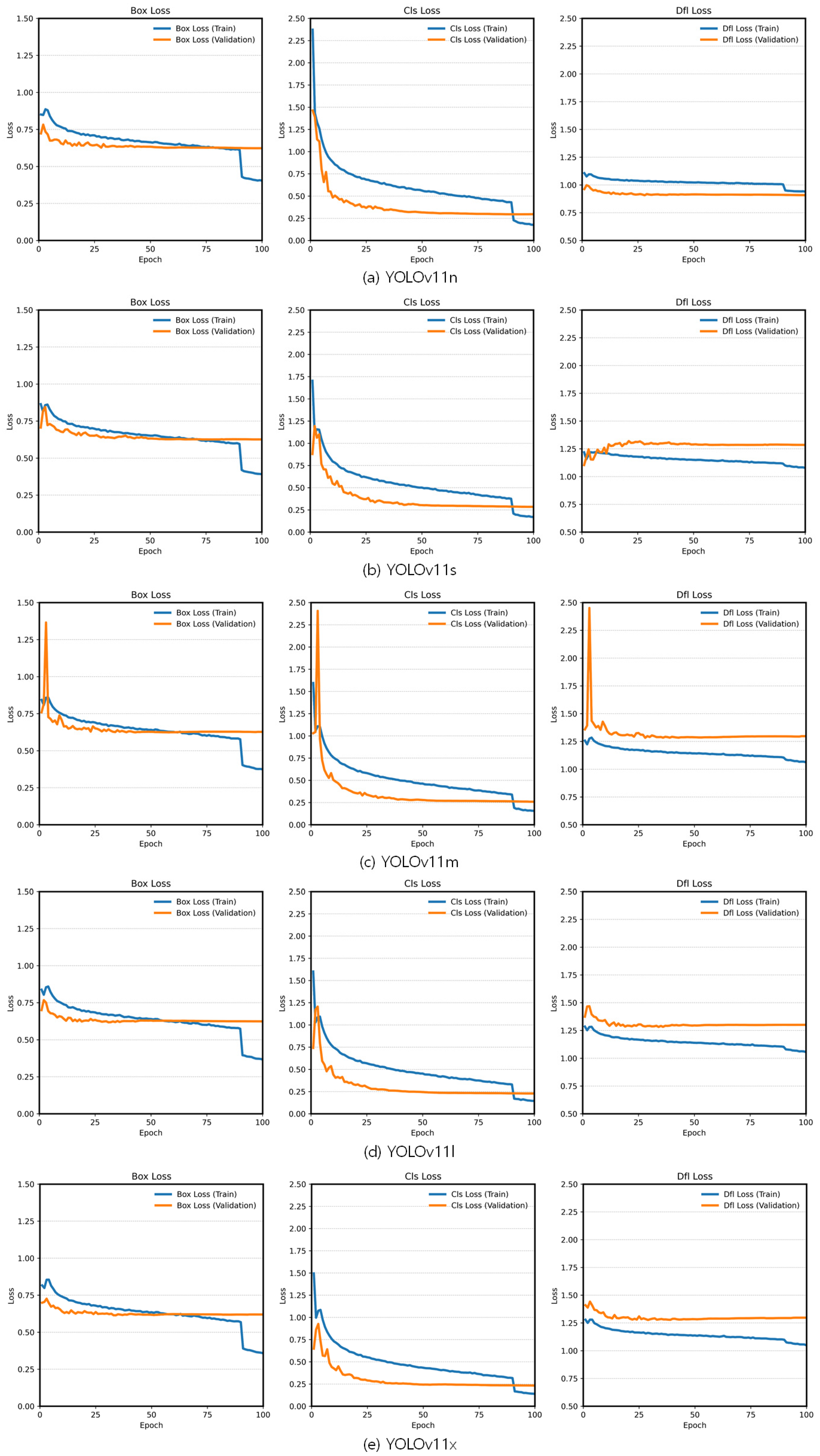
3.1. Fine-Tuning Results Based on the Pretrained YOLOv11 Variants
3.2. Hyperparameter Optimization
3.2.1. OFAT
Batch Size
Optimizer
Learning Rate
Weight Decay
Momentum
Dropout
Epoch
3.2.2. RS
3.3. Correlation Analysis Between Hyperparameters and Evaluation Metrics
3.4. Comparison Experiments with Other Models
4. Conclusions and Future Works
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jing, J.; Li, S.; Qiao, C.; Li, K.; Zhu, X.; Zhang, L. A tomato disease identification method based on leaf image automatic labeling algorithm and improved YOLOv5 model. J. Sci. Food Agric. 2023, 103, 7070–7082. [Google Scholar] [CrossRef] [PubMed]
- Panno, S.; Davino, S.; Caruso, A.G.; Bertacca, S.; Crnogorac, A.; Mandić, A.; Noris, E.; Matić, S. A review of the most common and economically important diseases that undermine the cultivation of tomato crop in the mediterranean basin. Agronomy 2021, 11, 2188. [Google Scholar] [CrossRef]
- Li, N.; Wu, X.; Zhuang, W.; Xia, L.; Chen, Y.; Wu, C.; Rao, Z.; Du, L.; Zhao, R.; Yi, M. Tomato and lycopene and multiple health outcomes: Umbrella review. Food Chem. 2021, 343, 128396. [Google Scholar] [CrossRef] [PubMed]
- Sainju, U.M.; Dris, R.; Singh, B. Mineral nutrition of tomato. Food Agric. Environ. 2003, 1, 176–183. [Google Scholar]
- Jones, J.B.; Zitter, T.A.; Momol, T.M.; Miller, S.A. Compendium of Tomato Diseases and Pests; APS: College Park, MD, USA, 2014. [Google Scholar]
- Kannan, V.R.; Bastas, K.K.; Devi, R.S. 20 Scientific and Economic Impact of Plant Pathogenic Bacteria. In Sustainable Approaches to Controlling Plant Pathogenic Bacteria; CRC Press: Boca Raton, FL, USA, 2015; p. 369. [Google Scholar]
- Jones, J. Compendium of tomato diseases. In American Phytopathological Society; APS: College Park, MD, USA, 1991. [Google Scholar]
- Subedi, B.; Poudel, A.; Aryal, S. The impact of climate change on insect pest biology and ecology: Implications for pest management strategies, crop production, and food security. J. Agric. Food Res. 2023, 14, 100733. [Google Scholar] [CrossRef]
- Van Der Werf, H.M. Assessing the impact of pesticides on the environment. Agric. Ecosyst. Environ. 1996, 60, 81–96. [Google Scholar] [CrossRef]
- Lykogianni, M.; Bempelou, E.; Karamaouna, F.; Aliferis, K.A. Do pesticides promote or hinder sustainability in agriculture? The challenge of sustainable use of pesticides in modern agriculture. Sci. Total Environ. 2021, 795, 148625. [Google Scholar] [CrossRef]
- Shoaib, M.; Shah, B.; Ei-Sappagh, S.; Ali, A.; Ullah, A.; Alenezi, F.; Gechev, T.; Hussain, T.; Ali, F. An advanced deep learning models-based plant disease detection: A review of recent research. Front. Plant Sci. 2023, 14, 1158933. [Google Scholar]
- Appe, S.N.; Arulselvi, G.; Balaji, G. CAM-YOLO: Tomato detection and classification based on improved YOLOv5 using combining attention mechanism. PeerJ Comput. Sci. 2023, 9, e1463. [Google Scholar] [CrossRef]
- Qi, J.; Liu, X.; Liu, K.; Xu, F.; Guo, H.; Tian, X.; Li, M.; Bao, Z.; Li, Y. An improved YOLOv5 model based on visual attention mechanism: Application to recognition of tomato virus disease. Comput. Electron. Agric. 2022, 194, 106780. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, S.; Zhou, G.; Hu, Y.; Li, L. Identification of tomato leaf diseases based on multi-channel automatic orientation recurrent attention network. Comput. Electron. Agric. 2023, 205, 107605. [Google Scholar] [CrossRef]
- Alif, M.A.R. YOLOv11 for Vehicle Detection: Advancements, Performance, and Applications in Intelligent Transportation Systems. arXiv 2024, arXiv:2410.22898. [Google Scholar]
- Buja, I.; Sabella, E.; Monteduro, A.G.; Chiriacò, M.S.; De Bellis, L.; Luvisi, A.; Maruccio, G. Advances in plant disease detection and monitoring: From traditional assays to in-field diagnostics. Sensors 2021, 21, 2129. [Google Scholar] [CrossRef] [PubMed]
- Touko Mbouembe, P.L.; Liu, G.; Park, S.; Kim, J.H. Accurate and fast detection of tomatoes based on improved YOLOv5s in natural environments. Front. Plant Sci. 2024, 14, 1292766. [Google Scholar] [CrossRef]
- Ferentinos, K.P. Deep learning models for plant disease detection and diagnosis. Comput. Electron. Agric. 2018, 145, 311–318. [Google Scholar] [CrossRef]
- Khan, A.I.; Quadri, S.; Banday, S.; Shah, J.L. Deep diagnosis: A real-time apple leaf disease detection system based on deep learning. Comput. Electron. Agric. 2022, 198, 107093. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Annual Conference on Advances in Neural Information Processing Systems, Montreal, QC, Cananda, 7–12 December 2015; Volume 28. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Liu, J.; Wang, X. Tomato diseases and pests detection based on improved Yolo V3 convolutional neural network. Front. Plant Sci. 2020, 11, 898. [Google Scholar] [CrossRef]
- Samal, S.; Zhang, Y.D.; Gadekallu, T.R.; Nayak, R.; Balabantaray, B.K. SBMYv3: Improved MobYOLOv3 a BAM attention-based approach for obscene image and video detection. Expert Syst. 2023, 40, e13230. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. Scaled-YOLOv4: Scaling cross stage partial network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13029–13038. [Google Scholar]
- Chen, J.-W.; Lin, W.-J.; Cheng, H.-J.; Hung, C.-L.; Lin, C.-Y.; Chen, S.-P. A smartphone-based application for scale pest detection using multiple-object detection methods. Electronics 2021, 10, 372. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, J.; Kim, S. ECAP-YOLO: Efficient channel attention pyramid YOLO for small object detection in aerial image. Remote Sens. 2021, 13, 4851. [Google Scholar] [CrossRef]
- Chen, S.; Zou, X.; Zhou, X.; Xiang, Y.; Wu, M. Study on fusion clustering and improved YOLOv5 algorithm based on multiple occlusion of Camellia oleifera fruit. Comput. Electron. Agric. 2023, 206, 107706. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, P.; Tian, S. Tomato leaf disease detection based on attention mechanism and multi-scale feature fusion. Front. Plant Sci. 2024, 15, 1382802. [Google Scholar] [CrossRef] [PubMed]
- Norkobil Saydirasulovich, S.; Abdusalomov, A.; Jamil, M.K.; Nasimov, R.; Kozhamzharova, D.; Cho, Y.-I. A YOLOv6-based improved fire detection approach for smart city environments. Sensors 2023, 23, 3161. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Xing, Z.; Wang, H.; Dong, X.; Gao, X.; Liu, Z.; Zhang, X.; Li, S.; Zhao, Y. Maize-YOLO: A new high-precision and real-time method for maize pest detection. Insects 2023, 14, 278. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Wang, X.; Sheng, Y.; Tian, W.; Ren, Y. A tree species classification model based on improved YOLOv7 for shelterbelts. Front. Plant Sci. 2024, 14, 1265025. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Qiao, S. ALF-YOLO: Enhanced YOLOv8 based on multiscale attention feature fusion for ship detection. Ocean Eng. 2024, 308, 118233. [Google Scholar] [CrossRef]
- Fang, C.; Li, C.; Yang, P.; Kong, S.; Han, Y.; Huang, X.; Niu, J. Enhancing Livestock Detection: An Efficient Model Based on YOLOv8. Appl. Sci. 2024, 14, 4809. [Google Scholar] [CrossRef]
- Elshawi, R.; Maher, M.; Sakr, S. Automated machine learning: State-of-the-art and open challenges. arXiv 2019, arXiv:1906.02287. [Google Scholar]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.; Blum, M.; Hutter, F. Efficient and robust automated machine learning. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning (PMLR), Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; Volume 28, pp. 1551–1559. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Ramos, L.; Casas, E.; Bendek, E.; Romero, C.; Rivas-Echeverría, F. Hyperparameter optimization of YOLOv8 for smoke and wildfire detection: Implications for agricultural and environmental safety. Artif. Intell. Agric. 2024, 12, 109–126. [Google Scholar] [CrossRef]
- Solimani, F.; Cardellicchio, A.; Dimauro, G.; Petrozza, A.; Summerer, S.; Cellini, F.; Renò, V. Optimizing tomato plant phenotyping detection: Boosting YOLOv8 architecture to tackle data complexity. Comput. Electron. Agric. 2024, 218, 108728. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Patil, M.P.; Kim, J.G.; Choi, S.S.; Seo, Y.B.; Kim, G.-D. Improved Tomato Leaf Disease Recognition Based on the YOLOv5m with Various Soft Attention Module Combinations. Agriculture 2024, 14, 1472. [Google Scholar] [CrossRef]
- Khan, Q. Tomato Disease Multiple Sources; Kaggle: San Francisco, CA, USA, 2022. [Google Scholar]
- Khanam, R.; Hussain, M. YOLOv11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar]
- Sapkota, R.; Meng, Z.; Churuvija, M.; Du, X.; Ma, Z.; Karkee, M. Comprehensive performance evaluation of yolo11, yolov10, yolov9 and yolov8 on detecting and counting fruitlet in complex orchard environments. arXiv 2024, arXiv:2407.12040. [Google Scholar]
- Ultralytics. Ultralytics YOLO Docs. 2023. Available online: https://docs.ultralytics.com/ (accessed on 10 September 2024).
- Redmon, J.; Farhadi, A. YOLOv3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Czitrom, V. One-factor-at-a-time versus designed experiments. Am. Stat. 1999, 53, 126–131. [Google Scholar] [CrossRef]
- Schmeiser, B. Batch size effects in the analysis of simulation output. Oper. Res. 1982, 30, 556–568. [Google Scholar] [CrossRef]
- Radiuk, P.M. Impact of training set batch size on the performance of convolutional neural networks for diverse datasets. Inform. Technol. Manag. Sci. 2017, 20, 20–24. [Google Scholar] [CrossRef]
- He, F.; Liu, T.; Tao, D. Control batch size and learning rate to generalize well: Theoretical and empirical evidence. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Takase, T.; Oyama, S.; Kurihara, M. Effective neural network training with adaptive learning rate based on training loss. Neural Netw. 2018, 101, 68–78. [Google Scholar] [CrossRef] [PubMed]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv 2016, arXiv:1609.04836. [Google Scholar]
- Loshchilov, I.; Hutter, F. Fixing weight decay regularization in adam. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Krogh, A.; Hertz, J. A simple weight decay can improve generalization. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference, Vancouver, CO, USA, 6–7 December 1991; Volume 4. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning (PMLR), Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 1139–1147. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the 4th International Conference on Learning Respresentations, Workshop Track, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–4. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ko, B.; Kim, H.-G.; Oh, K.-J.; Choi, H.-J. Controlled dropout: A different approach to using dropout on deep neural network. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Republic of Korea, 13–16 February 2017; pp. 358–362. [Google Scholar]
- Baldi, P.; Sadowski, P.J. Understanding dropout. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference, Lake Tahoe, NV, USA, 5–10 December 2013; Volume 26. [Google Scholar]
- Brownlee, J. What is the Difference Between a Batch and an Epoch in a Neural Network. Mach. Learn. Mastery 2018, 20, 1–5. [Google Scholar]
- Hastomo, W.; Karno, A.S.B.; Kalbuana, N.; Meiriki, A. Characteristic parameters of epoch deep learning to predict COVID-19 data in Indonesia. J. Phys. Conf. Ser. 2021, 1933, 012050. [Google Scholar] [CrossRef]
- Komatsuzaki, A. One epoch is all you need. arXiv 2019, arXiv:1906.06669. [Google Scholar]
- Hoffer, E.; Hubara, I.; Soudry, D. Train longer, generalize better: Closing the generalization gap in large batch training of neural networks. arXiv 2018, arXiv:1705.08741. [Google Scholar]
- Meng, C.; Liu, S.; Yang, Y. DMAC-YOLO: A High-Precision YOLO v5s Object Detection Model with a Novel Optimizer. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Li, S.; Sun, S.; Liu, Y.; Qi, W.; Jiang, N.; Cui, C.; Zheng, P. Real-time lightweight YOLO model for grouting defect detection in external post-tensioned ducts via infrared thermography. Autom. Constr. 2024, 168, 105830. [Google Scholar] [CrossRef]
- Arora, S.; Dalal, S.; Sethi, M.N. Interpretable features of YOLO v8 for Weapon Detection-Performance driven approach. In Proceedings of the 2024 International Conference on Emerging Innovations and Advanced Computing (INNOCOMP), Sonipat, India, 25–26 May 2024; pp. 87–93. [Google Scholar]
- Santos, C.; Aguiar, M.; Welfer, D.; Belloni, B. A new approach for detecting fundus lesions using image processing and deep neural network architecture based on YOLO model. Sensors 2022, 22, 6441. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Li, H.; Xu, Z.; Taylor, G.; Studer, C.; Goldstein, T. Visualizing the loss landscape of neural nets. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference, Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Wan, R.; Zhu, Z.; Zhang, X.; Sun, J. Spherical motion dynamics: Learning dynamics of normalized neural network using sgd and weight decay. In Proceedings of the Advances in Neural Information Processing Systems Annual Conference, Virtual, 6–14 December 2024; Volume 34, pp. 6380–6391. [Google Scholar]
- Nakamura, K.; Hong, B.-W. Adaptive weight decay for deep neural networks. IEEE Access 2019, 7, 118857–118865. [Google Scholar] [CrossRef]
- Cutkosky, A.; Mehta, H. Momentum improves normalized sgd. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Vienna, Austria, 12–18 July 2020; Volume 119, pp. 2260–2268. [Google Scholar]
- Yu, H.; Jin, R.; Yang, S. On the linear speedup analysis of communication efficient momentum SGD for distributed non-convex optimization. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 7184–7193. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. arXiv 2017, arXiv:1506.01186. [Google Scholar]



| Disease Name | Labels | Kaggle [44] | Previous Study [43] | This Study | |||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Valid | Train | Valid | Test | Train | Valid | Test | ||
| Healthy | HN | 3051 | 806 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Tomato_mosaic_virus | TV | 2153 | 584 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Spider_mites Two-spotted Spider_mite | SM | 1747 | 435 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Target_Spot | TS | 1827 | 457 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Tomato_Yellow_Leaf_Furl_Virus | TY | 2039 | 498 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Leaf_Mold | LM | 2754 | 739 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Septoria_leaf_spot | SL | 2882 | 746 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Early_blight | EB | 2455 | 643 | 400 | 50 | 50 | 1600 | 200 | 200 |
| powdery Mildew | PM | 1004 | 252 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Late_blight | LB | 3113 | 792 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Bacteria_spot | BS | 2826 | 732 | 400 | 50 | 50 | 1600 | 200 | 200 |
| Total | - | 25,851 | 6684 | 4400 | 550 | 550 | 17,600 | 2200 | 2200 |
| Models | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| YOLOv11n | Training | 0.97792 | 0.97850 | 0.97821 | 0.98776 | 0.86416 | 0.97917 | 1.519 | 0.81 |
| Test | 0.98379 | 0.98293 | 0.98336 | 0.98928 | 0.86988 | 0.98395 | - | 0.78 | |
| YOLOv11s | Training | 0.98542 | 0.97826 | 0.98183 | 0.98886 | 0.86739 | 0.98255 | 1.539 | 0.80 |
| Test | 0.98742 | 0.98784 | 0.98763 | 0.99202 | 0.87400 | 0.98807 | - | 0.95 | |
| YOLOv11m | Training | 0.98505 | 0.98263 | 0.98384 | 0.99045 | 0.87092 | 0.98450 | 1.861 | 0.95 |
| Test | 0.99104 | 0.98597 | 0.98850 | 0.99197 | 0.87666 | 0.98885 | - | 1.14 | |
| YOLOv11l | Training | 0.98690 | 0.98128 | 0.98408 | 0.99122 | 0.87247 | 0.98480 | 2.523 | 0.84 |
| Test | 0.99259 | 0.98682 | 0.98970 | 0.99350 | 0.87751 | 0.99008 | - | 1.31 | |
| YOLOv11x | Training | 0.98482 | 0.98248 | 0.98365 | 0.98987 | 0.87206 | 0.98427 | 2.702 | 1.23 |
| Test | 0.99177 | 0.99112 | 0.99144 | 0.99321 | 0.87811 | 0.99162 | - | 1.87 |
| Batch Size | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 8 | Training | 0.98366 | 0.98250 | 0.98308 | 0.99130 | 0.87100 | 0.98390 | 3.108 | 1.03 |
| Test | 0.98645 | 0.98730 | 0.98687 | 0.99208 | 0.87695 | 0.98740 | - | 1.24 | |
| 16 | Training | 0.98505 | 0.98263 | 0.98384 | 0.99045 | 0.87092 | 0.98450 | 1.861 | 0.95 |
| Test | 0.99104 | 0.98597 | 0.98850 | 0.99197 | 0.87666 | 0.98885 | - | 1.14 | |
| 24 | Training | 0.98263 | 0.98649 | 0.98456 | 0.99108 | 0.86922 | 0.98521 | 1.305 | 0.77 |
| Test | 0.99233 | 0.98824 | 0.99028 | 0.99224 | 0.87517 | 0.99048 | - | 1.00 | |
| 32 | Training | 0.98528 | 0.98231 | 0.98379 | 0.99140 | 0.86879 | 0.98456 | 1.116 | 0.74 |
| Test | 0.98969 | 0.98707 | 0.98838 | 0.99241 | 0.87551 | 0.98878 | - | 1.10 | |
| 48 | Training | 0.98705 | 0.97781 | 0.98241 | 0.99120 | 0.87156 | 0.98331 | 1.003 | 0.81 |
| Test | 0.98911 | 0.98681 | 0.98796 | 0.99272 | 0.87582 | 0.98843 | - | 1.10 | |
| 64 | Training | 0.98818 | 0.98185 | 0.98500 | 0.99165 | 0.86990 | 0.98568 | 0.901 | 0.81 |
| Test | 0.99121 | 0.98649 | 0.98884 | 0.99256 | 0.87461 | 0.98922 | - | 1.12 | |
| 72 | Training | 0.98639 | 0.98601 | 0.98485 | 0.99091 | 0.87154 | 0.98545 | 0.862 | 0.75 |
| Test | 0.98901 | 0.98793 | 0.98847 | 0.99130 | 0.87309 | 0.98875 | - | 1.23 | |
| 80 | Training | 0.98735 | 0.98306 | 0.98520 | 0.99144 | 0.87064 | 0.98583 | 0.874 | 0.82 |
| Test | 0.99249 | 0.99041 | 0.99145 | 0.99137 | 0.87309 | 0.99144 | - | 1.10 | |
| 88 | Training | 0.98612 | 0.98173 | 0.98392 | 0.99152 | 0.86745 | 0.98469 | 0.823 | 0.73 |
| Test | 0.98767 | 0.98780 | 0.98773 | 0.99188 | 0.87099 | 0.98815 | - | 1.01 |
| Optimizer | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| SGD | Training | 0.98735 | 0.98306 | 0.98520 | 0.99144 | 0.87064 | 0.98583 | 0.874 | 0.82 |
| Test | 0.99249 | 0.99041 | 0.99145 | 0.99137 | 0.87309 | 0.99144 | - | 1.10 | |
| Adam | Training | 0.94279 | 0.93403 | 0.93839 | 0.97474 | 0.83159 | 0.94204 | 0.932 | 0.90 |
| Test | 0.93105 | 0.92667 | 0.92885 | 0.96391 | 0.82911 | 0.93237 | - | 1.19 | |
| Adamax | Training | 0.97629 | 0.96717 | 0.97171 | 0.98791 | 0.85754 | 0.98335 | 1.079 | 0.89 |
| Test | 0.97011 | 0.97847 | 0.97427 | 0.98771 | 0.86213 | 0.97563 | - | 1.05 | |
| AdamW | Training | 0.92219 | 0.89974 | 0.91083 | 0.96372 | 0.80630 | 0.91624 | 0.866 | 0.92 |
| Test | 0.89851 | 0.88714 | 0.89279 | 0.93736 | 0.79382 | 0.89718 | - | 1.03 | |
| NAdam | Training | 0.94700 | 0.94129 | 0.94414 | 0.97978 | 0.84308 | 0.94771 | 0.958 | 0.97 |
| Test | 0.94373 | 0.93709 | 0.94040 | 0.96984 | 0.83613 | 0.94336 | - | 1.06 | |
| RAdam | Training | 0.94760 | 0.93541 | 0.94147 | 0.98027 | 0.83654 | 0.94538 | 0.952 | 0.84 |
| Test | 0.94815 | 0.92201 | 0.93490 | 0.96862 | 0.83696 | 0.93843 | - | 1.04 |
| Learning Rate | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 0.0001 | Training | 0.98220 | 0.97163 | 0.97689 | 0.98854 | 0.84849 | 0.97808 | 0.899 | 0.88 |
| Test | 0.98660 | 0.97901 | 0.98279 | 0.98948 | 0.86391 | 0.98347 | - | 0.97 | |
| 0.0005 | Training | 0.98606 | 0.98215 | 0.98410 | 0.99126 | 0.86062 | 0.98482 | 0.895 | 0.82 |
| Test | 0.98964 | 0.98675 | 0.98819 | 0.99175 | 0.86588 | 0.98855 | - | 1.07 | |
| 0.0010 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.0050 | Training | 0.98609 | 0.98233 | 0.98421 | 0.99070 | 0.86578 | 0.98486 | 0.912 | 0.82 |
| Test | 0.99206 | 0.98756 | 0.98980 | 0.99086 | 0.86782 | 0.98991 | - | 1.10 | |
| 0.0100 | Training | 0.98735 | 0.98306 | 0.98520 | 0.99144 | 0.87064 | 0.98583 | 0.874 | 0.82 |
| Test | 0.99249 | 0.99041 | 0.99145 | 0.99137 | 0.87309 | 0.99144 | - | 1.10 | |
| 0.0500 | Training | 0.98240 | 0.97295 | 0.97765 | 0.99063 | 0.86788 | 0.97897 | 0.896 | 0.81 |
| Test | 0.98472 | 0.98239 | 0.98355 | 0.99025 | 0.87157 | 0.98423 | - | 1.05 |
| Weight Decay | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 0.00001 | Training | 0.98883 | 0.98564 | 0.98723 | 0.99074 | 0.86145 | 0.98759 | 0.904 | 0.84 |
| Test | 0.98995 | 0.99098 | 0.99046 | 0.99203 | 0.86382 | 0.99062 | - | 1.12 | |
| 0.00005 | Training | 0.98794 | 0.98453 | 0.98472 | 0.99116 | 0.86154 | 0.98538 | 0.901 | 0.88 |
| Test | 0.98580 | 0.98860 | 0.98720 | 0.99199 | 0.86733 | 0.98768 | - | 1.02 | |
| 0.00010 | Training | 0.98857 | 0.98351 | 0.98603 | 0.99103 | 0.86009 | 0.98654 | 0.903 | 0.90 |
| Test | 0.99091 | 0.98796 | 0.98938 | 0.99186 | 0.86582 | 0.98953 | - | 1.03 | |
| 0.00050 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.00100 | Training | 0.98718 | 0.98171 | 0.98444 | 0.98976 | 0.85468 | 0.98498 | 0.918 | 0.73 |
| Test | 0.99142 | 0.98796 | 0.98969 | 0.99175 | 0.86643 | 0.98990 | - | 1.03 | |
| 0.00500 | Training | 0.98765 | 0.98227 | 0.98495 | 0.99100 | 0.86265 | 0.98556 | 0.918 | 0.87 |
| Test | 0.99238 | 0.98928 | 0.99083 | 0.99159 | 0.87045 | 0.99090 | - | 1.09 | |
| 0.01000 | Training | 0.98494 | 0.98469 | 0.98481 | 0.98930 | 0.86261 | 0.98526 | 0.901 | 0.88 |
| Test | 0.98982 | 0.99293 | 0.99137 | 0.99283 | 0.87170 | 0.99152 | - | 1.12 | |
| 0.05000 | Training | 0.97012 | 0.96706 | 0.96859 | 0.98925 | 0.84438 | 0.97066 | 0.918 | 0.91 |
| Test | 0.97066 | 0.96466 | 0.96765 | 0.98237 | 0.86042 | 0.96913 | - | 1.04 |
| Momentum | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 0.859 | Training | 0.98665 | 98044 | 0.98354 | 0.98988 | 0.85896 | 0.98418 | 0.906 | 0.79 |
| Test | 0.99132 | 0.98887 | 0.99009 | 0.99285 | 0.86553 | 0.99037 | - | 1.22 | |
| 0.885 | Training | 0.98479 | 0.98425 | 0.98452 | 0.99014 | 0.85877 | 0.98508 | 0.904 | 0.83 |
| Test | 0.98983 | 0.98585 | 0.98784 | 0.99118 | 0.86357 | 0.98817 | - | 1.13 | |
| 0.911 | Training | 0.98023 | 0.98380 | 0.98201 | 0.98986 | 0.85966 | 0.98280 | 0.903 | 0.83 |
| Test | 0.98749 | 0.98606 | 0.98677 | 0.99199 | 0.86667 | 0.98730 | - | 1.12 | |
| 0.937 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.963 | Training | 0.98732 | 0.98293 | 0.98512 | 0.99146 | 0.86502 | 0.98576 | 0.909 | 0.92 |
| Test | 0.98248 | 0.99037 | 0.98641 | 0.99189 | 0.86805 | 0.98697 | - | 1.13 | |
| 0.989 | Training | 0.98598 | 0.98361 | 0.98479 | 0.99050 | 0.86744 | 0.98537 | 0.906 | 0.87 |
| Test | 0.99127 | 0.98963 | 0.99045 | 0.99081 | 0.87057 | 0.99049 | - | 1.21 |
| Dropout | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.1 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.3 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.5 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 0.7 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 |
| Epoch | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| 100 | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| 150 | Training | 0.98885 | 0.98327 | 0.98605 | 0.99092 | 0.86289 | 0.98655 | 1.335 | 0.84 |
| Test | 0.99246 | 0.98939 | 0.99092 | 0.99202 | 0.86583 | 0.99103 | - | 1.11 | |
| 200 | Training | 0.98757 | 0.98401 | 0.98579 | 0.99048 | 0.86649 | 0.98626 | 1.238 | 0.83 |
| Test | 0.99099 | 0.98827 | 0.98963 | 0.99273 | 0.87320 | 0.98994 | - | 1.05 | |
| 250 | Training | 0.98789 | 0.98308 | 0.98548 | 0.99153 | 0.86662 | 0.98597 | 1.482 | 0.92 |
| Test | 0.99028 | 0.99214 | 0.99121 | 0.99170 | 0.86748 | 0.99126 | - | 1.02 | |
| 300 | Training | 0.98730 | 0.98368 | 0.98549 | 0.99024 | 0.86624 | 0.98597 | 1.447 | 0.80 |
| Test | 0.99014 | 0.99183 | 0.99098 | 0.99304 | 0.86990 | 0.99119 | - | 1.09 | |
| 350 | Training | 0.98709 | 0.98154 | 0.98431 | 0.98967 | 0.86261 | 0.98485 | 1.365 | 0.81 |
| Test | 0.98978 | 0.98995 | 0.98986 | 0.99078 | 0.86801 | 0.98995 | - | 1.04 | |
| 400 | Training | 0.98801 | 0.98362 | 0.98581 | 0.99051 | 0.86185 | 0.98628 | 2.093 | 0.86 |
| Test | 0.99158 | 0.99183 | 0.99170 | 0.99174 | 0.86475 | 0.99171 | - | 1.03 |
| Hyperparameter | Values/Ranges |
|---|---|
| Batch size | 24, 80, 96, 128 |
| Learning rate | 0.0001~0.0100 |
| Weight decay | 0.00001~0.00100 |
| Momentum | 0.800~0.990 |
| Model | Batch Size | Learning Rate | Weight Decay | Momentum | Model | Batch Size | Learning Rate | Weight Decay | Momentum |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 24 | 0.0025 | 0.00004 | 0.835 | C51 | 80 | 0.0005 | 0.00075 | 0.823 |
| C2 | 128 | 0.0088 | 0.00017 | 0.897 | C52 | 80 | 0.0010 | 0.00010 | 0.861 |
| C3 | 96 | 0.0004 | 0.00005 | 0.848 | C53 | 128 | 0.0038 | 0.00003 | 0.806 |
| C4 | 24 | 0.0020 | 0.00008 | 0.819 | C54 | 128 | 0.0071 | 0.00008 | 0.833 |
| C5 | 96 | 0.0012 | 0.00010 | 0.845 | C55 | 96 | 0.0029 | 0.00002 | 0.898 |
| C6 | 24 | 0.0005 | 0.00015 | 0.897 | C56 | 24 | 0.0027 | 0.00002 | 0.888 |
| C7 | 96 | 0.0001 | 0.00002 | 0.873 | C57 | 80 | 0.0012 | 0.00014 | 0.871 |
| C8 | 24 | 0.0015 | 0.00007 | 0.889 | C58 | 80 | 0.0017 | 0.00061 | 0.88 |
| C9 | 80 | 0.0089 | 0.00051 | 0.801 | C59 | 128 | 0.0076 | 0.00007 | 0.809 |
| C10 | 128 | 0.0019 | 0.00012 | 0.902 | C60 | 128 | 0.0099 | 0.00007 | 0.826 |
| C11 | 96 | 0.0033 | 0.00052 | 0.826 | C61 | 24 | 0.0021 | 0.00002 | 0.919 |
| C12 | 128 | 0.0024 | 0.00002 | 0.909 | C62 | 24 | 0.0036 | 0.00004 | 0.938 |
| C13 | 80 | 0.0078 | 0.00003 | 0.889 | C63 | 80 | 0.0005 | 0.00009 | 0.856 |
| C14 | 24 | 0.0002 | 0.00083 | 0.854 | C64 | 96 | 0.0009 | 0.00005 | 0.881 |
| C15 | 96 | 0.0006 | 0.00042 | 0.891 | C65 | 128 | 0.0095 | 0.00012 | 0.816 |
| C16 | 96 | 0.0047 | 0.00034 | 0.831 | C66 | 128 | 0.0013 | 0.00020 | 0.955 |
| C17 | 24 | 0.0004 | 0.00003 | 0.831 | C67 | 24 | 0.0007 | 0.00001 | 0.944 |
| C18 | 24 | 0.0008 | 0.00002 | 0.860 | C68 | 24 | 0.0006 | 0.00030 | 0.969 |
| C19 | 96 | 0.0004 | 0.00017 | 0.894 | C69 | 24 | 0.0006 | 0.00001 | 0.988 |
| C20 | 24 | 0.0016 | 0.00039 | 0.951 | C70 | 24 | 0.0003 | 0.00001 | 0.937 |
| C21 | 24 | 0.0008 | 0.00001 | 0.931 | C71 | 80 | 0.0003 | 0.00003 | 0.960 |
| C22 | 80 | 0.0003 | 0.00024 | 0.965 | C72 | 96 | 0.0017 | 0.00002 | 0.842 |
| C23 | 24 | 0.0047 | 0.00004 | 0.985 | C73 | 80 | 0.0004 | 0.00073 | 0.865 |
| C24 | 24 | 0.0002 | 0.00001 | 0.932 | C74 | 80 | 0.0003 | 0.00043 | 0.826 |
| C25 | 80 | 0.0002 | 0.00027 | 0.975 | C75 | 128 | 0.0040 | 0.00003 | 0.854 |
| C26 | 24 | 0.0051 | 0.00004 | 0.800 | C76 | 128 | 0.0044 | 0.00008 | 0.832 |
| C27 | 24 | 0.0001 | 0.00001 | 0.926 | C77 | 96 | 0.0029 | 0.00004 | 0.905 |
| C28 | 80 | 0.0002 | 0.00089 | 0.977 | C78 | 96 | 0.0062 | 0.00003 | 0.896 |
| C29 | 128 | 0.0060 | 0.00004 | 0.803 | C79 | 96 | 0.0030 | 0.00002 | 0.890 |
| C30 | 24 | 0.0029 | 0.00002 | 0.918 | C80 | 24 | 0.0024 | 0.00014 | 0.884 |
| C31 | 80 | 0.0010 | 0.00092 | 0.871 | C81 | 80 | 0.0009 | 0.00037 | 0.847 |
| C32 | 128 | 0.0075 | 0.00006 | 0.807 | C82 | 80 | 0.0013 | 0.00099 | 0.853 |
| C33 | 24 | 0.0034 | 0.00002 | 0.917 | C83 | 128 | 0.0084 | 0.00006 | 0.812 |
| C34 | 80 | 0.0010 | 0.00009 | 0.874 | C84 | 128 | 0.0053 | 0.00007 | 0.823 |
| C35 | 128 | 0.0098 | 0.00008 | 0.815 | C85 | 24 | 0.0020 | 0.00005 | 0.927 |
| C36 | 24 | 0.0014 | 0.00021 | 0.949 | C86 | 128 | 0.0044 | 0.00009 | 0.910 |
| C37 | 24 | 0.0007 | 0.00001 | 0.950 | C87 | 24 | 0.0034 | 0.00004 | 0.913 |
| C38 | 24 | 0.0006 | 0.00001 | 0.939 | C88 | 24 | 0.0005 | 0.00009 | 0.867 |
| C39 | 80 | 0.0003 | 0.00011 | 0.963 | C89 | 96 | 0.0008 | 0.00005 | 0.857 |
| C40 | 80 | 0.0021 | 0.00062 | 0.848 | C90 | 96 | 0.0006 | 0.00012 | 0.879 |
| C41 | 24 | 0.0040 | 0.00003 | 0.836 | C91 | 96 | 0.0011 | 0.00016 | 0.837 |
| C42 | 24 | 0.0064 | 0.00005 | 0.984 | C92 | 128 | 0.0090 | 0.00022 | 0.804 |
| C43 | 96 | 0.0001 | 0.00002 | 0.879 | C93 | 24 | 0.0007 | 0.00024 | 0.955 |
| C44 | 128 | 0.0002 | 0.00014 | 0.907 | C94 | 128 | 0.0019 | 0.00018 | 0.943 |
| C45 | 80 | 0.0014 | 0.00028 | 0.863 | C95 | 24 | 0.0006 | 0.00029 | 0.977 |
| C46 | 80 | 0.0002 | 0.00018 | 0.819 | C96 | 24 | 0.0015 | 0.00006 | 0.970 |
| C47 | 24 | 0.0024 | 0.00004 | 0.840 | C97 | 24 | 0.0004 | 0.00001 | 0.980 |
| C48 | 96 | 0.0055 | 0.00005 | 0.811 | C98 | 24 | 0.0001 | 0.00001 | 0.989 |
| C49 | 24 | 0.0001 | 0.00003 | 0.919 | C99 | 80 | 0.0003 | 0.00050 | 0.960 |
| C50 | 24 | 0.0017 | 0.00002 | 0.879 | C100 | 96 | 0.0002 | 0.00003 | 0.840 |
| Model | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| OFAT | Training | 0.98468 | 0.98455 | 0.98461 | 0.99034 | 0.86196 | 0.98519 | 0.909 | 0.86 |
| Test | 0.99085 | 0.99312 | 0.99198 | 0.99319 | 0.86615 | 0.99211 | - | 1.07 | |
| C1 | Training | 0.99022 | 0.98154 | 0.98586 | 0.99128 | 0.86481 | 0.98642 | 1.355 | 0.82 |
| Test | 0.99055 | 0.99409 | 0.99232 | 0.99178 | 0.86894 | 0.99227 | - | 1.21 | |
| C47 | Training | 0.98609 | 0.98293 | 0.98451 | 0.99086 | 0.86359 | 0.98514 | 1.421 | 0.93 |
| Test | 0.99190 | 0.99348 | 0.99269 | 0.99262 | 0.86842 | 0.99268 | - | 1.12 | |
| C56 | Training | 0.98831 | 0.98650 | 0.98740 | 0.99150 | 0.86662 | 0.98782 | 1.382 | 0.91 |
| Test | 0.99502 | 0.98943 | 0.99222 | 0.99236 | 0.87094 | 0.99224 | - | 1.09 | |
| C95 | Training | 0.99021 | 0.98060 | 0.98538 | 0.99060 | 0.86548 | 0.98593 | 1.439 | 0.94 |
| Test | 0.99243 | 0.99198 | 0.99220 | 0.99200 | 0.87179 | 0.99218 | - | 1.13 |
| Model | Process | Precision | Recall | F1-Score | mAP@.5 | mAP@.5:.95 | Fitness | Time (Hours) | Speed (ms) |
|---|---|---|---|---|---|---|---|---|---|
| YOLOv3µ | Training | 0.99046 | 0.98117 | 0.98579 | 0.99036 | 0.86732 | 0.98627 | 2.220 | 1.16 |
| Test | 0.98564 | 0.98971 | 0.98767 | 0.99157 | 0.87301 | 0.98807 | - | 1.92 | |
| YOLOv5m | Training | 0.98520 | 0.97657 | 0.98087 | 0.99161 | 0.87153 | 0.98196 | 1.601 | 0.92 |
| Test | 0.98785 | 0.98885 | 0.98835 | 0.99069 | 0.87159 | 0.98858 | - | 0.97 | |
| YOLOv7 | Training | 0.91633 | 0.84273 | 0.87799 | 0.93863 | 0.77301 | 0.88544 | 3.842 | - |
| Test | 0.90212 | 0.83679 | 0.86826 | 0.93029 | 0.75676 | 0.87554 | - | - | |
| YOLOv8m | Training | 0.98597 | 0.97636 | 0.98114 | 0.98906 | 0.87060 | 0.98195 | 1.455 | 0.87 |
| Test | 0.98565 | 0.98997 | 0.98781 | 0.99188 | 0.87443 | 0.98821 | - | 1.04 | |
| YOLOv9m | Training | 0.98840 | 0.97812 | 0.98323 | 0.99115 | 0.86930 | 0.98405 | 2.199 | 0.93 |
| Test | 0.98612 | 0.98994 | 0.98803 | 0.99160 | 0.87643 | 0.98839 | - | 1.16 | |
| YOLOv10m | Training | 0.98359 | 0.97809 | 0.98083 | 0.99095 | 0.86954 | 0.98185 | 2.322 | 0.63 |
| Test | 0.98575 | 0.98678 | 0.98626 | 0.99218 | 0.87218 | 0.98686 | - | 0.76 | |
| C47 | Training | 0.98609 | 0.98293 | 0.98451 | 0.99086 | 0.86359 | 0.98514 | 1.421 | 0.93 |
| Test | 0.99190 | 0.99348 | 0.99269 | 0.99262 | 0.86842 | 0.99268 | - | 1.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-S.; Patil, M.P.; Kim, J.G.; Seo, Y.B.; Ahn, D.-H.; Kim, G.-D. Hyperparameter Optimization for Tomato Leaf Disease Recognition Based on YOLOv11m. Plants 2025, 14, 653. https://doi.org/10.3390/plants14050653
Lee Y-S, Patil MP, Kim JG, Seo YB, Ahn D-H, Kim G-D. Hyperparameter Optimization for Tomato Leaf Disease Recognition Based on YOLOv11m. Plants. 2025; 14(5):653. https://doi.org/10.3390/plants14050653
Chicago/Turabian StyleLee, Yong-Suk, Maheshkumar Prakash Patil, Jeong Gyu Kim, Yong Bae Seo, Dong-Hyun Ahn, and Gun-Do Kim. 2025. "Hyperparameter Optimization for Tomato Leaf Disease Recognition Based on YOLOv11m" Plants 14, no. 5: 653. https://doi.org/10.3390/plants14050653
APA StyleLee, Y.-S., Patil, M. P., Kim, J. G., Seo, Y. B., Ahn, D.-H., & Kim, G.-D. (2025). Hyperparameter Optimization for Tomato Leaf Disease Recognition Based on YOLOv11m. Plants, 14(5), 653. https://doi.org/10.3390/plants14050653







