A Model of the Ectomycorrhizal Contribution to Forest Soil C and N Dynamics and Tree N Supply Within the EFIMOD3 Model System
Abstract
1. Introduction
2. Materials and Methods
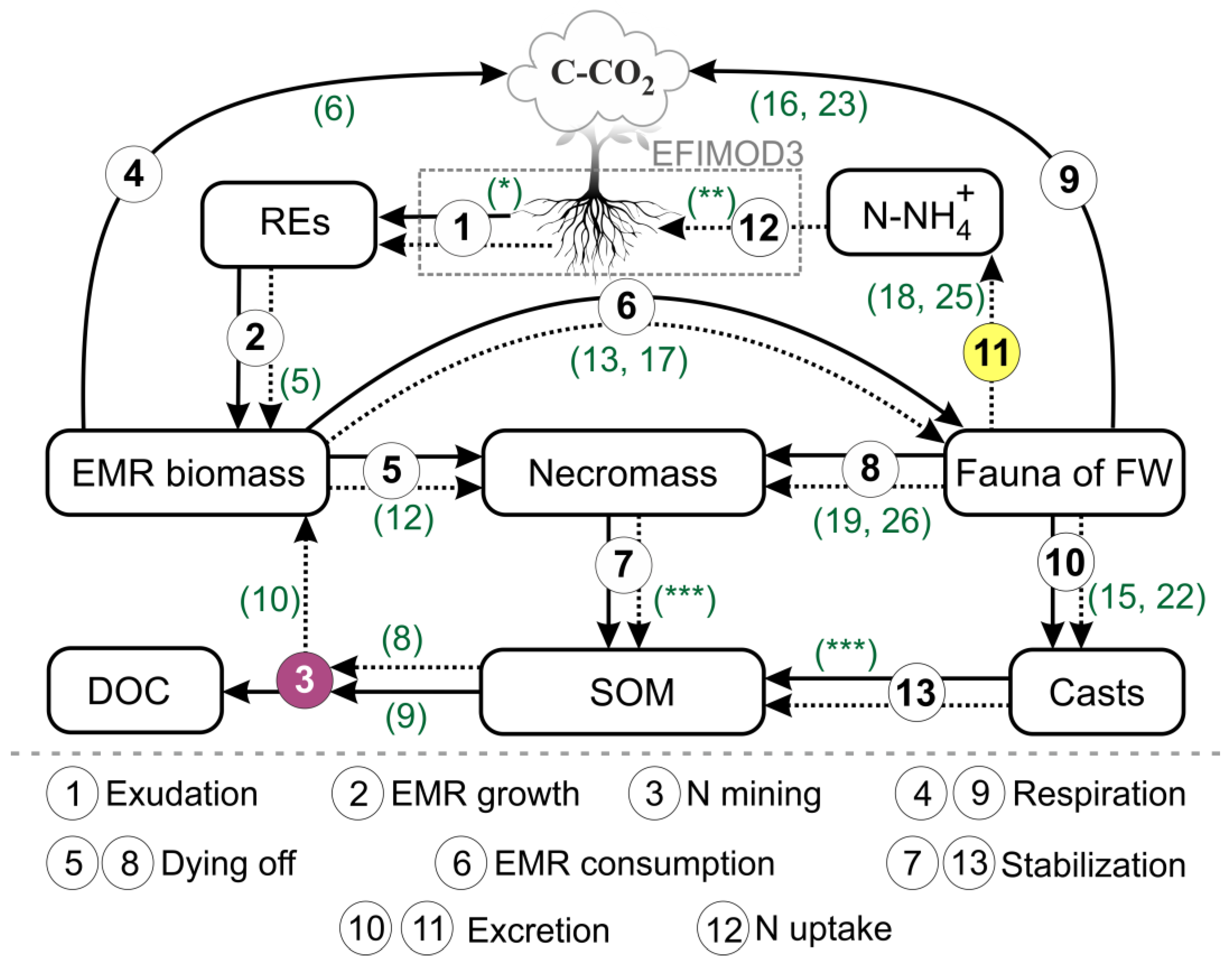
2.1. Model Description
2.1.1. Basic Postulates
2.1.2. Initialization
2.1.3. Root Exudates Input
2.1.4. EMM Growth
2.1.5. N Mining
2.1.6. EMM Consumption and Mortality
2.1.7. Food Webs’ Dynamics
2.2. Sensitivity Analysis
2.3. Model Validation
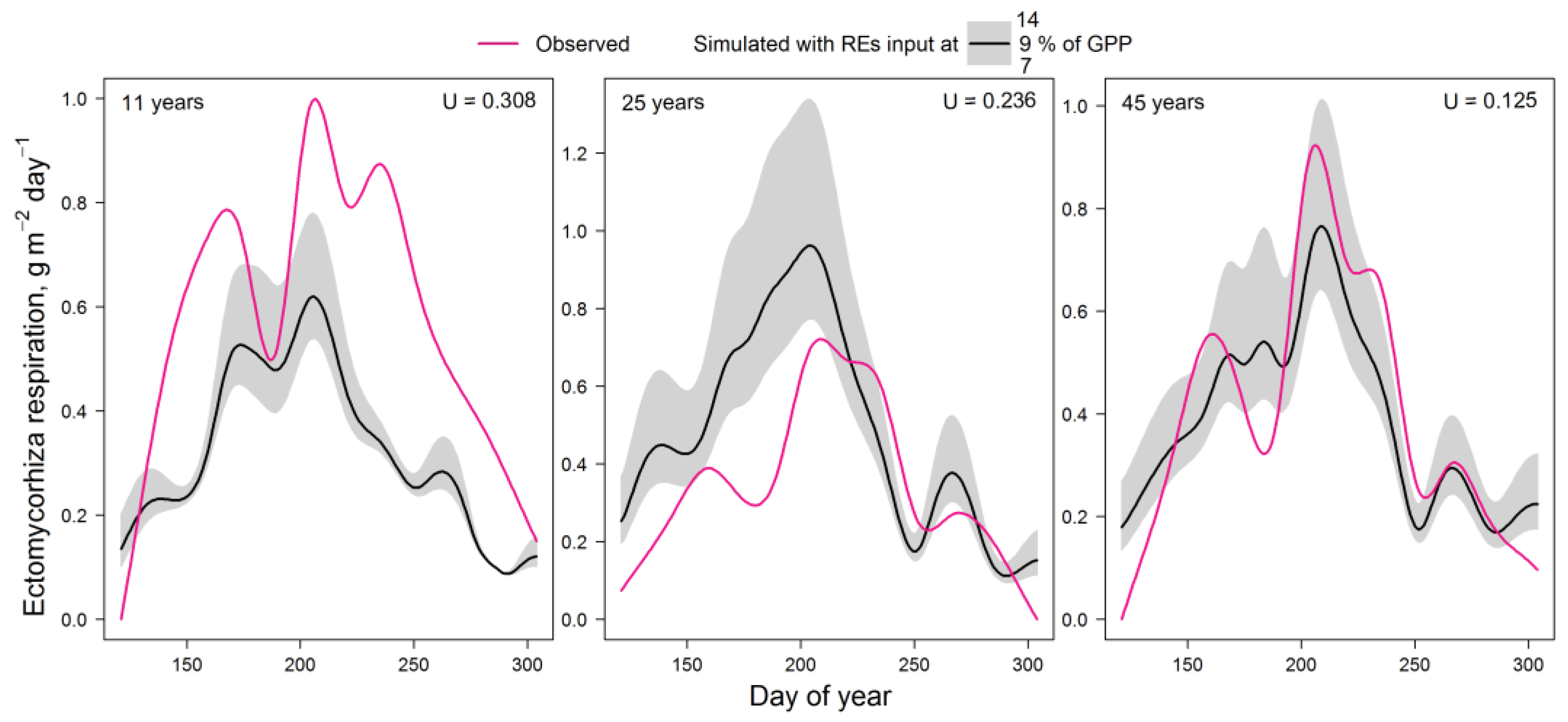
2.4. Testing the EMR Model
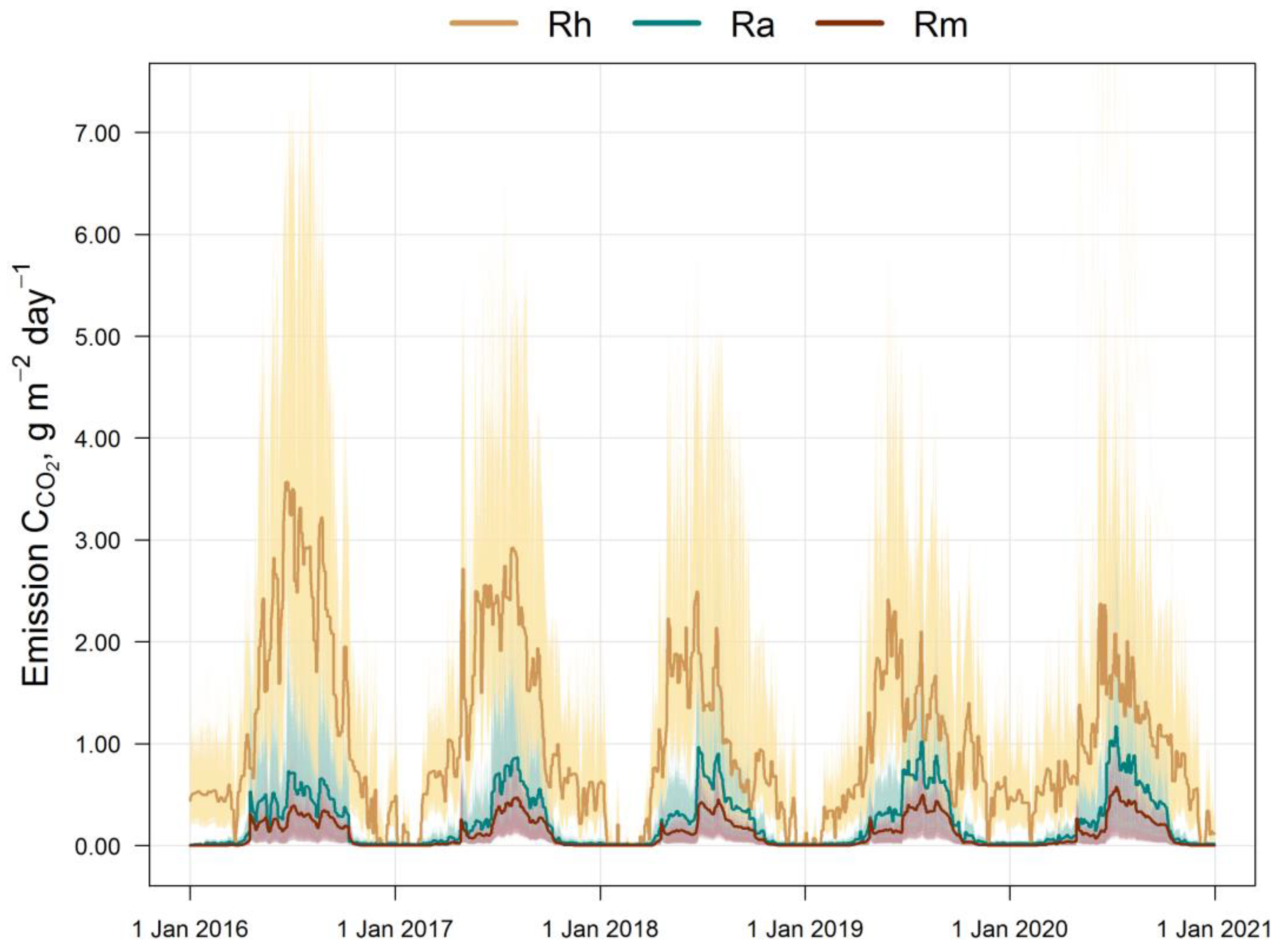
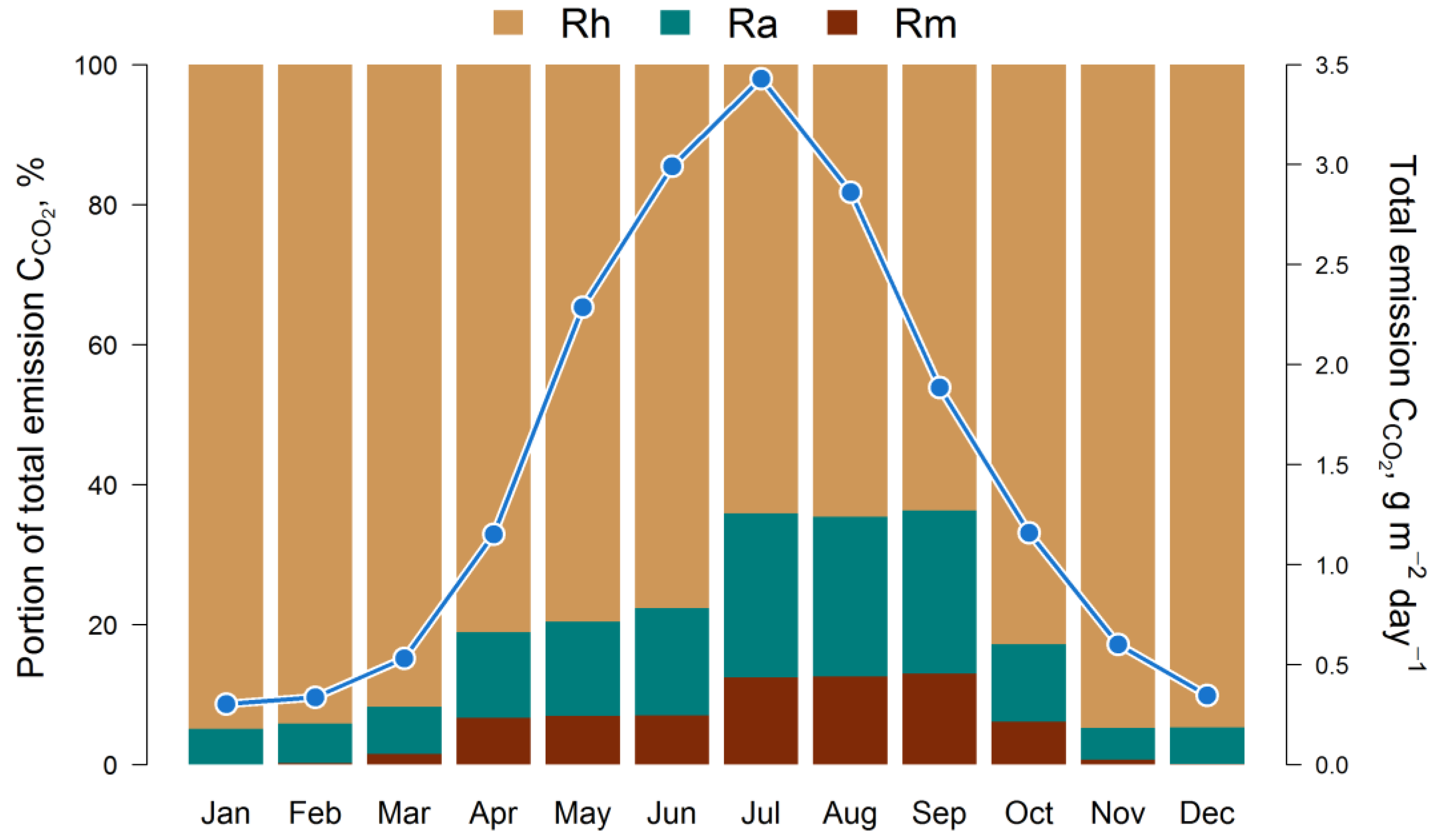
3. Results
4. Discussion
4.1. Theoretical Background and Structure of the Model
4.2. Sensitivity Analysis, Validation, and Testing
4.3. Role of EMR and Food Webs in the Soil Organic Matter Dynamics
4.4. Role of EMR in Nitrogen Dynamics and Supply for Tree Growth
4.5. Aspects of the EMR Functioning
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, P.; Smith, J.U.; Powlson, D.S.; McGill, W.B.; Arah, J.R.M.; Chertov, O.G.; Coleman, K.; Franko, U.; Frolking, S.; Jenkinson, D.S.; et al. A Comparison of the Performance of Nine Soil Organic Matter Models Using Datasets from Seven Long-Term Experiments. Geoderma 1997, 81, 153–225. [Google Scholar] [CrossRef]
- Chertov, O.G.; Komarov, A.S. SOMM—A model of soil organic matter dynamics. Ecol. Model. 1997, 94, 177–189. [Google Scholar] [CrossRef]
- Braakhekke, M.C.; Beer, C.; Hoosbeek, M.R.; Reichstein, M.; Kruijt, B.; Schrumpf, M.; Kabat, P. SOMPROF: A Vertically Explicit Soil Organic Matter Model. Ecol. Model. 2011, 222, 1712–1730. [Google Scholar] [CrossRef]
- Brzostek, E.R.; Fisher, J.B.; Phillips, R.P. Modeling the Carbon Cost of Plant Nitrogen Acquisition: Mycorrhizal Trade-Offs and Multipath Resistance Uptake Improve Predictions of Retranslocation. J. Geophys. Res. Biogeosci. 2014, 119, 1684–1697. [Google Scholar] [CrossRef]
- Huang, Y.; Guenet, B.; Ciais, P.; Janssens, I.A.; Soong, J.L.; Wang, Y.; Goll, D.; Blagodatskaya, E.; Huang, Y. ORCHIMIC (v1.0), a Microbe-Mediated Model for Soil Organic Matter Decomposition. Geosci. Model. Dev. 2018, 11, 2111–2138. [Google Scholar] [CrossRef]
- Berardi, D.; Brzostek, E.; Blanc-Betes, E.; Davison, B.; DeLucia, E.H.; Hartman, M.D.; Kent, J.; Parton, W.J.; Saha, D.; Hudiburg, T.W. 21st-century Biogeochemical Modeling: Challenges for Century-based Models and Where Do We Go from Here? GCB Bioenergy 2020, 12, 774–788. [Google Scholar] [CrossRef]
- Fitch, A.A.; Goldsmith, S.B.; Lankau, R.A.; Wurzburger, N.; Shortt, Z.D.; Vrattos, A.; Laurent, E.N.; Hicks Pries, C.E. Mycorrhizal Associations of Temperate Forest Seedlings Mediate Rhizodeposition, but Not Soil Carbon Storage, under Elevated Nitrogen Availability. Glob. Change Biol. 2024, 30, e17446. [Google Scholar] [CrossRef]
- Komarov, A.; Chertov, O.; Bykhovets, S.; Shaw, C.; Nadporozhskaya, M.; Frolov, P.; Shashkov, M.; Shanin, V.; Grabarnik, P.; Priputina, I.; et al. Romul_Hum model of soil organic matter formation coupled with soil biota activity. I. Problem formulation, model description, and testing. Ecol. Model. 2017, 345, 113–124. [Google Scholar] [CrossRef]
- Parton, W.J. The CENTURY model. In Evaluation of Soil Organic Matter Models; Powlson, D.S., Smith, P., Smith, J.U., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 283–293. ISBN 9783642646928. [Google Scholar]
- Komarov, A.; Chertov, O.; Nadporozhskaya, M.; Mikhailov, A.; Bykhovets, S.; Zudina, E.; Zoubkova, E. EFIMOD 2—A Model of Growth and Cycling of Elements in Boreal Forest Ecosystems. Ecol. Model. 2003, 170, 373–392. [Google Scholar] [CrossRef]
- Komarov, A.S.; Chertov, O.G.; Nadporozhskaya, M.A.; Priputina, I.V.; Bykhovets, S.S.; Larionova, A.A.; Grabarnik, P.Y.; Zudin, S.L.; Mikhailov, A.V.; Zubkova, E.V.; et al. Modelling the Organic Matter Dynamics in Forest Ecosystems; Kudeyarov, V.N., Ed.; Nauka Publishing: Moscow, Russia, 2007; 380p, ISBN 5-02-034053-7. (In Russian with English Content). [Google Scholar]
- Blagodatskaya, E.; Kuzyakov, Y. Mechanisms of Real and Apparent Priming Effects and Their Dependence on Soil Microbial Biomass and Community Structure: Critical Review. Biol. Fertil. Soils 2008, 45, 115–131. [Google Scholar] [CrossRef]
- Bastida, F.; García, C.; Fierer, N.; Eldridge, D.J.; Bowker, M.A.; Abades, S.; Alfaro, F.D.; Asefaw Berhe, A.; Cutler, N.A.; Gallardo, A.; et al. Global Ecological Predictors of the Soil Priming Effect. Nat. Commun. 2019, 10, 3481. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.E.; Read, D. Mycorrhizal Symbiosis, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2008; 787p, ISBN 978-0-12-370526-6. [Google Scholar]
- Martin, F. (Ed.) Molecular Mycorrhizal Symbiosis; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016; 506p, ISBN 978-1-118-95144-6. [Google Scholar]
- Zhou, J.; Zang, H.; Loeppmann, S.; Gube, M.; Kuzyakov, Y.; Pausch, J. Arbuscular Mycorrhiza Enhances Rhizodeposition and Reduces the Rhizosphere Priming Effect on the Decomposition of Soil Organic Matter. Soil Biol. Biochem. 2020, 140, 107641. [Google Scholar] [CrossRef]
- Lukina, N.V. (Ed.) Carbon Accumulation in Forest Soils and Forest Successional Status; KMK Scientific Press Ltd.: Moscow, Russia, 2018; 232p, ISBN 978-5-907099-47-0. (In Russian with English Contents). [Google Scholar]
- Aasfar, A.; Bargaz, A.; Yaakoubi, K.; Hilali, A.; Bennis, I.; Zeroual, Y.; Meftah Kadmiri, I. Nitrogen Fixing Azotobacter Species as Potential Soil Biological Enhancers for Crop Nutrition and Yield Stability. Front. Microbiol. 2021, 12, 628379. [Google Scholar] [CrossRef] [PubMed]
- Threatt, S.D.; Rees, D.C. Biological Nitrogen Fixation in Theory, Practice, and Reality: A Perspective on the Molybdenum Nitrogenase System. FEBS Lett. 2022, 597, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Blagodatsky, S.; Blagodatskaya, E.; Yuyukina, T.; Kuzyakov, Y. Model of Apparent and Real Priming Effects: Linking Microbial Activity with Soil Organic Matter Decomposition. Soil Biol. Biochem. 2010, 42, 1275–1283. [Google Scholar] [CrossRef]
- Chertov, O.; Kuzyakov, Y.; Priputina, I.; Frolov, P.; Shanin, V.; Grabarnik, P. Modelling the Rhizosphere Priming Effect in Combination with Soil Food Webs to Quantify Interaction between Living Plant, Soil Biota and Soil Organic Matter. Plants 2022, 11, 2605. [Google Scholar] [CrossRef] [PubMed]
- Högberg, M.N.; Högberg, P. Extramatrical Ectomycorrhizal Mycelium Contributes One-third of Microbial Biomass and Produces, Together with Associated Roots, Half the Dissolved Organic Carbon in a Forest Soil. New Phytol. 2002, 154, 791–795. [Google Scholar] [CrossRef]
- Nehls, U.; Das, A.; Neb, D. Carbohydrate Metabolism in Ectomycorrhizal Symbiosis. In Molecular Mycorrhizal Symbiosis; Martin, F., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016; pp. 159–177. ISBN 978-1-118-95144-6. [Google Scholar]
- Kuzyakov, Y.; Hill, P.W.; Jones, D.L. Root Exudate Components Change Litter Decomposition in a Simulated Rhizosphere Depending on Temperature. Plant Soil 2006, 290, 293–305. [Google Scholar] [CrossRef]
- Pena, R. Nitrogen Acquisition in Ectomycorrhizal Symbiosis. In Molecular Mycorrhizal Symbiosis; Martin, F., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016; pp. 179–196. ISBN 978-1-118-95144-6. [Google Scholar]
- Chalot, M.; Brun, A. Physiology of Organic Nitrogen Acquisition by Ectomycorrhizal Fungi and Ectomycorrhizas. FEMS Microbiol. Rev. 1998, 22, 21–44. [Google Scholar] [CrossRef] [PubMed]
- Stuart, E.K.; Plett, K.L. Digging Deeper: In Search of the Mechanisms of Carbon and Nitrogen Exchange in Ectomycorrhizal Symbioses. Front. Plant Sci. 2020, 10, 1658. [Google Scholar] [CrossRef] [PubMed]
- Agerer, R.; Hartmann, A.; Pritsch, K.; Raidl, S.; Schloter, M.; Verma, R.; Weigt, R. Plants and Their Ectomycorrhizosphere: Cost and Benefit of Symbiotic Soil Organisms. In Ecological Studies; Springer: Berlin/Heidelberg, Germany, 2012; pp. 213–242. ISBN 9783642306440. [Google Scholar]
- Tunlid, A.; Floudas, D.; Koide, R.; Rineau, F. Soil organic matter decomposition mechanisms in ectomycorrhizal fungi. In Molecular Mycorrhizal Symbiosis; Martin, F., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 257–275. ISBN 978-1-118-95144-6. [Google Scholar]
- Talbot, J.M.; Bruns, T.D.; Smith, D.P.; Branco, S.; Glassman, S.I.; Erlandson, S.; Vilgalys, R.; Peay, K.G. Independent Roles of Ectomycorrhizal and Saprotrophic Communities in Soil Organic Matter Decomposition. Soil Biol. Biochem. 2013, 57, 282–291. [Google Scholar] [CrossRef]
- Rineau, F.; Shah, F.; Smits, M.M.; Persson, P.; Johansson, T.; Carleer, R.; Troein, C.; Tunlid, A. Carbon Availability Triggers the Decomposition of Plant Litter and Assimilation of Nitrogen by an Ectomycorrhizal Fungus. ISME J. 2013, 7, 2010–2022. [Google Scholar] [CrossRef]
- van Breemen, N.; Finlay, R.; Lundström, U.; Jongmans, A.G.; Giesler, R.; Olsson, M. Mycorrhizal weathering: A true case of mineral plant nutrition? Biogeochemistry 2000, 49, 53–67. [Google Scholar] [CrossRef]
- Gadd, G.M. Geomycology: Biogeochemical Transformations of Rocks, Minerals, Metals and Radionuclides by Fungi, Bioweathering and Bioremediation. Mycol. Res. 2007, 111, 3–49. [Google Scholar] [CrossRef]
- Staddon, P.L.; Ramsey, C.B.; Ostle, N.; Ineson, P.; Fitter, A.H. Rapid Turnover of Hyphae of Mycorrhizal Fungi Determined by AMS Microanalysis of 14C. Science 2003, 300, 1138–1140. [Google Scholar] [CrossRef]
- Gorka, S.; Dietrich, M.; Mayerhofer, W.; Gabriel, R.; Wiesenbauer, J.; Martin, V.; Zheng, Q.; Imai, B.; Prommer, J.; Weidinger, M.; et al. Rapid Transfer of Plant Photosynthates to Soil Bacteria via Ectomycorrhizal Hyphae and Its Interaction With Nitrogen Availability. Front. Microbiol. 2019, 10, 168. [Google Scholar] [CrossRef] [PubMed]
- Godbold, D.L.; Hoosbeek, M.R.; Lukac, M.; Cotrufo, M.F.; Janssens, I.A.; Ceulemans, R.; Polle, A.; Velthorst, E.J.; Scarascia-Mugnozza, G.; De Angelis, P.; et al. Mycorrhizal Hyphal Turnover as a Dominant Process for Carbon Input into Soil Organic Matter. Plant Soil 2006, 281, 15–24. [Google Scholar] [CrossRef]
- Ekblad, A.; Wallander, H.; Godbold, D.L.; Cruz, C.; Johnson, D.; Baldrian, P.; Björk, R.G.; Epron, D.; Kieliszewska-Rokicka, B.; Kjøller, R.; et al. The Production and Turnover of Extramatrical Mycelium of Ectomycorrhizal Fungi in Forest Soils: Role in Carbon Cycling. Plant Soil 2013, 366, 1–27. [Google Scholar] [CrossRef]
- Klink, S.; Keller, A.B.; Wild, A.J.; Baumert, V.L.; Gube, M.; Lehndorff, E.; Meyer, N.; Mueller, C.W.; Phillips, R.P.; Pausch, J. Stable Isotopes Reveal That Fungal Residues Contribute More to Mineral-Associated Organic Matter Pools than Plant Residues. Soil Biol. Biochem. 2022, 168, 108634. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Wang, X.; Hartley, I.P.; Zhang, J.; Zhang, Y. Fungal Necromass Contributes More to Soil Organic Carbon and More Sensitive to Land Use Intensity than Bacterial Necromass. Appl. Soil Ecol. 2022, 176, 104492. [Google Scholar] [CrossRef]
- Chertov, O.G.; Priputina, I.V.; Shanin, V.N.; Frolov, P.V. Role of woody plants’ ectomycorrhiza in the dynamic of forest soil organic matter: Synthesis and conceptualization of available data. For. Sci. Issues 2024, 7, 141, (In Russian with English Summary). [Google Scholar] [CrossRef]
- Manzoni, S.; Porporato, A. Soil Carbon and Nitrogen Mineralization: Theory and Models across Scales. Soil Biol. Biochem. 2009, 41, 1355–1379. [Google Scholar] [CrossRef]
- Cotrufo, M.F.; Lavallee, J.M. Soil Organic Matter Formation, Persistence, and Functioning: A Synthesis of Current Understanding to Inform Its Conservation and Regeneration. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1–66. ISBN 9780323989534. [Google Scholar]
- King, A.E.; Amsili, J.P.; Córdova, S.C.; Culman, S.; Fonte, S.J.; Kotcon, J.; Liebig, M.; Masters, M.D.; McVay, K.; Olk, D.C.; et al. A Soil Matrix Capacity Index to Predict Mineral-Associated but Not Particulate Organic Carbon across a Range of Climate and Soil pH. Biogeochemistry 2023, 165, 1–14. [Google Scholar] [CrossRef]
- Zhou, Z.; Ren, C.; Wang, C.; Delgado-Baquerizo, M.; Luo, Y.; Luo, Z.; Du, Z.; Zhu, B.; Yang, Y.; Jiao, S.; et al. Global Turnover of Soil Mineral-Associated and Particulate Organic Carbon. Nat. Commun. 2024, 15, 5329. [Google Scholar] [CrossRef] [PubMed]
- Geisen, S.; Koller, R.; Hünninghaus, M.; Dumack, K.; Urich, T.; Bonkowski, M. The Soil Food Web Revisited: Diverse and Widespread Mycophagous Soil Protists. Soil Biol. Biochem. 2016, 94, 10–18. [Google Scholar] [CrossRef]
- Lukac, M.; Godbold, D.L. Soil Ecology in Northern Forests. A Belowground View of a Changing World; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780511976100. [Google Scholar]
- Zanella, A.; Ponge, J.-F.; Gobat, J.-M.; Juilleret, J.; Blouin, M.; Aubert, M.; Chertov, O.; Rubio, J.L. Humusica 1, Article 1: Essential Bases—Vocabulary. Appl. Soil Ecol. 2018, 122, 10–21. [Google Scholar] [CrossRef]
- Holtkamp, R.; van der Wal, A.; Kardol, P.; van der Putten, W.H.; de Ruiter, P.C.; Dekker, S.C. Modelling C and N Mineralisation in Soil Food Webs during Secondary Succession on Ex-Arable Land. Soil Biol. Biochem. 2011, 43, 251–260. [Google Scholar] [CrossRef]
- Moore, J.C.; de Ruiter, P.C.; McCann, K.S.; Wolters, V. (Eds.) Adaptive Food Webs; Cambridge University Press: Cambridge, UK, 2018; 416p, ISBN 9781316871867. [Google Scholar]
- Odum, E.P.; Barrett, G.W. Fundamentals of Ecology; Thomson Brooks/Cole: Boston, MA, USA, 2005; 598p, ISBN 0534420664/9780534420666. [Google Scholar]
- Moore, J.C.; de Ruiter, P.C. Energetic Food Webs: An Analysis of Real and Model Ecosystems; Oxford University Press: Oxford, UK, 2012; 352p, ISBN 978-0-19-856618-2. [Google Scholar]
- de Vries, F.T.; Thébault, E.; Liiri, M.; Birkhofer, K.; Tsiafouli, M.A.; Bjørnlund, L.; Bracht Jørgensen, H.; Brady, M.V.; Christensen, S.; de Ruiter, P.C.; et al. Soil Food Web Properties Explain Ecosystem Services across European Land Use Systems. Proc. Natl. Acad. Sci. USA 2013, 110, 14296–14301. [Google Scholar] [CrossRef] [PubMed]
- Chertov, O.; Komarov, A.; Shaw, C.; Bykhovets, S.; Frolov, P.; Shanin, V.; Grabarnik, P.; Priputina, I.; Zubkova, E.; Shashkov, M. Romul_Hum—A Model of Soil Organic Matter Formation Coupling with Soil Biota Activity. II. Parameterisation of the Soil Food Web Biota Activity. Ecol. Model. 2017, 345, 125–139. [Google Scholar] [CrossRef]
- Zelenev, V.V.; van Bruggen, A.H.C.; Semenov, A.M. “BACWAVE,” a Spatial–Temporal Model for Traveling Waves of Bacterial Populations in Response to a Moving Carbon Source in Soil. Microb. Ecol. 2000, 40, 260–272. [Google Scholar] [CrossRef]
- Zelenev, V.V.; van Bruggen, A.H.C.; Leffelaar, P.A.; Bloem, J.; Semenov, A.M. Oscillating Dynamics of Bacterial Populations and Their Predators in Response to Fresh Organic Matter Added to Soil: The Simulation Model ‘BACWAVE-WEB’. Soil Biol. Biochem. 2006, 38, 1690–1711. [Google Scholar] [CrossRef]
- DeForest, J.L.; Snell, R.S. Tree Growth Response to Shifting Soil Nutrient Economy Depends on Mycorrhizal Associations. New Phytol. 2019, 225, 2557–2566. [Google Scholar] [CrossRef] [PubMed]
- Anthony, M.A.; Crowther, T.W.; van der Linde, S.; Suz, L.M.; Bidartondo, M.I.; Cox, F.; Schaub, M.; Rautio, P.; Ferretti, M.; Vesterdal, L.; et al. Forest Tree Growth Is Linked to Mycorrhizal Fungal Composition and Function across Europe. ISME J. 2022, 16, 1327–1336. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.D.; Durall, D.M.; Tinker, P.B. Fluxes of Carbon and Phosphorus between Symbionts in Willow Ectomycorrhizas and Their Changes with Time. New Phytol. 1991, 119, 99–106. [Google Scholar] [CrossRef]
- Read, D.J.; Perez-Moreno, J. Mycorrhizas and Nutrient Cycling in Ecosystems—A Journey towards Relevance? New Phytol. 2003, 157, 475–492. [Google Scholar] [CrossRef] [PubMed]
- Wright, W.; Fitter, A.; Meharg, A. Reproductive Biomass in Holcus lanatus Clones That Differ in Their Phosphate Uptake Kinetics and Mycorrhizal Colonization. New Phytol. 2000, 146, 493–501. [Google Scholar] [CrossRef]
- Brunner, I.; Børja, I.; Dalsgaard, L.; Deckmyn, G.; Ekblad, A.; Godbold, D.L.; Guerra Avalos, I.; Lukac, M.; Kalbitz, K.; Kriiska, K.; et al. Belowground Carbon Turnover in European Forests: Fine Roots, Mycorrhizal Mycelia, Soil Organic Matter and Soil Models; Birmensdorf WSL: Zürich, Switzerland, 2013; 67p, ISBN 978-3-905621-54-9. [Google Scholar]
- Deckmyn, G.; Meyer, A.; Smits, M.M.; Ekblad, A.; Grebenc, T.; Komarov, A.; Kraigher, H. Simulating Ectomycorrhizal Fungi and Their Role in Carbon and Nitrogen Cycling in Forest Ecosystems. Can. J. For. Res. 2014, 44, 535–553. [Google Scholar] [CrossRef]
- Cagnarini, C.; Blyth, E.; Emmett, B.A.; Evans, C.D.; Griffiths, R.I.; Keith, A.; Jones, L.; Lebron, I.; McNamara, N.P.; Puissant, J.; et al. Zones of Influence for Soil Organic Matter Dynamics: A Conceptual Framework for Data and Models. Glob. Change Biol. 2019, 25, 3996–4007. [Google Scholar] [CrossRef] [PubMed]
- Simard, S.W.; Beiler, K.J.; Bingham, M.A.; Deslippe, J.R.; Philip, L.J.; Teste, F.P. Mycorrhizal Networks: Mechanisms, Ecology and Modelling. Fungal Biol. Rev. 2012, 26, 39–60. [Google Scholar] [CrossRef]
- Shao, S.; Wurzburger, N.; Sulman, B.; Hicks Pries, C. Ectomycorrhizal Effects on Decomposition Are Highly Dependent on Fungal Traits, Climate, and Litter Properties: A Model-Based Assessment. Soil Biol. Biochem. 2023, 184, 109073. [Google Scholar] [CrossRef]
- Meyer, A.; Grote, R.; Polle, A.; Butterbach-Bahl, K. Simulating Mycorrhiza Contribution to Forest C- and N Cycling-the MYCOFON Model. Plant Soil 2009, 327, 493–517. [Google Scholar] [CrossRef]
- Meyer, A.; Grote, R.; Butterbach-Bahl, K. Integrating Mycorrhiza in a Complex Model System: Effects on Ecosystem C and N Fluxes. Eur. J. For. Res. 2012, 131, 1809–1831. [Google Scholar] [CrossRef]
- Shanin, V.N.; Frolov, P.V.; Priputina, I.V.; Chertov, O.G.; Bykhovets, S.S.; Zubkova, E.V.; Portnov, A.M.; Frolova, G.G.; Stamenov, M.N.; Grabarnik, P.Y. Modeling forest ecosystems dynamic taking into account their structural heterogeneity at different functional and spatial levels. For. Sci. Issues 2023, 6, 112. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: http://www.R-project.org/ (accessed on 12 December 2024).
- Bengtson, P.; Barker, J.; Grayston, S.J. Evidence of a Strong Coupling between Root Exudation, C and N Availability, and Stimulated SOM Decomposition Caused by Rhizosphere Priming Effects. Ecol. Evol. 2012, 2, 1843–1852. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.P.; Erlitz, Y.; Bier, R.; Bernhardt, E.S. New Approach for Capturing Soluble Root Exudates in Forest Soils. Funct. Ecol. 2008, 22, 990–999. [Google Scholar] [CrossRef]
- Liu, T.; Chen, X.; Gong, X.; Lubbers, I.M.; Jiang, Y.; Feng, W.; Li, X.; Whalen, J.K.; Bonkowski, M.; Griffiths, B.S.; et al. Earthworms Coordinate Soil Biota to Improve Multiple Ecosystem Functions. Curr. Biol. 2019, 29, 3420–3429.e5. [Google Scholar] [CrossRef]
- Ostonen, I.; Lõhmus, K. Proportion of Fungal Mantle, Cortex and Stele of Ectomycorrhizas in Picea abies (L.) Karst. in Different Soils and Site Conditions. Plant Soil 2003, 257, 435–442. [Google Scholar] [CrossRef]
- Balestrini, R.; Kottke, I. Structure and Development of Ectomycorrhizal Roots. In Molecular Mycorrhizal Symbiosis; Martin, F., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016; pp. 47–61. ISBN 978-1-118-95144-6. [Google Scholar]
- Lukac, M.; Calfapietra, C.; Godbold, D.L. Production, Turnover and Mycorrhizal Colonization of Root Systems of Three Populus Species Grown under Elevated CO2 (POPFACE). Glob. Change Biol. 2003, 9, 838–848. [Google Scholar] [CrossRef]
- Anderson, T.-H.; Domsch, K.H. Ratios of Microbial Biomass Carbon to Total Organic Carbon in Arable Soils. Soil Biol. Biochem. 1989, 21, 471–479. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to Avoid a Perfunctory Sensitivity Analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Yan, T.; Qu, T.; Song, H.; Sun, Z.; Zeng, H.; Peng, S. Ectomycorrhizal Fungi Respiration Quantification and Drivers in Three Differently-Aged Larch Plantations. Agric. For. Meteorol. 2019, 265, 245–251. [Google Scholar] [CrossRef]
- Ma, Y.; Piao, S.; Sun, Z.; Lin, X.; Wang, T.; Yue, C.; Yang, Y. Stand Ages Regulate the Response of Soil Respiration to Temperature in a Larix principis-Rupprechtii Plantation. Agric. For. Meteorol. 2014, 184, 179–187. [Google Scholar] [CrossRef]
- de Boor, C.R. A Practical Guide to Splines. Math. Comput. 1980, 34, 325. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, L.; Peng, S.; Peñuelas, J.; Zeng, H.; Piao, S. Age-Related Modulation of the Nitrogen Resorption Efficiency Response to Growth Requirements and Soil Nitrogen Availability in a Temperate Pine Plantation. Ecosystems 2016, 19, 698–709. [Google Scholar] [CrossRef]
- Chari, N.R.; Tumber-Dávila, S.J.; Phillips, R.P.; Bauerle, T.L.; Brunn, M.; Hafner, B.D.; Klein, T.; Obersteiner, S.; Reay, M.K.; Ullah, S.; et al. Estimating the Global Root Exudate Carbon Flux. Biogeochemistry 2024, 167, 895–908. [Google Scholar] [CrossRef]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net Primary Production of Forests: A Constant Fraction of Gross Primary Production? Tree Physiol. 1998, 18, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Landsberg, J.J.; Waring, R.H.; Williams, M. The Assessment of NPP/GPP Ratio. Tree Physiol. 2020, 40, 695–699. [Google Scholar] [CrossRef]
- Theil, H. Applied Economic Forecasting; Rand McNally: Chicago, IL, USA, 1966; 474p. [Google Scholar]
- Priputina, I.V.; Frolova, G.G.; Shanin, V.N.; Myakshina, T.N.; Grabarnik, P.Y. Spatial Distribution of Organic Matter and Nitrogen in the Entic Podzols of the Prioksko-Terrasnyi Reserve and Its Relationship with the Structure of Forest Phytocenoses. Eurasian Soil Sci. 2020, 53, 1021–1032. [Google Scholar] [CrossRef]
- The Prioksko-Terrasny Biosphere Reserve: Environmental Monitoring. Available online: https://pt-zapovednik.org/nauchnaya-deyatelnost/ (accessed on 3 December 2024).
- Kurganova, I.N.; Lopes de Gerenyu, V.O.; Khoroshaev, D.A.; Myakshina, T.N.; Sapronov, D.V.; Zhmurin, V.A.; Kudeyarov, V.N. Analysis of the Long-Term Soil Respiration Dynamics in the Forest and Meadow Cenoses of the Prioksko-Terrasny Biosphere Reserve in the Perspective of Current Climate Trends. Eurasian Soil Sci. 2020, 53, 1421–1436. [Google Scholar] [CrossRef]
- Pena, R.; Tibbett, M. Mycorrhizal Symbiosis and the Nitrogen Nutrition of Forest Trees. Appl. Microbiol. Biotechnol. 2024, 108, 461. [Google Scholar] [CrossRef]
- Vanwalleghem, T.; Meentemeyer, R.K. Predicting Forest Microclimate in Heterogeneous Landscapes. Ecosystems 2009, 12, 1158–1172. [Google Scholar] [CrossRef]
- Díaz-Calafat, J.; Uria-Diez, J.; Brunet, J.; De Frenne, P.; Vangansbeke, P.; Felton, A.; Öckinger, E.; Cousins, S.A.O.; Bauhus, J.; Ponette, Q.; et al. From broadleaves to conifers: The effect of tree composition and density on understory microclimate across latitudes. Agric. For. Meteorol. 2023, 341, 109684. [Google Scholar] [CrossRef]
- Heinemeyer, A.; Hartley, I.P.; Evans, S.P.; Carreira De La Fuente, J.A.; Ineson, P. Forest Soil CO2 Flux: Uncovering the Contribution and Environmental Responses of Ectomycorrhizas. Glob. Change Biol. 2007, 13, 1786–1797. [Google Scholar] [CrossRef]
- Heinemeyer, A.; Wilkinson, M.; Vargas, R.; Subke, J.-A.; Casella, E.; Morison, J.I.L.; Ineson, P. Exploring the Overflow Tap Theory: Linking Forest Soil CO2 Fluxes and Individual Mycorrhizosphere Components to Photosynthesis. Biogeosciences 2012, 9, 79–95. [Google Scholar] [CrossRef]
- Hughes, J.K.; Hodge, A.; Fitter, A.H.; Atkin, O.K. Mycorrhizal Respiration: Implications for Global Scaling Relationships. Trends Plant Sci. 2008, 13, 583–588. [Google Scholar] [CrossRef] [PubMed]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N.; et al. Soil Organic Carbon Storage as a Key Function of Soils—A Review of Drivers and Indicators at Various Scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Harris, C. Geomorphological Applications of Soil Micromorphology with Particular Reference to Periglacial Sediments and Processes. In Geomorphology and Soils; Routledge: London, UK, 2020; pp. 219–232. ISBN 9780429320781. [Google Scholar]
- Longhi, A.; Trombino, L.; Guglielmin, M. Soil Micromorphology as Tool for the Past Permafrost and Paleoclimate Reconstruction. CATENA 2021, 207, 105628. [Google Scholar] [CrossRef]
- Bouché, M.B.; Al-Addan, F. Earthworms, Water Infiltration and Soil Stability: Some New Assessments. Soil Biol. Biochem. 1997, 29, 441–452. [Google Scholar] [CrossRef]
- Kim, G.; Jo, H.; Kim, H.-S.; Kwon, M.; Son, Y. Earthworm Effects on Soil Biogeochemistry in Temperate Forests Focusing on Stable Isotope Tracing: A Review. Appl. Biol. Chem. 2022, 65, 88. [Google Scholar] [CrossRef]
- Zhang, W.; Hendrix, P.F.; Dame, L.E.; Burke, R.A.; Wu, J.; Neher, D.A.; Li, J.; Shao, Y.; Fu, S. Earthworms Facilitate Carbon Sequestration through Unequal Amplification of Carbon Stabilization Compared with Mineralization. Nat. Commun. 2013, 4, 2576. [Google Scholar] [CrossRef] [PubMed]
- Pausch, J.; Kramer, S.; Scharroba, A.; Scheunemann, N.; Butenschoen, O.; Kandeler, E.; Marhan, S.; Riederer, M.; Scheu, S.; Kuzyakov, Y.; et al. Small but Active—Pool Size Does Not Matter for Carbon Incorporation in Below-ground Food Webs. Funct. Ecol. 2015, 30, 479–489. [Google Scholar] [CrossRef]
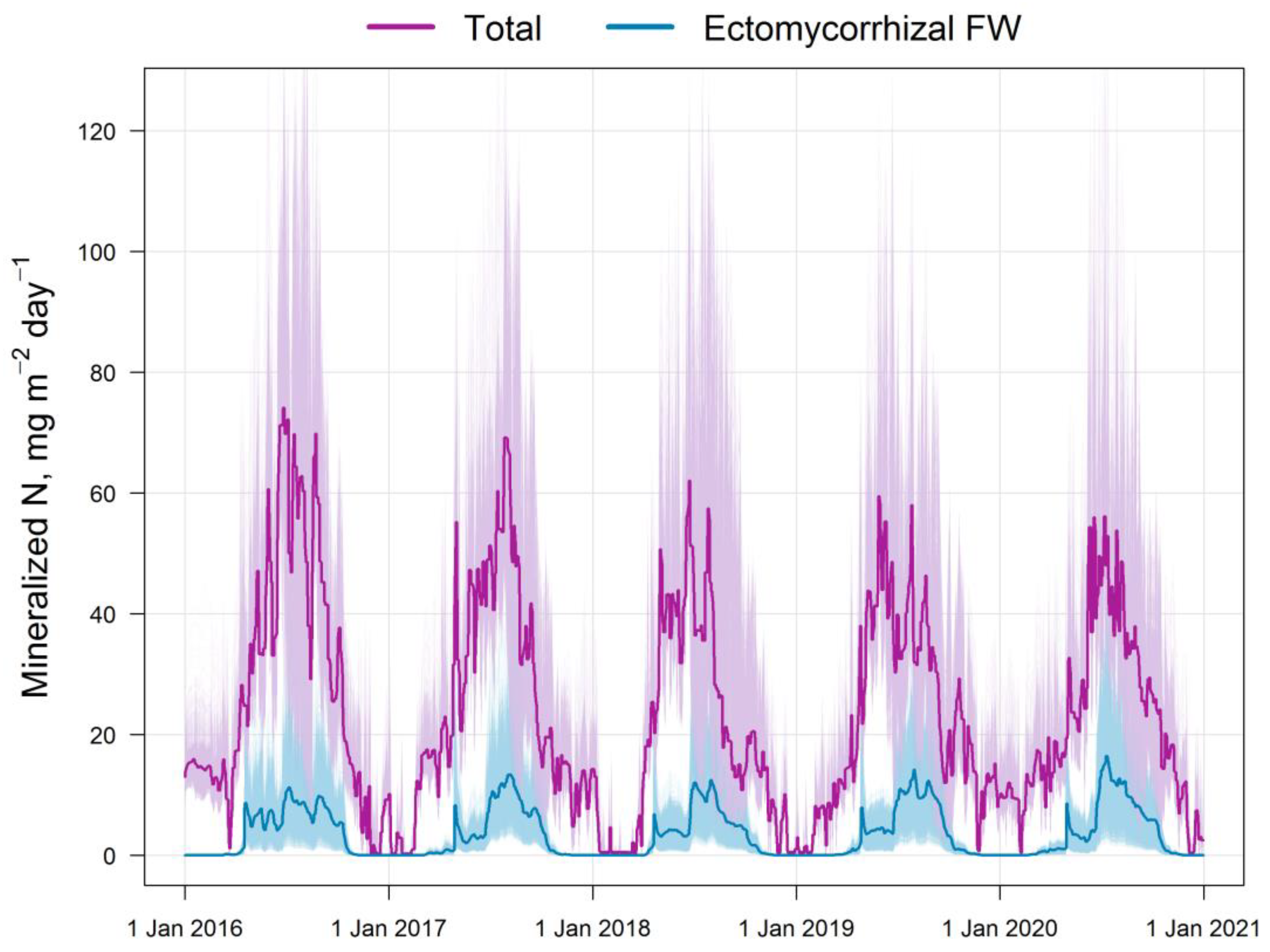
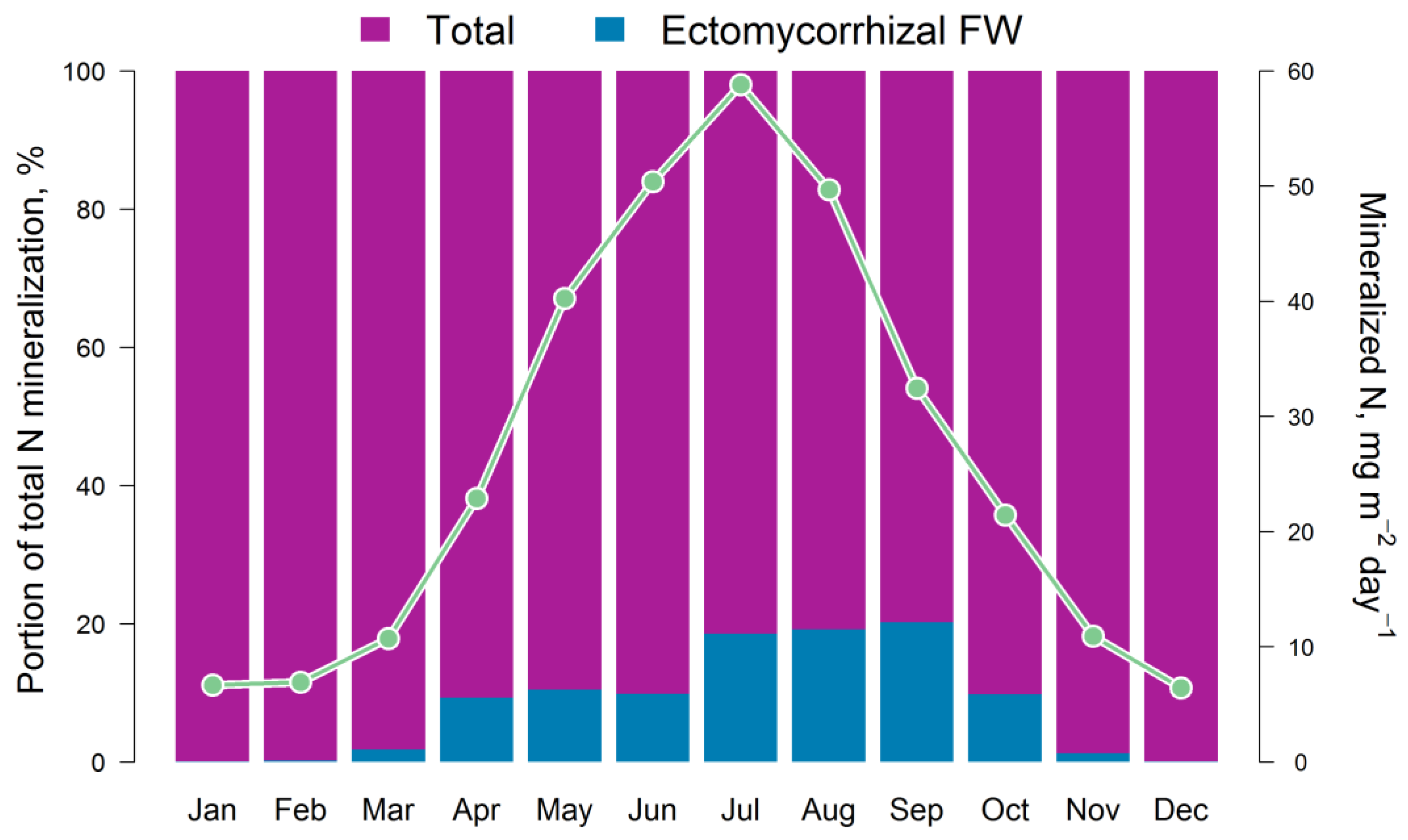
| Parameters | Dimension |
|---|---|
| Input parameters | |
| Total soil C | kg m−2 |
| Total soil N | kg m−2 |
| Root exudates input in terms of C | kg m−2 day−1 |
| Root exudates C:N ratio | dimensionless |
| Extramatrical mycelium biomass in terms of C | kg m−2 |
| Ectomycorrhiza C:N ratio | dimensionless |
| Microfauna biomass in terms of C | kg m−2 |
| Microfauna C:N ratio | dimensionless |
| Output parameters | |
| Total C-CO2 emission at ectomycorrhiza functioning | kg m−2 day−1 |
| N produced at SOC mining via ectomycorrhiza | kg m−2 day−1 |
| DOC produced at SOC mining via ectomycorrhiza | kg m−2 day−1 |
| Sum of microfauna excreta and all necromass C for labile SOC pool | kg m−2 |
| Sum of N produced for labile SOC pool | kg m−2 |
| N-NH4 excreted by food webs fauna | kg m−2 |
| Parameters | Valid Range | Default Value |
|---|---|---|
| REs assimilation rate via EMM | 0.00–1.00 | 1.00 |
| Coefficient of competition for REs between EMR (fungi) and rhizosphere priming (bacteria) | 0.00–1.00 | 1.00 |
| EMM C:N ratio | 9.00–25.00 | 13.10 |
| EMM respiration coefficient | 0.50–0.90 | 0.70 |
| EMM production/growth coefficient | 0.10–0.50 | 0.30 |
| EMM consumption coefficient | 0.00–0.25 | 0.24 |
| EMM mortality coefficient | 0.00–0.25 | 0.01 |
| Micro- and mesofauna C:N ratio | 8.00–11.00 | 10.00 |
| Macrofauna C:N ratio | 6.00–10.00 | 8.00 |
| Micro-, meso-, and macrofauna respiration coefficient | 0.50–0.80 | 0.60 |
| Soil fauna * consumption coefficient | 0.00–0.25 | 0.20 |
| Soil fauna * excretion coefficient | 0.10–0.40 | 0.20 |
| Soil fauna * mortality coefficient | 0.00–0.25 | 0.01 |
| Parameter | Parameter Name | Standardized Coefficient of Linear Regression |
|---|---|---|
| C:N ratio of root exudates | −0.245 *** | |
| C:N ratio of ectomycorrhiza | 0.723 *** | |
| C:N ratio of soil mesofauna | −0.344 *** | |
| C:N ratio of soil macrofauna | −0.164 *** | |
| Respiration rate of ectomycorrhiza | 0.238 *** | |
| Mortality rate of ectomycorrhiza | −0.0553 *** | |
| Consumption rate of ectomycorrhiza | 0.0730 *** | |
| Mortality rate of soil micro- and mesofauna | −0.0126 *** | |
| Consumption rate of soil micro- and mesofauna | 0.0167 *** | |
| Respiration rate of soil micro- and mesofauna | 0.326 *** | |
| Respiration rate of soil macrofauna | 0.142 *** | |
| Intercept | ~0 | |
| R2 | 0.921 | |
| Metric | Formula | 11 Years | 25 Years | 45 Years |
|---|---|---|---|---|
| Mean Squared Error | 0.0936 | 0.0508 | 0.0125 | |
| Root Mean Squared Error | 0.306 | 0.225 | 0.112 | |
| Mean Absolute Error | 0.269 | 0.179 | 0.0936 | |
| Symmetric Mean Absolute Percent Error | 0.628 | 0.464 | 0.284 | |
| Mean Squared Log Error | 0.0410 | 0.0224 | 0.00615 | |
| Root Mean Squared Log Error | 0.202 | 0.149 | 0.0784 | |
| Relative Squared Error | 1.589 | 1.355 | 0.228 | |
| Root Relative Squared Error | 1.260 | 1.164 | 0.477 | |
| Relative Absolute Error | 1.312 | 1.139 | 0.471 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chertov, O.; Frolov, P.; Shanin, V.; Priputina, I.; Bykhovets, S.; Geraskina, A. A Model of the Ectomycorrhizal Contribution to Forest Soil C and N Dynamics and Tree N Supply Within the EFIMOD3 Model System. Plants 2025, 14, 417. https://doi.org/10.3390/plants14030417
Chertov O, Frolov P, Shanin V, Priputina I, Bykhovets S, Geraskina A. A Model of the Ectomycorrhizal Contribution to Forest Soil C and N Dynamics and Tree N Supply Within the EFIMOD3 Model System. Plants. 2025; 14(3):417. https://doi.org/10.3390/plants14030417
Chicago/Turabian StyleChertov, Oleg, Pavel Frolov, Vladimir Shanin, Irina Priputina, Sergey Bykhovets, and Anna Geraskina. 2025. "A Model of the Ectomycorrhizal Contribution to Forest Soil C and N Dynamics and Tree N Supply Within the EFIMOD3 Model System" Plants 14, no. 3: 417. https://doi.org/10.3390/plants14030417
APA StyleChertov, O., Frolov, P., Shanin, V., Priputina, I., Bykhovets, S., & Geraskina, A. (2025). A Model of the Ectomycorrhizal Contribution to Forest Soil C and N Dynamics and Tree N Supply Within the EFIMOD3 Model System. Plants, 14(3), 417. https://doi.org/10.3390/plants14030417







