Phosphorus Dynamics in Managed and Natural Soils: SEM-PLS Analysis of Vaccinium, Forest, and Grassland Ecosystems
Abstract
1. Introduction
2. Materials and Methods
2.1. Global Data Collection and Processing
2.2. Soil Sampling and Processing in Japanese Blueberry Fields
2.3. Identification of AM and ERM Fungal Layers in Vaccinium Soils
2.4. Statistical Analysis
3. Results
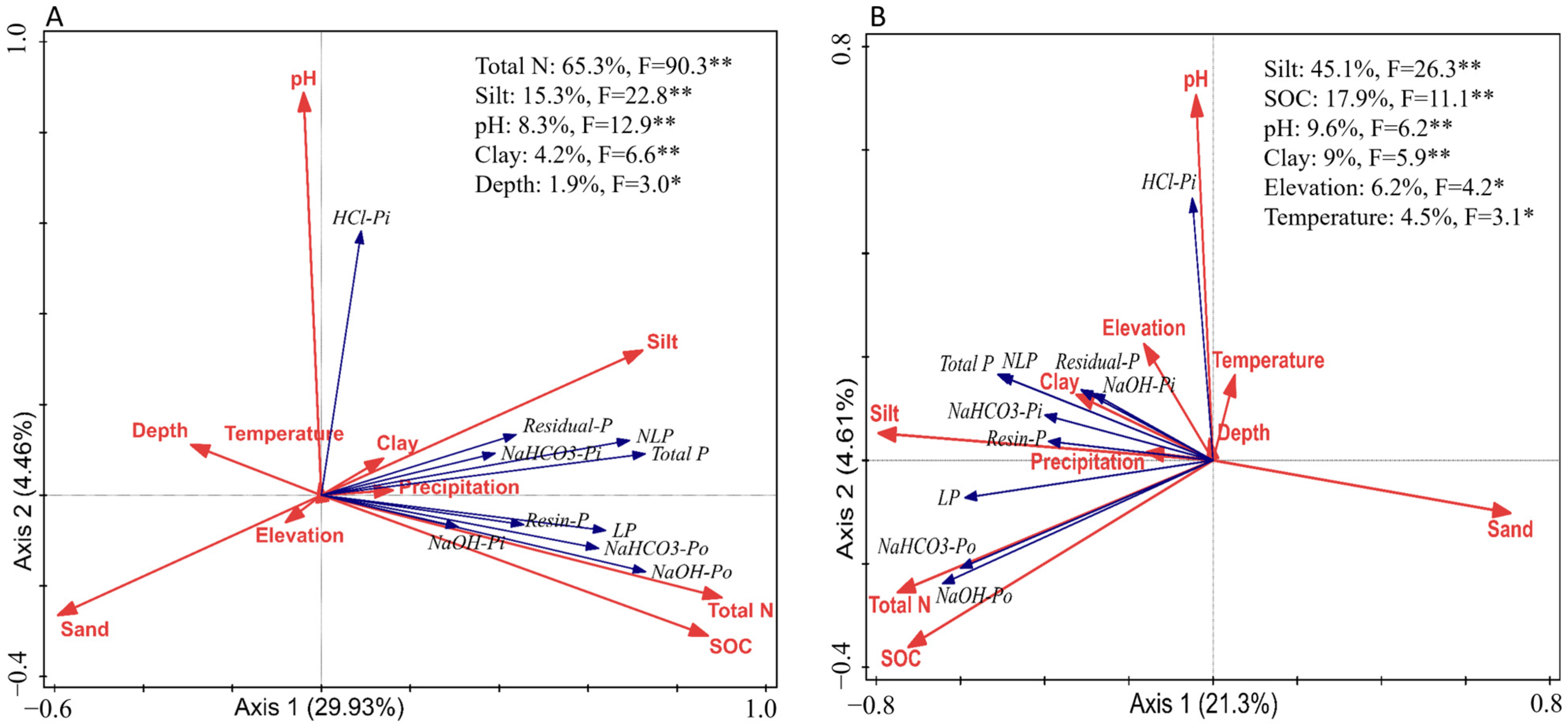
3.1. SEM Models for N and P Accumulation and Phosphorus Fractionation in Global Soils (0–30 cm and Below 30 cm)
3.2. SEM Models for Nitrogen and Phosphorus Accumulation and Their Fractionation Across Various Biomes in Global Soils Within the Top 30 cm
3.3. SEM Models for N and P Accumulation and Phosphorus Fractionation in Japanese Blueberry Soils at Depths of 0–30 cm and 30–60 cm
3.4. SEM Models Addressing Nitrogen and Phosphorus Accumulation and Phosphorus Fractionation in Active and Inactive Symbiotic Fungal Layers
3.5. Summary of Key Findings from SEM Models
4. Discussion
4.1. SEM Models for N and P Accumulation and Phosphorus Fractionation in Global Soils (0–30 cm and Below 30 cm)
4.2. SEM Models for Nitrogen and Phosphorus Accumulation and Their Fractionation Across Various Biomes in Global Soils Within the Top 30 cm
4.3. SEM Models for N and P Accumulation and Phosphorus Fractionation in Japanese Blueberry Soils at Depths of 0–30 cm and 30–60 cm
4.4. SEM Models Addressing Nitrogen and Phosphorus Accumulation and Phosphorus Fractionation in Active and Inactive Symbiotic Fungal Layers
4.5. Implications for Long-Term Soil Management and Global Soil Health
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matson, P.; Lohse, K.A.; Hall, S.J. The globalization of nitrogen deposition: Consequences for terrestrial ecosystems. Ambio 2002, 31, 113–119. [Google Scholar] [CrossRef]
- Menge, D.N.L.; Hedin, L.O.; Pacala, S.W. Nitrogen and phosphorus limitation over long-term ecosystem development in terrestrial ecosystems. PLoS ONE 2012, 7, e42045. [Google Scholar] [CrossRef] [PubMed]
- Güsewell, S. N:P ratios in terrestrial plants: Variation and functional significance. New Phytol. 2004, 164, 243–266. [Google Scholar] [CrossRef] [PubMed]
- Bünemann, E.K.; Smernik, R.J.; Marschner, P.; McNeill, A.M. Microbial synthesis of organic and condensed forms of phosphorus in acid and calcareous soils. Soil Biol. Biochem. 2008, 40, 932–946. [Google Scholar] [CrossRef]
- Mullan, A.; Quinn, J.P.; McGrath, J.W. Enhanced phosphate uptake and polyphosphate accumulation in Burkholderia cepacia grown under low-pH conditions. Microb. Ecol. 2002, 44, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Bernhardt, E.S. Biogeochemistry: An Analysis of Global Change; Academic Press: London, UK, 2013. [Google Scholar]
- Vitousek, P.M.; Porder, S.; Houlton, B.Z.; Chadwick, O.A. Terrestrial phosphorus limitation: Mechanisms, implications, and nitrogen–phosphorus interactions. Ecol. Appl. 2010, 20, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.L.; Frossard, E.; Baldwin, D.S. (Eds.) Organic Phosphorus in the Environment; CABI Publishing: Wallingford, UK, 2005. [Google Scholar]
- Azene, B.; Qiu, P.; Zhu, R.; Pan, K.; Sun, X.; Nigussie, Y.; Zhang, L. Response of soil phosphorus fractions to land use change in the subalpine ecosystems of Southeast margin of Qinghai-Tibet Plateau, Southwest China. Ecol. Indic. 2022, 144, 109432. [Google Scholar] [CrossRef]
- Ding, Z.; Kheir, A.M.; Ali, M.G.; Ali, O.A.; Abdelaal, A.I.; Lin, X.E.; He, Z. The integrated effect of salinity, organic amendments, phosphorus fertilizers, and deficit irrigation on soil properties, phosphorus fractionation, and wheat productivity. Sci. Rep. 2020, 10, 2736. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Vancov, T.; Si, H.; Yang, W.; Tong, K.; Chen, W.; Fang, Y. Isolation and characterization of endomycorrhizal fungi associated with growth promotion of blueberry plants. J. Fungi 2021, 7, 584. [Google Scholar] [CrossRef]
- Baba, T.; Nakaba, S.; Noma, S.; Funada, R.; Ban, T. Heterorhizy and fine root architecture of rabbiteye blueberry (Vaccinium virgatum) softwood-cuttings. J. Plant Res. 2018, 131, 271–284. [Google Scholar] [CrossRef]
- Caspersen, S.; Svensson, B.; Håkansson, T.; Winter, C.; Khalil, S.; Asp, H. Blueberry—Soil interactions from an organic perspective. Sci. Hortic. 2016, 208, 78–91. [Google Scholar] [CrossRef]
- Whiteside, M.D.; Treseder, K.K.; Atsatt, P.R. The brighter side of soils: Quantum dots track organic nitrogen through fungi and plants. Ecology 2009, 90, 100–108. [Google Scholar] [CrossRef]
- Smith, S.E.; Smith, F.A. Roles of arbuscular mycorrhizas in plant nutrition and growth: New paradigms from cellular to ecosystem scales. Annu. Rev. Plant Biol. 2011, 62, 227–250. [Google Scholar] [CrossRef]
- Smith, S.E.; Read, D.J. Mycorrhizal Symbiosis, 3rd ed.; Academic Press: London, UK, 2010. [Google Scholar]
- Widdig, M.; Schleuss, P.M.; Weig, A.R.; Guhr, A.; Biederman, L.A.; Borer, E.T.; Spohn, M. Nitrogen and phosphorus additions alter the abundance of phosphorus-solubilizing bacteria and phosphatase activity in grassland soils. Front. Environ. Sci. 2019, 7, 185. [Google Scholar] [CrossRef]
- Lu, C.; Sugihara, S.; Tanaka, H.; Tajima, R.; Matsumoto, S.; Ban, T. Phosphorus Dynamics in Japanese Blueberry Field: Long-Term Accumulation and Fractionation across Soil Types and Depths. Agronomy 2024, 14, 1947. [Google Scholar] [CrossRef]
- Lambers, H.; Raven, J.A.; Shaver, G.R.; Smith, S.E. Plant nutrient-acquisition strategies change with soil age. Trends Ecol. Evol. 2008, 23, 95–103. [Google Scholar] [CrossRef]
- Wang, R.; Liu, H.; Sardans, J.; Feng, X.; Xu, Z.; Peñuelas, J. Interacting effects of urea and water addition on soil mineral-bound phosphorus dynamics in semi-arid grasslands with different land-use history. Eur. J. Soil Sci. 2021, 72, 946–962. [Google Scholar] [CrossRef]
- Richardson, A.E.; Simpson, R.J. Soil microorganisms mediating phosphorus availability: Update on microbial phosphorus. Plant Physiol. 2011, 156, 989–996. [Google Scholar] [CrossRef] [PubMed]
- Grace, J.B.; Anderson, T.M.; Seabloom, E.W.; Borer, E.T.; Adler, P.B.; Harpole, W.S.; Smith, M.D. Integrative modelling reveals mechanisms linking productivity and plant species richness. Nature 2016, 529, 390–393. [Google Scholar] [CrossRef] [PubMed]
- Grace, J.B.; Anderson, T.M.; Olff, H.; Scheiner, S.M. On the specification of structural equation models for ecological systems. Ecol. Monogr. 2010, 80, 67–87. [Google Scholar] [CrossRef]
- Eisenhauer, N.; Bowker, M.A.; Grace, J.B.; Powell, J.R. From patterns to causal understanding: Structural equation modeling (SEM) in soil ecology. Pedobiologia 2015, 58, 65–72. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, J.; Shirkey, G.; John, R.; Wu, S.R.; Park, H.; Shao, C. Applications of structural equation modeling (SEM) in ecological studies: An updated review. Ecol. Process. 2016, 5, 19. [Google Scholar] [CrossRef]
- He, X.; Augusto, L.; Goll, D.S.; Ringeval, B.; Wang, Y.; Helfenstein, J.; Hou, E. Global patterns and drivers of soil total phosphorus concentration. Earth Syst. Sci. Data Discuss. 2021, 2021, 1–21. [Google Scholar] [CrossRef]
- Gaffert, P.; Meinfelder, F.; Bosch, V. Towards an MI-proper predictive mean matching. January 2016. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=5f13dd8d367c9b0ebc127c24487aa06773a2f00f (accessed on 7 January 2025).
- IUSS Working Group WRB. World Reference Base for Soil Resources 2022, 4th ed.; International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; International Union of Soil Sciences (IUSS): Vienna, Austria, 2022; Available online: https://wrb.isric.org/documents/ (accessed on 7 January 2025).
- Hedley, M.J.; Stewart, J.W.B.; Chauhan, B. Changes in inorganic and organic soil phosphorus fractions induced by cultivation practices and by laboratory incubations. Soil Sci. Soc. Am. J. 1982, 46, 970–976. [Google Scholar] [CrossRef]
- Tiessen, H.; Stewart, J.W.B. Characterization of available P by sequential extraction. In Soil Sampling and Methods of Analysis; Carter, M.R., Ed.; Canadian Society of Soil Science: Boca Raton, FL, USA, 1993; pp. 75–86. [Google Scholar]
- Cade-Menun, B.J.; O’Halloran, I.P. Total and organic phosphorus. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2007; pp. 265–292. [Google Scholar]
- Gaiji, S.; Chavan, V.; Ariño, A.H.; Otegui, J.; Hobern, D.; Sood, R.; Robles, E. Content assessment of the primary biodiversity data published through GBIF network: Status, challenges, and potentials. Biodivers. Inform. 2013, 8, 94–172. [Google Scholar]
- Zizka, A.; Silvestro, D.; Andermann, T.; Azevedo, J.; Duarte Ritter, C.; Edler, D.; Antonelli, A. CoordinateCleaner: Standardized cleaning of occurrence records from biological collection databases. Methods Ecol. Evol. 2019, 10, 744–751. [Google Scholar] [CrossRef]
- Poggio, L.; Simonetti, E.; Gimona, A. Enhancing the WorldClim data set for national and regional applications. Sci. Total Environ. 2018, 625, 1628–1643. [Google Scholar] [CrossRef]
- Ringle, C.M.; Wende, S.; Becker, J.M. SmartPLS 4; SmartPLS GmbH: Bönningstedt, Germany, 2024; Available online: https://www.smartpls.com (accessed on 7 January 2025).
- Jindo, K.; Audette, Y.; Olivares, F.L.; Canellas, L.P.; Smith, D.S.; Voroney, P.R. Biotic and abiotic effects of soil organic matter on the phytoavailable phosphorus in soils: A review. Chem. Biol. Technol. Agric. 2023, 10, 29. [Google Scholar] [CrossRef] [PubMed]
- Chapin, F.S.; Matson, P.A.; Mooney, H.A.; Vitousek, P.M. Principles of Terrestrial Ecosystem Ecology, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Japan Meteorological Agency. Historical Weather Data. Available online: https://www.data.jma.go.jp/stats/etrn/index.php (accessed on 7 January 2025).
- Emami-Karvani, Z.; Chitsaz-Esfahani, Z. Phosphorus solubilization: Mechanisms, recent advancement and future challenge. In Soil Microbiomes for Sustainable Agriculture: Functional Annotation; Springer: Cham, Switzerland, 2021; pp. 85–131. [Google Scholar]
- Hou, P.; Hu, C.; Yu, J.; Gao, Q.; Zhou, M.; Gao, L.; Tian, Z. Increasing topdressing ratio of nitrogen fertilizer improves grain yield and nitrogen use efficiency of winter wheat under winter and spring night-warming. J. Soil Sci. Plant Nutr. 2024, 24, 3459–3473. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Q.; Dai, H.; Feng, J.; Zeng, Q.; Sun, X.; Chen, Y. Nitrogen addition promotes the accumulation of soil particulate organic carbon in a subtropical forest. Forests 2024, 15, 619. [Google Scholar] [CrossRef]
- Ibrahim, M.; Iqbal, M.; Tang, Y.T.; Khan, S.; Guan, D.X.; Li, G. Phosphorus mobilization in plant–soil environments and inspired strategies for managing phosphorus: A review. Agronomy 2022, 12, 2539. [Google Scholar] [CrossRef]
- Gray, J.M.; Bishop, T.F.; Wilson, B.R. Factors controlling soil organic carbon stocks with depth in eastern Australia. Soil Sci. Soc. Am. J. 2015, 79, 1741–1751. [Google Scholar] [CrossRef]
- Gerke, J. The central role of soil organic matter in soil fertility and carbon storage. Soil Syst. 2022, 6, 33. [Google Scholar] [CrossRef]
- Crews, T.E.; Kitayama, K.; Fownes, J.H.; Riley, R.H.; Herbert, D.A.; Mueller-Dombois, D.; Vitousek, P.M. Changes in soil phosphorus fractions and ecosystem dynamics across a long chronosequence in Hawaii. Ecology 1995, 76, 1407–1424. [Google Scholar] [CrossRef]
- Zavišić, A.; Yang, N.; Marhan, S.; Kandeler, E.; Polle, A. Forest soil phosphorus resources and fertilization affect ectomycorrhizal community composition, beech P uptake efficiency, and photosynthesis. Front. Plant Sci. 2018, 9, 463. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Fan, H.; Yan, B.; Zhao, D.; Wei, X. Soil C, N, and P and C:N:P stoichiometry associated with environmental factors in two typical alpine grasslands in northern Tibet. J. Soils Sediments 2023, 23, 3735–3747. [Google Scholar] [CrossRef]
- Rasmussen, C.; Heckman, K.; Wieder, W.R.; Keiluweit, M.; Lawrence, C.R.; Berhe, A.A.; Wagai, R. Beyond clay: Towards an improved set of variables for predicting soil organic matter content. Biogeochemistry 2018, 137, 297–306. [Google Scholar] [CrossRef]
- Filippelli, G.M. The global phosphorus cycle: Past, present, and future. Elements 2008, 4, 89–95. [Google Scholar] [CrossRef]
- Penn, C.J.; Camberato, J.J. A critical review on soil chemical processes that control how soil pH affects phosphorus availability to plants. Agriculture 2019, 9, 120. [Google Scholar] [CrossRef]
- Maaroufi, N.I.; De Long, J.R. Global change impacts on forest soils: Linkage between soil biota and carbon-nitrogen-phosphorus stoichiometry. Front. For. Glob. Chang. 2020, 3, 16. [Google Scholar] [CrossRef]
- Ahmed, W.; Jing, H.; Kaillou, L.; Qaswar, M.; Khan, M.N.; Jin, C.; Zhang, H. Changes in phosphorus fractions associated with soil chemical properties under long-term organic and inorganic fertilization in paddy soils of southern China. PLoS ONE 2019, 14, e0216881. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, W.; Qaswar, M.; Jing, H.; Wenjun, D.; Geng, S.; Kailou, L.; Huimin, Z. Tillage practices improve rice yield and soil phosphorus fractions in two typical paddy soils. J. Soils Sediments 2020, 20, 850–861. [Google Scholar] [CrossRef]
- Cross, A.F.; Schlesinger, W.H. A literature review and evaluation of the Hedley fractionation: Applications to the biogeochemical cycle of soil phosphorus in natural ecosystems. Geoderma 1995, 64, 197–214. [Google Scholar] [CrossRef]
- Hinsinger, P. Bioavailability of soil inorganic P in the rhizosphere as affected by root-induced chemical changes: A review. Plant Soil 2001, 237, 173–195. [Google Scholar] [CrossRef]
- Kafle, A.; Cope, K.R.; Raths, R.; Yakha, J.K.; Subramanian, S.; Bücking, H.; Garcia, K. Harnessing soil microbes to improve plant phosphate efficiency in cropping systems. Agronomy 2019, 9, 127. [Google Scholar] [CrossRef]
- Ge, G.; Li, Z.; Fan, F.; Chu, G.; Hou, Z.; Liang, Y. Soil biological activity and their seasonal variations in response to long-term application of organic and inorganic fertilizers. Plant Soil 2010, 326, 31–44. [Google Scholar] [CrossRef]
- Pantigoso, H.A.; Manter, D.K.; Vivanco, J.M. Phosphorus addition shifts the microbial community in the rhizosphere of blueberry (Vaccinium corymbosum L.). Rhizosphere 2018, 7, 1–7. [Google Scholar] [CrossRef]
- Johnson, N.C.; Graham, J.H.; Smith, F.A. Functioning of mycorrhizal associations along the mutualism–parasitism continuum. New Phytol. 1997, 135, 575–585. [Google Scholar] [CrossRef]
- Vance, C.P. Symbiotic nitrogen fixation and phosphorus acquisition. Plant nutrition in a world of declining renewable resources. Plant Physiol. 2001, 127, 390–397. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.L.; Haygarth, P.M. Phosphorus solubilization in rewetted soils. Nature 2001, 411, 258. [Google Scholar] [CrossRef]
- Schröder, J.J.; Smit, A.L.; Cordell, D.; Rosemarin, A. Improved phosphorus use efficiency in agriculture: A key requirement for its sustainable use. Chemosphere 2011, 84, 822–831. [Google Scholar] [CrossRef] [PubMed]
- Blackwell, M.S.A.; Darch, T.; Haslam, R.P. Phosphorus use efficiency and fertilizers: Future opportunities for improvements. Front. Agric. Sci. Eng. 2019, 6, 332–340. [Google Scholar] [CrossRef]
- El Attar, I.; Hnini, M.; Taha, K.; Aurag, J. Phosphorus availability and its sustainable use. J. Soil Sci. Plant Nutr. 2022, 22, 5036–5048. [Google Scholar] [CrossRef]












| Soil Depth | Biomes | Number of Literature Data | Number of References | Publication Year Range |
|---|---|---|---|---|
| 0–30 cm | Desert | 17 | 4 | 2007–2020 |
| Forest | 280 | 93 | 1985–2021 | |
| Grassland | 169 | 38 | 1985–2021 | |
| Permanent | 16 | 5 | 1999–2011 | |
| Savan | 20 | 10 | 1992–2019 | |
| Shrubland | 37 | 16 | 1990–2020 | |
| Tundra | 18 | 4 | 2012–2017 | |
| Wetland | 33 | 8 | 2005–2018 | |
| Below 30 cm | Desert | 1 | 1 | 2020 |
| Forest | 51 | 18 | 1999–2021 | |
| Grassland | 20 | 9 | 1985–2020 | |
| Savan | 3 | 1 | 2011 | |
| Shrubland | 11 | 4 | 2004–2016 |
| Figure Caption | The Core Factor in P Fractions | SRMR | d_ULS | d_G | Chi-Square | NFI | Notes |
|---|---|---|---|---|---|---|---|
| Figure 5A | NaOH-Po | 0.07 | 0.53 | 0.18 | 485.03 | 0.93 | Global model for the upper 30 cm of soil |
| Figure 5B | NaHCO3-Po | 0.07 | 0.51 | 0.11 | 318.30 | 0.96 | Global model for the upper 30 cm of soil |
| Figure 6A | Resin-P | 0.08 | 0.57 | 0.35 | 151.53 | 0.86 | Global model for soil layers beneath 30 cm depth |
| Figure 6B | NaHCO3-Pi | 0.08 | 0.59 | 0.39 | 159.06 | 0.86 | Global model for soil layers beneath 30 cm depth |
| Figure 6C | NaOH-Po | 0.07 | 0.48 | 0.36 | 146.59 | 0.87 | Global model for soil layers beneath 30 cm depth |
| Figure 6D | HCl-Pi | 0.08 | 0.51 | 0.34 | 137.73 | 0.88 | Global model for soil layers beneath 30 cm depth |
| Figure 8A | NaHCO3-Po | 0.07 | 0.57 | 0.12 | 165.06 | 0.96 | Global model of forest soil within the upper 30 cm layer |
| Figure 8B | NaOH-Po | 0.07 | 0.50 | 0.21 | 258.60 | 0.93 | Global model of forest soil within the upper 30 cm layer |
| Figure 8C | NaHCO3-Po | 0.07 | 0.33 | 0.07 | 60.90 | 0.94 | Global model of grassland soil within the upper 30 cm layer |
| Figure 8D | NaOH-Po | 0.06 | 0.28 | 0.10 | 78.09 | 0.93 | Global model of grassland soil within the upper 30 cm layer |
| Figure 10A | Resin-P | 0.06 | 0.11 | 0.20 | 60.60 | 0.88 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10B | NaOH-Pi | 0.05 | 0.06 | 0.11 | 36.41 | 0.93 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10C | NaOH-Po | 0.06 | 0.09 | 0.15 | 48.10 | 0.92 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10D | NaHCO3-Pi | 0.06 | 0.09 | 0.17 | 53.88 | 0.90 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10E | NaHCO3-Po | 0.06 | 0.09 | 0.14 | 45.53 | 0.89 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10F | HCl-Pi | 0.04 | 0.05 | 0.11 | 38.22 | 0.91 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 10G | Residual-P | 0.06 | 0.09 | 0.17 | 53.02 | 0.87 | Model of Japan’s soil profile in the uppermost 30 cm |
| Figure 11A | Resin-P | 0.07 | 0.12 | 0.10 | 34.33 | 0.91 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11B | NaOH-Pi | 0.06 | 0.11 | 0.12 | 40.77 | 0.91 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11C | NaOH-Po | 0.07 | 0.14 | 0.15 | 49.11 | 0.91 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11D | NaHCO3-Pi | 0.06 | 0.11 | 0.10 | 33.05 | 0.93 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11E | NaHCO3-Po | 0.06 | 0.10 | 0.09 | 31.30 | 0.90 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11F | HCl-Pi | 0.06 | 0.12 | 0.15 | 49.48 | 0.88 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 11G | Residual-P | 0.06 | 0.10 | 0.09 | 32.38 | 0.92 | Model of Japan’s soil profile at depths of 30–60 cm |
| Figure 13A | NaHCO3-Po | 0.08 | 0.62 | 0.19 | 88.24 | 0.93 | Global model of symbiotic microbial activity within the upper 30 cm of soil |
| Figure 13B | NaHCO3-Po | 0.06 | 0.35 | 0.14 | 137.84 | 0.94 | Global model of inactive symbiotic microbes within the upper 30 cm of soil |
| Figure 13C | NaOH-Po | 0.06 | 0.34 | 0.21 | 178.55 | 0.92 | Global model of inactive symbiotic microbes within the upper 30 cm of soil |
| Figure Caption | The Core Factor in P Fractions (Key Variables) | Path Relationships | Significance (p-Value) | Key Findings |
|---|---|---|---|---|
| Figure 5A | NaOH-Po (pH, NLP, Silt, LP) | pH positively affects NLP; silt positively affects NaOH-Po; NLP positively affects LP. | pH→NLP (p < 0.01). Silt→NaOH-Po (p < 0.01). NLP→LP (p < 0.01). | pH and silt content regulate phosphorus availability and retention in upper soils. Acidic conditions promote the release of phosphorus from these non-labile pools. |
| Figure 5B | NaHCO3-Po (pH, NLP, Silt, LP) | pH positively regulates NLP; silt positively affects NaHCO3-Po; NLP positively affects LP. | pH→NLP (p < 0.01). Silt→NaHCO3-Po (p < 0.05). NLP→LP (p < 0.05). | Higher pH enhances NLP. Precipitation reduces phosphorus accumulation. |
| Figure 6A | Resin-P (pH, NLP, LP, SOC, N Accumulation) | pH positively regulates NLP and Resin-P; Resin-P positively affects NLP, LP, SOC, and N accumulation; NLP positively affects LP. | pH→NLP (p < 0.01). pH→ Resin-P (p < 0.05). Resin-P→NLP (p < 0.01). Resin-P→LP (p < 0.01). Resin-P→SCO and N Accumulation (p < 0.01). | SOC and N accumulation are consistently positively and significantly correlated. Weak silt influences deeper soils. |
| Figure 6B | NaHCO3-Pi (pH, NLP, LP, Precipitation) | pH positively regulates NLP; NaHCO3-Pi positively affects NLP and LP; precipitation positively affects NLP. | pH→NLP (p < 0.01). NaHCO3-Pi→NLP (p < 0.01). NaHCO3-Pi→LP (p < 0.01). Precipitation→NLP (p < 0.05). | Precipitation drives NLP accumulation in deeper soil layers. |
| Figure 6C | NaOH-Po (pH, NLP, Precipitation, Temperature) | pH positively regulates NLP, while its effect on NaOH-Po is negative; NaOH-Po positively affects NLP; precipitation positively affects NLP, while temperature negatively affects NLP. | pH→NLP (p < 0.01). pH←NaOH-Po (p < 0.05). NaOH-Po→NLP (p < 0.01). Precipitation→NLP (p < 0.05). Temperature←NLP (p < 0.01). | Precipitation drives NLP accumulation, whereas temperature reduces NLP accumulation in deeper soil layers. |
| Figure 6D | HCl-Pi (pH, NLP, LP) | pH negatively regulates NLP, while its effect on HCl-Pi is positive; HCl-Pi positively affects NLP; NLP positively affects LP. | pH←NLP (p < 0.05). pH→HCl-Pi (p < 0.01). HCl-Pi→NLP (p < 0.01). NLP→LP (p < 0.01). | In the SEM model depicting the dynamics of HCl-Pi in deeper soil layers, the regulation of LP by NLP is the most significant. |
| Figure 8A | NaHCO3-Po (pH, NLP, LP, P and N Accumulation, SOC) | pH positively regulates NLP, while its effect on NaHCO3-Po is negative; NaHCO3-Po positively affects NLP and LP; NLP and LP positively affects P and N accumulation; N accumulation positively affects SOC. | pH→NLP (p < 0.01). pH←NaHCO3-Po (p < 0.01). NaHCO3-Po→NLP and LP (p < 0.01). NLP and LP→P and N Accumulation (p < 0.01). N Accumulation→SOC (p < 0.01). | Depth reduces phosphorus availability in forest soils. SOC played a central role in N accumulation but did not directly influence P accumulation in forest ecosystems. |
| Figure 8B | NaOH-Po (pH, NLP, LP, P and N Accumulation, SOC) | pH positively regulates NLP, while its effect on NaOH-Po is negative; NaOH-Po positively affects NLP; NLP and LP positively affect P and N accumulation; N accumulation positively affects SOC; NLP positively affects LP. | pH→NLP (p < 0.01). pH←NaOH-Po (p < 0.01). NaOH-Po→NLP (p < 0.01). NLP and LP→P and N Accumulation (p < 0.01). N Accumulation→SOC (p < 0.01). NLP→LP (p < 0.05). | Climatic factors influence N and P accumulation in forest soils. |
| Figure 8C | NaHCO3-Po (pH, NLP, LP, N Accumulation) | pH positively regulates NLP, while its effect on NaHCO3-Po is negative; NaHCO3-Po positively affects NLP, LP, and N accumulation; NLP positively affects LP. | pH→NLP (p < 0.01). pH←NaHCO3-Po (p < 0.01). NaHCO3-Po→NLP, LP and N Accumulation (p < 0.01). NLP→LP (p < 0.01). | Unlike forest soil, temperature and precipitation had weaker and non-significant effects on NLP, LP, and N accumulation in grasslands soil. |
| Figure 8D | NaOH-Po (pH, NLP, LP, N Accumulation) | pH positively regulates NLP, while its effect on NaOH-Po and LP is negative; NaOH-Po positively affects NLP and N accumulation; LP positively affects N accumulation; NLP positively affects LP. | pH→NLP (p < 0.01). pH←NaOH-Po and LP (p < 0.05). NaOH-Po→NLP and N Accumulation (p < 0.01). LP→N Accumulation (p < 0.01). NLP→LP (p < 0.01). | Grassland nutrient dynamics differ from forest biomes. LP exhibited a strong positive impact on N accumulation in the NaOH-Po model. |
| Figure 10A | Resin-P (pH, EC, NLP, N Accumulation, LP) | pH and EC positively regulate NLP, while their effect on Resin-P is negative; Resin-P negatively regulates N accumulation, while its effect on LP is positive. | pH and EC→NLP (p < 0.01). pH and EC←Resin-P (p < 0.01). Resin-P←N Accumulation (p < 0.01). Resin-P→LP (p < 0.01). | Resin-P is suppressed by both pH and EC in upper Japanese soils. |
| Figure 10B | NaOH-Pi (pH, EC, NLP, LP, P and N Accumulation) | pH and EC positively regulate NLP and NaOH-Pi, while pH negatively regulates LP; NaOH-Pi positively affects NLP, LP, P, and N accumulation; NLP negatively affects LP. | pH and EC→NLP and NaOH-Pi (p < 0.01). pH←LP (p < 0.01). NaOH-Pi→ NLP, LP, P and N Accumulation (p < 0.01). NLP←LP (p < 0.01). | pH enhances stable phosphorus forms. |
| Figure 10C | NaOH-Po (pH, LP, NLP, EC, P and N Accumulation) | pH negatively regulates LP and NLP, EC negatively regulates P accumulation, while pH and EC positively regulate NaOH-Po; NaOH-Po positively affects NLP and N accumulation, while its effect on LP is negative; NLP positively affects LP. | pH←LP (p < 0.05). pH←NLP (p < 0.01). EC←P Accumulation (p < 0.01). pH and EC→NaOH-Po (p < 0.01). NaOH-Po→NLP and N Accumulation (p < 0.01). NaOH-Po←LP (p < 0.01). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of NaOH-Po in the 0–30 cm layer of Japanese blueberry soils, the regulation of LP by NLP exhibits the most significant effect. |
| Figure 10D | NaHCO3-Pi (pH, EC, NLP, LP, N Accumulation) | pH and EC positively regulate NLP, while their effect on NaHCO3-Pi is negative; pH negatively affects LP; NaHCO3-Pi positively affects NLP and N accumulation. | pH and EC→NLP (p < 0.01). pH and EC←NaHCO3-Pi (p < 0.01). pH←LP (p < 0.01). NaHCO3-Pi→LP and N Accumulation (p < 0.01). | Higher pH and EC reduce phosphorus mobility and enhance their stabilization in upper soil layers. |
| Figure 10E | NaHCO3-Po (pH, EC, NLP, LP, P Accumulation) | pH and EC positively regulate NLP and NaHCO3-Po, while their effect on LP is negative; NaHCO3-Po positively affects NLP and LP, while its effect on P accumulation is negative. | pH and EC→NLP and NaHCO3-Po (p < 0.01). pH and EC←LP (p < 0.01). NaHCO3-Po→NLP and LP (p < 0.01). NaHCO3-Po←P Accumulation (p < 0.01). | Higher pH and EC reduce phosphorus mobility and enhance their stabilization in upper soil layers. |
| Figure 10F | HCl-Pi (pH, EC, NLP, LP, P and N Accumulation) | pH and EC positively regulate NLP and HCl-Pi, while their effect on LP is negative; HCl-Pi positively affects NLP, while its effect on P and N accumulation is negative. | pH and EC→NLP and HCl-Pi (p < 0.01). pH and EC←LP (p < 0.01). HCl-Pi→NLP (p < 0.01). HCl-Pi←P and N Accumulation (p < 0.01). | HCl-Pi in the upper soil layers reduces both P accumulation and N accumulation. |
| Figure 10G | Residual-P (pH, EC, NLP, LP, N Accumulation) | pH and EC positively regulate NLP, while their effect on LP is negative; pH negatively affects Residual-P; EC positively affects Residual-P; Residual-P positively affects NLP, while its effect on N accumulation is negative. | pH and EC→NLP (p < 0.01). pH and EC←LP (p < 0.01). pH←Residual-P (p < 0.05). EC→Residual-P (p < 0.05). Residual-P→NLP (p < 0.01). Residual-P←N Accumulation (p < 0.01). | In the upper soil layers, pH inhibits Residual-P, while EC promotes its accumulation. |
| Figure 11A | Resin-P (pH, EC, NLP, LP) | pH and EC positively regulate NLP, while their effect on Resin-P is negative; EC negatively affects LP; Resin-P positively affects LP; NLP positively affects LP. | pH and EC→NLP (p < 0.01). pH and EC←Resin-P (p < 0.01). EC←LP (p < 0.05). Resin-P→LP (p < 0.01). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of Resin-P in the 30–60 cm soil layer of Japanese blueberry fields, the regulation of LP by NLP shows a statistically significant effect. |
| Figure 11B | NaOH-Pi (pH, EC, NLP, LP, P Accumulation) | pH and EC positively regulate NLP, while their effect on LP is negative; EC positively regulates NaOH-Pi; NaOH-Pi positively affects NLP, LP, and P accumulation. | pH and EC→NLP (p < 0.01). pH and EC←LP (p < 0.01). EC→NaOH-Pi (p < 0.01). NaOH-Pi→NLP, LP and P Accumulation (p < 0.01). | EC promotes the stabilization of phosphorus in deeper soil layers of Japanese blueberry fields. |
| Figure 11C | NaOH-Po (pH, EC, NLP, N Accumulation, LP) | pH and EC positively regulate NaOH-Po; EC negatively affects LP; pH negatively affects NLP; NaOH-Po positively regulates NLP and N accumulation, while its effect on LP is negative; NLP positively affects LP. | pH and EC→NaOH-Po (p < 0.01). EC←LP (p < 0.01). pH←NLP (p < 0.01). NaOH-Po→NLP (p < 0.01). NaOH-Po→N Accumulation (p < 0.05). NaOH-Po←LP (p < 0.01). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of NaOH-Po in the 30–60 cm layer of Japanese blueberry soils, the regulation of LP by NLP exhibits the most significant effect. |
| Figure 11D | NaHCO3-Pi (pH, EC, NLP, LP) | pH and EC positively regulate NLP, while their effect on NaHCO3-Pi is negative; NaHCO3-Pi positively affects LP and NLP. | pH and EC→NLP (p < 0.01). pH and EC←NaHCO3-Pi (p < 0.01). NaHCO3-Pi→LP and NLP (p < 0.01). | Inorganic phosphorus, such as NaHCO3-Pi, NaOH-Pi and HCl-Pi play a critical role in supporting P cycling through its influence on LP and NLP. |
| Figure 11E | NaHCO3-Po (pH, EC, LP, NLP, N Accumulation) | pH and EC positively regulate NaHCO3-Po, while their effect on LP is negative; EC positively regulates NLP; NaHCO3-Po positively regulates NLP, while its effect on N accumulation is negative; NLP positively affects LP. | pH and EC→NaHCO3-Po (p < 0.01). pH and EC←LP (p < 0.01). EC→NLP (p < 0.01). NaHCO3-Po→NLP (p < 0.01). NaHCO3-Po←N Accumulation (p < 0.05). NLP→LP (p < 0.05). | In the SEM model describing the dynamics of NaHCO3-Po in the 30–60 cm soil layer of Japanese blueberry fields, the regulation of LP by NLP shows a statistically significant effect. |
| Figure 11F | HCl-Pi (pH, EC, LP, NLP, N Accumulation) | pH and EC positively regulate HCl-Pi, while their effect on LP is negative; EC positively regulates NLP; HCl-Pi positively regulates NLP and LP, while its effect on N accumulation is negative; NLP negatively affects LP. | pH and EC→HCl-Pi (p < 0.01). pH and EC←LP (p < 0.01). EC→NLP (p < 0.01). HCl-Pi→NLP and LP (p < 0.01). HCl-Pi←N Accumulation (p < 0.01). NLP←LP (p < 0.01). | In the SEM model describing the dynamics of HCl-Pi in the 30–60 cm layer of Japanese blueberry soils, NLP exhibits a significant negative effect on LP. |
| Figure 11G | Residual-P (pH, EC, LP, NLP, P Accumulation) | pH and EC negatively regulate LP, while pH positively affects NLP; pH negatively affects Residual-P, while EC positively affects Residual-P; Residual-P positively affects NLP, while its effect on P accumulation is negative; NLP positively affects LP. | pH and EC←LP (p < 0.01). pH→NLP (p < 0.01). pH←Residual-P (p < 0.01). EC→Residual-P (p < 0.01). Residual-P→NLP (p < 0.01). Residual-P←P Accumulation (p < 0.05). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of Residual-P in the 30–60 cm soil layer of Japanese blueberry fields, the regulation of LP by NLP shows a statistically significant effect. |
| Figure 13A | NaHCO3-Po (pH, Depth, NLP, LP, P and N Accumulation, Temperature) | pH and depth negatively regulate NaHCO3-Po, while NaHCO3-Po positively affects NLP and LP; NLP and LP positively affect P and N accumulation; temperature positively affects N accumulation; NLP positively affects LP. | pH←NaHCO3-Po (p < 0.05). Depth←NaHCO3-Po (p < 0.01). NaHCO3-Po→NLP and LP (p < 0.01). NLP and LP→P and N Accumulation (p < 0.01). Temperature→N Accumulation (p < 0.01). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of NaHCO3-Po in the symbiotic microbial activity layer, the regulation of LP by NLP demonstrates a statistically significant effect, and temperature exerts a positive influence on N accumulation. |
| Figure 13B | NaHCO3-Po (pH, Depth, Silt, NLP, LP, P and N Accumulation) | pH and depth negatively regulate NaHCO3-Po, while silt positively regulates NaHCO3-Po; pH positively affects NLP; NaHCO3-Po positively affects NLP and LP; LP positively affects P and N accumulation; NLP positively affects P accumulation; NLP positively affects LP. | pH and depth←NaHCO3-Po (p < 0.01). Silt→NaHCO3-Po (p < 0.05). pH→NLP (p < 0.05). NaHCO3-Po→NLP and LP (p < 0.01). LP→P and N Accumulation (p < 0.01). NLP→P Accumulation (p < 0.01). NLP→LP (p < 0.05). | In the SEM model describing the dynamics of NaHCO3-Po in the inactive symbiotic microbial layer, the regulation of LP by NLP demonstrates a statistically significant effect. |
| Figure 13C | NaOH-Po (pH, LP, NLP, P and N Accumulation) | pH negatively regulates NaOH-Po and LP, while its effect on NLP is positive; NaOH-Po positively affects NLP; LP positively affects P and N accumulation; NLP positively affects P accumulation; NLP positively affects LP. | pH←NaOH-Po and LP (p < 0.05). pH→NLP (p < 0.01). NaOH-Po→NLP (p < 0.01). LP→P and N Accumulation (p < 0.01). NLP→P Accumulation (p < 0.01). NLP→LP (p < 0.01). | In the SEM model describing the dynamics of NaOH-Po in the inactive symbiotic microbial layers, the regulation of LP by NLP is more pronounced compared to that in the dynamics of NaHCO3-Po. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Sugihara, S.; Noma, S.; Tanaka, H.; Tajima, R.; Matsumoto, S.; Hirose, D.; Zhang, X.; Wang, N.; Ban, T. Phosphorus Dynamics in Managed and Natural Soils: SEM-PLS Analysis of Vaccinium, Forest, and Grassland Ecosystems. Plants 2025, 14, 189. https://doi.org/10.3390/plants14020189
Lu C, Sugihara S, Noma S, Tanaka H, Tajima R, Matsumoto S, Hirose D, Zhang X, Wang N, Ban T. Phosphorus Dynamics in Managed and Natural Soils: SEM-PLS Analysis of Vaccinium, Forest, and Grassland Ecosystems. Plants. 2025; 14(2):189. https://doi.org/10.3390/plants14020189
Chicago/Turabian StyleLu, Chun, Soh Sugihara, Satoshi Noma, Haruo Tanaka, Ryosuke Tajima, Shingo Matsumoto, Dai Hirose, Xueyan Zhang, Ning Wang, and Takuya Ban. 2025. "Phosphorus Dynamics in Managed and Natural Soils: SEM-PLS Analysis of Vaccinium, Forest, and Grassland Ecosystems" Plants 14, no. 2: 189. https://doi.org/10.3390/plants14020189
APA StyleLu, C., Sugihara, S., Noma, S., Tanaka, H., Tajima, R., Matsumoto, S., Hirose, D., Zhang, X., Wang, N., & Ban, T. (2025). Phosphorus Dynamics in Managed and Natural Soils: SEM-PLS Analysis of Vaccinium, Forest, and Grassland Ecosystems. Plants, 14(2), 189. https://doi.org/10.3390/plants14020189






