Canopy-Mediated Shifts in Grassland Diversity and Heterogeneity: A Power Law Approach from China’s Loess Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Site
2.2. Experimental Methods
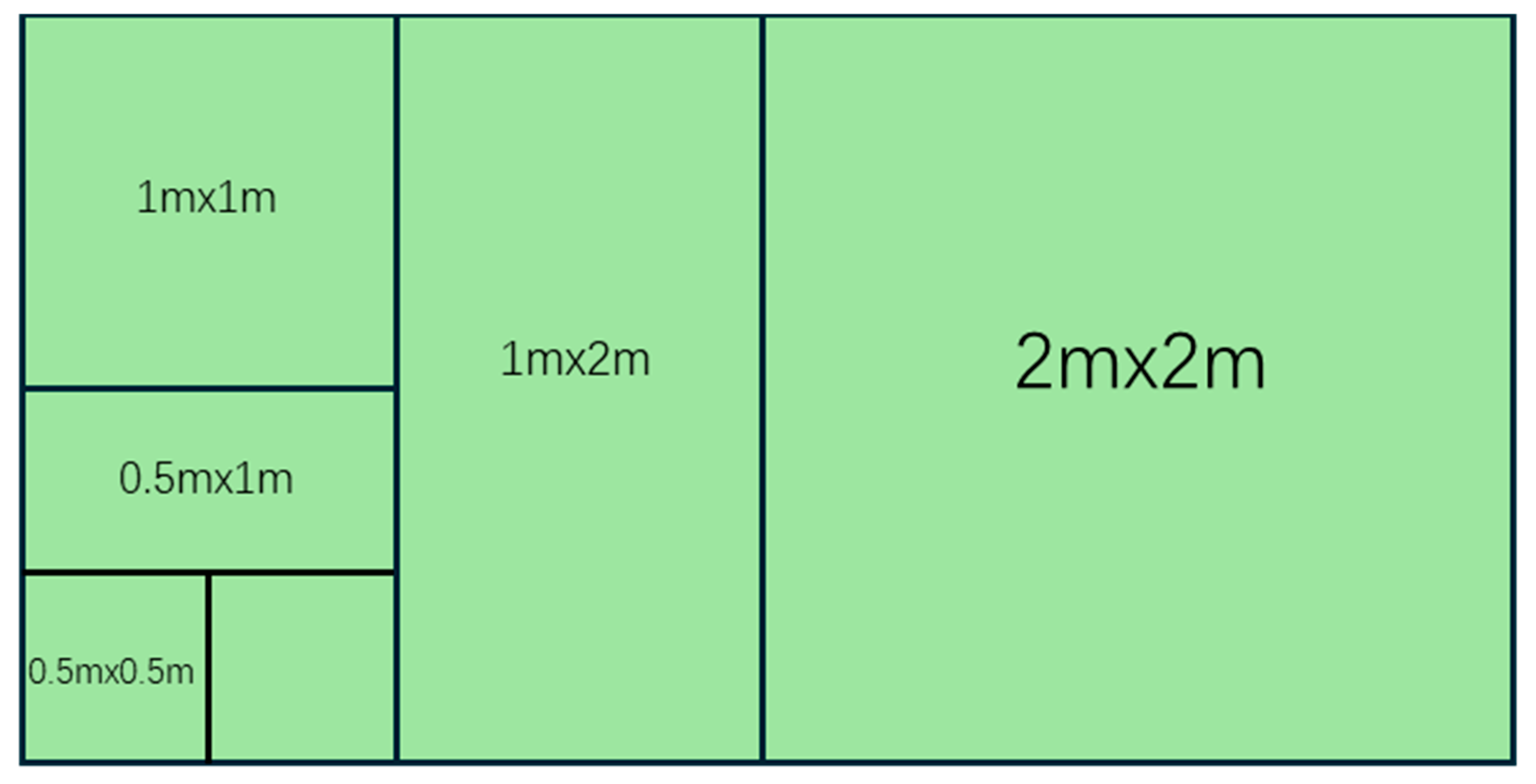
2.2.1. Species–Area Relationship Analysis
2.2.2. Taylor’s Power Law Model Principle
2.3. Statistical Analysis
3. Results
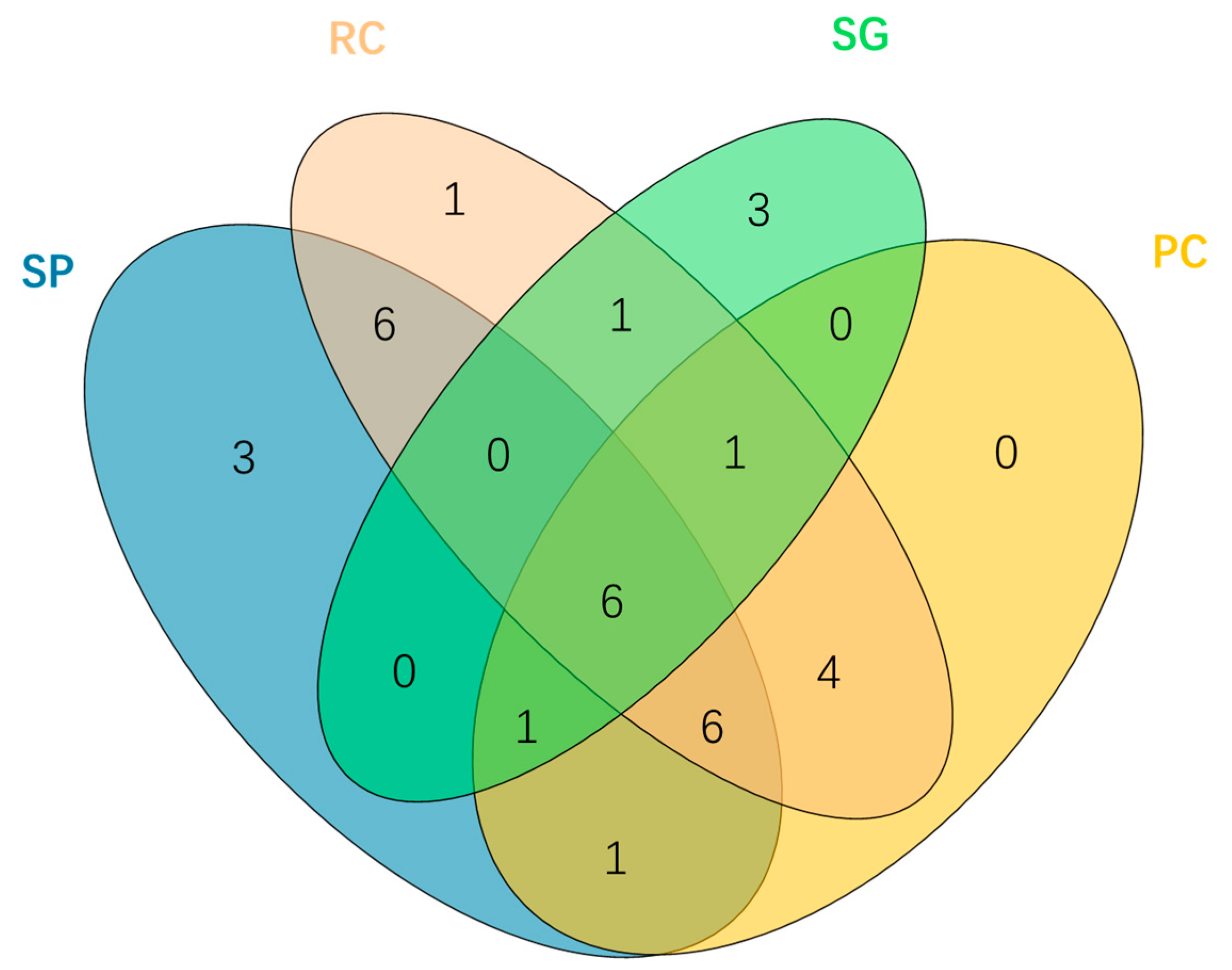
3.1. Species Composition and Distribution Patterns Across Vegetation Types
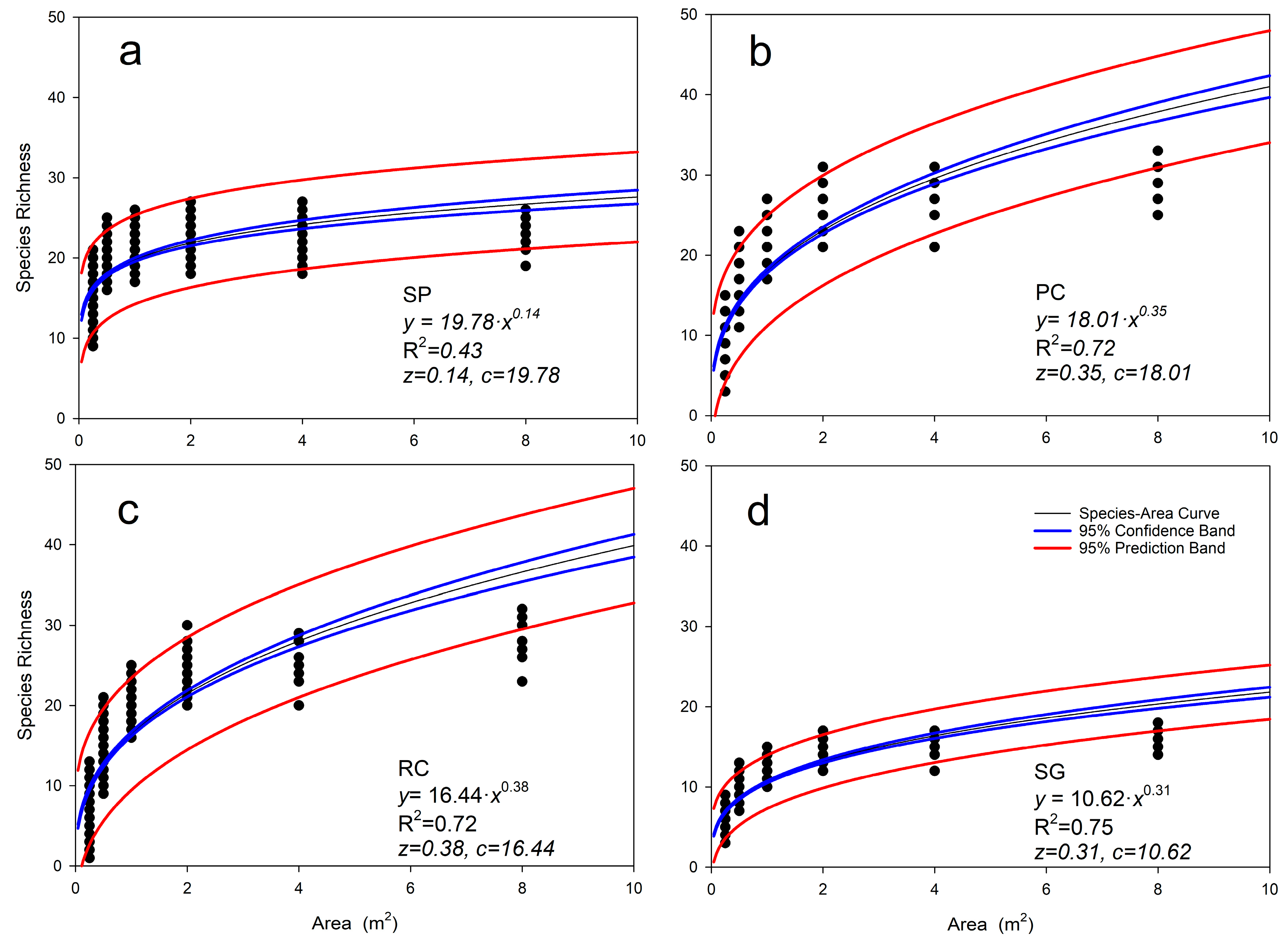
3.2. Species–Area Relationships of Herbaceous Layer
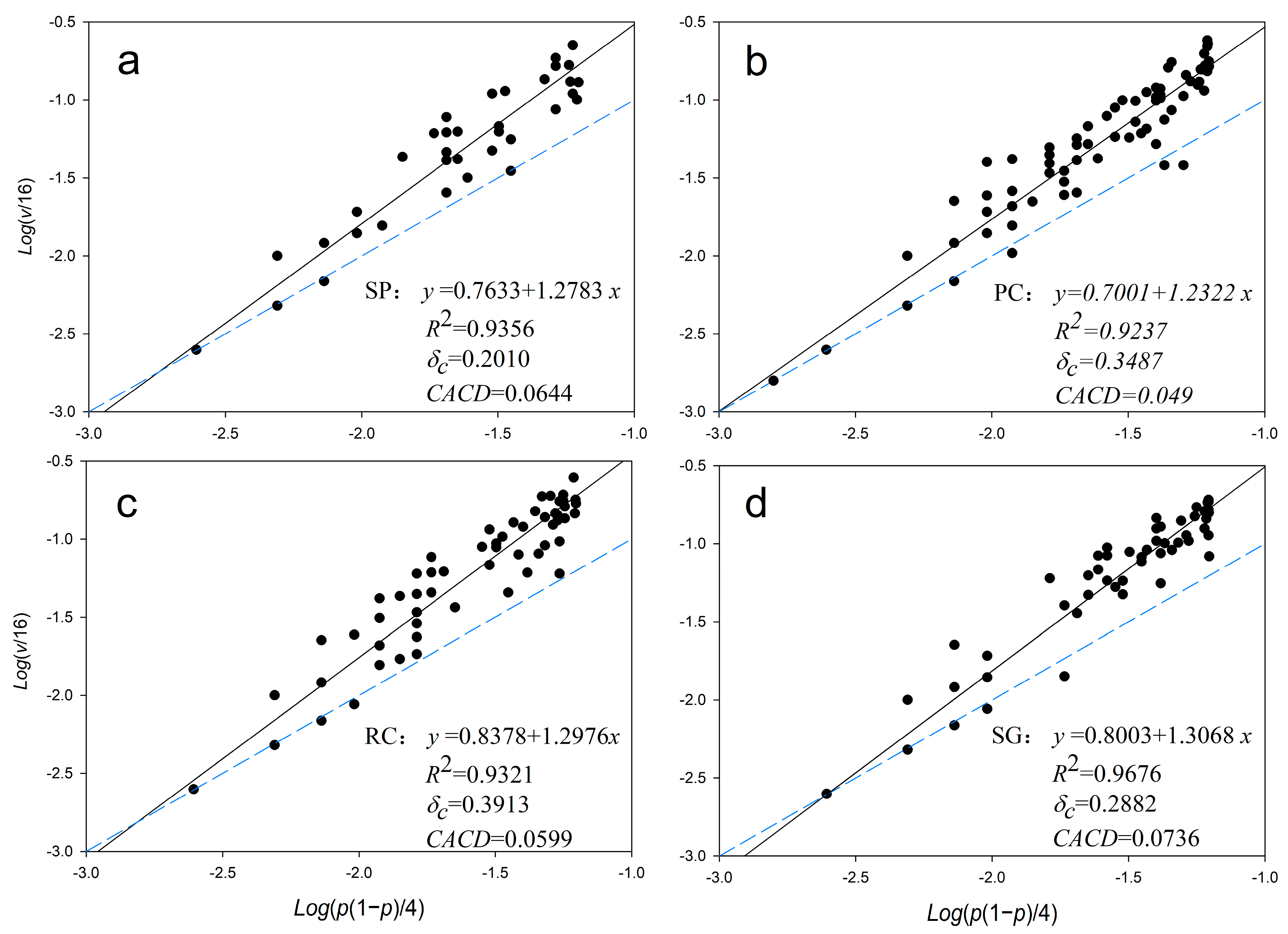
3.3. Community Spatial Heterogeneity Parameters
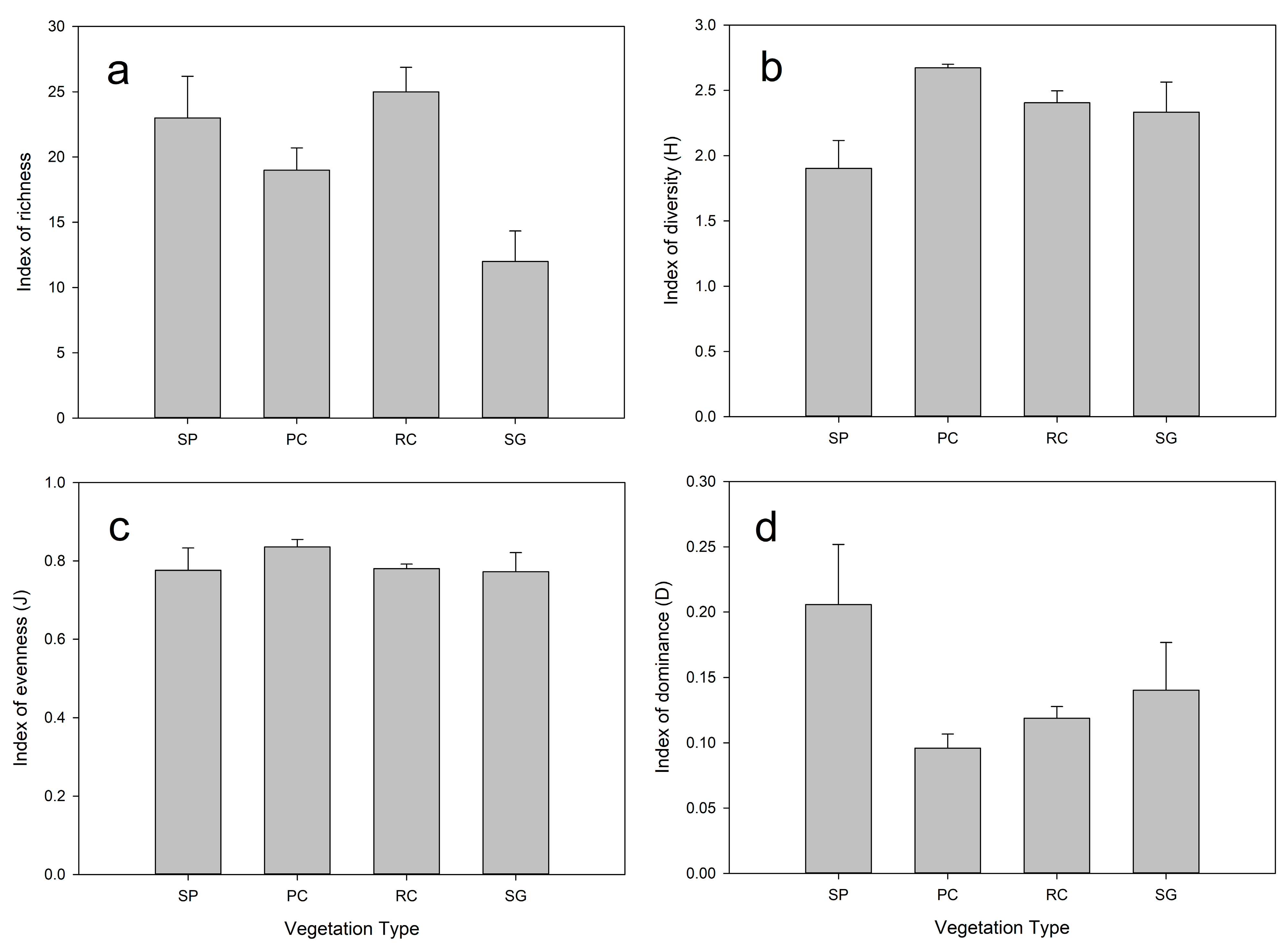
3.4. Community Spatial Diversity Parameters
4. Discussion
4.1. Synthesis of Key Innovations: The Integration of the Minimum Area Quantification and the Power Law Model Unravel Vegetation Dynamics
4.2. Ecological Implications in Theoretical Context: Convergence and Divergence with Existing Paradigms
4.3. Practical Implications: Optimizing Canopy Structures for Sustainability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SP | Small-leaf poplar forest |
| PC | Pine–caragana mixed forest |
| RC | Row-seeded caragana shrubland |
| SG | Linear dichroism saline grassland |
| SAR | Species–area relationship |
| CACD | Community aggregation critical diversity |
Appendix A
| Species Name | Functional Group | Life Form | Aboveground Biomass (g/m2) | |||
|---|---|---|---|---|---|---|
| SP | PC | RC | SG | |||
| Agropyron cristatum (L.) Gaertn. | Grass | Perennial herb | - | 35 ± 5.45 | 23 ± 3.65 | 8.8 ± 1.29 |
| Allium chrysanthum Regel | Forb | Perennial herb | - | 10 ± 1.7 | 10 ± 1.81 | - |
| Artemisia brachyloba Franch. | Forb | Perennial herb | 42 ± 2.8 | - | 15 ± 2.33 | - |
| Artemisia frigida Willd. | Forb | Perennial herb | 15 ± 1.98 | 20 ± 3.2 | 28 ± 4.4 | - |
| Aster altaicus Willd. | Forb | Annual herb | - | 25 ± 3.95 | 12 ± 1.95 | - |
| Astragalus melilotoides Pall. | Legume | Perennial herb | - | 28 ± 4.4 | 18 ± 3.13 | - |
| Carex duriuscula subsp. rigescens (Franch) S.Y.Liang et Y.C.Tang | Forb | Perennial herb | 65 ± 3.5 | 40 ± 6.2 | 35 ± 5.45 | 12 ± 2 |
| Cleistogenes squarrosa (Trin.) Keng | Grass | Perennial herb | 39 ± 3.6 | 46 ± 7.1 | 50 ± 8.2 | - |
| Cynanchum thesioides (Freyn) K. Schum | Forb | Perennial herb | 11 ± 1.58 | - | 15 ± 2.45 | - |
| Festuca ovina L. | Grass | Perennial herb | 51 ± 2.6 | 60 ± 7.6 | 55 ± 8.45 | 9.8 ± 1.55 |
| Gentiana scabra Bunge | Forb | Perennial herb | 11 ± 1.99 | - | 18 ± 2.9 | - |
| Hippophae rhamnoides L. | Shrub | Shrub | 46 ± 2.6 | - | - | - |
| Inula japonica Thunb. | Forb | Perennial herb | 20 ± 2.5 | 40 ± 5.12 | 50 ± 7.7 | 8.2 ± 1.7 |
| Ixeridium sonchifolium (Maxim.) Shih | Forb | Annual herb | - | - | 12 ± 2.16 | 20 ± 3.2 |
| Lespedeza bicolor Turcz. | Legume | Shrub | 12 ± 1.95 | 36 ± 5.6 | 40 ± 6.2 | - |
| Leymus chinensis (Trin. ex Bunge) Tzvelev | Grass | Perennial herb | 45 ± 3.5 | 52 ± 8 | 65 ± 9.95 | 13 ± 2.15 |
| Leymus secalinus (Georgi) Tzvelev | Grass | Perennial herb | 40 ± 4 | 42 ± 6.5 | 20 ± 3.2 | 10 ± 1.59 |
| Medicago ruthenica (L.) Trautv. | Legume | Perennial herb | 30.5 ± 3.1 | 42 ± 5.9 | - | - |
| Medicago sativa L. | Legume | Perennial herb | 38 ± 3.3 | 12 ± 2 | 15 ± 2.79 | - |
| Oxytropis caerulea (Pallas) Candolle | Legume | Perennial herb | 8.6 ± 1.47 | - | - | - |
| Parthenocissus chinensis C. L. Li | Forb | Annual herb | 12 ± 2.6 | - | 8 ± 1.4 | - |
| Potentilla acaulis L. | Forb | Perennial herb | - | - | 13 ± 2.15 | - |
| Potentilla supina L. | Forb | Perennial herb | - | - | - | 16 ± 2.6 |
| Puccinellia distans (Jacq.) Parl. | Grass | Perennial herb | - | - | - | 25 ± 3.95 |
| Salsola collina Pall. | Forb | Annual herb | 18 ± 2.5 | 8 ± 1.4 | - | 17 ± 2.75 |
| Setaria viridis (L.) P. Beauv. | Grass | Annual herb | 21 ± 4 | - | 25 ± 3.95 | - |
| Sibbaldianthe bifurca (L.) Kurtto & T. Erikss. | Forb | Perennial herb | 5 ± 1.21 | 8 ± 1.35 | 8 ± 1.2 | - |
| Stipa capillata L. | Grass | Perennial herb | 42 ± 3.9 | 60 ± 9.2 | 62 ± 9.5 | - |
| Teloxys aristata (L.) Moq. | Forb | Annual herb | 19 ± 2.8 | 15 ± 2.45 | 10 ± 1.53 | 15 ± 2.45 |
| Tephroseris kirilowii (Turcz. ex DC.) Holub | Forb | Perennial herb | 15 ± 2.71 | - | - | - |
| Thymus mongolicus (Ronniger) Ronniger | Shrub | Shrub | - | 23.5 ± 3.725 | 80.1 ± 12.215 | - |
| Viola yedoensis Makino | Forb | Perennial herb | 10 ± 1.26 | - | 8 ± 1.3 | - |
| Unverified forb | Forb | Herb | - | - | - | 10 ± 1.55 |
References
- Dietrich, P.; Ebeling, A.; Meyer, S.T.; Asato, A.E.B.; Bröcher, M.; Gleixner, G.; Huang, Y.; Roscher, C.; Schmid, B.; Eisenhauer, N. Plant diversity and community age stabilize ecosystem multifunctionality. Glob. Change Biol. 2024, 30, e17225. [Google Scholar] [CrossRef]
- Hautier, Y.; Tilman, D.; Isbell, F.; Seabloom, E.W.; Borer, E.T.; Reich, P.B. Anthropogenic environmental changes affect ecosystem stability via biodiversity. Science 2015, 348, 336–340. [Google Scholar] [CrossRef]
- Eisenhauer, N.; Hines, J.; Isbell, F.; Van Der Plas, F.; Hobbie, S.E.; Kazanski, C.E.; Lehmann, A.; Liu, M.; Lochner, A.; Rillig, M.C.; et al. Plant diversity maintains multiple soil functions in future environments. eLife 2018, 7, e41228. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Fang, S.; Fang, X.; Jin, Y.; Kuang, Y.; Lin, F.; Liu, J.; Ma, J.; Nie, Y.; Ouyang, S.; et al. Forest understory vegetation study: Current status and future trends. For. Res. 2023, 3, 6. [Google Scholar] [CrossRef]
- Salemaa, M.; Hotanen, J.P.; Oksanen, J.; Tonteri, T.; Merilä, P. Broadleaved trees enhance biodiversity of the understorey vegetation in boreal forests. For. Ecol. Manag. 2023, 546, 121357. [Google Scholar] [CrossRef]
- Bump, J.K.; Webster, C.R.; Vucetich, J.A.; Peterson, R.O.; Shields, J.M.; Powers, M. DUngulate carcasses perforate ecological filters and create biogeochemical hotspots in forest herbaceous layers allowing trees a competitive advantage. Ecosystems 2009, 12, 996–1007. [Google Scholar] [CrossRef]
- Deng, T.; Du, Q.; Zhu, Y.; Queenborough, S.A. Environmental drivers of herbaceous plant diversity in the understory community of a warm-temperate forest. Plant Divers. 2025, 47, 282–290. [Google Scholar] [CrossRef]
- Wrońska-Pilarek, D.; Rymszewicz, S.; Jagodziński, A.M.; Gawryś, R.; Dyderski, M.K. Temperate forest understory vegetation shifts after 40 years of conservation. Sci. Total Environ. 2023, 895, 165164. [Google Scholar] [CrossRef]
- Santi, I.; Carrari, E.; De Frenne, P.; Valerio, M.; Gasperini, C.; Cabrucci, M.; Selvi, F. Impact of coppicing on microclimate and understory vegetation diversity in an ancient Mediterranean oak forest. Sci. Total Environ. 2024, 918, 170531. [Google Scholar] [CrossRef] [PubMed]
- Kartalaei, Z.M.; Kooch, Y.; Tilaki, G.A.D. Litter and soil properties under woody and non-woody vegetation types: Implication for ecosystem management in a mountainous semi-arid landscape. J. Environ. Manag. 2023, 348, 119238. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Q.; Luo, Y.; Liu, S.; Zhang, Y.; Li, X.; Hou, G.; Chen, G.; Zhao, K.; Fan, C.; Li, X. Forest gaps alter the soil bacterial community of weeping cypress plantations by modulating the understory plant diversity. Front. Plant Sci. 2022, 13, 920905. [Google Scholar] [CrossRef]
- Anderson, M.J.; Walsh, D.C.; Sweatman, W.L.; Punnett, A.J. Non-linear models of species’ responses to environmental and spatial gradients. Ecol. Lett. 2022, 25, 2739–2752. [Google Scholar] [CrossRef]
- Chen, J.; Shiyomi, M. Spatial pattern model of herbaceous plant mass at species level. Ecol. Inform. 2014, 24, 124–131. [Google Scholar] [CrossRef]
- Chen, J.; Shiyomi, M. A power law model for analyzing spatial patterns of vegetation abundance in terms of cover, biomass, density, and occurrence: Derivation of a common rule. J. Plant Res. 2019, 132, 481–497. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Li, J.; Wang, K.; Wang, Z.; Zhang, S. Determination of intertidal macroalgae community patterns using the power law model. PLoS ONE 2022, 17, e0277101. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Chen, J.; Wei, Z.; Wang, Y.; Shiyomi, M.; Yang, Y. Analyzing the spatial heterogeneity of number of plant individuals in grassland community by using power law model. Ecol. Model. 2016, 320, 316–321. [Google Scholar] [CrossRef]
- Lin, Y.; Han, G.; Zhao, M.; Chang, S.X. Spatial vegetation patterns as early signs of desertification: A case study of a desert steppe in Inner Mongolia, China. Landsc. Ecol. 2010, 25, 1519–1527. [Google Scholar] [CrossRef]
- Gibson, R.; Driscoll, D.; Macdonald, K.; Williamson, G.; Nolan, R.; Doherty, T.; Nimmo, D.; Ritchie, E.; Tozer, M.; Tasker, L.; et al. Remotely Sensed Fire Heterogeneity and Biomass Recovery Predicts Empirical Biodiversity Responses. Glob. Ecol. Biogeogr. 2025, 34, 567–580. [Google Scholar] [CrossRef]
- Mou, X.M.; Yu, Y.W.; Li, X.G.; Degen, A.A. Presence frequency of plant species can predict spatial patterns of the species in small patches on the Qinghai-Tibetan Plateau. Glob. Ecol. Conserv. 2020, 21, e00831. [Google Scholar] [CrossRef]
- He, C.; Fan, F.; Qiao, X.; Zhou, Z.; Xu, H.; Li, S.; Zhu, J.; Wang, S.; Tang, Z.; Fang, J. Sampling origins and directions affect the minimum sampling area in forest plots. J. Veg. Sci. 2024, 35, e13232. [Google Scholar] [CrossRef]
- Navarro-Rosales, F.; Bell, M.B.V. Woody vegetation within semi-abandoned olive groves: Species-area relationships and minimum area values. Mediterr. Bot. 2022, 43, e71377. [Google Scholar] [CrossRef]
- May, R.M.; Stumpf, M.P. Ecology. Species-area relations in tropical forests. Science 2000, 290, 2084–2086. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, J.; Zhao, X. Species-Area Relationship and Its Scale-Dependent Effects in Natural Forests of North Eastern China. Forests 2019, 10, 422. [Google Scholar] [CrossRef]
- Liu, J.; MacDonald, Z.G.; Si, X.; Wu, L.; Zeng, D.; Hu, G.; Ding, P.; Yu, M. SLOSS-based inferences in a fragmented landscape depend on fragment area and species-area slope. J. Biogeogr. 2022, 49, 1075–1085. [Google Scholar] [CrossRef]
- Zhang, H.; Chase, J.M.; Liao, J. Habitat amount modulates biodiversity responses to fragmentation. Nat. Ecol. Evol. 2024, 8, 1477–1487. [Google Scholar] [CrossRef]
- Yan, Y.; Jarvie, S.; Zhang, Q.; Han, P.; Liu, Q.; Zhang, S.; Liu, P. Habitat heterogeneity determines species richness on small habitat islands in a fragmented landscape. J. Biogeogr. 2023, 50, 976–986. [Google Scholar] [CrossRef]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Dengler, J. Which function describes the species–area relationship best? A review and empirical evaluation. J. Biogeogr. 2009, 36, 728–744. [Google Scholar] [CrossRef]
- Shiyomi, M.; Takahashi, S.; Yoshimura, J.; Yasuda, T.; Tsutsumi, M.; Tsuiki, M.; Hori, Y. Spatial heterogeneity in a grassland community: Use of power law. Ecol. Res. 2001, 16, 487–495. [Google Scholar] [CrossRef]
- Ma, Z. Power law analysis of the human microbiome. Mol. Ecol. 2015, 24, 5428–5445. [Google Scholar] [CrossRef] [PubMed]
- Horník, J.; Janeček, Š.; Klimešová, J.; Doležal, J.; Janečková, P.; Jiráská, Š.; Lanta, V. Species-area curves revisited: The effects of model choice on parameter sensitivity to environmental, community, and individual plant characteristics. Plant Ecol. 2012, 213, 1675–1686. [Google Scholar] [CrossRef]
- Song, Z.; Huang, D.; Shiyomi, M.; Wang, Y.; Takahashi, S.; Yoshimichi, H.; Yamamuru, Y.; Chen, J. Spatial heterogeneity and variability of a large-scale vegetation community using a power-law model. Tsinghua Sci. Technol. 2005, 10, 469–477. [Google Scholar] [CrossRef]
- Brooker, R.W.; Maestre, F.T.; Callaway, R.M.; Lortie, C.L.; Cavieres, L.A.; Kunstler, G.; Liancourt, P.; TielböRger, K.; Travis, J.M.J.; Anthelme, F.; et al. Facilitation in plant communities: The past, the present, and the future. J. Ecol. 2008, 96, 18–34. [Google Scholar] [CrossRef]
- Devagiri, G.M.; Khaple, A.K.; Mohan, S.; Venkateshamurthy, P.; Tomar, S.; Arunkumar, A.N.; Joshi, G. Species diversity, regeneration and dominance as influenced by canopy gaps and their characteristics in tropical evergreen forests of Western Ghats, India. J. For. Res. 2016, 27, 799–810. [Google Scholar] [CrossRef]
- Plotkin, J.B.; Potts, M.D.; Leslie, N.; Manokaran, N.; LaFrankie, J.; Ashton, P.S. Species-area curves, spatial aggregation, and habitat specialization in tropical forests. J. Theor. Biol. 2000, 207, 81–99. [Google Scholar] [CrossRef]
- Liu, J.; Feng, C.; Wang, D.; Wang, L.; Wilsey, B.J.; Zhong, Z. Impacts of grazing by different large herbivores in grassland depend on plant species diversity. J. Appl. Ecol. 2015, 52, 1053–1062. [Google Scholar] [CrossRef]
- Tilman, D. Resource Competition and Community Structure; Princeton University Press: Princeton, NJ, USA, 1982. [Google Scholar]
- Sun, C.; Chai, Z.; Liu, G.; Xue, S. Changes in species diversity patterns and spatial heterogeneity during the secondary succession of grassland vegetation on the Loess Plateau, China. Front. Plant Sci. 2017, 8, 1465. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Huang, D.; Shiyomi, M.; Hori, Y.; Yamamura, Y.; Yiruhan. Spatial heterogeneity and diversity of vegetation at the landscape level in Inner Mongolia, China, with special reference to water resources. Landsc. Urban Plan. 2007, 82, 222–232. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; ElAich, A.; De Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jiang, Y.; Shipley, B.; Li, B.; Luo, W.; Chen, Y.; Zhao, K.; He, D.; Rodríguez, D.; Chu, C. The complexity of trait-environment performance landscapes in a local subtropical forest. New Phytol. 2021, 229, 1388–1397. [Google Scholar] [CrossRef]
- Moeslund, J.E.; Arge, L.; Bøcher, P.K.; Dalgaard, T.; Ejrnæs, R.; Odgaard, M.V.; Svenning, J.C. Topographically controlled soil moisture drives plant diversity patterns within grasslands. Biodivers. Conserv. 2013, 22, 2151–2166. [Google Scholar] [CrossRef]
- Brockerhoff, E.G.; Ecroyd, C.E.; Leckie, A.C.; Kimberley, M.O. Diversity and succession of adventive and indigenous vascular understorey plants in Pinus radiata plantation forests in New Zealand. For. Ecol. Manag. 2003, 185, 307–326. [Google Scholar] [CrossRef]
- Zhao, X.; Feng, Y.; Xu, K.; Cao, M.; Hu, S.; Yang, Q.; Liu, X.; Ma, Q.; Hu, T.; Kelly, M.; et al. Canopy structure: An intermediate factor regulating grassland diversity-function relationships under human disturbances. Fundam. Res. 2023, 3, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.C.; Williams, C.J.; Guertin, D.P.; Archer, S.R.; Heilman, P.; Pierson, F.B.; Wei, H. Restoration of a shrub-encroached semi-arid grassland: Implications for structural, hydrologic, and sediment connectivity. Ecohydrology 2021, 14, e2281. [Google Scholar] [CrossRef]
- Deng, J.; Chong, Y.; Dan, Z.; Kang, D.; Han, X.; Yang, G. Aggregated Distribution of Herbaceous Plants in Restored Vegetation Community in a Semi-arid Area: Evidence from the Loess Plateau of China. Russ. J. Ecol. 2020, 51, 136–143. [Google Scholar] [CrossRef]
- Han, J.; Wu, N.; Wu, Y.; Zhou, S.; Bi, X. Spatial effects of shrub encroachment on wetland soil pH and salinity in the Yellow River Delta, China. J. Coast. Conserv. 2024, 28, 60. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, L.; Wu, C.; Jing, S.; Meng, L.; Liu, S.; Hou, X.; Lu, W.; Zhao, X. Canopy-Mediated Shifts in Grassland Diversity and Heterogeneity: A Power Law Approach from China’s Loess Plateau. Plants 2025, 14, 3008. https://doi.org/10.3390/plants14193008
Qian L, Wu C, Jing S, Meng L, Liu S, Hou X, Lu W, Zhao X. Canopy-Mediated Shifts in Grassland Diversity and Heterogeneity: A Power Law Approach from China’s Loess Plateau. Plants. 2025; 14(19):3008. https://doi.org/10.3390/plants14193008
Chicago/Turabian StyleQian, Lili, Cong Wu, Sipu Jing, Li Meng, Shuo Liu, Xiangyang Hou, Wenjie Lu, and Xiang Zhao. 2025. "Canopy-Mediated Shifts in Grassland Diversity and Heterogeneity: A Power Law Approach from China’s Loess Plateau" Plants 14, no. 19: 3008. https://doi.org/10.3390/plants14193008
APA StyleQian, L., Wu, C., Jing, S., Meng, L., Liu, S., Hou, X., Lu, W., & Zhao, X. (2025). Canopy-Mediated Shifts in Grassland Diversity and Heterogeneity: A Power Law Approach from China’s Loess Plateau. Plants, 14(19), 3008. https://doi.org/10.3390/plants14193008






