PCA-Driven Multivariate Trait Integration in Alfalfa Breeding: A Selection Model for High-Yield and Stable Progenies
Abstract
1. Introduction
2. Results
2.1. Agronomic Trait Characterization in Parental Lines and F1 Hybrids
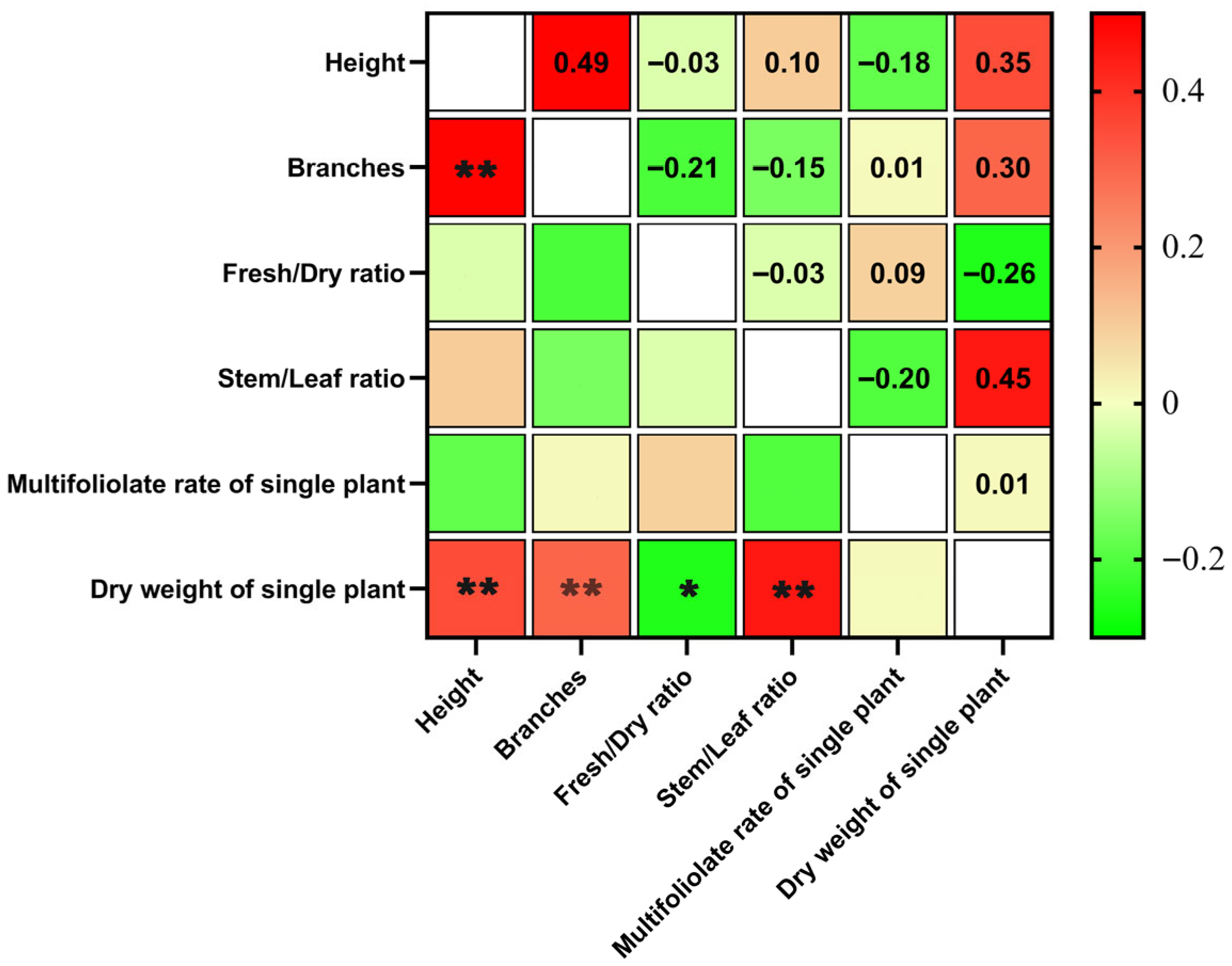
2.2. Correlations Among Agronomic Traits in the F1 Generation of Alfalfa Crosses
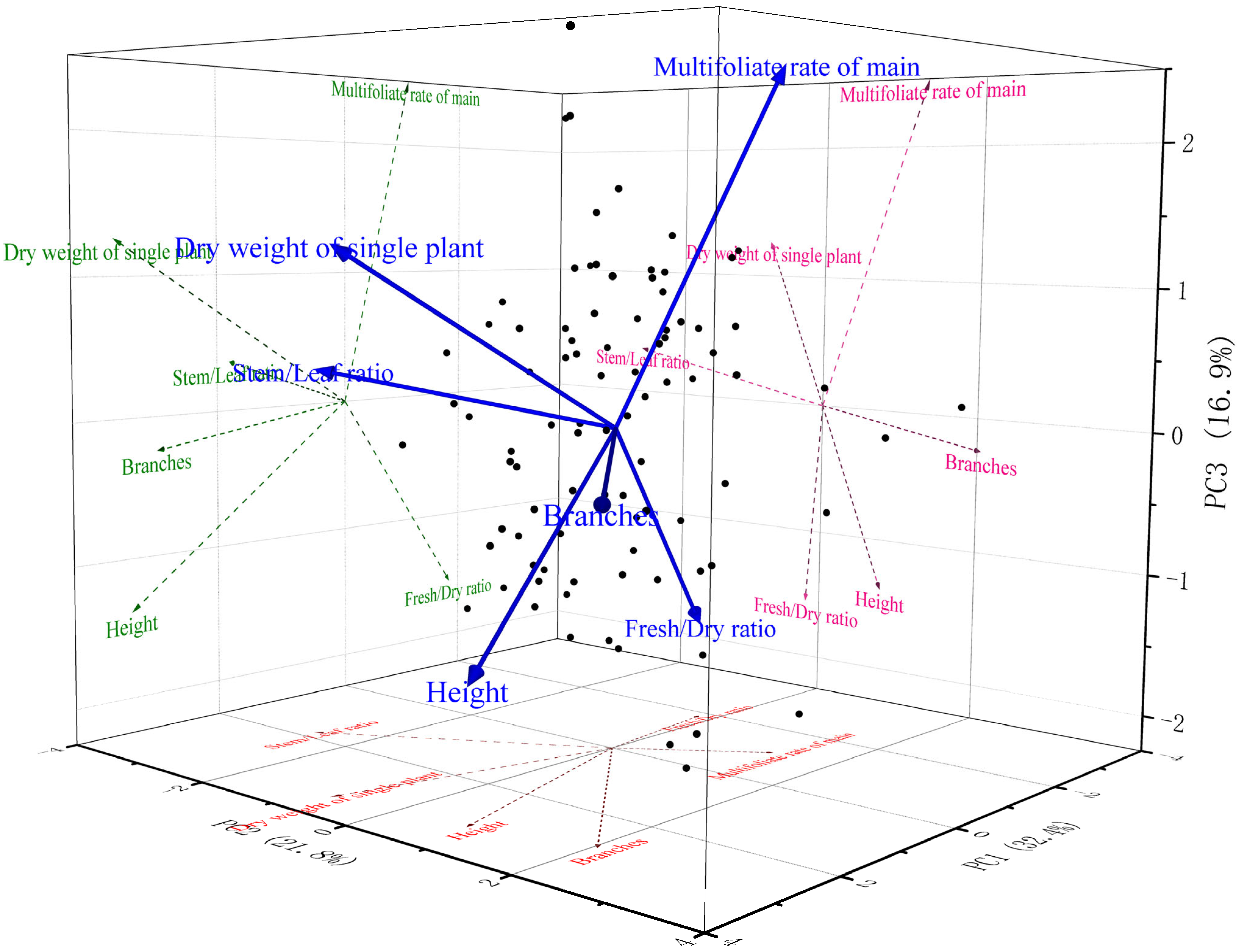
2.3. Principal Component Analysis (PCA) for Dimensionality Reduction
2.4. Selection of Elite Hybrids Using a Multivariate Approach
2.5. Validation of Selection Efficacy in F2 Progenies
3. Discussion
4. Materials and Methods
4.1. Research Design and Materials
4.2. Measurement and Analytical Methods for Agronomic Traits
4.2.1. Agronomic Trait Quantification
- Plant height (PH): the distance between the ground (seedling from cotyledonary node) and the top of the main stem (growing point) after the individual plant has been straightened (cm) [48].
- Branch number (BN): Total primary branches above root crown (parallel to ground) [48].
- Multifoliolate trait frequency (MF): The multifoliolate trait frequency (MF) is a species-specific indicator used in alfalfa to evaluate the occurrence of compound leaves with an increased number of leaflets. To determine MF, the total number of compound leaves on a representative branch was recorded, and leaves with four or more leaflets were classified as multifoliolate [48]. The MF was then calculated as the proportion of multifoliolate leaves to the total number of compound leaves on the branch, using the following formula:
- Fresh weight (FW): Fresh biomass per plant after cutting (g) [49].
- The leaf/stem ratio (LSR) was determined as the ratio of leaf dry weight to stem dry weight. After harvest, plant samples were manually separated into leaf and stem components. Each component was oven-dried at 65 °C to a constant weight. The LSR was calculated using the following formula:
- Dry weight (DW): Constant weight after 105 °C enzyme deactivation (30 min) followed by 65 °C drying (g) until a constant weight was achieved [51].
- The fresh/hay yield ratio (FHR) was calculated as the ratio of fresh biomass weight to dry biomass weight. Fresh weight was measured immediately after harvesting each plant. To determine dry weight, the same plant samples were oven-dried at 65 °C until a constant weight was achieved (typically 48–72 h). The FHR was then calculated using the formula:
4.2.2. Statistical Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dayananda, B.; Chahwala, P.; Cozzolino, D. The Ability of Near-Infrared Spectroscopy to Discriminate Plant Protein Mixtures: A Preliminary Study. AppliedChem 2023, 3, 428–436. [Google Scholar] [CrossRef]
- Gill, T.; Gill, S.K.; Saini, D.K.; Chopra, Y.; de Koff, J.P.; Sandhu, K.S. A Comprehensive Review of High Throughput Phenotyping and Machine Learning for Plant Stress Phenotyping. Phenomics 2022, 2, 156–183. [Google Scholar] [CrossRef]
- da Piedade, G.N.; Vieira, L.V.; dos Santos, A.R.P.; Amorim, D.J.; Zanotto, M.D.; Sartori, M.M.P. Principal Component Analysis for Identification of Superior Castor Bean Hybrids. J. Agric. Sci. 2019, 11, 179. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Chen, Z.; Lu, H.; Liu, Y.; Zhang, Z.; Liang, C. An Overview of Genome-wide Association Studies in Plants. Chin. Bull. Bot. 2020, 55, 715–732. [Google Scholar] [CrossRef]
- Varanasi, Y.V.P.; Isetty, S.R.; Revadi, P.; Balakrishnan, D.; Hajira, S.; Prasad, M.S.; Laha, G.S.; Perraju, P.; Singh, U.M.; Singh, V.K.; et al. Molecular and Morphological Characterization of Introgression Lines with Resistance to Bacterial Leaf Blight and Blast in Rice. Plants 2023, 12, 3012. [Google Scholar] [CrossRef] [PubMed]
- Phahom, T.; Mano, J. Integration of Multiple Linear Regression, Principal Component Analysis, and Hierarchical Cluster Analysis for Optimizing Dried Fingerroot (Boesenbergia rotunda) Extraction Process. J. Appl. Res. Med. Aromat. Plants 2023, 36, 100511. [Google Scholar] [CrossRef]
- Placide, R.; Shimelis, H.; Laing, M.; Gahakwa, D. Application of Principal Component Analysis to Yield and Yield Related Traits to Identify Sweet Potato Breeding Parents. Trop. Agric. 2015, 92, 1. [Google Scholar]
- Wang, M.; Ahmad, I.; Qin, B.; Chen, L.; Bu, W.; Zhu, G.; Zhou, G. Identification and Comprehensive Evaluation of Drought Tolerance in Sorghum During Germination and Seedling Stages. Plants 2025, 14, 1793. [Google Scholar] [CrossRef]
- Baha, J.; Liu, W.; Ma, X.; Li, Y.; Zhao, X.; Zhai, X.; Cao, X.; Guo, W. Comprehensive Evaluation of 202 Cotton Varieties (Lines) and Their Physiological Drought Resistance Response During Seedling Stage. Plants 2025, 14, 1770. [Google Scholar] [CrossRef] [PubMed]
- Shojaei, S.H.; Bihamta, M.R.; Mousavi, S.M.N.; Qasemi, S.H.; Keshavarzi, M.H.B.; Omrani, A. Application of Graphical Analysis and Principal Components to Identify the Effect of Genotype × Trait in Maize Hybrids. Agrosystems Geosci. Environ. 2024, 7, e20548. [Google Scholar] [CrossRef]
- Ferreira, E.A.; de Abreu, J.G.; Martinez, J.C.; dos Santos Braz, T.G.; Ferreira, D.P. Cutting Ages of Elephant Grass for Chopped Hay Production. Pesqui. Agropecuária Trop. 2018, 48, 245–253. (In Portuguese) [Google Scholar] [CrossRef]
- Alatürk, F. Effects of Harvest Height and Time on Hay Yield and Quality of Some Sweet Sorghum and Sorghum Sudangrass Hybrid Varieties. PeerJ 2024, 12, e17274. [Google Scholar] [CrossRef]
- Cao, Z.; Li, J.; Wang, C.; Min, X.; Wei, Z. Stem Coloration in Alfalfa: Anthocyanin Accumulation Patterns and Nutrient Profiles of Red- and Green-Stemmed Variants. Agronomy 2025, 15, 862. [Google Scholar] [CrossRef]
- Kloda, J.M.; Dean, P.D.G.; Maddren, C.; MacDonald, D.W.; Mayes, S. Using Principle Component Analysis to Compare Genetic Diversity across Polyploidy Levels within Plant Complexes: An Example from British Restharrows (Ononis spinosa and Ononis repens). Heredity 2008, 100, 253–260. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fatima, S.; Rashid, M.; Hameed, A.; Fiaz, S.; Rebouh, N.Y.; Zaman, Q.U. Development of Rice Mutants with Enhanced Resilience to Drought and Brown Spot (Bipolaris oryzae) and Their Physiological and Multivariate Analysis. BMC Plant Biol. 2025, 25, 1040. [Google Scholar] [CrossRef]
- Rodriguez, D.F.C.; Urban, M.O.; Santaella, M.; Gereda, J.M.; Contreras, A.D.; Wenzl, P. Using Phenomics to Identify and Integrate Traits of Interest for Better-Performing Common Beans: A Validation Study on an Interspecific Hybrid and Its Acutifolii Parents. Front. Plant Sci. 2022, 13, 1008666. [Google Scholar] [CrossRef]
- Filho, A.C.; Toebe, M. Sample size for principal component analysis in corn. Pesqui. Agropecuária Bras. 2021, 56, e02510. (In Portuguese) [Google Scholar] [CrossRef]
- Qaraei, M.; Abbaasi, S.; Ghiasi-Shirazi, K. Randomized Non-Linear PCA Networks. Inf. Sci. 2021, 545, 241–253. [Google Scholar] [CrossRef]
- Björklund, M. Be Careful with Your Principal Components. Evolution 2019, 73, 2151–2158. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Principal Component Analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Yao, Y.; Ochoa, A. Limitations of Principal Components in Quantitative Genetic Association Models for Human Studies. eLife 2023, 12, e79238. [Google Scholar] [CrossRef]
- Semagn, K.; Crossa, J.; Cuevas, J.; Iqbal, M.; Ciechanowska, I.; Henriquez, M.A.; Randhawa, H.; Beres, B.L.; Aboukhaddour, R.; McCallum, B.D.; et al. Comparison of Single-Trait and Multi-Trait Genomic Predictions on Agronomic and Disease Resistance Traits in Spring Wheat. Theor. Appl. Genet. 2022, 135, 2747–2767. [Google Scholar] [CrossRef]
- Shahi, D.; Guo, J.; Pradhan, S.; Khan, J.; Avci, M.; Khan, N.; Mcbreen, J.; Bai, G.; Reynolds, M.; Foulkes, J.; et al. Multi-Trait Genomic Prediction Using in-Season Physiological Parameters Increases Prediction Accuracy of Complex Traits in US Wheat. BMC Genom. 2022, 23, 298. [Google Scholar] [CrossRef]
- Osterman, J.; Gutiérrez, L.; Öhlund, L.; Ortiz, R.; Hammenhag, C.; Parsons, D.; Geleta, M. Comparison of Single-Trait and Multi-Trait GBLUP Models for Genomic Prediction in Red Clover. Agronomy 2024, 14, 2445. [Google Scholar] [CrossRef]
- Jing, F.; Shi, S.; Kang, W.; Guan, J.; Lu, B.; Wu, B.; Wang, W. The Physiological Basis of Alfalfa Plant Height Establishment. Plants 2024, 13, 679. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, R.; Yang, K.; Ma, C.; Zhang, Q. Effects of Nitrogen and Phosphorus Fertilization on Photosynthetic Properties of Leaves and Agronomic Characters of Alfalfa over Three Consecutive Years. Agriculture 2022, 12, 1187. [Google Scholar] [CrossRef]
- Ames, N.; McElroy, A.R.; Akin, D.E.; Lyon, C.E. Evaluation of Stem Strength of Alfalfa (Medicago sativa L.) Genotypes. Anim. Feed. Sci. Technol. 1995, 54, 267–274. [Google Scholar] [CrossRef]
- Annicchiarico, P. Alfalfa Forage Yield and Leaf/Stem Ratio: Narrow-Sense Heritability, Genetic Correlation, and Parent Selection Procedures. Euphytica 2015, 205, 409–420. [Google Scholar] [CrossRef]
- Claessens, A.; Thériault, M.; Bertrand, A.; Lajeunesse, J.; Rocher, S.; Biligetu, B. High-Energy Alfalfa (Medicago sativa L.) Developed by Recurrent Phenotypic Selection for Nonfiber Carbohydrate Concentration in Stems. Crop Sci. 2025, 65, e70054. [Google Scholar] [CrossRef]
- Min, X.; Luo, K.; Liu, W.; Zhou, K.; Li, J.; Wei, Z. Molecular Characterization of the miR156/MsSPL Model in Regulating the Compound Leaf Development and Abiotic Stress Response in Alfalfa. Genes 2022, 13, 331. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Medina, C.A.; Boge, B.; Hu, J.; Fransen, S.; Norberg, S.; Yu, L.-X. Identification of Genetic Loci Associated with Forage Quality in Response to Water Deficit in Autotetraploid Alfalfa (Medicago sativa L.). BMC Plant Biol. 2020, 20, 303. [Google Scholar] [CrossRef]
- Mnafgui, W.; Jabri, C.; Jihnaoui, N.; Maiza, N.; Guerchi, A.; Zaidi, N.; Basson, G.; Keyster, E.M.; Djébali, N.; Pecetti, L.; et al. Discovering New Genes for Alfalfa (Medicago sativa) Growth and Biomass Resilience in Combined Salinity and Phoma Medicaginis Infection through GWAS. Front. Plant Sci. 2024, 15, 1348168. [Google Scholar] [CrossRef]
- Aruna, C.; Rakshit, S.; Shrotria, P.K.; Pahuja, S.K.; Jain, S.K.; Kumar, S.S.; Modi, N.D.; Deshmukh, D.T.; Kapoor, R.; Patil, J.V. Assessing Genotype-by-Environment Interactions and Trait Associations in Forage Sorghum Using GGE Biplot Analysis. J. Agric. Sci. 2016, 154, 73–86. [Google Scholar] [CrossRef]
- Leitão, S.T.; Alves, M.L.; Pereira, P.; Zerrouk, A.; Godinho, B.; Barradas, A.; Vaz Patto, M.C. Towards a Trait-Based Approach to Potentiate Yield under Drought in Legume-Rich Annual Forage Mixtures. Plants 2021, 10, 1763. [Google Scholar] [CrossRef]
- Volenec, J.J. Physiological Control of Alfalfa Growth and Yield. In Crop Yield: Physiology and Processes; Smith, D.L., Hamel, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 425–442. ISBN 978-3-642-58554-8. [Google Scholar]
- Volenec, J.J.; Cherney, J.H.; Johnson, K.D. Yield Components, Plant Morphology, and Forage Quality of Alfalfa as Influenced by Plant Population. Crop Sci. 1987, 27, 321–326. [Google Scholar] [CrossRef]
- Lorenzo, C.D.; García-Gagliardi, P.; Antonietti, M.S.; Sánchez-Lamas, M.; Mancini, E.; Dezar, C.A.; Vazquez, M.; Watson, G.; Yanovsky, M.J.; Cerdán, P.D. Improvement of Alfalfa Forage Quality and Management through the Down-regulation of MsFTa1. Plant Biotechnol. J. 2019, 18, 944–954. [Google Scholar] [CrossRef] [PubMed]
- Yun, A.; Shi, S.; Gong, W.; Zhang, J.; Zhang, X.; Zhang, J. Cross-Breeding Improvement and Performance Analysis of Dominant Production Traits in Grazing-Type Alfalfa (Medicago sativa L.). BioMed Res. Int. 2022, 2022, 1252310. [Google Scholar] [CrossRef]
- Behera, P.P.; Singode, A.; Bhat, B.V.; Ronda, V.; Borah, N.; Verma, H.; Gogoi, L.R.; Borah, J.L.; Majhi, P.K.; Saharia, N.; et al. Genetic Gains in Forage Sorghum for Adaptive Traits for Non—Conventional Area through Multi-Trait-Based Stability Selection Methods. Front. Plant Sci. 2024, 15, 1248663. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Stephens, M. Efficient Multivariate Linear Mixed Model Algorithms for Genome-Wide Association Studies. Nat. Methods 2014, 11, 407–409. [Google Scholar] [CrossRef]
- Pan, X.; Wang, P.; Wei, X.; Zhang, J.; Xu, B.; Chen, Y.; Wei, G.; Wang, Z. Exploring Root System Architecture and Anatomical Variability in Alfalfa (Medicago sativa L.) Seedlings. BMC Plant Biol. 2023, 23, 449. [Google Scholar] [CrossRef]
- Hakl, J.; Mofidian, S.M.A.; Kozová, Z.; Fuksa, P.; Jaromír, Š. Estimation of Lucerne Yield Stability for Enabling Effective Cultivar Selection under Rainfed Conditions. Grass Forage Sci. 2019, 74, 687–695. [Google Scholar] [CrossRef]
- McDonagh, J.; O’Donovan, M.; McEvoy, M.; Gilliland, T.J. Genetic Gain in Perennial Ryegrass (Lolium perenne) Varieties 1973 to 2013. Euphytica 2016, 212, 187–199. [Google Scholar] [CrossRef]
- Caradus, J.R.; Chapman, D.F. Evaluating Pasture Forage Plant Breeding Achievements: A Review. New Zealand J. Agric. Res. 2025, 68, 1146–1220. [Google Scholar] [CrossRef]
- Crain, J.; Mondal, S.; Rutkoski, J.; Singh, R.P.; Poland, J. Combining High-Throughput Phenotyping and Genomic Information to Increase Prediction and Selection Accuracy in Wheat Breeding. Plant Genome 2018, 11, 170043. [Google Scholar] [CrossRef]
- Juliana, P.; Montesinos-López, O.A.; Crossa, J.; Mondal, S.; González Pérez, L.; Poland, J.; Huerta-Espino, J.; Crespo-Herrera, L.; Govindan, V.; Dreisigacker, S.; et al. Integrating Genomic-Enabled Prediction and High-Throughput Phenotyping in Breeding for Climate-Resilient Bread Wheat. Theor. Appl. Genet. 2019, 132, 177–194. [Google Scholar] [CrossRef]
- Wang, W.; Guo, W.; Le, L.; Yu, J.; Wu, Y.; Li, D.; Wang, Y.; Wang, H.; Lu, X.; Qiao, H.; et al. Integration of High-Throughput Phenotyping, GWAS, and Predictive Models Reveals the Genetic Architecture of Plant Height in Maize. Mol. Plant 2023, 16, 354–373. [Google Scholar] [CrossRef]
- Wu, Z. Research of Alfalfa Multifoliate traits and anther culture. Ph.D. Thesis, Yangzhou University, Yangzhou, China, 2013. [Google Scholar]
- Jabborova, D.; Abdrakhmanov, T.; Jabbarov, Z.; Abdullaev, S.; Azimov, A.; Mohamed, I.; AlHarbi, M.; Abu-Elsaoud, A.; Elkelish, A. Biochar Improves the Growth and Physiological Traits of Alfalfa, Amaranth and Maize Grown under Salt Stress. PeerJ 2023, 11, e15684. [Google Scholar] [CrossRef]
- Liu, J.; Lu, S.; Liu, C.; Hou, D. Nutrient Reallocation between Stem and Leaf Drives Grazed Grassland Degradation in Inner Mongolia, China. BMC Plant Biol. 2022, 22, 505. [Google Scholar] [CrossRef]
- GB/T 6435-2014; Determination of Moisture in Feed Stuffs. Standardization Administration of PRC (SAC) Standards Press of China: Beijing, China, 2014.
| Traits 1 | Parents 2 | p-Value 3 | F1 Mean | |
|---|---|---|---|---|
| Paternal Mean (♂) | Maternal Mean (♀) | |||
| Height (cm) | 80.85 ± 14.92 | 72.48 ± 16.23 | 0.036 | 75.66 ± 17.64 |
| Branches | 7.31 ± 1.90 | 9.16 ± 3.28 | 0.008 | 8.34 ± 3.08 |
| FHR | 4.33 ± 0.24 | 4.04 ± 0.29 | 0.001 | 4.16 ± 0.29 |
| LSR | 1.64 ± 0.35 | 1.50 ± 0.29 | 0.134 | 1.57 ± 0.31 |
| MF of individual plants (%) | 0.00 | 68.87 ± 4.29 | 0.000 | 29.03 ± 5.29 |
| Dry weight of individual plants (g) | 119.69 ± 29.17 | 142.26 ± 43.59 | 0.034 | 124.34 ± 47.46 |
| Component 2 | Extraction Sums of Squared Loadings 1 | ||
|---|---|---|---|
| Total | Percentage of Variance (%) | Cumulative % | |
| 1 | 1.946 | 32.435 | 32.435 |
| 2 | 1.306 | 21.771 | 54.206 |
| 3 | 1.016 | 16.937 | 71.143 |
| Component | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Z-score (Height) | 0.729 | 0.247 | −0.398 |
| Z-score (Branches) | 0.645 | 0.621 | −0.071 |
| Z-score (FHR) | −0.412 | −0.057 | −0.454 |
| Z-score (LSR) | 0.410 | −0.805 | 0.102 |
| Z-score (Multifoliolate trait frequency of individual plants) | −0.245 | 0.395 | 0.711 |
| Z-score (Dry weight of individual plants) | 0.775 | −0.229 | 0.363 |
| Overall Ranking | Combined Score | Overall Ranking | Combined Score | Overall Ranking | Combined Score |
|---|---|---|---|---|---|
| 1 | 35.40 | 31 | 0.65 | 61 | −2.54 |
| 2 | 18.89 | 32 | 0.62 | 62 | −2.73 |
| 3 | 15.28 | 33 | 0.46 | 63 | −2.84 |
| 4 | 13.97 | 34 | 0.44 | 64 | −2.92 |
| 5 | 10.82 | 35 | 0.33 | 65 | −2.97 |
| 6 | 10.70 | 36 | 0.10 | 66 | −3.06 |
| 7 | 10.46 | 37 | 0.08 | 67 | −3.15 |
| 8 | 10.31 | 38 | −0.32 | 68 | −3.67 |
| 9 | 10.05 | 39 | −0.34 | 69 | −4.09 |
| 10 | 8.79 | 40 | −0.41 | 70 | −4.26 |
| 11 | 7.79 | 41 | −0.52 | 71 | −4.49 |
| 12 | 7.49 | 42 | −0.53 | 72 | −4.89 |
| 13 | 7.30 | 43 | −0.63 | 73 | −5.55 |
| 14 | 7.10 | 44 | −0.65 | 74 | −5.99 |
| 15 | 6.77 | 45 | −0.66 | 75 | −6.60 |
| 16 | 6.42 | 46 | −0.72 | 76 | −6.78 |
| 17 | 6.15 | 47 | −0.78 | 77 | −7.06 |
| 18 | 6.06 | 48 | −1.02 | 78 | −7.16 |
| 19 | 5.69 | 49 | −1.05 | 79 | −7.71 |
| 20 | 4.88 | 50 | −1.17 | 80 | −7.97 |
| 21 | 4.75 | 51 | −1.44 | 81 | −8.41 |
| 22 | 4.55 | 52 | −1.70 | 82 | −9.37 |
| 23 | 4.01 | 53 | −1.78 | 83 | −9.46 |
| 24 | 3.93 | 54 | −1.83 | 84 | −9.57 |
| 25 | 3.14 | 55 | −1.99 | 85 | −10.26 |
| 26 | 2.86 | 56 | −2.06 | 86 | −10.45 |
| 27 | 1.82 | 57 | −2.17 | 87 | −13.84 |
| 28 | 1.54 | 58 | −2.18 | 88 | −14.19 |
| 29 | 0.95 | 59 | −2.42 | 89 | −14.67 |
| 30 | 0.83 | 60 | −2.52 | 90 | −15.83 |
| F1 Generation Selected Plants | All F1 Generation Hybrid Plants | Selected Single Natural Cross F2 Generation Plants | Non-Selected Single Natural Cross F2 Generation Plants | All F2 Generation Plants | |
|---|---|---|---|---|---|
| Height/cm | 86.45 ± 12.04 a | 75.66 ± 17.64 c | 80.68 ± 9.77 b | 69.27 ± 11.09 d | 74.98 ± 11.90 c |
| Branches | 11.11 ± 3.02 a | 8.34 ± 3.08 b | 8.57 ± 1.64 b | 7.92 ± 1.81 b | 8.24 ± 1.75 b |
| Ratio of fresh and hay | 3.99 ± 0.26 b | 4.16 ± 0.29 a | 3.83 ± 0.30 c | 4.14 ± 0.35 a | 3.97 ± 0.36 b |
| Ratio of stem and leaf | 1.60 ± 0.19 | 1.57 ± 0.31 | 1.62 ± 0.27 | 1.59 ± 0.24 | 1.61 ± 0.25 |
| Multifoliolate trait frequency of individual plants/% | 34.68 ± 7.86 c | 29.03 ± 5.29 c | 50.74 ± 9.92 a | 42.71 ± 6.35 b | 46.73 ± 8.13 ab |
| Dry weight of individual plants/g | 161.21 ± 45.34 a | 124.34 ± 19.46 cd | 143.69 ± 44.67 b | 112.80 ± 27.65 d | 128.24 ± 40.15 c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Li, J.; Lei, H.; Yan, M.; Wang, Q.; Ji, R.; Zhang, S.; Min, X.; Sun, Z.; Wei, Z. PCA-Driven Multivariate Trait Integration in Alfalfa Breeding: A Selection Model for High-Yield and Stable Progenies. Plants 2025, 14, 2906. https://doi.org/10.3390/plants14182906
Cao Z, Li J, Lei H, Yan M, Wang Q, Ji R, Zhang S, Min X, Sun Z, Wei Z. PCA-Driven Multivariate Trait Integration in Alfalfa Breeding: A Selection Model for High-Yield and Stable Progenies. Plants. 2025; 14(18):2906. https://doi.org/10.3390/plants14182906
Chicago/Turabian StyleCao, Zhengfeng, Jiaqing Li, Huanwei Lei, Mengyu Yan, Qianxi Wang, Runqin Ji, Siqi Zhang, Xueyang Min, Zhengguo Sun, and Zhenwu Wei. 2025. "PCA-Driven Multivariate Trait Integration in Alfalfa Breeding: A Selection Model for High-Yield and Stable Progenies" Plants 14, no. 18: 2906. https://doi.org/10.3390/plants14182906
APA StyleCao, Z., Li, J., Lei, H., Yan, M., Wang, Q., Ji, R., Zhang, S., Min, X., Sun, Z., & Wei, Z. (2025). PCA-Driven Multivariate Trait Integration in Alfalfa Breeding: A Selection Model for High-Yield and Stable Progenies. Plants, 14(18), 2906. https://doi.org/10.3390/plants14182906






