Global Sensitivity Analyses of the APSIM-Wheat Model at Different Soil Moisture Levels
Abstract
1. Introduction
2. Results
2.1. Analysis Using the Morris Method
2.1.1. Morris Results for WAGT
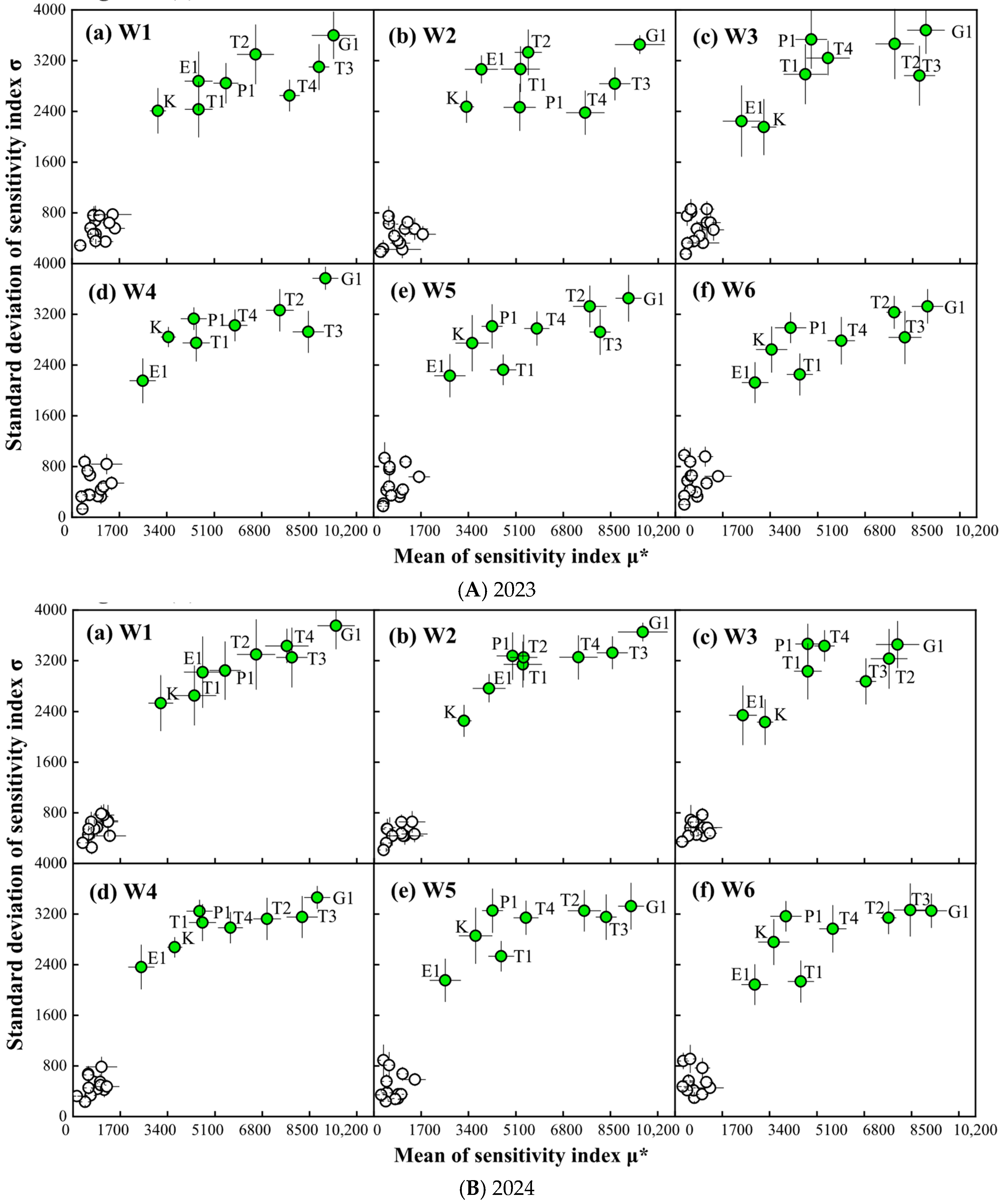
2.1.2. Morris Results for Wheat Yield
2.2. Analysis Using the EFAST Method
2.2.1. EFAST Results for WAGT
2.2.2. EFAST Results for Wheat Yield
2.3. Consistency Test of SA
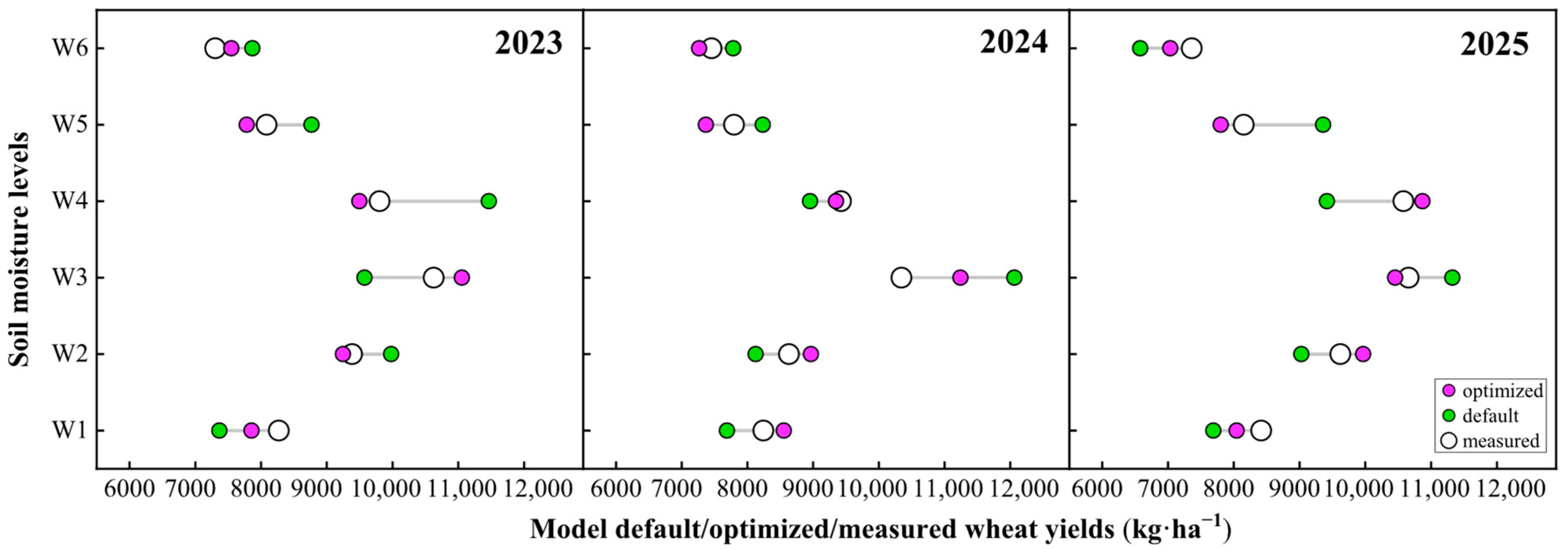
2.4. Results of Parameter Optimization and Model Evaluation
3. Discussion
4. Materials and Methods
4.1. Site Description
4.2. Field Experiment
4.3. APSIM-Wheat Model
4.4. Global SA Methods
4.4.1. Morris Method
4.4.2. EFAST Method
4.5. Parameter Selection and SA Plan
- (1)
- The range of model parameters was defined in SimLab2.2 and a uniform distribution was assumed for these parameters.
- (2)
- The input parameters were sampled. The Morris method required setting t = 10 (repetitions), n = 21 (parameters) × 3 (years), and sampling a total of 640 groups of 10 × (21 × 3 + 1). The EFAST method generated 4410 sets of 21 (parameters) × 3 (years) × 70 (times). The EFAST method deemed valid when the number of samples exceeded 65 times the number of parameters; accordingly, this study adopted a sampling size 70 times greater than the number of parameters.
- (3)
- The R language was used to modify parameters, run in batches, and organize the results for the APSIM-Wheat model.
- (4)
- The batch-processed simulation results were organized into a format recognizable by SimLab2.2, inputted into the software for analysis, and the SA results were obtained.
4.6. Consistency Test of SA Results
4.7. Parameter Optimization and Model Evaluation
4.8. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lei, Q.; Tao, W.; Lin, S.; Su, L.; Deng, M.; Wang, Q.; Yang, F.; Zhu, T.; Ma, L. The Synergistic Production Effect of Water and Nitrogen on Winter Wheat in Southern Xinjiang. Plants 2024, 13, 1391. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yang, G.; Chang, C.; Wang, H.; Jin, X.; Peng, Z. Study on the Appropriate Degree of Water-Saving Measures in Arid Irrigated Areas Considering Groundwater Level. Agronomy 2024, 14, 1611. [Google Scholar] [CrossRef]
- Latifmanesh, H.; Deng, A.; Nawaz, M.M.; Liang, L.; Chen, Z.; Zheng, Y.; Wang, P.; Song, Z.; Zhang, J.; Zheng, C.; et al. Integrative impacts of rotational tillage on wheat yield and dry matter accumulation under corn-wheat cropping system. Soil Tillage Res. 2018, 184, 100–108. [Google Scholar] [CrossRef]
- Contreras, J.I.; Alonso, F.; Cánovas, G.; Baeza, R. Irrigation management of greenhouse zucchini with different soil matric potential level. Agronomic and environmental effects. Agric. Water Manag. 2017, 183, 26–34. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Meng, Y.; Cao, N.; Li, D.; Zhou, Z.; Chen, B.; Dou, F. The effects of soil moisture and salinity as functions of groundwater depth on wheat growth and yield in coastal saline soils. J. Integr. Agric. 2019, 18, 2472–2482. [Google Scholar] [CrossRef]
- Smethurst, P.J.; Huth, N.I.; Masikati, P.; Sileshi, G.W.; Akinnifesi, F.K.; Wilson, J. Fergus Sinclair Accurate crop yield predictions from modelling tree-crop interactions in gliricidia-maize agroforestry. Agric. Syst. 2017, 155, 70–77. [Google Scholar] [CrossRef]
- Chen, S.; He, L.; Dong, W.; Li, R.; Jiang, T.; Li, L.; Feng, H.; Zhao, K.; Yu, Q.; He, J. Weather records from recent years performed better than analogue years when merging with real-time weather measurements for dynamic within-season predictions of rainfed maize yield. Agric. For. Meteorol. 2022, 315, 108810. [Google Scholar] [CrossRef]
- Liu, K.; Harrison, M.T.; Yan, H.; Liu, D.; Meinke, H.; Hoogenboom, G.; Wang, B.; Peng, B.; Guan, K.; Jaegermeyr, J. Silver lining to a climate crisis in multiple prospects for alleviating crop waterlogging under future climates. Nat. Commun. 2023, 14, 765. [Google Scholar] [CrossRef]
- Rugira, P.; Ma, J.; Zheng, L.; Wu, C.; Liu, E.K. Application of DSSAT CERES-Maize to Identify the Optimum Irrigation Management and Sowing Dates on Improving Maize Yield in Northern China. Agronomy 2021, 11, 674. [Google Scholar] [CrossRef]
- Pei, W.; Hao, L.; Fu, Q.; Ren, Y.; Li, T. Study on Agricultural Drought Risk Assessment Based on Information Entropy and a Cluster Projection Pursuit Model. Water Resour. Manag. 2022, 37, 619–638. [Google Scholar] [CrossRef]
- Wang, E.L.; Brown, H.E.; Rebetzke, G.E.; Zhao, Z.; Zheng, B.; Chapman, S.C. Improving process-based crop models to better capture genotype environment management interactions. J. Exp. Bot. 2019, 70, 2389–2401. [Google Scholar] [CrossRef]
- Wang, E.L.; Martre, P.; Zhao, Z.; Ewert, F.; Maiorano, A.; Rötter, R.P.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W. The uncertainty of crop yield projections is reduced by improved temperature response functions. Nat. Plants 2017, 3, 17102. [Google Scholar] [CrossRef]
- Anar, M.J.; Lin, Z.L.; Hoogenboom, G.; Shelia, V.; Batchelor, W.D.; Teboh, J.M.; Ostlie, M.; Schatz, B.G.; Khan, M. Modeling growth, development and yield of Sugarbeet using DSSAT. Agric. Syst. 2019, 169, 58–70. [Google Scholar] [CrossRef]
- Guo, Y.H.; Hao, F.H.; Zhang, X.; He, Y.H.; Fu, Y.S. Improving maize yield estimation by assimilating UAV-based LAI into WOFOST model. Field Crops Res. 2024, 315, 109477. [Google Scholar] [CrossRef]
- Takeda, N.; Friedl, J.; Rowlings, D.; Haas, E.; Kraus, D.; Grace, P.; Scheer, C. In-situ N2O and N2 data improved N budget simulation with APSIM and Landscape DNDC in tropical sugarcane systems. Agric. Ecosyst. Environ. 2024, 375, 109193. [Google Scholar] [CrossRef]
- Yang, H.B.; Li, Z.L.; Du, Q.Y.; Duan, Z. Winter Wheat Drought Risk Assessment by Coupling Improved Moisture-Sensitive Crop Model and Gridded Vulnerability Curve. Remote Sens. 2023, 15, 3197. [Google Scholar] [CrossRef]
- Dong, Z.; Jiang, M.; Xue, X.; Pan, Z.; Li, N.; Zhao, H.; Hou, Y. The applicability evaluation and drought validation of the WOFOST model for the simulation of winter wheat growth in Shandong Province, China. Heliyon 2022, 8, e12004. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, E.; Xue, L.; Wu, Y.; Zang, H.; Qin, X.; Zhang, J.; Wang, Z. Accuracy of root modelling and its impact on simulated wheat yield and carbon cycling in soil. Field Crops Res. 2014, 165, 99–110. [Google Scholar] [CrossRef]
- Kumar, U.; Hansen, E.M.; Kaag, I.; Thomsen, I.K.; Vogeler, I. Performance of APSIM to Simulate the Dynamics of Winter Wheat Growth, Phenology, and Nitrogen Uptake from Early Growth Stages to Maturity in Northern Europe. Plants 2023, 12, 986. [Google Scholar] [CrossRef]
- Asseng, S.; Keating, B.A.; Fillery, I.R.P.; Gregory, P.J.; Bowden, J.W.; Turner, N.C.; Palta, J.A.; Abrecht, D.G. Performance of the APSIM-wheat model in Western Australia. Field Crops Res. 1998, 57, 163–179. [Google Scholar] [CrossRef]
- Ahmed, M.; Stöckle, C.O.; Nelson, R.; Higgins, S.; Ahmad, S.; Raza, M.A. Novel multimodel ensemble approach to evaluate the sole effect of elevated CO2 on winter wheat roductivity. Sci. Rep. 2019, 9, 7813. [Google Scholar] [CrossRef]
- Akhavizadegan, F.; Ansarifar, J.; Wang, L.Z.; Huber, I.; Archontoulis, S.V. A time-dependent parameter estimation framework for crop modeling. Sci. Rep. 2021, 11, 11437. [Google Scholar] [CrossRef]
- Cui, W.N.; Nie, Z.G.; Li, G.; Yuan, J.Y. Optimization of Parameters Related to Grain Growth of Spring Wheat in Dryland Based on the Next-Generation APSIM. Agronomy 2023, 13, 1915. [Google Scholar] [CrossRef]
- Feng, K.; Lu, Z.; Yang, C. Enhanced Morris method for global sensitivity analysis: Good proxy of Sobol’ index. Struct. Multidiscip. Optim. 2019, 59, 373–387. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method. Environ. Model. Softw. 2013, 48, 171–182. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Zhu, A.; Shen, F.; Lei, Q.; Duan, Z. Global sensitivity analysis of the APSIM-Oryza rice growth model under different environmental conditions. Sci. Total Environ. 2019, 651, 953–968. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Safikhani, H. Sensitivity analysis of the effective centrifugal pump parameters using the EFAST method. Sci. Iran. 2019, 26, 421–427. [Google Scholar] [CrossRef]
- Li, Y.; Yao, Y.; Du, M.; Dong, L.; Yuan, J.; Li, G. APSIM NG Model Simulation of Soil N2O Emission from the Dry-Crop Wheat Field and Its Parameter Sensitivity Analysis. Agronomy 2025, 15, 834. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Willems, P. Global sensitivity analysis of yield output from the water productivity model AquaCrop. Environ. Model. Softw. 2014, 51, 323–332. [Google Scholar] [CrossRef]
- Fan, Y.; Tian, Z.; Yan, Y.; Hu, C.; Abid, M.; Jiang, D.; Ma, C.; Huang, Z.; Dai, T. Winter Night-Warming Improves Post-anthesis Physiological Activities and Sink Strength in Relation to Grain Filling in Winter Wheat (Triticum aestivum L.). Front. Plant Sci. 2017, 8, 992. [Google Scholar] [CrossRef]
- Djanaguiraman, M.; Narayanan, S.; Erdayani, E.; Prasad, P.V.V. Effects of high temperature stress during anthesis and grain filling periods on photosynthesis, lipids and grain yield in wheat. BMC Plant Biol. 2020, 20, 268. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Wei, Q.; Yang, Y.; Pan, H. Variation in Leaf Type, Canopy Architecture, and Light and Nitrogen Distribution Characteristics of Two Winter Wheat (Triticum aestivum L.) Varieties with High Nitrogen-Use Efficiency. Agronomy 2022, 12, 2411. [Google Scholar] [CrossRef]
- Du, X.; Gao, Z.; Sun, X.; Bian, D.; Ren, J.; Yan, P.; Cui, Y. Increasing temperature during early spring increases winter wheat grain yield by advancing phenology and mitigating leaf senescence. Sci. Total Environ. 2021, 812, 152557. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Qiu, X.; Yin, T.; Liao, Z.; Liu, B.; Liu, L. The Impact of Global Warming on the Winter Wheat Production of China. Agronomy 2021, 11, 1845. [Google Scholar] [CrossRef]
- Feng, X.; Huai, Y.; Kang, S.; Yang, L.; Li, Y.; Feng, J.; Zhang, Z.; Maw, M.J.W.; Cui, Z.L.; Ning, P. Reproductive resilience of growth and nitrogen uptake underpins yield improvement in winter wheat with forced delay of sowing. Sci. Total Environ. 2024, 949, 175108. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Lv, Z.; Qin, B.; Yang, J.; Ren, K.; Liu, Q.; Jiang, F.; Zhang, W.; Ma, S.; Ma, C.; et al. Night warming at the vegetative stage improves pre-anthesis photosynthesis and plant productivity involved in grain yield of winter wheat. Plant Physiol. Biochem. 2022, 186, 19–30. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, Y.; Zaman, A.M.; Zhang, M.; Li, Q. Delayed irrigation at the jointing stage increased the post-flowering dry matter accumulation and water productivity of winter wheat under wide-precision planting pattern. J. Sci. Food Agric. 2022, 103, 1925–1934. [Google Scholar] [CrossRef]
- Nicholas, C.C.; Boris, P. Diverging temperature responses of CO2 assimilation and plant development explain the overall effect of temperature on biomass accumulation in wheat leaves and grains. AoB Plants 2017, 9, 92. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, N.; Zhang, H.; Huo, Z.; Yang, Z. Effect of Low Temperature on Photosynthetic Characteristics, Senescence Characteristics, and Endogenous Hormones of Winter Wheat “Ji Mai 22” during the Jointing Stage. Agronomy 2023, 13, 2650. [Google Scholar] [CrossRef]
- Ahmed, M.; Akram, M.N.; Asim, M.; Aslam, M.; Hassan, F.; Higgins, S.; Stöckle, C.O.; Hoogenboom, G. Calibration and validation of APSIM-Wheat and CERES-Wheat for spring wheat under rainfed conditions: Models evaluation and application. Comput. Electron. Agric. 2016, 123, 384–401. [Google Scholar] [CrossRef]
- Sexton, J.; Everingham, Y.; Inman-Bamber, G. A theoretical and real world evaluation of two Bayesian techniques for the calibration of variety parameters in a sugarcane crop model. Environ. Model. Softw. 2016, 83, 126–142. [Google Scholar] [CrossRef]
- Kuang, N.K.; Hao, C.C.; Liu, D.Z.; Maimaitiming, M.; Xiaokaitijiang, K.; Zhou, Y.P.; Li, Y.K. Modeling of cotton yield responses to different irrigation strategies in Southern Xinjiang Region, China. Agric. Water Manag. 2024, 303, 109018. [Google Scholar] [CrossRef]
- Balcão, L.F.; Andreucci, M.; Snow, V.; Holzworth, D.; Brunetti, H.C.; dos Santos, M.L.; Bosi, C.; Pezzopane, J.R.M.; Santos, P.M. Pasture growth simulation and sensitivity analysis using APSIM-related models in a tropical silvopastoral system. Eur. J. Agron. 2024, 160, 127307. [Google Scholar] [CrossRef]
- Asseng, S.; Keulen, H.V.; Stol, W. Performance and application of the APSIM Nwheat model in the Netherlands. Eur. J. Agron. 2000, 12, 37–54. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Touhami, H.B.; Lardy, R.; Barra, V.; Bellocchi, G. Screening parameters in the pasture simulation model using the Morris method. Ecol. Model. 2013, 266, 42–57. [Google Scholar] [CrossRef]
- DeJonge, K.C.; Ascough, J.C.; Ahmadi, M.; Andales, A.A.; Arabi, M. Global sensitivity and uncertainty analysis of a dynamic agroecosystem model under different irrigation treatments. Ecol. Model. 2012, 231, 113–125. [Google Scholar] [CrossRef]
- Zhao, G.; Bryan, B.A.; Song, X. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar, environmental, and management parameters. Ecol. Model. 2014, 279, 1–11. [Google Scholar] [CrossRef]
- Zheng, B.; Chenu, K.; Doherty, A. The APSIM-Wheat Module (7.5 R3008). Agricultural Production Systems Simulator (APSIM) Initiative. 2014, 615. Available online: http://www.apsim.info/ (accessed on 15 May 2025).
- Iman, R.L.; Conover, W.J. A Measure of Top-Down Correlation. Technometrics 1987, 29, 351–357. [Google Scholar] [CrossRef]
- Confalonieri, R.; Bellocchi, G.; Tarantola, S.; Acutis, M.; Donatelli, M.; Genovese, G. Sensitivity analysis of the rice model WARM in Europe: Exploring the effects of different locations, climates and methods of analysis on model sensitivity to crop parameters. Environ. Model. Softw. 2010, 25, 479–488. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Ai, P.; Ma, Y.; Hai, Y. Comparing Simulated Jujube Evapotranspiration from P–T, Dual Kc, and S–W Models against Measurements Using a Large Weighing Lysimeter under Drip Irrigation in an Arid Area. Agriculture 2023, 13, 437. [Google Scholar] [CrossRef]








| Years | Items | W1 | W2 | W3 | W4 | W5 | W6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TDCC | p | TDCC | p | TDCC | p | TDCC | p | TDCC | p | TDCC | p | ||
| 2023 | WAGT | 0.775 | <0.01 | 0.758 | <0.01 | 0.847 | <0.01 | 0.738 | <0.01 | 0.725 | <0.01 | 0.712 | <0.01 |
| Yield | 0.786 | <0.01 | 0.723 | <0.01 | 0.768 | <0.01 | 0.747 | <0.01 | 0.708 | <0.01 | 0.756 | <0.01 | |
| 2024 | WAGT | 0.834 | <0.01 | 0.766 | <0.01 | 0.863 | <0.01 | 0.767 | <0.01 | 0.832 | <0.01 | 0.789 | <0.01 |
| Yield | 0.778 | <0.01 | 0.709 | <0.01 | 0.787 | <0.01 | 0.872 | <0.01 | 0.756 | <0.01 | 0.862 | <0.01 | |
| 2025 | WAGT | 0.767 | <0.01 | 0.722 | <0.01 | 0.885 | <0.01 | 0.745 | <0.01 | 0.824 | <0.01 | 0.752 | <0.01 |
| Yield | 0.824 | <0.01 | 0.706 | <0.01 | 0.759 | <0.01 | 0.854 | <0.01 | 0.732 | <0.01 | 0.816 | <0.01 | |
| Years | Items | W1 | W2 | W3 | W4 | W5 | W6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TDCC | p | TDCC | p | TDCC | p | TDCC | p | TDCC | p | TDCC | p | ||
| 2023 | WAGT | 0.821 | <0.01 | 0.801 | <0.01 | 0.883 | <0.01 | 0.844 | <0.01 | 0.763 | <0.01 | 0.892 | <0.01 |
| Yield | 0.746 | <0.01 | 0.658 | <0.01 | 0.757 | <0.01 | 0.665 | <0.01 | 0.754 | <0.01 | 0.767 | <0.01 | |
| 2024 | WAGT | 0.808 | <0.01 | 0.726 | <0.01 | 0.698 | <0.01 | 0.753 | <0.01 | 0.714 | <0.01 | 0.722 | <0.01 |
| Yield | 0.738 | <0.01 | 0.665 | <0.01 | 0.734 | <0.01 | 0.711 | <0.01 | 0.765 | <0.01 | 0.752 | <0.01 | |
| 2025 | WAGT | 0.767 | <0.01 | 0.785 | <0.01 | 0.776 | <0.01 | 0.816 | <0.01 | 0.763 | <0.01 | 0.843 | <0.01 |
| Yield | 0.676 | <0.01 | 0.661 | <0.01 | 0.712 | <0.01 | 0.704 | <0.01 | 0.697 | <0.01 | 0.726 | <0.01 | |
| Year | Parameter Set | R2 | d-Index | RMSE (kg·ha–1) | MAE (kg·ha–1) | NSE | RSR | Grade |
|---|---|---|---|---|---|---|---|---|
| 2023 | Default | 0.526 | 0.822 | 985.28 | 910.32 | 0.24 | 0.85 | Unacceptable |
| Optimized | 0.877 | 0.941 | 642.69 | 473.21 | 0.68 | 0.57 | Good | |
| 2024 | Default | 0.768 | 0.885 | 821.07 | 669.80 | 0.30 | 0.82 | Unacceptable |
| Optimized | 0.955 | 0.961 | 454.83 | 373.34 | 0.79 | 0.46 | Excellent | |
| 2025 | Default | 0.666 | 0.918 | 889.55 | 856.61 | 0.49 | 0.70 | Unacceptable |
| Optimized | 0.974 | 0.995 | 319.45 | 314.69 | 0.93 | 0.26 | Excellent |
| Soil Layer cm | Organic Matter g·kg−1 | Available P mg·kg−1 | Available K mg·kg−1 | Nitrate Nitrogen mg·kg−1 | Ammonium Nitrogen mg·kg−1 | Total N g·kg−1 | Total P g·kg−1 | Total K g·kg−1 | pH |
|---|---|---|---|---|---|---|---|---|---|
| 0~20 | 15.04 | 6.54 | 339.86 | 13.32 | 4.50 | 0.56 | 1.12 | 18.54 | 7.60 |
| 20~40 | 12.23 | 5.61 | 203.43 | 10.65 | 4.86 | 0.42 | 1.01 | 16.52 | 7.81 |
| 40~60 | 9.12 | 4.12 | 160.12 | 12.43 | 4.65 | 0.33 | 0.89 | 15.16 | 8.03 |
| Treatment | Seedling Period | Wintering Period | Greening Period | Jointing Period | Heading Period | Grain Filling Period | Maturity Period |
|---|---|---|---|---|---|---|---|
| W1 | 65 | 65 | 65 | 65 | 65 | 65 | 65 |
| 9.15% | 9.15% | 9.15% | 9.15% | 9.15% | 9.15% | 9.15% | |
| W2 | 65 | 65 | 65 | 65 | 50 | 50 | 65 |
| 9.15% | 9.15% | 9.15% | 9.15% | 13.07% | 13.07% | 9.15% | |
| W3 | 65 | 65 | 65 | 65 | 80 | 80 | 65 |
| 9.15% | 9.15% | 9.15% | 9.15% | 5.23% | 5.23% | 9.15% | |
| W4 | 65 | 65 | 80 | 80 | 65 | 65 | 65 |
| 9.15% | 9.15% | 5.23% | 5.23% | 9.15% | 9.15% | 9.15% | |
| W5 | 65 | 65 | 50 | 50 | 65 | 65 | 65 |
| 9.15% | 9.15% | 13.07% | 13.07% | 9.15% | 9.15% | 9.15% | |
| W6 | 65 | 65 | 50 | 50 | 50 | 65 | 65 |
| 9.15% | 9.15% | 13.07% | 13.07% | 13.07% | 9.15% | 9.15% |
| Abbreviation | Definition | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| P1 | potential daily grain filling rate during the grain filling period | g·grain−1·d−1 | 0.001 | 0.004 |
| P2 | potential daily grain filling rate from flowering to grain filling stage | g·grain−1·d−1 | 0.0005 | 0.0015 |
| P3 | daily potential grain nitrogen accumulation rate | g·grain−1·d−1 | 0.0000275 | 0.0000825 |
| M1 | lower limit of daily nitrogen accumulation rate in grains | g·grain−1·d−1 | 0.0000075 | 0.0000225 |
| P4 | crop photoperiod sensitivity index | / | 0 | 5 |
| V1 | crop vernalization sensitivity index | / | 0 | 5 |
| G1 | number of grains per unit stem | grain·g−1 | 10 | 40 |
| M2 | maximum grain weight per plant | g | 0.02 | 0.06 |
| T1 | accumulated temperature from seedling to jointing stage | °C·d | 200 | 600 |
| T2 | accumulated temperature from jointing to flowering period | °C·d | 250 | 800 |
| T3 | accumulated temperature from flowering to grain filling period | °C·d | 60 | 180 |
| T4 | accumulated temperature from grain filling to maturity | °C·d | 200 | 900 |
| K | extinction coefficient | / | 0 | 1 |
| R1 | light energy utilization rate | g·MJ−1 | 1.116 | 1.364 |
| Y1 | maximum specific leaf area | mm2·g−1 | 22,000 | 45,000 |
| I1 | leaf area at the beginning of the plant | mm2 | 100 | 300 |
| S1 | slope of water stress in photosynthetic leaf aging | / | 0.05 | 0.15 |
| E1 | crop water demand | / | 0.75 | 2.25 |
| N1 | multiple effects of nitrogen deficiency on photosynthesis | / | 0.75 | 2.25 |
| I2 | maximum leaf area index of aging caused by shading | m2·m–2 | 3.5 | 10.5 |
| X1 | daily average temperature affects the grouting rate | / | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ai, P.; Ma, Y.; Fu, Q.; Ma, X. Global Sensitivity Analyses of the APSIM-Wheat Model at Different Soil Moisture Levels. Plants 2025, 14, 2608. https://doi.org/10.3390/plants14172608
Zhang Y, Ai P, Ma Y, Fu Q, Ma X. Global Sensitivity Analyses of the APSIM-Wheat Model at Different Soil Moisture Levels. Plants. 2025; 14(17):2608. https://doi.org/10.3390/plants14172608
Chicago/Turabian StyleZhang, Ying, Pengrui Ai, Yingjie Ma, Qiuping Fu, and Xiaopeng Ma. 2025. "Global Sensitivity Analyses of the APSIM-Wheat Model at Different Soil Moisture Levels" Plants 14, no. 17: 2608. https://doi.org/10.3390/plants14172608
APA StyleZhang, Y., Ai, P., Ma, Y., Fu, Q., & Ma, X. (2025). Global Sensitivity Analyses of the APSIM-Wheat Model at Different Soil Moisture Levels. Plants, 14(17), 2608. https://doi.org/10.3390/plants14172608








