Characteristics of Hydrodynamic Parameters of Different Understory Vegetation Patterns
Abstract
1. Introduction
2. Materials and Methods
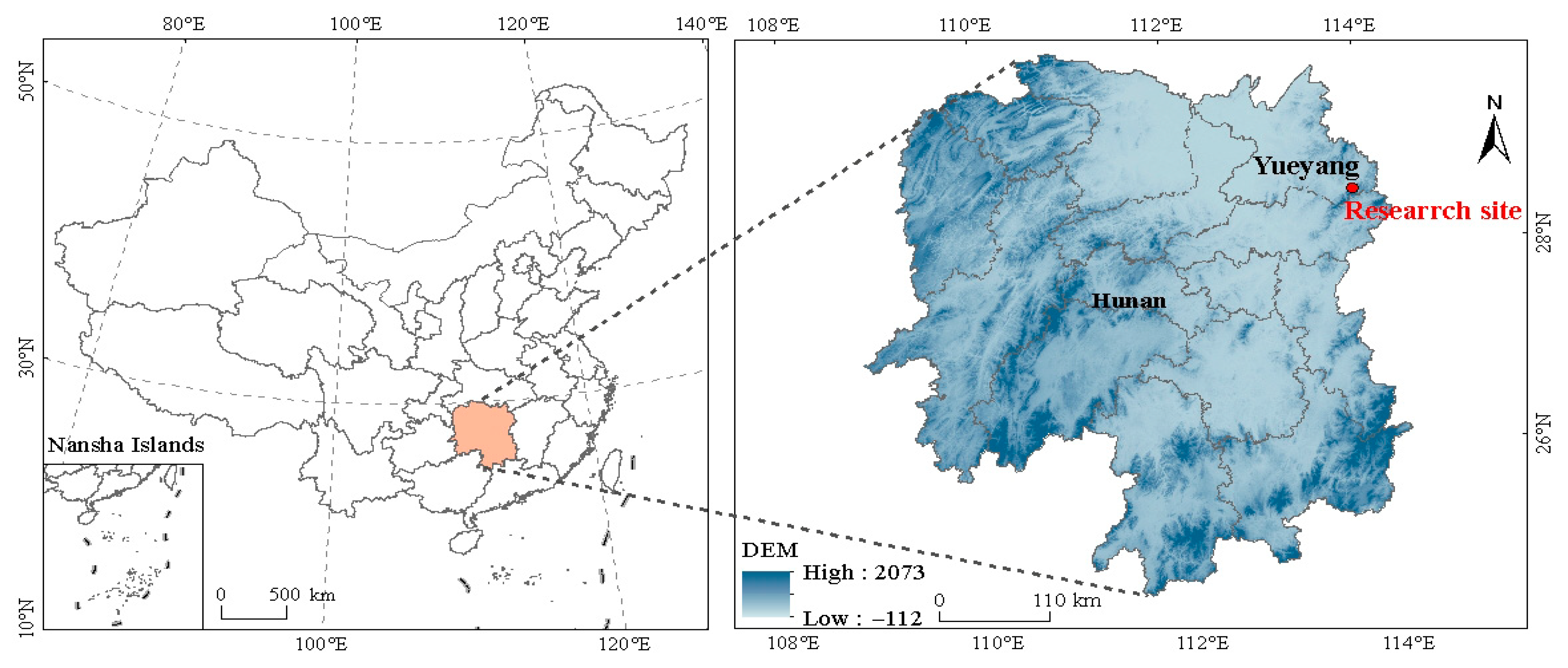
2.1. Study Area
2.2. Experiment Design
2.3. The Test Process
2.4. Indicator Calculation
- (1)
- The equation for calculating the average velocity of runoff is:
- (2)
- The runoff depth calculation equation is:
- (3)
- The Reynolds number is calculated using the following equation:
- (4)
- The Froude number is calculated using the following equation:
- (5)
- The calculation equation of Darcy–Weisbach resistance coefficient is:
- (6)
- The calculation equation of Manning roughness coefficient is:
- (7)
- The runoff shear stress is calculated using the following equation:
- (8)
- The runoff power is calculated using the following equation:
2.5. Data Analysis and Plotting Tools
3. Results and Analysis
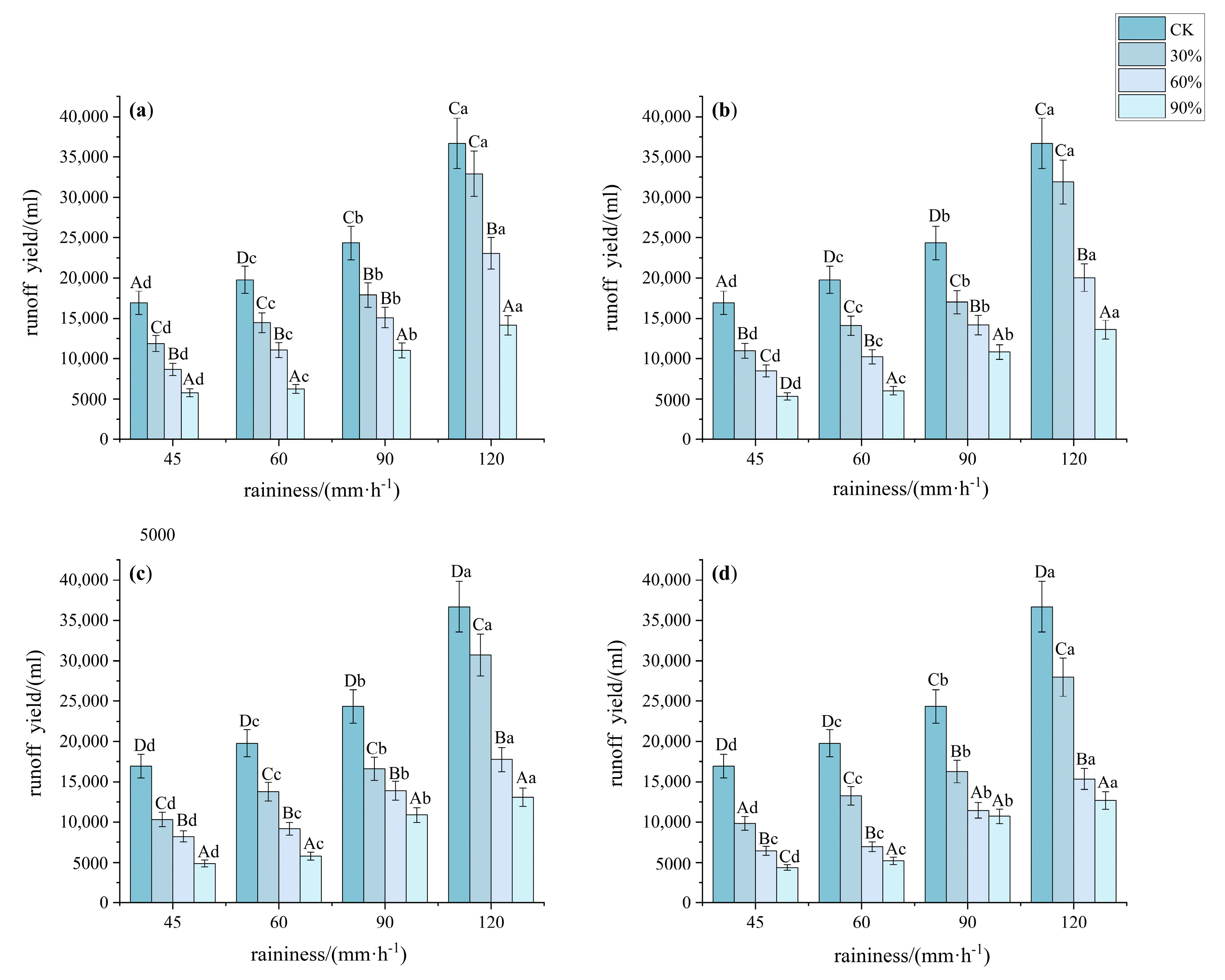
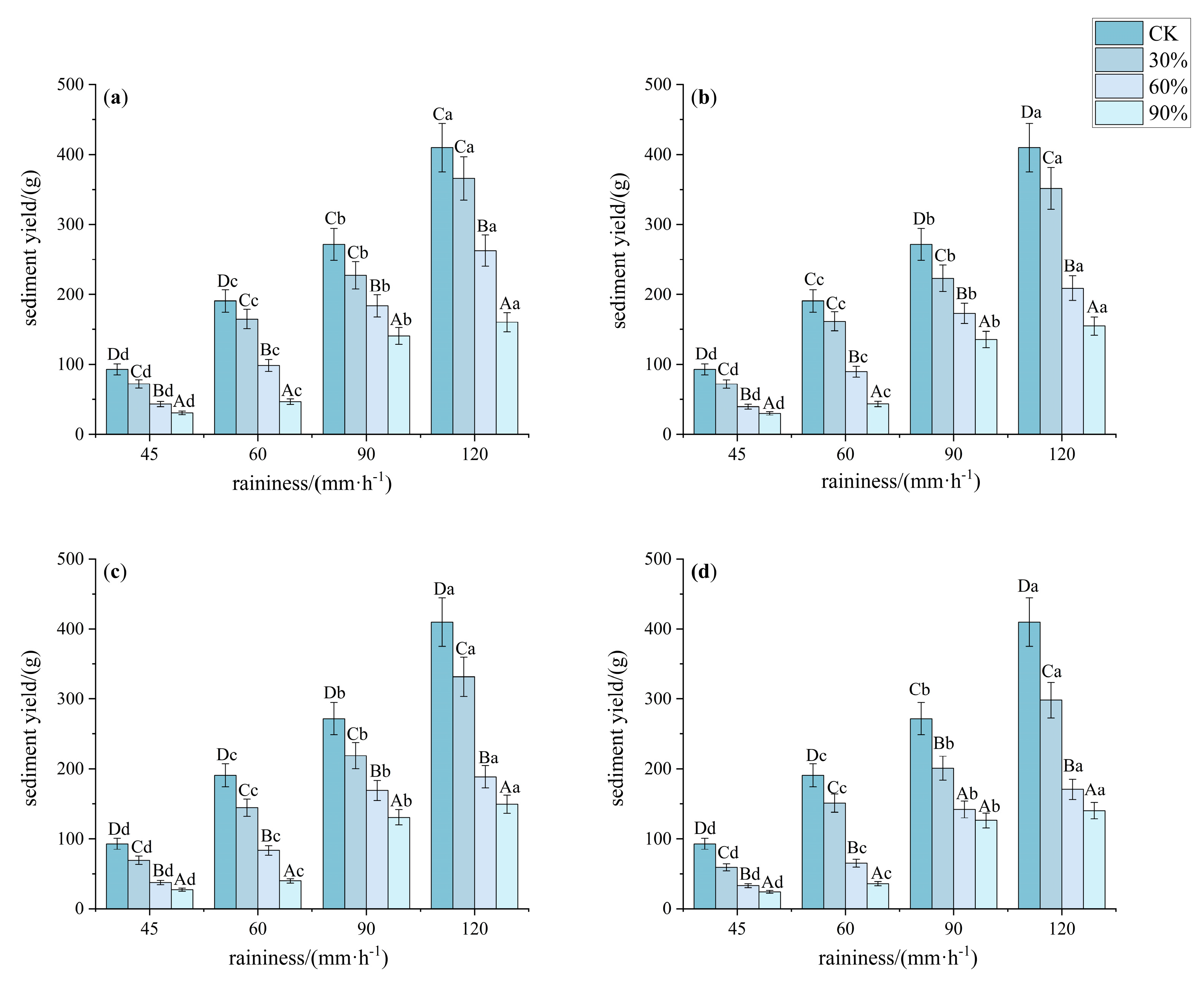
3.1. Characteristics of Runoff and Sediment Yield on Slopes Under Different Understory Vegetation Patterns
3.1.1. Characteristics of Slope Runoff Under Different Understory Vegetation Patterns
3.1.2. Characteristics of Slope Sediment Yield Under Different Understory Vegetation Patterns
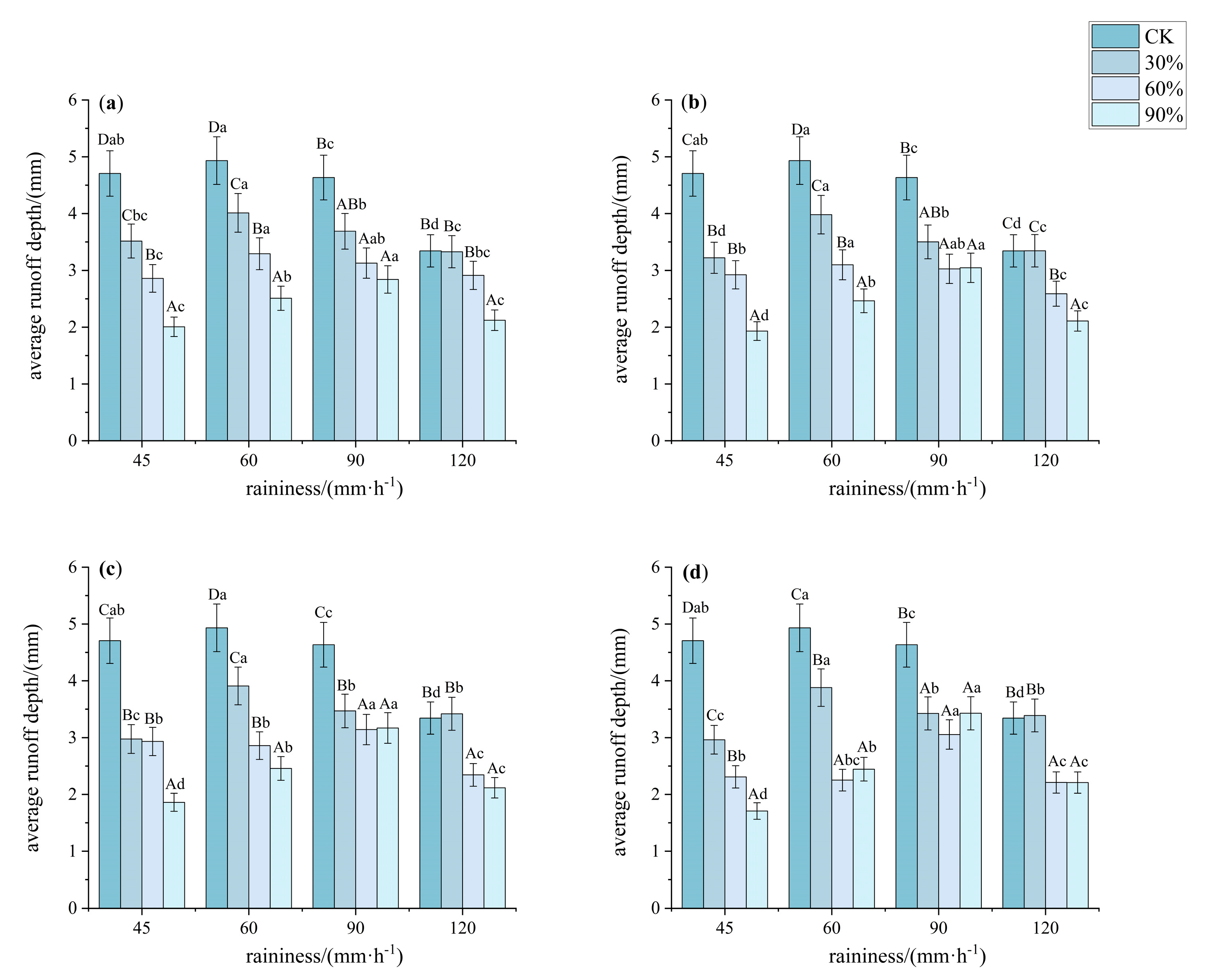
3.2. Characteristics of Slope Hydraulic Parameters Under Different Understory Vegetation Patterns
3.2.1. Average Flow Velocity and Average Runoff Depth of Slope Flow
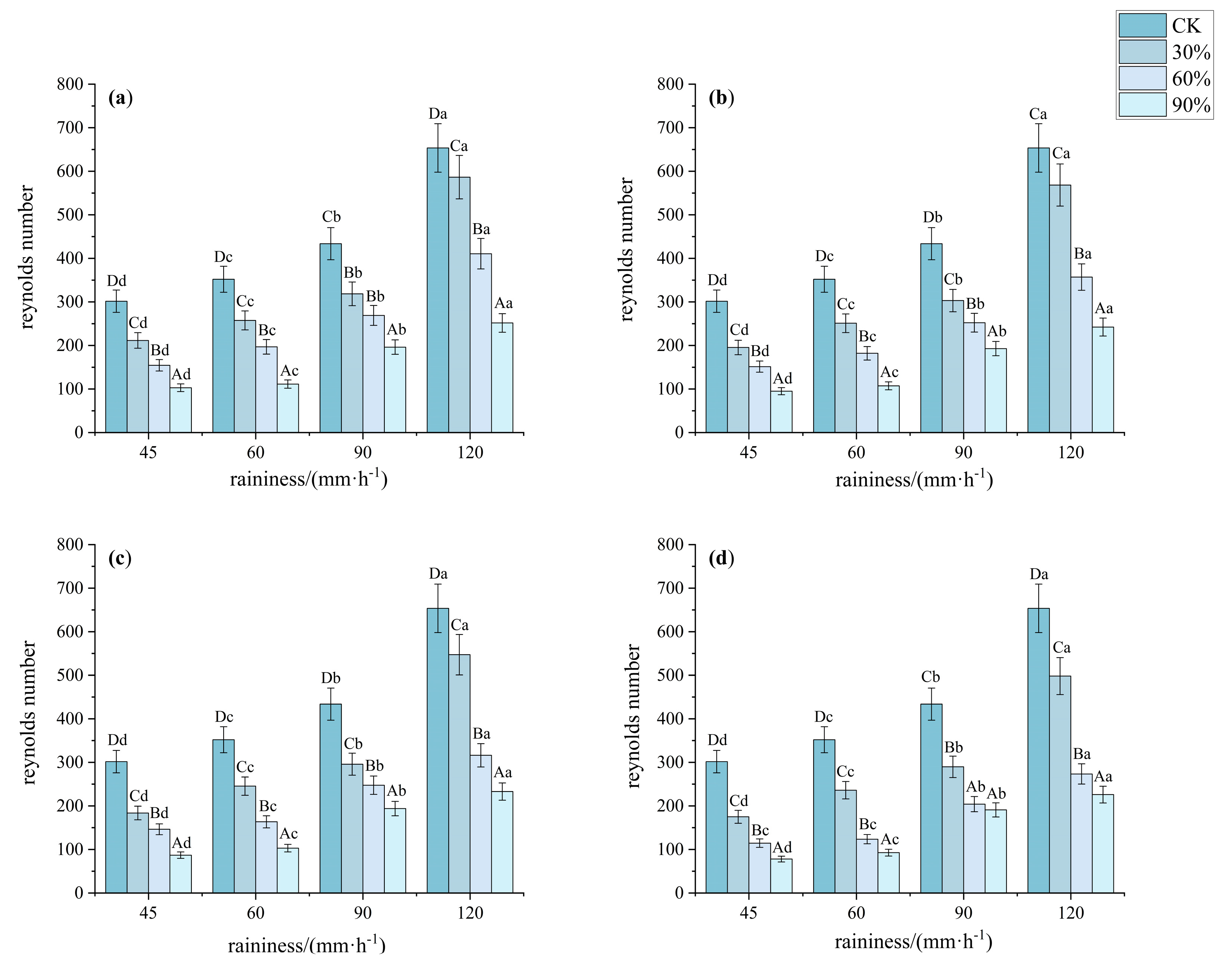
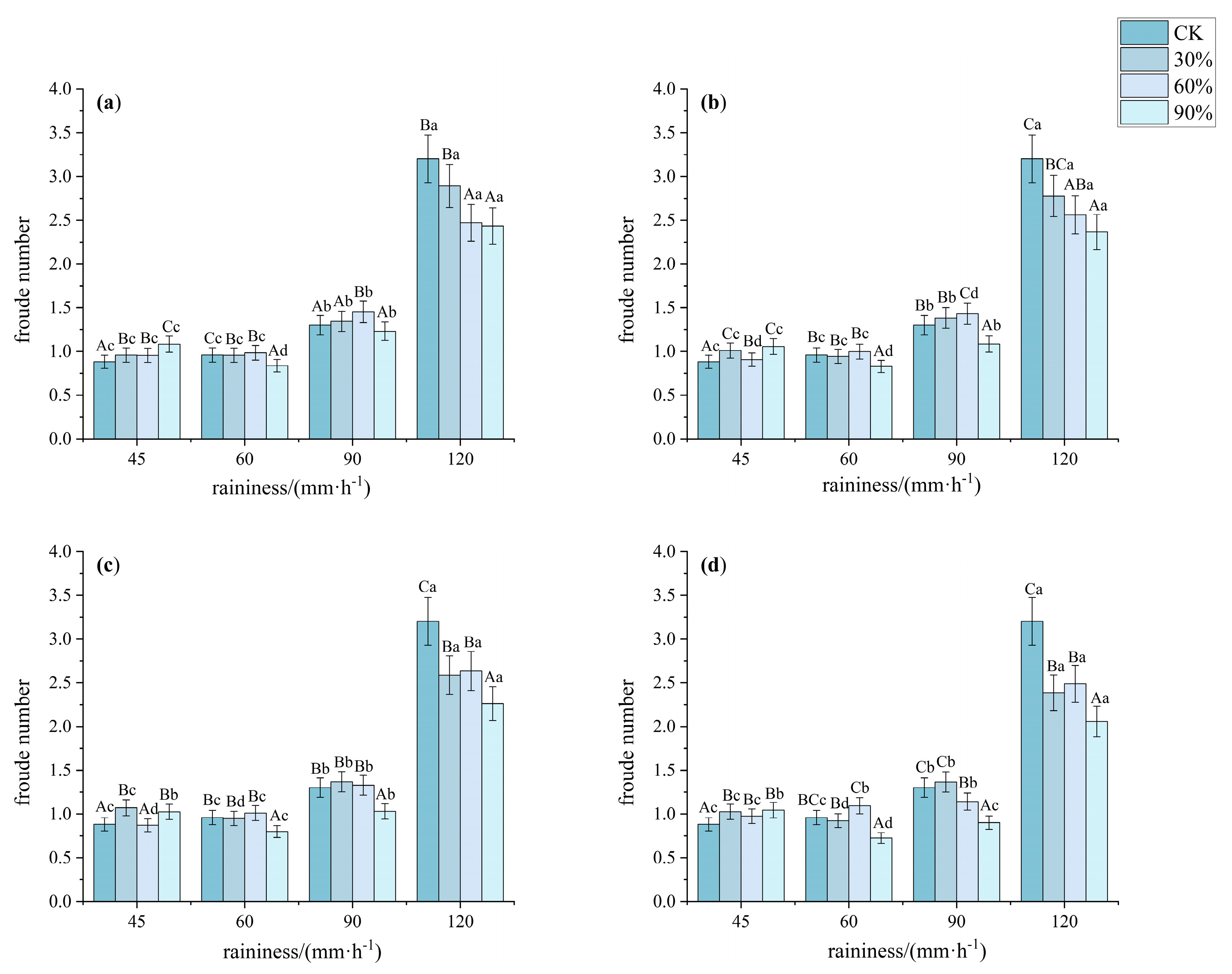
3.2.2. Reynolds Number and Froude Number
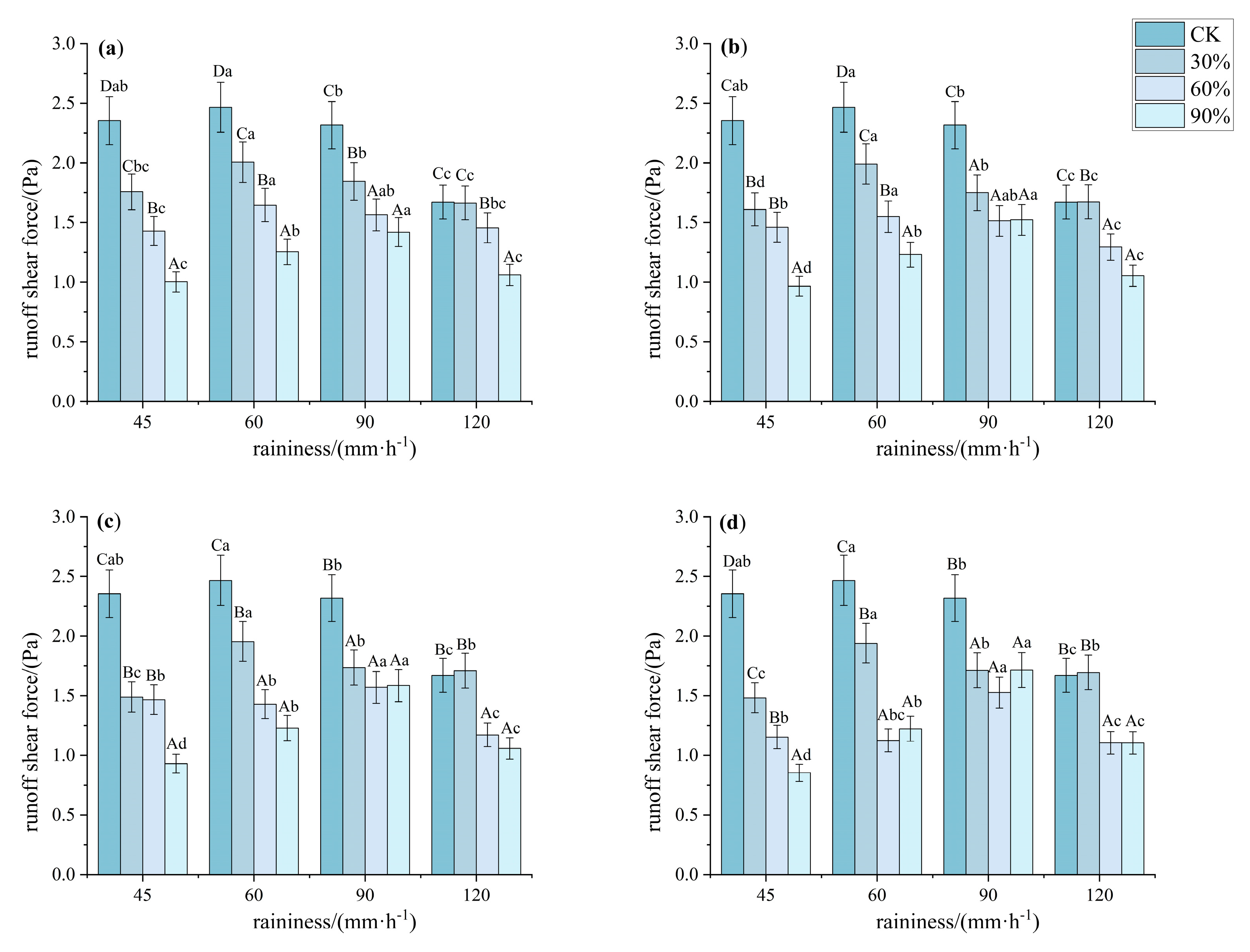
3.3. Characteristics of Slope Dynamic Parameters of Different Understory Vegetation Patterns
4. Discussion
4.1. Effects of Different Understory Vegetation Patterns on Runoff and Sediment Yield on Slopes
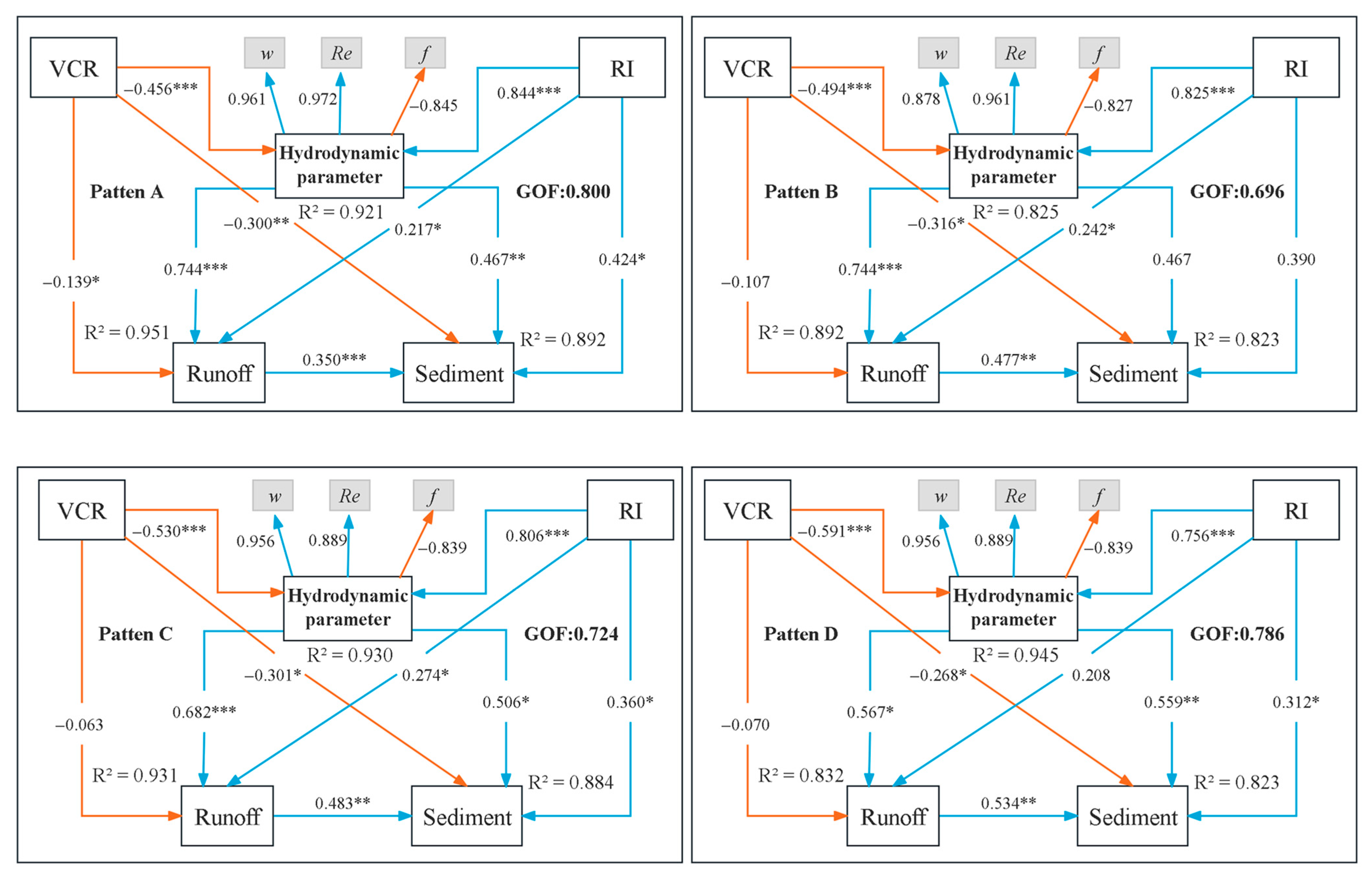
4.2. Effects of Different Understory Vegetation Patterns on Hydrodynamic Parameters of Overland Flow
4.3. Effects of Different Vegetation Patterns on Hydrodynamic Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guerra, C.A.; Rosa, I.M.; Valentini, E.; Wolf, F.; Filipponi, F.; Karger, D.N.; Nguyen Xuan, A.; Mathieu, J.; Lavelle, P.; Eisenhauer, N. Global vulnerability of soil ecosystems to erosion. Landsc. Ecol. 2020, 35, 823–842. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Panagos, P.; Lugato, E.; Yang, J.E.; Alewell, C.; Wuepper, D.; Montanarella, L.; Ballabio, C. Land use and climate change impacts on global soil erosion by water (2015–2070). Proc. Natl. Acad. Sci. USA 2020, 117, 21994–22001. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Wang, Z.; Zhang, X.; Chen, C.; Liu, H. The challenge of soil loss control and vegetation restoration in the karst area of southwestern China. Int. Soil Water Conserv. Res. 2020, 8, 26–34. [Google Scholar] [CrossRef]
- Schilling, K.E.; Jha, M.K.; Zhang, Y.K.; Gassman, P.W.; Wolter, C.F. Impact of land use and land cover change on the water balance of a large agricultural watershed: Historical effects and future directions. Water Resour. Res. 2008, 44, 7. [Google Scholar] [CrossRef]
- Zhao, L.; Fang, Q.; Hou, R.; Wu, F. Effect of rainfall intensity and duration on soil erosion on slopes with different microrelief patterns. Geoderma 2021, 396, 115085. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, H.; Li, Z.; Liu, C.; Wang, D.; Wang, L.; Tang, C. Threshold effects of vegetation coverage on soil erosion control in small watersheds of the red soil hilly region in China. Ecol. Eng. 2019, 132, 109–114. [Google Scholar] [CrossRef]
- Zuazo, V.H.D.; Pleguezuelo, C.R.R. Soil-erosion and runoff prevention by plant covers: A review. Sustain. Agric. 2009, 28, 65–86. [Google Scholar]
- Liu, Y.-F.; Liu, Y.; Shi, Z.-H.; Lopez-Vicente, M.; Wu, G.-L. Effectiveness of re-vegetated forest and grassland on soil erosion control in the semi-arid Loess Plateau. Catena 2020, 195, 104787. [Google Scholar] [CrossRef]
- Nilsson, M.-C.; Wardle, D.A. Understory vegetation as a forest ecosystem driver: Evidence from the northern Swedish boreal forest. Front. Ecol. Environ. 2005, 3, 421–428. [Google Scholar] [CrossRef]
- Han, C.; Liu, J.; Ding, Y.; Chai, P.; Bian, X. Recognition of area without understory vegetation based on the RGB-UAV ultra-high resolution images in red soil erosion area. Remote Sens. 2023, 15, 1470. [Google Scholar] [CrossRef]
- Li, G.; Wan, L.; Cui, M.; Wu, B.; Zhou, J. Influence of canopy interception and rainfall kinetic energy on soil erosion under forests. Forests 2019, 10, 509. [Google Scholar] [CrossRef]
- Neyret, M.; Robain, H.; De Rouw, A.; Janeau, J.-L.; Durand, T.; Kaewthip, J.; Trisophon, K.; Valentin, C. Higher runoff and soil detachment in rubber tree plantations compared to annual cultivation is mitigated by ground cover in steep mountainous Thailand. Catena 2020, 189, 104472. [Google Scholar] [CrossRef]
- Deng, J.; Fang, S.; Fang, X.; Jin, Y.; Kuang, Y.; Lin, F.; Liu, J.; Ma, J.; Nie, Y.; Ouyang, S. Forest understory vegetation study: Current status and future trends. For. Res. 2023, 3, 6. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, F.; Luo, Z.; Badreldin, N.; Benoy, G.; Xing, Z. Soil and water conservation effects of different types of vegetation cover on runoff and erosion driven by climate and underlying surface conditions. Catena 2023, 231, 107347. [Google Scholar] [CrossRef]
- Shi, P.; Li, P.; Li, Z.; Sun, J.; Wang, D.; Min, Z. Effects of grass vegetation coverage and position on runoff and sediment yields on the slope of Loess Plateau, China. Agric. Water Manag. 2022, 259, 107231. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Li, Z.B.; Yu, G.Q.; Li, C. Effects of precipitation and different distributions of grass strips on runoff and sediment in the loess convex hillslope. Catena 2018, 162, 130–140. [Google Scholar] [CrossRef]
- Zhu, B.; Li, Z.; Li, P.; You, Z. Effect of grass coverage on sediment yield of rain on slope. Int. J. Sediment Res. 2010, 47, 401–407. [Google Scholar]
- Dey, B.; Abir, K.A.M.; Ahmed, R.; Salam, M.A.; Redowan, M.; Miah, M.D.; Iqbal, M.A. Monitoring groundwater potential dynamics of north-eastern Bengal Basin in Bangladesh using AHP-Machine learning approaches. Ecol. Indic. 2023, 154, 110886. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, X. Effects of slope vegetation patterns on erosion sediment yield and hydraulic parameters in slope-gully system. Ecol. Indic. 2022, 145, 109723. [Google Scholar] [CrossRef]
- Sun, W.; Mu, X.; Gao, P.; Zhao, G.; Li, J.; Zhang, Y.; Chiew, F. Landscape patches influencing hillslope erosion processes and flow hydrodynamics. Geoderma 2019, 353, 391–400. [Google Scholar] [CrossRef]
- Chen, X.; Liang, Z.; Zhang, Z.; Zhang, L. Effects of soil and water conservation measures on runoff and sediment yield in red soil slope farmland under natural rainfall. Sustainability 2020, 12, 3417. [Google Scholar] [CrossRef]
- Léonard, J.; Richard, G. Estimation of runoff critical shear stress for soil erosion from soil shear strength. Catena 2004, 57, 233–249. [Google Scholar] [CrossRef]
- Xiao, P.; Yao, W.; Römkens, M.J.M. Effects of grass and shrub cover on the critical unit stream power in overland flow. Int. J. Sediment Res. 2011, 26, 387–394. [Google Scholar] [CrossRef]
- Tang, C.; Liu, Y.; Li, Z.; Guo, L.; Xu, A.; Zhao, J. Effectiveness of vegetation cover pattern on regulating soil erosion and runoff generation in red soil environment, southern China. Ecol. Indic. 2021, 129, 107956. [Google Scholar] [CrossRef]
- El Kateb, H.; Zhang, H.; Zhang, P.; Mosandl, R. Soil erosion and surface runoff on different vegetation covers and slope gradients: A field experiment in Southern Shaanxi Province, China. Catena 2013, 105, 1–10. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, G.; Wang, G. Effects of canopy and roots of patchy distributed Artemisia capillaris on runoff, sediment, and the spatial variability of soil erosion at the plot scale. Soil Sci. 2012, 177, 409–415. [Google Scholar] [CrossRef]
- Mhaske, S.N.; Pathak, K.; Basak, A. A comprehensive design of rainfall simulator for the assessment of soil erosion in the laboratory. Catena 2019, 172, 408–420. [Google Scholar] [CrossRef]
- Pan, C.; Shangguan, Z. Runoff hydraulic characteristics and sediment generation in sloped grassplots under simulated rainfall conditions. J. Hydrol. 2006, 331, 178–185. [Google Scholar] [CrossRef]
- Zhang, L.-T.; Gao, Z.-L.; Yang, S.-W.; Li, Y.-H.; Tian, H.-W. Dynamic processes of soil erosion by runoff on engineered landforms derived from expressway construction: A case study of typical steep spoil heap. Catena 2015, 128, 108–121. [Google Scholar] [CrossRef]
- Hou, G.; Bi, H.; Huo, Y.; Wei, X.; Zhu, Y.; Wang, X.; Liao, W. Determining the optimal vegetation coverage for controlling soil erosion in Cynodon dactylon grassland in North China. J. Clean. Prod. 2020, 244, 118771. [Google Scholar] [CrossRef]
- Sun, J.; Fan, D.; Yu, X.; Li, H. Hydraulic characteristics of varying slope gradients, rainfall intensities and litter cover on vegetated slopes. Hydrol. Res. 2018, 49, 506–516. [Google Scholar] [CrossRef]
- Omidvar, E.; Hajizadeh, Z.; Ghasemieh, H. Sediment yield, runoff and hydraulic characteristics in straw and rock fragment covers. Soil Tillage Res. 2019, 194, 104324. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, Y.; Zhao, C.; Mao, J.; Li, Z.; Jia, L.; Zhang, Y.; Wang, B. Effects of driving factors at multi-spatial scales on seasonal runoff and sediment changes. Catena 2023, 222, 106867. [Google Scholar] [CrossRef]
- Wang, J.; Fan, H.; Jia, Y. Spatial variation characteristics and influencing factors of sediment connectivity in the black soil region of northeast China. Geoderma 2024, 446, 116895. [Google Scholar] [CrossRef]
- Lou, Y.; Zhu, Y.; Wei, J.; Wang, W.; Guo, M.; Kang, H.; Feng, L.; Yang, H. Effects of vegetation on runoff hydrodynamics and erosion morphologies in headcut erosion processes in the loess tableland region. Water Resour. Res. 2025, 61, e2024WR038274. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Z.; Ren, Z.; Li, P.; Lu, K.; Li, C.; Tang, S.; Wang, T. Effect of different positions of grass strips on hydrological connectivity in slope-gully system. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2018, 34, 170–176. [Google Scholar]
- Shang, H.; Zhang, K.; Wang, Z.; Yang, J.; He, M.; Pan, X.; Fang, C. Effect of varying wheatgrass density on resistance to overland flow. J. Hydrol. 2020, 591, 125594. [Google Scholar] [CrossRef]
- Han, L.; Zeng, Y.; Chen, L.; Li, M. Modeling streamwise velocity and boundary shear stress of vegetation-covered flow. Ecol. Indic. 2018, 92, 379–387. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Li, Z.B.; Yu, G.Q. Effects of grass strips distribution on soil erosion and its optimal configuration on hillslopes. Catena 2024, 238, 107882. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Calomino, F.; Alfonsi, G.; Lauria, A. Flow resistance in open channel due to vegetation at reach scale: A review. Water 2021, 13, 116. [Google Scholar] [CrossRef]
- Wang, T.; Li, P.; Liu, Y.; Hou, J.; Li, Z.; Ren, Z.; Cheng, S.; Zhao, J.; Hinkelmann, R. Experimental investigation of freeze-thaw meltwater compound erosion and runoff energy consumption on loessal slopes. Catena 2020, 185, 104310. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Wang, Y.; Wang, Y.; Zhang, W. Improved interrill erosion prediction by considering the impact of the near-surface hydraulic gradient. Soil Tillage Res. 2020, 203, 104687. [Google Scholar] [CrossRef]
- Li, C.; Pan, C. Overland runoff erosion dynamics on steep slopes with forages under field simulated rainfall and inflow. Hydrol. Process. 2020, 34, 1794–1809. [Google Scholar] [CrossRef]
- Yan, Y.; Hu, Z.; Wang, L.; Jiang, J.; Dai, Q.; Gan, F.; Almaliki, A.H.; Hashim, M.A.; Hussein, E.E.; Ghoneim, S.S. Impact of extreme rainfall events on soil erosion on karst Slopes: A study of hydrodynamic mechanisms. J. Hydrol. 2024, 638, 131532. [Google Scholar] [CrossRef]
- Zhang, B.-J.; Zhang, G.-H.; Yang, H.-Y.; Zhu, P.-Z. Temporal variation in soil erosion resistance of steep slopes restored with different vegetation communities on the Chinese Loess Plateau. Catena 2019, 182, 104170. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Jia, J.; Zhen, Q.; Zhang, X. Effect of vegetation on the flow pathways of steep hillslopes: Overland flow plot-scale experiments and their implications. Catena 2021, 204, 105438. [Google Scholar] [CrossRef]
- Shen, H.; Zheng, F.; Wen, L.; Han, Y.; Hu, W. Impacts of rainfall intensity and slope gradient on rill erosion processes at loessial hillslope. Soil Tillage Res. 2016, 155, 429–436. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wang, J.; Jia, J. Characteristics of Hydrodynamic Parameters of Different Understory Vegetation Patterns. Plants 2025, 14, 2556. https://doi.org/10.3390/plants14162556
Zhang C, Wang J, Jia J. Characteristics of Hydrodynamic Parameters of Different Understory Vegetation Patterns. Plants. 2025; 14(16):2556. https://doi.org/10.3390/plants14162556
Chicago/Turabian StyleZhang, Chenhui, Jiali Wang, and Jianbo Jia. 2025. "Characteristics of Hydrodynamic Parameters of Different Understory Vegetation Patterns" Plants 14, no. 16: 2556. https://doi.org/10.3390/plants14162556
APA StyleZhang, C., Wang, J., & Jia, J. (2025). Characteristics of Hydrodynamic Parameters of Different Understory Vegetation Patterns. Plants, 14(16), 2556. https://doi.org/10.3390/plants14162556






