Accuracy of Increment Core Method for Measuring Basic Wood Density and Moisture Content in Three Catalpa Species
Abstract
1. Introduction
2. Results and Discussion
3. Materials and Methods
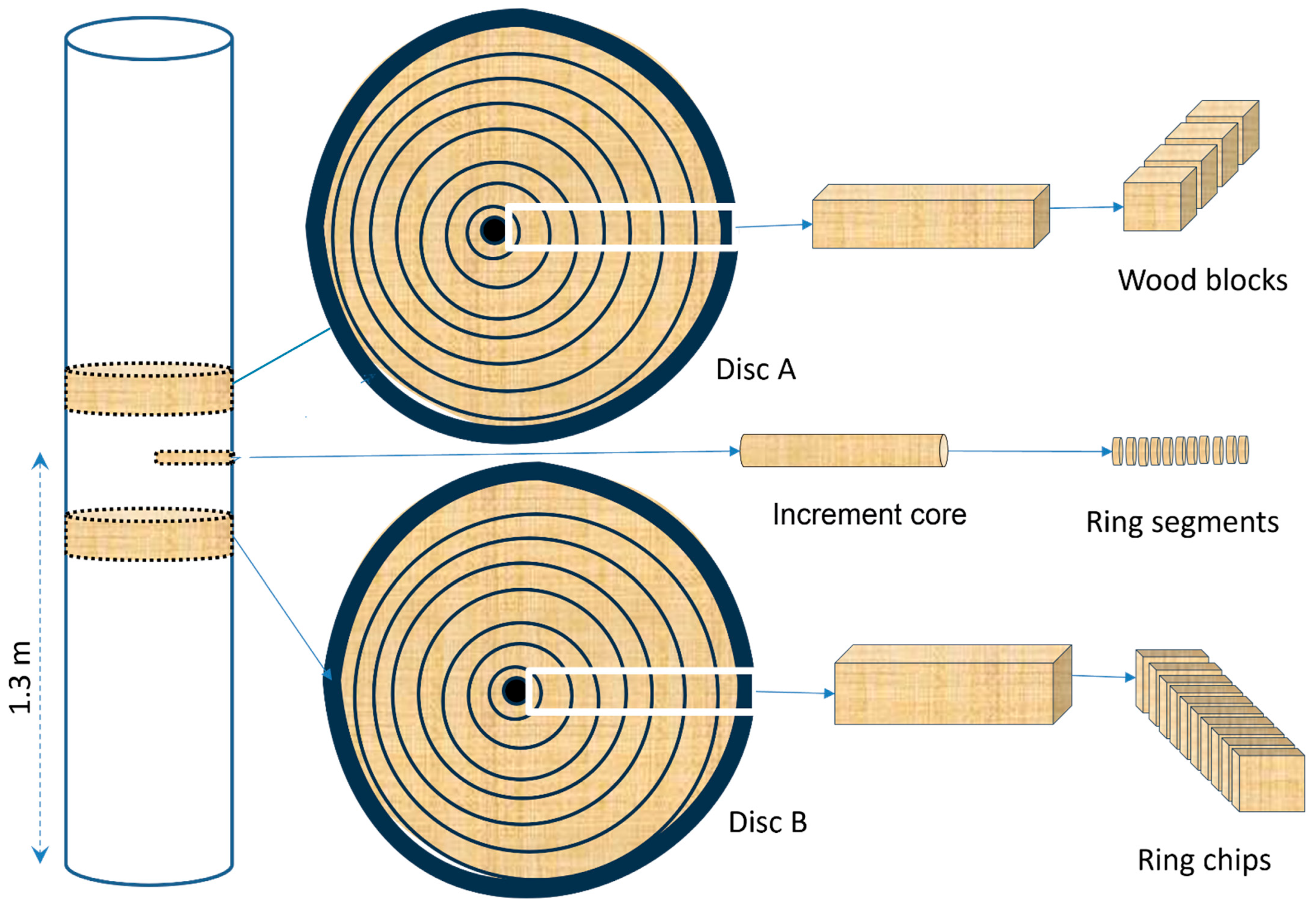
3.1. Sample Preparations
3.2. Determination of Basic Wood Density and Moisture Content
3.3. Statistical Analyses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC | Moisture content |
| WD | Wood density |
| S.D. | Standard deviation |
| C.V. | Coefficient of variation |
| SMC | Moisture content of ring segment |
| BMC | Moisture content of wood block |
| CMC | Moisture content of ring chip |
| SWD | Wood density of ring segment |
| BWD | Wood density of wood block |
| CWD | Wood density of ring chip |
| R2 | Square of regression coefficient |
| RMSE | Root mean square error |
| SL | Length of ring segments |
References
- Ji, G.; Cui, T. Utilization value and cultivation techniques of Catalpa bungei. For. By-Prod. Spec. China 2012, 35–37. [Google Scholar] [CrossRef]
- Ke, S.; Wang, C.; Liu, X.; Zi, X. Wood qualities and uses of Chinese Catalpa (Catalpa ovata G. Don). J. Anhui Agric. Univ. 1994, 21, 362–365. [Google Scholar]
- Ding, P.; Zhao, Q.; An, S. Analysis and evaluation of early wood character variation of Catalpa fargesii clones. J. Gansu For. Sci. Technol. 2024, 49, 11–17. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, S.; Wang, J.; Zhai, W.; Cui, Y.; Wang, Q. Timber physical and mechanical properties of new Catalpa bungei clones. Sci. Silvae Sin. 2013, 49, 126–134. [Google Scholar]
- Catalpa Wood. Sci. Am. 1878, 38, 395. [CrossRef]
- Wang, R.; Shi, L.; Wang, Y. Physical and mechanical properties of Catalpa bungei clones and estimation of the properties by near-Infrared spectroscopy. J. Renew. Mater. 2022, 10, 3285–3302. [Google Scholar] [CrossRef]
- Gilman, E.F.; Watson, D.G.; Klein, R.W.; Koeser, A.K.; Hilbert, D.R.; McLean, D.C. Catalpa spp.: Catalpa. In Environmental Horticulture; University of Florida: Gainesville, FL, USA, 2019. [Google Scholar]
- Jian, S.; Zhu, T.; Wang, J.; Yan, D. The current and future potential geographical distribution and evolution process of Catalpa bungei in China. Forests 2022, 13, 96. [Google Scholar] [CrossRef]
- Jiang, K. Overview of the current status and breeding cultivation of catalpa tree resources. Friends Farmers Get. Rich 2021, 13, 197. [Google Scholar]
- Guo, P.; Zhao, X.; Yang, Z.; Wang, Y.; Li, H.; Zhang, L. Water, starch, and nuclear behavior in ray parenchyma during heartwood formation of Catalpa bungei ‘Jinsi’. Heliyon 2024, 10, e27231. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Dergunov, D.R.; Belokopytova, L.V.; Zhirnova, D.F.; Upadhyay, K.K.; Tripathi, S.K.; Zharkov, M.S.; Vaganov, E.A. Non-linear response to cell number revealed and eliminated from long-term tracheid measurements of Scots pine in Southern Siberia. Front. Plant Sci. 2021, 12, 719796. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Zhao, X.; Wang, X.; Feng, Q.; Li, X.; Tan, Y. Wood density and carbon concentration jointly drive wood carbon density of five Rosaceae tree species. Forests 2024, 15, 1102. [Google Scholar] [CrossRef]
- Nakada, R.; Okada, N.; Nakai, T.; Kuroda, K.; Nagai, S. Water potential gradient between sapwood and heartwood as a driving force in water accumulation in wetwood in conifers. Wood Sci. Technol. 2019, 53, 407–424. [Google Scholar] [CrossRef]
- Petrea, S.; Radu, G.R.; Braga, C.I.; Cucu, A.B.; Serban, T.; Zaharia, A.; Pepelea, D.; Ienasoiu, G.; Petritan, I.C. The role of wood density variation and biomass allocation in accurate forest carbon stock estimation of European beech (Fagus sylvatica L.) mountain forests. Forests 2024, 15, 404. [Google Scholar] [CrossRef]
- Pompa-García, M.; Julio Camarero, J.; Vivar-Vivar, E.D. Contrasting climate drivers of seasonal growth in western vs. eastern Mexican mountain conifer forests. For. Ecosyst. 2023, 10, 100091. [Google Scholar] [CrossRef]
- Neo, L.; Ky, C.; Cy, K.; Sy, T.N.; Jw, L.; Rcj, L.; Ww, S.; Htw, T. Short-term external effects of increment coring on some tropical trees. J. Trop. For. Sci. 2017, 29, 519–529. [Google Scholar] [CrossRef]
- Park, B.B.; Lim, J.H.; Park, P.S.; Lee, K.H. Accuracy test of coring for measuring annual increment in Quercus mongolica, Kalopanax septemlobus, and Pinus densiflora. J. Korean For. Soc. 2010, 99, 682–685. [Google Scholar]
- Wahlgren, H.E.; Fassnacht, D.L. Estimating Tree Specific Gravity from a Single Increment Core; Rpt. 2146; Forest Products Laboratory U.S.: Madison, WI, USA, 1959; p. 9.
- Gilmore, A.R.; Metcalf, G.E.; Boggess, W.R. Specific gravity of shortleaf pine and loblolly pine in Southern Illinois. J. For. 1961, 59, 894–896. [Google Scholar]
- Tomczak, K.; Tomczak, A.; Jelonek, T. Measuring radial variation in basic density of pendulate oak: Comparing Increment core samples with the iml power drill. Forests 2022, 13, 589. [Google Scholar] [CrossRef]
- Dierickx, S.; Genbrugge, S.; Beeckman, H.; Hubau, W.; Kibleur, P.; van den Bulcke, J. Non-destructive wood identification using X-ray μCT scanning: Which resolution do we need? Plant Methods 2024, 20, 14. [Google Scholar] [CrossRef]
- Yang, T.; Wang, J.; Zhou, J. Recent research progress in X-ray spectrometry-based detection of wood moisture content. For. Mach. Woodwork. Equip. 2015, 43, 6–9. [Google Scholar] [CrossRef]
- Galleguillos-Hart, C.; Fernández, M.; Guesalaga, A. A portable method to estimate wood basic density from increment cores using spectroscopic techniques. J. Near Infrared Spectrosc. 2010, 18, 465–472. [Google Scholar] [CrossRef]
- Raymond, C.A.; Muneri, A. Nondestructive sampling of Eucalyptus globulus and E. nitens for wood properties. I. Basic density. Wood Sci. Technol. 2001, 35, 27–39. [Google Scholar] [CrossRef]
- Martínez, R.D.; Balmori, J.-A.; F. Llana, D.; Bobadilla, I. Wood density and moisture content estimation by drilling chips extraction technique. Materials 2020, 13, 1699. [Google Scholar] [CrossRef]
- Yao, X.; Shu-Jun, Y.; Gui-Juan, Y.; Ming-Gang, Z.; Fang-Qun, O.; Jun-Hui, W.; Wen-Jun, M. Early variations of wood property of Catalpa fargesii f. duclouxii clone and their evaluation. For. Res. 2019, 32, 79–87. [Google Scholar]
- Xiao, Y.; Yun, H.; Yang, G.; Ma, J.; Ma, W.; Qu, G.-Z. Genetic evaluation and combined selection for the simultaneous improvement of growth and wood properties in Catalpa bungei clones. Forests 2021, 12, 868. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Gao, J.; Wang, J. Micromorphological structure and physical properties of unearthed catalpa wood. J. Beijing For. Univ. 2008, 30, 134–138. [Google Scholar]
- Molteberg, D. Methods for the determination of wood properties, Kraft pulp yield and wood fibre dimensions on small wood samples. Wood Sci. Technol. 2004, 37, 395–410. [Google Scholar] [CrossRef]
- Young, P.J.; Cleaveland, M.K. Twisted increment cores: Getting it straight. Tree-Ring Bull. 2000, 56, 21–23. [Google Scholar]
- Pérez-Harguindeguy, N.; Diaz, S.; Garnier, E.; Lavorel, S.; Poorter, H.; Jaureguiberry, P.; Bret-Harte, M.S.; Cornwell, W.K.; Craine, J.; Gurvich, D.; et al. New handbook for standardise measurement of plant functional traits worldwide. Aust. J. Bot. 2013, 61, 167–234. [Google Scholar] [CrossRef]
- Thybring, E.E.; Fredriksson, M.; Zelinka, S.L.; Glass, S.V. Water in wood: A Review of current understanding and knowledge gaps. Forests 2022, 13, 2051. [Google Scholar] [CrossRef]
- GB/T 1927.5-2021; Test Methods for Physical and Mechanical Properties of Small Clear Wood Specimens—Part 5: Determination of Density. State Administration for Market Regulation: Beijing, China, 2021; pp. 1–12.
- Vermaas, H.F. Combination of a special water immersion method with the maximum moisture content method for bulk wood density determination. Holzforschung 1988, 42, 131–134. [Google Scholar] [CrossRef]
- Gendvilas, V.; Downes, G.M.; Neyland, M.; Hunt, M.; Jacobs, A.; O’Reilly-Wapstra, J. Friction correction when predicting wood basic density using drilling resistance. Holzforschung 2021, 75, 508–516. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Link, R.; Li, R.; Deng, L.; Schuldt, B.; Jiang, X.; Zhao, R.; Zheng, J.; Li, S.; et al. Influence of cambial age and axial height on the spatial patterns of xylem traits in Catalpa bungei, a ring-porous tree species native to China. Forests 2019, 10, 662. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, F.; Guo, P.; Feng, Q.; Wang, D.; Hao, Z. Distribution of starch in trunkwood of Catalpa bungei ‘Jinsi’: A revelation on the metabolic process of energy storage substances. Forests 2025, 16, 242. [Google Scholar] [CrossRef]
- GB/T 1927.4-2021; Test Methods for Physical and Mechanical Properties of Small Clear Wood Specimens—Part 4: Determination of Moisure Content. State Administration for Market Regulation: Beijing, China, 2021; pp. 1–11.
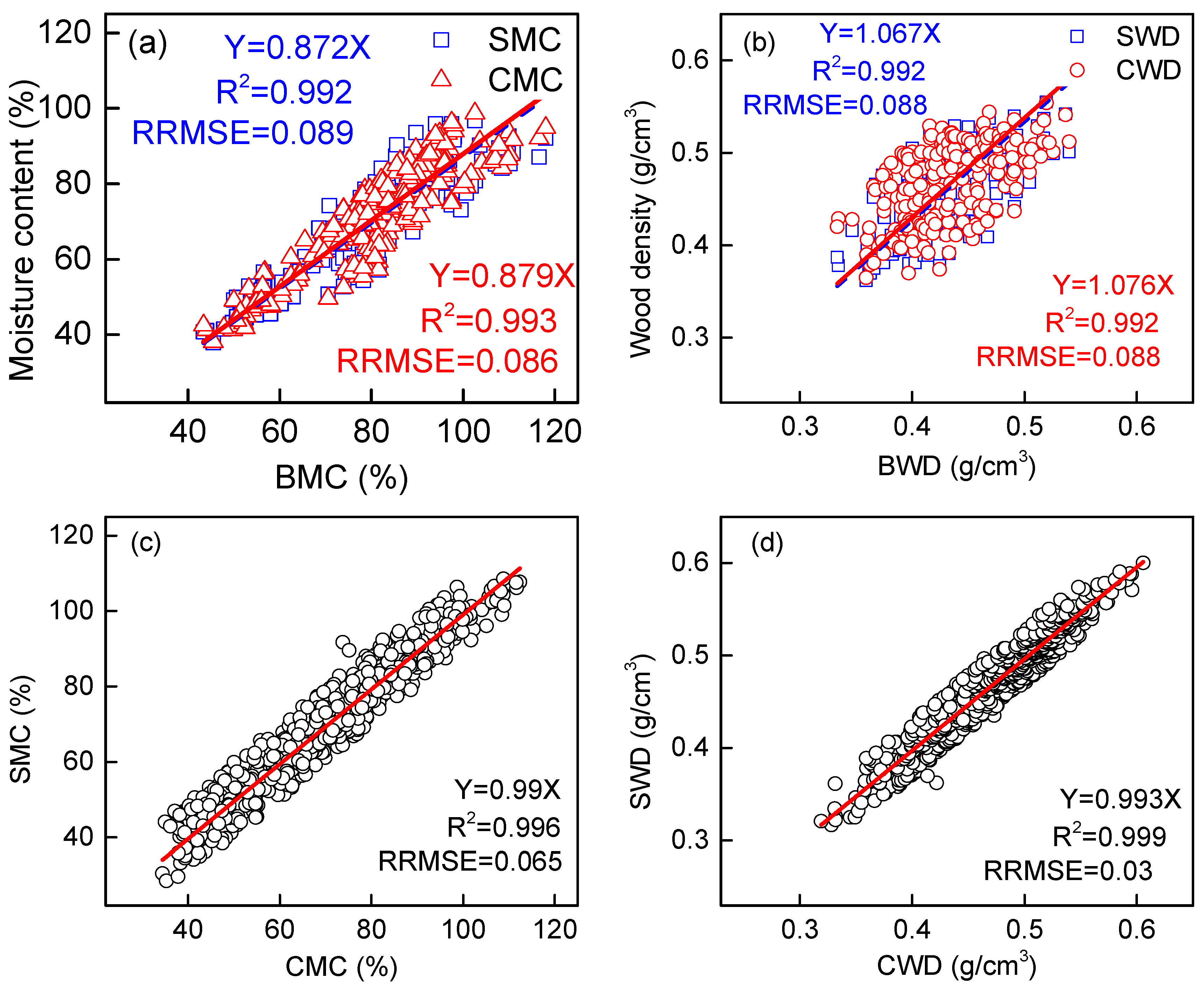
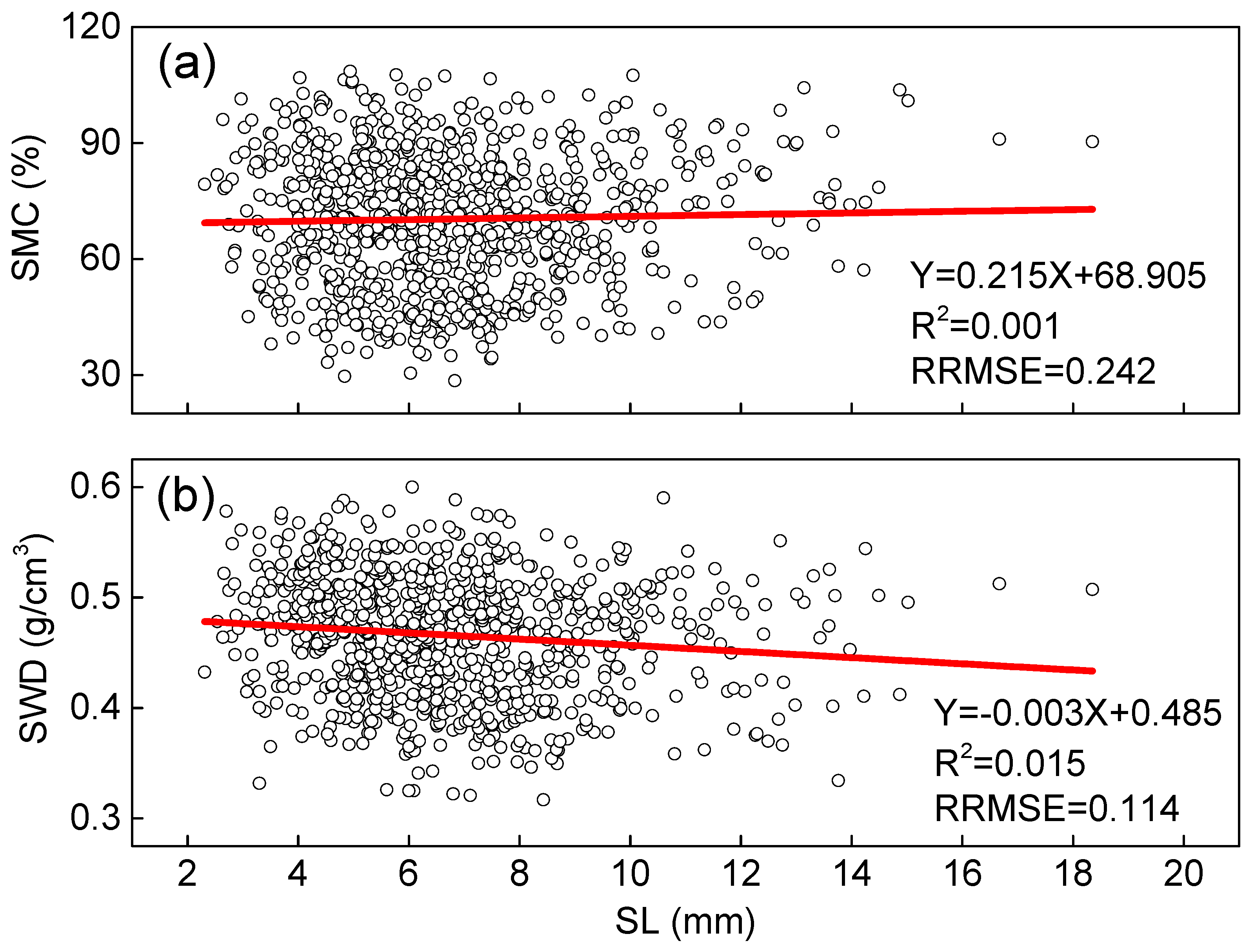
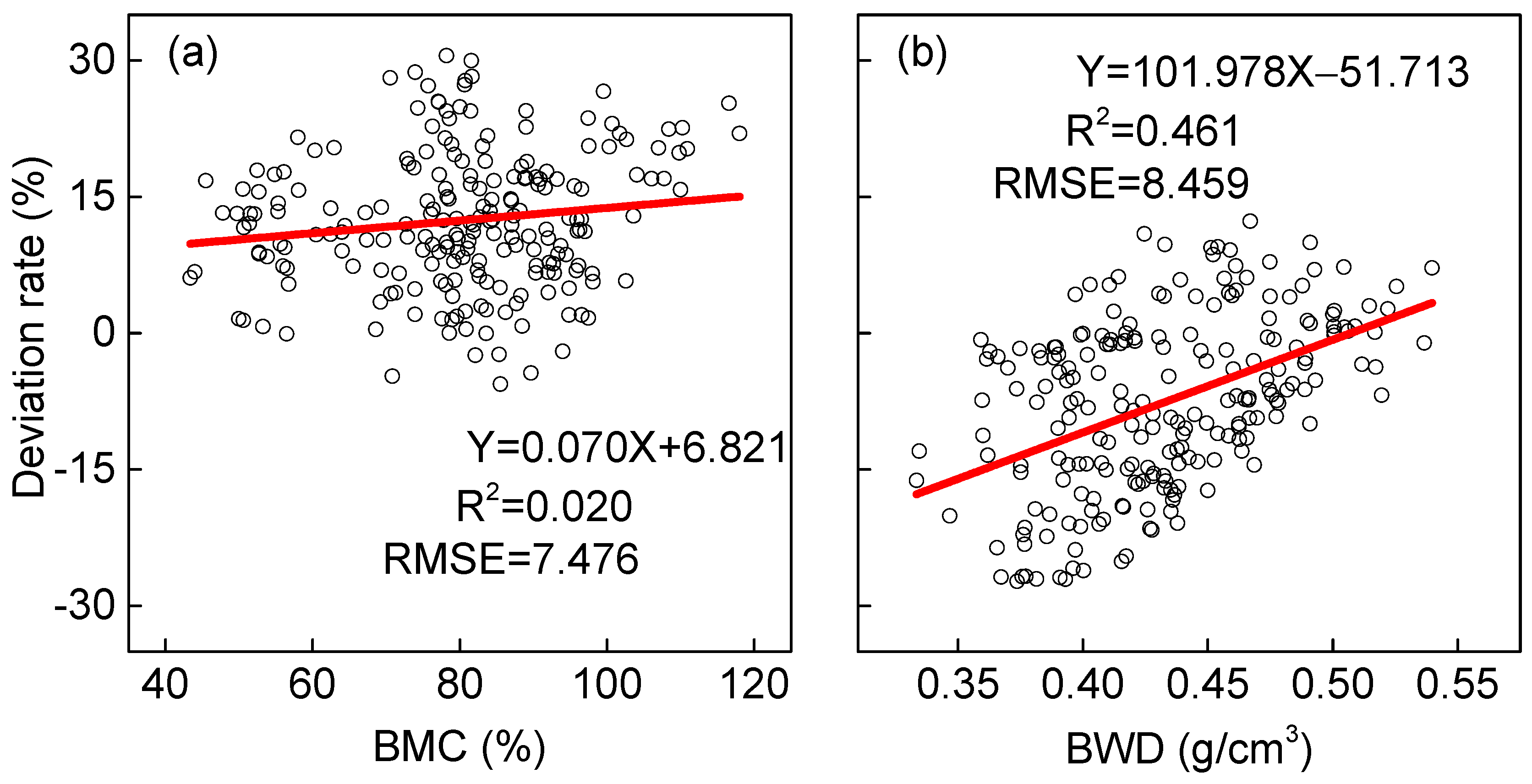
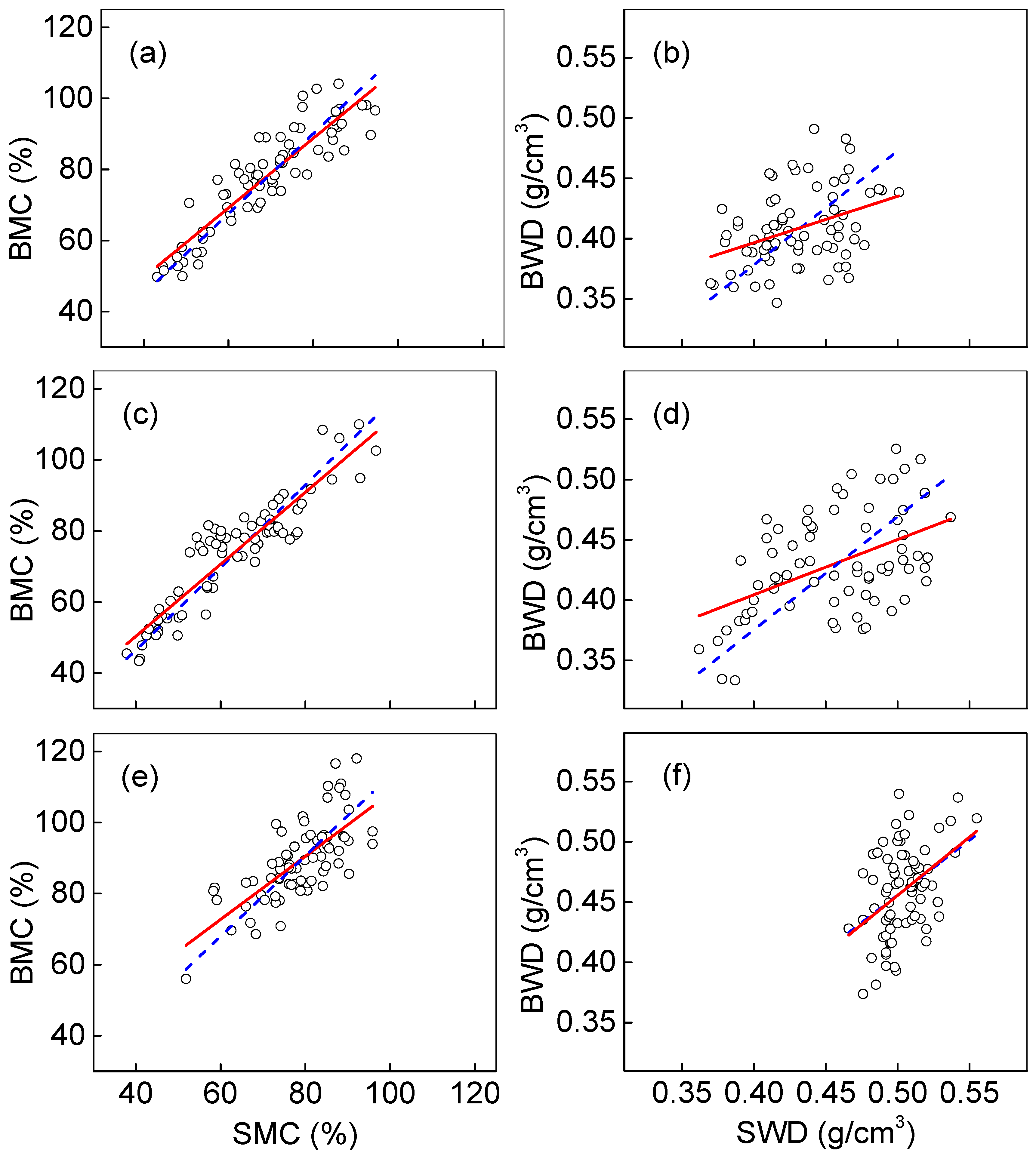

| Variable | Sample Shape | Number | Minimum | Maximum | Average | S.D. | C.V. |
|---|---|---|---|---|---|---|---|
| MC/% | Ring segment | 895 | 28.55 | 108.56 | 70.35 b | 16.99 | 0.24 |
| Ring chip | 894 | 34.40 | 112.38 | 70.89 b | 17.09 | 0.24 | |
| Wood block | 216 | 43.38 | 118.03 | 80.21 a | 15.29 | 0.19 | |
| WD/(g∙cm−3) | Ring segment | 895 | 0.32 | 0.60 | 0.47 a | 0.054 | 0.12 |
| Ring chip | 894 | 0.32 | 0.61 | 0.47 a | 0.05 | 0.11 | |
| Wood block | 216 | 0.33 | 0.54 | 0.43 b | 0.04 | 0.10 |
| Tree Species | Deviation Rate | |
|---|---|---|
| Moisture Content | Wood Density | |
| Catalpa bungei | 11.402 ± 0.829 b | −5.874 ± 1.047 b |
| Catalpa fargesii | 14.286 ± 0.862 a | −6.6 ± 1.363 b |
| Catalpa ovata | 11.501 ± 0.513 b | −10.316 ± 0.975 a |
| Variable | Tree Species | Linear Regression Equation | R2 | RRMSE |
|---|---|---|---|---|
| MC | Catalpa bungei | BMC = 1.125 × SMC | 0.993 | 0.083 |
| BMC = 0.978 × SMC + 10.480 | 0.821 | 0.080 | ||
| Catalpa fargesii | BMC = 1.162 × SMC | 0.993 | 0.088 | |
| BMC = 1.014 × SMC + 9.803 | 0.842 | 0.084 | ||
| Catalpa ovata | BMC = 1.132 × SMC | 0.992 | 0.091 | |
| BMC = 0.888 × SMC + 19.429 | 0.512 | 0.089 | ||
| WD | Catalpa bungei | BWD = 0.945 × SWD | 0.993 | 0.083 |
| BWD = 0.386 × SWD + 0.242 | 0.143 | 0.074 | ||
| Catalpa fargesii | Y = 0.938 × SWD | 0.990 | 0.10 | |
| BWD = 0.458 × SWD + 0.221 | 0.226 | 0.088 | ||
| Catalpa ovata | Y = 0.912 × SWD | 0.995 | 0.074 | |
| BWD = 0.967 × SWD − 0.028 | 0.171 | 0.074 |
| Species | Number | Diameter at Breast Height (cm) | Height (m) | Height of the Lowest Branch (m) |
|---|---|---|---|---|
| Catalpa bungei | 24 | 11.6 ± 1.6 | 8.4 ± 0.4 | 2.8 ± 0.4 |
| Catalpa fargesii | 24 | 12.3 ± 6.6 | 8.3 ± 1.7 | 2.7 ± 0.2 |
| Catalpa ovata | 24 | 11.4 ± 2.2 | 12.8 ± 0.3 | 2.4 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Wang, D.; Guo, P.; Feng, Q.; Deng, Y. Accuracy of Increment Core Method for Measuring Basic Wood Density and Moisture Content in Three Catalpa Species. Plants 2025, 14, 2339. https://doi.org/10.3390/plants14152339
Zhao X, Wang D, Guo P, Feng Q, Deng Y. Accuracy of Increment Core Method for Measuring Basic Wood Density and Moisture Content in Three Catalpa Species. Plants. 2025; 14(15):2339. https://doi.org/10.3390/plants14152339
Chicago/Turabian StyleZhao, Xiping, Dongfang Wang, Pingping Guo, Qi Feng, and Yuanping Deng. 2025. "Accuracy of Increment Core Method for Measuring Basic Wood Density and Moisture Content in Three Catalpa Species" Plants 14, no. 15: 2339. https://doi.org/10.3390/plants14152339
APA StyleZhao, X., Wang, D., Guo, P., Feng, Q., & Deng, Y. (2025). Accuracy of Increment Core Method for Measuring Basic Wood Density and Moisture Content in Three Catalpa Species. Plants, 14(15), 2339. https://doi.org/10.3390/plants14152339





