Wheat Soil-Borne Mosaic Virus Disease Detection: A Perspective of Agricultural Decision-Making via Spectral Clustering and Multi-Indicator Feedback
Abstract
1. Introduction
1.1. The Historical Context and Recent Advancements in Plants
1.2. LSGDM Models with Enhanced Spectral Clustering and Decision Indicator Sets
1.3. The Summary of Research Challenges and Motivations
- (1)
- How to address the ambiguity in field assessments caused by evaluator subjectivity, environmental noise, and symptom overlap with non-disease factors.
- (2)
- How to manage inconsistent evaluations and estimate missing trust relationships among geographically dispersed planting sites.
- (3)
- How to reduce decision complexity and effectively identify opinion divergence within ecologically similar subgroups.
- (4)
- How to structure the group decision-making process to ensure convergence, credibility, and interpretability of the final outcome.
- (1)
- Field-collected WSBM symptom data are encoded using IFNs to represent degrees of infection belief, skepticism, and hesitation, effectively capturing observation ambiguity and assessment uncertainty.
- (2)
- A trust network is constructed based on ecological similarity and spatial proximity. Missing or weak trust values are inferred via graph reasoning to ensure that regional influence and consistency are embedded in the evaluation process.
- (3)
- Combining numerical deviation and rank order differences, a customized distance metric is used to identify subgroups of plots with similar evaluation behaviors. This reduces complexity while preserving ecological interpretability.
- (4)
- ADISs derived from agricultural disease metrics guide iterative revisions of plot-level assessments until opinion differences are reconciled and consensus is achieved. Finally, using ADISs based on MGRS, the consensus matrix is processed to generate robust, explainable rankings of planting plots. This enables targeted interventions, such as deploying resistant varieties or applying localized treatments.
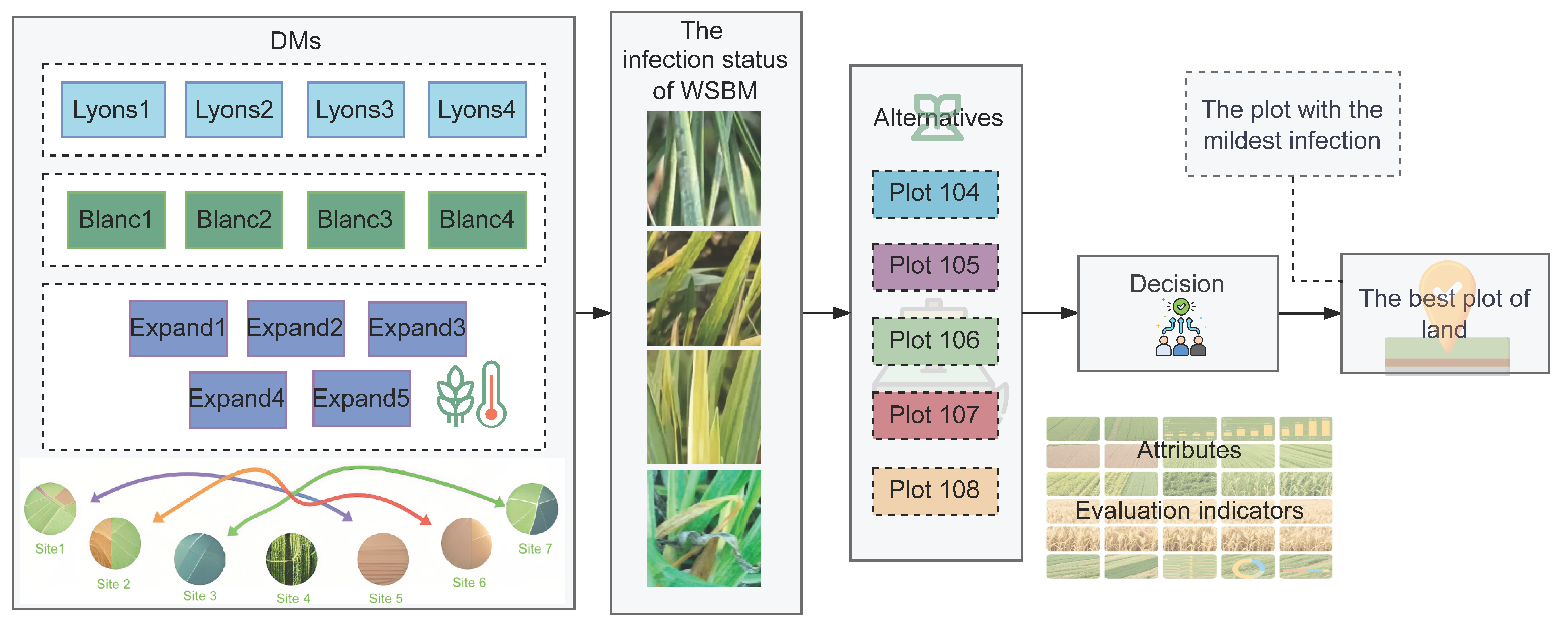
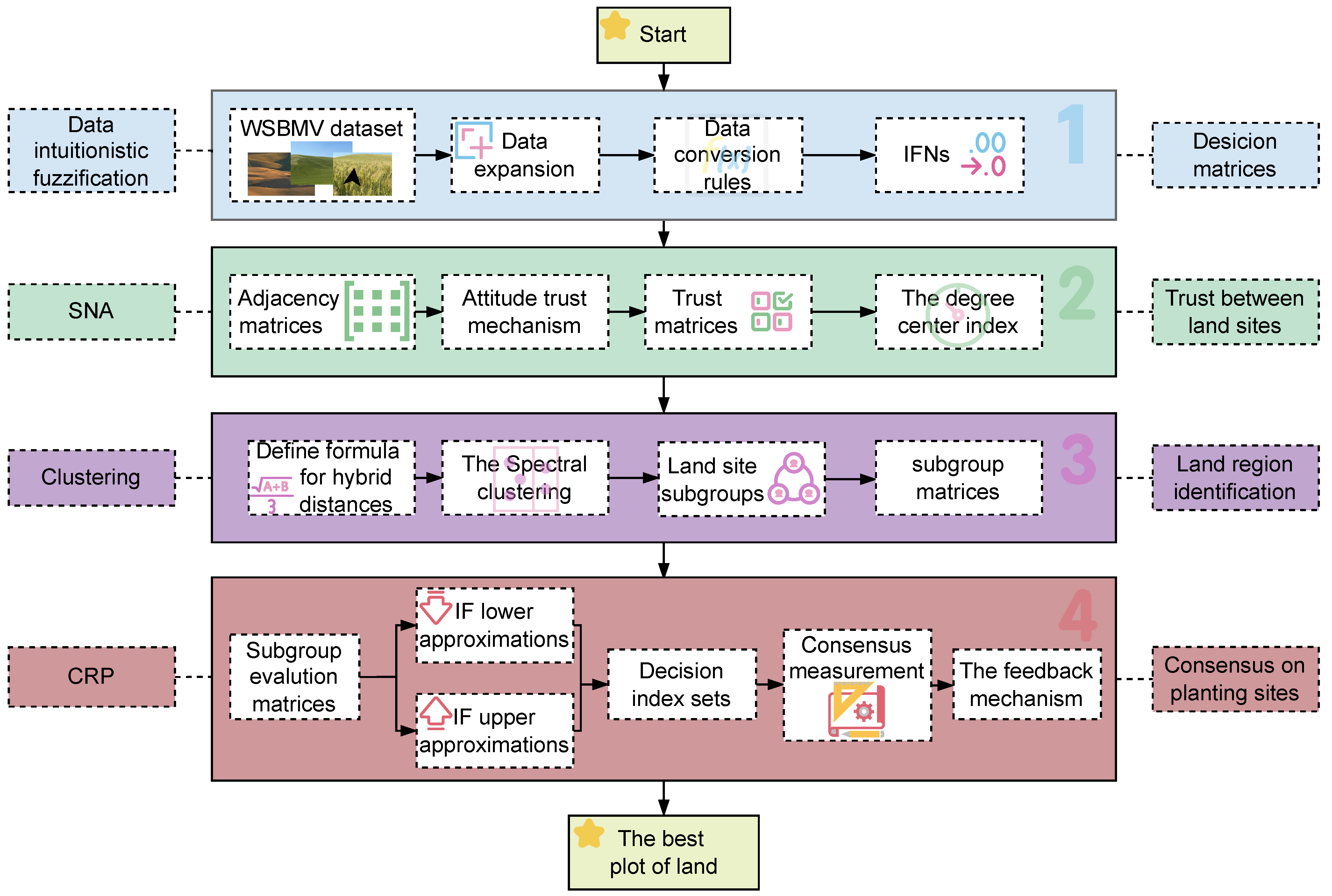
2. Materials and Methods
2.1. Datasets
2.1.1. Data Acquisition and Background
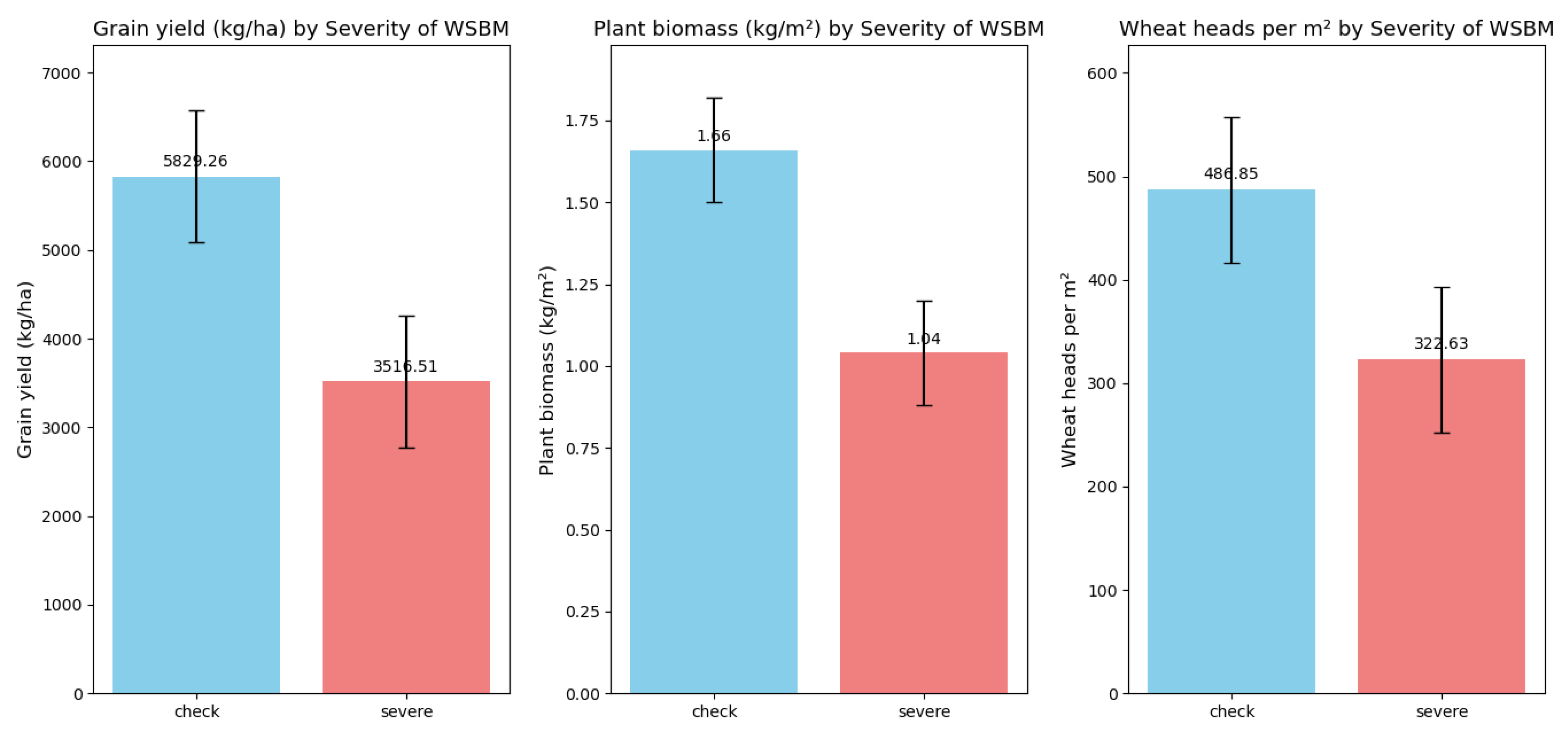
- Grain yield (kg/ha): Core for measuring wheat production. High yield means efficient conversion of resources to grains; low yield relates to poor pollination, affecting profits and supply.
- Above-ground biomass (kg/m2): Reflects photosynthetic capacity. More biomass supports grain development; less (due to stress) limits yield and reduces stress resistance.
- Wheat head count (heads/m2): A basic yield-structuring index. Proper count (via density/management) balances population and individual growth for more grains.
- Spikelets per head: Determines potential grains per ear. Affected by genetics and environment; more spikelets (with good conditions) boost yield potential.
- Test weight (kg/l): Shows grain quality/fullness. Higher weight means better quality (more starch, good for milling); lower weight signals poor grain development from stress, linking to yield/quality.
2.1.2. Data Preprocessing and Transformation into Intuitionistic Fuzzy Numbers
2.2. Methodology
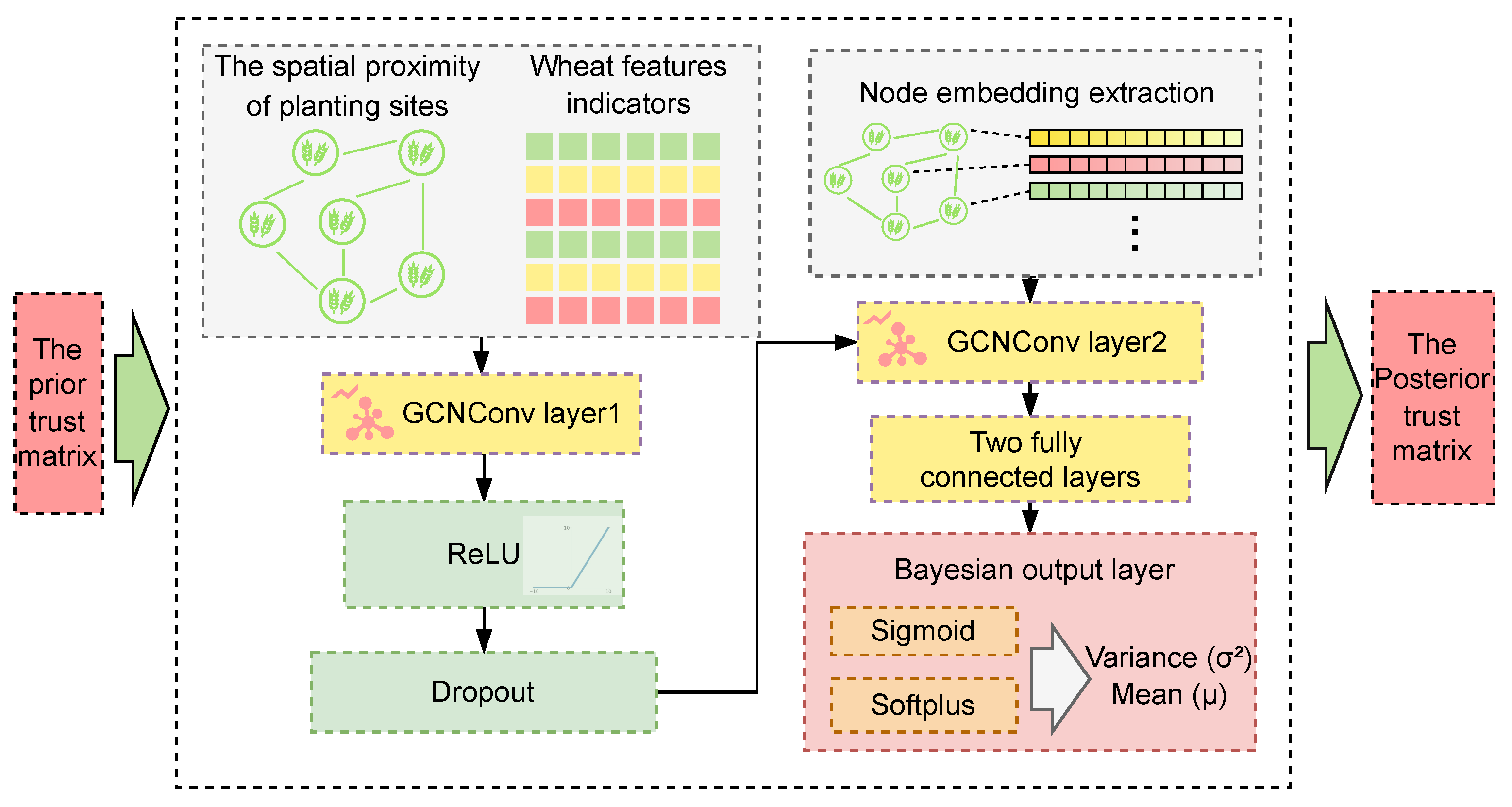
2.2.1. Trust Propagation Analysis of Planting Sites Based on Bayesian Graph Neural Model
2.2.2. The Similarity Analysis and Grouping of Planting Sites Based on Wheat Growth and Yield Indicators
| Algorithm 1. The enhanced spectral clustering with subgroup interpretation |
| Input:
Data points , a kernel bandwidth , the number of subgroups k Output: Subgroup labels , Step 1: Construct similarity matrix W for to n do for to n do Compute hybrid distance using Equation (6) Compute similarity end for end for Step 2: Compute graph Laplacian L Step 3: Eigendecomposition Compute eigenvectors and eigenvalues: Select top-k eigenvectors: Step 4: Embedding normalization for to n do Normalize row the vector end for Step 5: K-means clustering return Subgroup labels |
2.2.3. The Weight Calculation Framework
2.2.4. The Consensus Measurement with ADISs-MGRS
- (1)
- Lower approximation: Plots that are definitely considered severely infected under the subgroup definition, as shown in Equation (11)is the equivalence class of plot x under the index , where it is required that the plot is judged as the least infected among all similar plots.
- (2)
- Upper approximation: It indicates the existence of similar plots that belong to the least infected category, as shown in Equation (12).
- (1)
- Optimistic MGRSs: In the optimistic MGRS framework, a plot is deemed consensually severe if it appears in the lower or upper approximation of at least one subgroup. This embodies a permissive consensus rule, where granular support from any single subgroup (among b subgroups ) is sufficient to recognize severity. Mathematically, the optimistic membership degrees are calculated as Equations (13) and (14):where the indicator function marks membership (1) or non-membership (0) in these approximations, and averaging across subgroups quantifies the fraction of subgroups endorsing the plot’s severity (definite or possible).
- (2)
- Pessimistic MGRSs: A plot is deemed consensually severe under the pessimistic MGRS strategy only if it is present in the lower (or upper) approximation of all subgroups simultaneously. This reflects a strict consensus criterion, where a plot’s severity must be consistently recognized across every subgroup’s granular perspective. Mathematically, the pessimistic membership functions are defined as Equations (15) and (16):
- (1)
- Optimistic DIS:
- (2)
- Pessimistic DIS:
- (3)
- Conprehensive DIS:
- (1)
- Full consensus: When , it indicates consistent evaluation across granularity levels, and plot risk rankings can be directly generated;
- (2)
- Partial consensus: If and both hold, feedback adjustment mechanisms must be initiated for divergent indicators;
- (3)
- No consensus: When , systematic divergence is identified, so the feedback adjustment mechanisms must be initiated.
2.2.5. Feedback-Driven Preference Evolution and Consensus Convergence
- is the trust score of subgroup h from Bayesian-GCN inference;
- is the size of subgroup h;
- N is the total number of plots;
- is the learning rate;
- is the entropy control parameter.
| Algorithm 2 The CRP method based on ADISs-MGRS and feedback-driven weight adjustment |
| Input: Subgroup partitions , the initial subgroup weights , the initial target matrix Output: The final ranking result Step 1: The consensus measurement via ADISs-MGRS repeat Compute optimistic consensus using Equation (17) Compute pessimistic consensus using Equation (18) Compute comprehensive consensus using Equation (19) Check convergence condition: whether until Consensus is reached or maximum iterations exceeded Step 2: Subgroups weight update (trust-prospect-entropy-based) for each subgroup do Compute reference point using Equation (20) Compute deviation using Equation (21) Transform deviation into prospect utility using Equation (22) Compute adjustment factor capturing disagreement Using Equation (23) Aggregate total utility value using Equation (24) Update weights Using Equation (25) Normalize weights: ensure end for Step 3: The evaluation matrix feedback adjustment if Consensus stagnates then for each evaluation pair do Update membership using Equation (27) Update non-membership Using Equation (28) end for end if Step 4: Target matrix evolution Aggregate subgroup matrices using updated weights to obtain consensus matrix B Step 5: Output final result Compute comprehensive scores from return The final ranking |
3. Result
3.1. IFN Conversion: Embedding Diagnostic Uncertainty
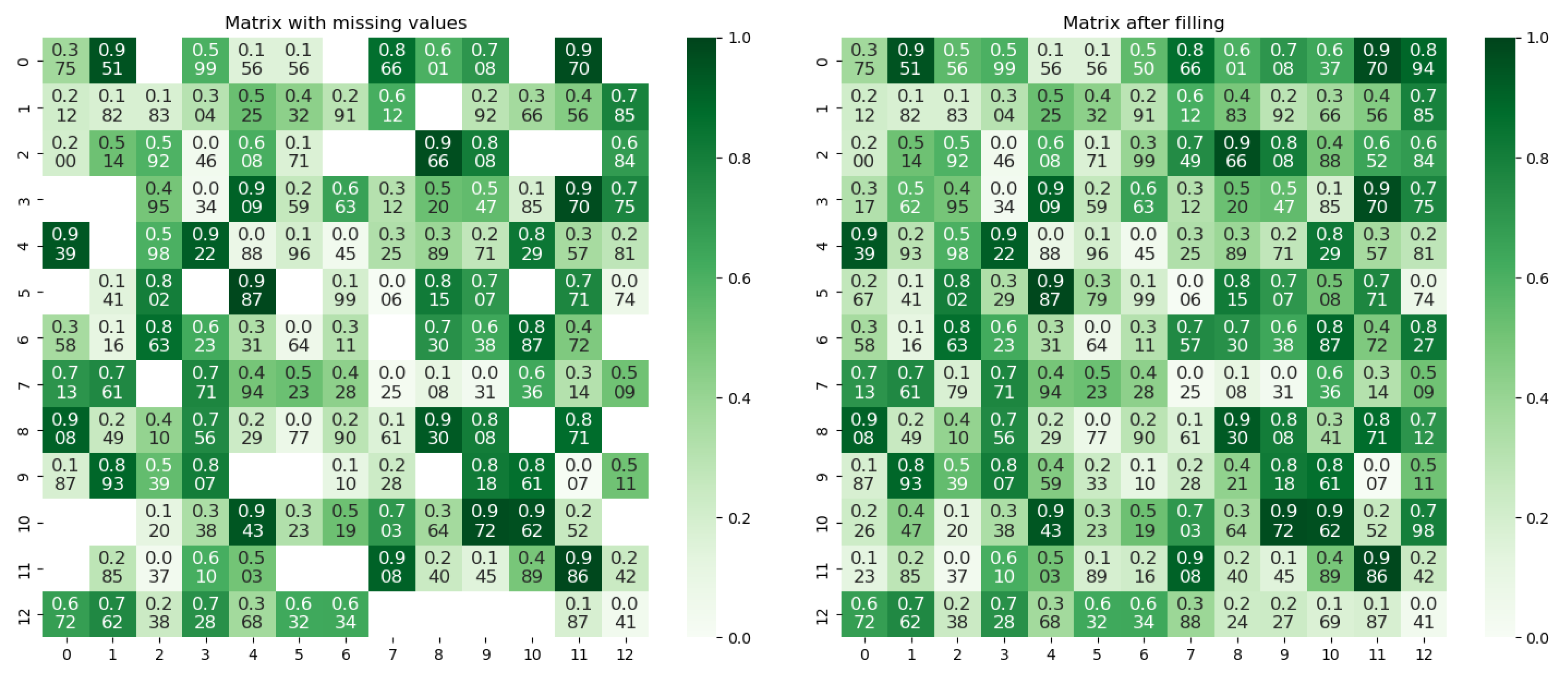
3.2. The Trust Matrix Completion: Based on Spatial–Ecological Similarity
3.3. The Enhanced Spectral Clustering: Eco-Cognitive Dual-Dimensional Grouping
3.4. The Weight Calculation and Subgroup Aggregation: Incorporating Trust Propagation
3.5. The Consensus Measurement: Different Subgroup of Planting Sites
3.6. Feedback Regulation: Iterative Optimization of Evaluation Consistency
4. Discussions
4.1. Sensitivity Analysis Under Agricultural Heterogeneity
4.1.1. The Impact of Distance Weighting Parameter on Plot Clustering Consistency
4.1.2. The Effect of Learning Rate () on CRP
4.2. Comparison Analysis
4.2.1. Ablation Study: Role of Key Modules in Agricultural Decision Making
4.2.2. Comparative Performance Evaluation with Existing Models
4.3. Theoretical and Practical Value of Plant-Based Decision Modeling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| The DMs’ evaluation matrices | |
Appendix B
| The matrix with missing values |
| The matrix after filling |
Appendix C
| The subgroup evaluation matrices | |
References
- Dolatabadian, A.; Neik, T.X.; Danilevicz, M.F.; Upadhyaya, S.R.; Batley, J.; Edwards, D. Image-based crop disease detection using machine learning. Plant Pathol. 2025, 74, 18–38. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Xia, W.K.; Chu, H.Q.; Su, W.H.; Wang, R.F.; Wang, H. A comprehensive review of deep learning applications in cotton industry: From field monitoring to smart processing. Plants 2025, 14, 1481. [Google Scholar] [CrossRef]
- Jose, A.; Nandagopalan, S.; Akana, C. Artificial intelligence techniques for agriculture revolution: A survey. Ann. Rom. Soc. Cell Biol. 2021, 25, 2580–2597. [Google Scholar]
- Rao, X.; Liu, W. A guide to metabolic network modeling for plant biology. Plants 2025, 14, 484. [Google Scholar] [CrossRef] [PubMed]
- Avila, F.; Barbosa, J. Smart environments in digital agriculture: A systematic review and taxonomy. Comput. Electron. Agric. 2025, 236, 110393. [Google Scholar] [CrossRef]
- González-Mon, B.; Mancilla-García, M.; Bodin, Ö.; Malherbe, W.; Sitas, N.; Pringle, C.; Biggs, R.; Schlüter, M. The importance of cross-scale social relationships for dealing with social-ecological change in agricultural supply chains. J. Rural Stud. 2024, 105, 103191. [Google Scholar] [CrossRef]
- Jafar, A.; Bibi, N.; Naqvi, R.; Sadeghi-Niaraki, A.; Jeong, D. Revolutionizing agriculture with artificial intelligence: Plant disease detection methods, applications, and their limitations. Front. Plant Sci. 2024, 15, 1356260. [Google Scholar] [CrossRef]
- Espinel, R.; Herrera-Franco, G.; Rivadeneira García, J.; Escandón-Panchana, P. Artificial intelligence in agricultural mapping: A review. Agriculture 2024, 14, 1071. [Google Scholar] [CrossRef]
- World Health Organization. The State of Food Security and Nutrition in the World 2019: Safeguarding Against Economic Slowdowns and Downturns; Food & Agriculture Org.: Rome, Italy, 2019. [Google Scholar]
- Agrios, G. Plant Pathology; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Saleem, S.; Hussain, A.; Majeed, N.; Akhtar, Z.; Siddique, K. A multi-scale feature extraction and fusion deep learning method for classification of wheat diseases. arXiv 2025, arXiv:2501.09938. [Google Scholar] [CrossRef]
- Krishnan, V.; Saradhi, M.; Dhanalakshmi, G.; Somu, C.; Theresa, W. Design of M3FCM based convolutional neural network for prediction of wheat disease. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 203. [Google Scholar]
- Upadhyay, A.; Chandel, N.; Singh, K.; Chakraborty, S.; Nandede, B.; Kumar, M.; Subeesh, A.; Upendar, K.; Salem, A.; Elbeltagi, A. Deep learning and computer vision in plant disease detection: A comprehensive review of techniques, models, and trends in precision agriculture. Artif. Intell. Rev. 2025, 58, 92. [Google Scholar] [CrossRef]
- Singh, J.; Chhabra, B.; Raza, A.; Yang, S.; Sandhu, K. Important wheat diseases in the US and their management in the 21st century. Front. Plant Sci. 2023, 13, 1010191. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, K.; Strauch, C.; Bonse, S.; Bauer, P.; Heidler, C.; Niehl, A. Detection and quantification of soil-borne wheat mosaic virus, soil-borne cereal mosaic virus and Japanese soil-borne wheat mosaic virus by ELISA and one-step SYBR Green real-time quantitative RT-PCR. Viruses 2024, 16, 1579. [Google Scholar] [CrossRef] [PubMed]
- Hariri, D.; Fouchard, M.; Prud’Homme, H. Incidence of soil-borne wheat mosaic virus in mixtures of susceptible and resistant wheat cultivars. Eur. J. Plant Pathol. 2001, 107, 625–631. [Google Scholar] [CrossRef]
- Yang, J.; Liu, P.; Zhong, K.; Ge, T.; Chen, L.; Hu, H.; Zhang, T.; Zhang, H.; Guo, J.; Sun, B.; et al. Advances in understanding the soil-borne viruses of wheat: From the laboratory bench to strategies for disease control in the field. Phytopathol. Res. 2022, 4, 27. [Google Scholar] [CrossRef]
- Okada, K.; Xu, W.; Mishina, K.; Oono, Y.; Kato, T.; Namai, K.; Komatsuda, T. Genetic resistance in barley against Japanese soil-borne wheat mosaic virus functions in the roots. Front. Plant Sci. 2023, 14, 1149752. [Google Scholar] [CrossRef]
- Liu, S.; Bai, G.; Lin, M.; Luo, M.; Zhang, D.; Jin, F.; Tian, B.; Trick, H.; Yan, L. Identification of candidate chromosome region of Sbwm1 for soil-borne wheat mosaic virus resistance in wheat. Sci. Rep. 2020, 10, 8119. [Google Scholar] [CrossRef]
- Kroese, D.R.; Schonneker, L.; Bag, S.; Frost, K.; Cating, R.; Hagerty, C.H. Wheat soil-borne mosaic: Yield loss and distribution in the US Pacific Northwest. Crop Prot. 2020, 132, 105102. [Google Scholar] [CrossRef]
- Haagsma, M.; Hagerty, C.H.; Kroese, D.R.; Selker, J.S. Detection of soil-borne wheat mosaic virus using hyperspectral imaging: From lab to field scans and from hyperspectral to multispectral data. Precis. Agric. 2023, 24, 1030–1048. [Google Scholar] [CrossRef]
- Ziegler, A.; Golecki, B.; Kastirr, U. Occurrence of the New York strain of soil-borne wheat mosaic virus in Northern Germany. J. Phytopathol. 2013, 161, 290–292. [Google Scholar] [CrossRef]
- Tidakbi, L.; Wang, H.; Bian, R.; Redila, C.; Zhu, D.; Amand, P.; Bernatdo, A.; Bruce, M.; Zhang, G.; Frita, A.; et al. Genome-wide association study identifies novel associations with barley yellow dwarf virus and soil-borne wheat mosaic virus resistance in winter wheat association mapping panel. Crop Sci. 2025, 65, e70016. [Google Scholar] [CrossRef]
- Ansari, R.; Manna, A.; Hazra, S.; Bose, S.; Chatterjee, A.; Sen, P. Breeding 4.0 vis-à-vis application of artificial intelligence (AI) in crop improvement: An overview. N. Z. J. Crop Hortic. Sci. 2024, 53, 812–854. [Google Scholar] [CrossRef]
- Zhang, T.; Cai, Y.; Zhuang, P.; Li, J. Remotely sensed crop disease monitoring by machine learning algorithms: A review. Unmanned Syst. 2024, 12, 161–171. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, W.; Wang, H. Crop disease monitoring and recognizing system by soft computing and image processing models. Multimed. Tools Appl. 2020, 79, 30905–30916. [Google Scholar] [CrossRef]
- Azizi, A.; Zhang, Z.; Rui, Z.; Li, Y.; Igathinathane, C.; Flores, P.; Mathew, J.; Pourreza, A.; Han, X.; Zhang, M. Comprehensive wheat lodging detection after initial lodging using UAV RGB images. Expert Syst. Appl. 2024, 238, 121788. [Google Scholar] [CrossRef]
- Devran, Z.; Goknur, A. Molecular diagnosis and differentiation of Meloidogyne arenaria, Meloidogyne javanica and Meloidogyne incognita using SNP-based KASP assays. Crop Prot. 2023, 174, 106388. [Google Scholar] [CrossRef]
- Gautam, D.; Mawardi, Z.; Elliott, L.; Loewensteiner, D.; Whiteside, T.; Brooks, S. Detection of invasive species (Siam weed) using drone-based imaging and YOLO deep learning model. Remote Sens. 2025, 17, 120. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, M.; Zeng, H.; Tian, F.; Potgieter, A.; Qin, X.; Yan, N.; Chang, S.; Zhao, Y.; Dong, Q.; et al. Challenges and opportunities in remote sensing-based crop monitoring: A review. Natl. Sci. Rev. 2023, 10, 290. [Google Scholar] [CrossRef]
- Nagasubramanian, G.; Sakthivel, R.K.; Patan, R.; Sankayya, M.; Daneshmand, M.; Gandomi, A.H. Ensemble classification and IoT-based pattern recognition for crop disease monitoring system. IEEE Internet Things J. 2021, 8, 12847–12854. [Google Scholar] [CrossRef]
- Chen, H.; Lin, M.; Liu, J.; Yang, H.; Zhang, C.; Xu, Z. NT-DPTC: A non-negative temporal dimension preserved tensor completion model for missing traffic data imputation. Inf. Sci. 2024, 653, 119797. [Google Scholar] [CrossRef]
- Lin, M.; Liu, J.; Chen, H.; Xu, X.; Luo, X.; Xu, Z. A 3D convolution-incorporated dimension preserved decomposition model for traffic data prediction. IEEE Trans. Intell. Transp. Syst. 2024, 26, 673–690. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Li, W. Incorporating artificial intelligence in detecting crop diseases: Agricultural decision-making based on group consensus model with MULTIMOORA and evidence theory. Crop Prot. 2024, 179, 106632. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Liu, H.; Wu, C.; Wan, Y.; Zhu, L.; Yang, J.; Cai, P.; Chen, J.; Ge, T. Combating wheat yellow mosaic virus through microbial interactions and hormone pathway modulations. Microbiome 2024, 12, 200. [Google Scholar] [CrossRef] [PubMed]
- Palomares, I.; Martinez, L.; Herrera, F. A consensus model to detect and manage noncooperative behaviors in large-scale group decision making. IEEE Trans. Fuzzy Syst. 2013, 22, 516–530. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, K.; Wang, P.; Wang, F. A clustering-and maximum consensus-based model for social network large-scale group decision making with linguistic distribution. Inf. Sci. 2022, 602, 269–297. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, C.; Li, D.; Li, W.; Zhan, J. A three-way large-scale group decision-making method integrating sentiment analysis and quantum interference-based prospect theory for the selection of new energy vehicles. Expert Syst. Appl. 2025, 275, 126940. [Google Scholar] [CrossRef]
- Li, J.; Niu, L.; Chen, Q.; Wang, Z.; Li, W. Group decision making method with hesitant fuzzy preference relations based on additive consistency and consensus. Complex Intell. Syst. 2022, 8, 2203–2225. [Google Scholar] [CrossRef]
- Yu, B.; Zheng, Z.; Xiao, Z.; Fu, Y.; Xu, Z. A large-scale group decision-making method based on group-oriented rough dominance relation in scenic spot service improvement. Expert Syst. Appl. 2023, 233, 120999. [Google Scholar] [CrossRef]
- Guo, L.; Zhan, J.; Zhang, C.; Xu, Z. A large-scale group decision-making method fusing three-way clustering and regret theory under fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2023, 32, 4846–4860. [Google Scholar] [CrossRef]
- Wu, X.; Nie, S.; Liao, H.; Gupta, P. A large-scale group decision making method with a consensus reaching process under cognitive linguistic environment. Int. Trans. Oper. Res. 2023, 30, 1340–1365. [Google Scholar] [CrossRef]
- Wu, X.; Liu, Q.; Liu, L.; Yang, M.; Zhang, X. New Jensen-Shannon divergence measures for intuitionistic fuzzy sets with the construction of a parametric intuitionistic fuzzy TOPSIS. Complex Intell. Syst. 2025, 11, 134. [Google Scholar] [CrossRef]
- Chaira, T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl. Soft Comput. 2011, 11, 1711–1717. [Google Scholar] [CrossRef]
- Wu, J.; Gou, F.; Tian, X. Disease control and prevention in rare plants based on the dominant population selection method in opportunistic social networks. Comput. Intell. Neurosci. 2022, 2022, 1489988. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Xu, Y.; Hao, W.; Yu, X. A signed network analysis-based consensus reaching process in group decision making. Appl. Soft Comput. 2021, 100, 106926. [Google Scholar] [CrossRef]
- Kalimuthu, T.; Kalpana, P.; Kuppusamy, S.; Sreedharan, V. Intelligent decision-making framework for agriculture supply chain in emerging economies: Research opportunities and challenges. Comput. Electron. Agric. 2024, 219, 108766. [Google Scholar] [CrossRef]
- Gemtou, M.; Kakkavou, K.; Anastasiou, E.; Fountas, S.; Pedersen, S.; Isakhanyan, G.; Erekalo, K.; Pazos-Vidal, S. Farmers’ transition to climate-smart agriculture: A systematic review of the decision-making factors affecting adoption. Sustainability 2024, 16, 2828. [Google Scholar] [CrossRef]
- Hou, X.; Xu, T.; Zhang, C. Building consensus with enhanced K-means++ clustering: A group consensus method based on minority opinion handling and decision indicator set-guided opinion divergence degrees. Electronics 2025, 14, 1638. [Google Scholar] [CrossRef]
- Xu, T.; He, S.; Yuan, X.; Zhang, C. Enhancing group consensus in social networks: A two-stage dual-fine tuning consensus model based on adaptive Leiden algorithm and minority opinion management with non-cooperative behaviors. Electronics 2024, 13, 4930. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Zhang, X.; Liu, P. A dynamic dual-trust network-based consensus model for individual non-cooperative behaviour management in group decision-making. Inf. Sci. 2024, 674, 120750. [Google Scholar] [CrossRef]

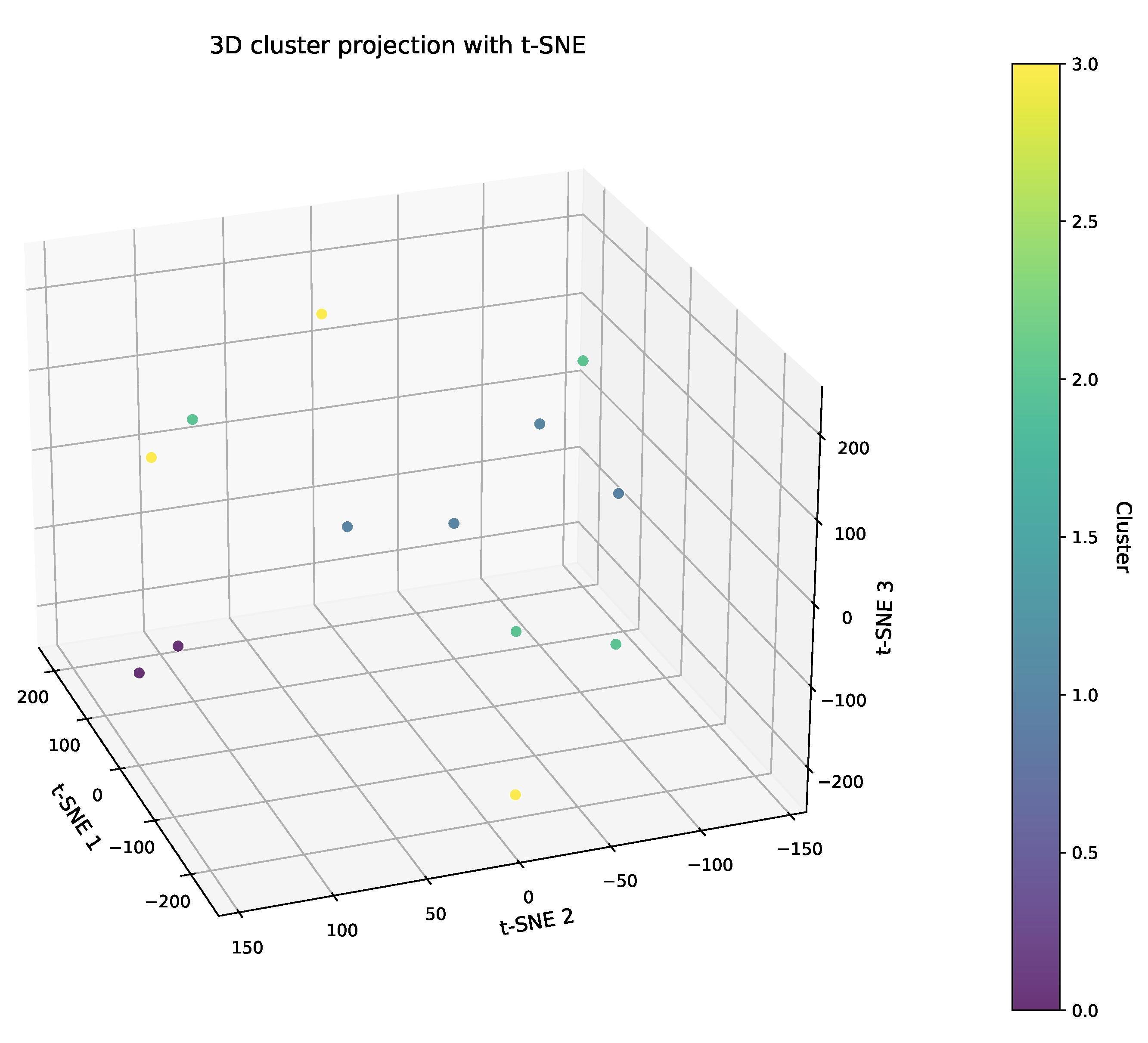
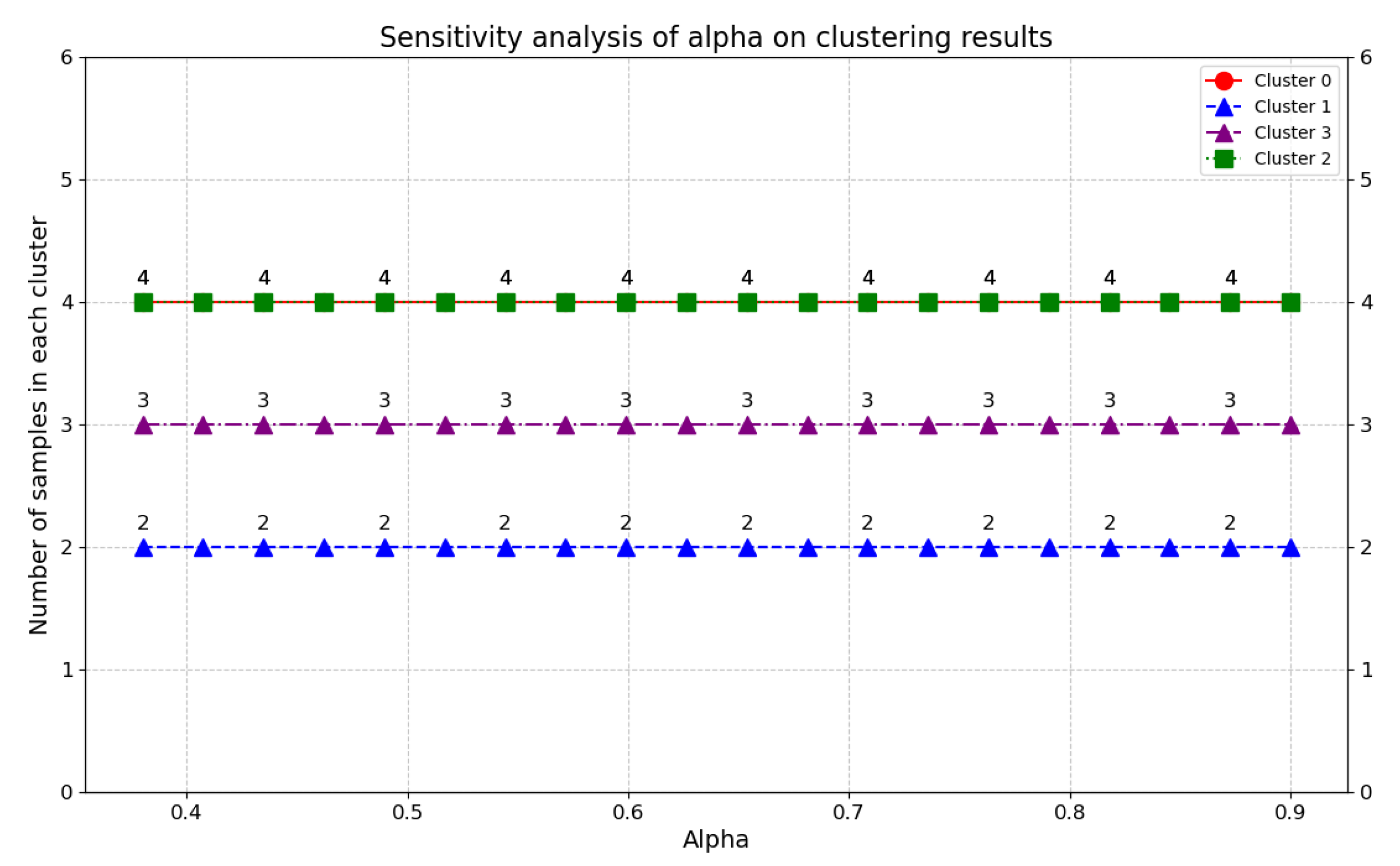
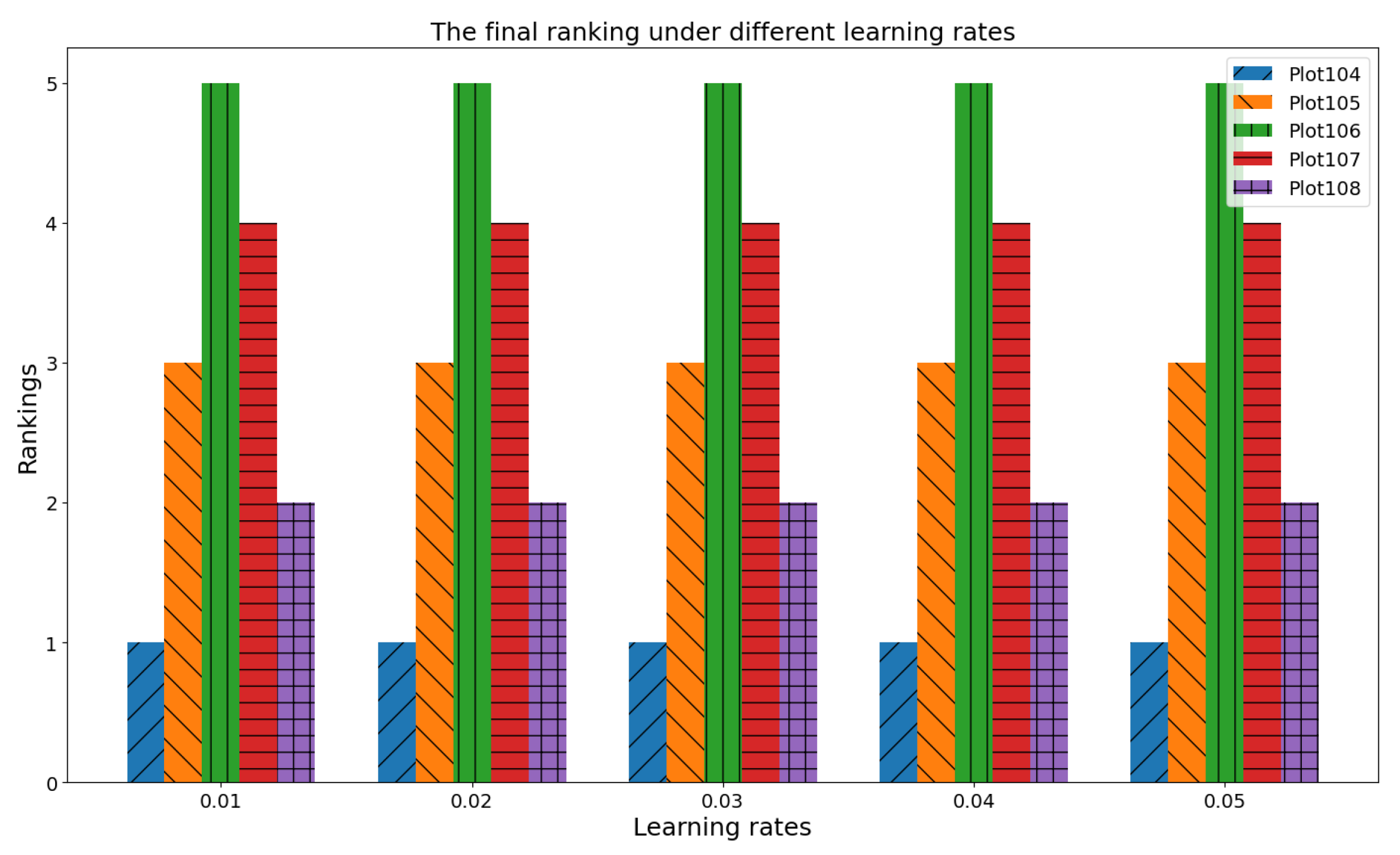
| Subgroups | Planting Sites |
|---|---|
| 0.068 | 0.076 | 0.070 | 0.085 | 0.082 | 0.045 | 0.058 |
| 0.075 | 0.084 | 0.087 | 0.091 | 0.090 | 0.089 |
| 3.402 | 0.435 | |
| 2.079 | 0.291 | |
| 2.079 | 0.173 | |
| 2.495 | 0.101 |
| ADISs | Values | Max Triples |
|---|---|---|
| Original Method | |
|---|---|
| Method removes the cardinal distance. | |
| Method removes ordinal distance. | |
| Method removes SNA. | |
| Method removes prospect–regret theory. | |
| Method replaces DISs with linear fusion. |
| Method | Total Time (s) | The Clustering Time (s) | The CRP Time (s) | The Final Ranking |
|---|---|---|---|---|
| 5.282 | 0.648 | 0.258 | ||
| 4.973 | 0.603 | 0.351 | ||
| 5.186 | 0.628 | 0.336 | ||
| 1.184 | 0.604 | 0.258 | ||
| 5.105 | 0.643 | 0.232 | ||
| 5.410 | 0.644 | 0.262 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Zhang, C.; Song, Y.; Alghamdi, T.; Aborokbah, M.; Zhang, H.; La, H.; Wang, Y. Wheat Soil-Borne Mosaic Virus Disease Detection: A Perspective of Agricultural Decision-Making via Spectral Clustering and Multi-Indicator Feedback. Plants 2025, 14, 2260. https://doi.org/10.3390/plants14152260
Hou X, Zhang C, Song Y, Alghamdi T, Aborokbah M, Zhang H, La H, Wang Y. Wheat Soil-Borne Mosaic Virus Disease Detection: A Perspective of Agricultural Decision-Making via Spectral Clustering and Multi-Indicator Feedback. Plants. 2025; 14(15):2260. https://doi.org/10.3390/plants14152260
Chicago/Turabian StyleHou, Xue, Chao Zhang, Yunsheng Song, Turki Alghamdi, Majed Aborokbah, Hui Zhang, Haoyue La, and Yizhen Wang. 2025. "Wheat Soil-Borne Mosaic Virus Disease Detection: A Perspective of Agricultural Decision-Making via Spectral Clustering and Multi-Indicator Feedback" Plants 14, no. 15: 2260. https://doi.org/10.3390/plants14152260
APA StyleHou, X., Zhang, C., Song, Y., Alghamdi, T., Aborokbah, M., Zhang, H., La, H., & Wang, Y. (2025). Wheat Soil-Borne Mosaic Virus Disease Detection: A Perspective of Agricultural Decision-Making via Spectral Clustering and Multi-Indicator Feedback. Plants, 14(15), 2260. https://doi.org/10.3390/plants14152260








