Abstract
Tropical trees represent an important potential archive of climate and ecological information, but their dendrochronology based on conventional techniques has been challenging. We conducted a pilot study of the wood anatomy and dendroclimatological potential of Juglans neotropica Diels (Juglandaceae), an IUCN Red List species, using 225 radii sampled from 57 trees in Piura (4°55′ S, 79° 56′ W), northern Peru. A total of 112 radii from 40 trees passed quality control and are included in the tree-ring width chronology for this species. J. neotropica has demonstrably annual rings, and results are consistent with reports that the species has a dormant period during the dry season, which locally is approximately June–November. Local precipitation is correlated (p = 0.10, 1-tailed test) with tree-ring growth, lagged by one year, consistent with other studies of tropical tree species. The age distribution of the sample collection of J. neotropica is young and invariant, probably because of selective cutting by local villagers. To supplement ring-width analysis, we conducted the first oxygen isotopic (δ18O) and radiocarbon (∆14C) analysis for this species on radii from two individuals; results are preliminary given sample size limitations, but consistent with dendrochronological dating, within uncertainties, in all three chronometric analyses. A two-sample composite annually-averaged δ18O anomaly data series is correlated significantly with gridded regional growing season (December–May) precipitation (1973/74–2005/06). Qualitatively consistent with simulation of ring width and δ18O, responses to El Niño events are manifested in positive ring-growth anomalies and negative isotopic anomalies following known event years. The combination of tree-ring, radiocarbon, stable isotopic analyses, and the application of sensor and chronological modeling provides a degree of confidence in the results that would not have been possible by relying on any single approach and indicates the potential for further investigation of this and other tropical tree species with uncertain ring boundaries.
1. Introduction
Tropical forests remain substantially understudied dendrochronologically relative to their distribution and ecological importance [1,2,3]. Investigations of growth periodicity in tropical tree species have been conducted over the last century [4,5,6,7,8,9], but annual tree-ring chronologies remain rare in the neotropics compared to other biomes [3,10,11,12]. Tropical trees may be problematic for dendrochronology for several reasons: (1) although tropical climates are often hydrologically and phenologically seasonal [13,14], they may lack distinct seasonal variation in temperature, so trees do not always produce visible and reliably annual rings associated with seasonal thermal dormancy [15]; (2) perhaps because of hydrologically mediated seasonal dormancy ([16] and references therein), tropical trees may form false rings and individuals may present missing rings, making the establishment of proxy records with absolute chronologies more difficult [17,18,19]; (3) species that produce long time series can be difficult to locate and sample; and (4) trees may be disturbed by human activities, making the climate-growth signal difficult to interpret [20,21,22,23,24]. Identifying species useful for tropical dendrochronology thus remains a challenge in this field [23,25], although progress has been made for high elevation sites and species in Peru [19,26,27,28], southern Ecuador, northern Argentina and Chile, and elsewhere [1,29,30,31,32,33,34], as well as the Amazon Nordeste region [14].
Seasonal and interannual variation in climate regulates tree growth and demography in tropical regions [27,35,36]. El Niño/Southern Oscillation (ENSO) events occur irregularly approximately every two to seven years [37], and their effects on tropical regional climate are pronounced [38]. Northern coastal Peru is often a focal point for initiation of large storm events and high precipitation periods during El Niño events, which can cause precipitation anomalies of up to 60 times the climatological mean [39,40,41,42,43]. This makes northern Peru especially relevant for studies of ENSO effects on terrestrial climate ([27] and references therein).
Tree-ring studies on Prosopis spp. [42,44,45,46] and Bursera graveolens [42] in northern Peru and Chile indicated an El Niño growth increase in lowland areas. Investigations of Prosopis spp. in northern Peru concluded that lowland tree species respond strongly to precipitation variation [44]. Expansion of dendrochronological work into regional highland tree species, including the establishment of multi-species networks, might complement these studies by improving cross-site replication and dating precision, producing generalized environmental growth response functions for the Peruvian dry forest, and strengthening spatial and temporal climate reconstruction efforts and hydroclimate response patterns across species [27,47,48,49,50].
Radiocarbon dating can be used as a supplemental method in tropical dendrochronology to determine tree ages and/or support the determination of annual rings [17,19,51,52,53,54,55,56,57], or to construct isotope chronologies for tree species without visible annual rings [54,58]. During the late 1950s and early 1960s the concentration of radiocarbon (14C) doubled in the Earth’s atmosphere due to atmospheric nuclear weapons testing [51,59,60]. Tropospheric 14C subsequently decreased with the flux of carbon into biological, land surface and ocean reservoirs [61]. Since living plants assimilate the concurrent atmospheric radiocarbon concentration, so-called ‘bomb radiocarbon’ can be used to date recent organic material, such as wood from living or recent trees [19,51]. Radiocarbon dating has been used in tropical trees to determine growth rates [62] and to investigate whether visible wood anatomical features are annual growth rings [17,19,52,53,55,56] or not [54,57,58,63]. Radiocarbon analysis has also been used to validate analyses of tree-ring growth response to climatic events, including flooding [52], rainfall events [17,64], or ENSO events [55,65], and to develop isotope age models [58,64,65].
Stable isotope techniques permit advances in tropical dendrochronology beyond those possible from visual tree-ring width analysis alone (e.g., [15,25,65,66,67,68,69,70,71,72]). Because wood cellulose tends to be stable at surface conditions (e.g., [73]), and because the environmental controls on its stable isotope composition are relatively well understood (e.g., [74,75,76]), carbon, oxygen and hydrogen isotope records from cellulose can be developed [77]. The oxygen isotopic composition of tree cellulose reflects air temperature, relative humidity, and the isotopic composition of source water [58,78,79], the latter determined by temperature path history of atmospheric moisture [80,81], as well as leaf-level evaporative effects and tree physiological processes [76,82,83]. In our study area (montane western South America), temperature is relatively constant through the year; thus, it has been proposed that variations in the oxygen isotopic composition of wood cellulose primarily reflect variations in the amount of precipitation [15,65,66,67] and/or the temperature path history of the precipitating moisture [71,84]. Based on these empirical studies, as well as forward modeling ([76,85] and references therein), we expect that, for tropical locations with high and constant temperature, high humidity, and pronounced seasonal and/or interannual variations, higher precipitation amounts will be expressed as lower cellulose δ18O values, and lower precipitation amounts will be expressed as higher cellulose δ18O values. For sub-annually resolved sampling, we can use the hypothesized annual cycle in cellulose δ18O to develop a relative age model by assigning periodic isotopic maxima to the beginning and end of the climatological dry season (e.g., [65]).
Juglans neotropica Diels [86] (Juglandaceae: walnut family), common name: ‘nogal’ is a highland species first described by Diels [87]. It is found primarily in dry to humid lower montane forests between 1000 m and 2800 m elevation, and ranges from northwestern Venezuela and northern Colombia through Ecuador and Peru [88,89,90]; it is also used for forestry in New Zealand [91]. J. neotropica is valued as a timber, medicinal, and nutritional resource; a bark extract is used to dye wool (personal communication; Luis Gongolo Córdova; carpenter and owner of J. neotropica trees in Frias; [90,92,93]). J. neotropica is a conservation priority because of its extensive use and documented decline [93,94,95,96] and is on the Red List of endangered species [97], due in part to over-exploitation for timber [90,98]. Because of its wide range over a region affected directly by ENSO in the eastern Pacific Ocean, and its socioeconomic importance, J. neotropica is a prime candidate for dendrochronological and dendroclimatological analysis [19,27].
Relatively few dendrochronological studies have been published for the genus Juglans, but its dendrochronological importance and potential have been recognized [3,19,27]. Juglans are generally diffuse-porous [99,100], meaning that the vessels are of approximately equal diameter throughout the ring [101]. J. australis cross-dates both within and among trees [11,29,102,103,104]. Wood growth in tropical areas generally starts soon after the beginning of the rainy season, and in deciduous species growth stops at the end of the rainy season [105]. J. neotropica is reported to be dormant during the winter months [91], which normally extend from June to August. Villalba et al. [29] indicate that the growth period of J. australis lasts from September to April/May in Argentina and western Bolivia. However, there is disagreement as to whether J. neotropica is evergreen [95,96,106] or deciduous [89,91,99].
We present dendrochronological, oxygen isotopic and radiocarbon analyses in this pilot study to establish a preliminary regional growth chronology for J. neotropica from the Pacific slopes of the Andean foothills of northwestern Peru, with reference to effects of El Niño on growth patterns. We couple ring studies with isotopic analysis and radiocarbon dating to strengthen inferences about the timing of tree growth in tropical locations, such as our northern Peru study area. In addition, we calibrate the isotopic signature of climatic variations associated with the regional expression of El Niño activity, the first step toward using the species as an archive of paleoclimatic indicators in this key geographic area. In northwest coastal tropical Peru, we expect an annual precipitation cycle to produce anatomically distinct annual ring structures associated primarily with moisture availability [15,42], for which cross-dated chronologies should be in agreement with radiocarbon dates from hypothesized 1970s–1980s wood. Although seasonal dormancy has not been observed directly, we postulate that growth occurs in J. neotropica within the rainy season, based on studies in closely related taxa (e.g., [29]). On interannual timescales, we expect growth of J. neotropica to be controlled by variation in precipitation amount, as found for Juglans australis [103] and other tropical tree species [31,44,103,107,108]. Specifically, during ENSO warm phase conditions, when precipitation is unusually high, we expect increased ring widths (e.g., [16,42]) and lower oxygen isotopic composition [15,85] during or shortly after such events. Our specific research questions are as follows:
- Can J. neotropica be cross-dated [109] accurately using visible wood anatomical features?
- Are ring-based age estimates consistent with radiocarbon and stable isotopic estimates?
- Are variations in growth rates and oxygen isotopic composition of J. neotropica, and their relationship to regional precipitation variations and ENSO, consistent with that demonstrated for other species?
2. Data and Methods
2.1. Study Site
Field work was conducted in 2005 and 2007 in the north Peruvian villages of Frias and Pueblo Nuevo (04°55′ S, 79°56′ W, elevation 1765–1870 m a.s.l.), Piura Province, Peru (Figure 1). The study sites are classified as ‘premontane dry forest’ (‘bosque seco premontaño’ [110]. Premontane dry forest occurs in tropical areas along the lower slopes of mountains where there is a long dry season, alternating with a 5–6 month precipitation period. The study area consists of variably dense forest, with tree canopy coverage of 40–70% on soils of mostly sand, silt and clay overlying Cretaceous intrusive units (diorites, granodiorites, tonalites, granites) and volcanic units; landslides and seepage erosion are frequent following periods of higher precipitation [111,112]. The combination of elevation and latitude produces relatively warm days and cool nights (see below; [112]). The study area supports rich species diversity; typical tree and bush species include Juglans neotropica (nogal), Persea americana (palto) and other P. spp., Erythrina edulis (pajul), Baccharis latifolia (chilca), Nectandra reticulata (paltaguiro), Rubus spp. (blackberry), Croton spp., Tibouchina spp. and Heliotropicum spp. [112].
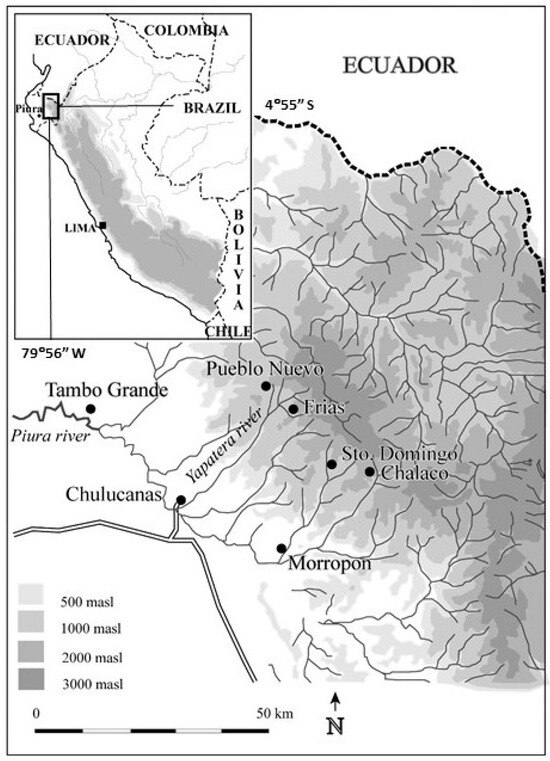
Figure 1.
Study area and locations of sampling and climate stations.
Forest canopy height in these areas is approximately 15–25 m, but trees could probably grow higher in areas without human extraction of forest resources. Toro and Roldán [90] document a tree height of J. neotropica in South America of 15–48 m, with deep roots that can reach more than three meters in depth. Small-scale subsistence agriculture, cattle breeding and forestry are the main activities of the inhabitants [112]. Households are clustered, with agricultural areas spread out in the local area. To minimize risk of pests and disease, several species are cultivated together on a small scale, where farmers often change cultivated species from year to year. Areas of natural vegetation are mainly in areas that are difficult to cultivate, relatively far from villages, or as natural boundaries and windbreaks between small-scale agricultural plots.
Precipitation in Frias is generally received from December to May/June (5–6 months) (precipitation data from Frias 1963–1992 and 2002–2003 [113], with a dry season from May/June to November (Figure 2). Because local precipitation data from Frias are missing for the periods January 1993–December 2001 and January 2004–December 2007, we compiled additional precipitation data from Santo Domingo (05°02′ S, 79°52′ W, 1475 m a.s.l.), 14 km away [113] SENAMHI, 2025; Figure 1). We analyzed historic annual precipitation data, designating the water year from September to August. Santo Domingo and Frias precipitation data series are correlated significantly (r = 0.82, df = 31, p < 0.05) for the period 1963/64–1991/92, 2001/02–2002/03 for which data are available for both stations. During the El Niño event of 1982/83, Frias experienced five times more precipitation (above 3400 mm rain from September 1982 to August 1983) than the mean annual precipitation of 648 mm (data range: 1964–2007, excluding the El Niño events of 1982/83 and 1997/98). During the same El Niño event, Santo Domingo experienced nearly seven times more rain (more than 3100 mm from September 1982 to June 1983) compared to a mean annual precipitation period of 533 mm (data range: (1964–2007, without the El Niño events of 1982/83 and 1997/98).
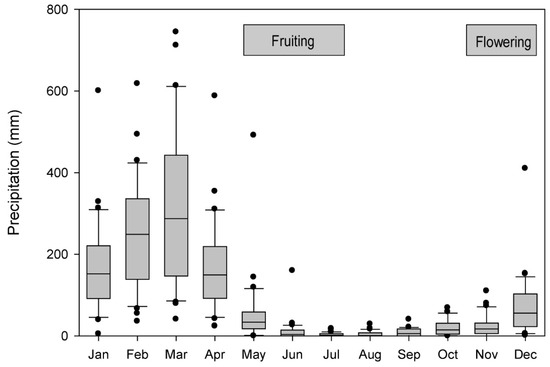
Figure 2.
Monthly maximum, mean and minimum precipitation (mm) in Frias, Peru for 1963–2003. (Source: [113]). Standard box plot convention is followed (box encloses 25th–75th percentile with median line; outer bars are 10th and 90th percentiles; outliers are shown as dots). Horizontal bars indicate the mean periods of flowering and fruiting of J. neotropica [93].
Temperature data at the immediate study site are unavailable, but Sausal de Curucan, 27 km distant at an elevation of 980 m a.s.l., had a yearly mean temperature of 22.5 °C, and a mean annual range of 17.1–29.3 °C during 1972–1996 [113]. Based on the moist Environmental Lapse Rate (ELR) and the International Standard Atmosphere (ISA; [114]), mean temperature decreases at a moist adiabatic rate of 6.49 °C/1000 m; using this correction, we estimate the yearly mean temperature in Frias to be 16.7–17.4 °C, which is consistent with other estimates of the growing season temperature range for J. neotropica of 16–28 °C [115] and 11–19 °C [116]. Mean interannual variation in temperature is about 4 °C, although records for 1972–1996 indicate a temperature range of 14–30 °C [113]. Based on these data, we infer that temperature variations in Frias are not likely to limit growth for J. neotropica.
2.2. Field Sampling
We sampled 225 radii of J. neotropica from 56 trees using Haglöf increment borers of 5.1 mm diameter/600 mm length and 4.3 mm diameter/200 mm length, following standard dendrochronological methods [109]. One additional cross-sectional sample was also recovered from a cambial active stump (adventitious cambial growth) of a previously felled tree (total N = 57). Because sampled J. neotropica produced colored fluids when cored, it was difficult to identify the intersection of cores with, or proximity to, the pith in the field. We sampled four radii from each tree, one from each cardinal direction. Cores were stored in paper straws and air dried, then stored in a freezer to prevent disease or pathogen transport. Subsequent sample preparation and analysis were performed at the Laboratory of Tree-Ring Research, University of Arizona, Tucson, AZ, USA.
2.3. Wood Anatomy
We prepared microtome slices of two radii from two J. neotropica trees to examine wood structure. We first let the wood soak in three parts water to two parts glycerin to soften samples for cutting. We then used a sliding microtome to cut slices as thin as possible without breaks; this procedure yielded slide thicknesses of 50–70 µm. We mounted the sections on glass slides and took images of each slide using a light microscope (Nikon SMZ-U; Nikon, Tokyo, Japan) equipped with a digital camera (Olympus E-330; Olympus, Tokyo, Japan). We used the microtome slides to complement traditional visual investigation of tree samples under a dissecting microscope to investigate the cell structure and wood anatomy of J. neotropica.
The determination of annual ring boundaries in diffuse porous species can be based on a variety of characteristics (e.g., [23]). We examined pore size, wood density, presence of parenchyma, and differences in vessel diameter and color from the beginning to the end of the growth band. We classified our observations as indicating growth rings in J. neotropica if (a) they were present in all samples, (b) the ring was uninterrupted by vessel cells going through the parenchyma line, and (c) there was a clear discontinuity of late wood cells and early wood cells. We noted differences in ring sequences in radii within and among sampled trees.
2.4. Dendrochronological Sample Preparation, Tree-Ring Analysis and Modeling
We sanded samples with progressively finer sandpaper to grit size 1200. We visually cross-dated radii from 57 trees to the innermost ring of the radius. Of these, we excluded 17 trees that were younger than 12 years of age (1995/96) because juveniles can be more prone to competition stress, geomorphic and wind stress that can complicate the climatic signal [101], leaving 112 radii (n = 40) for analysis. We measured annual rings to the nearest ± 0.001 mm under a binocular stereoscope with a Velmex measuring machine connected to a computer [117]. We measured rings perpendicularly to a line tangent to the curve of the ring to maintain measurement accuracy despite variations in the coring angle [118].
We cross-dated and checked ring data using the skeleton plot method [119] and used the computer program ARSTAN (v.6; [120]) to detrend each tree series for the period 1963–2006. We detrended tree series with a negative exponential curve or linear regression to minimize non-climatic growth influences, such as competition, tree age and diameter, forest disturbances and defoliation [121]; indices were computed by division. We calculated correlation statistics for the years that were common to the trees used in analysis (1977–2006) (Table 1b).

Table 1.
Chronology statistics for J. neotropica.
We used the process-based model VS-Lite [122] to explore the mechanistic relationship of tree growth to climate variables (Supplementary Information). VS-Lite provides a realistic nonlinear multivariate tree growth model based on the principle of limiting factors [123]. We generated cumulative age-growth plots by integrating annual ring widths over time, to examine growth trends and variation among trees with varying years of origin [124,125]. We plotted and compared cumulative actual and normalized diameter growth to both calendar and normalized age for each tree in the analysis set.
2.5. Oxygen Isotopic Analysis
2.5.1. Sample Preparation and Data Analysis
We chose one radius from each of two trees (JN37-1W and JN41-2N) from which to analyze oxygen isotopes and develop both an age model and analysis of interannual variations. Trees for this analysis were selected based on their potential for time series length, absence of breaks or twists, and an intersection of the core with the tree pith. One radius (JN41-2N) was sanded with sandpaper to grit size 1200; the other (JN37-1W) was left un-sanded for subsequent radiocarbon analysis to avoid cross-contamination across the steep bomb radiocarbon curve or through intraseasonal oxygen isotopic variations [126].
We used a rotary microtome to sample increment cores perpendicular to the sampled axis of growth, at thicknesses ranging between 0.15 and 0.30 mm per slice, accumulated into sequential independent samples each of about 1 mg wood [15,127]. Alpha-cellulose was extracted using a modified Brendel technique [128]. We wrapped 300–350 μg samples of alpha-cellulose in silver capsules and converted them to carbon monoxide (CO) at ≳1500 °C using a Costech High Temperature Generator (Milan, Italy) [129] and passed the CO to a Thermo Finnigan Delta Plus XP mass spectrometer (Thermo Fisher Scientific, Waltham, MA, USA) via Conflo II open split interface for isotopic analysis. Data were quality controlled for chromatographic evidence of incomplete sample conversion and insufficient sample amplitude (<1V at M44 collector), and trend-corrected using periodic in-run working standard alpha cellulose and monitoring gas measurements. The 1-sigma measurement precision, based on replicate homogeneous working standard alpha cellulose (Sigma Alpha Cellulose (Sigma-Aldrich, St. Louis, MO USA), assigned δ18O = 31.0‰, relative to the V-SMOW reference standard), was ±0.3‰. We analyzed a total of 2184 isotopic samples (1315 from radius JN37-1W and 869 from radius JN41-2N).
To age model the δ18O data independently from wood anatomical and dendrochronological analyses, we worked backwards from the known collection date in May 2007 to assign periodic isotopic maxima to December and May of prior years, based on precipitation records and following the oxygen isotope chronometric hypothesis (Section 1; see [15,65]). We then linearly interpolated to obtain date estimates for isotopic data within each growing season December to May, and assumed growth hiatus during the dry season (between May and December). The age-modeled series were then averaged across growing season and core series to form a composite δ18O data series at annual resolution.
To model the chronological uncertainty in these data, we applied the banded age model (BAM) of Comboul et al. [130], which assumes a cumulative error of omission or addition of annual growth increments as a function of a specified error rate. Based on the radiocarbon and oxygen isotope based chronometric results and the method of age model development, for which either sampling or date assignments are relative to a known distance from bark or date of collection, we specify a Poisson distribution of errors and an error rate of 10%. We applied the same model to the TRW chronology with an error rate of 5%.
2.5.2. Isotopic Modeling
Interpretation of the annually resolved composite δ18O was facilitated by comparison with simulated δ18O, in which the simulated values were those predicted using the model of Evans [85], updated to sample forcing uncertainty [131]. In contrast to linear or multivariate linear modeling, the isotopic model reflects the combined influences of temperature (T), precipitation (P) and humidity (q) variations at monthly resolution, based on eco-physiological and stable isotope modeling [75,76,85]. It thus provides a basis for comparing observed δ18O to local climate variations. We used the CRU TS4.08 [132] gridded monthly Dec-May precipitation amount, temperature and specific humidity as modeling inputs. We averaged the simulated δ18O to December–May values for comparison with the observed δ18O composite. Parameters used in the simulation exercise were as in Table 1 and Table 2 of [85]), with a prescribed uncertainty of 20% for T, P and q inputs.

Table 2.
Radiocarbon results (14C) of five samples from J. neotropica, radius JN37-1W.
2.6. Correlation Analysis
We examined the relationships between the tree-ring width of J. neotropica and precipitation, and between isotope composition and precipitation, using correlation functions. We tested correlations between standard tree-ring width chronology and mean isotope values per growing season with local growing season precipitation records from Frias and Santo Domingo. Because we found that the tree-ring widths (TRWs) were serially autocorrelated (Table 1), we used the effective degrees of freedom (edf) as where n = number of observations and AR1 = first order autocorrelation coefficient ([133] and references therein). We used a one-tailed t-test because we did not hypothesize a negative slope for the regression of TRW on precipitation, a positive slope for the regression of cellulose δ18O on precipitation, or a negative slope for the regression of simulated on observed cellulose δ18O. Because isotopic composition of precipitation in equatorial regions is driven by hydrological processes at regional scales [133,134], we also used gridded precipitation data (CRU T4.08; resolution 0.5° × 0.5°), based on regional interpolation and quality control, from 82.25–77.75° W to 7.25–2.75° S, using mean December–May precipitation in the correlation analysis in addition to station data [135]. The time series used for the gridded precipitation data were 1959/60 to 2005/06.
2.7. Radiocarbon Analysis
To validate the isotopic and dendrochronological age models of J. neotropica, we selected five wood samples from JN37-1W for radiocarbon analysis. Based on the oxygen isotopic age model, radiocarbon samples were selected from core intervals corresponding to 1–2 years each and spanning the full estimated age of the cored tree. Samples containing 4–5 mg of wood were treated following the procedure described in [136] to extract cellulose [128]. Treated samples were submitted to the NSF-Arizona Accelerator Mass Spectrometry (AMS) Laboratory, University of Arizona, for combustion to CO2, purification, and high-precision 14C analysis; calibrated ages were developed using OxCal version 4.1 [137,138]. Results from radiocarbon analyses, including measurement uncertainty (two year sampling age resolution) were fitted to the observed Southern Hemisphere bomb radiocarbon dataset [61], with the constraint that samples must be ordered in age as they are ordered in depth toward the tree core pith [137]. Age ranges reported are for the two sigma ranges estimated by OxCal 4.1 [138], which indicates a 95.4% probability that the correct calendar date falls within this range [139].
3. Results
3.1. Wood Anatomy of J. neotropica
Once samples are prepared in the laboratory, heartwood and sapwood in J. neotropica can be differentiated by coloration. Heartwood tends to be dark grey–brown, with some lightening towards the end of the growing season, whereas sapwood tends to be a more uniform creamy yellow (Figure 3B). We defined ring termination by a rapid narrowing of the parenchyma cells to produce a thin dark line, usually about two to four cells wide, tangential to the direction of growth (Figure 3A–C). Parenchyma cells forming the sharp boundary in heartwood can be difficult to discern without extensive preparation of the core surface (Figure 3D). However, an increased number of vessels in the earlywood, often in clusters, and an increased number of wood rays tangential to the direction on latewood growth can also be used to identify a growth boundary (Figure 3A,D). Ring boundaries within the sapwood are visible as darker bands than those that typically occur in the heartwood.

Figure 3.
Microscope images of J. neotropica microtone slices showing ring boundaries (arrows) near the core (A), in the transition zone from heartwood to sapwood (B) and near the bark (C). A piece of the bark is seen in the lowermost part of (C), indicating the direction of growth from top to bottom. Scale bars in mm. (D,E) Wood structure images. All photos by T.M. Ektvedt.
3.2. Tree-Ring Chronology of J. neotropica
Our samples showed large variability in ring width among trees. Within a single radius, the mean range factor between smallest and largest ring is 26, but the difference could be as extreme as 1:233 (0.074 mm: 17.274 mm). Mean minimum ring value among samples is 0.84 mm, while mean maximum value is 10.41 mm. Among trees, mean ring width and standard deviation is 4.87 ± 1.49 mm (min among all trees 1.67 mm/yr, max 8.02 mm/yr). Although we cannot eliminate the possibility of missing rings, cross-dating analyses did not indicate dating errors in the ring width chronology.
For the common interval time span (1977–2006), mean correlation across 28 radii from 17 trees of J. neotropica is high (0.76), indicating relatively strong within-tree consistency in growth variations around the tree circumference (Table 1b). However, the correlation of all radii compared to the sample mean is relatively low (0.18), and mean inter-tree correlation is near zero, indicating a weak inter-tree correlation (r-bar = 0.176).
The total set of measured tree samples from 1963/64–2005/06 covered few trees in the early period (especially 1963/64–1973/74) (Figure 4, top), resulting in relatively few reliable ring-width values during this early period. The earliest rings show a period of larger radial growth compared with rings in the later stage of the chronology, probably reflecting inherent variability due to small sample size during this period, but possibly also reflecting more vigorous growth rates in younger trees [101,140]. Sample size by year (Figure 4, top) reflects only the innermost measured rings and not actual tree ages, since some cores were an unknown number of years from pith. Using pith estimators [141], we estimated that the mean years to pith was 2.1 years (maximum 5 yr). Some chronology values from 1962 to 1971 may not be reliable due to low sample size (<10 samples). The resulting J. neotropica standard chronology provides a record of tree ring growth of more than 30 years with sufficient sample size (Figure 4, top).
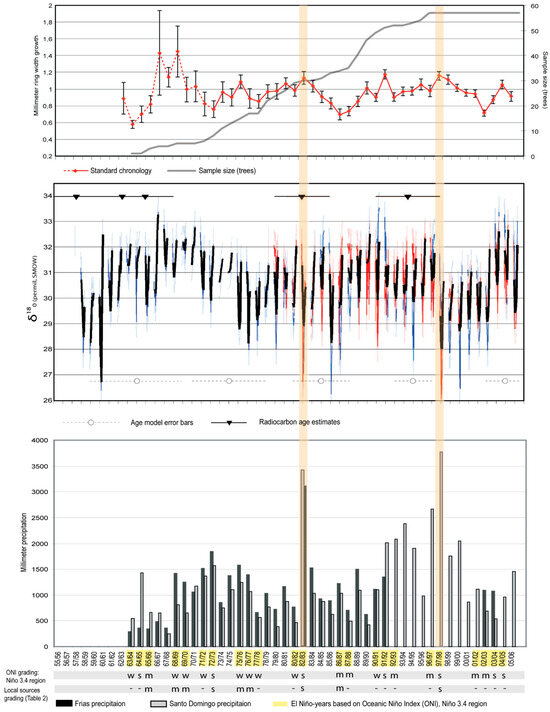
Figure 4.
(Top) J. neotropica standard chronology from 1962/63–2005/06 compared to sample size (number of trees, grey line). The bars on the standard chronology are ±1 standard error of the standard chronology among the samples. Chronology values from 1962–1971, which may not be reliable due to small sample size, are indicated as a dashed line. (Middle) Age-modeled oxygen isotope records of JN37-1W (blue) and JN41-2N (red), with monthly-interpolated mean values in black, and radiocarbon age estimates (see Table 2) plotted as nablas with 2s error bars (top). Bottom lines with circles are error bars by decade centered on the decade midpoint: 2000s ± 2 years, 1990s ± 2 years, 1980s ± 3 years, 1970s ± 4 years, 1960s ± 5 years. (Bottom) Precipitation at Frias (black bars) and Santo Domingo (grey bars). El Niño years (yellow shading on years) are based on the Oceanic Niño Index [142], with event intensity grading (weak (w), moderate (m), strong (s) and no info (-) (Table 3). The two strong El Niño-events that resulted in precipitation of more than 3000 mm are shaded for comparison across panels.
3.3. Stable Isotopic and Radiocarbon
Oxygen isotopic analyses (Figure 4, middle) and age modeling revealed a quasi-cyclical climatic signal associated with the stable isotopic age model (§2.5), with interannual variation. The oxygen isotopic age model indicated that JN37-1W dates to 1958 ± 5 years, with uncertainty based on differences between plausible age models (Figure S1); this is consistent, within error, with both ring width and radiocarbon age estimation (Figure 4: middle section: blue curve). The isotopic interpretation of JN41-2N (Figure 4: middle section: red curve) was dated to 1978 ± 4 years, consistent within age model error with the ring width measurement of the same sample. Radiocarbon results (14C) of the five samples taken from the J. neotropica radius JN37-1W (Table 2) bracket the ages estimated by dendrochronological and isotopic analysis, given uncertainties in the age model estimates (Figure 4, middle). Our fraction of modern radiocarbon (F14C) values revealed an age range from zero (expected age) to eleven years compared to our expected age model. Our youngest radiocarbon sample (sample 5) had a younger calibrated age than expected, while our oldest sample (sample 1) was older than expected.
3.4. Correlation of Tree Growth with Local and Regional Climate
Growth modeling with VS-Lite confirmed that ring growth is regulated primarily by soil moisture (r = 0.31, edf = 8, p = 0.07, one-tailed test; Table 4; Figure S3, Supplementary Information). Two particularly strong El Niño events occurred during the period of analysis, in 1982/83 and 1997/98. Other strong El Niño events occurred in 1991/92 and 2003-05 [142] (Table 3; Figure 4). During the period with more than ten sampled trees (1973/74–2005/06), we found a generally positive (but non-significant) relationship between ring width and gridded precipitation (r = 0.25, p = 0.10, edf = 14, one-tailed test); Table 4). For the same period, correlation between the 2-sample composite δ18O and gridded precipitation is slightly less likely to arise by chance (r = −0.31, p = 0.06, edf = 12, one tailed test). Correlation between composite δ18O and median simulated δ18O [85] is significant (r = 0.32, p = 0.05, edf = 12, one-tailed test) and not sensitive to forcing uncertainty. Correlation between composite δ18O and ring width is nonsignificant (r = −0.21, p = 0.15, edf = 12, one tailed test). Correlations (Table 4) of observed TRW and δ18O with the NINO12 SST anomaly index (0–10° S, 90–80° W) are 0.34 and –0.35, respectively, significant at p = 0.04; however, when age model uncertainty is sampled, significance is preserved for TRW (95th percentile confidence interval > 0), but not for δ18O (Figures S2 and S3).

Table 3.
El Niño events affecting climate in Peru from 1950 to 1998 classified by [143] as moderate (M) and strong (S).
Table 3.
El Niño events affecting climate in Peru from 1950 to 1998 classified by [143] as moderate (M) and strong (S).
| Period | Strength | Source |
|---|---|---|
| 1951 | M | [41,144] |
| 1953 | M+ | [41,144] |
| 1957/58 | S | [41,144] |
| 1965 | M+ | [41,144] |
| 1968/69 | M− | [41] |
| 1972/73 | S | [41,144] |
| 1976 | M | [41,144] |
| 1982/83 | S+ | [41,113,144] |
| 1987 | M | [41,143] |
| 1997/98 | S+ | [113,144,145] |

Table 4.
Correlation of tree ring width (TRW), and oxygen isotopic composition (δ18O) and simulated δ18O [85] with nearest grid point precipitation (P) from CRU TS4.08 [134] and NINO12 sea surface temperature (SST) index [142].
Table 4.
Correlation of tree ring width (TRW), and oxygen isotopic composition (δ18O) and simulated δ18O [85] with nearest grid point precipitation (P) from CRU TS4.08 [134] and NINO12 sea surface temperature (SST) index [142].
| Correlated Variables | r | Student’s t | EDF | p |
|---|---|---|---|---|
| P, TRW | 0.25 | 1.35 | 14 | 0.10 |
| P, observed δ18O | −0.31 | −1.71 | 12 | 0.06 |
| Observed δ18O, simulated δ18O | 0.32 | −1.74 | 12 | 0.03 |
| Observed δ18O, TRW | −0.21 | −1.09 | 12 | 0.15 |
| Observed TRW, NINO12 SST index | 0.34 (0.04, 0.37) | 1.85 | 12 | 0.04 |
| Observed δ18O, NINO12 SST index | −0.35 (−0.39, 0.44) | −1.96 | 12 | 0.04 |
EDF = minimum (across correlated variables), estimated degrees of freedom [(1 − r1)/(1 + r1)] × N; r1 = AR(1) coefficient; p = significance (one-tailed test) of the correlation coefficient given EDF. NINO12 SST index = Dec–May mean climatological SST anomaly for the area (0–10° S, 90° W–80° W; CPC 2025 [145]). For the correlations with NINO12, values in parentheses are the 2.5th and 97.5th percentile values considering age uncertainty estimates, following [130], with a Poisson distribution and annual growth error rates of 5% and 10%, respectively.
3.5. Cumulative Tree Growth
Sampled trees were recruited over a 33-year period (1963–1995 inclusive), with the majority recruited in the 1980s and 1990s (Figure 5a, Table 1a). Trees that were recruited during the early portion of the record (1960s–1970s) had higher sustained growth rates than those recruited later (Figure 5b). The 1982/3 EN event is notable as a period of accelerated growth among many of the sampled trees (dashed line in Figure 5c). Plots of normalized growth as a function of normalized time (Figure 5d) indicate that trees achieved their median total growth after only 39% of total time, with the growth curve downwardly inflected, indicating a declining growth rate.
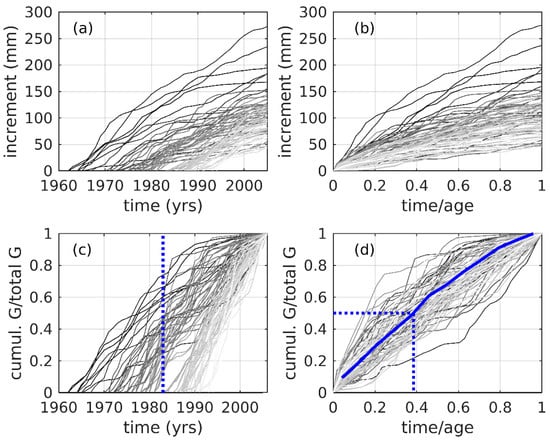
Figure 5.
Cumulative growth analyses for study samples of J. neotropica. (a) Cumulative incremental growth (mm) vs. time for 83 increment series in the J. neotropica chronology reported in this study. Darker (lighter) greyscale indicates longer (shorter) time interval spanned per increment core. (b) As in (a), except for time normalized to the length of each increment series, respectively. (c) As in (a), except for cumulative growth normalized by total growth of each series, respectively. The vertical dashed line indicates the 1982/83 El Niño event. (d) As in (c), except for time normalized by length of each increment series, respectively. Blue curve is the median of the median normalized growth-time values, with all normalized cumulative growth series interpolated to a common 12-point linear normalized timescale. Dashed lines trace the values of the median normalized cumulative growth (0.5), reached at 0.39 of the median normalized interpolated age.
4. Discussion
4.1. Can J. neotropica Be Crossdated Accurately Using Visible Wood Anatomical Features?
Some authors have described the wood anatomy and the appearance of J. neotropica [92,93,94,96,116,146,147,148,149] but could not determine if the observed growth bands were annual or seasonal. Ref. [99] claims that the genus Juglans forms annual growth rings, but did not mention J. neotropica specifically. The growth rings were seen as a ‘thin layer of flattened fibers and a uniseriate row of parenchyma cells on outer margin’ [99]. Ref. [100] found terminal parenchyma present in J. neotropica that they identified as growth rings. However, [150]’s work on wood anatomy of the genus Juglans claimed that ‘growth rings are distinct in the temperate species and generally lacking in the tropical species’. Refs. [19,151,152] later concluded that J. neotropica had annual rings.
Our results are in accordance with [19,100,151,152], who found annual growth rings. Our study thus contributes to the literature confirming that growth rings can be detected in seasonally dry tropical species. Interannual differences in ring width were observed in the samples of J. neotropica (§3.1). To our knowledge, no other studies have reported similar magnitude growth differences in tropical Juglans spp.; we cannot evaluate whether such interannual differences are common in the region. Mean ring width of all rings in J. neotropica was 4.87 mm, similar to mean ring width of 5.29 mm in Bursera graveolens [42] (Rodríguez et al., 2005), which also occurs in the region, but not Prosopis pallida [44] (mean ring width of 0.93 ± 0.620 mm). Ref. [30] found that different tropical tree species in the same region can vary from 0.6 mm year−1 to 5.7 mm year−1. The cumulative radial growth rate was highest during the early years for most trees in our sample (Figure 5d).
The 112 radii from 40 trees of J. neotropica in this study suggest dendrochronological potential, beginning with a coherent common signal (r = 0.76 for increment cores within the same tree) for this species at this site. However, the low common signal among different trees represents a challenge to dendrochronological reconstruction and merits additional sampling and analysis. Low among-tree correlation may reflect the extensive human modification and use of J. neotropica stands; juvenile trees can also be more prone to ecological factors, such as competition, geomorphic events, and wind stress, which can complicate a purely climatic signal [101]. In the effort to obtain a sufficiently large sample size, we sampled both open and closed canopy stands, which may further contribute to variability in the resulting ring width chronology. Refs. [19,27] found high intercorrelation among radii of J. neotropica in studies conducted in areas with less human impact, which may indicate that the selection of a study site with less human impact is important. Ref. [90] (and references therein) confirm that J. neotropica grows well under conditions of moderate disturbance, such as in agroforestry systems and areas with soils degraded by mining activity. However, if J. neotropica could also be sampled in areas with less human impact, longer and more accurate chronologies may be developed.
Accurate precipitation data were scarce at this site, and local temperature, humidity and evaporation data are lacking entirely, as was also challenging in other studies [27]. This uncertainty affects the calibration process of comparing the known record of an environmental variable to the tree-ring chronology for the purpose of determining tree growth response [109].
A low common signal has been observed for some other tropical trees. Ref. [124] found ring width to be highly variable between different radii of the stem, with low correlations among individual trees for six tropical Bolivian species. J. australis has a similar mean within-tree correlation of radii (0.68–0.70) to those found in our study (0.760), but J. australis shows a higher among-tree correlation (0.449–0.503) than J. neotropica [29].
Wood formation in a given year is dependent partly on growing conditions in the prior year [153,154]. Growth of J. neotropica is influenced by precipitation during previous and current growing season [27], similar to studies of J. australis [103]. Worbes’ [105] study of 37 tropical tree species in a semi-deciduous forest in Venezuela found that evergreen species tended to have a short growth interruption (during the latter part of the dry season), whereas deciduous species stopped growth completely at the end of the rainy season. Our findings of annual bands in J. neotropica suggest a complete cessation of growth during the dry season in this environment. Consistent with our conclusions, ref. [27] found that tree-ring chronologies were most highly correlated with the precipitation period from November (year t) to October (year t + 1).
4.2. Are Ring-Based Age Estimates Consistent with Radiocarbon and Stable Isotopic Estimates?
The radiocarbon result and the visual dating of JN37-1W yielded different age estimates of up to ±five years (±12%) (Table 2). This difference in age interpretation is within the uncertainty of the respective age models but may be partly due to undetected dating errors in tree sample JN37-1W, due to surface irregularities that remained because we wished to avoid sample cross-dust contamination in isotope and radiocarbon processing [126]. As emphasized earlier (e.g., Figure 3D), annual rings can be difficult to detect visually if not sanded. Oxygen isotopic results at intraseasonal resolution suggest a quasi-cyclical climatic signal (Figure 4, middle), which, if interpreted as variation over the course of the growing season, produces a chronology consistent (within uncertainty) with independently derived radiocarbon and ring width age models.
All three of the dating methods used in this study are imperfect and involve uncertainties. The cross dating of tree rings produced chronologies with a low signal-to-noise-ratio and may also have been influenced by the relative youth of the sampled trees. Although the derived signal appears to reflect quasiperiodic annual cycles, oxygen isotopic analyses are expensive and time consuming to replicate. Radiocarbon dating uncertainties arise from dendrochronological uncertainty, and the bimodal distribution of the peak atmospheric radiocarbon concentrations with latitude, and measurement uncertainties [155,156,157,158]. Despite these uncertainties, results from all three chronological methods are convergent, and provide a more coherent picture of the extent to which precipitation variations may be reflected in proxy observations than might be derived from a single approach [25].
This study revealed that the Juglans collection from northern Piura is probably not more than 45 years old. This conclusion is consistent across all proxy measurements employed (tree-ring chronology, isotope age interpretation and radiocarbon results). Considering the challenges in working with tropical tree species, our results are encouraging for the potential of tropical dendroclimatology. Our investigation suggests useful implications for climate reconstruction, sustainable forestry and carbon cycle dynamics in the dry forests of tropical South America. Human use of J. neotropica is intensive in the study area, which emphasizes the importance of long-term planning and protection to maintain sustainable populations of the species.
4.3. Are Variations in Ring Widths, Growth Rates and Oxygen Isotopic Composition of J. neotropica at Piura Related to Regional Climate and ENSO, and If So, How?
Growth modeling results are consistent with our expectation that tree growth in J. neotropica is conditioned primarily on growing season precipitation, not temperature (Supplementary Information, Figure S3). A growth lag response of one year of J. neotropica with respect to local and regional precipitation was evident in some periods in our standard growth curve, such as 1973/74, 1987/88, 1989/90 and 1995/96 (Figure 4, top). Ref. [159] proposed the ‘pulse-reserve hypothesis’ to explain how arid and semi-arid plants respond to trigger events (e.g., precipitation events) versus time. He argued that the response to a sequence of rain events depends in part on the time interval between events relative to the ‘relaxation time’ of the system (dry periods) in response to individual events. If rain events are clustered or the plant has a slow response, the effects of the input pulses (rain) will accumulate to produce one single response pulse (growth). This response will often be delayed in time, which can be manifested as a lagged response in the J. neotropica growth curve, such as 1973/74, 1987/88, 1989/90 and 1995/96 (Figure 4, top). Correlation analysis for J. neotropica during the period 1973/74–2005/06 indicates a significant positive relationship between ring width lagged one year behind Santo Domingo precipitation (r = 0.47, p = 0.004, edf = 16). We also found a positive (but not significant) relationship between ring width lagged with respect to Frias precipitation by one year (r = 0.32, p = 0.10, edf = 8.5). These relationships could be explored more fully with larger sample sizes and longer time series; differences in correlation may result from real spatial variations in precipitation anomalies, chronological uncertainty, and meteorological data uncertainty. A growth lag response of one year of J. neotropica with respect to gridded precipitation in Peru was also found by [27].
Because of the significant positive correlation between Santo Domingo precipitation and ring width growth, and the marginally significant correlation with Frias precipitation, we tentatively reject the null hypothesis that wood growth of J. neotropica is independent of precipitation. Investigations of Prosopis spp. in northern Peru report a significant relationship to precipitation events from October the previous year until June of the current year [44]. Our interpretation is consistent with [103], who found that growth in several tropical tree species (including J. australis) was associated positively with precipitation, although there were differences in the timing of the response between species: some species showed a strong positive relationship to precipitation during the previous growing season, while other species showed a positive relationship only to current growing season precipitation, and others responded to both current and previous growing season precipitation. Understanding the mechanisms of a lagged growth response to environmental variability would be an important direction for further research with these species.
Increased ring width growth is consistent with anomalously high precipitation resulting from the strong El Niño events of 1982/83, 1991/92, 1997/98 and 2003-05. Refs. [105,160] found similar correlations between El Niño events and wood growth in tropical tree species. The El Niño events of 1982/83 and 1997/98 produced five and seven times the mean of annual precipitation in Frias and Santo Domingo, respectively; tree-ring growth for these years increases to local maxima during those years compared to the previous and following years, but 1972/73 and 1982/83 seems to precede the appearance of new cohort of trees in the sample (Figure 4, top and Figure 5a,c). The moderate growth increase associated with the El Niño events of 1982/83 and 1997/98 may be due to water saturation (i.e., too much water for plant utilization in a short time period). The strong El Niño event of 1973/74 seems to show a lag effect of one year (Figure 4, top) and appears to be explained by clustered rain events in previous years and/or a slow response of the species. This is consistent with the results of [103], showing that growth variations of Juglans australis were controlled largely by precipitation during previous and current growing seasons. Our results are also consistent with Bursera graveolens [42] and Prosopis pallida [44,45] in northern Peru, which show increased tree ring growth in response to El Niño events.
Although we found that J. neotropica responds to the previous season’s precipitation, this effect seemed to be moderated during especially high precipitation periods, such as strong El Niño events. The threshold–delay (T–D) model [161] in arid and semi-arid environments proposes that antecedent water availability affects a plant’s ability to use precipitation [162,163]; this effect can be incorporated into the lag or threshold response, such as the precipitation thresholds, for which plant response is reduced. This model might account for the immediate growth response in the tree-ring chronology related to some large precipitation events, whereas a lag occurs in years of less precipitation (Figure 5).
The significant negative correlation between gridded precipitation and isotopic composition supports the hypothesis that isotopic composition in J. neotropica is controlled by the regional precipitation amount, itself influenced by ENSO variation [72]. Isotopic age interpretations of JN37-1W and JN41-2N showed a response to precipitation; the two El Niño events of 1982/83 and 1997/98 are manifested as a ~−3‰ magnitude variation in δ18Ocellulose in both age interpretations, most clearly in JN41-2N (Figure 4, middle). Ref. [15] found that Prosopis pallida in Piura can respond to El Niño events with a similarly large magnitude variation in δ18Ocellulose [65] found that the variation in cellulose δ18O of cloud forest trees was consistent with both simulated δ18O and anomalous winds and sea surface temperatures associated with the footprint of ENSO in the tropical Atlantic and Pacific. Our findings support [81], who suggested that large-scale atmospheric circulation features should be considered when interpreting tree ring oxygen isotope signals, because circulation represents not only large-scale processes fundamental to source water δ18O, but also the extent of enrichment due to evapotranspiration in the leaf.
We found a significant relationship between tree-ring growth lagged by one year relative to local precipitation, whereas the isotope interpretation showed a significant relationship to gridded precipitation and simulated isotopic composition in the same year. Considering the biological facts of cell processing in a tree, compared with isotopic theory in dendrochronology, we expected a similar response between the two proxies, because the isotopic composition of water is primarily recorded in new cells, as part of the growth of the tree (but see [164], who proposed and modeled a carry-over mechanism from the prior year’s stored photosynthate). It is well established that antecedent rainfall affects tree growth in arid and semiarid environments [159,161,165], and that mixing processes and lag-times in the soil may vary from year to year and thus influence the tree-ring signal [81]. Many questions remain unanswered and need further investigation in this ecosystem, but our study suggests the merits of using ring width and isotopic data in combination to further understand the environmental information encoded in trees, compared to either measurement in isolation. Unlike other studies (e.g., [25], review by [72]), the oxygen isotopic data in this study were age modeled independently of cross-dating, using their interannual cyclicity and also radiocarbon data, with subsequent environmental interpretation of their interannual variations. Such a strategy might be useful in future studies of J. neotropica and other species from our study region, where ring-width cross-dating is uncertain.
Low replication of the observations presented here is a valid limitation on the strength and generality of the interpretations we develop. Although we found a significant correlation between seasonal δ18O and gridded precipitation for 1973/4–2001/2002, gridded precipitation data were not significantly correlated with isotope interpretations of current or previous seasons for 1959/60–2005/2006. This is likely to reflect the lack of a two-sample composite prior to 1978/9, and that oxygen isotope age model error is cumulative and increases with time since present [15,85,130]. If these preliminary correlations are valid, then improved age model uncertainty with additional replicate analyses should improve ring width chronology statistics (Table 1), and the significance of correlation of isotopic data with gridded regional precipitation, modeled cellulose δ18O and large-scale climate variations (Table 4).
Lower replication records, such as those presented here, have been shown repeatedly to be of value, at least as preliminary indicators. With respect to cellulose δ18O records, [69] published interpretable and statistically significant correlations simulated with four cores from three trees. [65] used two radiocarbon-dated increment cores to form an age model with n = 2 replication for 1900–1969, with significant r across the two records, and significant correlation with environmental variation associated with ENSO activity. [25] averaged δ18O data from three cores from three trees to show significant precipitation-related correlation with ENSO activity at a site in Queensland, Australia. [131] averaged data from three cores from three trees for the period 1971–2005, and showed significant correlation with both local precipitation amount, itself a local response associated with remote ENSO activity. That interpretation has recently been replicated independently by correlation of an expanded composite δ18O record with NINO34 SST anomaly, 1856–2005 [166].
5. Conclusions
Juglans neotropica has annual rings and a dormant period during the dry season of the annual year cycle; we developed a ring-width chronology for this species in a semi-arid, mid-elevation environment at ≤5 °S. This study also demonstrates that variation in δ18Ocellulose and radiocarbon analyses provide complementary and independent chronological control. Both ring width and oxygen isotopic composition provide consistent and plausible indicators of the precipitation variation most clearly associated with interannual ENSO warm phase events.
The age of the J. neotropica sample in this study is young, probably as a consequence of human exploitation of the species, but the techniques applied here may be applied to other species, including some with greater longevity. Such studies might be used to test the hypothesis that El Niño events can initiate changes in stand demography. The combination of wood anatomy, tree-ring chronologies, radiocarbon analyses and stable isotopic analyses provide a greater degree of confidence in our chronological results that would have been possible using only a single proxy. Increased sample replication, geographic range, and more controlled study of the environmental controls on J. neotropica growth and wood isotopic composition would be beneficial to fully exploit the dendrochronological potential of this species to record aspects of climate and carbon cycle dynamics in the dry forests of tropical South America [167].
This study contributes to the increasing inventory of tree-ring chronologies near the equator and in montane areas of South America. The expanded study of tropical forests has the potential to illuminate how these ecosystems influence the dynamics of the global carbon cycle, as well as deeper insights into how climate variability modulates tree growth, survival [168,169], and reproduction in tropical forest ecosystems. Tropical dendrochronology has much to contribute to insights into climate and forest dynamics, both regionally and globally.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/plants14111704/s1. Figure S1: Banded age model (BAM) simulation of age uncertainty of tree-ring width (upper panel; 5% error rate) and δ18O (lower panel; 5% error rate.; Figure S2: Correlation of plausible age simulated TRW (left) and δ18O (right) series with the NINO12 (upper) and NINO34 SST (lower) anomaly indices.; Figure S3: VS-Lite modeling of temperature and moisture controls on growth. Relative effects of monthly temperature (GT, upper left) and moisture (GM, upper right) on TRW. Resulting simulated TRW time series with propagated age model errors (lower left), and comparison of simulated and observed TRW (lower right).
Author Contributions
T.M.E. conceived and initiated the study, organized primary funding, conducted all fieldwork and collected samples; performed all anatomical, ring-width analysis and measuring, led manuscript writing and revision. Research questions were defined by T.M.E. and refined in cooperation with M.N.E. and D.A.F. M.N.E. conducted stable isotope analyses, performed isotopic modeling and statistical analysis of results, and participated in manuscript writing and revision. D.A.F. provided guidance and participated in dendrochronological data analysis, manuscript writing and revision. P.R.S. conducted statistical analysis in dendrochronology and participated in manuscript revision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Norwegian Research Council (Grant 166045/V10 (TME)) and US National Science Foundation Grant NSF/ATM0349356 (MNE).
Data Availability Statement
The original contributions presented in the study are included in the article and Supplementary Material. Tree-ring width and isotopic data collected for this study will be available through the NOAA/NCEI World Data Service (https://www.ncei.noaa.gov/products/paleoclimatology). Further inquiries can be directed to the authors.
Acknowledgments
T.M.E. stayed ten months in Piura, Peru to collect field data: thanks to informants who shared information and local companions. Thanks for assistance in the field by Luis Flores Caucha (Laboratorio Dendrochonología, Universidad de Piura) and student Luis Urbina Zapata (Unidad de proyectos ambientales, Universidad de Piura). Grover Otero (Projecto Especial Chira Piura) and Hector Yuari Quispe (Servicio Nacional de Meteorológica e Hidrológica del Perú) were contact persons for obtaining climate data. Permission to bring tree samples to Norway was given by INRENA, Lima, Peru. T.M.E. worked ten months at Laboratory of Tree-Ring Research, University of Arizona, USA; thanks to staff and students for knowledge sharing, especially Rex Adams, Erica Bigio, April Chiriboga, Adam Csank, Rebecca Franklin, Steve Leavitt, Kiyomi Morino, and Scott St. George. Thanks to Melissa Kingston for dendrochronology laboratory work (ring-width analysis and measuring), and to Ruth Penniston and Sarah White for isotopic laboratory work and isotope processing. Kjell Helge Sjøstrøm, University of Bergen, gave good advice for improving the layout of figures. Thanks to Erling Moxnes, Kerstin Potthoff, and Ulysses S. Ninnemann, all University of Bergen, for sharing knowledge and insights. The authors thank three anonymous reviewers for their helpful insights and contributions to the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- von Schnakenburg, P.; Bräuning, A.; Helle, G. Detecting annual growth rhythms from high-frequency densitometry and carbon isotopes in tropical mountain rain forest trees in southern Ecuador. In TRACE—Tree Rings in Archaeology, Climatology and Ecology; Elferts, D., Brumelis, G., Gartner, H., Helle, G., Schleser, G., Eds.; Scientific Technical Report STR 07/05; GFZ Potsdam: Potsdam, Germany, 2008; Volume 6, pp. 96–99. [Google Scholar]
- Fichtler, E. Dendroclimatology using tropical broad-leaved tree species—A review. Erdkunde 2017, 71, 5–22. [Google Scholar] [CrossRef]
- Sánchez-Calderón, O.D.; Carlón-Allende, T.; Mendoza, M.E.; Villanueva-Díaz, J. Dendroclimatology in Latin America: A Review of the State of the Art. Atmosphere 2022, 13, 748. [Google Scholar] [CrossRef]
- Mariaux, A. Growth Periodicity in Tropical Trees. Preface. Int. Assoc. Wood Anat. (IAWA) J. 1995, 16, 327–328. [Google Scholar]
- Eckstein, D.; Sass, U.; Baas, P. Growth periodicity in tropical trees. Kew Bull. 1995, 16, 323–442. [Google Scholar]
- Worbes, M. One hundred years of tree-ring research in the tropics—A brief history and an outlook to future challenges. Dendrochronologia 2002, 20, 217–231. [Google Scholar] [CrossRef]
- Zuidema, P.A.; Baker, P.J.; Groenendijk, P.; Schippers, P.; van der Sleen, P.; Vlam, M.; Sterck, F. Tropical forests and global change: Filling knowledge gaps. Trends Plant Sci. 2013, 18, 413–419. [Google Scholar] [CrossRef]
- Zuidema, P.A.; Groenendijk, P.; Rahman, M.; Trouet, V.; Abiyu, A.; Acuña-Soto, R.; Adenesky-Filho, E.; Alfaro-Sánchez, R.; Anholetto, C.R., Jr.; Vieira Aragão, J.R.; et al. Pantropical tree rings show small effects of drought on stem growth. Science 2025, in press.
- Brienen, R.J.W.; Schöngart, J.; Zuidema, P.A. Tree rings in the tropics: Insights into the ecology and climate sensitivity of tropical trees. In Tropical Tree Physiology; Goldstein, G., Santiago, L., Eds.; Tree Physiology; Springer: Cham, Switzerland, 2016; Volume 6. [Google Scholar] [CrossRef]
- Stahle, D.W.; D’Arrigo, R.D.; Krusic, P.J.; Cleaveland, M.K.; Cook, E.R.; Allan, R.J.; Cole, J.E.; Dunbar, R.B.; Therrell, M.D.; Gay, D.A.; et al. Experimental dendroclimatic reconstruction of the Southern Oscillation. Bull. Am. Meteorol. Soc. 1998, 79, 2137–2152. [Google Scholar] [CrossRef]
- Villalba, R.; Grau, H.R.; Boninsegna, J.A.; Jacoby, G.C.; Ripalta, A. Tree-ring evidence for long-term precipitation changes in subtropical South America. Int. J. Clim. 1998, 18, 1463–1478. [Google Scholar] [CrossRef]
- Borchert, R. Climatic Periodicity, Phenology, and Cambium Activity in Tropical Dry Forest Trees. IAWA J. 1999, 20, 239–247. [Google Scholar] [CrossRef]
- Ciemer, C.; Boers, N.; Hirota, M.; Kurths, J.; Müller-Hansen, F.; Oliveira, R.S.; Winkelmann, R. Higher resilience to climatic disturbances in tropical vegetation exposed to more variable rainfall. Nat. Geosci. 2019, 12, 174–179. [Google Scholar] [CrossRef]
- Granato-Souza, D.; Stahle, D.W.; Barbosa, A.C.; Feng, S.; Torbenson, M.C.A.; Pereira, G.d.A.; Schöngart, J.; Barbosa, J.P.; Griffin, D. Tree rings and rainfall in the equatorial Amazon. Clim. Dyn. 2019, 52, 1857–1869. [Google Scholar] [CrossRef]
- Evans, M.N.; Schrag, D.P. A stable isotope-based approach to tropical dendroclimatology. Geochim. Cosmochim. Acta 2004, 68, 3295–3305. [Google Scholar] [CrossRef]
- Brienen, R.J.W.; Lebrija-Trejos, E.; Van Breugel, M.; Pérez-García, E.A.; Bongers, F.; Meave, J.A.; Martínez-Ramos, M. The Potential of Tree Rings for the Study of Forest Succession in Southern Mexico. Biotropica 2009, 41, 186–195. [Google Scholar] [CrossRef]
- Brienen, R.J.W.; Zuidema, P.A. Relating tree growth to rainfall in Bolivian rain forests: A test for six species using tree ring analysis. Oecologia 2005, 146, 1–12. [Google Scholar] [CrossRef]
- Boninsegna, J.; Argollo, J.; Aravena, J.; Barichivich, J.; Christie, D.; Ferrero, M.; Lara, A.; Le Quesne, C.; Luckman, B.; Masiokas, M.; et al. Dendroclimatological reconstructions in South America: A review. Palaeogeogr. Palaeoclim. Palaeoecol. 2009, 281, 210–228. [Google Scholar] [CrossRef]
- Inga, J.G.; del Valle, J.I. Log-relative growth: A new dendrochronological approach to study diameter growth in Cedrela odorata and Juglans neotropica, Central Forest, Peru. Dendrochronologia 2017, 44, 117–129. [Google Scholar] [CrossRef]
- Alvim, P.d.T. Tree growth periodicity in tropical climates. In The Formation of Wood in Forest Trees; Zimmermann, M.H., Ed.; Academic Press: New York, NY, USA; London, UK; San Francisco, CA, USA, 1964; pp. 479–495. [Google Scholar]
- Boninsegna, J.A.; Villalba, R.; Amarilla, L.; Ocampo, J. Studies on tree rings, growth rates and age-size relationships of tropical trees in Misiones, Argentina. Int. Assoc. Wood Anat. (IAWA) Bull. 1989, 10, 161–169. [Google Scholar]
- Jacoby, G.C. Overview of tree-ring analysis in tropical regions. Int. Assoc. Wood Anat. (IAWA) Bull. 1989, 10, 99–108. [Google Scholar] [CrossRef]
- Stahle, D.W. Useful Strategies for the Development of Tropical Tree-Ring Chronologies. IAWA J. 1999, 20, 249–253. [Google Scholar] [CrossRef]
- Worbes, M. Wood Anatomy and Tree-Ring Structure and Their Importance for Tropical Dendrochronology. In Amazonian Floodplain Forests; Ecological Studies; Junk, W., Piedade, M., Wittmann, F., Schöngart, J., Parolin, P., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 210, pp. 329–346. [Google Scholar] [CrossRef]
- Boysen, B.M.; Evans, M.N.; Baker, P.J. δ18O in the tropical conifer Agathis robusta records ENSO-related precipitation variations. PLoS ONE 2014, 9, e102336. [Google Scholar] [CrossRef] [PubMed]
- Layme-Huaman, E.; Ferrero, M.; Palacios-Lazaro, K.; Requena-Rojas, E. Cedrela nebulosa: A novel species for dendroclimatological studies in the montane tropics of South America. Dendrochronologia 2018, 50, 105–112. [Google Scholar] [CrossRef]
- Humanes-Fuente, V.; Ferrero, M.E.; Muñoz, A.A.; González-Reyes, Á.; Requena-Rojas, E.J.; Barichivich, J.; Inga, J.G.; Layme-Huaman, E.T. Two centuries of hydroclimatic variability reconstructed from tree-ring records over the Amazonian Andes of Peru. J. Geophys. Res. Atmos. 2020, 125, e2020JD032565. [Google Scholar] [CrossRef]
- Marcelo-Peña, J.L.; Roig, F.A.; Goodwin, Z.A.; Tomazello-Filho, M. Characterizing growth rings in the trees of Perú: A wood anatomical overview for potential applications in dendroecological-related fields. Dendrochronologia 2020, 62, 125728. [Google Scholar] [CrossRef]
- Villalba, R.; Boninsegna, J.A.; Holmes, R.L. Cedrela augstifolia and Juglans australis: Two new tropical species useful in dendrochronology. Tree-Ring Bull. 1985, 45, 25–35. [Google Scholar]
- Bräuning, A.; Homeier, J.; Cueva, E.; Beck, E.; Günter, S. Growth dynamics of trees in tropical mountain ecosystems. In Gradients in a Tropical Mountain Ecosystem of Ecuador; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Ecological Studies 198; Springer: Berlin, Germany, 2008; pp. 347–359. ISBN 978-3-540-73526-7. [Google Scholar]
- Bräuning, A.; von Schnakenburg, P.; Volland-Voigt, F.; Peters, T. Seasonal growth dynamics and its climate forcing in a tropical mountain rain forest in southern Ecuador. In TRACE—Tree Rings in Archaeology, Climatology and Ecology; Elferts, D., Brumelis, G., Gartner, H., Helle, G., Schleser, G., Eds.; Scientific Technical Report STR 07/05; GFZ Potsdam: Potsdam, Germany, 2008; Volume 6, pp. 27–30. [Google Scholar]
- Barichivich, J.; Sauchyn, D.J.; Lara, A. Climate signals in high elevation tree-rings from the semiarid Andes of north-central Chile: Responses to regional and large-scale variability. Palaeogeogr. Palaeoclim. Palaeoecol. 2009, 281, 320–333. [Google Scholar] [CrossRef]
- Luckman, B.H. Using multiple high-resolution proxy climate records to reconstruct natural climate variability: An example from the Canadian Rockies. In Mountain Environments in Changing Climates; Beniston, M., Ed.; Routledge: London, UK, 1994; pp. 42–59. [Google Scholar]
- Villalba, R.; Boninsegna, J.A.; Veblen, T.T.; Schmelter, A.; Rubulis, S. Recent trends in tree-ring records from high elevation sites in the andes of northern patagonia. Clim. Change 1997, 36, 425–454. [Google Scholar] [CrossRef]
- Lara, A.; Villalba, R.; Urrutia, R. A 400-year tree-ring record of the Puelo River summer–fall streamflow in the Valdivian Rainforest eco-region, Chile. Clim. Change 2008, 86, 331–356. [Google Scholar] [CrossRef]
- Pucha-Cofrep, D.; Jumbo, N.; Moncada, V.; Burneo, M.; Narvaez, L.; César, F.; Barrera, E.; Castro, J.; Ruiz, J.; Bräuning, A. Impacto de las condiciones climáticas en el crecimiento diamétrico de especies forestales de alto valor comercial. In Efectos del Cambio Climático en el Hábitat de las Especies y los O.D.S. Memorias del Congreso Internacional de Cambio Climático; Benavides-Muñoz, H., Pucha-Cofrep, F., Eds.; La Universidad Católica de Loja: Loja, Equador, 2020; pp. 20–22. [Google Scholar]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an Integrating Concept in Earth Science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef]
- Diaz, H.F.; Hoerling, M.P.; Eischeid, J.K. ENSO variability, teleconnections and climate change. Int. J. Climatol. 2001, 21, 1845–1862. [Google Scholar] [CrossRef]
- Goldberg, R.A.; Tisnado, M.G.; Scofield, R.A. Characteristics of extreme rainfall events in northwestern Peru during the 1982–1983 El Niño period. J. Geophys. Res. Oceans 1987, 92, 14225–14241. [Google Scholar] [CrossRef]
- D’Arrigo, R.D.; Jacoby, G.C. Past changes in climate and tree growth in the Western Americas. In High-Latitude Rainforests and Associated Ecosystems of the West Coast of the Americas: Climate, Hydrology, Ecology, and Conservation; Lawford, R.G., Alaback, P.B., Fuentes, E., Eds.; Ecological Studies 116; Springer: Berlin/Heidelberg, Germany, 1996; pp. 75–88. [Google Scholar]
- Ortlieb, L. The documented historical record of El Niño events in Peru: An update of the Quinn record (sixteenth through nineteenth centuries). In El Niño and the Southern Oscillation: Multiscale Variability and Global and Regional Impacts; Díaz, H.F., Markgraf, V., Eds.; Cambridge University Press: Cambridge, UK, 2000; pp. 207–295. [Google Scholar]
- Rodríguez, R.; Mabres, A.; Luckman, B.; Evans, M.; Masiokas, M.; Ektvedt, T.M. ‘El Niño’ events recorded in dry-forest species of the lowlands of northwest Peru. Dendrochronologia 2005, 22, 181–187. [Google Scholar] [CrossRef]
- Holmgren, M.; López, B.C.; Gutiérrez, J.R.; Squeo, F.A. Herbivory and plant growth rate determine the success of El Niño Southern Oscillation-driven tree establishment in semiarid South America. Glob. Change Biol. 2006, 12, 2263–2271. [Google Scholar] [CrossRef]
- López, B.; Sabaté, S.; Gracia, C.; Rodríguez, R. Wood anatomy, description of annual rings, and responses to ENSO events of Prosopis pallida H.B.K., a wide-spread woody plant of arid and semi-arid lands of Latin America. J. Arid. Environ. 2005, 61, 541–554. [Google Scholar] [CrossRef]
- López, B.C.; Rodríguez, R.; Gracia, C.A.; Sabaté, S. Climatic signals in growth and its relation to ENSO events of two Prosopis species following a latitudinal gradient in South America. Glob. Change Biol. 2006, 12, 897–906. [Google Scholar] [CrossRef]
- López, B.C.; Holmgren, M.; Sabaté, S.; Garcia, C.A. Estimating annual rainfall threshold for establishment of tree species in water-limited ecosystems using tree-ring data. J. Arid. Environ. 2008, 72, 602–611. [Google Scholar] [CrossRef]
- Locosselli, G.M.; Buckeridge, M.S.; Moreira, M.Z.; Ceccantini, G. A multi-proxy dendroecological analysis of two tropical species (Hymenaea spp., Leguminosae) growing in a vegetation mosaic. Trees 2013, 27, 25–36. [Google Scholar] [CrossRef]
- López, L.; Rodríguez-Catón, M.; Villalba, R. Convergence in growth responses of tropical trees to climate driven by water stress. Ecography 2019, 42, 1899–1912. [Google Scholar] [CrossRef]
- Babst, F.; Bodesheim, P.; Charney, N.; Friend, A.D.; Girardin, M.P.; Klesse, S.; Moore, D.J.; Seftigen, K.; Björklund, J.; Bouriaud, O. When tree rings go global: Challenges and opportunities for retro-and prospective insight. Quat. Sci. Rev. 2018, 197, 1–20. [Google Scholar] [CrossRef]
- Rodriguez-Caton, M.; Morales, M.S.; Rao, M.P.; Nixon, T.; Vuille, M.; Rivera, J.A.; Oelkers, R.; Christie, D.A.; Varuolo-Clarke, A.M.; Ferrero, M.E.; et al. A 300-year tree-ring δ18O-based precipitation reconstruction for the South American Altiplano highlights decadal hydroclimate teleconnections. Commun. Earth Environ. 2024, 5, 269. [Google Scholar] [CrossRef]
- Worbes, M.; Junk, W.J. Dating Tropical Trees by Means of 14C from Bomb Tests. Ecology 1989, 70, 503–507. [Google Scholar] [CrossRef]
- Dezzeo, N.; Worbes, M.; Ishii, I.; Herrera, R. Annual tree rings revealed by radiocarbon dating in seasonally flooded forest of the Mapire River, a tributary of the lower Orinoco River, Venezuela. Plant Ecol. 2003, 168, 165–175. [Google Scholar] [CrossRef]
- Fichtler, E.; Clark, D.A.; Worbes, M. Age and Long-term Growth of Trees in an Old-growth Tropical Rain Forest, Based on Analyses of Tree Rings and 14C1. Biotropica 2003, 35, 306. [Google Scholar] [CrossRef]
- Robertson, I.; Froyd, C.A.; Walsh, R.P.D.; Newbery, D.M.; Woodborne, S.; Ong, R.C. The dating of dipterocarp tree rings: Establishing a record of carbon cycling and climatic change in the tropics. J. Quat. Sci. 2004, 19, 657–664. [Google Scholar] [CrossRef]
- Robertson, I.; Loader, N.; Froyd, C.; Zambatis, N.; Whyte, I.; Woodborne, S. The potential of the baobab (Adansonia digitata L.) as a proxy climate archive. Appl. Geochem. 2006, 21, 1674–1680. [Google Scholar] [CrossRef]
- Westbrook, J.A.; Guilderson, T.P.; Colinvaux, P.A. Annual growth rings in a sample of Hymenaea courbaril. Int. Assoc. Wood Anat. (IAWA) J. 2006, 27, 193–197. [Google Scholar] [CrossRef]
- Wils, T.H.; Robertson, I.; Eshetu, Z.; Sass-Klaassen, U.G.; Koprowski, M. Periodicity of growth rings in Juniperus procera from Ethiopia inferred from crossdating and radiocarbon dating. Dendrochronologia 2009, 27, 45–58. [Google Scholar] [CrossRef]
- Norström, E.; Holmgren, K.; Mörth, C.-M. A 600-year-long δ18O record from cellulose of Breonadia salicina trees, South Africa. Dendrochronologia 2008, 26, 21–33. [Google Scholar] [CrossRef]
- Nydal, R.; Lövseth, K. Tracing bomb 14C in the atmosphere 1962–1980. J. Geophys. Res. Ocean. 1983, 88, 3621–3642. [Google Scholar] [CrossRef]
- Reimer, P.J.; Brown, T.A.; Reimer, R.W. Discussion: Reporting and calibration of post-bomb 14C data. Radiocarbon 2004, 46, 1299–1304. [Google Scholar]
- Hua, Q.; Barbetti, M. Review of Tropospheric Bomb 14C Data for Carbon Cycle Modeling and Age Calibration Purposes. Radiocarbon 2004, 46, 1273–1298. [Google Scholar] [CrossRef]
- Mozeto, A.A.; Fritz, P.; Moreira, M.Z.; Vetter, E.; Aravena, R.; Salati, E.; Drimmie, R.J. Growth Rates of Natural Amazonian Forest Trees Based on Radiocarbon Measurements. Radiocarbon 1988, 30, 1–6. [Google Scholar] [CrossRef]
- Biondi, F.; Fessenden, J.E. Radiocarbon Analysis of Pinus lagunae Tree Rings: Implications for Tropical Dendrochronology. Radiocarbon 1999, 41, 241–249. [Google Scholar] [CrossRef]
- Norström, E.; Holmgren, K.; Mörth, C.-M. Rainfall-driven variations in δ13C composition and wood anatomy of Breonadia salicina trees from South Africa between AD 1375 and 1995. S. Afr. J. Sci. 2005, 101, 162–168. [Google Scholar]
- Anchukaitis, K.J.; Evans, M.N. Tropical cloud forest climate variability and the demise of the Monteverde golden toad. Proc. Natl. Acad. Sci. USA 2010, 107, 5036–5040. [Google Scholar] [CrossRef] [PubMed]
- Verheyden, A.; Helle, G.; Schleser, G.H.; Dehairs, F.; Beeckman, H.; Koedam, N. Annual cyclicity in high-resolution stable carbon and oxygen isotope ratios in the wood of the mangrove tree Rhizophora mucronata. Plant Cell Environ. 2004, 27, 1525–1536. [Google Scholar] [CrossRef]
- Poussart, P.F.; Evans, M.N.; Schrag, D.P. Resolving seasonality in tropical trees: Multi-decade, high-resolution oxygen and carbon isotope records from Indonesia and Thailand. Earth Planet. Sci. Lett. 2004, 218, 301–316. [Google Scholar] [CrossRef]
- Poussart, P.F.; Schrag, D.P. Seasonally resolved stable isotope chronologies from northern Thailand deciduous trees. Earth Planet. Sci. Lett. 2005, 235, 752–765. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Evans, M.N.; Wheelwright, N.T.; Schrag, D.P. Stable isotope chronology and climate signal calibration in neotropical montane cloud forest trees. J. Geophys. Res. Biogeosci. 2008, 113, G03030. [Google Scholar] [CrossRef]
- Managave, S.R.; Ramesh, R. Isotope dendroclimatology: A review with a special emphasis on tropics. In Handbook of Environmental Isotope Geochemistry, Advances in Isotope Geochemistry; Baskaran, M., Ed.; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Brienen, R.J.W.; Helle, G.; Pons, T.L.; Guyot, J.-L.; Gloor, M. Oxygen isotopes in tree rings are a good proxy for Amazon precipitation and El Niño-Southern Oscillation variability. Proc. Natl. Acad. Sci. USA 2012, 109, 16957–16962. [Google Scholar] [CrossRef]
- van der Sleen, P.; Zuidema, P.A.; Pons, T.L. Stable isotopes in tropical tree rings: Theory, methods and applications. Funct. Ecol. 2017, 31, 1674–1689. [Google Scholar] [CrossRef]
- Wolfe, A.P.; Csank, A.Z.; Reyes, A.V.; McKellar, R.C.; Tappert, R.; Muehlenbachs, K. Pristine Early Eocene Wood Buried Deeply in Kimberlite from Northern Canada. PLoS ONE 2012, 7, e45537. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Ehleringer, J.R.; Hubick, K.T. Carbon isotope discrimination and photosynthesis. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1989, 40, 503–537. [Google Scholar] [CrossRef]
- Roden, J.S.; Ehleringer, J.R. Hydrogen and oxygen isotope ratios of leaf water and tree-ring cellulose for field-grown riparian trees. Oecologia 2000, 123, 481–489. [Google Scholar] [CrossRef]
- Barbour, M.M.; Roden, J.S.; Ehleringer, J.R.; Farquhar, G.D. Expressing leaf water and cellulose oxygen isotope ratios as enrichment above source water reveals evidence of a Péclet effect. Oecologia 2004, 138, 426–435. [Google Scholar] [CrossRef] [PubMed]
- McCarroll, D.; Loader, N.J. Stable isotopes in tree rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Dawson, T.E. Water uptake by plants: Perspectives from stable isotope composition. Plant Cell Environ. 1992, 15, 1073–1082. [Google Scholar] [CrossRef]
- Dawson, T.E.; Mambelli, S.; Plamboeck, A.H.; Templer, P.H.; Tu, K.P. Stable isotopes in plant ecology. Annu. Rev. Ecol. Syst. 2002, 33, 507–559. [Google Scholar] [CrossRef]
- Vuille, M.; Werner, M. Stable isotopes in precipitation recording South American summer monsoon and ENSO variability: Observations and model results. Clim. Dyn. 2005, 25, 401–413. [Google Scholar] [CrossRef]
- Saurer, M.; Kress, A.; Leuenberger, M.; Rinne, K.T.; Treydte, K.S.; Siegwolf, R.T.W. Influence of atmospheric circulation patterns on the oxygen isotope ratio of tree rings in the Alpine region. J. Geophys. Res. Atmos. 2012, 117, D5. [Google Scholar] [CrossRef]
- Gessler, A.; Brandes, E.; Keitel, C.; Boda, S.; Kayler, Z.E.; Granier, A.; Barbour, M. The oxygen isotope enrichment of leaf-exported assimilates–does it always reflect lamina leaf water enrichment? New Phytol. 2013, 200, 144–157. [Google Scholar] [CrossRef] [PubMed]
- Gessler, A.; Ferrio, J.P.; Hommel, R.; Treydte, K.; Werner, R.A.; Monson, R.K.; Schnitzler, J.-P. Stable isotopes in tree rings: Towards a mechanistic understanding of isotope fractionation and mixing processes from the leaves to the wood. Tree Physiol. 2014, 34, 796–818. [Google Scholar] [CrossRef]
- Rodriguez-Caton, M.; Andreu-Hayles, L.; Morales, M.S.; Daux, V.; Christie, D.A.; Coopman, R.E.; Alvarez, C.; Rao, M.P.; Aliste, D.; Flores, F.; et al. Different climate sensitivity for radial growth, but uniform for tree-ring stable isotopes along an aridity gradient in Polylepis tarapacana, the world’s highest elevation tree species. Tree Phys. 2021, 41, 1353–1371. [Google Scholar] [CrossRef]
- Evans, M.N. Toward forward modeling for paleoclimatic proxy signal calibration: A case study with oxygen isotopic composition of tropical woods. Geochem. Geophys. Geosyst. 2007, 8, Q07008. [Google Scholar] [CrossRef]
- Tropicos v.3.4.2; Missouri Botanical Garden: St. Louis, MO, USA, 2025; Available online: https://tropicos.org/name/16700014 (accessed on 27 May 2025).
- Diels, L. Juglans neotropica. In Urban, Plantae Novae Andinae Imprimis Weberbauerianae; Botanishe Jahrbüchen: Stuttgart, Germany, 1906; Volume 37, p. 398. [Google Scholar]
- Manning, W.E. The Genus Juglans in South America and the West Indies. Brittonia 1960, 12, 1–26. [Google Scholar] [CrossRef]
- Aradhya, M.K.; Potter, D.; Gao, F.; Simon, C.J. Molecular phylogeny of Juglans (Juglandaceae): A biogeographic perspective. Tree Genet. Genomes 2007, 3, 363–378. [Google Scholar] [CrossRef]
- Toro Vanegas, E.; Roldan Rojas, I.E. Estado del arte, progagación y conservación de Juglans neotropica Diels, en zonas Andinas (State of the Art, propagation and conservation of Juglans neotropica Diels., in Andean zones). Madera Bosques 2018, 24, 1. [Google Scholar] [CrossRef]
- Ministry of Agriculture and Forestry. Juglans (Walnut)—Post Entry Quarantine Testing Manual; Biosecurity New Zealand, Ministry of Agriculture and Forestry: Auckland, New Zealand, 2008; 27p. [Google Scholar]
- Pennington, T.D.; Reyel, C.; Daza, A. Illustrated Guide to the Trees of Peru; D Hunt Books: Wallingford, UK, 2004; 848p. [Google Scholar]
- Reynel, C.; Pennington, T.D.; Pennington, R.T.; Marcelo, J.; Daza, A. Árboles Útiles del Ande Peruano. Una guía de Identificación, Ecología y Propagación de las Especies de la Sierra y los Bosques Montaños en el Perú; Darwin Initiative Project: Lima, Peru, 2006; 466p. [Google Scholar]
- Amaya Cubas, J.A. Tratamientos Pre-Germinativos de Juglans neotropica Diels y Podocarpus rospigliosii Pilger, en Inmersiones de agua y Ácido Giberélico. Ph.D. Thesis, Universidad Nacional del Centro del Peru, Facultad de Ingenierio Forestal, Huancayo, Peru, 1985. [Google Scholar]
- Cotler, H.; Maass, J.M. Tree Management in the Northwestern Andean Cordillera of Peru. Mt. Res. Dev. 1999, 19, 153. [Google Scholar] [CrossRef]
- National Research Council (NRC). The Lost Crops of the Incas: Little-Known Plants of the Andes with Promise for Worldwide Cultivation; National Academy Press: Washington, DC, USA, 1989; 415p.
- IUCN (International Union for the Conservation of Nature). Americas Regional Workshop (Conservation & Sustainable Management of Trees, Costa Rica) 1998. Juglans neotropica. In IUCN 2010. IUCN Red List of Threatened Species; Version 2010.2; 2010; Available online: www.iucnredlist.org (accessed on 1 September 2010).
- Lamb, D.; Erskine, P.D.; Parrotta, J.A. Restoration of Degraded Tropical Forest Landscapes. Science 2005, 310, 1628–1632. [Google Scholar] [CrossRef]
- Kribs, D.A. Comparative anatomy of the woods of the Juglandaceae. Trop. Woods 1927, 12, 16–21. [Google Scholar]
- Heimsch, C., Jr.; Wetmore, R.H. The significance of wood anatomy in the taxonomy of the Juglandaceae. Am. J. Bot. 1939, 26, 651–660. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; The Blackburn Press: Caldwell, NJ, USA, 1976; 567p. [Google Scholar]
- Villalba, R.; Holmes, R.L.; Boninsegna, J.A. Spatial Patterns of Climate and Tree Growth Variations in Subtropical Northwestern Argentina. J. Biogeogr. 1992, 19, 631. [Google Scholar] [CrossRef]
- Morales, M.S.; Villalba, R.; Grau, H.R.; Paolini, L. Rainfall-controlled tree growth in high-elevation subtropical treelines. Ecology 2004, 85, 3080–3089. [Google Scholar] [CrossRef]
- Morales, M.S.; Villalba, R. Tree rings as a surrogate for economic stress—An example from the Puna of Jujuy, Argentina in the 19th century. Dendrochronologia 2005, 22, 141–147. [Google Scholar]
- Worbes, M. Annual growth rings, rainfall-dependent growth and long-term growth patterns of tropical trees from the Caparo Forest Reserve in Venezuela. J. Ecol. 1999, 87, 391–403. [Google Scholar] [CrossRef]
- Nugent, J.; Boniface, J. Permaculture Plants—A Selection; Chelsea Green Publishing Company: White River Junction, VT, USA, 2005; 160p. [Google Scholar]
- Leuschner, C. Are high elevations in tropical mountains arid environments for plants? Ecology 2000, 81, 1425–1436. [Google Scholar] [CrossRef]
- Biondi, F. A 400-year tree-ring chronology from the tropical treeline of North America. AMBIO J. Hum. Environ. 2001, 30, 162–166. [Google Scholar] [CrossRef]
- Speer, J.H. Fundamentals of Tree-Ring Research; The University of Arizona Press: Tucson, AZ, USA, 2010; 333p. [Google Scholar]
- Instituto Nacional de Recursos Naturales (INRENA). Mapa de Bosques Secos del Departamento de Piura. Memoria Descriptive; Ministerio de Agricultura, Dirección de Estudios y Proyectos de Recursos Naturales: Lima, Peru, 1998; 86p. [Google Scholar]
- Mettier, R.; Schlunegger, F.; Schneider, H.; Rieke-Zapp, D.; Schwab, M. Relationships between landscape morphology, climate and surface erosion in northern Peru at 5°S latitude. Int. J. Earth Sci. (Geol. Rundsch.) 2009, 98, 2009–2022. [Google Scholar] [CrossRef]
- Ektvedt, T.M. Firewood consumption amongst poor inhabitants in a semiarid tropical forest: A case study from Piura, northern Peru. Nor. Geogr. Soc. 2011, 65, 28–41. [Google Scholar] [CrossRef]
- Servicio Nacional de Meteorológica e Hidrológica del Perú (SENAMHI). 2025. Available online: https://www.senamhi.gob.pe/?&p=estaciones (accessed on 17 May 2025).
- ISO 2533:1975.9; Standard Atmosphere. International Organization for Standardization (ISO): Geneva, Switzerland, 1975.
- Bockor, I.; Gamboa, H. Documentación del Proyecto. Resúmenes de publicaciones. INFOR-GTZ. Proyecto Peruano-Alemán; Desarrollo Forestal y Agroforestal en la Selva Central: Lima, Peru, 1987; p. 86. [Google Scholar]
- Estrada, A.W. Manual para la Producción de Nogal. Juglans neotropica Diels; Editorial EDI-U: Loja, Ecuador, 1997; 47p. [Google Scholar]
- Robinson, W.J.; Evans, R. A microcomputer-based tree-ring measuring system. Tree-Ring Bull. 1980, 40, 59–64. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree Ring Dating; The University of Arizona Press: Tucson, AZ, USA, 1996; 73p. [Google Scholar]
- Cook, E. The Concept and Methodology of Program ARSTAN, Program Site; Tree-Ring Laboratory, Lamont-Doherty Earth Observatory of Columbia University in Palisades: New York, NY, USA, 1985. [Google Scholar]
- Cook, E.R.; Briffa, K.R.; Shiyatov, S.; Mazepa, V. Tree-ring standardization and growth-trend estimation. In Methods of Dendrochronology: Applications in the Environmental Sciences; Cook, E.R., Kairiukstis, L.A., Eds.; International Institute for Applied Systems Analysis, Kluwer Academic Publishers: Boston, MA, USA, 1990; pp. 104–123. [Google Scholar]
- Tolwinski-Ward, S.E.; Evans, M.N.; Hughes, M.K.; Anchukaitis, K.J. An efficient forward model of the climate controls on interannual variation in tree-ring width. Clim. Dyn. 2010, 36, 2419–2439. [Google Scholar] [CrossRef]
- Evans, M.; Smerdon, J.E.; Kaplan, A.; Tolwinski-Ward, S.; González-Rouco, J.F. Climate field reconstruction uncertainty arising from multivariate and nonlinear properties of predictors. Geophys. Res. Lett. 2014, 41, 9127–9134. [Google Scholar] [CrossRef]
- Brienen, R.J.; Zuidema, P.A. Lifetime growth patterns and ages of Bolivian rain forest trees obtained by tree ring analysis. J. Ecol. 2006, 94, 481–493. [Google Scholar] [CrossRef]
- Groenendijk, P.; Sass-Klaassen, U.; Bongers, F.; Zuidema, P.A. Potential of tree-ring analysis in a wet tropical forest: A case study on 22 commercial tree species in Central Africa. For. Ecol. Manag. 2014, 323, 65–78. [Google Scholar] [CrossRef]
- Pearson, C.; Manning, S.W.; Coleman, M.; Jarvis, K. Can tree-ring chemistry reveal absolute dates for past volcanic eruptions? J. Archaeol. Sci. 2005, 32, 1265–1274. [Google Scholar] [CrossRef]
- Schollaen, K.; Heinrich, I.; Neuwirth, B.; Krusic, P.J.; D’Arrigo, R.D.; Karyanto, O.; Helle, G. Multiple tree-ring chronologies (ring width, δ13C and δ18O) reveal dry and rainy season signals of rainfall in Indonesia. Quat. Sci. Rev. 2013, 73, 170–181. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Evans, M.N.; Lange, T.; Smith, D.R.; Leavitt, S.W.; Schrag, D.P. Purity and isotopic results from a rapid cellulose extraction method. Anal. Chem. 2008, 80, 2035–2041. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.N. A reactor for high-temperature pyrolysis and oxygen isotopic analysis of cellulose via induction heating. Rapid Commun. Mass Spectrom. 2008, 22, 2211–2219. [Google Scholar] [CrossRef]
- Comboul, M.; Emile-Geay, J.; Evans, M.N.; Mirnateghi, N.; Cobb, K.M.; Thompson, D.M. A probabilistic model of chronological errors in layer-counted climate proxies: Applications to annually banded coral archives. Clim. Past 2014, 10, 825–841. [Google Scholar] [CrossRef]
- Nurhati, I.S.; Evans, M.N.; Cahyarini, S.Y.; D’arrigo, R.D.; Yoshimura, K.; Herho, S.H.S. δ18O of Marine-Influenced Tectona grandis L. f. From Equatorial Indonesia: A Local Rainfall Amount and Remote ENSO Indicator. Paleoceanogr. 2024, 39, e2023PA004758. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Bradley, R.S.; Vuille, M.; Hardy, D.; Thompson, L.G. Low latitude ice cores record Pacific sea surface temperatures. Geophys. Res. Lett. 2003, 30, 1174. [Google Scholar] [CrossRef]
- Cobb, K.M.; Adkins, J.F.; Partin, J.W.; Clark, B. Regional-scale climate influences on temporal variations of rainwater and cave dripwater oxygen isotopes in northern Borneo. Earth Planet. Sci. Lett. 2007, 263, 207–220. [Google Scholar] [CrossRef]
- Hu, J.; Emile-Geay, J.; Partin, J. Correlation-based interpretations of paleoclimate data—Where statistics meet past climates. Earth Planet. Sci. Lett. 2017, 459, 362–371. [Google Scholar] [CrossRef]
- Leavitt, S.W.; Danzer, S.R. Method for batch processing small wood samples to holocellulose for stable-carbon isotope analysis. Anal. Chem. 1993, 65, 87–89. [Google Scholar] [CrossRef]
- Bronk Ramsey, C. Bayesian Analysis of Radiocarbon Dates. Radiocarbon 2009, 51, 337–360. [Google Scholar] [CrossRef]
- Oxcal 4.1. Available online: https://c14.arch.ox.ac.uk/oxcal/OxCal.html (accessed on 1 May 2010).
- Banning, E.B. Interpreting radiocarbon dates. In The Archaeologist’s Laboratory. The Analysis of Archeological Data; Banning, E.B., Ed.; Kluwer Academic: Hingham, MA, USA, 2000; pp. 265–275. [Google Scholar]
- Biondi, F.; Queadan, F. A theory-driven approach to tree-ring standardization: Defining the biological trend from expected basal area increment. Tree-Ring Res. 2008, 64, 81–96. [Google Scholar] [CrossRef]
- Applequist, M.B. A simple pith locator for use with off-center increment cores. J. For. 1958, 56, 141. [Google Scholar]
- Block, M.; Richter, M. Impacts of heavy rainfall in El Nino 1997/98 on the vegetation of Sechura Desert in Northern Peru (A preliminary report). Phytocoenologia 2000, 30, 491–517. [Google Scholar] [CrossRef]
- Chen, D.; Cane, M.A. El Niño prediction and predictability. J. Comput. Phys. 2008, 227, 3625–3640. [Google Scholar] [CrossRef]
- Quinn, W.H.; Neal, V.T.; Antinez de Mayolo, S.E. El Nino Occurrences over the past four and a half centuries. J. Geophys. Res. 1987, 92, 14449–14461. [Google Scholar] [CrossRef]
- Climate Prediction Center (CPC). NOAA Oceanic NINO Indices. 2025. Available online: https://www.cpc.ncep.noaa.gov/data/indices/ersst5.nino.mth.91-20.ascii (accessed on 17 March 2025).
- Dode, L.A. Contribution de l’étude du genre Juglans. In Bulletin de la Société Botanique de France; Société Botanique de France: Paris, France, 1909; pp. 165–215. [Google Scholar]
- Loján Idrobo, L. El verdor de Los Andes. Arboles y Arbustos Nativos para el Desarrollo Forestal Altoandino; Proyecto Desarrollo Forestal Participativo en Los Andes; FAO: Quito, Ecuador, 1992; pp. 67–73. [Google Scholar]
- Arias Ninán, E.S. Ensayos de Desinfección y Medios de Cultivo para la Micropropagación del nogal (Juglans neotropica Diels). Bachelor’s Thesis, Universidad Nacional Agraria La Molina, Facultad de Ciencias Forestales, Lima, Peru, 1995. [Google Scholar]
- Van den Eynden, V.; Cueva, E.; Cabrera, O. Plantas Silvestres Comestibles del sur del Ecuador—Wild edible Plants of Southern Ecuador; Ediciones Abya-Yala: Quito, Ecuador, 1999; 221p. [Google Scholar]
- Miller, R.B. Wood Anatomy and Identification of Species of Juglans. Bot. Gaz. 1976, 137, 368–377. [Google Scholar] [CrossRef]
- Vera, A.; Ortega, R.; Pérez, P.; Rosero, J.; Chavesta, M. Avances en la caracterización e identificción anatómica de los anillos de crecimiento de la especie Juglans neotropica Diels (Nogal) para estudios dendrocronológicos en el fundo La Génova, Junín (Perú). XILEMA 2011, 24, 5–11. [Google Scholar]
- Beltrán, L.A.; Valencia, G.M. Anatomía de anillos de crecimiento de 80 especies arbóreas potenciales para estudios dendrochronológicos en la selva central, Peru. Rev. Biol. Trop. 2013, 61, 21–36. [Google Scholar]
- Hoff, J.C. A Practical Guide to BOX-JENKINS Forecasting; Lifetime Learning Publications: Belmont, CA, USA, 1983; pp. 4–93. [Google Scholar]
- Schweingruber, F.H. Trees and Wood in Dendrochronology; Springer: Berlin, Germany, 1993; 402p. [Google Scholar]
- Godwin, H. The value of plant materials for radiocarbon dating. Am. J. Bot. 1969, 56, 723–731. [Google Scholar] [CrossRef]
- Broecker, W.S.; Peng, T.-H. Tracers in the Sea; Eldigio Press: Palisades, NY, USA, 1982; 705p. [Google Scholar]
- Toggweiler, J.R.; Dixon, K.; Bryan, K. Simulations of radiocarbon in a coarse-resolution world ocean model, 2. Distributions of bomb-produced Carbon-14. J. Geophys. Res. 1989, 94, 8243–8264. [Google Scholar] [CrossRef]
- Currie, L. The remarkable metrological history of radiocarbon dating [II]. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 185–217. [Google Scholar] [CrossRef]
- Noy-Meir, I. Desert Ecosystems: Environment and Producers. Annu. Rev. Ecol. Syst. 1973, 4, 25–51. [Google Scholar] [CrossRef]
- Christie, D.A.; Lara, A.; Barichivich, J.; Villalba, R.; Morales, M.S.; Cuq, E. El Niño Southern Oscillation signal in the world’s highest tree-ring chronologies from the Altiplano, Central Andes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 309–319. [Google Scholar] [CrossRef]
- Ogle, K.; Reynolds, J.F. Plant responses to precipitation in desert ecosystems: Integrating functional types, pulses, thresholds, and delays. Oecologia 2004, 141, 282–294. [Google Scholar] [CrossRef] [PubMed]
- Borchert, R. Soil and Stem Water Storage Determine Phenology and Distribution of Tropical Dry Forest Trees. Ecology 1994, 75, 1437–1449. [Google Scholar] [CrossRef]
- Reynolds, J.F.; Kemp, P.R.; Ogle, K.; Fernandez, R.J. Modifying the ‘Pulse-Reserve’ paradigm for deserts of North America: Precipitation pulses, soil water and plant responses. Oecologia 2004, 141, 194–210. [Google Scholar] [CrossRef]
- Roden, J.S.; Lin, G.; Ehleringer, J.R. Response to the comment of V. J. Terwilliger on “A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose,” by J. S. Roden, G. Lin, and J. R. Ehleringer (2000) Geochim. Cosmochim. Acta 64: 21–35. Geochim. Cosmochim. Acta 2002, 64, 733–734. [Google Scholar] [CrossRef]
- Schwinning, S.; Sala, O.E. Hierarchy of responses to resource pulses in arid and semi-arid ecosystems. Oecologia 2004, 141, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.N.; Herho, S.H.S.; Wollney, J.C.; Carter, A.N.; Gbenro, M.A.; Tripp, G.R.; D’Arrigo, R.D.; Cahyarin, S.Y. Three centuries of ENSO variability from Muna, Indonesia teak: Limited response to radiative forcing. Geophy. Res. Lett. 2024, in press.
- Zuidema, P.A.; Poulter, B.; Frank, D.C. A Wood Biology Agenda to Support Global Vegetation Modelling. Trends Plant Sci. 2018, 23, 1006–1015. [Google Scholar] [CrossRef]
- Babst, F.; Friend, A.D.; Karamihalaki, M.; Wei, J.; von Arx, G.; Papale, D.; Peters, R.L. Modeling Ambitions Outpace Observations of Forest Carbon Allocation. Trends Plant Sci. 2021, 26, 210–219. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Ballesteros-Cánovas, J.A.; George, S.S.; Stoffel, M. Tropical and subtropical dendrochronology: Approaches, applications, and prospects. Ecol. Indic. 2022, 144, 109506. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).