The Spatial-Comprehensiveness (S-COM) Index: Identifying Optimal Spatial Extents in Volunteered Geographic Information Point Datasets
Abstract
1. Introduction
2. Background
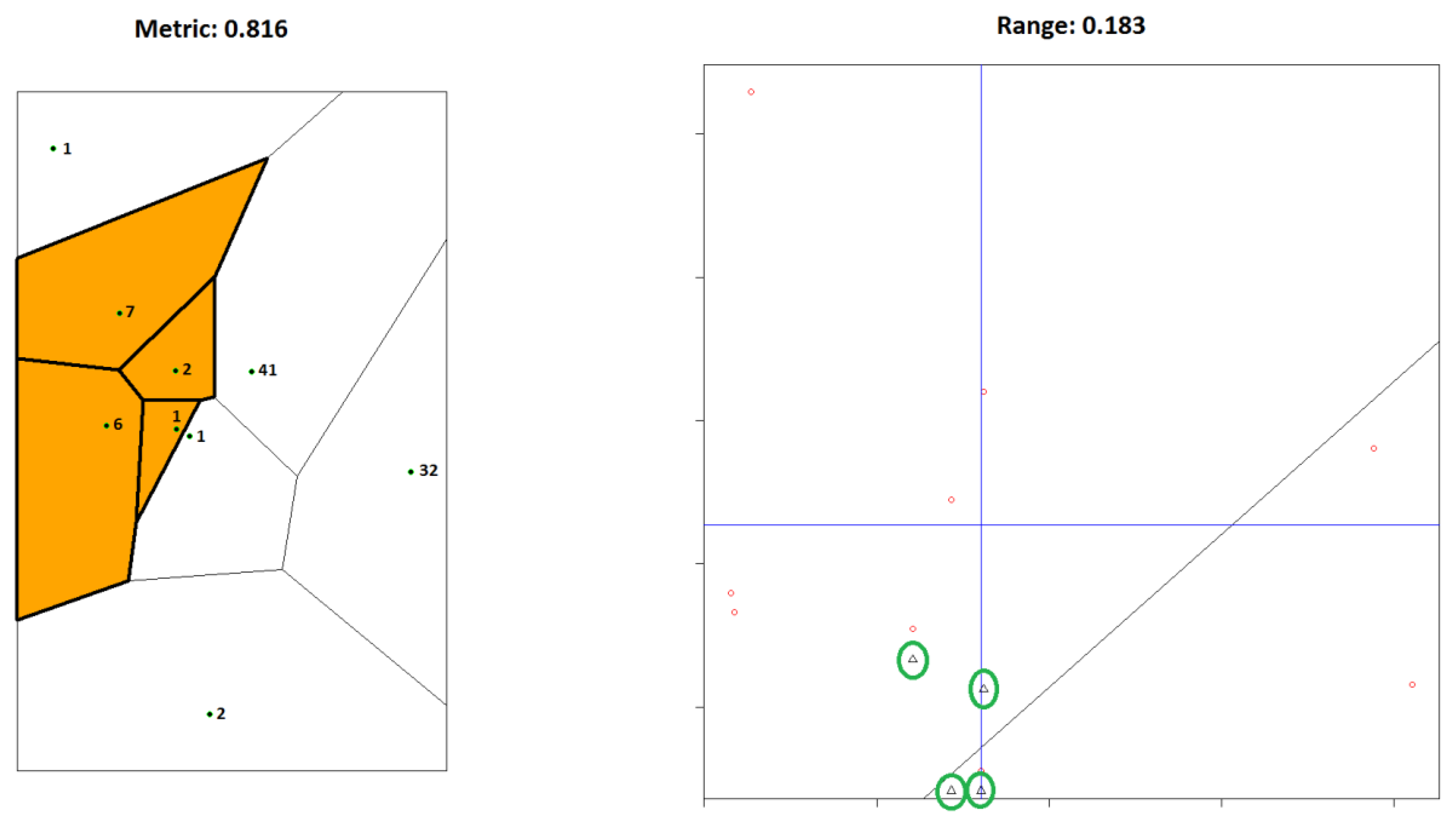
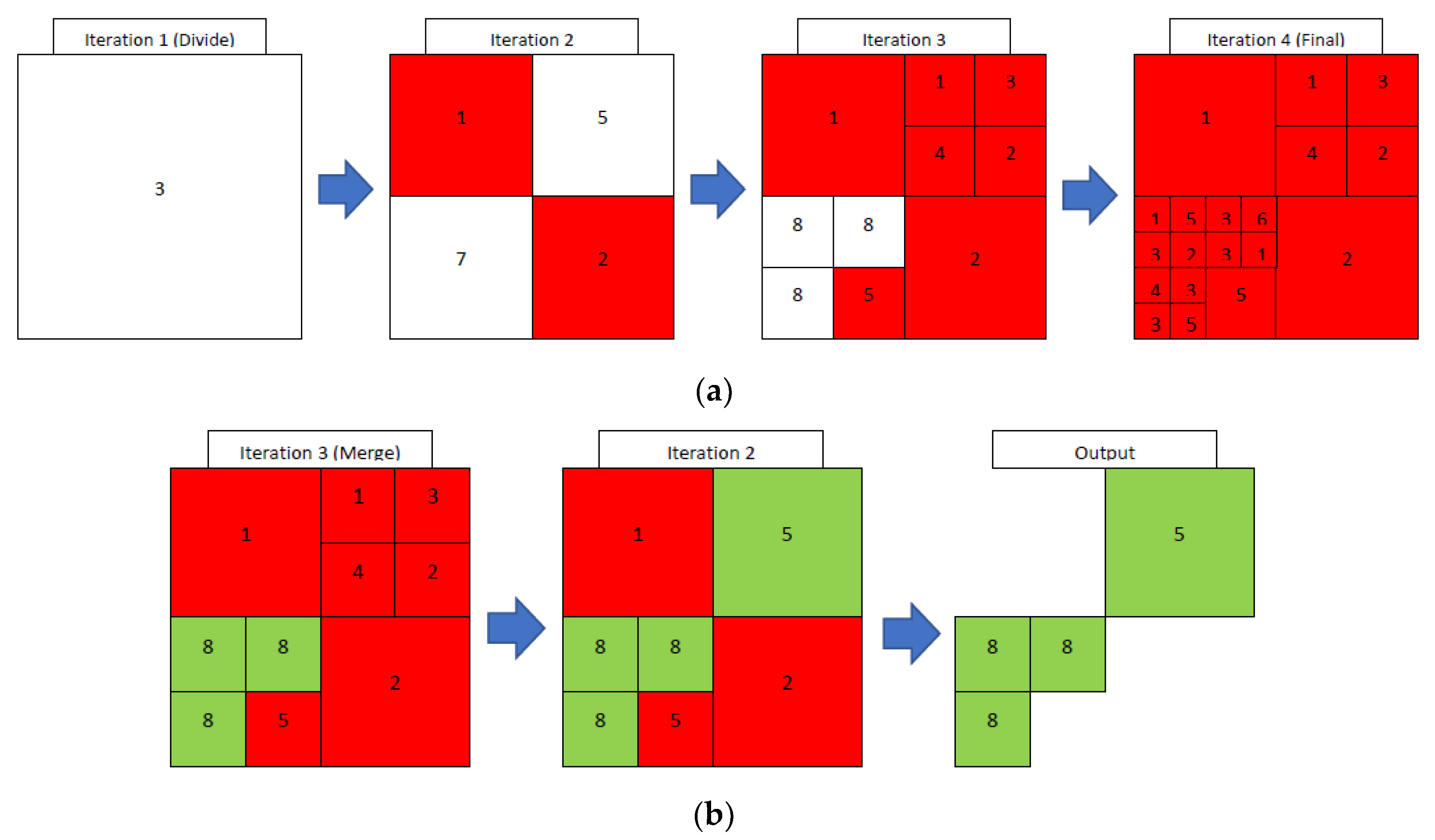
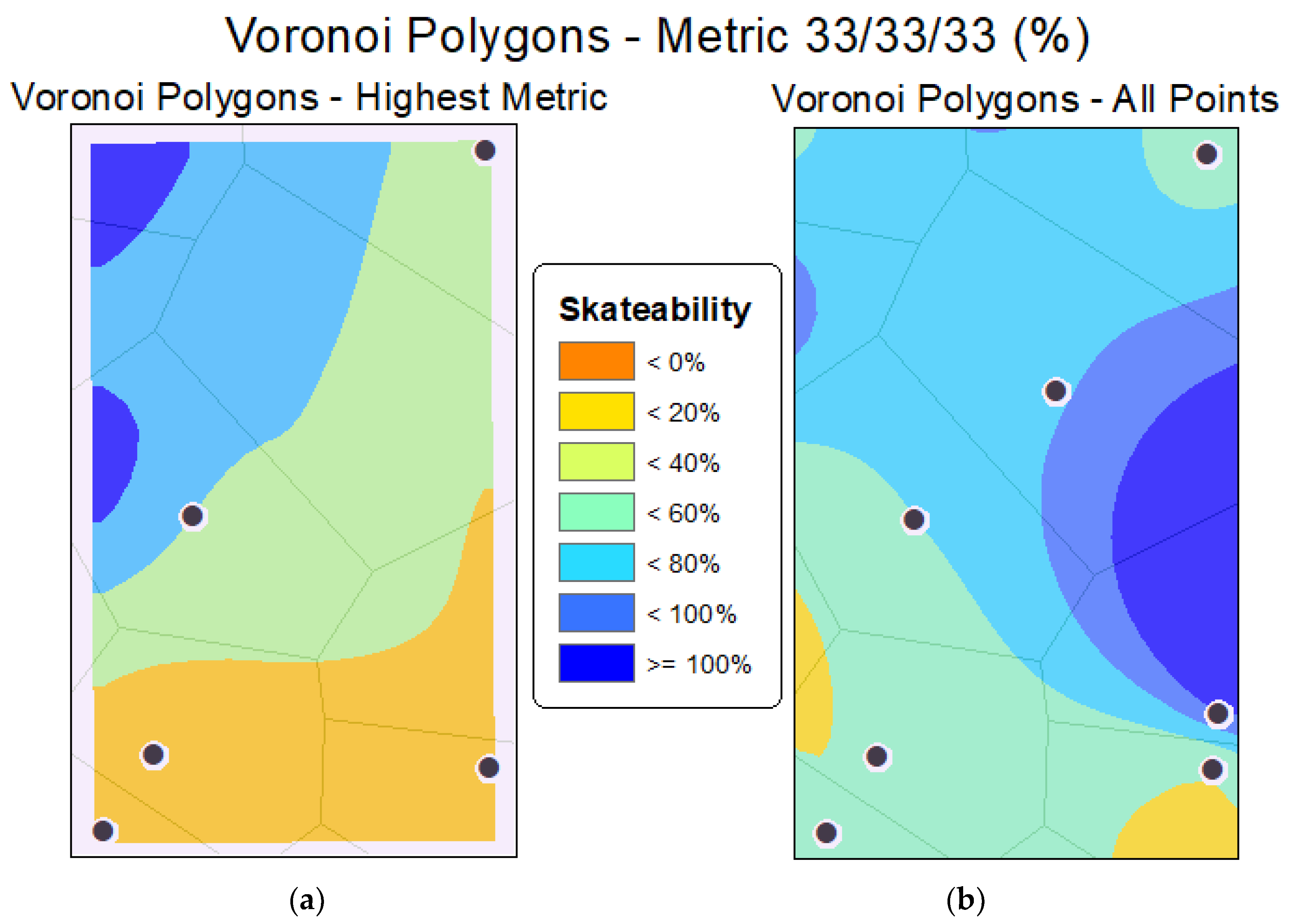
3. Methods
4. Data Sources and Study Area
5. Case Study
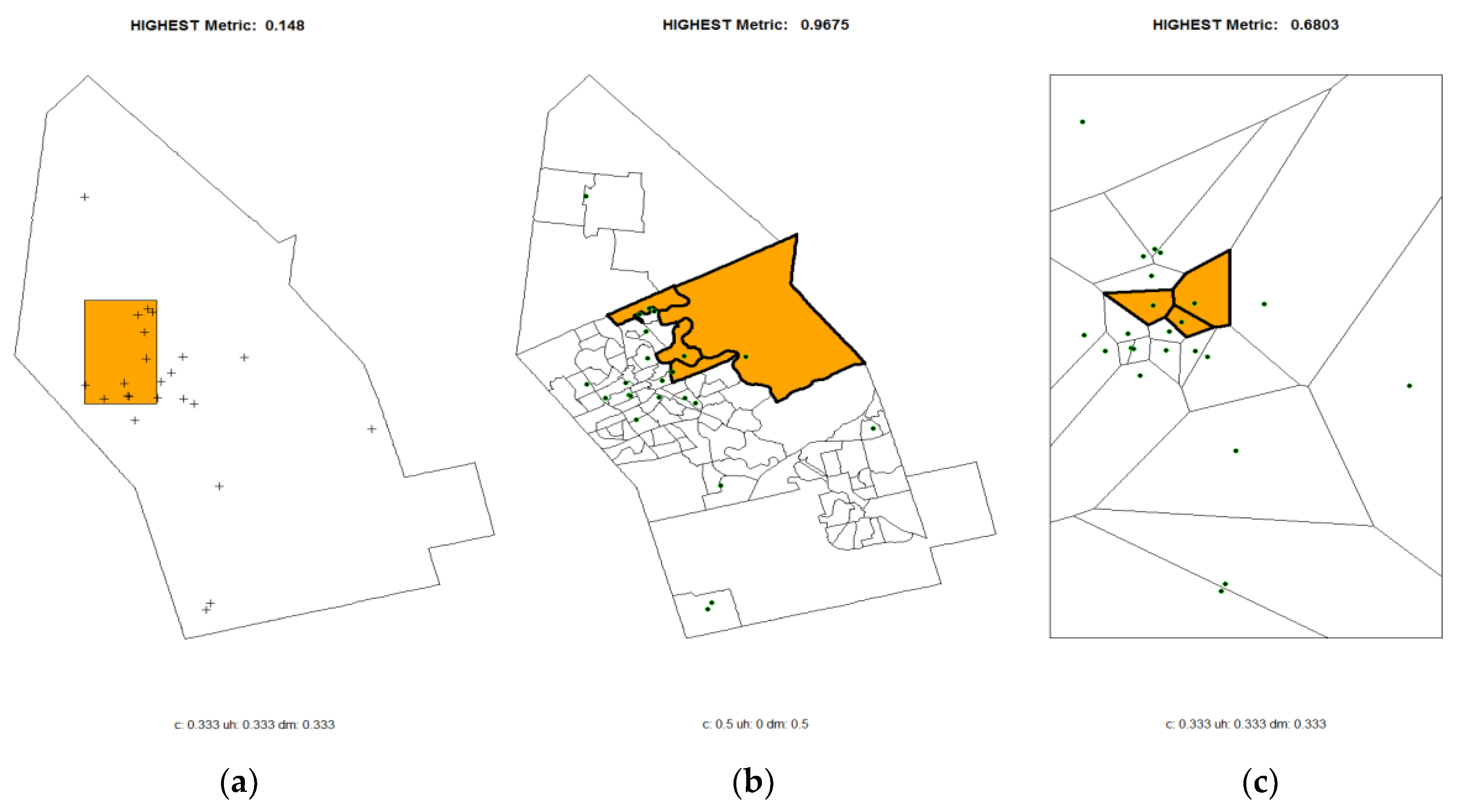
6. Results
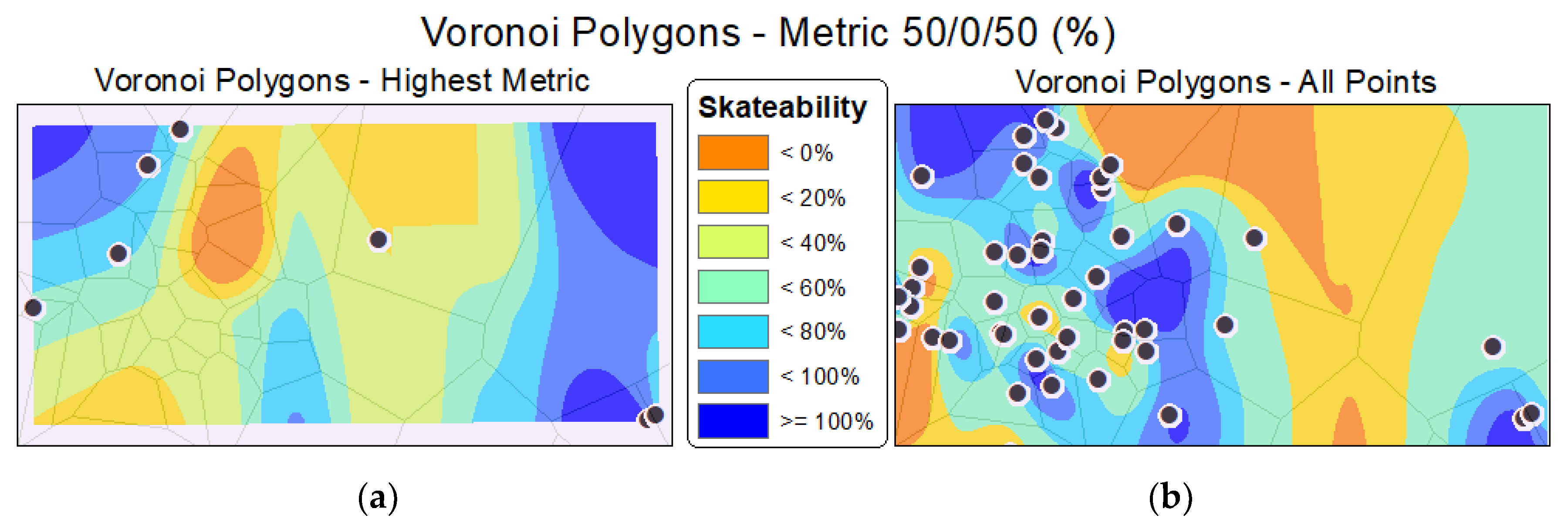
6.1. RinkWatch
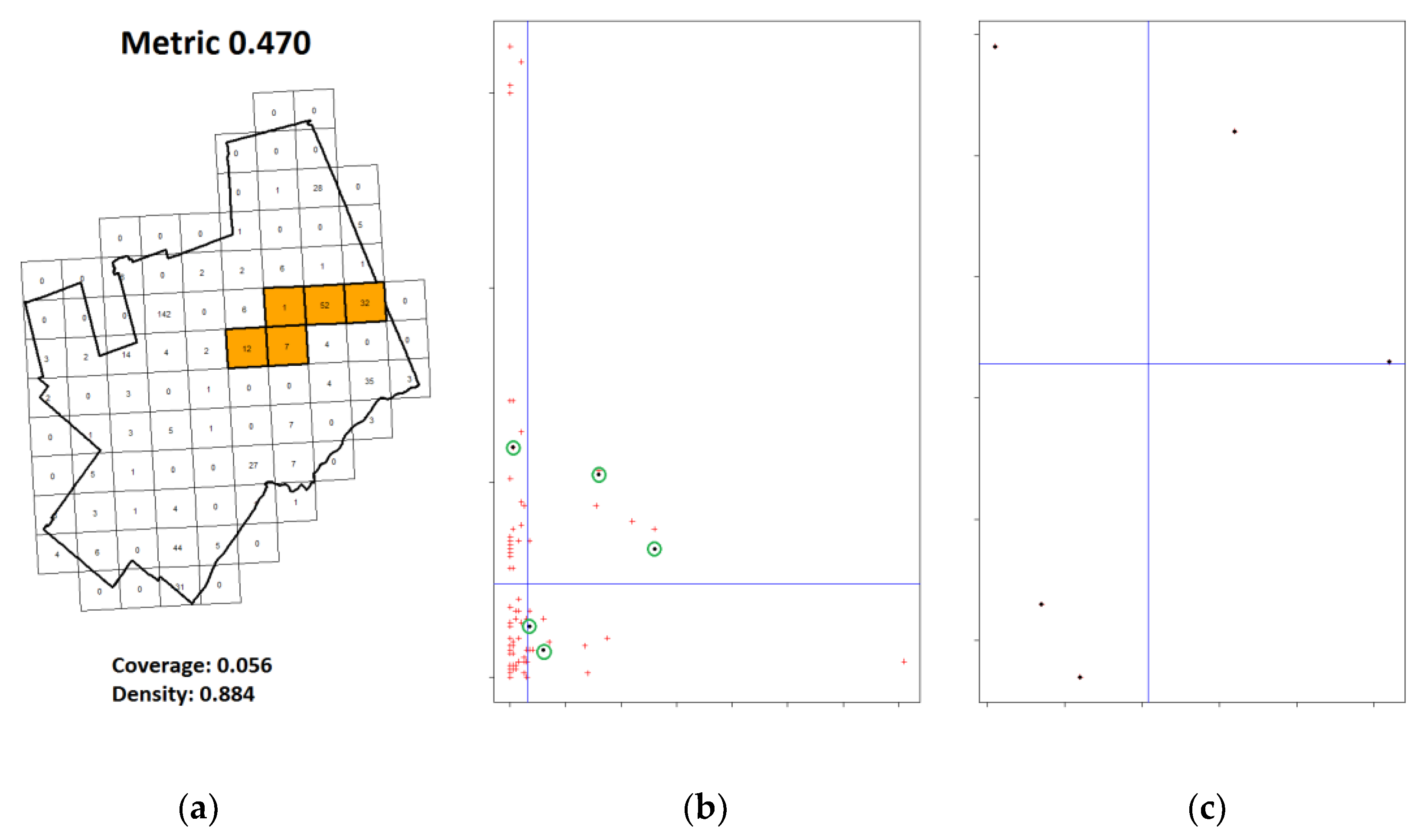
6.2. FrogWatch
7. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Li, W.; Goodchild, M.F.; Church, R.L.; Zhou, B. Geospatial Data Mining on the Web: Discovering Locations of Emergency Service Facilities. In Proceedings of the Advanced Data Mining and Applications, Beijing, China, 17–19 December 2011; Zhou, S., Zhang, S., Karypis, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 552–563. [Google Scholar]
- Elwood, S. Geographic information science: Visualization, visual methods, and the geoweb. Prog. Hum. Geogr. 2011, 35, 401–408. [Google Scholar] [CrossRef]
- Goetz, M.; Zipf, A. Towards defining a framework for the automatic derivation of 3D CityGML models from volunteered geographic information. Int. J. 3 Inf. Model. IJ3DIM 2012, 1, 1–16. [Google Scholar] [CrossRef]
- Tenney, M.; Hall, G.B.; Sieber, R.E. A crowd sensing system identifying geotopics and community interests from user-generated content. Int. J. Geogr. Inf. Sci. 2019, 33, 1497–1519. [Google Scholar] [CrossRef]
- Senaratne, H.; Mobasheri, A.; Ali, A.L.; Capineri, C.; Haklay, M. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2017, 31, 139–167. [Google Scholar] [CrossRef]
- Brown, G.; Rhodes, J.; Lunney, D.; Goldingay, R.; Fielding, K.; Garofano, N.; Hetherington, S.; Hopkins, M.; Green, J.; McNamara, S. The influence of sampling design on spatial data quality in a geographic citizen science project. Trans. GIS 2019, 23, 1184–1203. [Google Scholar] [CrossRef]
- Barron, C.; Neis, P.; Zipf, A. A comprehensive framework for intrinsic OpenStreetMap quality analysis. Trans. GIS 2014, 18, 877–895. [Google Scholar] [CrossRef]
- Mooney, P.; Corcoran, P.; Winstanley, A.C. Towards quality metrics for OpenStreetMap. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; Association for Computing Machinery: San Jose, CA, USA, 2010; pp. 514–517. [Google Scholar]
- Girres, J.-F.; Touya, G. Quality assessment of the French OpenStreetMap dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Devillers, R.; Stein, A.; Bédard, Y.; Chrisman, N.; Fisher, P.; Shi, W. Thirty years of research on spatial data quality: Achievements, failures, and opportunities. Trans. GIS 2010, 14, 387–400. [Google Scholar] [CrossRef]
- Jeansoulin, R.; Devillers, R. Chapter 2. Spatial Data Quality: Concepts. In Fundamentals of Spatial Data Quality; Devillers, R., Jeansoulin, R., Eds.; ISTE: London, UK, 2006; pp. 31–42. [Google Scholar]
- Basiri, A.; Haklay, M.; Foody, G.; Mooney, P. Crowdsourced geospatial data quality: Challenges and future directions. Int. J. Geogr. Inf. Sci. 2019, 33, 1588–1593. [Google Scholar] [CrossRef]
- Lansley, G.; de Smith, M.; Goodchild, M.; Longley, P. Big Data and Geospatial Analysis. arXiv 2019, arXiv:1902.06672. [Google Scholar]
- Lawrence, H.; Robertson, C.; Feick, R.; Nelson, T. Identifying Optimal Study Areas and Spatial Aggregation Units for Point-Based VGI from Multiple Sources. In Advances in Spatial Data Handling and Analysis: Select Papers from the 16th IGU Spatial Data Handling Symposium; Harvey, F., Leung, Y., Eds.; Advances in Geographic Information Science; Springer International Publishing: Cham, Switzerland, 2015; pp. 65–84. ISBN 978-3-319-19950-4. [Google Scholar]
- Coleman, D.; Georgiadou, Y.; Labonte, J. Volunteered geographic information: The nature and motivation of produsers. Int. J. Spat. Data Infrastruct. Res. 2009, 4, 332–358. [Google Scholar]
- Coleman, D.J. Potential contributions and challenges of VGI for conventional topographic base-mapping programs. In Crowdsourcing Geographic Knowledge; Sui, D., Elwood, S., Goodchild, M., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 245–263. [Google Scholar]
- Budhathoki, N.R.; Haythornthwaite, C. Motivation for open collaboration: Crowd and community models and the case of OpenStreetMap. Am. Behav. Sci. 2013, 57, 548–575. [Google Scholar] [CrossRef]
- Robertson, C.; Feick, R. Defining local experts: Geographical expertise as a basis for geographic information quality. In Proceedings of the 13th International Conference on Spatial Information Theory (COSIT 2017), L’Aquila, Italy, 4–8 September 2017; Clementini, E., Donnelly, M., Yuan, M., Kray, C., Fogliaroni, P., Ballatore, A., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017; Volume 86, pp. 22:1–22:14. [Google Scholar]
- Dickinson, J.L.; Zuckerberg, B.; Bonter, D.N. Citizen science as an ecological research tool: Challenges and benefits. Annu. Rev. Ecol. Evol. Syst. 2010, 41, 149–172. [Google Scholar] [CrossRef]
- Haklay, M. Citizen science and volunteered geographic information: Overview and typology of participation. In Crowdsourcing Geographic Knowledge; Sui, D., Elwood, S., Goodchild, M., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 105–122. [Google Scholar]
- Antoniou, V.; Capineri, C.; Haklay, M.E. VGI and beyond: From data to mapping. In Routledge Handbook of Mapping and Cartography; Kent, A., Vujakovic, P., Eds.; Routledge: Abingdon, UK, 2017; pp. 475–488. [Google Scholar]
- Neis, P.; Zielstra, D.; Zipf, A. The street network evolution of crowdsourced maps: OpenStreetMap in Germany 2007–2011. Future Internet 2012, 4, 1–21. [Google Scholar] [CrossRef]
- Czepkiewicz, M.; Jankowski, P.; Młodkowski, M. Geo-questionnaires in urban planning: Recruitment methods, participant engagement, and data quality. Cartogr. Geogr. Inf. Sci. 2017, 44, 551–567. [Google Scholar] [CrossRef]
- Hay, S.I.; George, D.B.; Moyes, C.L.; Brownstein, J.S. Big data opportunities for global infectious disease surveillance. PLoS Med. 2013, 10, e1001413. [Google Scholar] [CrossRef]
- Kitchin, R. Big data and human geography: Opportunities, challenges and risks. Dialogues Hum. Geogr. 2013, 3, 262–267. [Google Scholar] [CrossRef]
- Goodchild, M.F. The quality of big (geo) data. Dialogues Hum. Geogr. 2013, 3, 280–284. [Google Scholar] [CrossRef]
- Lazer, D.; Kennedy, R.; King, G.; Vespignani, A. The parable of google flu: Traps in big data analysis. Science 2014, 343, 1203–1205. [Google Scholar] [CrossRef]
- Li, L.; Goodchild, M.F.; Xu, B. Spatial, temporal, and socioeconomic patterns in the use of Twitter and Flickr. Cartogr. Geogr. Inf. Sci. 2013, 40, 61–77. [Google Scholar] [CrossRef]
- Hecht, B.; Stephens, M. A tale of cities: Urban biases in volunteered geographic information. In Proceedings of the Eighth International AAAI Conference on Weblogs and Social Media, Ann Arbor, MI, USA, 1–4 June 2014; pp. 197–205. [Google Scholar]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Neis, P.; Zielstra, D. Recent developments and future trends in volunteered geographic information research: The case of OpenStreetMap. Future Internet 2014, 6, 76–106. [Google Scholar] [CrossRef]
- Jeffery, C.; Ozonoff, A.; Pagano, M. The effect of spatial aggregation on performance when mapping a risk of disease. Int. J. Health Geogr. 2014, 13, 9. [Google Scholar] [CrossRef] [PubMed]
- Hollenstein, L.; Purves, R. Exploring place through user-generated content: Using Flickr tags to describe city cores. J. Spat. Inf. Sci. 2010, 2010, 21–48. [Google Scholar]
- Feick, R.; Robertson, C. A multi-scale approach to exploring urban places in geotagged photographs. Comput. Environ. Urban Syst. 2015, 53, 96–109. [Google Scholar] [CrossRef]
- Derungs, C.; Purves, R.S. From text to landscape: Locating, identifying and mapping the use of landscape features in a Swiss Alpine corpus. Int. J. Geogr. Inf. Sci. 2014, 28, 1272–1293. [Google Scholar] [CrossRef]
- Shelton, T.; Poorthuis, A.; Graham, M.; Zook, M. Mapping the data shadows of Hurricane Sandy: Uncovering the sociospatial dimensions of ‘big data’. Geoforum 2014, 52, 167–179. [Google Scholar] [CrossRef]
- Robertson, C.; Feick, R. Inference and analysis across spatial supports in the big data era: Uncertain point observations and geographic contexts. Trans. GIS 2018, 22, 455–476. [Google Scholar] [CrossRef]
- Antoniou, V.; Skopeliti, A. Measures and indicators of VGI quality: An overview. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. Present. ISPRS Geospatial Week 2015, II-3/W5, 345–351. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spat. Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Fuchs, G.; Andrienko, N.; Andrienko, G.; Bothe, S.; Stange, H. Tracing the German centennial flood in the stream of tweets: First lessons learned. In Proceedings of the Second ACM SIGSPATIAL International Workshop on Crowdsourced and Volunteered Geographic Information, Orlando, FL, USA, 5 November 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 31–38. [Google Scholar]
- Foody, G.M.; See, L.; Fritz, S.; Van der Velde, M.; Perger, C.; Schill, C.; Boyd, D.S.; Comber, A. Accurate attribute mapping from volunteered geographic information: Issues of volunteer quantity and quality. Cartogr. J. 2015, 52, 336–344. [Google Scholar] [CrossRef]
- Haklay, M.; Basiouka, S.; Antoniou, V.; Ather, A. How many volunteers does it take to map an area well? The validity of Linus’ law to volunteered geographic information. Cartogr. J. 2010, 47, 315–322. [Google Scholar] [CrossRef]
- Brisaboa, N.R.; Cerdeira-Pena, A.; de Bernardo, G.; Navarro, G.; Pedreira, Ó. Extending general compact querieable representations to GIS applications. Inf. Sci. 2020, 506, 196–216. [Google Scholar] [CrossRef]
- Gagie, T.; González-Nova, J.I.; Ladra, S.; Navarro, G.; Seco, D. Faster compressed quadtrees. In Proceedings of the 2015 Data Compression Conference, Snowbird, UT, USA, 7–9 April 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 93–102. [Google Scholar]
- Bereuter, P.; Weibel, R. Real-time generalization of point data in mobile and web mapping using quadtrees. Cartogr. Geogr. Inf. Sci. 2013, 40, 271–281. [Google Scholar] [CrossRef]
- Ramanathan, V.; Mishra, S.; Mitra, P. Quadtree decomposition based extended vector space model for image retrieval. In Proceedings of the 2011 IEEE Workshop on Applications of Computer Vision (WACV), Kona, HI, USA, 5–7 January 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 139–144. [Google Scholar]
- Zhang, C.; Chen, R.; Zhu, L.; Liu, A.; Lin, Y.; Huang, F. Hierarchical information quadtree: Efficient spatial temporal image search for multimedia stream. Multimed. Tools Appl. 2019, 78, 30561–30583. [Google Scholar] [CrossRef]
- Popinet, S. Quadtree-adaptive tsunami modelling. Ocean Dyn. 2011, 61, 1261–1285. [Google Scholar] [CrossRef]
- Qiu, L.; Du, Z.; Zhu, Q.; Fan, Y. An integrated flood management system based on linking environmental models and disaster-related data. Environ. Model. Softw. 2017, 91, 111–126. [Google Scholar] [CrossRef]
- Valles, G. AMOEBA: A Multidirectional Optimum Ecotope-Based Algorithm; R package; CRAN: Toronto, ON, Canada, 2014. [Google Scholar]
- Connors, J.P.; Lei, S.; Kelly, M. Citizen science in the age of neogeography: Utilizing volunteered geographic information for environmental monitoring. Ann. Assoc. Am. Geogr. 2012, 102, 1267–1289. [Google Scholar] [CrossRef]
- Robertson, C.; McLeman, R.; Lawrence, H. Winters too warm to skate? Citizen-science reported variability in availability of outdoor skating in Canada. Can. Geogr. Géographe Can. 2015, 59, 383–390. [Google Scholar] [CrossRef]
- Statistics Canada Historic Climate Data. Available online: http://climate.weather.gc.ca/ (accessed on 12 December 2019).
- Statistics Canada Population of Census Metropolitan Areas. Available online: http://www.statcan.gc.ca/tables-tableaux/sum-som/l01/cst01/demo05a-eng.htm (accessed on 26 March 2017).
- Mackaness, W.A.; Chaudhry, O. Assessing the Veracity of Methods for Extracting Place Semantics from Flickr Tags. Trans. GIS 2013, 17, 544–562. [Google Scholar] [CrossRef]
- Truong, Q.T.; De Runz, C.; Touya, G. Analysis of collaboration networks in OpenStreetMap through weighted social multigraph mining. Int. J. Geogr. Inf. Sci. 2019, 33, 1651–1682. [Google Scholar] [CrossRef]
- Purves, R.; Edwardes, A.; Wood, J. Describing place through user generated content. First Monday 2011, 16. [Google Scholar] [CrossRef][Green Version]
- Elwood, S.; Goodchild, M.; Sui, D. Prospects for VGI research and the emerging fourth paradigm. In Crowdsourcing Geographic Knowledge; Sui, D., Elwood, S., Goodchild, M., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 361–375. [Google Scholar]
- Mooney, P. Understanding the activity of contributors to VGI projects. How, why, where, and when do they contribute geographic information? In Proceedings of the 26th International Cartographic Conference (ICC), Dresden, Germany, 25–30 August 2013. [Google Scholar]
- Gardner, Z.; Mooney, P.; De Sabbata, S.; Dowthwaite, L. Quantifying gendered participation in OpenStreetMap: Responding to theories of female (under) representation in crowdsourced mapping. GeoJournal 2019, 1–18. [Google Scholar] [CrossRef]
- McLafferty, S.; Schneider, D.; Abelt, K. Placing volunteered geographic health information: Socio-spatial bias in 311 bed bug report data for New York City. Health Place 2020, 62, 102282. [Google Scholar] [CrossRef]
- Bastin, L.; Schade, S.; Schill, C. Data and metadata management for better VGI reusability. In Mapping and the Citizen Sensor; Foody, G., See, L., Fritz, S., Mooney, P., Olteanu-Raimond, A.-M., Fonte, C., Antoniou, V., Eds.; Ubiquity Press: London, UK, 2017; pp. 249–272. [Google Scholar]
- Brown, G. A review of sampling effects and response bias in internet participatory mapping (PPGIS/PGIS/VGI). Trans. GIS 2017, 21, 39–56. [Google Scholar] [CrossRef]
- Mirahsan, M.; Schoenen, R.; Szyszkowicz, S.S.; Yanikomeroglu, H. Measuring the spatial heterogeneity of outdoor users in wireless cellular networks based on open urban maps. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 2834–2838. [Google Scholar]
- Feng, J.; Zhang, M.; Wang, H.; Yang, Z.; Zhang, C.; Li, Y.; Jin, D. Dplink: User identity linkage via deep neural network from heterogeneous mobility data. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 459–469. [Google Scholar]
- Zielstra, D.; Zipf, A. A comparative study of proprietary geodata and volunteered geographic information for Germany. In Proceedings of the 13th AGILE International Conference on Geographic Information Science, Guimarães, Portugal, 11–14 May 2010; Volume 2010. [Google Scholar]
- Galpern, P.; Manseau, M.; Wilson, P. Grains of connectivity: Analysis at multiple spatial scales in landscape genetics. Mol. Ecol. 2012, 21, 3996–4009. [Google Scholar] [CrossRef]
- Sester, M.; Jokar Arsanjani, J.; Klammer, R.; Burghardt, D.; Haunert, J.-H. Integrating and Generalising Volunteered Geographic Information. In Abstracting Geographic Information in a Data Rich World: Methodologies and Applications of Map Generalisation; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Lecture Notes in Geoinformation and Cartography; Springer International Publishing: Cham, Switzerland, 2014; pp. 119–155. [Google Scholar]
- Nayini, S.E.Y.; Geravand, S.; Maroosi, A. A novel threshold-based clustering method to solve K-means weaknesses. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, Tamil Nadu, India, 1–2 August 2017; IEEE Computer Society: Washington, DC, USA, 2017; pp. 47–52. [Google Scholar]
- Patel, K.M.A.; Thakral, P. The best clustering algorithms in data mining. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, Tamil Nadu, India, 6–8 April 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 2042–2046. [Google Scholar]
- Brown, G.; Kelly, M.; Whitall, D. Which ‘public’? Sampling effects in public participation GIS (PPGIS) and volunteered geographic information (VGI) systems for public lands management. J. Environ. Plan. Manag. 2014, 57, 190–214. [Google Scholar] [CrossRef]
- Fonte, C.C.; Antoniou, V.; Bastin, L.; Estima, J.; Arsanjani, J.J.; Bayas, J.-C.L.; See, L.; Vatseva, R. Assessing VGI data quality. In Mapping and the Citizen Sensor; Foody, G., See, L., Fritz, S., Mooney, P., Olteanu-Raimond, A.-M., Fonte, C., Antoniou, V., Eds.; Ubiquity Press: London, UK, 2017; pp. 137–163. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawrence, H.; Robertson, C.; Feick, R.; Nelson, T. The Spatial-Comprehensiveness (S-COM) Index: Identifying Optimal Spatial Extents in Volunteered Geographic Information Point Datasets. ISPRS Int. J. Geo-Inf. 2020, 9, 497. https://doi.org/10.3390/ijgi9090497
Lawrence H, Robertson C, Feick R, Nelson T. The Spatial-Comprehensiveness (S-COM) Index: Identifying Optimal Spatial Extents in Volunteered Geographic Information Point Datasets. ISPRS International Journal of Geo-Information. 2020; 9(9):497. https://doi.org/10.3390/ijgi9090497
Chicago/Turabian StyleLawrence, Haydn, Colin Robertson, Rob Feick, and Trisalyn Nelson. 2020. "The Spatial-Comprehensiveness (S-COM) Index: Identifying Optimal Spatial Extents in Volunteered Geographic Information Point Datasets" ISPRS International Journal of Geo-Information 9, no. 9: 497. https://doi.org/10.3390/ijgi9090497
APA StyleLawrence, H., Robertson, C., Feick, R., & Nelson, T. (2020). The Spatial-Comprehensiveness (S-COM) Index: Identifying Optimal Spatial Extents in Volunteered Geographic Information Point Datasets. ISPRS International Journal of Geo-Information, 9(9), 497. https://doi.org/10.3390/ijgi9090497






