An Evaluation Model of Level of Detail Consistency of Geographical Features on Digital Maps
Abstract
1. Introduction
2. Methods
2.1. Graphical Unit and LoD
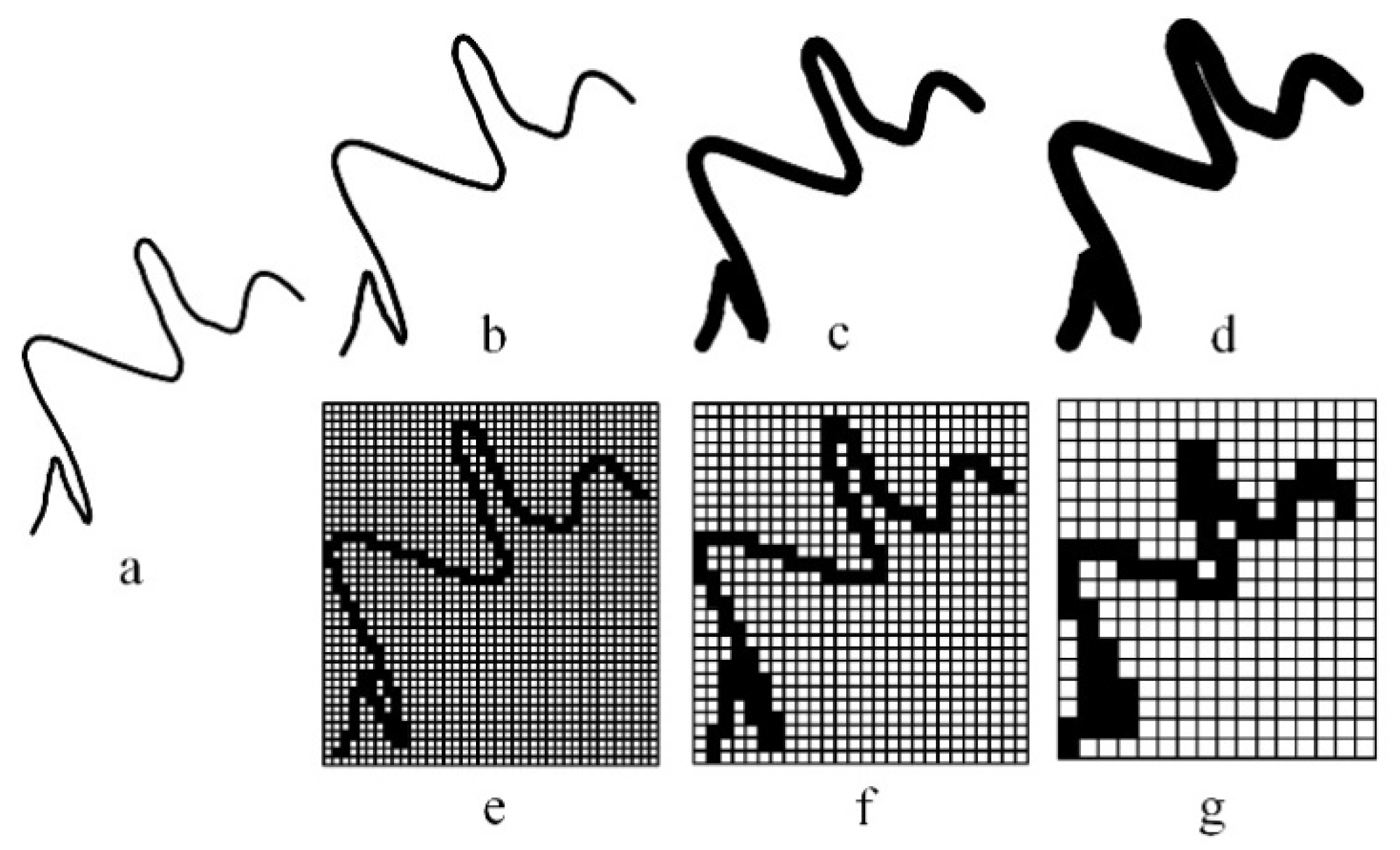
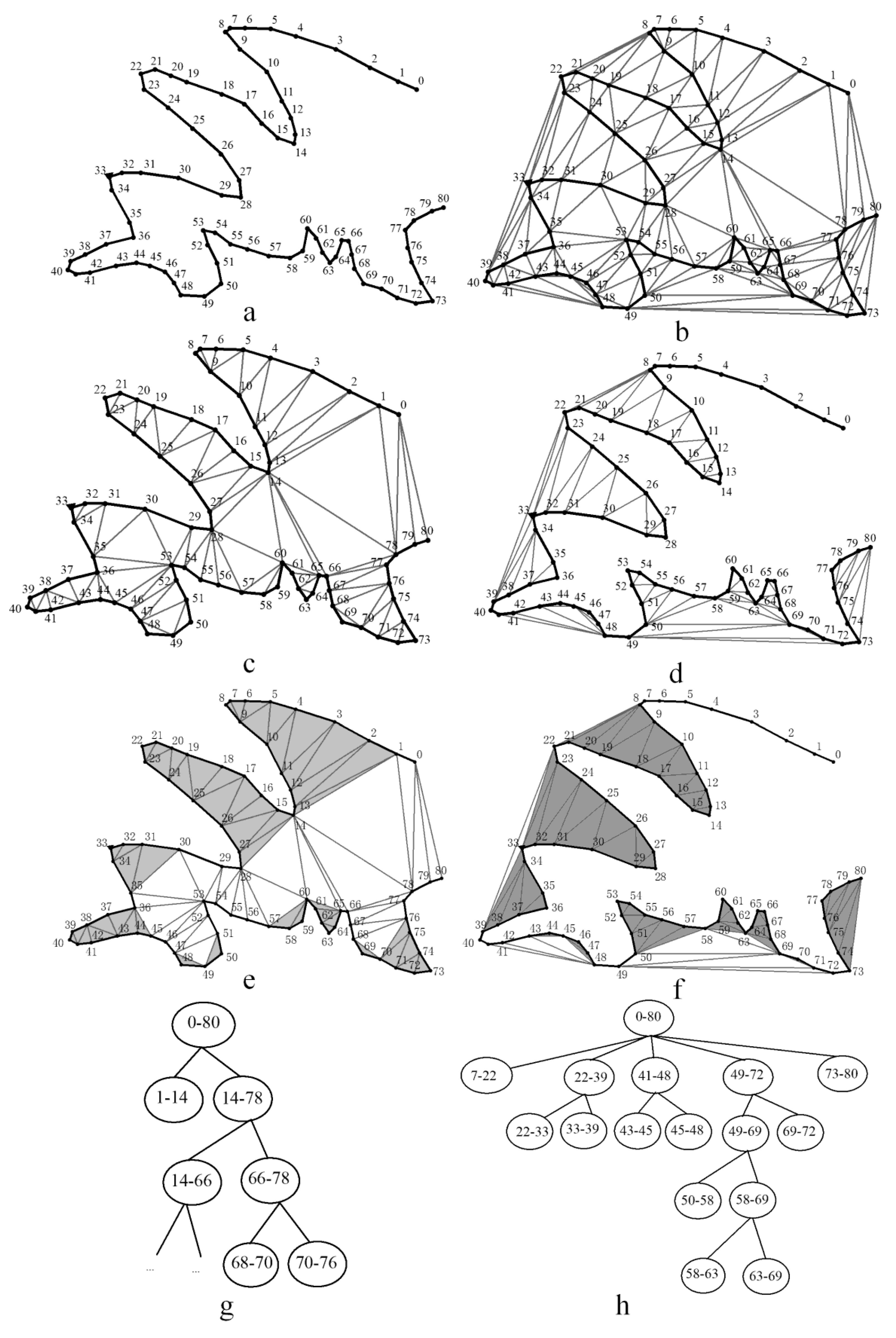
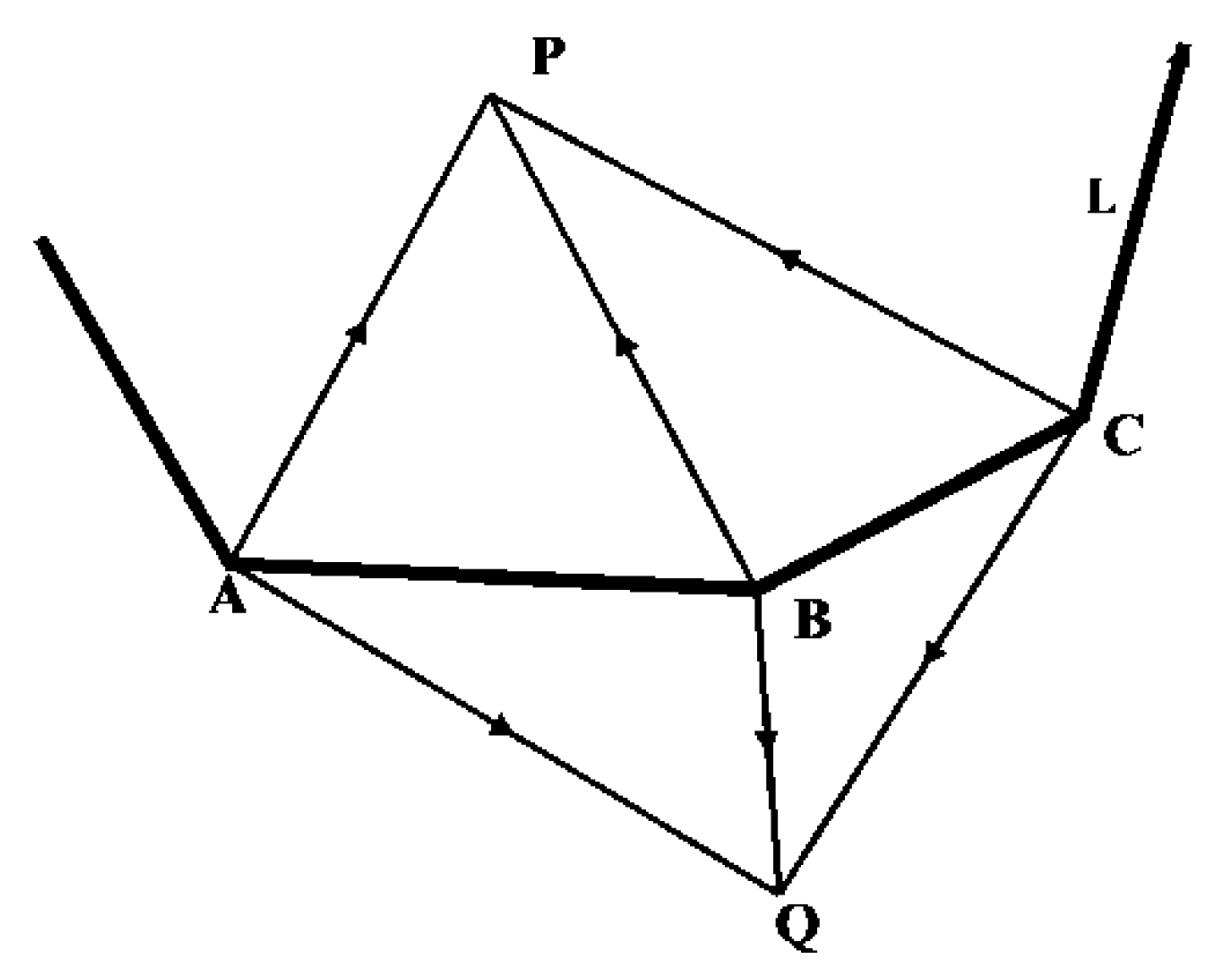
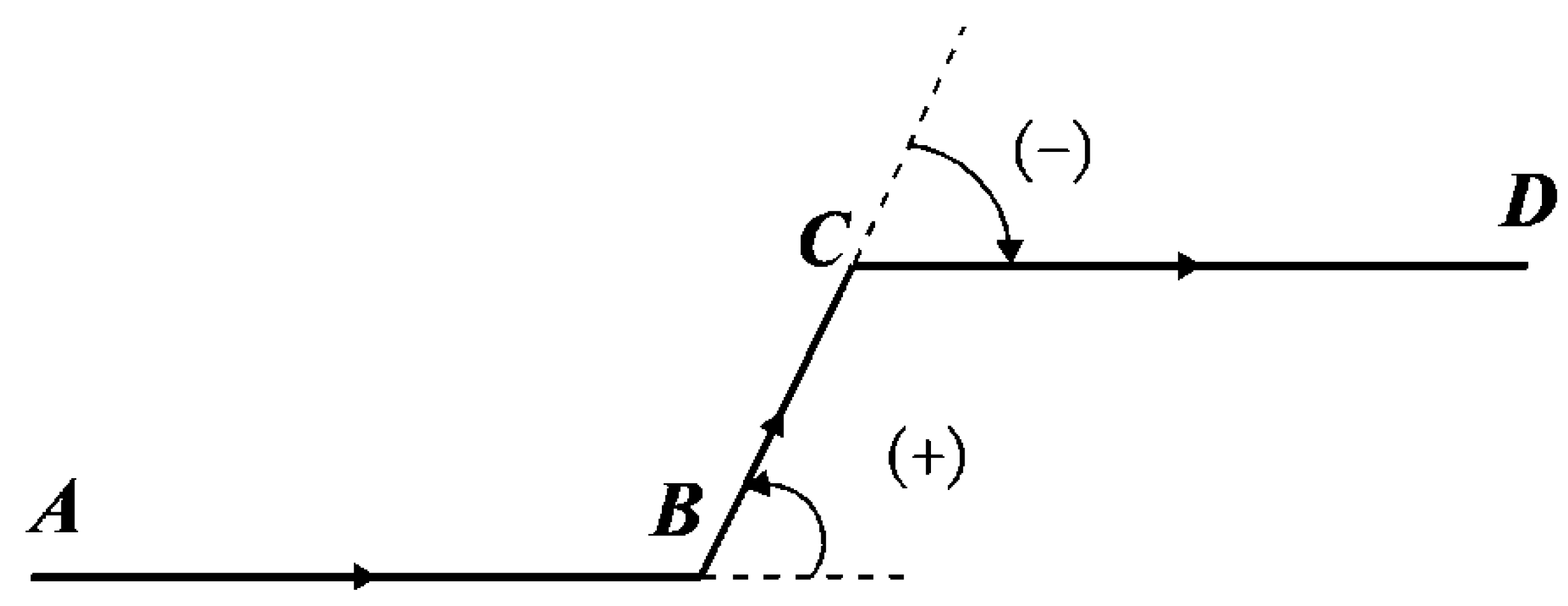
2.1.1. Bend of Curve as Graphical Unit
2.1.2. Graphical Unit of Natural Features
2.1.3. Graphical Unit of Humanmade Features
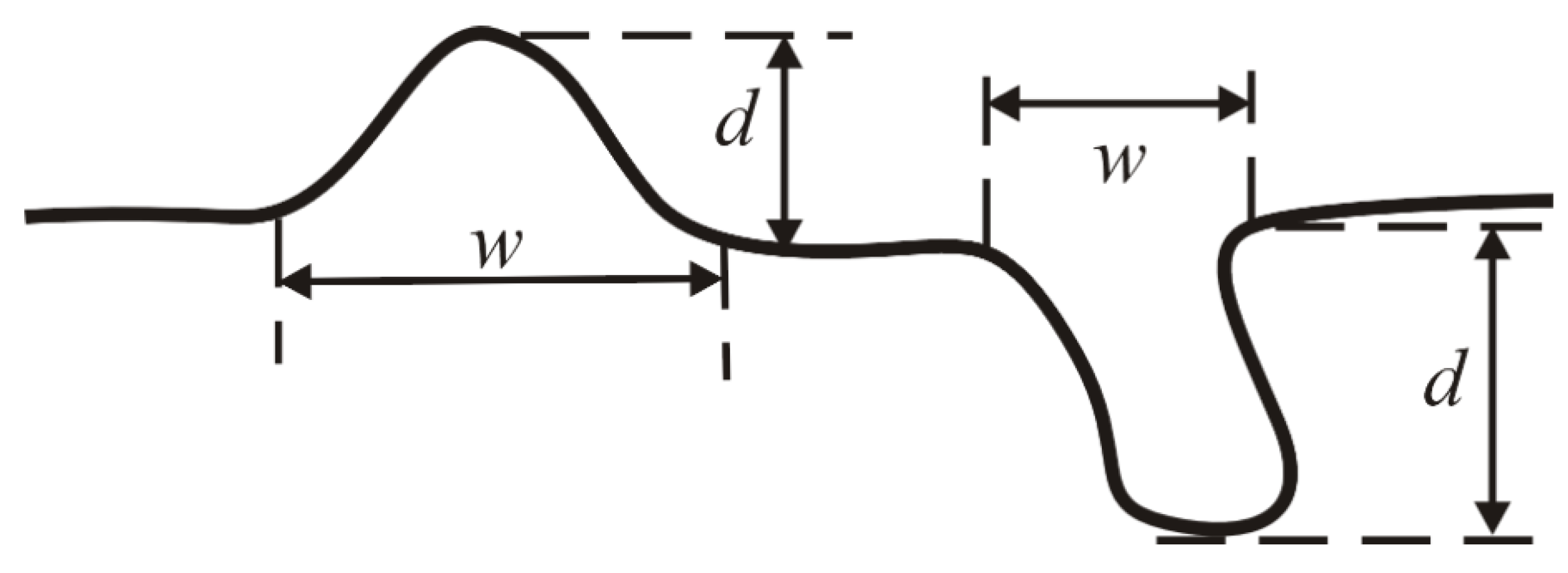
2.2. Minimum Representative Scale
3. Experiment and Analysis
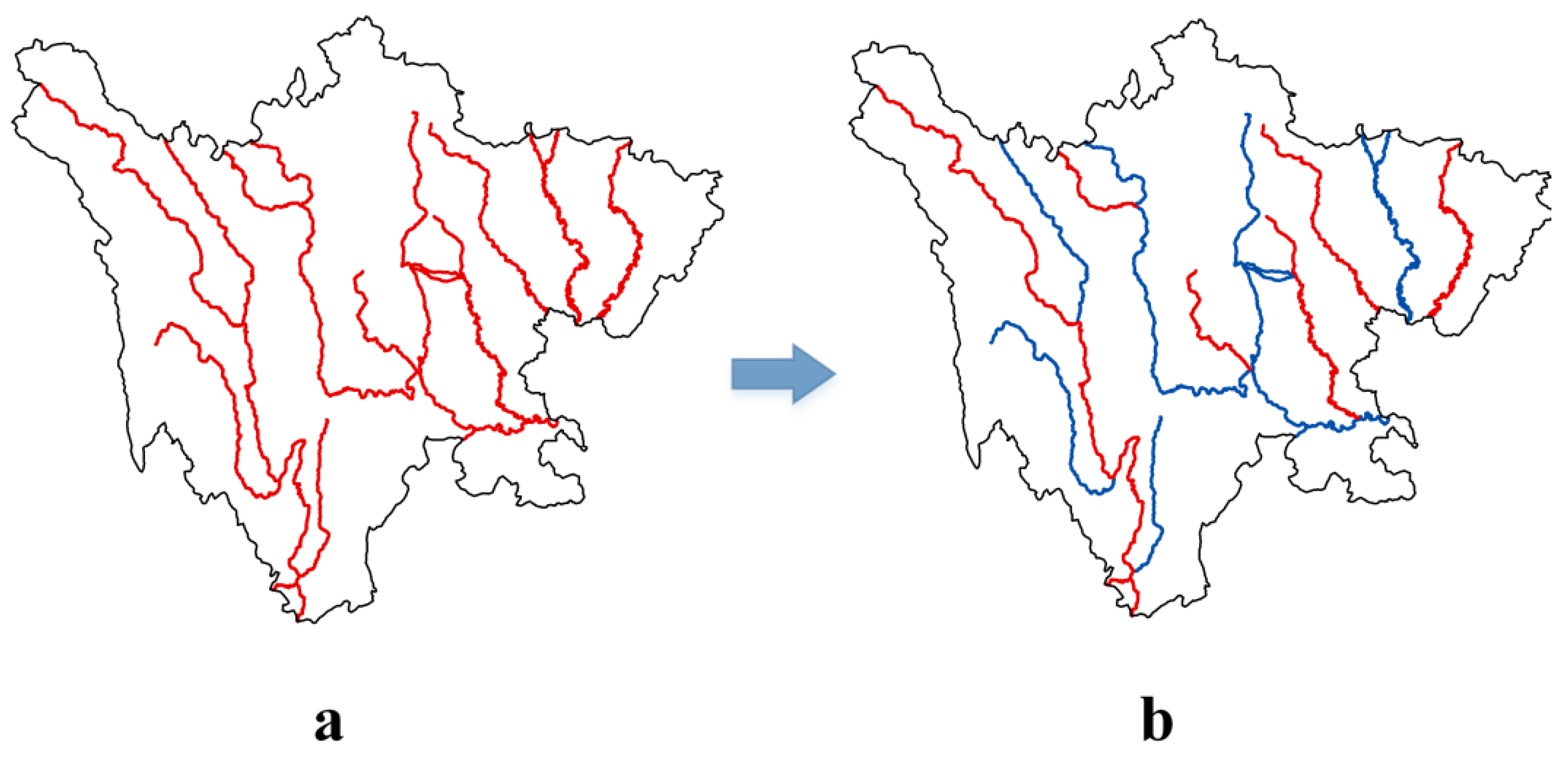
3.1. Contour Lines
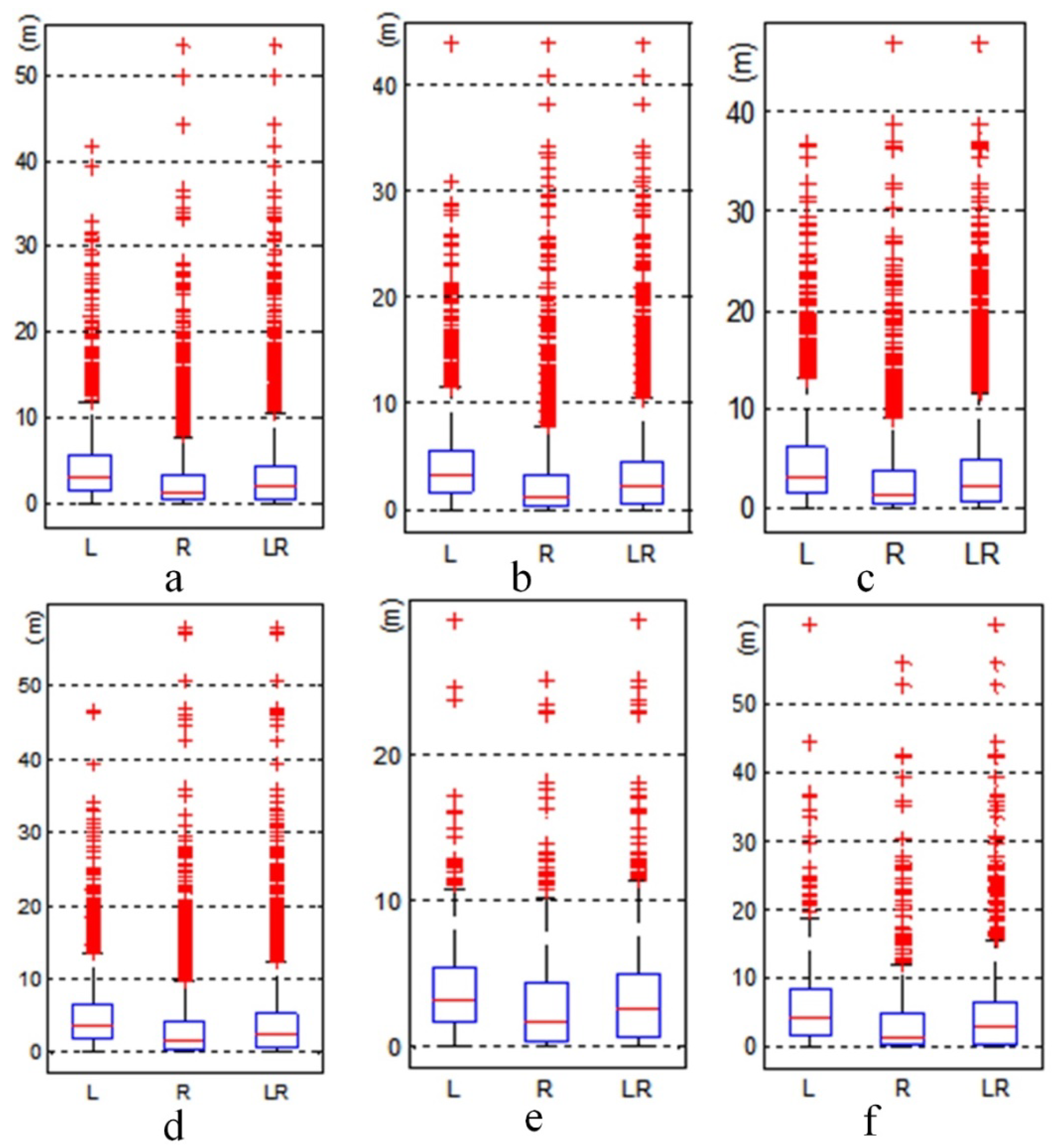
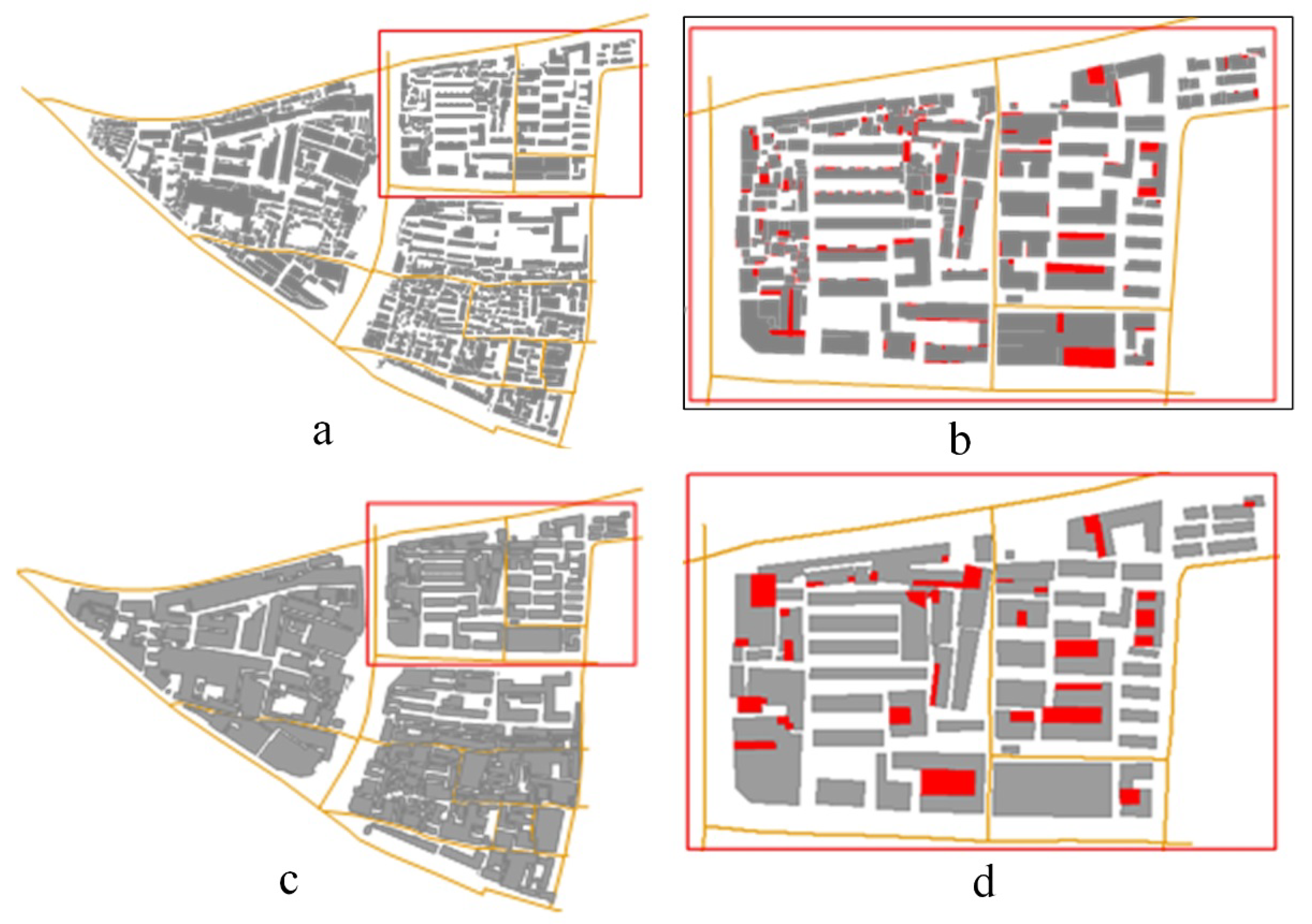
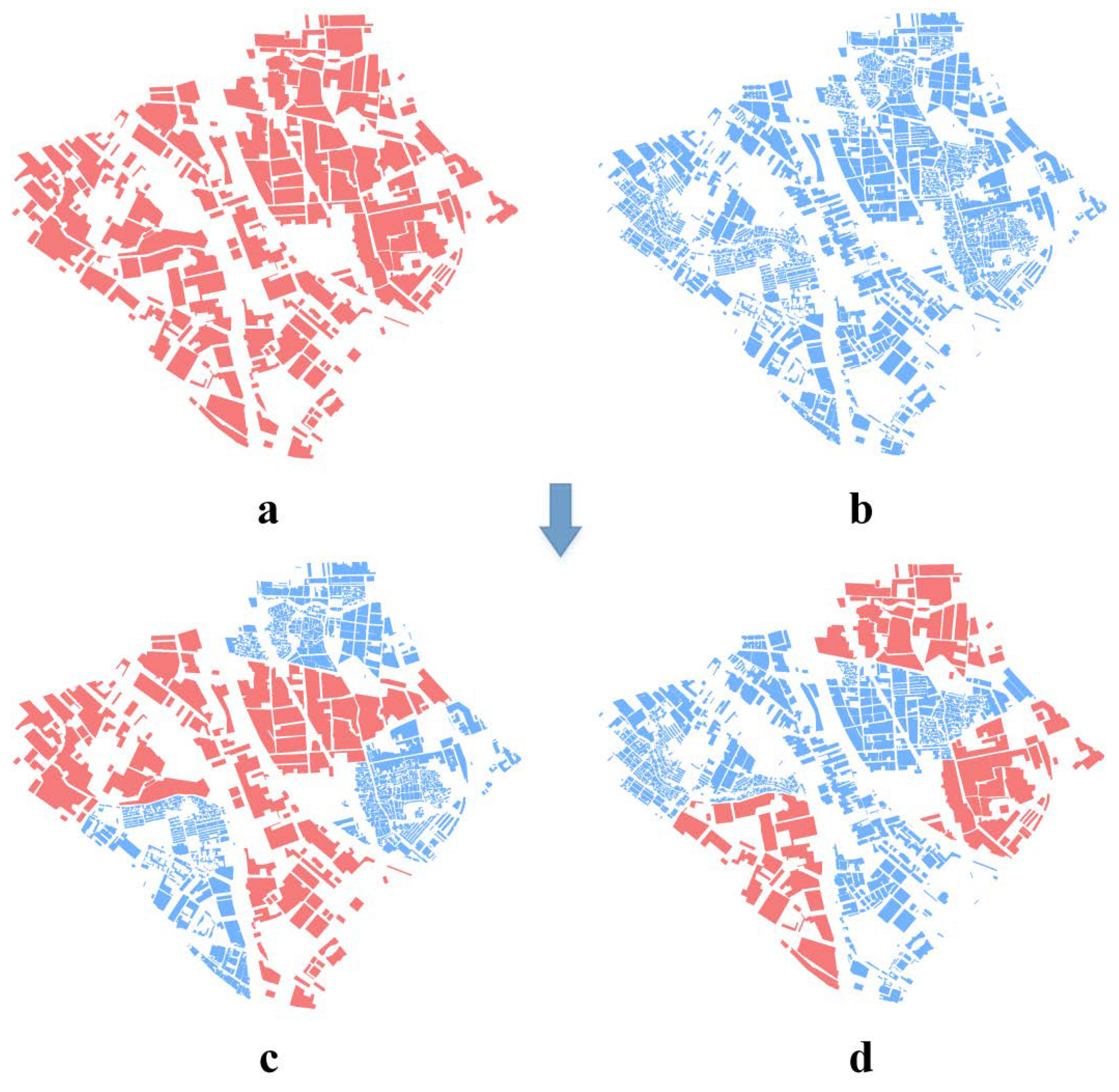
3.2. Buildings
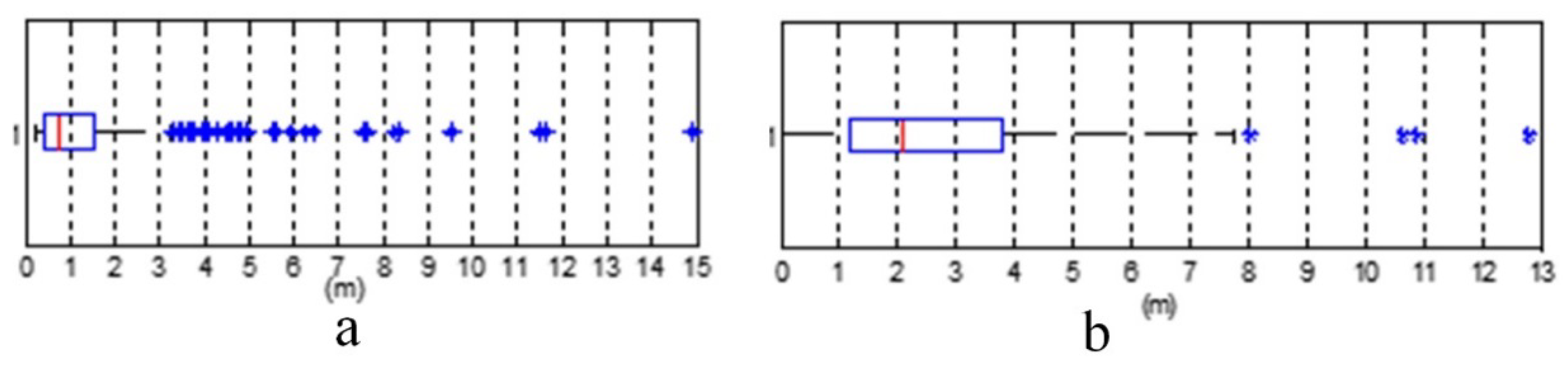
3.3. Scale Inconsistency Detection
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Girres, J.F.; Touya, G. Quality Assessment of the French OpenStreetMap Dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spat. Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Hung, K.C.; Kalantari, M.; Rajabifard, A. Methods for assessing the credibility of volunteered geographic information in flood response: A case study in Brisbane, Australia. Appl. Geogr. 2016, 68, 37–47. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Zhou, X.G. Version similarity-based model for volunteers’ reputation of volunteered geographic information: A case study of polygon. Acta Geod. Cartogr. Sin. 2015, 44, 578–584. [Google Scholar] [CrossRef]
- Stehman, S.V.; Fonte, C.C.; Foody, G.M.; See, L. Using volunteered geographic information (VGI) in design-based statistical inference for area estimation and accuracy assessment of land cover. Remote Sens. Environ. 2018, 212, 47–59. [Google Scholar] [CrossRef]
- Schultz, M.; Voss, J.; Auer, M.; Carter, S.; Zipf, A. Open land cover from OpenStreetMap and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 206–213. [Google Scholar] [CrossRef]
- Touya, G.; Brando-Escobar, C. Detecting level-of-detail inconsistencies in volunteered geographic information data sets. Int. J. Geogr. Inf. Geovis. 2013, 48, 134–143. [Google Scholar] [CrossRef]
- Brando, C.; Bucher, B.; Abadie, N. Specifications for user generated spatial content. In Advancing Geoinformation Science for a Changing World; Geertman, S., Reinhardt, W., Toppen, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 479–495. [Google Scholar]
- Duchêne, C.; Christophe, S.; Ruas, A. Generalisation symbol specification and map evaluation: Feedback from research done at COGIT laboratory, IGN France. Int. J. Digit. Earth 2011, 4 (Suppl. 1), 25–41. [Google Scholar] [CrossRef]
- Ai, T.; Liu, Y. A method of point cluster simplification with spatial distribution properties preserved. Acta Geod. Cartogr. Sin. 2002, 31, 175–181. [Google Scholar]
- Ai, T.; Li, Z.; Liu, Y.; Zhou, Y. The Changes Accumulation Model for Streaming Map Data Transferring over Web. Acta Geod. Cartogr. Sin. 2009, 38, 514–519. [Google Scholar]
- Huang, Y.; Ai, T.; Liu, H. The detection and removal of conflicts in road network generalization by Delaunay triangulation. In Proceedings of the 2009: 17th International Conference on Geoinformatics, Fairfax, VT, USA, 12–14 August 2009; IEEE: Fairfax, VA, USA, 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, H.; Ai, T.; Yang, M. Detail Resolution: A New Model to Describe Level of Detail Information of Vector Line Data. In Spatial Data Handling in Big Data Era. Advances in Geographic Information Science; Zhou, C., Su, F., Harvey, F., Xu, J., Eds.; Springer: Singapore, 2017; pp. 167–177. [Google Scholar]
- Ai, T. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Qian, H.Z.; Wu, F.; Chen, B.; Zhang, J.H.; Wang, J.Y. Simplifying line with oblique dividing curve method. Acta Geod. Cartogr. Sin. 2007, 36, 443–456. [Google Scholar]
- Guo, Q.S.; Huang, Y.; Zhang, L. The Method of Curve Bend Recognition. Geomat. Inf. Sci. Wuhan Univ. 2018, 33, 596–599. [Google Scholar]
- Liu, P.; Yang, W.; Li, C. Multi-branch tree model of bend for curve and its application in map generalization. Appl. Res. Comput. 2012, 29, 2793–2795. [Google Scholar]
- Lee, D.T.; Lin A, K. Generalized Delaunay triangulation for planar graphs. Discret. Comput. Geom. 1986, 1, 201–217. [Google Scholar] [CrossRef]
- Fang, T.P.; Piegl, L.A. Algorithm for constrained Delaunay triangulation. Vis. Comput. 1994, 10, 255–265. [Google Scholar] [CrossRef]
- Li, Z.; Openshaw, S. Algorithms for automated line generalization based on a natural principle of objective generalization. Int. J. Geogr. Inf. Syst. 1992, 6, 373–389. [Google Scholar] [CrossRef]
- Xu, W.; Long, Y.; Zhou, T.; Chen, L. Simplification of Building Polygon Based on Adjacent Four-Point Method. Acta Geod. Cartogr. Sin. 2013, 42, 929–936. [Google Scholar]
- Samsonov, T.E.; Yakimova, O.P. Shape-adaptive geometric simplification of heterogeneous line datasets. Int. J. Geogr. Inf. Sci. 2017, 31, 1485–1520. [Google Scholar] [CrossRef]
- Wang, Z.; Lee, D. Building Simplification Based on Pattern Recognition and Shape Analysis. In Proceedings of the China 2000: 9th International Symposium on Spatial Data Handling, Beijing, China, 10–12 August 2000; pp. 58–72. [Google Scholar]
- Wang, H.; Wu, F.; Zhang, L.; Deng, H. The application of mathematical morphology and pattern recognition to building polygon simplification. Acta Geod. Cartogr. Sin. 2005, 34, 269–276. [Google Scholar]
- Cai, A.; Zha, L.; Liu, D.; Gu, L. Analysis of Synthetical Multi-fuzzy Evaluation on the Quality of GIS Data. Geo-Inf. Sci. 2005, 7, 50–53. [Google Scholar]
- Deng, M.; Fan, Z.D.; Liu, H.M. Performance Evaluation of Line Simplification Algorithms Based on Hierarchical Information Content. Acta Geod. Cartogr. Sin. 2013, 42, 443–456. [Google Scholar]
- Zhang, X.; Guo, T.; Tang, T. An Adaptive Method for Incremental Updating of Vector Data. Acta Geod. Cartogr. Sin. 2012, 41, 613–619. [Google Scholar]
- Chen, B.; Zhu, K.; Xue, B. Quality Assessment of Linear Features Simplification Algorithms. J. Geomat. Sci. Technol. 2007, 24, 121–124. [Google Scholar]
- Liu, P.; Luo, J.; Ai, T.; Li, C. Evaluation Model for Similarity Based on Curve Generalization. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 114–117. [Google Scholar]
- Zhang, J.; Goodchild, M.F. Uncertainty in Geographical Information; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]

| No. | Pattern | Example | Regularity | Minimal Detail Distance (d) |
|---|---|---|---|---|
| 1 | convex | 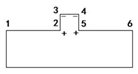 | The signs of the middle four consecutive turning angles are positive, negative, positive and negative; their angle value is approximately 90 degrees, and the angles of vector 12 and vector 56 are close to 0 degrees. | The minimal detail distance is the shorter length of edge 23 and edge 34, i.e., d = MIN(d23, d34), where d23 and d34 are the lengths of edge 23 and edge 34, respectively. |
| 2 | concave | 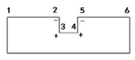 | The signs of the middle four consecutive turning angles are negative, positive, positive and negative; their angle value is approximately 90 degrees, and the angles of vectors 12 and 56 are close to 0 degrees. | The minimal detail distance is the shorter length of edge 23 and edge 34, i.e., d = MIN(d23, d34). |
| 3 | notch | 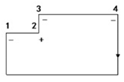 | The signs of the four consecutive turning angles are negative, positive, negative, negative or positive, negative, positive, positive; their angle value is approximately 90 degrees, and edges 12 and 23 are short edges. | The minimal detail distance is the shorter edge length of the notch, i.e., d = MIN(d12, d23). |
| 4 | multiple-step stair | 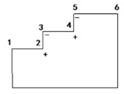 | The four consecutive turning angles’ values are approximately 90 degrees, the symbols are alternating, and edges 23 and 45 are short edges (i.e., the middle edges all are short edges). | The minimal detail distance is the shortest edge’s length, i.e., d = MIN (d12, d23, d34, d45). |
| 5 | spike | 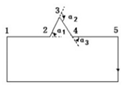 | The angle between vector 12 and vector 34 is approximately 0 degrees, edges 23 and 34 are short edges, and the angle between vector 12 and vector 34 is an acute angle. | The minimal detail is the shorter edge length of the acute angle, i.e., d=min(d23, d34) |
| 6 | Dull corner | 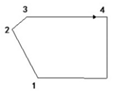 | The angle between vector 12 and vector 34 is an acute angle, edge 23 is the short edge, and edges 12 and 34 are long edges. | d= d23 |
| 7 | Curve steps | 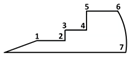 | The overall shape is a ladder above the sector; the four consecutive turning angles’ values are approximately 90 degrees. | The minimum detail distance is the length of the shortest edge including the sector arc segment, i.e., d = MIN(d12, d23, d34, d45, d67) |
| 8 | Perforated | 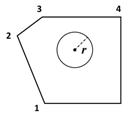 | A round hole in the middle of the building. | The minimum detail distance is the minimum value between the d value of the building profile and the diameter of the hole, i.e., d = MIN (d23, 2r) |
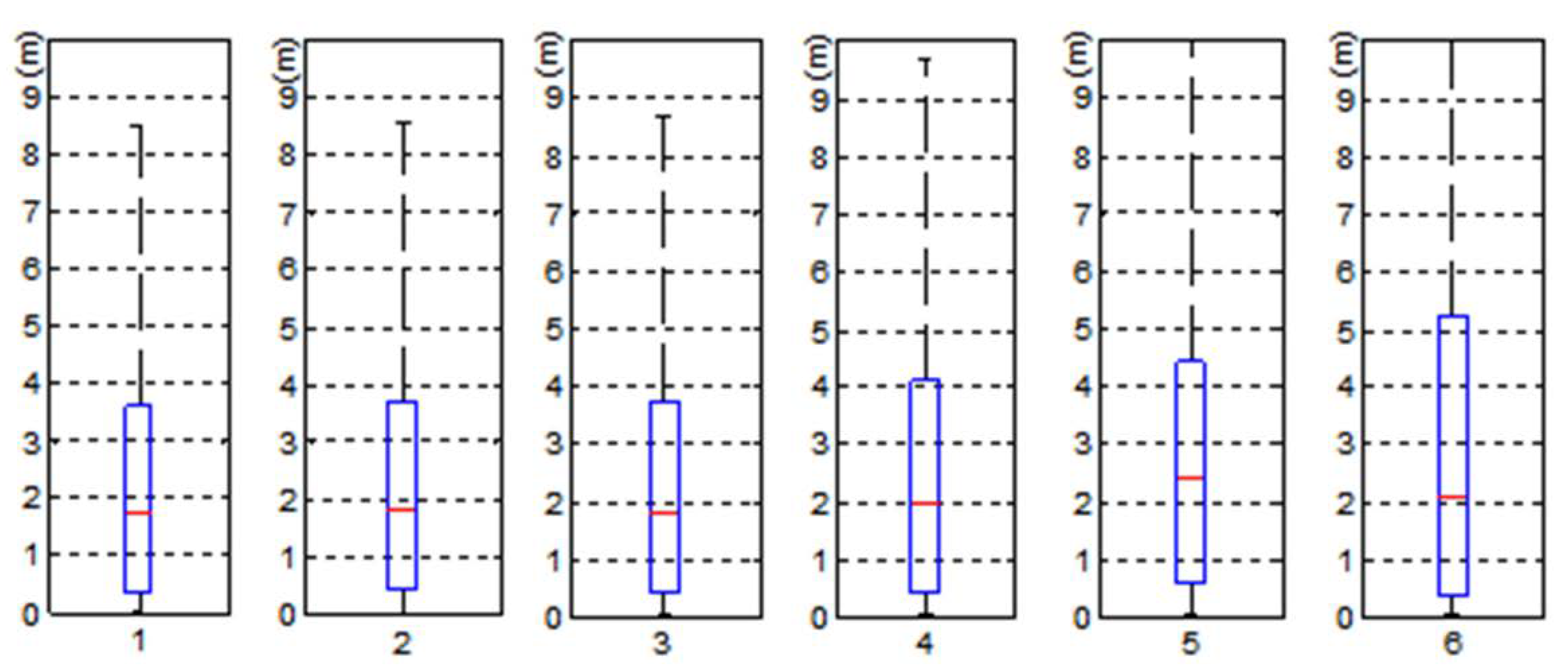
| No. | Thumbnail | # of Points | # of Left Leaf Bends | # of Right Leaf Bends | No. | Thumbnail | # of Points | # of Left Bends | # of Right Leaf Bends |
|---|---|---|---|---|---|---|---|---|---|
| 1 |  | 28399 | 2552 | 3491 | 4 |  | 24255 | 2085 | 2734 |
| 2 |  | 26392 | 2380 | 3296 | 5 |  | 4190 | 381 | 489 |
| 3 |  | 15060 | 1316 | 1708 | 6 |  | 7252 | 493 | 513 |
| Left Leaf Bend | Right Leaf Bend | ||||||
|---|---|---|---|---|---|---|---|
| NO. | w(m) | d(m) | l(m) | NO. | w(m) | d(m) | l(m) |
| 1 | 16.6 | 2.3 | 2.3 | 1 | 3.3 | 0.3 | 0.3 |
| 2 | 15.9 | 3.0 | 3.0 | 2 | 3.0 | 0.3 | 0.3 |
| 3 | 12.3 | 2.4 | 2.4 | 3 | 22.9 | 3.4 | 3.4 |
| 4 | 16.9 | 2.8 | 2.8 | 4 | 14.8 | 4.6 | 4.6 |
| 5 | 21.7 | 4.9 | 4.9 | 5 | 16.7 | 6.5 | 6.5 |
| 6 | 30.5 | 14.9 | 14.9 | 6 | 11.1 | 2.7 | 2.7 |
| 7 | 28.9 | 13.6 | 13.6 | 7 | 3.6 | 0.3 | 0.3 |
| 8 | 9.4 | 4.2 | 4.2 | 8 | 4.6 | 0.3 | 0.3 |
| 9 | 7.5 | 1.7 | 1.7 | 9 | 2.3 | 0.2 | 0.2 |
| 10 | 37.2 | 8.8 | 8.8 | 10 | 2.1 | 0.2 | 0.2 |
| 11 | 9.5 | 0.4 | 0.4 | 11 | 12.5 | 2.2 | 2.2 |
| … | … | … | … | … | … | … | … |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| LoD (m) | 1.529 | 1.5 | 1.566 | 1.651 | 1.872 | 1.378 | 1.543 | 1.653 | 1.453 | 1.621 |
| Scale denominator | 5097 | 5000 | 5220 | 5503 | 6240 | 4593 | 5143 | 5510 | 4843 | 5403 |
| Scale consistency | YES | YES | YES | YES | NO | NO | YES | NO | YES | YES |
| No. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| LoD (m) | 1.394 | 1.603 | 1.743 | 1.464 | 1.583 | 1.632 | 1.39 | 1.567 | 1.583 | 1.445 |
| Scale denominator | 4647 | 5343 | 5810 | 4880 | 5277 | 5440 | 4633 | 5223 | 5277 | 4817 |
| Scale consistency | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| No. | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| LoD (m) | 1.567 | 1.704 | 1.6 | 1.456 | 1.532 | 1.8 | 1.542 | 1.64 | 1.543 | 1.673 |
| Scale denominator | 5223 | 5680 | 5333 | 4853 | 5107 | 6000 | 5140 | 5467 | 5143 | 5577 |
| Scale consistency | YES | NO | YES | YES | YES | NO | YES | YES | YES | NO |
| No. | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| LoD (m) | 1.542 | 1.621 | 1.543 | 1.456 | 1.432 | 1.532 | 1.502 | 1.542 | 1.632 | 1.432 |
| Scale denominator | 5140 | 5403 | 5143 | 4853 | 4773 | 5107 | 5007 | 5140 | 5440 | 4773 |
| Scale consistency | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| No. | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| LoD (m) | 1.554 | 1.376 | 1.534 | 1.543 | 1.64 | 1.502 | 1.435 | 1.583 | 1.623 | 1.46 |
| Scale denominator | 5180 | 4587 | 5113 | 5143 | 5467 | 5007 | 4783 | 5277 | 5410 | 4867 |
| Scale consistency | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| Parameters | Original Map | Mixed Map | ||||
|---|---|---|---|---|---|---|
| L | R | LR(LoD) | L | R | LR(LoD) | |
| Q1 (m) | 2951.554 | 2986.015 | 2972.630 | 1274.871 | 1243.072 | 1255.090 |
| Q2 (m) | 4344.659 | 4411.786 | 4392.251 | 3234.362 | 3149.018 | 3207.992 |
| Q3 (m) | 6201.038 | 6386.454 | 6313.461 | 5316.651 | 5441.523 | 5385.743 |
| l (m) | 1976.980 | 2018.262 | 1997.362 | 813.389 | 825.634 | 819.442 |
| Nominal scale | 1:2,000,000 | 1:2,000,000 & 1:750,000 | ||||
| Calculated scale | 1:1,997,362 | 1:819,442 | ||||
| Parameters | Original Map | Map for Replacement | Mixed Map 1 | Mixed Map 2 |
|---|---|---|---|---|
| Q1 (m) | 17.157 | 3.969 | 4.259 | 4.212 |
| Q2 (m) | 24.495 | 7.128 | 8.043 | 7.752 |
| Q3 (m) | 42.157 | 11.467 | 12.893 | 14.925 |
| LoD (m) | 9.339 | 2.473 | 2.662 | 2.626 |
| Nominal scale | 1:30,000 | 1:10,000 | 1:30,000 & 1:10,000 | |
| Calculated scale | 1:31,130 | 1:8243 | 1:8873 | 1:8753 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Xiao, J. An Evaluation Model of Level of Detail Consistency of Geographical Features on Digital Maps. ISPRS Int. J. Geo-Inf. 2020, 9, 410. https://doi.org/10.3390/ijgi9060410
Liu P, Xiao J. An Evaluation Model of Level of Detail Consistency of Geographical Features on Digital Maps. ISPRS International Journal of Geo-Information. 2020; 9(6):410. https://doi.org/10.3390/ijgi9060410
Chicago/Turabian StyleLiu, Pengcheng, and Jia Xiao. 2020. "An Evaluation Model of Level of Detail Consistency of Geographical Features on Digital Maps" ISPRS International Journal of Geo-Information 9, no. 6: 410. https://doi.org/10.3390/ijgi9060410
APA StyleLiu, P., & Xiao, J. (2020). An Evaluation Model of Level of Detail Consistency of Geographical Features on Digital Maps. ISPRS International Journal of Geo-Information, 9(6), 410. https://doi.org/10.3390/ijgi9060410





