GroupSeeker: An Applicable Framework for Travel Companion Discovery from Vast Trajectory Data
Abstract
1. Introduction
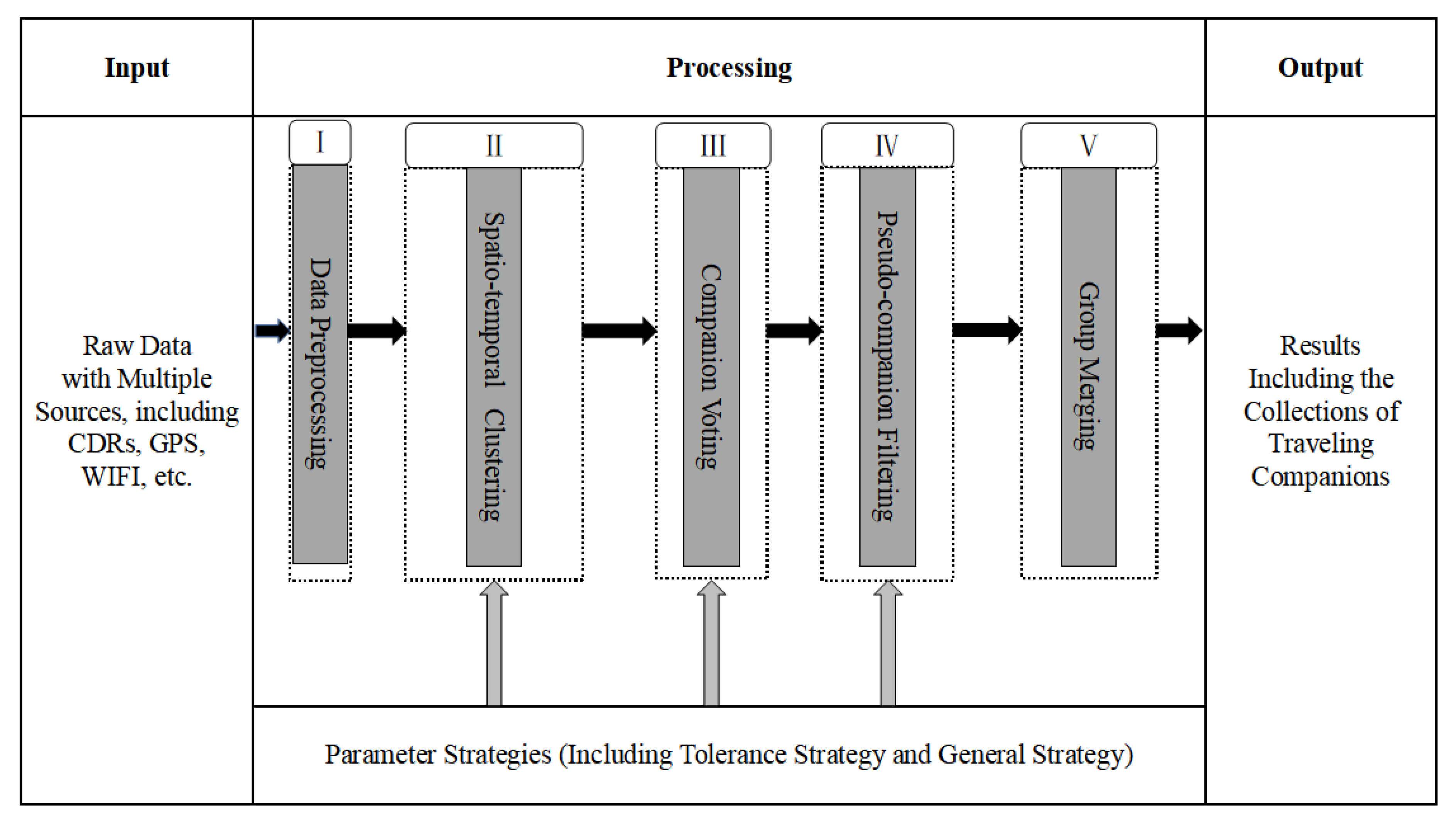
- A framework of traveling companion discovery named GroupSeeker is proposed. Through a five-stage processing flow, GroupSeeker can find potential traveling companions in a huge amount of trajectory data with high performance and accuracy.
- Parameter Setting Strategies are inherently embedded into GroupSeeker. Primary stages can determine their parameters according to the characteristic of datasets, which makes the framework much more practical and applicable.
- A novel Spatio-temporal clustering method is used to deal with trajectory data of long-term time slices and solve the omitting problem of companion candidates caused by improper short-term time segmentation in previous work.
- Experimental results on real-world and simulated datasets show the time cost of GroupSeeker is at a desirable level. Trajectory data for twenty-four hours can be processed within one and a half hours, which means GroupSeeker can be used in all-weather monitoring jobs.
2. Related Work
2.1. Trajectory Clustering
2.2. Companion Pattern Discovery
3. Materials and Methods
3.1. Problem Statement
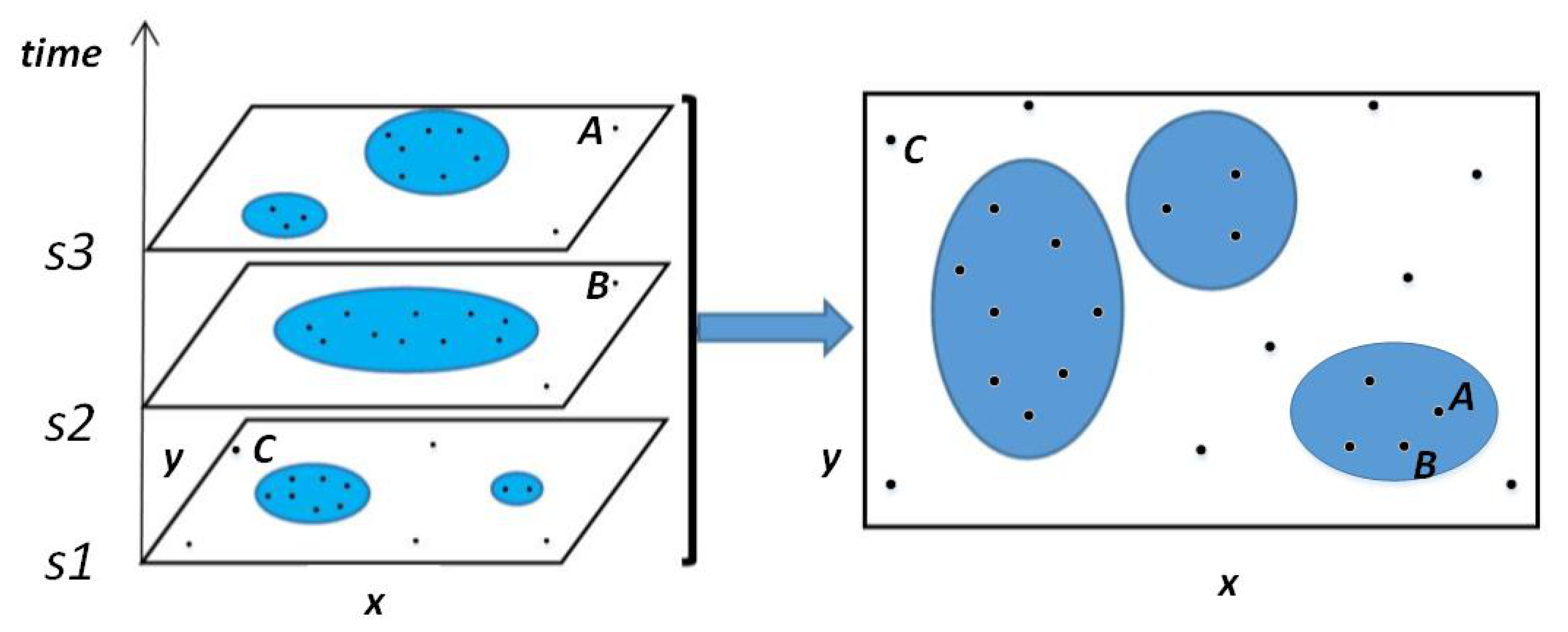
3.1.1. Companion Candidate Omitting Problem
- Signals of real-world positioning data may be blocked during acquisition and transmission. The reason for blocking is because users can actively turn off devices or terminate location service and the transmission of location information may be interfered or blocked by surrounding environments.
- Due to differences in sampling methods and loss of data transmission, trajectory data will be sparse or partially lost during data collection.
3.1.2. Problem Definition
- Definition 1 (Snapshot Set): A time snapshot set is a collection of series of short-time snapshots. which can be seen as an extension to a shorter-time snapshot.
- Definition 2 (Record Group): A Record Group is a collection of all moving object records in a snapshot set , n represents the number of moving objects within the time set. For a moving object , the number of the records is , and
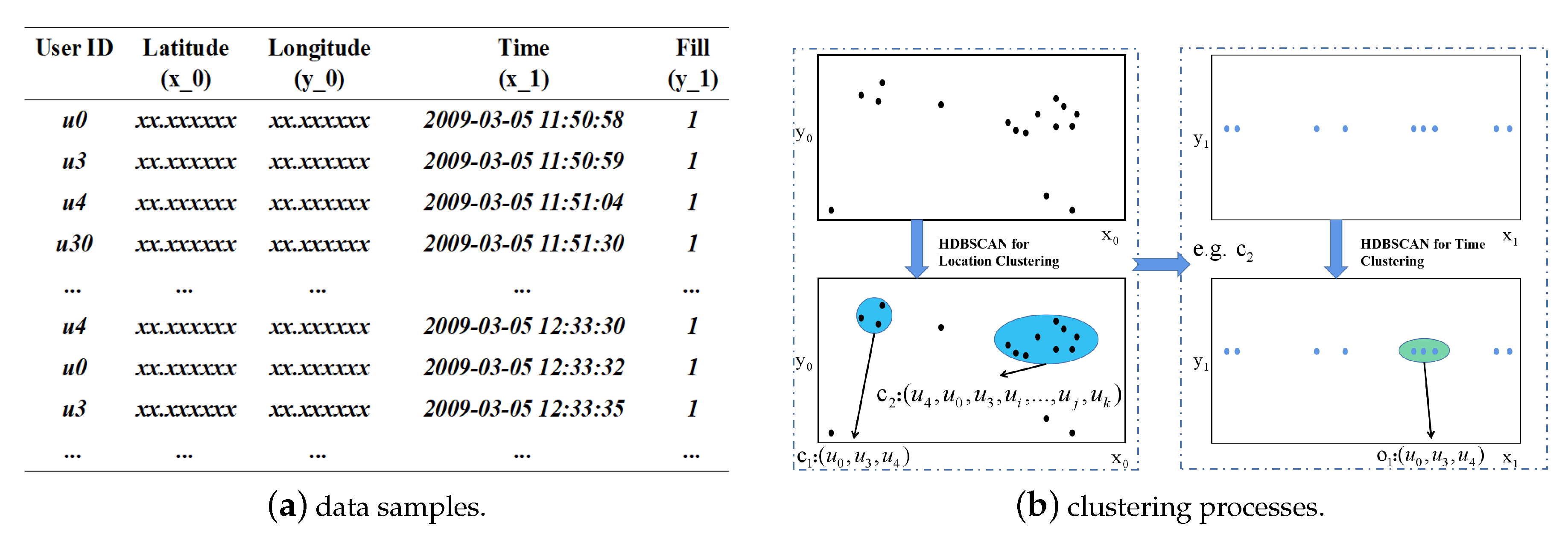
- Definition 3 (Locational Potential Candidate (LPC)): A Candidate Set is a set as a set of companion candidates clustered by location information, where m represents the number of clusters. This paper uses the density-based clustering algorithm. Some parameters need to be defined. is defined as a size threshold of clustering, is used as a distance threshold. The default distance formula of several clustering algorithms is based on the Euclidean distance formula, which can provide certain efficiency advantages. However, in order to facilitate the parameter setting of trajectory data mining and improve the accuracy of trajectory data mining results, the distance formula here may be replaced by a distance formula that better meets the needs of the scene. A locational potential candidate set is a cluster set satisfying w.r.t. and .
- Definition 4 (Time and Location Potential Candidate (TLPC)): On the basis of potential candidates for position, the clusters of the candidates satisfy clustering based on time to form clusters. The collection of objects in these clusters is regarded as Time and Location Potential Candidate. Among them, is defined as the minimum cluster size. In addition, because HDBSCAN is used to weaken another distance parameter, it is not defined here.
- Definition 5 (Associated Traveling Companion Candidate(ATCC)): is the minimum support threshold for the association analysis and is the minimum confidence threshold. The candidate set satisfies an association rule dictionary . The key-value pair of the dictionary corresponds to the frequent item and its support. is a frequent item with its support not less than the minimum support. The key of the association rule is a frequent item with its confidence is not less than the minimum confidence.
- Definition 6 (Pseudo-companion Scenarios): The Pseudo-companion scenarios refer to scenarios that already have potentially associated companionship while some important features do not fully conform to the accompanying pattern.
- Definition 7 (Tolerance Strategy): When performing trajectory data mining in a sparse data set, some parameters cannot be set strictly. Otherwise, it will be difficult to find the research objects that meet the relevant conditions. For this reason, a Tolerance Strategy needs to be considered to discover moving objects.
- Definition 8 (Traveling Companion (TC)): is a set of traveling companion, where a traveling companion group is a group that satisfies the number of records satisfying the potential accompany situation is greater than the frequency threshold , and the proportion of the records satisfying is greater than the percentage threshold within the time period S.
3.2. Methodology
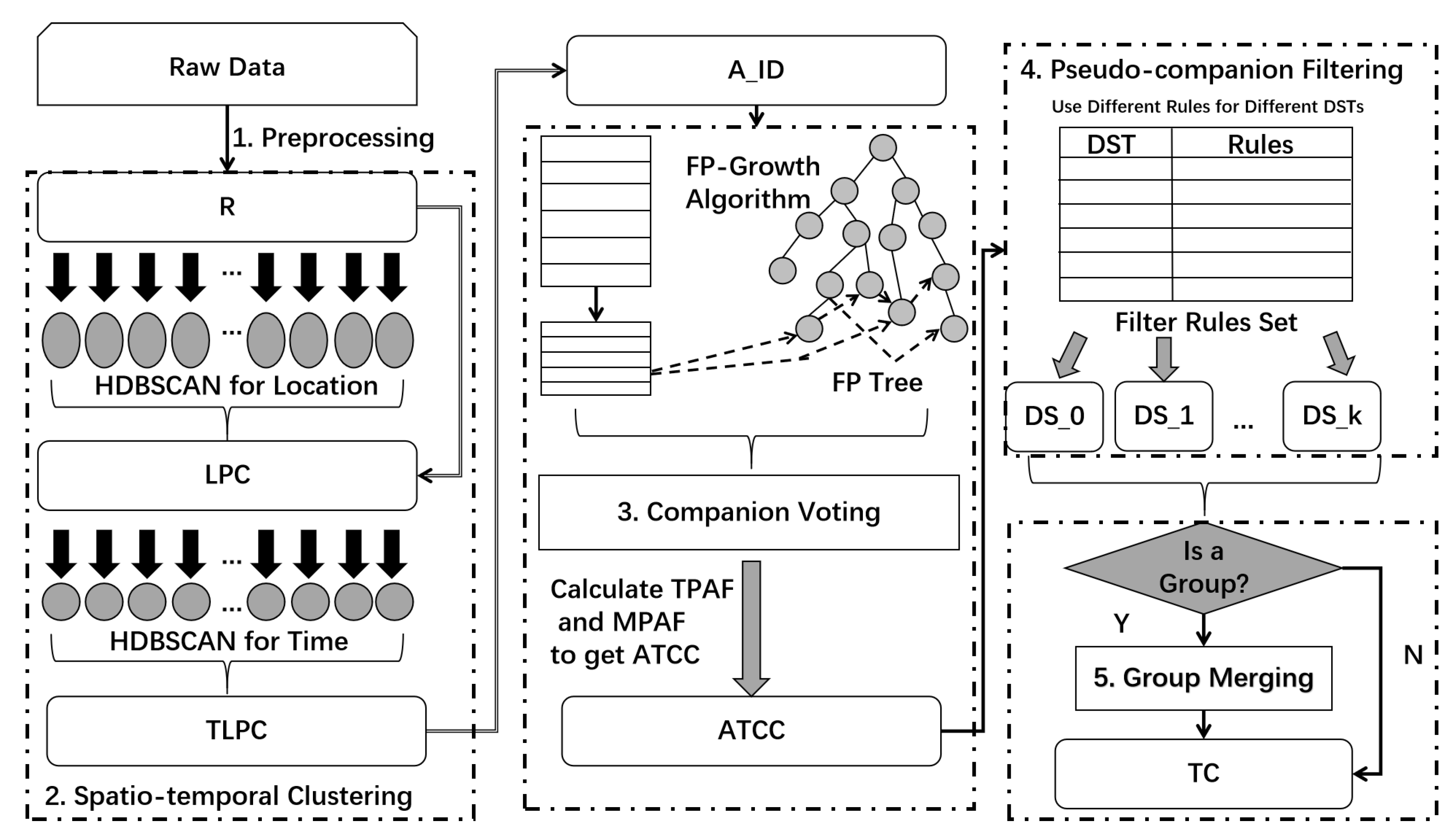
3.2.1. Framework
3.2.2. Data Preprocessing
3.2.3. Spatio-Temporal Clustering
| Algorithm 1: Spatio-temporal Clusteirng and Companion Voting Algorithm. |
 |
3.2.4. Companion Voting
3.2.5. Pseudo-Companion Filtering
3.2.6. Group Merging
| Algorithm 2: Pseudo-companion Filtering and Group Merging Algorithm. |
 |
3.2.7. Parameter Setting Strategy
- General Strategy: The general strategy is explained here in order to highlight the tolerance strategy. First, the haversine formula is a formula especially calculated to the distance between two points through their latitudes and longitudes. Many clustering algorithms include a parameter called “metric”, which can be set as “haversine”. Secondly, for discovering Traveling Companions, the minimal clustered number for clustering should be larger than 3 to reduce the number of clusters. Moreover, for the support-and-confidence setting, Table 4 shows a preliminary correspondence between participation and confidence level. We hope to guarantee a higher confidence level, so the default confidence value set in this study is 0.6. For the support level, we will focus on the frequency of the target object at the same time and not necessarily require to get a ratio. Finally, it is important for the consistency of the results of a data set to ensure the distance threshold parameter. For instance, for and , they are set to the same value in consideration of sampling accuracy at different stages. Absolutely, if the purpose of applications requires stricter filtering, it needs to set the latter parameter smaller.
- Tolerance Strategy: Compared with the strictness of the general strategy, the tolerance strategy provides good support for the data sets from some special data sources, such as CDRs. Besides, it is difficult to give a clear value range for some parameters for various data sets, while the proposed tolerance strategy can guide users to weaken some parameter setting ideas from the purpose of mining. The original intention of this strategy is that for data samples with higher sparseness, strict threshold constraints are bound to make the result set as small as possible. In fact, the setting of this strategy comes more from the practicality of the results. In this field, the sparseness of trajectory data has always been a major challenge. At the same time, it is difficult for some specific data sources to collect data information of all users in a specific geographic area within a long period of time. This results in the sparseness of real-world data that is reasonable and unavoidable. For this reason, researchers should hope to make full use of each recorded information (except obvious noise). Specifically, for some important scenarios, such as mining the behavior patterns of specific groups and specific individuals to discover the traveling companion pattern, sometimes various factors disturb the collecting process so that these data are caused to be sparse. In this case, the tolerance strategy can better prevent some records from being strictly filtered out, which is more likely to find other related moving objects. In our study, it is important for and in data source D1 to consider tolerance. These two parameters can be set to larger values to limit the confusion scenarios, such as only a small number of records are related and most of the records are far apart, or the number of records of an object is so small that it should be filtered out.
4. Experiment and Results
4.1. Data Sets
- The Sampling Frequency
- The Number of Records for Individuals
- Effective Duration
- Data Collection Period
- D1 (Traveling Users Dataset): This dataset is collected from real users in a certain region of China between 16 November 2014 and 18 November 2014, which was provided by a communication provider in China. The locations are from the cell-sites which are connected with many phones. The raw spatial trajectory data mainly includes the latitude and longitude coordinates, time-stamp and user information. When we got this dataset, personal-sensitive information in the dataset was anonymized and the coordinate information was re-adjusted by this provider for privacy protection.
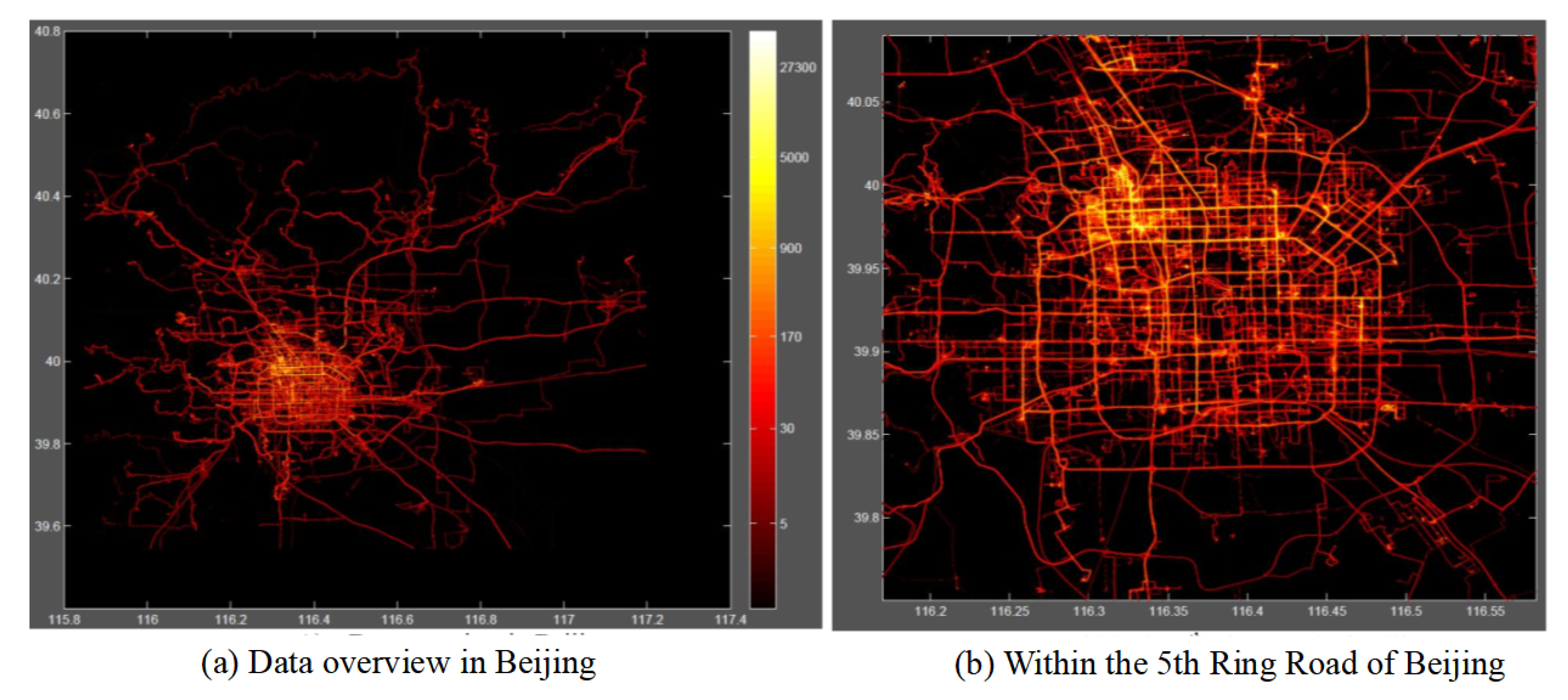
- D2 (Geolife Trajectory): This dataset was collected in (Microsoft Research Asia) Geolife project from 182 users between April 2007 and August 2012 [51,52,53]. A GPS trajectory from that set is represented by a sequence of time-stamped points containing information on latitude, longitude and altitude. of the tracks are in a dense representation, e.g., every 1–5 s or every 5–10 m per point, the overview of this data set shown in Figure 5:
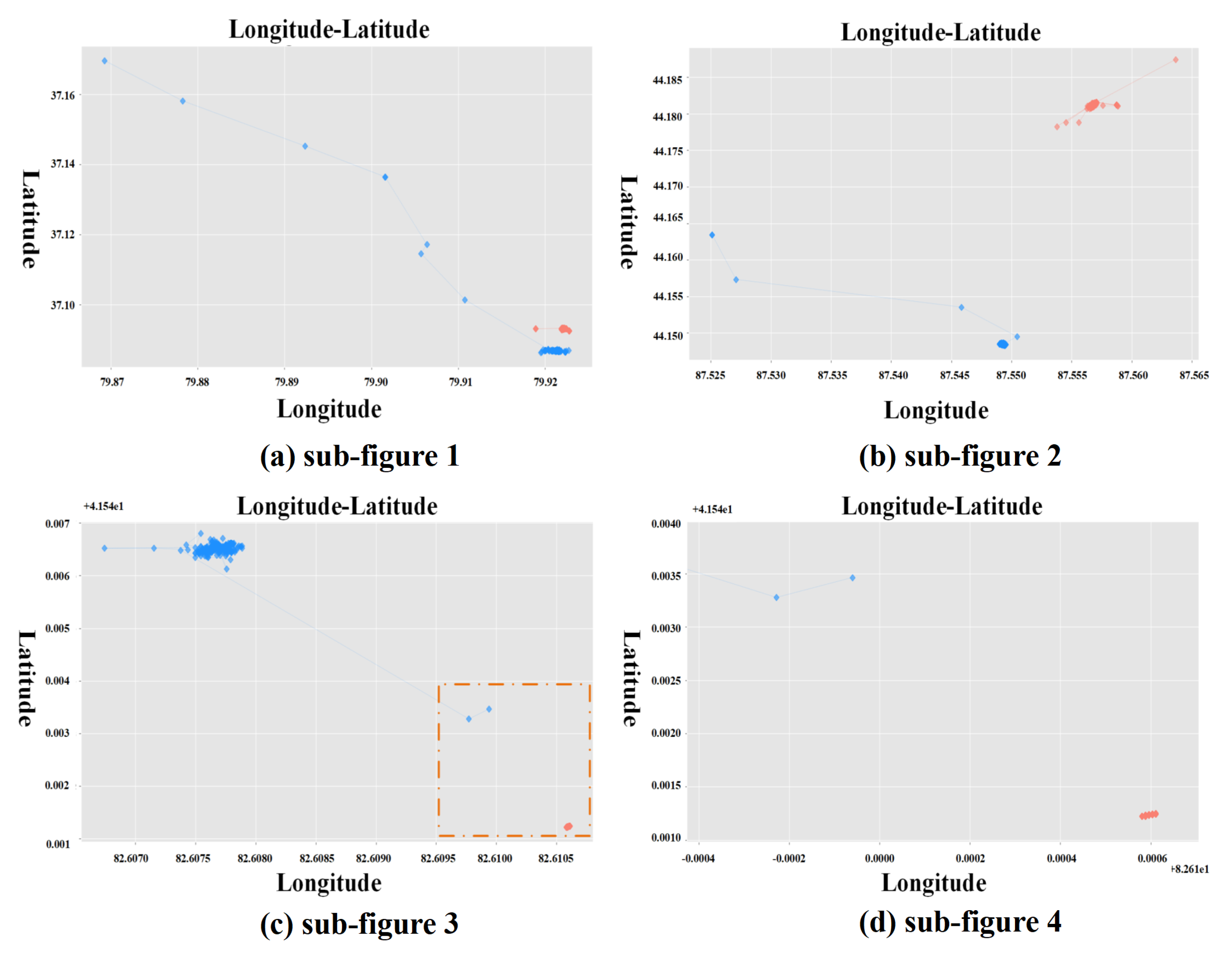
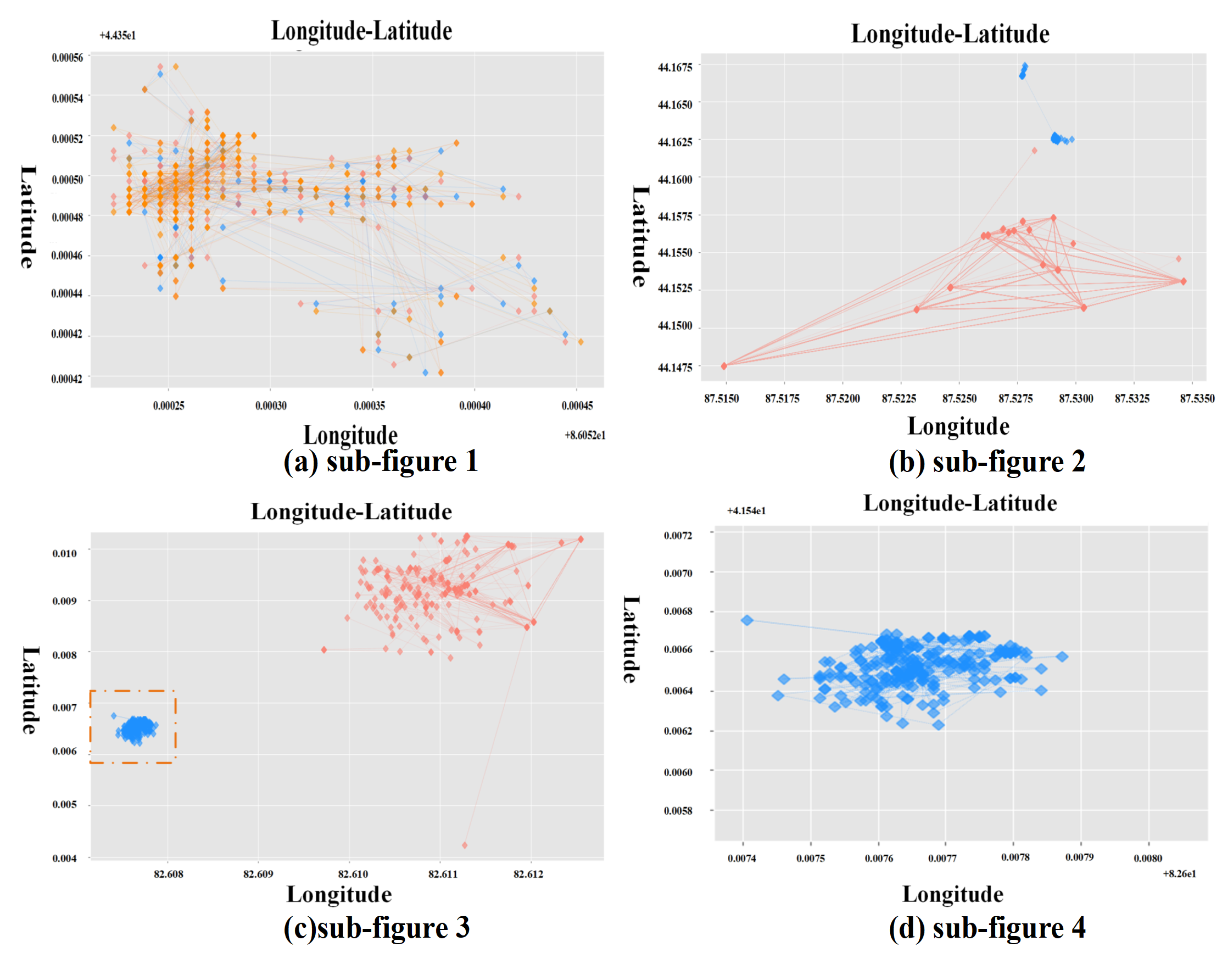
4.2. Pseudo-Companion Scenarios Filtering Display
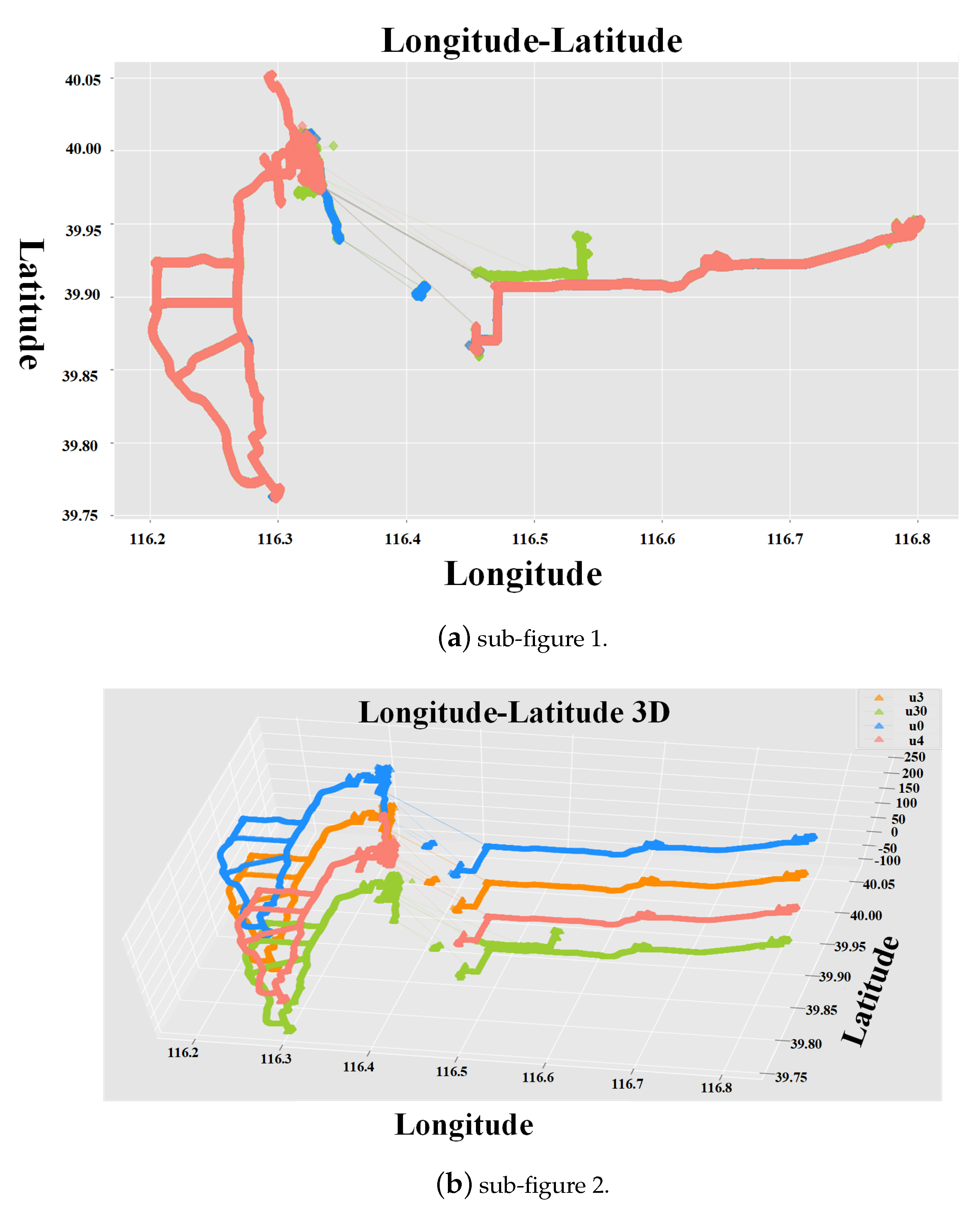
4.3. The Results of Traveling Companion Discovery and Validation
4.3.1. Measuring Time Overhead
4.3.2. Significant Result Analysis
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANPR | Automatic Number Plate Recognition |
| ATCC | Associated Traveling Companion Candidate |
| CDRs | call detial records |
| DBSCAN | density-based spatical clustiny of application with noise |
| DENCLUE | density-based clustering |
| DTS | Different Data Source |
| DTWD | Dynamic Time Warping Distance |
| HDBSCAN | Hierarchical Density-Based Spatial Clustering of Applications with Noise |
| HD-FIM | a breadth-first and depth-first hybrid distributed approach with Frequent itemset mining |
| ITs | intelligent system |
| LBS | Location-Based Service |
| LPC | Locational Potential Candidate |
| MBB | Minimal Bounding Box |
| MBR | Minimum Bounding Rectangle |
| MPAF | The Mutual Promotion of Accompanying Frequency |
| OPTICS | Ordering points to identify the clustering structure |
| TLPC | Time and Location Potential Candidate |
| TC | Traveling Companion |
| TPAF | The Total Proportion of Accompanying Frequency |
References
- National Bureau Statistics of China, Statistical Communiqué of the People’s Republic of China on National Economic and Social Development in 2019. Available online: http://www.stats.gov.cn/tjsj/zxfb/202002/t20200228_1728913.html (accessed on 28 February 2020).
- Gao, Q.; Zhang, F.L.; Wang, R.J.; Zhou, F. Trajectory Big Data: A Review of Key Techologies in Data Processing. Ruan Jian Xue Bao/J. Softw. 2017, 28, 959–992. (In Chinese) [Google Scholar]
- Elragal, A. Analysis of trajectory data in support of traffic management. Lect. Notes Comput. Sci. 2015, 8557, 174–188. [Google Scholar]
- Enami, S.; Shiomoto, K. Spatio-temporal human mobility prediction based on trajectory data mining for resource management in mobile communication networks. In Proceedings of the IEEE International Conference on High Performance Switching and Routing, Xi’An, China, 26–29 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Qin, T.; Shangguan, W.; Song, G.; Tang, J. Spatio-Temporal Routine Mining on Mobile Phone Data. ACM Trans. Knowl. Discov. Data 2018, 12, 56.1–56.24. [Google Scholar] [CrossRef]
- Li, H.; Gou, Y. Mining Mobile Sensor Data for Social Behaviors. In Proceedings of the 2nd International Workshop on Social Sensing, Pittsburgh, PA, USA, 21 April 2017. [Google Scholar]
- Chen, Y.; Crespi, N.; Ortiz, A.M.; Shu, L. Reality mining: A prediction algorithm for disease dynamics based on mobile big data. Inf. Sci. Int. J. 2017, 379, 82–93. [Google Scholar] [CrossRef]
- Liu, X.; Tian, Y.; Zhang, X.; Wan, Z. Identification of Urban Functional Regions in Chengdu Based on Taxi Trajectory Time Series Data. Int. J. Geo-Inf. 2020, 9, 158. [Google Scholar] [CrossRef]
- Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 29:1–29:41. [Google Scholar] [CrossRef]
- Tang, L.; Zheng, Y.; Yuan, J.; Han, J.; Leung, A.; Peng, W.; Porta, T.F.L. A framework of traveling companion discovery on trajectory data streams. ACM Trans. Intell. Syst. Technol. 2013, 5, 3:1–3:34. [Google Scholar] [CrossRef]
- Zhu, M.L.; Liu, C.; Wang, X.-B.; Han, Y.-B. Approach to discover companion pattern based on anpr data stream. Ruan Jian Xue Bao/J. Softw. 2017. (In Chinese) [Google Scholar]
- Zhu, X.; Sun, T.; Yuan, H.; Hu, Z.; Miao, J. Exploring Group Movement Pattern through Cellular Data: A Case Study of Tourists in Hainan. ISPRS Int. J. Geo-Inf. 2019, 8, 74. [Google Scholar] [CrossRef]
- Gudmundsson, J.; van Kreveld, M.J. Computing longest duration flocks in trajectory data. In Proceedings of the 14th ACM International Symposium on Geographic Information Systems, ACM-GIS 2006, Arlington, VA, USA, 10–11 November 2006; de By, R.A., Nittel, S., Eds.; ACM: New York, NY, USA, 2006; pp. 35–42. [Google Scholar]
- Tang, L.; Zheng, Y.; Yuan, J.; Han, J.; Leung, A.; Hung, C.; Peng, W. On Discovery of Traveling Companions from Streaming Trajectories. In Proceedings of the IEEE 28th International Conference on Data Engineering (ICDE 2012), Washington, DC, USA, 1–5 April 2012; Kementsietsidis, A., Salles, M.A.V., Eds.; IEEE Computer Society: Washington, DC, USA, 2012; pp. 186–197. [Google Scholar]
- Zhang, Y.; Ji, G.; Zhao, B.; Zhang, B. An Algorithm for Mining Gradual Moving Object Clusters Pattern From Trajectory Streams. CMC-Comput. Mater. Contin. 2019, 59, 885–901. [Google Scholar] [CrossRef]
- Yao, R.; Wang, F.; Chen, S. TCoD: A Traveling Companion Discovery Method Based on Clustering and Association Analysis. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Mcinnes, L.; Healy, J.; Astels, S. hdbscan: Hierarchical density based clustering. J. Open Sour. Softw. 2017, 2, 205. [Google Scholar] [CrossRef]
- Agrawal, R.; Faloutsos, C.; Swami, A.N. Efficient Similarity Search in Sequence Databases; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Faloutsos, C.; Ranganathan, M.; Manolopoulos, Y. Fast Subsequence Matching in Time-Series Databases. In Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data, Minneapolis, MN, USA, 24–27 May 1994; pp. 419–429. [Google Scholar]
- Chan, K.; Fu, A.W. Efficient time series matching by wavelets. In Proceedings of the 15th International Conference on Data Engineering (Cat. No.99CB36337), Sydney, Australia, 23–26 March 1999; pp. 126–133. [Google Scholar]
- Elnekave, S.; Last, M.; Maimon, O. Incremental Clustering of Mobile Objects. In Proceedings of the IEEE International Conference on Data Engineering Workshop, ICDE 2007, Istanbul, Turkey, 15–20 April 2007; pp. 585–592. [Google Scholar]
- De Vries, G.K.D.; Van Someren, M. Clustering Vessel Trajectories with Alignment Kernels under Trajectory Compression. In Proceedings of the Machine Learning and Knowledge Discovery in Databases, European Conference, ECML PKDD 2010, Barcelona, Spain, 20–24 September 2010; Volume 6321, pp. 296–311. [Google Scholar]
- Hightower, J.; Borriello, G. Particle Filters for Location Estimation in Ubiquitous Computing: A Case Study. In Proceedings of the UbiComp 2004: Ubiquitous Computing: 6th International Conference, Nottingham, UK, 7–10 September 2004; Volume 3205, pp. 88–106. [Google Scholar]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial Databases with Noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Peipei, Z.; Qinghai, D.; Haibo, L.; Xinglin, H. Trajectory outlier detection based on DBSCAN clustering algorithm. Infrared Laser Eng. 2017, 46, 528001. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.; Sander, J. OPTICS: Ordering points to identify the clustering structure. SIGMOD 1999. In Proceedings of the Proceedings ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 49–60. [Google Scholar]
- Hinneburg, A.; Keim, D.A. A general approach to clustering in large databases with noise. Knowl. Inf. Syst. 2003, 5, 387–415. [Google Scholar] [CrossRef]
- Hinneburg, A.; Gabriel, H.H. DENCLUE 2.0: Fast Clustering Based on Kernel Density Estimation. In Proceedings of the Advances in Intelligent Data Analysis VII, 7th International Symposium on Intelligent Data Analysis, IDA 2007, Ljubljana, Slovenia, 6–8 September 2007; Volume 4723, pp. 70–80. [Google Scholar]
- Yang, Y.; Cai, J.; Yang, H.; Zhang, J.; Zhao, X. TAD: A trajectory clustering algorithm based on spatial-temporal density analysis. Expert Syst. Appl. 2020, 139, 112846. [Google Scholar] [CrossRef]
- Gao, Y.; Zheng, B.; Chen, G.; Li, Q. Algorithms for constrainedk-nearest neighbor queries over moving object trajectories. Geoinformatica 2010, 14, 241–276. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Valladares, N. A GPU approach to subtrajectory clustering using the Fréchet distance. In Proceedings of the SIGSPATIAL 2012 International Conference on Advances in Geographic Information Systems (formerly known as GIS), SIGSPATIAL’12, Redondo Beach, CA, USA, 7–9 November 2012; pp. 259–268. [Google Scholar]
- Deng, Z.; Hu, Y.; Zhu, M.; Huang, X.; Du, B. A scalable and fast OPTICS for clustering trajectory big data. Clust. Comput. 2015, 18, 549–562. [Google Scholar] [CrossRef]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A review of moving object trajectory clustering algorithms. Artif. Intell. Rev. 2017, 47, 123–144. [Google Scholar] [CrossRef]
- Xiao, X.; Zheng, Y.; Luo, Q.; Xie, X. Finding similar users using category-based location history. In Proceedings of the 18th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems, ACM-GIS 2010, San Jose, CA, USA, 3–5 November 2010; pp. 442–445. [Google Scholar]
- Ying, J.J.C.; Lee, W.C.; Weng, T.C.; Tseng, V.S. Semantic trajectory mining for location prediction. In Proceedings of the 19th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems, ACM-GIS 2011, Chicago, IL, USA, 1–4 November 2011; pp. 34–43. [Google Scholar]
- Liu, S.L.Y.; Ni, L.M. Towards Mobility-based Clustering. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 919–928. [Google Scholar]
- Andrienko, G.; Andrienko, N.; Fuchs, G.; Garcia, J.M.C. Clustering Trajectories by Relevant Parts for Air Traffic Analysis. IEEE Trans. Vis. Comput. Graph. 2018, 24, 34–44. [Google Scholar] [CrossRef]
- Olive, X.; Morio, J. Trajectory Clustering of Air Traffic Flows around Airports. Aerosp. Sci. Technol. 2019, 84, 776–781. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Kreveld, M.J.V. Computing longest duration flocks in trajectory data. In Proceedings of the 14th ACM International Symposium on Geographic Information Systems, ACM-GIS 2006, Arlington, VA, USA, 10–11 November 2006. [Google Scholar]
- Jeung, H.; Yiu, M.L.; Zhou, X.; Jensen, C.S.; Shen, H.T. Discovery of convoys in trajectory databases. Proc. VLDB Endow. 2008, 1, 1068–1080. [Google Scholar] [CrossRef]
- Zhenhui, L.; Bolin, D.; Han, J. Swarm: Mining relaxed temporal moving object clusters. Proc. VLDB Endow. 2010, 3, 723–734. [Google Scholar]
- Kai, Z.; Yu, Z.; Yuan, N.J.; Shang, S. On Discovery of Gathering Patterns from Trajectories. In Proceedings of the 29th IEEE International Conference on Data Engineering, ICDE 2013, Brisbane, Australia, 8–12 April 2013; pp. 242–253. [Google Scholar]
- Wang, Z.; He, S.Y.; Leung, Y. Applying mobile phone data to travel behaviour research: A literature review. Travel Behav. Soc. 2017, 11, 141–155. [Google Scholar] [CrossRef]
- Fan, C.; Cavallaro, A. Detecting Group Interactions by Online Association of Trajectory Data. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1754–1758. [Google Scholar]
- Zhang, J.; Li, J.; Wang, S.; Liu, Z.; Yuan, Q.; Yang, F. On Retrieving Moving Objects Gathering Patterns from Trajectory Data via Spatio-temporal Graph. In Proceedings of the 2014 IEEE International Congress on Big Data, Anchorage, AK, USA, 27 June–2 July 2014; pp. 390–397. [Google Scholar]
- Puntheeranurak, S.; Shein, T.T.; Imamura, M. Efficient Discovery of Traveling Companion from Evolving Trajectory Data Stream. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference, Tokyo, Japan, 23–27 July 2018; Volume 1, pp. 448–453. [Google Scholar]
- Zhu, M.; Chen, L.; Wang, J.; Wang, X.; Han, Y. A Service-Friendly Approach to Discover Traveling Companions Based on ANPR Data Stream. In Proceedings of the IEEE International Conference on Services Computing, SCC 2016, San Francisco, CA, USA, 27 June–2 July 2016; pp. 171–178. [Google Scholar]
- Xia, D.; Lu, X.; Li, H.; Wang, W.; Li, Y.; Zhang, Z. A MapReduce-Based Parallel Frequent Pattern Growth Algorithm for Spatiotemporal Association Analysis of Mobile Trajectory Big Data. Complexity 2018, 2018, 2818251:1–2818251:16. [Google Scholar] [CrossRef]
- Wen-Bo, H.U.; Huang, W.; Guo-Chao, H.U. Trajectory Adjoint Pattern Analysis Based on OPTICS Clustering and Association Analysis. Comput. Mod. 2017. (In Chinese) [Google Scholar] [CrossRef]
- Albadwi, A.; Long, Z.; Zhang, Z.; Alhabib, M.; Alsabahi, K. A Novel Integrated Approach for Companion Vehicle Discovery Based on Frequent Itemset Mining on Spark. Arab. J. Sci. Eng. 2019, 44, 9517–9527. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W. Mining interesting locations and travel sequences from GPS trajectories. In Proceedings of the International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 791–800. [Google Scholar]
- Zheng, Y.; Li, Q.; Chen, Y.; Xie, X.; Ma, W. Understanding mobility based on GPS data. In Proceedings of the Ubicomp: Ubiquitous Computing, International Conference, Ubicomp, Seoul, Korea, 21–24 September 2008; pp. 312–321. [Google Scholar]
- Zheng, Y.; Xie, X.; Ma, W. GeoLife: A Collaborative Social Networking Service among User, location and trajectory. IEEE Data(base) Eng. Bull. 2010, 33, 32–39. [Google Scholar]
| Data_Source | Time | User_ID | Latitude | Longitude |
|---|---|---|---|---|
| Traveling User Dataset | 2014-11-16 14:53:56 | XXXXXXXXXXX | 4X.XXX627 | 8X.XXX317 |
| GeolifeV1.3 | 2009-04-09 18:28:10 | u3 | 39.999966 | 116.327415 |
| Data Source Type | Scenarios Names | Scenarios Description | Filtering Rules |
|---|---|---|---|
| Breif Contact | There is a small amount of close contact in the total record of A or B within a small area. | The number of pseudo-accompanying records is small and the total number of records is relatively small. If either is less than the relative threshold, the two objects are filtered. | |
| Traveling Users Data | No-contact | There is almost no close contact in the total record of A or B within a small area. | Pseudo-accompanying cases account for a so small proportion but the distance between the central geographic location of two objects is within the signal strength range of a base station. |
| Geolife | Breif Encounter | A and B have frequent contacts in a small area within a short-term period within a small area. | The time span of the accompanying records is short-term. The directions of these moving objects change after these records. There is no accompanying record for a long-term period. |
| Parameters | Description | Parameters | Description |
|---|---|---|---|
| the distance threshold in HDBSCAN | the minimal clustered number for location clustering | ||
| the minimal clustered number for time clustering | min_sup | the minimal support threshold for FP-growth | |
| min_conf | the minimal confident threshold for FP-growth | the minimal frequency threshold for the records number | |
| the minimal distance threshold between two records | the maximal time span threshold between two records | ||
| minimal records promotion threshold | metric | distance formula |
| min_conf | [0, 0.2] | [0.2, 0.4] | [0.4, 0.6] | [0.6, 0.8] | [0.8, 1.0] |
|---|---|---|---|---|---|
| Confidence Level | low | relatively low | medium | relatively high | high |
| Source | Data Set | Duration2 | Duration3 | Duration4 | Total Duration | Average Duration for D1/D2 | TC# | Total TC Users# |
|---|---|---|---|---|---|---|---|---|
| D1 | Set1 | 5724.4 | 2.1 | 50.3 | 5776.8 | 7 | 14 | |
| Set2 | 5572 | 2.1 | 55.5 | 5629.6 | 2 | 6 | ||
| Set3 | 5421.9 | 1.7 | 1.5 | 5425.1 | 1 | 2 | ||
| Set4 | 5381.5 | 2.8 | 145.8 | 5530.1 | 1 | 2 | ||
| Set5 | 5961.8 | 0.5 | 0 | 5962.3 | 5664.78 | 0 | 0 | |
| D2 | Geo1 | 3192.2 | 0.1 | 0 | 3192.3 | 0 | 0 | |
| Geo2 | 2428 | 0.2 | 0 | 2428.2 | 1 | 2 | ||
| Geo3 | 2702.8 | 0.2 | 0 | 2703 | 1 | 4 | ||
| Geo4 | 2890.3 | 0.2 | 0 | 2890.5 | 1 | 2 | ||
| Geo5 | 3023.3 | 0.2 | 0 | 3023.5 | 2847.5 | 1 | 3 | |
| D3 | Sim1 | 413.4 | 0.2 | 11.8 | 425.4 | 425.4 | 1 | 3 |
| Source | Data Set | Data Size | Number of Records | Duration |
|---|---|---|---|---|
| D1 | Set1 | 51,256 KB | 800,000 | 24H |
| Set2 | 51,246 KB | 800,000 | 24H | |
| Set3 | 50,880 KB | 800,000 | 10H | |
| Set4 | 50,930 KB | 800,000 | 8H | |
| Set5 | 29,469 KB | 464,746 | 5H | |
| D2 | Geo1 | 41,080 KB | 800,000 | 17D |
| Geo2 | 41,496 KB | 800,000 | 30D | |
| Geo3 | 41,874 KB | 800,000 | 17D | |
| Geo4 | 41,927 KB | 800,000 | 22D | |
| Geo5 | 41,927 KB | 800,000 | 31D | |
| D3 | Sim1 | 7848 KB | 125,367 | 80M |
| Source | min_sup | min_conf | ||||||
|---|---|---|---|---|---|---|---|---|
| D1 | 500 | 4 | 4 | 200 | 120 | 0.6 | 0.8 | 0.5 |
| D2 | 5 | 4 | 4 | 5 | 5 | 0.6 | 0.8 | - |
| D3 | 500 | 4 | 4 | 200 | 120 | 0.6 | 0.8 | 0.5 |
| Data Source | Time | User_ID | Latitude | Longitude |
|---|---|---|---|---|
| D2 | 2009-04-09 18:28:25 | u0 | 39.999912 | 116.32751 |
| 2009-04-09 18:28:25 | u3 | 39.999912 | 116.32751 | |
| 2009-04-09 18:28:27 | u30 | 40.000008 | 116.327446 | |
| 2009-04-09 18:28:28 | u4 | 39.99983 | 116.32712 | |
| 2009-04-09 18:28:29 | u30 | 40.000008 | 116.32754 | |
| 2009-04-09 18:28:30 | u30 | 39.999996 | 116.32745 | |
| 2009-04-09 18:28:30 | u3 | 39.999924 | 116.327484 | |
| 2009-04-09 18:28:30 | u0 | 39.999924 | 116.327484 | |
| 2009-04-09 18:28:31 | u30 | 39.99999 | 116.32748 | |
| 2009-04-09 18:28:33 | u4 | 39.99989 | 116.32744 | |
| 2009-04-09 18:28:35 | u0 | 39.9999 | 116.32745 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, R.; Wang, F.; Chen, S.; Zhao, S. GroupSeeker: An Applicable Framework for Travel Companion Discovery from Vast Trajectory Data. ISPRS Int. J. Geo-Inf. 2020, 9, 404. https://doi.org/10.3390/ijgi9060404
Yao R, Wang F, Chen S, Zhao S. GroupSeeker: An Applicable Framework for Travel Companion Discovery from Vast Trajectory Data. ISPRS International Journal of Geo-Information. 2020; 9(6):404. https://doi.org/10.3390/ijgi9060404
Chicago/Turabian StyleYao, Ruihong, Fei Wang, Shuhui Chen, and Shuang Zhao. 2020. "GroupSeeker: An Applicable Framework for Travel Companion Discovery from Vast Trajectory Data" ISPRS International Journal of Geo-Information 9, no. 6: 404. https://doi.org/10.3390/ijgi9060404
APA StyleYao, R., Wang, F., Chen, S., & Zhao, S. (2020). GroupSeeker: An Applicable Framework for Travel Companion Discovery from Vast Trajectory Data. ISPRS International Journal of Geo-Information, 9(6), 404. https://doi.org/10.3390/ijgi9060404




