1. Introduction
The river network is the skeleton element in multi-scale topographic maps. Due to scale sensitivity, hydrographic data requires frequent generalization to maintain the main and typical characteristics of the river network [
1]. Generally, dendritic river features are characterized by distinct hierarchical and fractal features [
2,
3], and coding is an effective approach for revealing the spatial structure of river features and the order of each stream. Therefore, the coding of dendritic river features has always been a focal point for map generalization studies [
4,
5].
Horton [
6] proposed the classic Horton coding system based on the natural river property, in which water flows under the effects of gravity. The Horton coding system distinguishes the order of each stream and provides an intuitive reflection of the subtree depth of the stream, which makes it a powerful tool in quantitative analyses of the structural features of river networks. For example, Moharir et al. [
7] and Harish et al. [
8] combined Horton’s stream ordering system with remote-sensing images to analyze the topographic features of watersheds. Most of all, since Horton’s coding system can be used to distinguish the stream order, the coding system was used for stream selection in the generalization of river systems [
9].
Strahler [
10] further developed Horton’s theories to establish the Strahler coding system, which is based on river segments. Strahler’s coding system reflects the sizes and morphological features of substreams, and it is useful for highlighting the dendritic features of a river network. Stanislawski et al. [
11] used the Strahler coding system as a criterion by which to identify the importance of a reach during stream generalization and selection. Since the reach-based coding system is a better fit for organizing river networks in computers, Shreve [
12], Horsfield and Cumming [
13] proposed their own hydrologic coding systems based on Strahler’s coding system to reflect features such as the number of tributaries and differences in the density of a river network. The aforementioned coding systems are widely applied in hydrographic analyses and river generalizations. However, these systems generally use a top-down approach, wherein streams are ordered from the end of a river system (i.e., river source) towards the main stem (i.e., estuary). When these coding systems are used to process large dendritic river systems, the resulting stream codes are not very suitable for highlighting the hierarchies of a river system, which are formed by catchment relationships.
Gravelius [
14] and Hack [
15] proposed a classic definition for the stream order according to catchment relationships. Based on this definition, an automated bottom-up hydrologic coding system was developed for dendritic river systems [
16,
17]. In the method, river entities are treated as elements, and the stream hierarchy is accounted for in the coding of the stream order. Compared to Horton’s stream coding system, this coding system cannot directly indicate the subtree depth of a stream, yet it does provide a better indication of the stream hierarchies produced by catchment relationships. In short, during stream selection and generalization, Horton’s stream coding system is better suited for dendritic river systems that have topologically deep structures, whereas the Gravelius [
14] and Hack [
15] stream coding system is better suited for topologically shallow dendritic river systems with a uniform distribution of tributaries.
In the traditional river selection method for topographic map generalization, the aforementioned two coding systems were used individually, scholars either choose a top-down approach or a bottom-up approach. However, the spatial distribution structure of river networks is complex and diverse in actual data, it is difficult for a single code system to describe the importance of each stream during the selection operation. As a result, some river subtrees can’t keep the original spatial distribution characteristics after automatic selection. Therefore, by combining the advantages of both of these methods, a selection method of dendritic river network based on hybrid coding is proposed in this paper.
The paper includes five sections.
Section 2 introduces the existing top-down and bottom-up coding methods, and simultaneously, their shortcomings are analyzed. The proposed selection method for dendritic river networks based on hybrid coding is explained in detail in
Section 3.
Section 4 explains the experiments and then presents and analyzes the results, followed by the discussions and conclusions in
Section 5.
2. Related Works
2.1. Current Stream Coding Methods
2.1.1. Top-Down Coding System
There are two classical top-down coding systems. One is Horton’s stream coding system, and the other is Strahler’s stream coding system.
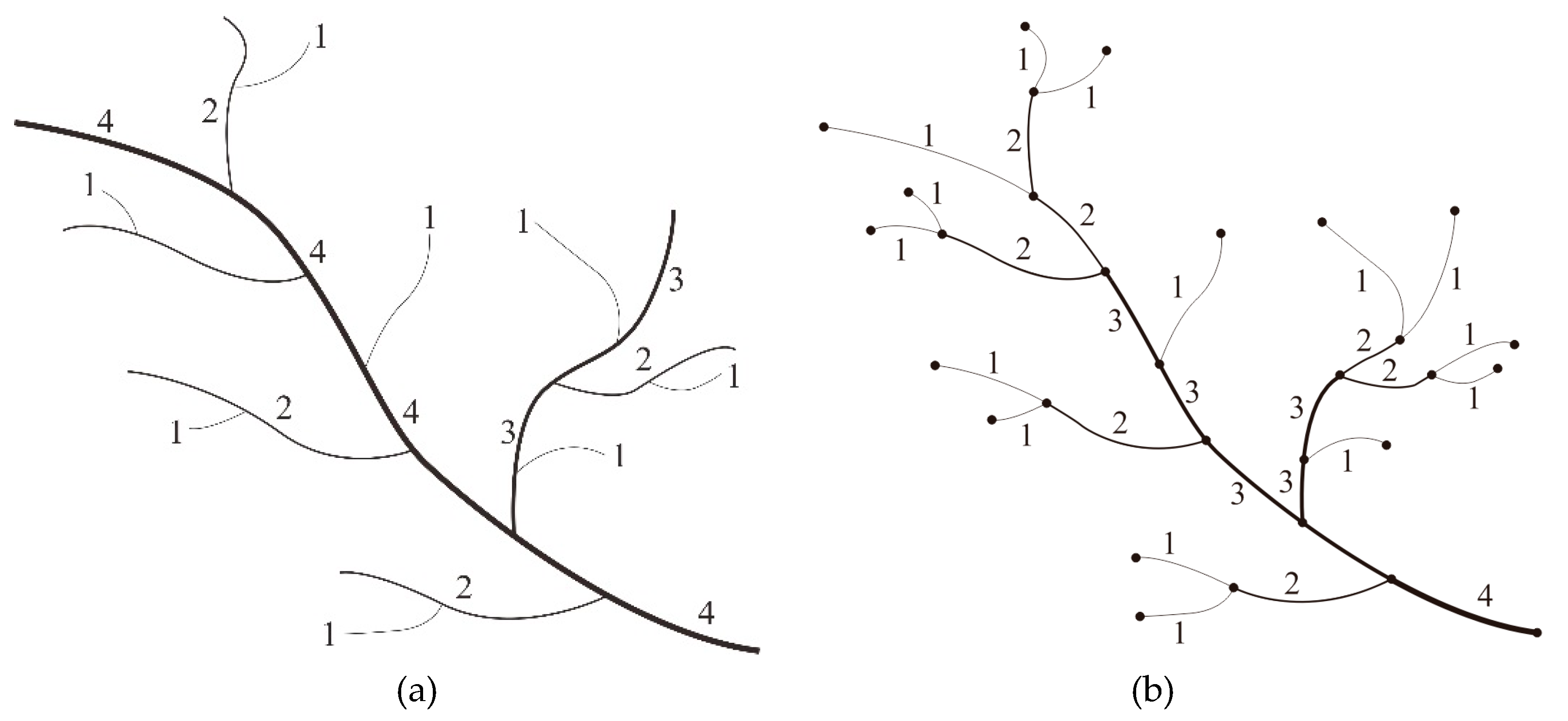
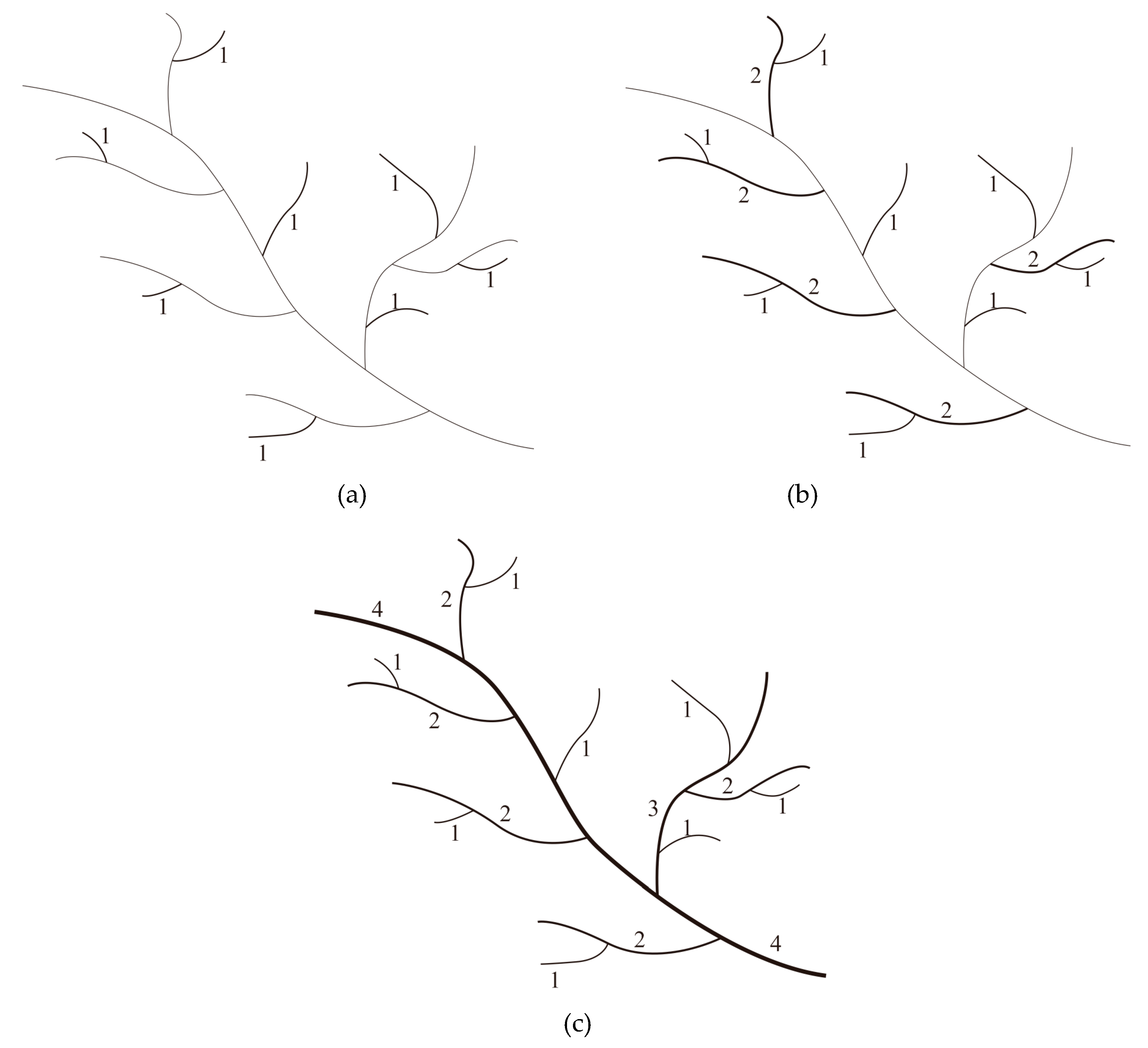
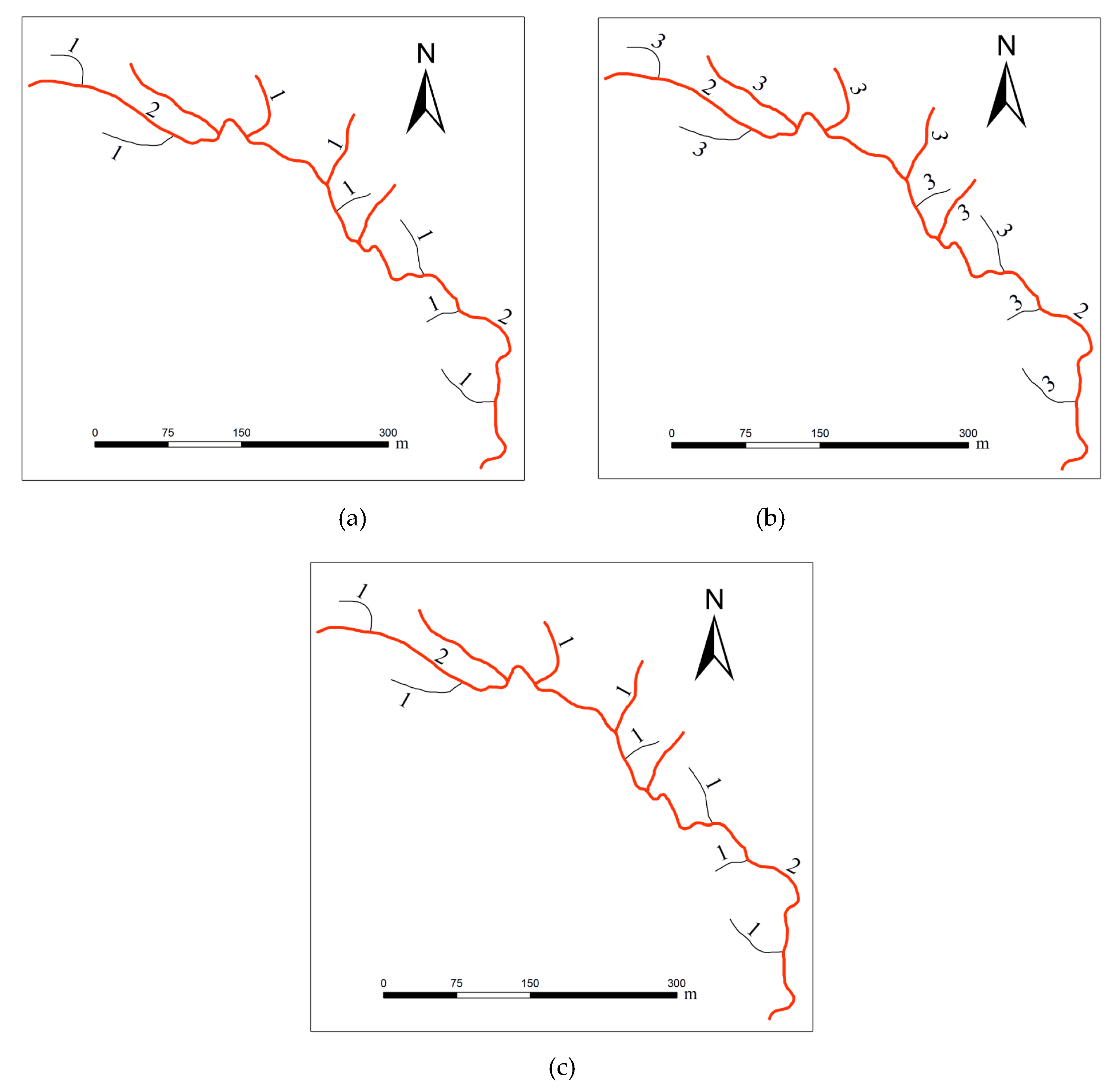
The objective of Horton’s coding system is to categorize river entities in different watersheds that have similar shapes and structural features into the same order. To this end, branchless terminal tributaries in a dendritic river feature are assigned an order of one in the Horton stream system. Based on the direction of each stream, rivers that only contain first-order streams are defined as second-order streams, while rivers that contain first- and second-order streams are defined as third-order streams. In this way, the main stem of a river system, which has the greatest number of tributaries, is defined as the highest-order stream (
nth-order), as shown in
Figure 1a.
Strahler stream ordering is performed on a dendritic river features based on river segments. River segments that are connected to river source nodes are defined as first-order reaches, while reaches formed by the convergence of two or more first-order reaches have a stream order of 2. In this way, any reach formed by two or more nth-order reaches has a stream order of n + 1. All of the reaches are traversed until all of the streams have been coded. The Strahler codes of a river system are then obtained, as shown in
Figure 1b.
2.1.2. Bottom-Up Coding System
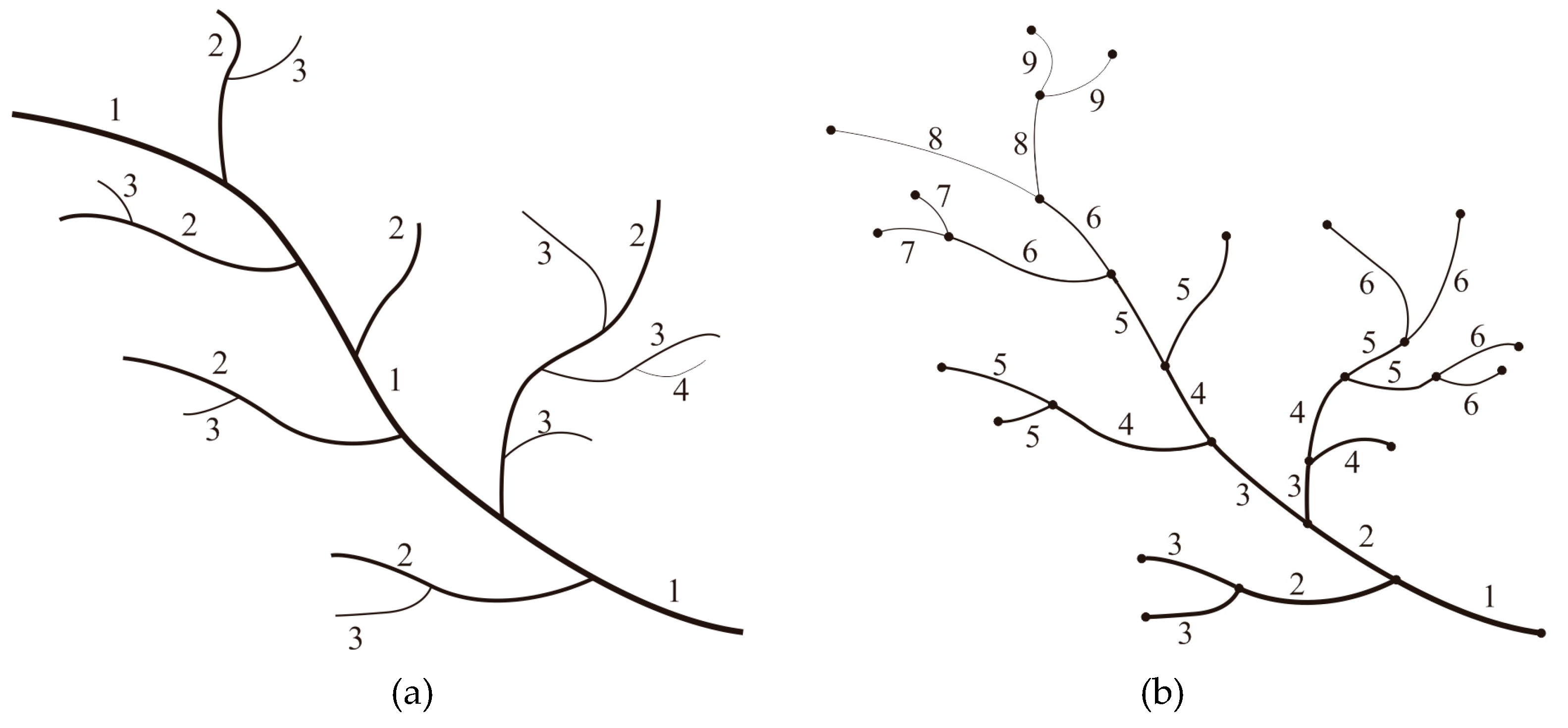
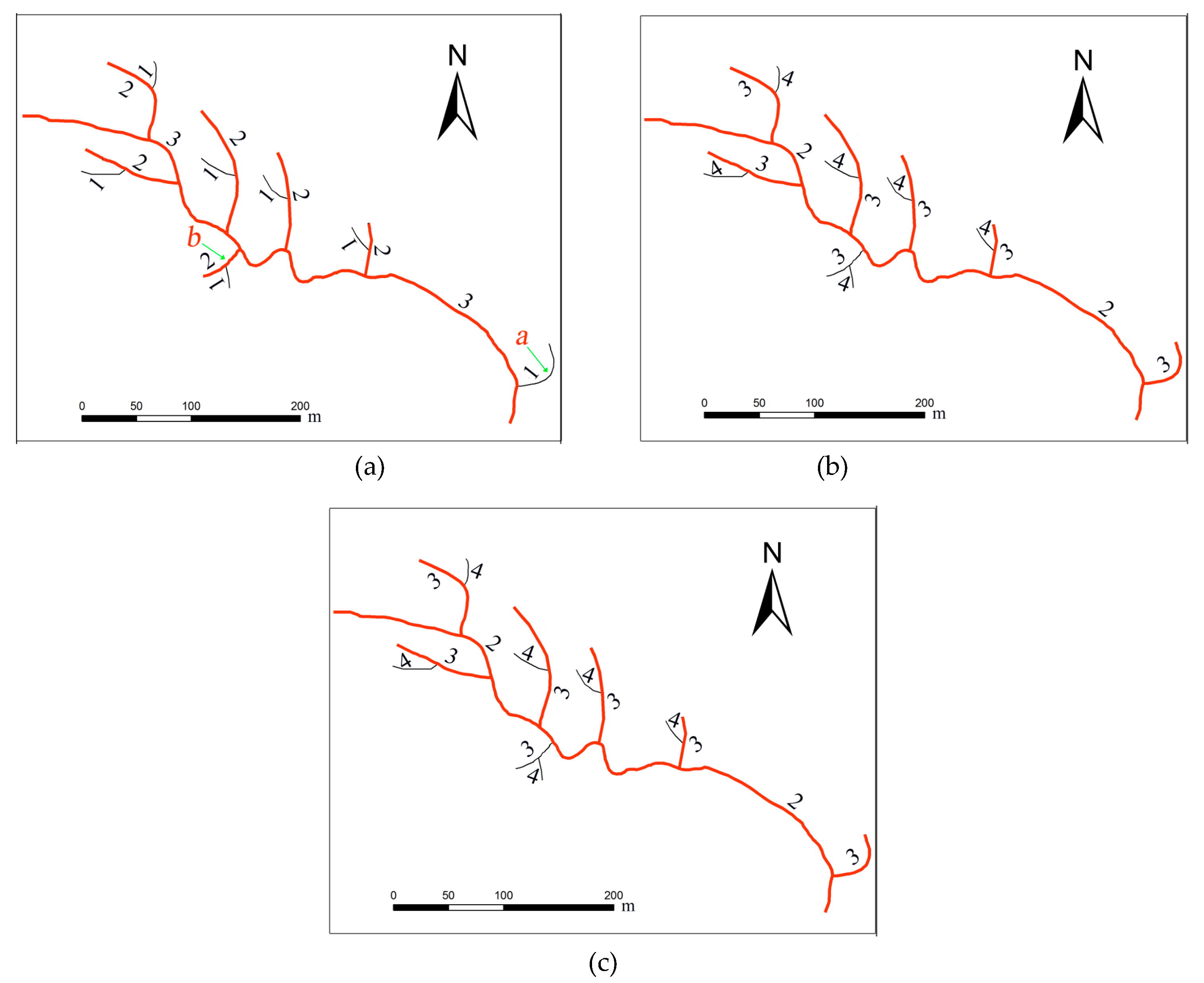
Just like the top-down coding system, there are two kinds of bottom-up coding systems. One is Hack’s stream coding system based on river streams, and the other is Marani’s stream coding system based on river segments. A bottom-up coding system was proposed and implemented [
14,
15,
16,
17] through a classic definition of the stream order, in which the main stem is defined as a first-order stream, while the tributaries connected to the main stem are second-order streams. In this way, branchless tributaries at the end of a river system are defined as the highest-order streams, as shown in
Figure 2a. This definition of the stream order clearly defines the hierarchies formed by catchment relationships in a river system. Marani et al. [
18] proposed a coding system based on river segments, which is also known as the topological diameter coding method [
16], as shown in
Figure 2b.
2.2. Inadequacies of the Current Methods
2.2.1. Inadequacies of the Top-Down Approach in River Selection
The top-down coding approach is often used in river generalization to reflect the importance of a river [
1,
11]. Compared to Strahler’s coding system, Horton’s coding system has more advantages in expressing the connectivity of a river because the unit in Horton’s coding is river entities.
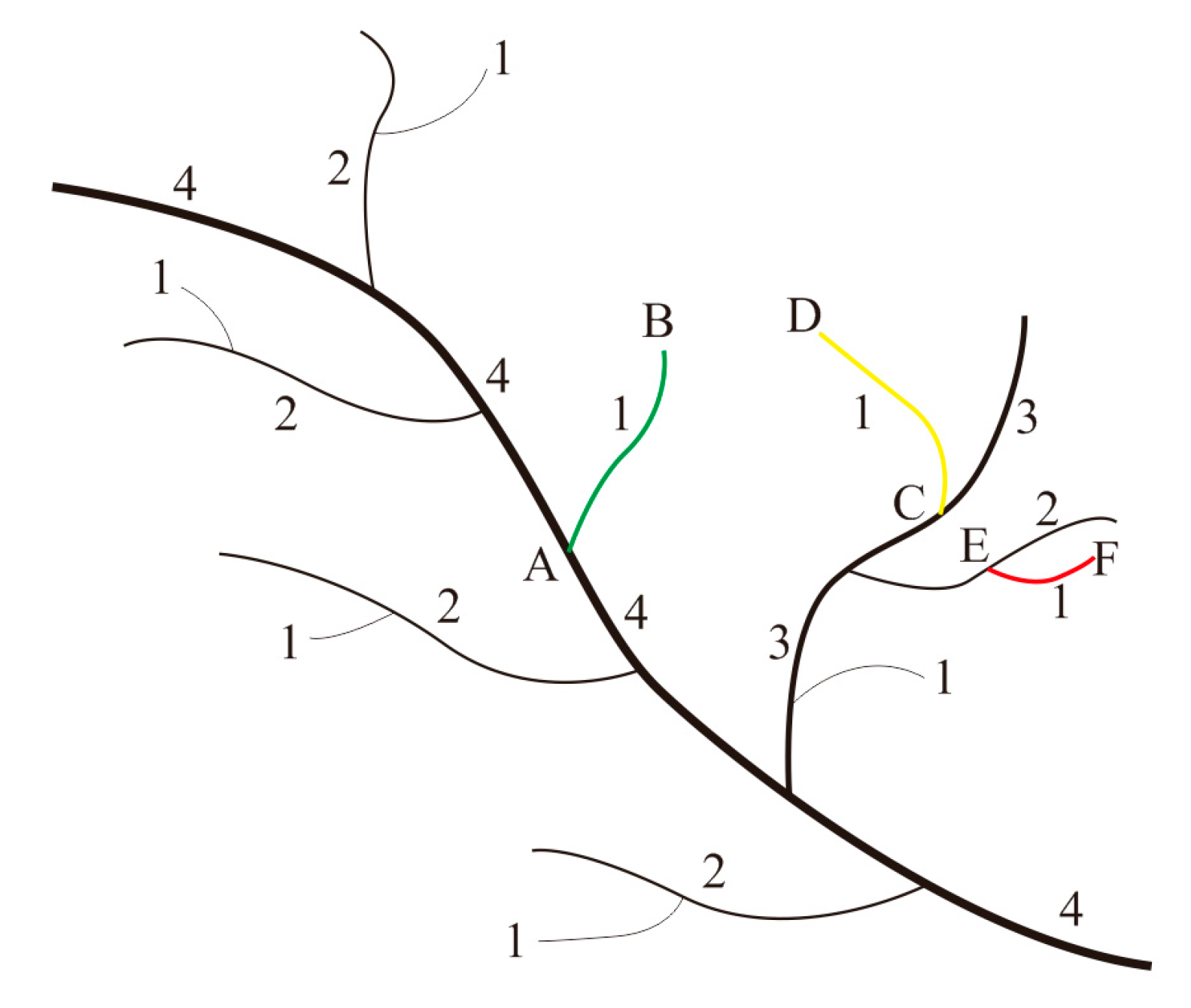
Figure 1a shows that Horton’s coding system (which is based on river entities) is an excellent method for distinguishing the stream order and describing the subtree depth of a stream. However, since Horton’s coding system uses a top-down approach, tributary entities that have the same Horton order in large river systems may not actually have the same stream order. In
Figure 3, the AB (green), CD (yellow) and EF (red) streams all have a Horton code of 1, despite having different stream orders in reality. Stream AB is connected to the main stem and is, therefore, a first-order stream; stream CD is connected to a first-order tributary and is, therefore, a second-order stream; and stream EF is connected to a second-order tributary and is, therefore, a third-order stream. Hence, river entities that have the same Horton stream order cannot be compared to each other, and the orders assigned by this system do not accurately reflect the stream hierarchies formed by the catchment relationships.
2.2.2. Inadequacies of the Bottom-Up Approach in River Selection
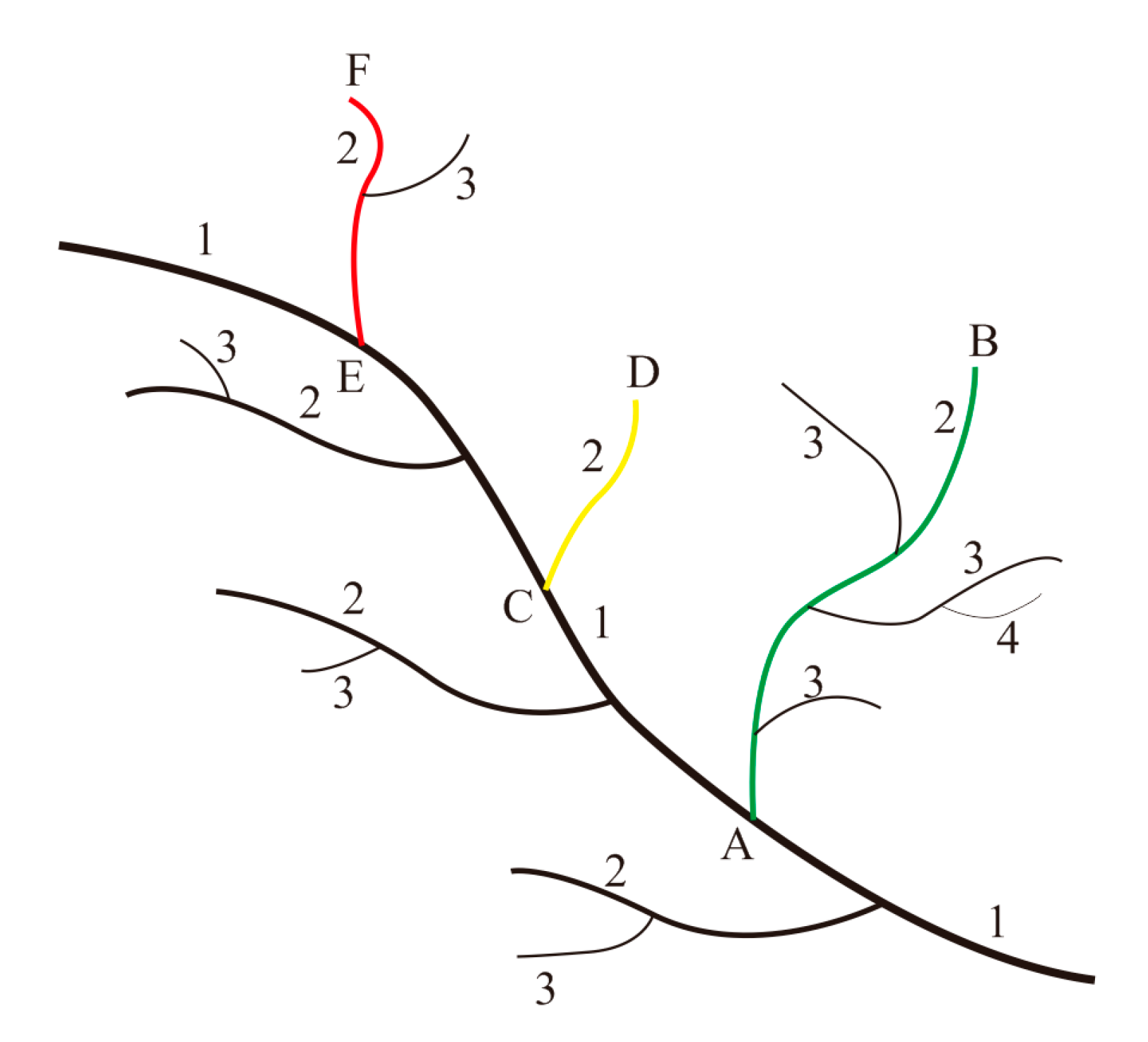
We still focus on the coding approach based on river streams, which code the streams rely on in the catchment relationships of each river [
15,
16] are shown in
Figure 4. However, since the coding system uses a top-down approach, tributary entities that have the same coding order in large river systems may not actually describe the subtree depth of a stream. In
Figure 4, the AB (green), CD (yellow) and EF (red) streams all have a code of two, despite their deep structures being different in reality.
3. Selection Method for Dendritic River Networks Based on Hybrid Coding
A selection method for dendritic river networks based on hybrid coding is proposed, and it consists of three parts: (1) the dendritic river network is coded by classical top-down Horton coding; (2) directed topology trees are constructed to organize the river network data, while stroke connections are calculated to code the river network in the bottom-up approach; and (3) the river network is marked through hybrid usage of the top-down approach and bottom-up approach, after which a selection algorithm for dendritic river features based on hybrid coding is put forward.
3.1. Top-Down Coding for Dendritic River Features
The first step of hybrid coding is to code the stream in the dendritic river network by top-down Horton coding. Terminal tributaries connected to river sources are assigned an order of 1. Based on the direction of each stream, streams that only contain first-order streams are defined as second-order streams and are assigned an order of 2. In this way, any stream containing nth-order streams has an order of n + 1. The main stem of a river system, which has the greatest number of tributaries, is defined as the highest-order stream (
nth-order), as depicted in
Figure 5. The detailed process of Horton coding has been described in existing research [
6,
9,
19]; thus, it is not covered here.
3.2. Bottom-Up Coding for Dendritic River Features
In fact, rivers are usually stored as a collection of reach elements in original map data. Regarding selection, it is important that a stream be processed as a whole. To code a stream in a dendritic river network by the bottom-up approach, directed topology trees are constructed to organize the river network data, and stroke connections are calculated from estuaries to track the main stream in this paper [
17].
3.2.1. Directed Topology Trees and Stroke Connections
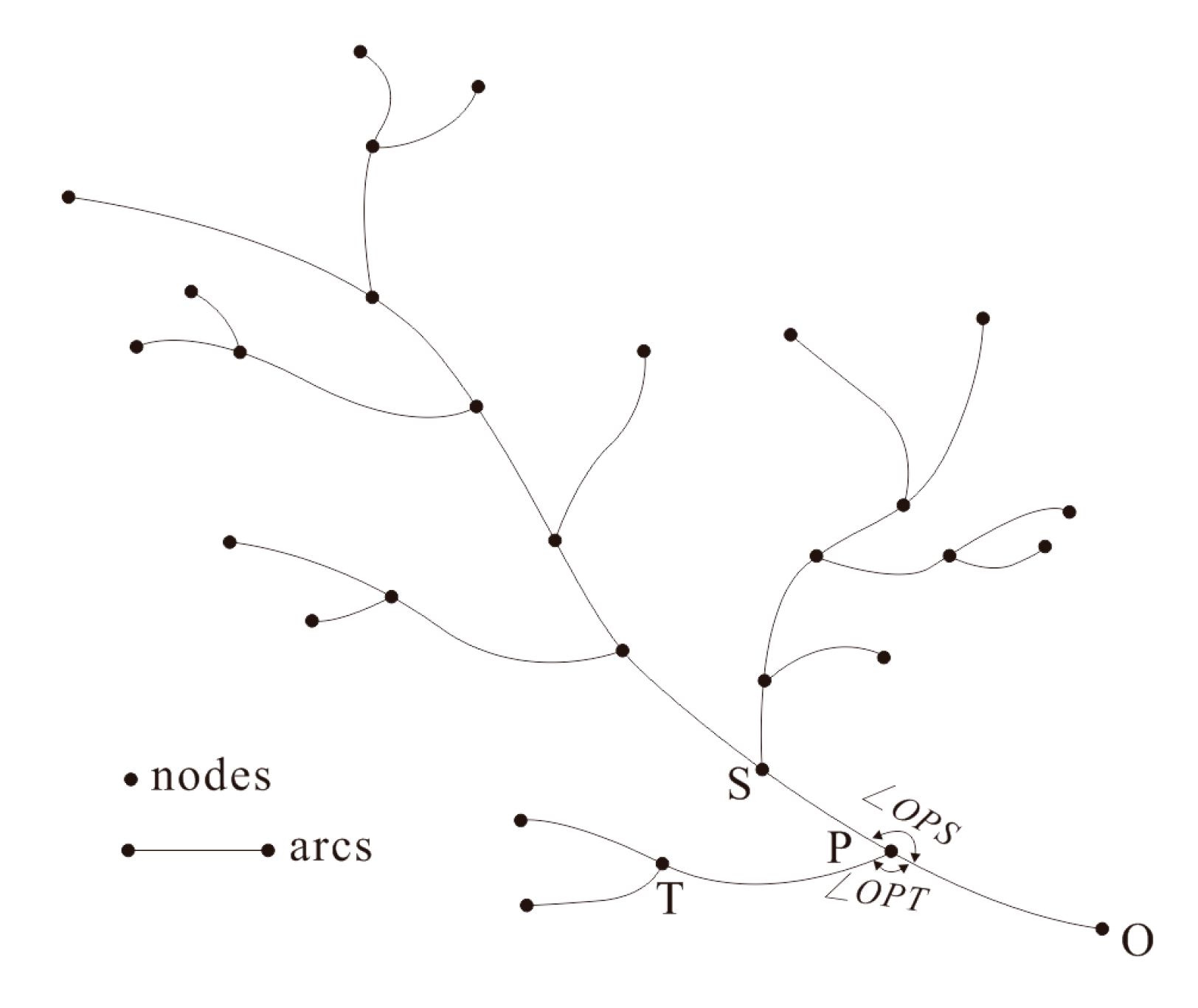
Topological structural diagrams of dendritic river features that contain flow directions are also known as DTTs [
20], which are collections of nodes and arcs that record information such as the degree, out-degree and in-degree of each node [
21]. The direction of each arc (edge) is defined as the direction from the source node to the terminal node. In addition, DTTs also contain semantic (e.g., name and type) and geometric (e.g., length and width) stream information.
The recognition of main stems is an important step in the coding of river systems. Some scholars have proposed that river reaches could be connected to form river entities using stream lengths and basin areas [
16]. However, these methods do not account for the flow direction characteristics of a stream. Thomson et al. [
22,
23] proposed that the principle of connectivity in Gestalt psychology could be used to construct strokes for river systems based on the semantics, geometries, topologies and directions of their streams. Excellent results have been obtained using this approach. In our method, the stroke connections of a dendritic river feature are iteratively calculated using DTTs based on the principles of semantic consistency, directional consistency and length prioritization (i.e., longer is better). The main stem is then identified on this basis. The procedures for the calculation of stroke connections and main stem identification are described below, with
Figure 6 being used as an illustrative example:
Step 1: In most cases, the downstream reaches of a dendritic river feature only have one estuary. Therefore, we have chosen the estuary as the origin (Point O) from which the stroke connections are traced. The arc associated with the estuary is the tracing arc (Arc OP), and the other node of this arc (Point P) is the tracing node.
Step 2: The arcs associated with P are incorporated into the set of candidate arcs for stroke connection R {PS, PT}. The angles of these arcs with respect to OP (i.e., {∠OPS, ∠OPT}, respectively) are also calculated.
Step 3: The arc in set R that forms a stroke with OP is selected according to the principles of semantic consistency, directional consistency and length prioritization. In this case, S is selected to form OS, and S is now the tracing node.
Step 4: Stroke connections are continuously calculated and traced according to the methods of Steps 2 and 3 until the stream has been traced to its source. The resulting stroke is then the main stem of the estuary.
Step 5: All of the stroke connections to the arc associated with the river source are then calculated to obtain the tributaries of the main stem.
Step 6: All of the stroke connections associated with the aforementioned tributaries are calculated until all of the arcs in the DTT have been calculated. The calculation of stroke connections terminates at this point.
3.2.2. Procedures of Automated Bottom-Up Coding
The procedures of the automated coding method for dendritic river features are described below, with the river system shown in
Figure 7 being used as an illustrative example:
Step 1: Stroke connections are calculated from the estuary, O, until the main stem of the river system has been calculated. The main stem is assigned a code (order) of 1, as shown in
Figure 7a.
Step 2: All of the stroke connections associated with the arc of the main stem are calculated to obtain the tributaries of the main stem. These tributaries are assigned a code of 2, as shown in
Figure 7b.
Step 3: All of the stroke connections to the tributary arcs are calculated and coded. The final results of the stream ordering process are shown in
Figure 7c.
3.3. Selection Algorithm for Dendritic River Features Based on Hybrid Coding
3.3.1. Hybrid Coding
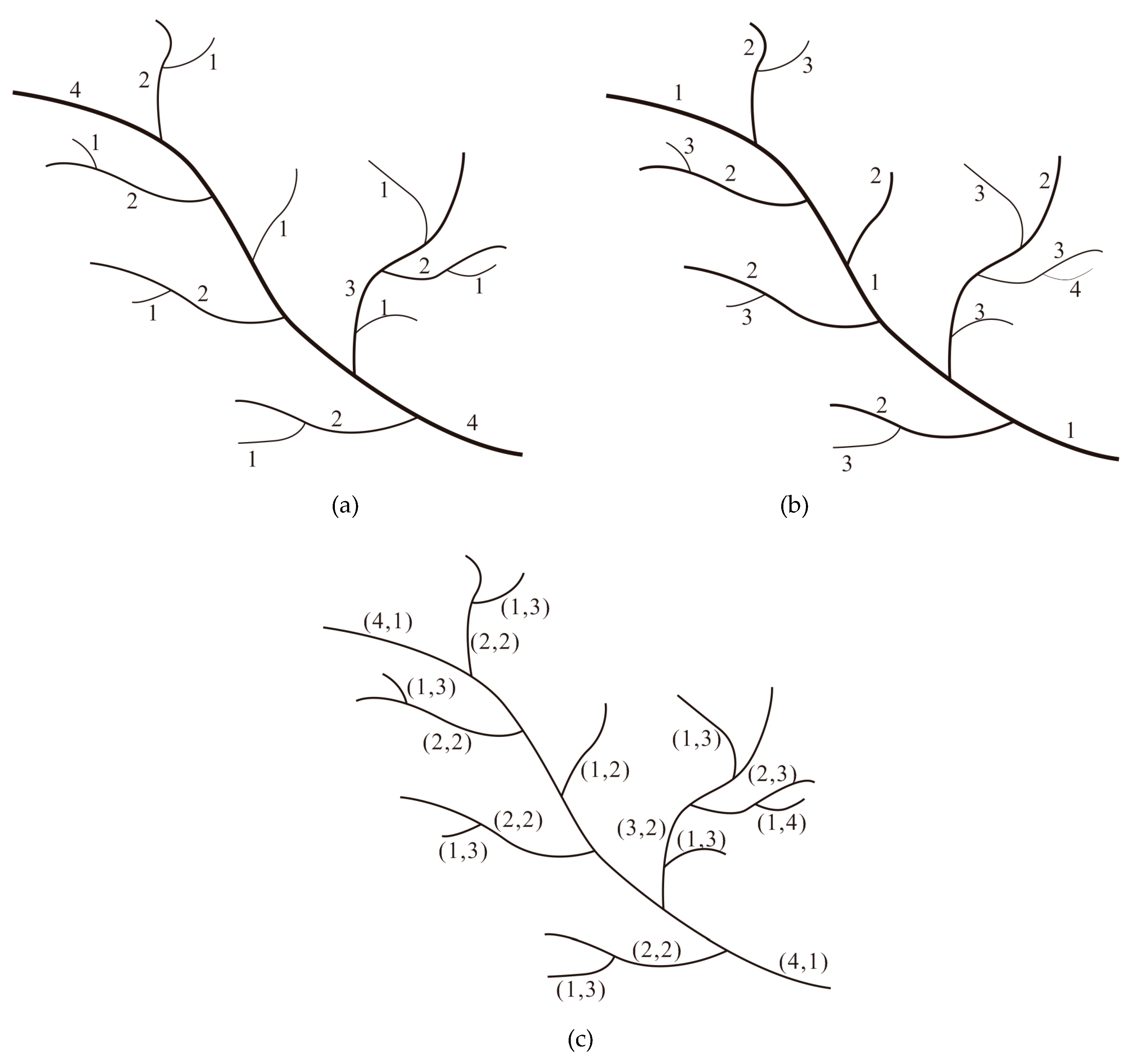
By combining the advantages of both coding methods, hybrid coding is proposed to describe the spatial characteristic of river networks. The basic idea is that any stream in a river network is marked through hybrid usage of the top-down approach and bottom-up approach, and the coding structure is described as (top-down coding, bottom-up coding), as shown in
Figure 8.
As can be seen from
Figure 8, the deep structure and hierarchical relationship can be described at the same time by hybrid coding.
3.3.2. Determination of the Dichotomy Threshold of Each Stream
According to the analysis in
Section 2.1, the information described by the two existing coding methods is different, which affects the judgment of the river network spatial structure. To make full use of the advantages of the two codes, the subtrees connected to the main stream of the river network are classified into different patterns.
First, the depth information of each stream (DS) is identified based on Horton’s coding, and the depth threshold (DT) is calculated on the basis of the variance of the depth information distribution to classify the streams into two categories. If DS > DT, the stream is a deep stream, which means that the stream is very important for maintaining the overall depth characteristics of the river network, and if DS ≤ DT, the stream is a shallow stream, which means that its importance in maintaining the overall depth characteristics is lesser.
The depth threshold (DT) is calculated by the Otsu’s method [
24], which is an effective algorithm for image segmentation and has been widely employed in various field applications. Let the depth distribution of a given river network be represented by
L levels
[1, 2, ,L]. The number of streams at level
i is denoted by
ni, and the total number of streams is represented by
N = n1 + n2 + + nL. Then, the probability distribution of each depth level is
pi= ni /
N.
Now, suppose that we dichotomize the depth into two classes,
C0 and
C1, by a threshold at level
k.
C0 denotes the depths of levels [1, … ,
k], and
C1 denotes the depths of levels [
k + 1, … ,
L]. Then the between-class variance is given by [
24]:
where
,
,
, and
are the probabilities of class occurrence and the class mean levels, respectively,
,
, and
.
The optimal threshold
k* is [
24]:
3.3.3. Classification of Dendritic River Networks
After the dichotomy of all streams is determined, each subtree connected to the main stream is classified into one of three patterns based on the spatial distribution and connection relationship of the two kinds of streams, as follows: (1) deep branch, which consists of deep streams and the shallow streams contained by these deep streams; (2) shallow branch, which consists of shallow streams or only of a deep stream and the shallow streams contained by this stream; and (3) modest branch, which consists of shallow streams without depth differences or among which the difference is 1. During the generalization process, the deep branches are coded using the top-down approach, the shallow branches are coded via the bottom-up approach, and the modest branches are coded by one of the aforementioned two approaches.
The classification is carried out based on the hybrid coding of each stream. The subtrees connected to the main stream can be extracted through bottom-up coding, and these streams are coded 2. Top-down coding is used for comparison with DT to classify the streams into the deep or shallow category, and subtrees are classified into different patterns based on the aforementioned classification rules.
3.3.4. Selection Algorithm
River selections are performed using the classic selection method proposed by Stanislawski et al. [
11]. The detailed procedure is as follows:
Step 1: The number of streams that should be retained is determined using the ‘Radical Law’ model [
25,
26],
, where
is the number of objects that can be shown at the target scale,
is the number of objects shown on the original map, and
and
are the scale denominators of the original and target maps, respectively.
Step 2: The river network is hybrid coded to describe the depth and hierarchy information of each stream, and then the depth threshold (DT) is calculated by Otsu’s method.
Step 3: The streams are classified into deep or shallow types, and the subtrees of the main stream are classified into deep, shallow and modest patterns based on the spatial characteristic and connection relationships of the streams.
Step 4: The deep branches are coded using the top-down approach, the shallow branches are coded via the bottom-up approach, and the modest branches are classified by one of the aforementioned two approaches to prepare the selection.
Step 5: The selection numbers are allocated unequally to each subtree based on the number of streams, , where is the number of streams shown at subtree i, is the total number of streams shown, is the number of streams at subtree i, and is the total number of streams across the whole river network.
Step 6: The selective principle is to preserve main streams and remove the tributaries. Specifically, for a subtree, selection starts from the main stream of the subtree and extends to the tributaries. Streams in the same order are selected according to their length information, and the longer streams are preserved.
Step 7: Because of the special structure of the modest branches with depth code 1, they are placed together and selected as a whole.
Step 8: Steps 6 and 7 are repeated until a sufficient number of streams (as defined by the square root model) have been selected, and then the selection algorithm ends.
4. Experiments and Analysis
4.1. Experimental Data and Environment
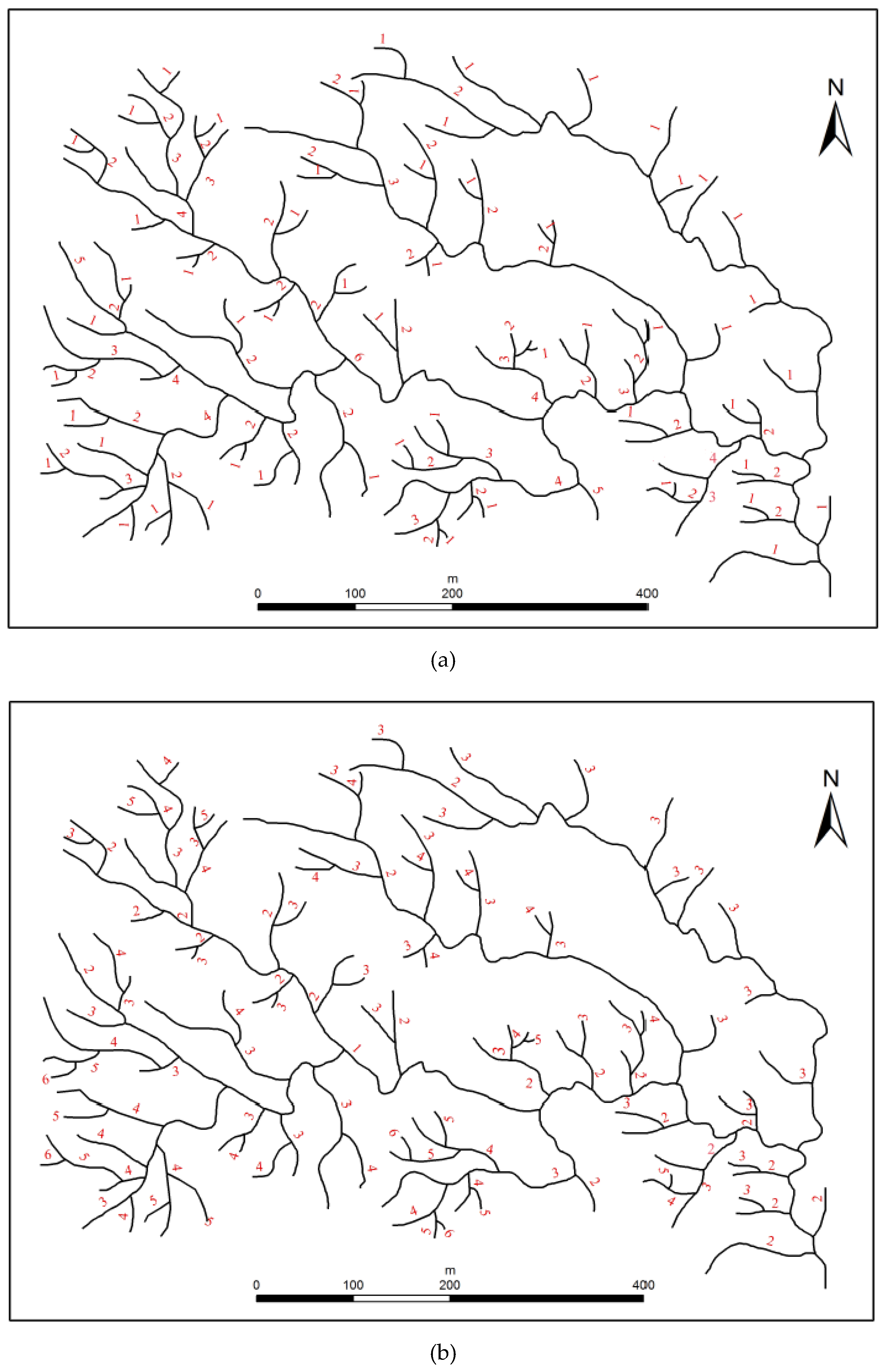
The hybrid coding method was embedded into the WJ-III mapping workstation developed by the Chinese Academy of Surveying and Mapping. The new stream coding method was experimentally validated via a comparison with the classic top-down coding method and bottom-up method. The experimental data correspond to part of a dendritic river feature in a city of Hubei Province in China. The original scale of these data is 1:100,000, and there is a total of 108 rivers in this dataset. The storage space of the experimental data is 55 KB. The hardware environment for this experiment runs on a Microsoft Windows 7 64-bit operating system equipped with an Intel Core i7-3770 running at 3.2 GHz, with 16 GB of RAM and a 1024 GB solid-state drive.
The experiment included two parts: first, coding the rivers in the same experimental area using three different coding methods to analyze their differences and characteristics; second, comparing the selection effect under three different coding methods via classifying of river subtrees in three typical areas.
The time consumed by the selection method based on river coding mainly includes three parts: data preparation time, river coding time and river selection time. For the same experimental area, the total time to complete the above three operations for each classical coding system is 8 s, and the total time based on the proposed method is 10 s.
4.2. Comparative Analysis of Each Coding Method
Figure 9 illustrates the coding results of the experimental river network obtained using three different coding methods, including (a) the top-down Horton’s coding method, (b) the bottom-up coding method and (c) the hybrid coding method. As depicted in
Figure 9, the ranges of the stream orders given by these three methods are identical, i.e., from 1 to 6. However, the spatial structural characteristics that they describe are different. (1) Horton coding coded the river network from the source to the estuary, so the depth information was recorded. For example, a stream that has a Horton stream order of 3 must contain a bifurcation of first-order and second-order tributaries, and the subtree depth of this stream is 3. (2) The bottom-up approach coded the river network from the estuary to the source, so the hierarchy formed by catchment relationships was recorded. For example, a stream that has a code of 2 must connect to the main stream, which is coded by 1. (3) The hybrid coding method combined the advantages of the aforementioned two coding methods, and the depth and hierarchy information of a stream can be read at the same time.
To further analyze the characteristics and differences of different coding methods, the number of streams corresponding to each stream order is shown in
Table 1.
As depicted in
Table 1, although the coding ranges of these two coding methods are identical, there are significant differences in the number of streams corresponding to each stream order. In the Horton method, the number of streams decreases with the stream order. Rivers with codes 1 and 2 at the boundary account for 82.4%, which means that the importance of these streams can be distinguished accurately by the coding. The distribution of streams corresponding to our coding method exhibits an n-type pattern, i.e., lower- and higher-order streams are fewer in number, whereas medium-order streams are greater in number, which makes it easy to judge the importance of the streams around the outside of river network but difficult to judge the streams in the middle.
In addition, a cross-check analysis was carried out in this paper. Taking Horton’s coding as the reference code, the numbers of streams with inverted codes and non-inverted codes in the bottom-up coding were recorded. As depicted in
Table 1, only 16.67% of the rivers are streams with inverted codes, which means that the comprehensive utilization of the two methods can’t be achieved through simple algebraic transformation but requires an in-depth analysis of the functions of the two methods in expressing different spatial structures.
4.3. Analyzing the Efficacy of Each Coding System in River Selection and Generalization
The target scale of river network generalization is 1:500,000. Therefore, 52 streams can be shown at the target scale based on the square root model. In addition, according to Otsu’s method [
24], for each depth level, the between-class variance was calculated. The results were as follows.
= 206.21,
= 222.25,
= 112.53,
= 41.84,
= 14.59, and
was the max value, so the depth threshold (DT) was set to 2. On the basis of the DT, 6 deep branches, 12 shallow branches and 4 modest branches were obtained.
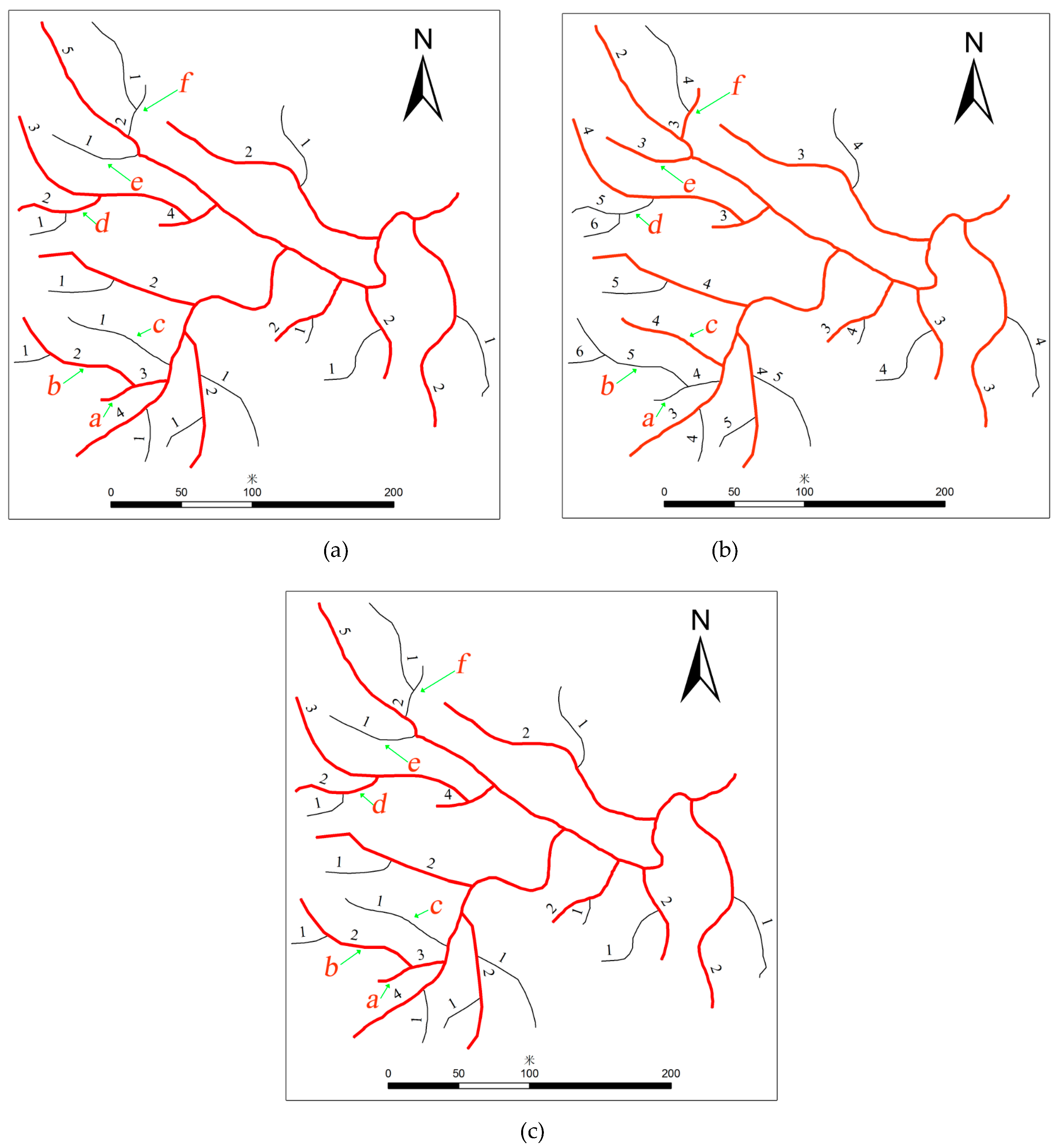
For each pattern, the subtrees with the largest numbers of streams are selected as typical areas for visual analysis of the selection results, as shown in
Figure 10,
Figure 11 and
Figure 12.
Figure 10 shows a modest branch, in which all of the tributaries connected to the main stem of the subtree have the same topological depth.
Figure 11 shows a shallow branch with uniformly distributed tributaries, in which the tributaries of the main stem are relatively shallow in terms of topological depth, and their depths do not vary significantly.
Figure 12 shows a topologically deep branch, in which the tributaries connected to the main stem have very large differences in topological depth.
There are 11 streams in the modest branch shown in
Figure 10. Based on the square root model, 5 streams need to be preserved, while 6 streams have to be removed. The spatial distribution characteristics of streams show that the hierarchies and depths of each tributary are the same, except for the main stream in this branch; hence, their codes have no difference, no matter which coding method is used. During the generalization process, Horton’s coding was selected as the coding method in this paper. The selection results for each method are shown in
Figure 10a–c, and the three ordering methods resulted in the same selection results in this scenario.
Figure 11 shows that there are 13 streams in the shallow branch. According to the square root model, 6 streams are retained, while 7 streams need to be removed. These streams are evenly uniformly distributed around the main stream of this branch, but the hierarchies and depths of each tributary have slight differences. For this pattern, bottom-up coding was selected as the coding method in this paper. The selection results for each method are shown in
Figure 11a–c. The results obtained using Horton’s coding method retain stream b and remove stream a. Conversely, the results obtained using bottom-up coding remove stream b and retain stream a. As can be seen from
Figure 11, although stream b has a depth of two, the depth structure in this branch is as not important as the hierarchy structure, which can better reflect the main spatial structure of this branch, as shown in stream a. Hence, the bottom-up coding method and the proposed method can efficiently preserve the spatial structures of the original map.
There are 27 streams in the deep branch shown in
Figure 12. Based on the square root model, 13 streams have to be retained, while 14 streams have to be removed. These rivers form a deeply nested structure, and the hierarchies and depths of each tributary have obvious differences. For this pattern, top-down coding was selected as the coding method in this paper. The selection results for each method are shown in
Figure 12a–c. The results obtained using Horton’s coding method retain streams a, b and d and remove streams c, e and f. Conversely, the results obtained using bottom-up coding remove streams a, b and d and retain streams c, e and f. As can be seen from
Figure 12, streams a, b and d with deeper depth structures are more important than are streams c, e and f in reflecting the main spatial structure of this branch. Removing streams a and b leads to the obvious loss of the tree structure. Hence, the top-down coding method and the proposed method can efficiently preserve the spatial structure of the original map.
5. Conclusions
River coding plays an important role in river network selection for topographic map generalization. Two existing classical coding methods show different characteristics—the top-down coding method is not appropriate for the stream selection of river networks with uniform distributions of tributaries, and the bottom-up coding method is not favorable for the stream selection of river systems that have topologically deep structures. The aforementioned two coding systems were used individually on the traditional river selection method, which leads to that the selection results of some river subtrees can’t keep the original spatial distribution characteristics. Therefore, a selection method for dendritic river networks based on hybrid coding is proposed in this paper, which combines the advantages of the above two methods and can preserve the spatial structural characteristics of river networks well by selecting the appropriate coding mode according to the spatial structure of the river subtrees. The following conclusions were drawn from the experimental validation using actual data:
(1) Only 16.67% of the rivers are inverted-coded, which means that the comprehensive utilization of the two methods can’t be achieved through simple algebraic transformation. The hybrid coding method proposed in this paper is effective, and the depth and hierarchy information of a stream can be read at the same time.
(2) The spatial distribution structure of river networks is determined based on the hybrid coding. First, streams were classified into deep or shallow streams based on the top-down coding approach, which reflects the depth information; second, river subtrees were identified based on the bottom-up coding approach, which reflects the hierarchy information; finally, the classified into three kinds of patterns based on the distribution characteristics and connection relationship of streams, which is deep branch, shallow branch and modest branch.
(3) For different patterns, the appropriate coding mode was selected automatically in this paper, which ensured that the selection results of different spatial structures was reasonable. For the modest branch, one of two coding approaches was used arbitrarily, because the selection result was the same. For the shallow branch and deep branch, the bottom-up coding method and the top-down coding method were selected, respectively.
The method proposed in this paper can be directly used in the river map generalization and also be helpful in the determination of river catchment regions. Future research will focus on (1) the generality of the proposed method in river selection of multi-scale and large-spatial range river network datasets; (2) exploring widely the applications of the proposed method in fields, such as hydrographic analyses, flood, retention activities, etc. At present, the proposed method embedded in WJ-III map station has been used in five provinces in China to perform multi-scale representation of river networks data in the National Geographic Census, such as Guizhou, Gansu, Guangdong, etc. The research results in river selection of multi-scale and large-spatial range river network datasets need further summarization.