Abstract
A digital model of the ground surface has many potential applications in forestry. Nowadays, Light Detection and Ranging (LiDAR) is one of the main sources for collecting morphological data. Point clouds obtained via laser scanning are used for modelling the ground surface by interpolation, a process which is affected by various errors. Using LiDAR data to collect ground surface data for forestry applications is a challenging scenario because the presence of forest vegetation will hinder the ability of laser pulses to reach the ground. The density of ground observations will be therefore reduced and not homogenous (as it is affected by the variations in canopy density). Furthermore, forest areas are generally present in mountainous areas, in which case the interpolation of the ground surface is more challenging. In this paper, we present a comparative analysis of interpolation accuracy for nine algorithms, which are used for generating Digital Terrain Models from Airborne Laser Scanning (ALS) data, in mountainous terrain covered by dense forest vegetation. For most of the algorithms we find a similar performance in terms of general accuracy, with RMSE values between 0.11 and 0.28 m (when model resolution is set to 0.5 m). Five of the algorithms (Natural Neighbour, Delauney Triangulation, Multilevel B-Spline, Thin-Plate Spline and Thin-Plate Spline by TIN) have vertical errors of less than 0.20 m for over 90 percent of validation points. Meanwhile, for most algorithms, major vertical errors (of over 1 m) are associated with less than 0.05 percent of validation points. Digital Terrain Model (DTM) resolution, ground slope and point cloud density influence the quality of the ground surface model, while for canopy density we find a less significant link with the quality of the interpolated DTMs.
1. Introduction
In the past, forestry research typically relied on two-dimensional representations (images) of forested areas [1,2,3]. The advent of Light Detection and Ranging (LiDAR) and the development of navigational systems such as Global Navigational Satellite System (GNSS) or Inertial Measurement Unit (IMU) enabled scientists to analyse the forest in a tri-dimensional space, using data formats such as point clouds or surface models [4]. Mounting a LiDAR sensor on an aerial platform (a method commonly referred to as Airborne Laser Scanning—ALS) allows efficient collection of high-precision data for relatively large areas. The result of LiDAR data collection is a data structure called point cloud, which can be used to obtain information related to the horizontal and vertical structure of the forest [5], from the top of the canopy to the ground level; in other words, laser scanning offers a new perception on forest structure and processes, at a local or regional level [6].
From a LiDAR point cloud, certain forest parameters can be determined, such as: aboveground forest biomass [7,8,9], Leaf Area Index (LAI) [10,11,12,13,14] or canopy density [15,16]. Furthermore, LiDAR data can be used for tree inventories [17,18,19,20], monitoring vegetation health [21,22,23,24] or generating Canopy Height Models (CHMs) [16,25].
The main advantage of LiDAR, with regard to forestry, is the fact that laser pulses can penetrate the canopy cover, with some of the pulses reaching the ground level. Therefore, geomorphological data is collected even if the ground is covered by forest vegetation, allowing the generation of a detailed and accurate ground surface model.
In general, a data structure that models the elevation over an area is called a Digital Elevation Model (DEM). In short, a DEM is simply a surface that represents the elevation of a certain area in reference to a common vertical datum. When this type of model is used for a representation of the bare-earth surface, it can also be termed as Digital Terrain Model (DTM). In this paper, we opted for the term DTM, in order to emphasize the fact that the models we analyse, while generally speaking classify as DEMs, are meant specifically to represent the surface of the bare-earth.
To obtain such a representation of the ground surface, a LiDAR point cloud must initially be filtered—a process which involves the separation of ground-level points from the original point cloud [26]. This filtered point cloud, containing only points which are at (or close to) the ground level, can afterwards serve for the interpolation of a continuous surface that models the variation of ground elevation.
A ground model obtained from ALS data can be used in forestry for various purposes, such as: (1) the development of forest road networks [27], (2) the identification of existing forest roads [28,29], (3) the optimisation of forest skid trails [30] and (4) finding optimal harvesting solutions [31,32,33]. Furthermore, a DTM is generally an intermediate product when estimating various forest parameters from LiDAR data [18,34,35,36,37]; the accuracy of the DTM will therefore influence the quality of subsequent estimations [38].
In the case of dense forest cover, the penetration rate of laser pulses is hindered, resulting in a lower density of ground-level observations [39]. Furthermore, ground points will not have a uniform spatial distribution, with most of them concentrating inside gaps in the canopy cover. In these conditions, proper processing of the LiDAR point cloud (ground filtering followed by DTM interpolation) is an important step to ensure a high-quality model of the ground surface is obtained. DTM accuracy will depend on: (1) the measurement accuracy and precision of the laser system, (2) the accuracy of point cloud filtering and (3) the method of interpolation. [40] carried out a classification of the error component affecting DTM accuracy in the case of LiDAR data, establishing that the interpolation error is the second-most important factor affecting DTM accuracy (after the measurement system error).
Numerous interpolation algorithms have been developed in the last decades, stimulating research into their relative accuracy [41]. Previous research has not established a definitive consensus regarding the performance of interpolation methods. For example, Inverse Distance Weighted (IDW), possibly the most widely used method, is found to have a relatively low accuracy in some studies [38,41,42,43,44], while in others it provides the most accurate ground surface [45,46]. However, when comparing previous research, one has to take into account the source of altimetry data. The accuracy of interpolation can be assessed using synthetic [41,47] or real data. The main sources of elevation data are: digital stereo-matching [42], topographical maps with isolines [46] and ground surveys carried out using topographical equipment [43,44], GNSS receivers [48] or LiDAR sensors [38,45,49].
Regarding the influence of external factors on DTM quality, the consensus is relatively better. Among the main factors that are usually taken into account when analysing DTM quality, the following are typically found to have some degree of influence on accuracy: morphological complexity of the ground surface [41,42,43,45,49], density of input data [42,43,50,51], model resolution [38,46] and the presence or characteristics of vegetation [44,45,49].
In this paper, we propose a quantitative analysis of the relative performance of nine interpolation algorithms, with the aim of testing the accuracy of DTM generation from LiDAR point cloud data in difficult conditions (mountainous terrain with a high degree of surface roughness and covered by dense forest vegetation). To compare algorithm performance, we used the cross-validation method, which involves the random separation of observations into two datasets: one used for prediction and the other for validation. This method provides a pseudo-external dataset, in situations where using an independent dataset for validation is not feasible. Any systematic error (e.g., the measurement error of the LiDAR system) will evidently not be taken into account, but the method can still provide an estimation of the relative accuracy of interpolation methods. External factors that were taken into account for the analysis of DTM accuracy are: model resolution, ground slope, ground point density and canopy cover density.
In addition, recognizing that free DEMs with worldwide coverage such as Advanced Spaceborne Thermal Emission Reflection Radiometer (ASTER) [52] or Shuttle Radar Topography Mission (SRTM) [53] are common products in forestry practice and research (especially at regional scales), we established the following as a secondary objective: a comparison between the most accurate model obtained from the interpolation of LiDAR data and the ASTER/SRTM datasets available for our test site. These models are global in coverage and operate at a different scale in terms of space (their resolution of 1-arcsecond corresponds to a cell-size of about 21 × 30 m at the latitude of our test area) and level of precision, so they are not suitable as validation data for ALS data or the interpolation methods that were tested. Therefore, results pertaining to this secondary objective are presented in Appendix A.
2. Materials and Methods
2.1. Test Site
The analysis was carried out in a test site with an area of 1.6 km2, located in the Latoriței Mountains of Romania, along the Bora River valley (Figure 1). Most of the area is covered with forest vegetation, mainly spruce (90 percent) and pine (10 percent). The majority of tree stands have an age of 90–95 years, with younger stands (55–75 years) also being present to a smaller extent. The most recent forest management plan indicates a high canopy density, with an average value of 0.8. The area is characterised by steep, mountainous relief, with ground slope having an average value of 26 degrees.
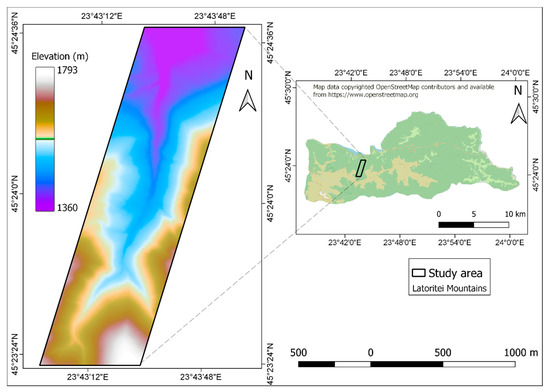
Figure 1.
Test site location.
2.2. LiDAR Data
LiDAR data was collected by ALS using a full-wave Riegl LMS-Q560 mounted on a Diamond Aircraft Industries airplane (the DA42 MPP). Parameters of the laser sensor and flight technical data are presented in Table 1.

Table 1.
Technical data for the Riegl LMS-Q560 laser sensor.
The resulting point cloud has an average density of 5.2 points m−2, which was achieved by scanning the same area two or three times. LiDAR data was delivered in the Universal Transversal Mercator (UTM) projection (zone 35N), with matched scan strips but unclassified point data.
As previously discussed, the initial point cloud contains both ground-level returns (or ground points) and returns caused by various above-ground objects, such as forest vegetation [54]. To accurately model the ground surface, above-ground laser returns have to be eliminated from the initial point cloud, in a process commonly called ground filtering [26]. To achieve this, we used a combined method: initially, we applied an automatic ground filter using the lasground algorithm included in the LasTools software package (rapidlasso GmbH). The filtered point cloud was then visually checked, in order to manually correct any noticeable filtering errors. Therefore, the filtered dataset should theoretically contain only points located at (or close to) the ground level. This final point cloud has an average density of 0.9 points m−2, corresponding to an average point spacing of 1.06 m.
2.3. Validation Data and Accuracy Assessment
To estimate the accuracy of interpolation, a validation dataset has to be used for comparison. To achieve this, we used the technique called cross-validation [55,56], which involves the separation of the initial dataset into two separate sets: one used for prediction and the other for validation. In some papers, this method is referred to as true validation [42,57]. In choosing the proportion between the subsets two aspects have to be considered [38]: (1) the validation data should contain enough observations to ensure the statistical significance of the results and (2) the integrity of the prediction set should be kept intact. There are no widely accepted guidelines for establishing the percentage of initial observations to be used for validation. As an example, we find that [42] uses 4 percent of input data for validation, while [38] uses 3 percent of data for the same purpose, [45] uses 0.1 percent of input data (but also carries out external validation using independent data) and [47] uses 10 percent of initial data to test a newly-developed method of DTM interpolation from LiDAR data.
Taking previous research into account and the specifics of our data, we established the following proportions: 95 percent of the initial ground points are used for prediction (1.06 mil. points) while the remaining 5 percent (n = 52,358) are used for validation. The validation dataset has an average density of 1 point per 31.9 m2 and an average distance between pairs of closest points of 2.48 m2 (SD = 1.58 m). It is reasonable to assume that this would ensure a sufficient reliability of the accuracy analysis.
In other words, we randomly select 95 percent of observations to represent the input data for DTM interpolation, with the remaining 5 percent used for estimating the accuracy of the resulting models.
The accuracy of a DTM is estimated by calculating the residual (or vertical error) for each validation point [58]:
where E(i) is the vertical error (or residual value) for validation point i, ZDTM(i) is the elevation value of the raster cell in which point i is located and ZALS(i) is the measured elevation for point i.
E(i) = ZDTM(i) − ZALS(i)
To clarify, ZDTM(i) is the elevation value estimated via interpolation for the centre of the DTM cell in which i is located, not for its exact location. Therefore, an extra error component is added, because of the distance between validation points and the cell centres of the raster model. This effect is evidently exacerbated in rougher terrain (where elevation has a higher local variance) and for lower modelling resolutions (larger cell sizes). Based on the residual values, accuracy estimates such as mean signed/unsigned error, standard deviation and Root Mean Square Error (RMSE) were calculated.
To get a clearer picture of the overall DTM accuracy, absolute (unsigned) vertical errors were calculated and classified. Error classification is by necessity subjective, as there is no accepted standard in the field of forestry for this aspect. In our case, we took into account the accuracy that is usually strived for in practice. For example, we considered absolute elevation errors of less than 0.20 m to be very low. In the end, we defined the following classification for absolute residual values: very low (less than 0.20 m), low (between 0.21 and 0.50 m), significant (between 0.51 and 1.00 m) and extreme (over 1.00 m).
We emphasize that the lack of independent data for external validation means that any of the reported accuracy estimates should be taken as a measure of the relative performance of interpolation methods, not as absolute indicators of the accuracy of elevation estimates. As previously stated, the main purpose of this paper is to compare the relative performance of different interpolation methods, not to estimate absolute geodetical errors, nor to model the error budget.
2.4. Interpolation Algorithms
In a general sense, an interpolation algorithm involves the definition of a prediction function, which can be used to estimate the values for unsampled points, based on the known values of neighbouring points.
Most methods of interpolation use weighted averages of known data points to predict values for unsampled points, with the difference being the method by which these weights are calculated. Therefore, for many of these algorithms the general formula for prediction can be written as follows [59]:
where denotes the estimated value for point , z(xi) is the measured value for point , is the weight asociated with observation z(xi) and n is the total number of reference points used for the estimation of .
Nine interpolation algorithms were tested:
- Inverse Distance Weighted (IDW) is one of the most widely used algorithms for surface modelling. The weight attributed to a reference point is based on its distance from the unsampled point for which the estimation is made, with reference points further away having a lower weight [60]. IDW is an intuitive method of interpolation, in that it assumes that there is a degree of spatial autocorrelation of measured values; in other words, closer points are likely to have similar values.
- Nearest Neighbour (NeN) is a simple approach: each unsampled point will be given the value of its closest measured point. This is achieved by constructing Thiessen polygons for all reference points. The Thiessen polygon of a point is the area of influence associated with that point; all unsampled points inside a polygon are closer to its centre than to any other reference point. Therefore, all unsampled points inside a Thiessen polygon will be assigned the value of the reference point in the centre of that polygon.
- Natural Neighbour (NN) is similar to Nearest Neighbour, but more complex [61]. The first step is the generation of a network of Thiessen polygons. Unsampled points for which the prediction is made are then overlaid with the network and a new set of Thiessen polygons are generated for them. Each new polygon will overlap with one or more of the original polygons. The centre points of those polygons are called the “natural neighbours” of the unsampled point used to generate the Thiessen polygon. The weight each reference value has in the interpolation of an unsampled point is based on the degree of overlap between initial Thiessen polygons and the polygon associated with the unsampled point.
- Delauney Triangulation (DT) involves the generation of a Triangular Irregular Network (TIN) from the input point data. The general principle of a Delauney triangulation network is that no known point is inside the circumcirle of any of the generated triangles [62]. By following this approach, a Delauney network will maximise the minimum angle of all triangles and ensure that triangle edges are relatively short. Each unsampled point is located inside a triangle of the network and its predicted value is calculated via a simple linear or polynomial interpolation using the known values for that triangle’s vertices.
- Spline-based interpolators are a class of global, non-convex interpolation algorithms, which involve the fitting of a flexible surface (commonly called spline) through a set of measured observations. The interpolation function will pass through (or close to) all measured values. These algorithms work on the assumption that each measured value has an inherent measurement error, which can be reduced by generating a smooth surface of minimal tension [43]. This local smoothing is achieved by generating a spline surface of minimal tension. The main difference between these algorithms is the mathematical form of the function used for surface generation. For this paper, we tested four spline-based algorithms:
- Multilevel B-Spline (BS), which uses a hierarchy of coarse-to-fine control lattices to generate a sequence of B-Spline functions, the sum of which is the final interpolation function [63].
- Cubic Spline (CS), which is based on the construction of a bivariate cubic spline function [64].
- Thin-Plate Spline (TPS), which uses the namesake function to generate surfaces. Thin-plate Spline is the 2D generalization of the cubic spline function [65].
- Thin-Plate Spline by TIN (TPSTIN) is a variant of TPS that involves the construction of a TIN (Triangular Irregular Network) prior to interpolation. A TIN is a 3D mesh composed of triangles of varying area, using the set of measured points as vertices. Instead of a global Thin-plate Spline function, TPSTIN involves the generation of a separate function for each triangle of the network.
- Ordinary Kriging (OK) is a geostatistical interpolation procedure that aims to quantify the degree of spatial auto-correlation of measured values. This is done by generating a semi-variogram, which depicts the overall shape, magnitude and spatial scale for the variation of the measured variable [66]. Over this graph a model is then fitted, which is used to assign weights to observations. These weights used for interpolation are therefore a function of the spatial co-variance of the observations [46].
A summary of the interpolation methods, their main characteristics and the abbreviations used going further are presented in Table 2. Most algorithms are deterministic, with the exception of Ordinary Kriging, which is geostatistical. Furthermore, prediction methods vary in terms of: scale of analysis (some estimate values on a global scale, rather than local), smoothing of predictions at sampled locations (exact vs. approximate methods) or shape (convex algorithms will always predict values inside the range of known values and predictions for non-convex algorithms can potentially fall outside the range of sampled values).

Table 2.
General characteristics of tested interpolation algorithms. Detailed explanation of terms can be found in [67].
2.5. Factors Considered for DTM Accuracy
The variation of DTM accuracy was analysed by taking into account the following factors:
- Spatial resolution, which is the main characteristic of a raster data structure (such as a DTM); four model resolutions were tested: 0.5 m, 1.0 m, 1.5 m and 2.0 m.
- Ground slope, which was determined using a reference DTM, generated from the complete dataset (both prediction and validation points) by Natural Neighbour interpolation at a 0.5 m resolution. Ground slope values were then classified as follows: 0–10, 11–20, 21–30, 31–40, 41–50 and >50 degrees.
- Point density, which was determined in a raster structure at a 1.0 m resolution. To reduce the noise level of the density model, a mean filter with a 5 × 5 kernel size was applied. Point density values were classified as follows: 0–0.25, 0.26–0.50, 0.51–0.75, 0.75–1.00 and >1.00 points m−2.
- Canopy density was determined in a raster structure, using the initial LiDAR point cloud and the formula proposed by [68], implemented in the FUSION LiDAR processing software:where δi is the canopy density for cell i of the model, n is the number of LiDAR returns inside cell i that are above a user-established height threshold and N is the total number of returns inside cell i. Height threshold was set to 3 m, assuming that LiDAR returns below this height are likely objects such as understory vegetation, fallen tree trunks, boulders etc.
To ensure that the estimated canopy density is meaningful, the model resolution has to be larger than a typical tree crown diameter. We took into account the fact that, at the time of LiDAR data collection, most tree stands in our test area were close to harvesting age, in which case Romanian forestry guidelines recommend an average distance between trees of 6–8 m [69]. Therefore, we set a value of 15 m for the resolution of the canopy density raster model, in the assumption that most, if not all, tree crowns should have a canopy diameter below this.
Estimated canopy density values were classified as follows: 0–10, 11–40, 41–60, 61–80 and 81–100 percent.
3. Results
3.1. General Acuraccy of Ground Surface Interpolation
By interpolation of a LiDAR point cloud containing ground returns, continuous surfaces that model the variation of ground elevation (or DTMs) were generated. A validation dataset was then overlaid with this surface in order to calculate residual values (or elevation errors). Statistical indices of these residuals, such as mean unsigned/signed error or RMSE, provide an estimate of the general accuracy of DTMs. Accuracy measures for DTMs generated from the filtered ALS point cloud are presented in Table 3, for the most accurate model resolution (0.5 m).

Table 3.
Accuracy of interpolation algorithms at the 0.5 m spatial resolution.
In all cases, regardless of interpolation method or model resolution, mean signed error is less than 0.01 m. This indicates that there is no apparent bias of interpolation; in other words, no significant tendency to over/under-estimate elevation values. Mean unsigned error and RMSE values are relatively similar between algorithms, for a given resolution. As an example, mean unsigned error at a model resolution of 0.5 m varies between 0.08 m (for five of the algorithms) and 0.20 m (for NeN and OK).
The classification of absolute residual values is presented in Table 4. Since the relative distribution of errors across classes is very similar between model resolutions, only the results for the 0.5 m resolution are presented.

Table 4.
Classification of absolute vertical errors, at the 0.5 m model resolution.
Classification of absolute vertical errors reveals that for most interpolation methods vertical errors of over 0.50 m are relatively rare (less than 1 percent of validation points). A different error distribution is found for NeN and OK, as both methods have about 7 percent of error values in the two uppermost classes. Interpolation methods which provide a relatively high accuracy overall in terms of RMSE values (NN, DT, BS, TPS and TPSTIN) have a large percentage (93–95%) of absolute vertical errors in the first category (<0.20 m).
In addition to the quantitative analysis of accuracy, we propose that a qualitative (or visual) analysis of generated surfaces is also of interest, especially in cases where interpolation methods do not have a significant difference in terms of RMSE values. A hillshade generated from the final DTMs (at the 0.5 m resolution) for a subset of the test area is presented in Figure 2. It is apparent that most interpolated surfaces have some degree of visual artefacts. Most distinctive artefacts are present for interpolation with NeN (which has a significant noise-level), DT (mostly in areas of lower point density, where the facets of the initial TIN are larger), IDW (also predominantly in areas of low point density) and CS. Visual analysis shows that spline-based methods generate smoother surfaces, closer in appearance to the real ground surface.

Figure 2.
Hillshade models derived from interpolated Digital Terrain Models (DTMs), for a subset of the test site (500 × 500 m).
3.2. Effect of Model Resolution on DTM Accuracy
RMSE values for each model resolution (0.5, 1.0, 1.5 and 2.0 m) are presented in Figure 3. For each interpolation algorithm, a lower general accuracy is observed for coarser resolutions. In other words, for a specific resolution, the relative performance of tested algorithms is for the most part similar.
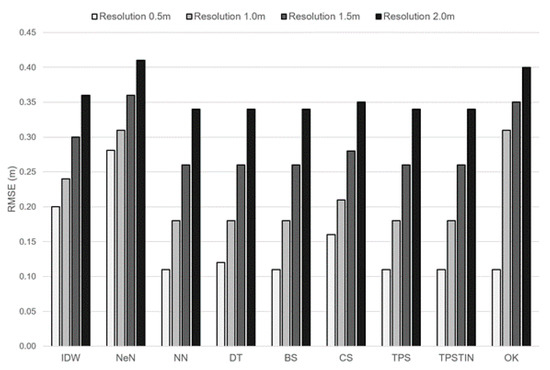
Figure 3.
Interpolation accuracy at different model resolutions.
3.3. Effect of External Conditions on DTM Accuracy
In order to analyse the manner in which accuracy varies depending on external factors, validation points were categorised according to established classes for each factor. Mean RMSE values for the resulting subsets of validation points were then calculated. Based on these mean RMSE values for each category, r correlation coefficients were calculated (Table 5).

Table 5.
Correlation coefficients (r) for RMSE values dependent on external factor categories.
Three external factors were considered in the analysis: ground slope (Figure 4), ground point density of the ALS point cloud (Figure 5) and canopy cover density (Figure 6). As we find that RMSE values follow a similar variation regardless of model resolution, only results for the 0.5 m resolution are shown.
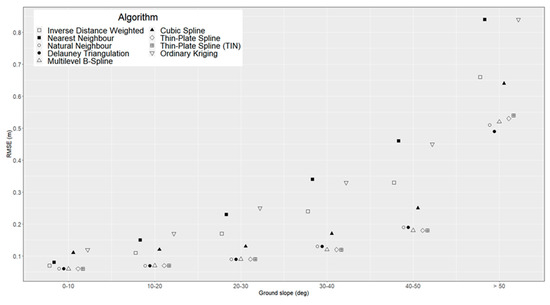
Figure 4.
Variation of interpolation accuracy by ground slope class (model resolution: 0.5 m). For clarity, points are horizontally offset.
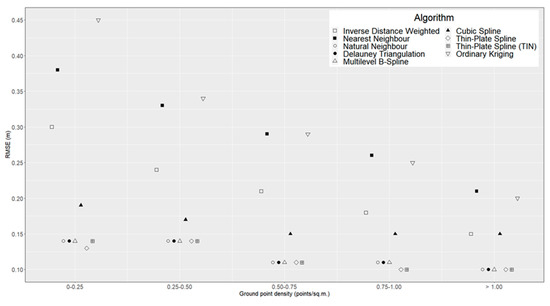
Figure 5.
Variation of interpolation accuracy by point density class (model resolution: 0.5 m). For clarity, points are horizontally offset.
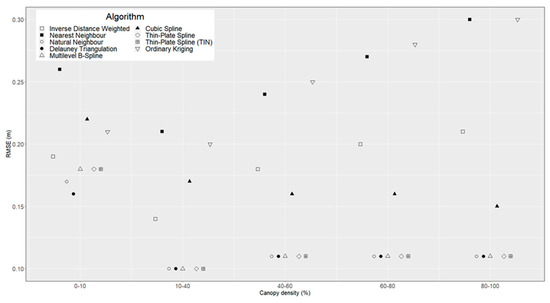
Figure 6.
Variation of interpolation accuracy by canopy density class (model resolution: 0.5 m). For clarity, points are horizontally offset.
4. Discussion
Results indicate that, for the most part, tested interpolation algorithms have a relatively similar performance, in terms of overall DTM accuracy. Mean signed errors are very close to zero in all cases, indicating the lack of a prediction bias. It is worth pointing out that some previous studies find a positive bias of elevation prediction, in the case of dense forest vegetation. For example, [70] reports a mean DTM error of 0.31 m for unlogged coniferous tree stands, while [45] report a mean DTM error of 0.23 m for uncut aspen tree stands. The effect (or lack thereof) of forest composition and/or harvesting practices on the bias of ground elevation estimates from ALS data is worth further investigation.
Accuracy estimation for different model resolutions shows that, regardless of interpolation algorithm, lower DTM resolutions are associated with higher RMSE values (Figure 3). This is in accordance with previous research [38,44,46], but it is worth pointing out that at lower resolutions the distance between raster cell centres (the points for which prediction is made during the interpolation) and validation points will likely increase.
With regard to ground slope, previous research indicates that it should have an impact on the accuracy of the ground surface representation [44,45,49,71]. This is indeed the case here, as we find that RMSE values for all algorithms increase with ground slope. However, not all algorithms are equally affected. This is especially observed in the case of very steep terrain (ground slope of over 40 degrees), where some of the algorithms have a comparatively poorer performance (Figure 4). This is confirmed by r correlation coefficient values, which highlight a very significant correlation between mean RMSE values and ground slope categories (p-value < 0.01) for these algorithms (Table 5). On the other hand, for most spline-based methods (which achieve a better overall performance) we find that the correlation between RMSE and ground slope is insignificant (p-value > 0.05). There is no clear provable explanation for this behaviour, but our assumption is that it has to do with what we called the ‘shape’ of algorithms (Table 2). As previously discussed, some algorithms (called convex) will always predict values inside the range of known values, while non-convex algorithms can predict values outside this range. In very rugged terrain (high slope values) it is unlikely that sampled points will cover the whole range of real elevation values. In other words, local maxima and minima will generally fall outside the sampled interval of elevation values, therefore will not be properly modelled by convex algorithms. On the other hand, non-convex algorithms (generally spline-based) are better suited to predict local maxima and minima even when those values fall outside the range of observations. This assumption is warranted by the fact that three out of the five convex algorithms that were tested have a degrading relative performance when ground slope increases (these being NeN, IDW and OK). This is in line with previous research: [42] tested IDW and three spline-based interpolation methods and noted that IDW has a lower performance in rugged test plots because of its inability to properly model local maxima/minima; [43] tested four interpolation methods in a hilly area and reported that IDW produced a higher rate of error clustering near the top of the hill (local maxima) when compared to non-convex methods like TPS or Multi-Quadratic.
On the other hand, at least one of the algorithms that we tested (DT) follows the opposite trend: even if DT is convex, this method actually has the best accuracy at the highest slope class (relative to the other algorithms). Further research is necessary to establish if this is something that has to do with DT’s approach to interpolation or random behaviour.
The next external factor that was considered is the ground point density (Figure 5). While the reduction of point density has a noticeable effect on RMSE for NeN, IDW and OK algorithms, the other interpolation methods that were tested have a lower variation of RMSE across point density classes. A higher variance of RMSE values between interpolation methods for lower point densities is also reported by [72]. For most algorithms, we find a significant negative correlation between mean RMSE values and point density categories (Table 5), with the sole exception of TPS (r = -.87, p-value > 0.05).
With regard to canopy density, we find that algorithms do not follow the same trend (Figure 6). Some of the methods that were tested (NN, DT, BS and spline-based methods except CS) have near-constant mean RMSE values across canopy density categories, while others have lower accuracy in dense canopy cover (NeN, IDW and OK). In addition, OK is the only algorithm for which we find a significant positive correlation between canopy density and RMSE (r = 0.95, p-value < 0.05).
It is worth pointing out that the distribution of validation points across canopy density categories is strongly skewed to the right: while only 4 percent of the validation points are assigned to the first canopy density category (0–10 percent canopy cover), the last category (80–100 percent canopy cover) includes 58 percent of the validation points. Therefore, mean RMSE values calculated for the lower canopy density classes have a relatively large 0.95 confidence interval.
There is no significant body of research that focuses on the effect that vegetation conditions have on the accuracy of ground-surface modelling from ALS data, especially for the specific case of forest eco-systems. Furthermore, vegetation conditions can be looked at from different perspectives: while in our study we only considered the density of the canopy cover, other researchers looked at DTM accuracy for different vegetation classes [45] or for varying understory vegetation heights [49]. As a result of this, it is difficult to put the results presented in Figure 6 into perspective.
Leaving aside the lowest canopy density class (0–10 percent) due to its unreliability (a higher 0.95 confidence interval due to a low number of validation points), it is apparent that, generally speaking, canopy density has a similar effect as ground point density (Figure 5), except inversed (since an increase of canopy cover density should cause a decrease of ground point density). Therefore, if we look at this two factor in conjunction, we can see that: (1) several algorithms are not affected by changes in ground point/canopy density—NN, DT, BS, TPS, TPSTIN; (2) some algorithms have a decreased performance at higher canopy density/lower ground point density—NeN, OK, IDW and (3) the rest of the algorithms seem to have random changes in terms of accuracy between classes of canopy density/ground point density.
In other words, results would indicate that canopy density acts as a proxy of ground point density, in terms of its influence on the accuracy of ground-surface modelling in dense forest environments. This is contrary to our initial assumption, which was that canopy density (while evidently linked to a certain extent with ground point density) would exhibit a different influence on DTM interpolation. This assumption was made by considering the theoretical effect that canopy density would have on the spatial distribution of ALS ground points. While in open terrain the variation of ground point density (for example by changing the altitude of the LiDAR sensor platform) would be evenly spread (point density is generally homogenous), increased canopy density would not only cause a general lowering of ground point density, but also an increase in the clustering of these points (with most of observations grouped under gaps in the canopy cover).
However, results show that this expected clustering of ground points in areas of higher canopy density is either not significant, or it does not have a noticeable influence on the interpolation of the ground surface model. Further research needs to be carried out before we can state that the effect of canopy density on DTM accuracy is fully explained by changes in terms of ground point density. This additional research should be ideally carried out in areas with different forest compositions and with a distribution of canopy densities closer to the normal (as stated, canopy density values for our test site are skewed to the right).
To sum up, results indicate that for our test conditions (mountainous areas with dense canopy cover), the relatively lower accuracy of some interpolation methods (namely Nearest Neighbour, Inverse Distance Weighted and Ordinary Kriging) is likely attributed to areas of steep slope and/or lower point densities caused by the presence of dense forest cover.
5. Conclusions
An accuracy assessment of DTM interpolation from LiDAR point cloud data in difficult terrain conditions (mountainous relief with dense forest cover) was carried out. In lack of independent data at a sufficient density and accuracy, we had to carry out the performance analysis of interpolation algorithms using cross-validation, which involves separating a certain proportion of the initial dataset (in our case 5 percent) to use as validation. The limitation of this approach is that any systematic errors (which affect the initial dataset in its entirety) are not taken into account, so none of the reported accuracy estimates are to be taken as global estimates of modelling accuracy. In other words, the results that were presented can only be considered as indicators of the relative performance of the tested interpolation methods in a densely-forested area, which was indeed our main purpose.
Nine interpolation methods were tested and results show that, as far as general DTM accuracy is concerned, algorithm performance is relatively similar. Therefore, we propose that a visual analysis of interpolated DTMs is warranted, alongside the quantitative one. In addition, such an analysis has the advantage that it can easily inform the end user about the quality of the ground surface model [73]. Significant visual artefacts are present for Inverse Distance Weighted, Nearest Neighbour and Ordinary Kriging. On the other hand, surfaces generated by spline-based methods are generally artefact-free; as they apply a degree of smoothing to the generated surface, DTMs obtained using these methods are more appealing (in terms of visualisation). This is not to say that visual analysis is as important as the quantitative one, since a better-looking model does not necessarily mean a more accurate prediction.
With regard to TPS and its variant TPSTIN, results do not highlight any significant difference between their respective DTMs. Therefore, the significantly longer processing time of TPSTIN (relative to TPS) is not justified.
The best overall accuracy is achieved by spline-based methods and the Natural Neighbour algorithm. These methods have a similar response to the variations of ground slope, ground point density and, to a lesser extent, canopy cover density. However, it is worth mentioning that spline-based algorithms generally involve a time-consuming process of parameter optimisation, while Natural Neighbour does not require any user input.
Overall, results indicate that ALS point clouds are a viable source for accurate ground surface modelling even in less than ideal conditions, such as steep slopes covered with dense forest vegetation. However, issues concerning model resolution, interpolation method and parameter optimisation need to be taken into account.
While the effect of model resolution, ground slope and the ground point density of the ALS point cloud have been established for our test area, the influence of canopy density on different interpolation algorithms is not entirely clear and warrants further research.
Author Contributions
Conceptualization, Mihnea Cățeanu and Arcadie Ciubotaru; methodology, Mihnea Cățeanu and Arcadie Ciubotaru; software processing, Mihnea Cățeanu; writing—original draft preparation, Mihnea Cățeanu; writing—review and editing, Mihnea Cățeanu and Arcadie Ciubotaru. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors extend their gratitude towards the National Institute for Research and Development in Forestry (INCDS) “Marin Drăcea” for kindly providing access to the ALS data used in this study. The authors would also like to express their sincere appreciation to the academic editor and the two anonymous reviewers, whose insightful observations were of great help in improving this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
A secondary objective of this paper was to provide a comparison between the most accurate DTM we obtained and two freely available elevation models that are commonly used in forestry operations and research (especially on a regional scale): ASTER and SRTM (both at v3, the latest version available) which will be identified as DTMASTER and DTMSRTM going forward. The DTM interpolated from ALS data that was chosen for this comparison was generated using the Natural Neighbour (NN) algorithm, and will be identified as DTMN. This algorithm was chosen not only because of its comparatively good performance (on par with spline-based methods), but also because of its advantages from the end-user perspective: no parameters to be set, easy to understand approach to interpolation and a faster generation of DTMs than most other algorithms. Elevation values of DTMNN were translated to the EGM96 vertical datum, in order to coincide with the datum of ASTER/SRTM data.
The comparison was carried out at five spatial resolutions: 0.5, 1.0, 1.5, 2.0 and 21.0 m. DTMASTER and DTMSRTM had an initial resolution of 1 arc-second (a cell-size of approx. 21 × 30 m at the latitude of our test site) so had to be resampled in order to get the appropriate resolutions. It is worth pointing out that resampling does not add any new information to the ASTER/SRTM models, but it is necessary in order to overlay and compare the models. Additionally, in order to test DTMASTER and DTMSRTM at their native resolution, one of the DTMNN models (initially at a 0.5 m resolution) was downgraded to a resolution of 21.0 m by averaging cell values.
Figure A1 presents the DTMs for a subset of the test site, for the three datasets that were compared. Visual analysis shows that DTMNN offers a much more detailed representation of the ground surface, highlighting local features such as gulleys or forest tracks. Meanwhile, DTMASTER and DTMSRTM only offer a more general perspective, representing larger changes of the landscape.
For a quantitative comparison, raster models of vertical deviation (Figure A2) were generated for the ASTER dataset (by subtracting cell values of DTMNN from DTMASTER) and for the SRTM dataset (by subtracting cell values of DTMNN from DTMSRTM). Since the purpose of this appendix is to compare (rather than validate) SRTM/ASTER data with a DTM interpolated from ALS data, we will refer to the differences of elevation values between these models as vertical deviation or vertical displacement instead of vertical error. General statistics for vertical displacement between ASTER/SRTM data and DTMNN are presented in Table A1.
While the mean signed displacement values show significant differences in terms of deviation from DTMNN for both DTMASTER and DTMSRTM, the other statistics (for example the root mean sq. of vertical displacement values) indicate that the two models have an overall similar deviation from DTMNN. No effect of changes in terms of model resolution on the overall displacement between ground-surface models is noticeable. This is not surprising, as between the original ASTER/SRTM model at a resolution of approx. 21.0 m and the models resampled at higher resolutions there are no functional differences. Going by the root mean sq. of vertical deviations, we can summarize that an overall difference of around 40–42 m is to be expected between ASTER/SRTM data and DTMNN, regardless of model resolution.
In addition, to get a better understanding of the distribution of vertical displacements, absolute vertical displacement values were classified as follows: under 1.0 m, between 1.0 and 5.0 m, between 5.0 and 10.0 m and over 10.0 m. Since the distribution of values in classes is very similar between resolutions, only the results for the 21.0 m resolution (closest to the native resolution of ASTER/SRTM data) are presented (Table A2).
Results show that, for both ASTER and SRTM models, a large proportion of vertical displacement values are over 10.0 m. While the distribution of values per classes is similar between the two models, DTMSRTM seems to deviate less from DTMNN, at least in some areas.
A representation of two vertical displacement raster models is presented in Figure A2. These models are very similar in appearance regardless of resolution so only the result for the 21.0 m resolution is shown.
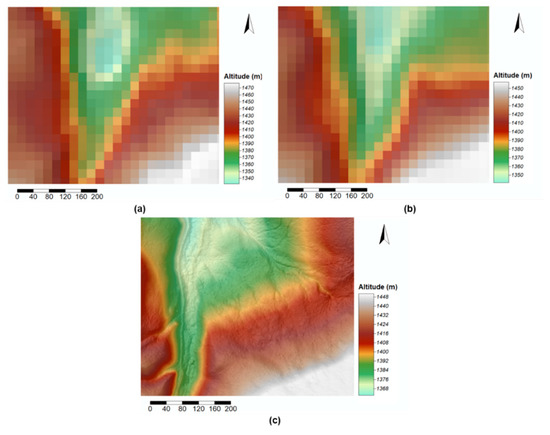
Figure A1.
DTMs for a subset of the test site, generated from: (a) ASTER data, at the original 21.0 m resolution, (b) SRTM data, at the original 21.0 m resolution and (c) ALS data, interpolated at 0.5 m resolution using the Natural Neighbour algorithm.
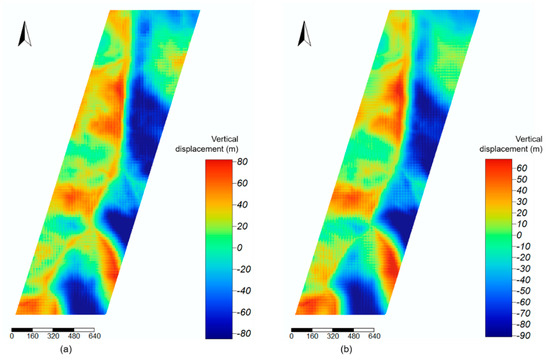
Figure A2.
Raster models of vertical displacement between: (a) DTMNN and DTMASTER and (b) DTMNN and DTMSRTM.

Table A1.
Statistics for vertical displacement between DTMNN and DTMASTER/DTMSRTM.
Table A1.
Statistics for vertical displacement between DTMNN and DTMASTER/DTMSRTM.
| Models Compared | Mean Signed Displ. (m) | Mean Unsigned Displ. (m) | Std. Dev. of Signed Displ. | Root Mean sq. of Vert. Displ. (m) |
|---|---|---|---|---|
| DTMNN vs. DTMASTER (0.5 m) | −1.57 | 33.95 | 24.30 | 40.90 |
| DTMNN vs. DTMSRTM (0.5 m) | −11.57 | 31.54 | 26.91 | 40.61 |
| DTMNN vs. DTMASTER (1.0 m) | −1.57 | 33.95 | 24.30 | 41.75 |
| DTMNN vs. DTMSRTM (1.0 m) | −11.57 | 31.54 | 26.90 | 41.45 |
| DTMNN vs. DTMASTER (1.5 m) | −1.57 | 33.95 | 24.31 | 41.75 |
| DTMNN vs. DTMSRTM (1.5 m) | −11.57 | 31.53 | 26.92 | 41.45 |
| DTMNN vs. DTMASTER (2.0 m) | −1.56 | 33.93 | 24.28 | 41.72 |
| DTMNN vs. DTMSRTM (2.0 m) | −11.56 | 31.52 | 26.89 | 41.43 |
| DTMNN vs. DTMASTER (21.0 m) | −1.59 | 34.05 | 24.22 | 41.79 |
| DTMNN vs. DTMSRTM (21.0 m) | −11.67 | 31.54 | 27.05 | 41.55 |
Visual analysis of these representations indicates a significant effect of slope exposition on the direction the vertical displacement takes, for both ASTER and SRTM models. Slopes facing westward (on the eastern side of the test plot) have negative deviations (ASTER/SRTM models are below DTMNN) with deviations seemingly increasing with altitude. Deviations for DTMASTER reach values as low as −82 m in the highest areas, while DTMSRTM deviations are as low as −90 m in the same areas. Meanwhile, slopes facing eastward (mostly on the western side of the test plot) have positive deviations (ASTER/SRTM models are above DTNNN) with deviations also seemingly increasing with altitude. On this side, deviations for DTMASTER go up to values as high as 80 m in the highest areas, while DTMSRTM deviations are as high as 66 m in the same areas.

Table A2.
Classification of absolute vertical displacement values, at the 21.0 m model resolution.
Table A2.
Classification of absolute vertical displacement values, at the 21.0 m model resolution.
| Models Compared | No. of Cells (% of Total no. Cells) | |||
|---|---|---|---|---|
| Abs. Vertical Displ. under 1.0 m | Abs. Vertical Displ. between 1.0 and 5.0 m | Abs. Vertical Displ. between 5.0 and 10.0 m | Abs. Vertical Displ. over 10.0 m | |
| DTMNN vs. DTMASTER | 1.8 | 6.0 | 7.8 | 84.4 |
| DTMNN vs. DTMSRTM | 2.8 | 10.7 | 12.2 | 74.3 |
References
- Brandtberg, T.; Walter, F. Automated delineation of individual tree crowns in high spatial resolution aerial images by multiple-scale analysis. Mach. Vis. Appl. 1998, 11, 64–73. [Google Scholar] [CrossRef]
- Coburn, C.; Roberts, A.C. A multiscale texture analysis procedure for improved forest stand classification. Int. J. Remote Sens. 2004, 25, 4287–4308. [Google Scholar] [CrossRef]
- Hagan, G.F.; Smith, J. Predicting tree groundline diameter from crown measurements made on 35-mm aerial photography. Photogramm. Eng. Remote Sens. 1986, 52, 687–690. [Google Scholar]
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geog. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Jacquemoud, S.; Gonçalves, G.; Silva, C.A.; Soares, P.; Tomé, M.; Pereira, L. Airborne Lidar Estimation of Aboveground Forest Biomass in the Absence of Field Inventory. Remote Sens. 2016, 8, 653. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite lidar vs. small footprint airborne lidar: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar]
- Jensen, J.L.; Humes, K.S.; Vierling, L.A.; Hudak, A.T. Discrete return lidar-based prediction of leaf area index in two conifer forests. Remote Sens. Environ. 2008, 112, 3947–3957. [Google Scholar] [CrossRef]
- Lin, Y.; West, G. Retrieval of effective leaf area index (LAIe) and leaf area density (LAD) profile at individual tree level using high density multi-return airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 150–158. [Google Scholar] [CrossRef]
- Pimont, F.; Soma, M.; Dupuy, J.-L. Accounting for Wood, Foliage Properties, and Laser Effective Footprint in Estimations of Leaf Area Density from Multiview-LiDAR Data. Remote Sens. 2019, 11, 1580. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ. 2006, 102, 364–376. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef]
- Chen, L.; Chiang, T.; Teo, T. Fusion of LIDAR data and high resolution images for forest canopy modelling. In Proceedings of the 26th Asian Conference on Remote Sensing, Hanoi, Vietnam, 7–11 November 2005. [Google Scholar]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne LiDAR data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Chen, W.; Hu, X.; Chen, W.; Hong, Y.; Yang, M. Airborne LiDAR remote sensing for individual tree forest inventory using trunk detection-aided mean shift clustering techniques. Remote Sens. 2018, 10, 1078. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Vertical stratification of forest canopy for segmentation of understory trees within small-footprint airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 385–392. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Rullan-Silva, C.D.; Olthoff, A.E.; de la Mata, J.A.D.; Pajares-Alonso, J.A. Remote Monitoring of Forest Insect Defoliation—A Review-. For. Syst. 2013, 22, 377–391. [Google Scholar] [CrossRef]
- Vastaranta, M.; Kantola, T.; Lyytikäinen-Saarenmaa, P.; Holopainen, M.; Kankare, V.; Wulder, M.A.; Hyyppä, J.; Hyyppä, H. Area-based mapping of defoliation of scots pine stands using airborne scanning LiDAR. Remote Sens. 2013, 5, 1220–1234. [Google Scholar] [CrossRef]
- Barnes, C.; Balzter, H.; Barrett, K.; Eddy, J.; Milner, S.; Suárez, J. Individual tree crown delineation from airborne laser scanning for diseased larch forest stands. Remote Sens. 2017, 9, 231. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Lange, H.; Bollandsås, O.M. Remote sensing of forest health. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004; 36, 8. [Google Scholar]
- Iqbal, I.A.; Dash, J.; Ullah, S.; Ahmad, G. A novel approach to estimate canopy height using ICESat/GLAS data: A case study in the New Forest National Park, UK. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 109–118. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Aruga, K.; Sessions, J.; Miyata, E.S. Forest road design with soil sediment evaluation using a high-resolution DEM. J. For. Res. 2005, 10, 471–479. [Google Scholar] [CrossRef]
- White, R.A.; Dietterick, B.C.; Mastin, T.; Strohman, R. Forest roads mapped using LiDAR in steep forested terrain. Remote Sens. 2010, 2, 1120–1141. [Google Scholar] [CrossRef]
- Pentek, T.; Picman, D.; Potocnik, I.; Dvoršcak, P.; Nevecerel, H. Analysis of an existing forest road network. Croat. J. For. Eng. 2005, 26, 39–50. [Google Scholar]
- Sterenczak, K.; Moskalik, T. Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network. iForest-Biogeosciences For. 2014, 8, 661. [Google Scholar] [CrossRef]
- Mohtashami, S.; Bergkvist, I.; Löfgren, B.; Berg, S. A GIS Approach to Analyzing Off-Road Transportation: A Case Study in Sweden. Croat. J. For. Eng. 2012, 33, 275–284. [Google Scholar]
- Chung, W. Optimization of Cable Logging Layout Using a Heuristic Algorithm for Network Programming . Ph.D. Thesis, Department of Forest Engineering, College of Forestry, Oregon State University, Corvallis, OR, USA, 2003. [Google Scholar]
- Vega-Nieva, D.J.; Murphy, P.N.; Castonguay, M.; Ogilvie, J.; Arp, P.A. A modular terrain model for daily variations in machine-specific forest soil trafficability. Can. J. Soil Sci. 2009, 89, 93–109. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef]
- Tinkham, W.T.; Smith, A.M.; Hoffman, C.; Hudak, A.T.; Falkowski, M.J.; Swanson, M.E.; Gessler, P.E. Investigating the influence of LiDAR ground surface errors on the utility of derived forest inventories. Can. J. For. Res. 2012, 42, 413–422. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Assessment of Individual Tree Detection and Canopy Cover Estimation using Unmanned Aerial Vehicle based Light Detection and Ranging (UAV-LiDAR) Data in Planted Forests. Remote Sens. 2019, 11, 908. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; She, G. Estimating forest structural parameters using canopy metrics derived from airborne LiDAR data in subtropical forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar]
- Maguya, A.S.; Junttila, V.; Kauranne, T. Adaptive algorithm for large scale dtm interpolation from lidar data for forestry applications in steep forested terrain. ISPRS J. Photogramm. Remote Sens. 2013, 85, 74–83. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne LiDAR-derived elevation. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Agüera, F.; Aguilar, M.A.; Carvajal, F. Effects of terrain morphology, sampling density, and interpolation methods on grid DEM accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar]
- Erdogan, S. A comparision of interpolation methods for producing digital elevation models at the field scale. Earth Surf. Processes Landforms 2009, 34, 366–376. [Google Scholar] [CrossRef]
- Ismail, Z.; Abdul Khanan, M.F.; Omar, F.Z.; Abdul Rahman, M.Z.; Mohd Salleh, M.R. Evaluating Error of LiDar Derived DEM Interpolation for Vegetation Area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 42. [Google Scholar]
- Su, J.; Bork, E. Influence of vegetation, slope, and lidar sampling angle on DEM accuracy. Photogramm. Eng. Remote Sens. 2006, 72, 1265–1274. [Google Scholar]
- Weng, Q. An Evaluation of Spatial Interpolation Accuracy of Elevation data. In Progress in Spatial Data Handling; Riedl, A., Kainz, W., Elmes, G.A., Eds.; Springer: Berlin, Germany, 2006; pp. 805–824. [Google Scholar]
- Chen, C.; Li, Y. A Fast Global Interpolation Method for Digital Terrain Model Generation from Large LiDAR-Derived Data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef]
- Arun, P.V. A comparative analysis of different DEM interpolation methods. Egypt. J. Remote Sens. Space Sci. 2013, 16, 133–139. [Google Scholar] [CrossRef]
- Stereńczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of topographic variability and lidar sampling density on several DEM interpolation methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. The effect of LiDAR data density on DEM accuracy. In Proceedings of the International Congress on Modelling and Simulation (MODSIM07), Christchurch, New Zealand, 10–13 December 2007; Oxley, L., Kulasiri, D., Eds.; Modelling and Simulation Society of Australia and New Zealand Inc.: Christchurch, New Zealand, 2007; pp. 1363–1369. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113.4, 711–715. [Google Scholar] [CrossRef]
- Zyl, J.J. van. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001; 48, 559–565. [Google Scholar]
- Cățeanu, M.; Arcadie, C. ALS for terrain mapping in forest environments: An analysis of lidar filtering algorithms. EARSeL eProceedings 2017, 16, 9–20. [Google Scholar]
- Anderson, E.; Thompson, J.; Austin, R. LIDAR density and linear interpolator effects on elevation estimates. Int. J. Remote Sens. 2005, 26, 3889–3900. [Google Scholar] [CrossRef]
- Davis, B.M. Uses and abuses of cross-validation in geostatistics. Math. Geol. 1987, 19, 241–248. [Google Scholar] [CrossRef]
- Voltz, M.; Webster, R. A comparison of kriging, cubic splines and classification for predicting soil properties from sample information. Journal of Soil Science 1990, 41, 473–490. [Google Scholar] [CrossRef]
- Li, Z. On the measure of digital terrain model accuracy. Photogramm. Rec. 1988, 12, 873–877. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons, Ltd.: Chichester, UK, 2007; pp. 37–38. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd National Conference of the Association for Computing Machinery, Princeton, NJ, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; Wiley: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Ripley, B.D. Spatial Statistics; Wiley: New York, NY, USA, 1981; pp. 39–43. [Google Scholar]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered data interpolation with multilevel B-splines. IEEE Trans. Vis. Comput. Graph. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Haber, J.; Zeilfelder, F.; Davydov, O.; Seidel, H.P. Smooth Approximation and Rendering of Large Scattered Data Sets. In Proceedings of the Conference on Visualization ’01, San Diego, CA, USA, 21–26 October 2001; IEEE Computer Society: Washington, DC, USA, 2001; pp. 341–348. [Google Scholar]
- Donato, G.; Belongie, S. Approximate thin plate spline mappings. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2002; pp. 21–31. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping of Environmental Variables; EUR 22904, EN; Office for Official Publications of the European Communities: Luxembourg, 2007; pp. 11–13. [Google Scholar]
- McGaughey, R. FUSION/LDV: Software for LiDAR data analysis and visualization; US Department of Agriculture, Forest Service: Seattle, WA, USA, 2014; pp. 28–31. [Google Scholar]
- Giurgiu, V.; Draghiciu, D. Modele Matematice-Auxologice Si Tabele de Productie Pentru Arborete (Mathematical Growth Models and Yield Tables for Stands); Ed. Ceres: Bucharest, Romania, 2004; pp. 120–122. [Google Scholar]
- Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.-E.; Carson, W.W. Accuracy of a high-resolution lidar terrain model under a conifer forest canopy. Can. J. Remote Sens. 2003, 29, 527–535. [Google Scholar] [CrossRef]
- Hyyppä, H.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Kaasalainen, S.; Honkavaara, E.; Rönnholm, P. Factors affecting the quality of DTM generation in forested areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, 85–90. [Google Scholar]
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Phachomphon, K. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Wood, J.D.; Fisher, P.F. Assessing interpolation accuracy in elevation models. IEEE Comput. Graph. Appl. 1993, 13, 48–56. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).