Figure 1.
Mercator map projection with as overlay the Tissot indicatrix.
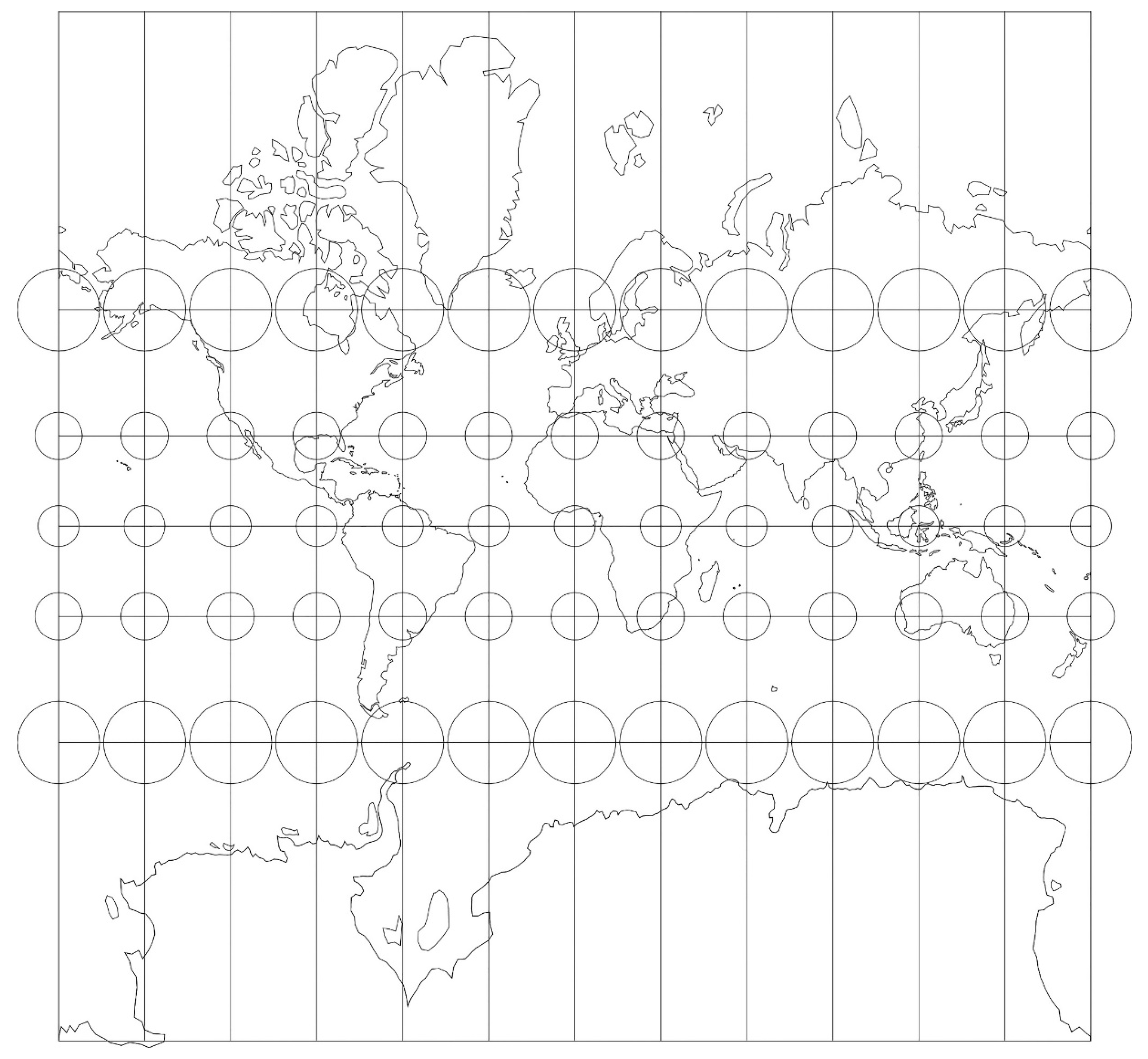
Figure 1.
Mercator map projection with as overlay the Tissot indicatrix.
Figure 2.
Gall–Peters map projection with as overlay the Tissot indicatrix.
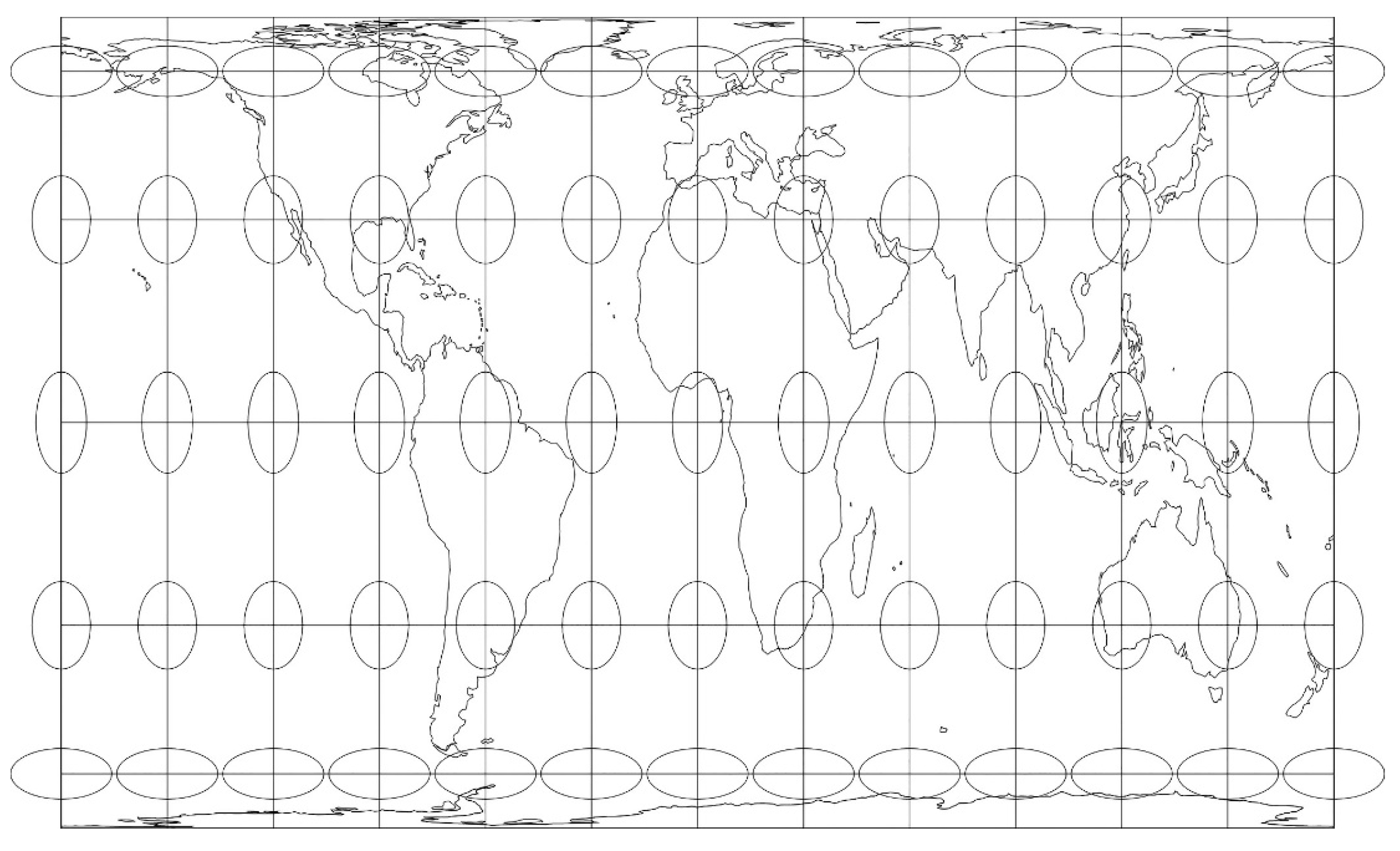
Figure 2.
Gall–Peters map projection with as overlay the Tissot indicatrix.
Figure 3.
Robinson map projection with as overlay the Tissot indicatrix.
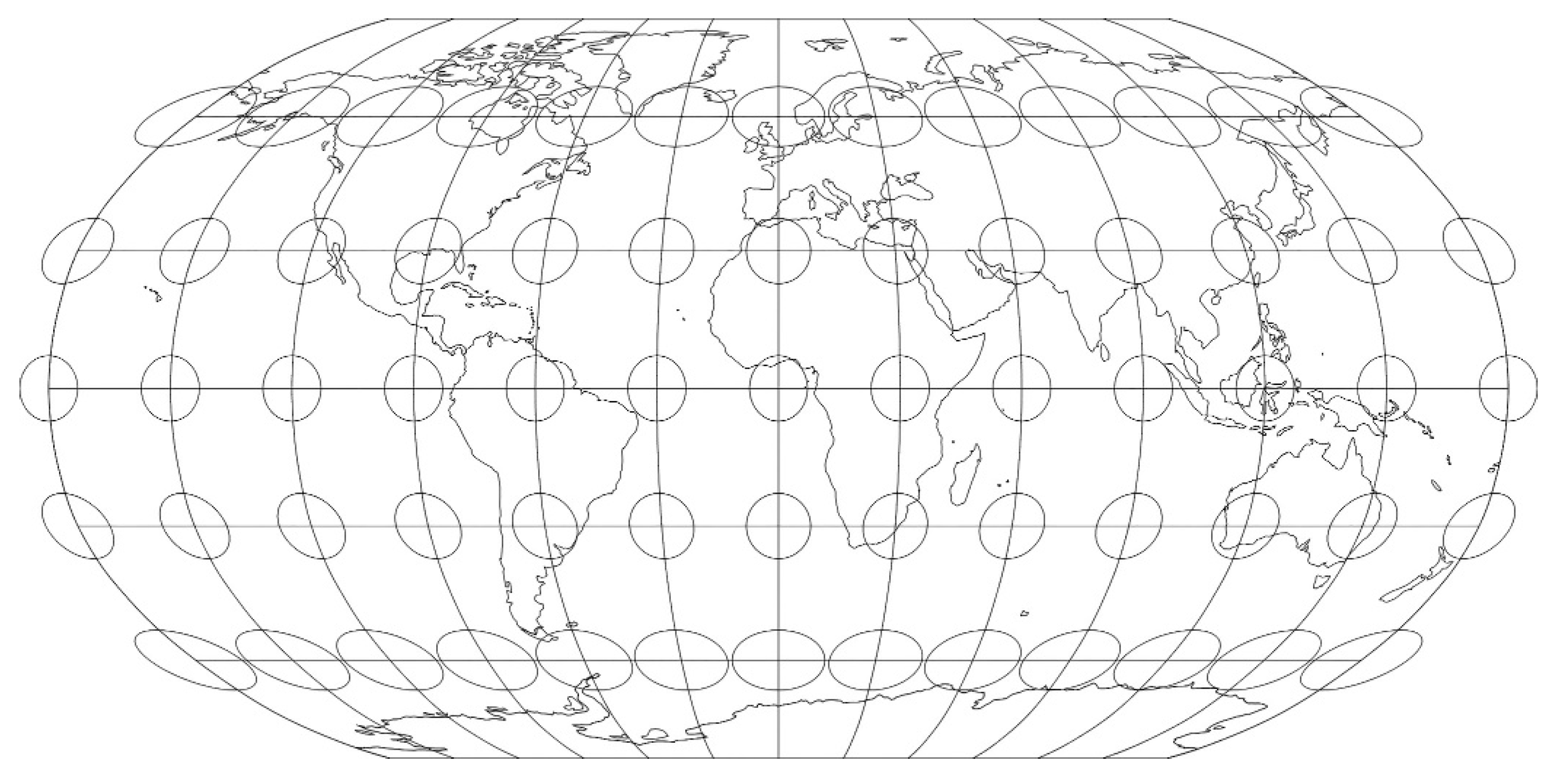
Figure 3.
Robinson map projection with as overlay the Tissot indicatrix.
Figure 4.
An example of the initial interface with as ‘test region 1’ Asia and as ‘test region 2’ Africa. The height of Africa corresponds with the maximum height of the box, while the width of Asia fits in the maximum width of the box.
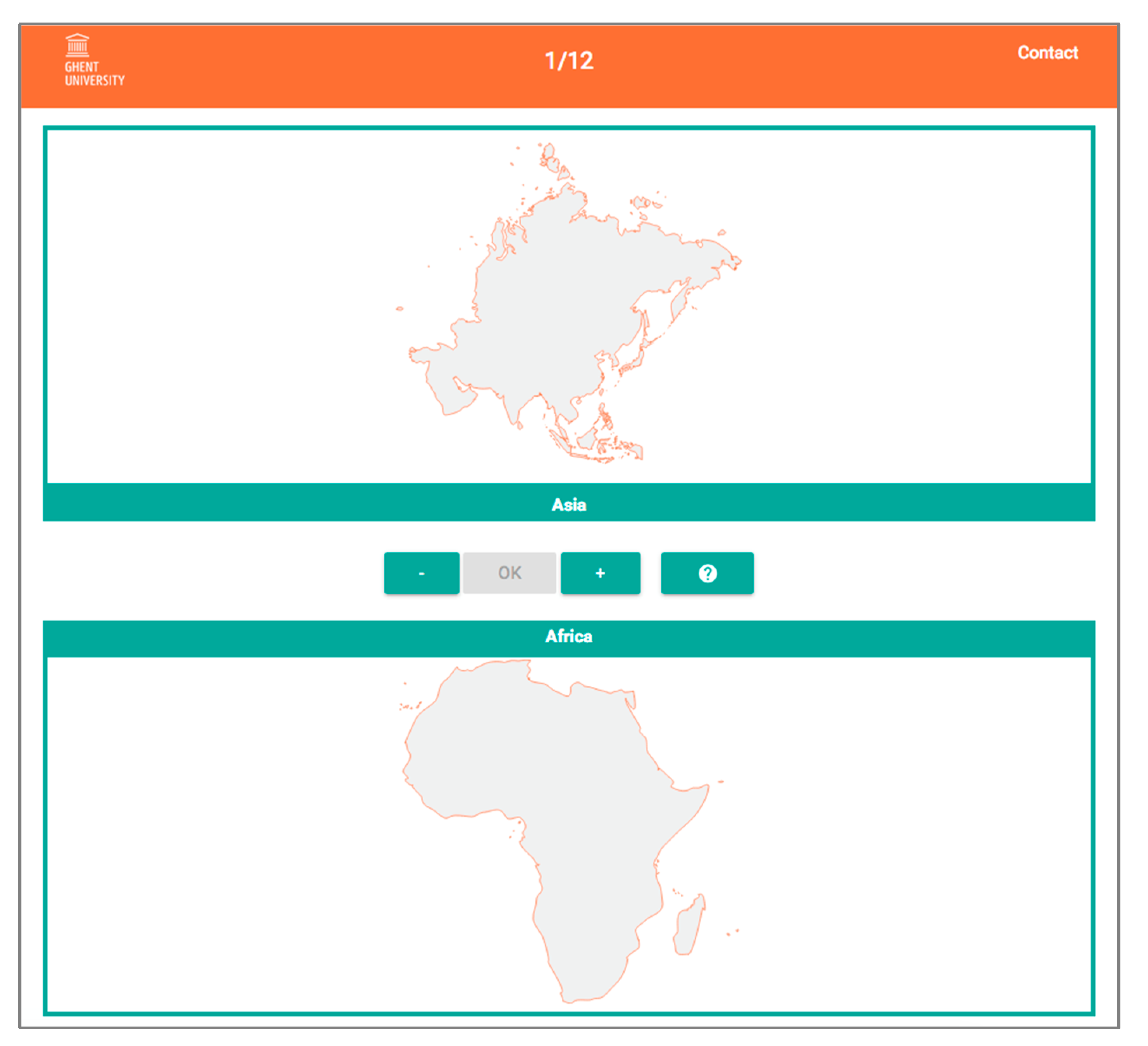
Figure 4.
An example of the initial interface with as ‘test region 1’ Asia and as ‘test region 2’ Africa. The height of Africa corresponds with the maximum height of the box, while the width of Asia fits in the maximum width of the box.
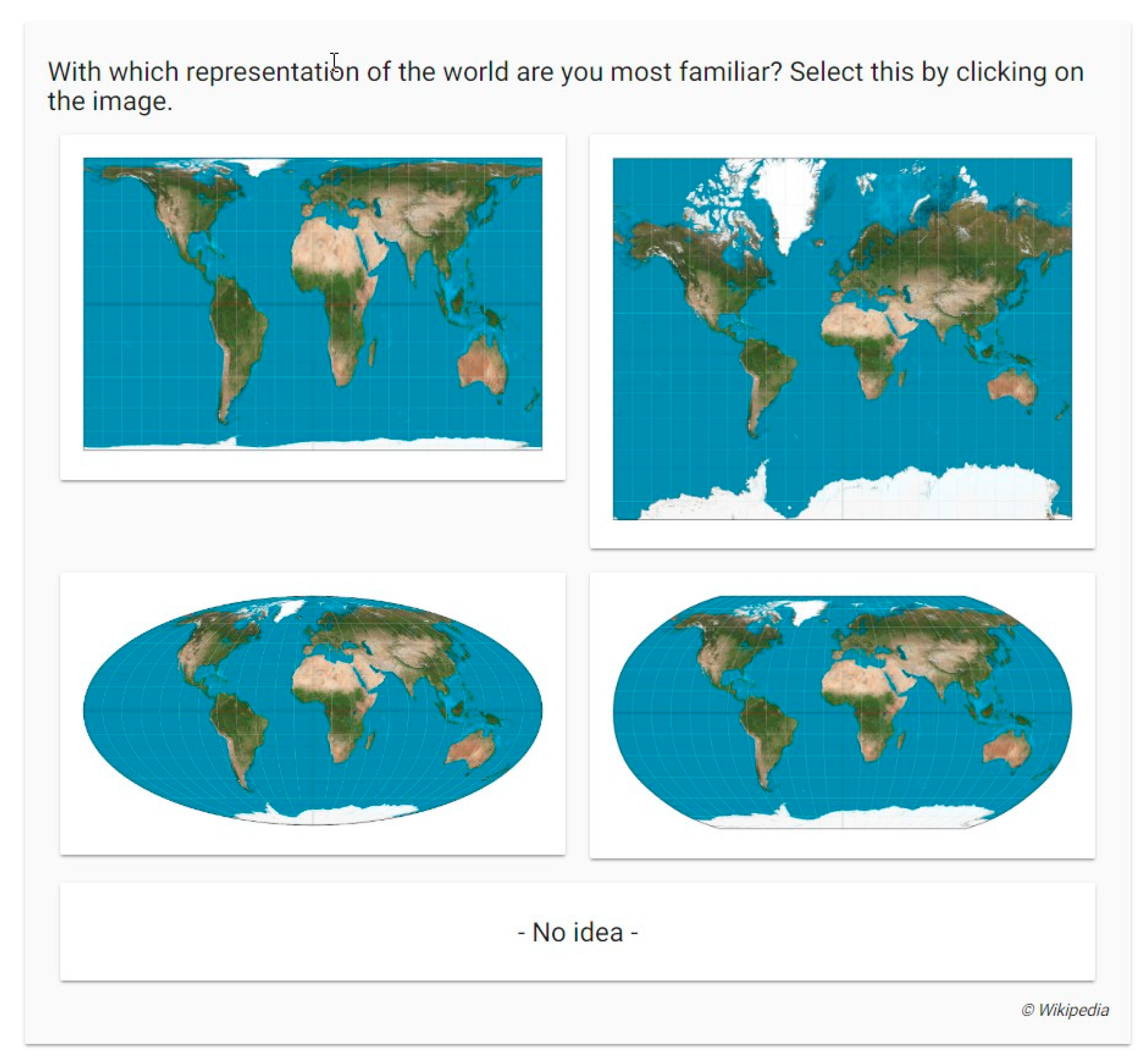
Figure 5.
Question: ‘With which representation of the world are you most familiar?’ and five possible answers: Gall–Peters projection, Mercator projection, Mollweide projection, Robinson projection, or ‘No idea’.
Figure 5.
Question: ‘With which representation of the world are you most familiar?’ and five possible answers: Gall–Peters projection, Mercator projection, Mollweide projection, Robinson projection, or ‘No idea’.
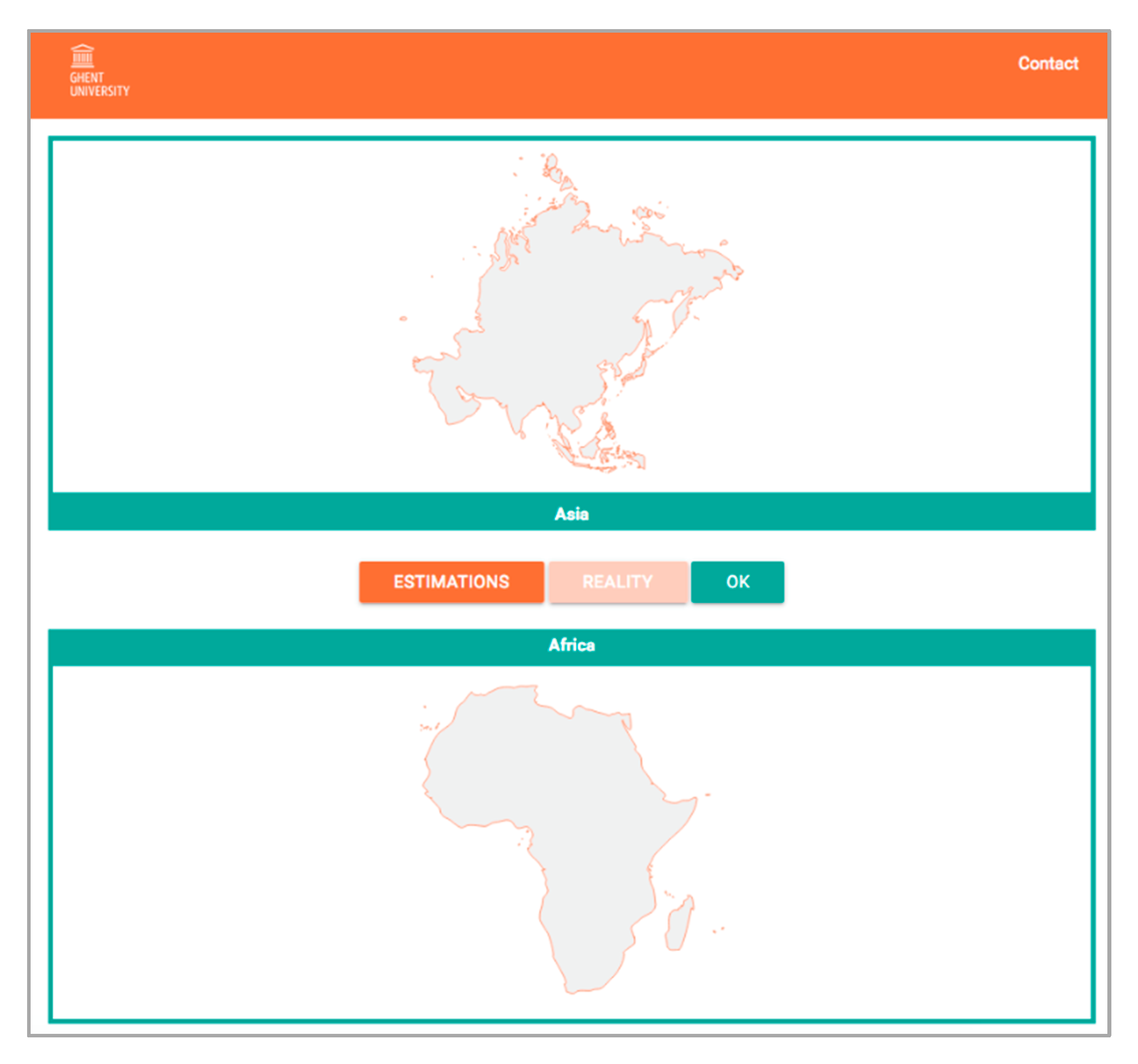
Figure 6.
Feedback-tool demonstrating the estimated (button “ESTIMATIONS”) and real (button “REALITY”) proportions of two test regions.
Figure 6.
Feedback-tool demonstrating the estimated (button “ESTIMATIONS”) and real (button “REALITY”) proportions of two test regions.
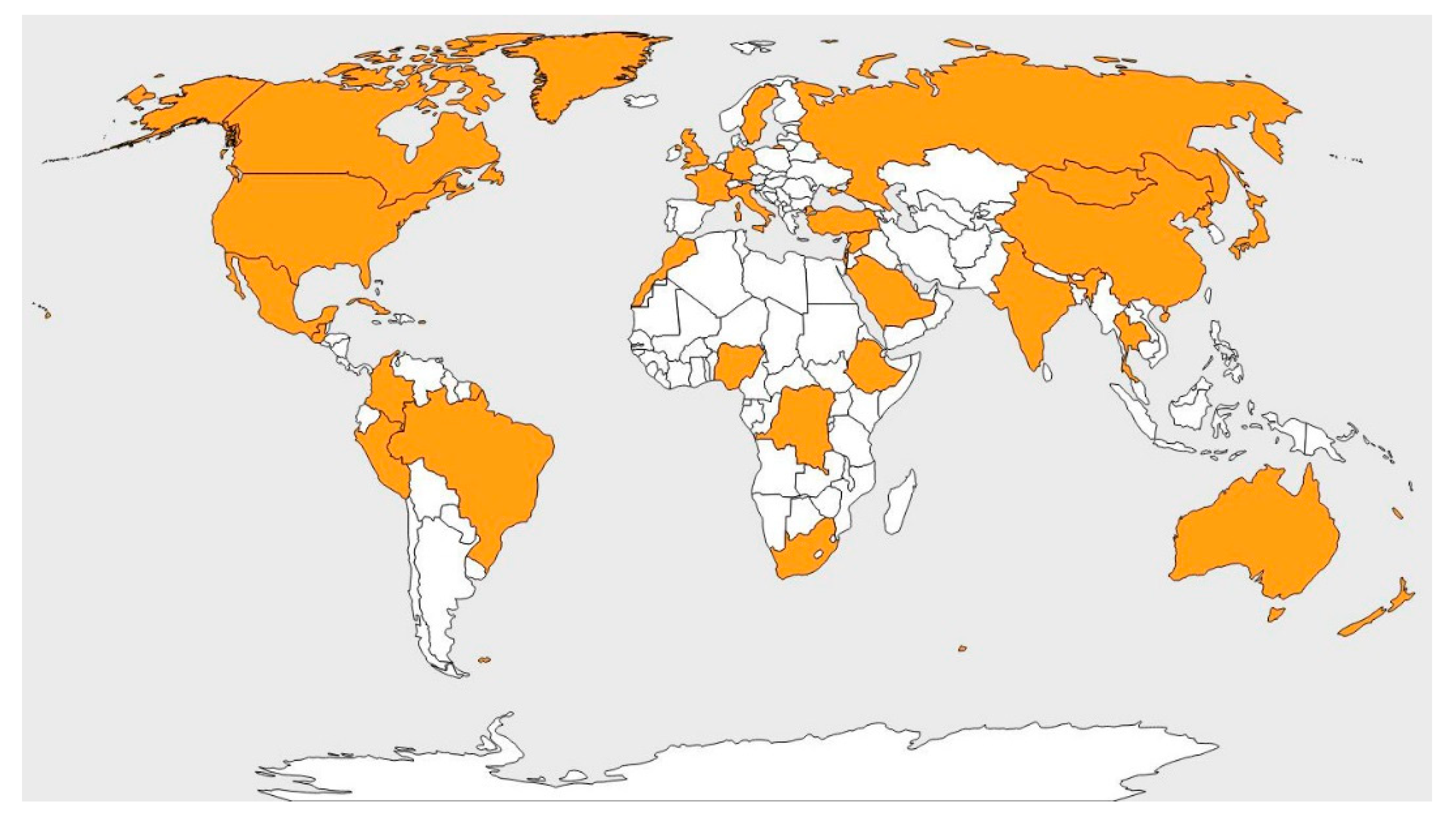
Figure 7.
Selection of the countries or regions as test regions.
Figure 7.
Selection of the countries or regions as test regions.
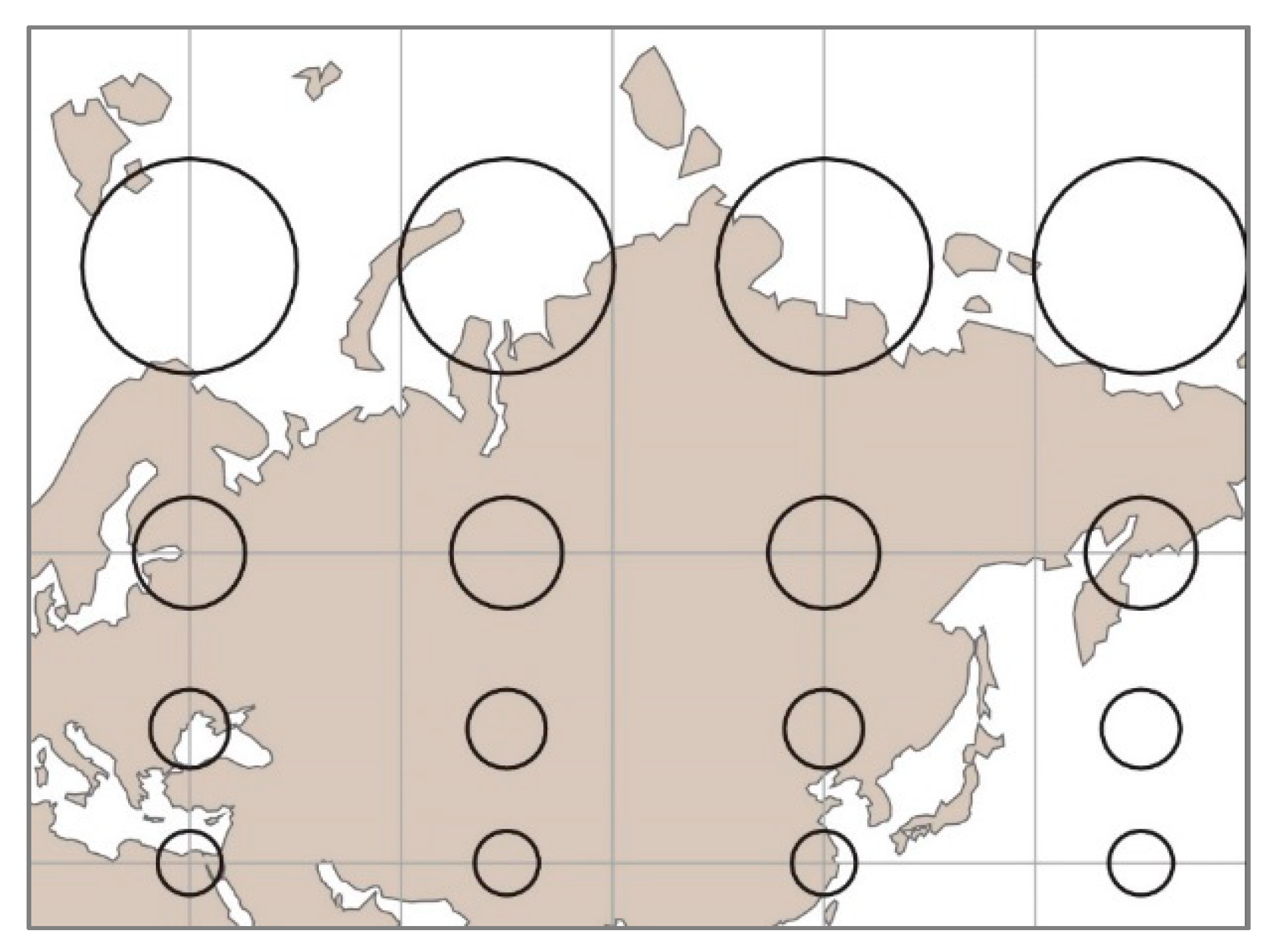
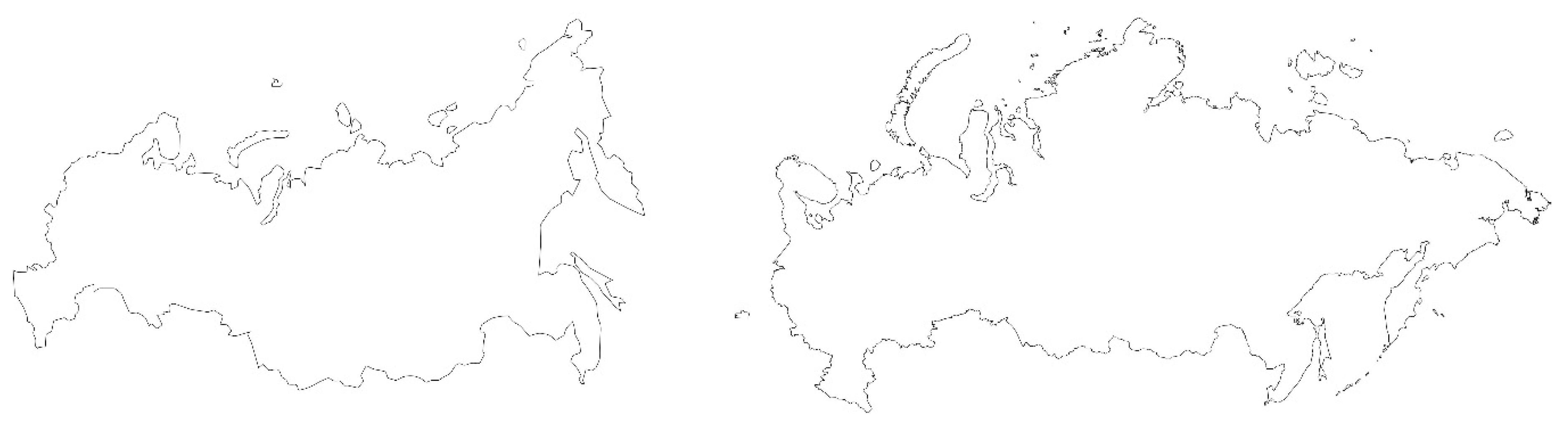
Figure 8.
Russia as on the Mercator projection with Tissot indicatrix.
Figure 8.
Russia as on the Mercator projection with Tissot indicatrix.
Figure 9.
Russia represented with Mercator versus Lambert projection (with standard parallels at 15° N and 65° N).
Figure 9.
Russia represented with Mercator versus Lambert projection (with standard parallels at 15° N and 65° N).
Table 1.
Overview of the 97,082 participants.
Table 1.
Overview of the 97,082 participants.
| Gender | Male | Female | X |
| 68,484 | 26,994 | 1604 |
| 71% | 28% | 2% |
| |
| Age Groups | 12–18 | 19–25 | 26–30 | 31–40 | 41–50 | 51–60 | 61–70 | 70 + |
| 5275 | 20,145 | 17,579 | 28,168 | 14,234 | 7475 | 3400 | 806 |
| 5% | 21% | 18% | 29% | 15% | 8% | 4% | 1% |
| |
| Diploma | None | Primary | Secondary | Higher |
| 475 | 4257 | 14,910 | 77,440 |
| 0.5% | 4% | 15% | 80% |
| |
| | > 20 Participants | > 100 Participants | > 1000 Participants |
| Residency | 76 countries | 55 countries | 15 countries |
| Place of Education | 79 countries | 53 countries | 17 countries |
Table 2.
Selection of pairs of test regions (tr1 and tr2) to analyze the Mercator effect.
Table 2.
Selection of pairs of test regions (tr1 and tr2) to analyze the Mercator effect.
| Tr1 | Latitude | Modulus Area | Tr2 | Latitude | Modulus Area | Mercator Area | Robinson Area | N |
|---|
| Colombia | 4° N | 1000 | Canada | 60° N | 8767 | 42,108 | 13,399 | 18,092 |
| DR Congo | 0° N | 1000 | Greenland | 72° N | 924 | 13,601 | 1806 | 18,173 |
| DR Congo | 0° N | 1000 | Sweden | 62° N | 192 | 867 | 284 | 6069 |
| Ethiopia | 8° N | 1000 | South Africa | 29° S | 1104 | 1461 | 1176 | 5916 |
| Nigeria | 10° N | 1000 | Sweden | 62° N | 487 | 2199 | 720 | 18,154 |
| India | 20° N | 1000 | Russia | 60° N | 5201 | 23,227 | 7655 | 18,486 |
| India | 20° N | 1000 | Canada | 60° N | 3037 | 14,587 | 4647 | 12,148 |
Table 3.
Overview of the Pearson correlation coefficients (cc) between the estimates and the true, Robinson, and Mercator areas.
Table 3.
Overview of the Pearson correlation coefficients (cc) between the estimates and the true, Robinson, and Mercator areas.
| (1) | cc estimates—Modulus | 0.807 * |
| (2) | cc estimates—Mercator | 0.636 * |
| (3) | cc estimates—Robinson | 0.756 * |
| (4) | cc Modulus—Mercator | 0.893 * |
| (5) | cc Modulus—Robinson | 0.964 * |
| (6) | cc Robinson—Mercator | 0.964 * |
Table 4.
Overview of the Pearson correlation coefficients per age group.
Table 4.
Overview of the Pearson correlation coefficients per age group.
| | Estimates—Modulus Area | Estimates—Mercator Area | Estimates—Robinson Area |
|---|
| 12–40 Years Old | 0.806 * | 0.635 * | 0.753 * |
| 41–80 Years Old | 0.808 * | 0.638 * | 0.763 * |
Table 5.
Overview of the Pearson correlation coefficients (cc) between the estimates and the ‘Modulus’, ‘Robinson’, and ‘Mercator areas’ (for the continents).
Table 5.
Overview of the Pearson correlation coefficients (cc) between the estimates and the ‘Modulus’, ‘Robinson’, and ‘Mercator areas’ (for the continents).
| Mercator-Projected Continents (N: 94,447) |
| (1) | cc estimates—Modulus | 0.843 * |
| (2) | cc estimates—Mercator | 0.651 * |
| (3) | cc estimates—Robinson | 0.821 * |
| Gall–Peters-Projected Continents (N: 84,706) |
| (4) | cc estimates—Modulus | 0.826 * |
| (5) | cc estimates—Mercator | 0.688 * |
| (6) | cc estimates—Robinson | 0.805 |
Table 6.
Average relative estimated accuracy (rea) values for countries/regions projected with Mercator or Lambert map projection.
Table 6.
Average relative estimated accuracy (rea) values for countries/regions projected with Mercator or Lambert map projection.
| | N | Average Rea | Significantly Different |
|---|
| Mercator Projected Countries/Regions | 117,004 | 0.29 | at 0.01 level |
| Lambert Conformal Projected Countries/Regions | 13,911 | 1.30 |
Table 7.
Average relative estimated accuracy (rea) values for continents projected with Mercator or Gall–Peters projection.
Table 7.
Average relative estimated accuracy (rea) values for continents projected with Mercator or Gall–Peters projection.
| | N | Average Rea | Significantly Different |
|---|
| Mercator-Projected Continents | 97,391 | 1.16 | at 0.01 level |
| Gall–Peters-Projected Continents | 96,758 | 1.54 |
Table 8.
Average relative estimated accuracy values for each continent (Mercator projection), in positive values are overestimations, negative values are underestimations.
Table 8.
Average relative estimated accuracy values for each continent (Mercator projection), in positive values are overestimations, negative values are underestimations.
| Europe Compared to… | / | 1.65 | 1.01 | 1.43 | 2.05 | 1.49 |
| South America Compared to… | −1.65 | / | −0.26 | −0.52 | 0.06 | −0.60 |
| North America Compared to… | −1.01 | 0.26 | / | −0.33 | 0.18 | −0.11 |
| Africa Compared to… | −1.43 | 0.52 | 0.33 | / | 0.55 | −0.04 |
| Asia Compared to… | −2.05 | −0.06 | −0.18 | −0.55 | / | −0.45 |
| | … Europe | … South America | … North America | … Africa | … Asia | … All |
| Area (km2) | 6,002,353 | 17,747,529 | 24,702,443 | 30,318,411 | 44,783,781 | |
Table 9.
Average relative estimated accuracy values for each continent (Gall–Peters projection), in positive values are overestimations, negative values are underestimations, in grey: more accurate values compared to the Mercator projection (
Table 8).
Table 9.
Average relative estimated accuracy values for each continent (Gall–Peters projection), in positive values are overestimations, negative values are underestimations, in grey: more accurate values compared to the Mercator projection (
Table 8).
| Europe Compared to… | / | 2.58 | 3.31 | 2.46 | 2.12 | 2.62 |
| South America Compared to… | −2.58 | / | 0.68 | −0.28 | −1.75 | −0.61 |
| North America Compared to… | −3.31 | −0.68 | / | −1.06 | −0.92 | −1.28 |
Africa
Compared to… | −2.46 | 0.28 | 1.06 | / | 0.19 | −0.27 |
Asia
Compared to… | −2.12 | 1.75 | 0.92 | −0.19 | / | −0.04 |
| | … Europe | … South America | … North America | … Africa | … Asia | … All |
| Area (km2) | 6,002,353 | 17,747,529 | 24,702,443 | 30,318,411 | 44,783,781 | |
Table 10.
Three reference regions (Japan, South Africa, USA) compared to certain test regions (with area as size of the country in km², latitude, and rea as the average of the relative estimated accuracy values for that particular test region), grey = least accurate estimations, smallest countries, and highest latitude.
Table 10.
Three reference regions (Japan, South Africa, USA) compared to certain test regions (with area as size of the country in km², latitude, and rea as the average of the relative estimated accuracy values for that particular test region), grey = least accurate estimations, smallest countries, and highest latitude.
| Reference Region Japan versus Test Region | Rea | Area of Test Region (km2) | Absolute Latitude of Test Region |
| China | 0.47 | 9,326,410 | 35° |
| United States | −0.65 | 9,147,593 | 38° |
| Saudi Arabia | 1.61 | 2,149,690 | 25° |
| Nigeria | 2.49 | 910,768 | 10° |
| Sweden | 1.71 | 410,335 | 62° |
| Germany | 6.97 | 348,672 | 51° |
| North Korea | 6.77 | 120,480 | 40° |
| Reference Region South Africa versus Test Region … | Rea | Area of Test Region (km2) | Absolute Latitude of Test Region |
| China | −1.96 | 9,326,410 | 35° |
| Australia | −1.42 | 7,682,300 | 27° |
| Peru | −1.67 | 1,279,996 | 10° |
| Ethiopia | −0.18 | 1,096,570 | 8° |
| Colombia | −1.13 | 1,038,700 | 4° |
| Japan | −1.61 | 364,485 | 36° |
| Italy | 0.34 | 294,140 | 42° |
| Reference Region USA versus Test Region … | Rea | Area of Test Region (km2) | Absolute Latitude of Test Region |
| China | 0.23 | 9,326,410 | 35° |
| Mongolia | 1.01 | 1,553,556 | 46° |
| Turkey | 2.14 | 769,632 | 39° |
| Italy | 2.73 | 294,140 | 42° |
| Japan | 0.65 | 364,485 | 36° |
| North Korea | 12.69 | 120,480 | 40° |
| Syria | 12.07 | 185,180 | 35° |
Table 11.
Number of participants (N), the average absolute values of the relative estimated accuracy (ABSrea), and the most familiar map projection per country/region. The data are ranked by ABSrea.
Table 11.
Number of participants (N), the average absolute values of the relative estimated accuracy (ABSrea), and the most familiar map projection per country/region. The data are ranked by ABSrea.
| | N | ABSrea | Continent | Percentages per Map Projection | Most Familiar Map Projection |
|---|
| Robinson | Mercator | Gall-Peters | Mollweide | Robinson ** | Mercator ** |
|---|
| Switzerland | 32 | 1.80 | Europe | 59.4 | 21.9 | 15.6 | 3.1 | X | |
| Hungary | 48 | 1.97 | Europe | 41.7 | 41.7 | 10.4 | 6.3 | | |
| Canada | 284 | 2.02 | N America | 46.1 | 41.5 | 6.3 | 6.0 | X | |
| Austria | 37 | 2.04 | Europe | 37.8 | 43.2 | 10.8 | 8.1 | | X |
| China | 41 | 2.05 | Asia | 48.8 | 39.0 | 7.3 | 4.9 | X | |
| United States | 1311 | 2.06 | N America | 49.3 | 36.9 | 6.5 | 5.0 | X | |
| Hong Kong | 28 | 2.07 | Asia | 50.0 | 28.6 | 10.7 | 10.7 | X | |
| Colombia | 45 | 2.07 | S America | 37.8 | 24.4 | 24.4 | 13.3 | X | |
| New Zealand | 27 | 2.11 | Oceania | 44.4 | 33.3 | 14.8 | 3.7 | X | |
| Finland | 36 | 2.12 | Europe | 55.6 | 36.1 | 2.8 | 2.8 | X | |
| Germany | 182 | 2.12 | Europe | 45.1 | 38.5 | 11.5 | 3.8 | X | |
| Group 1 * | 91% | 18% |
| Chili | 35 | 2.15 | Asia | 37.1 | 25.7 | 22.9 | 11.4 | X | |
| Indonesia | 20 | 2.24 | Asia | 30.0 | 50.0 | 20.0 | | | X |
| Rumania | 37 | 2.24 | Europe | 37.7 | 37.9 | 10.8 | 10.8 | | X |
| Great Britain | 536 | 2.25 | Europe | 35.1 | 47.9 | 7.5 | 8.2 | | X |
| Sweden | 86 | 2.34 | Europe | 31.4 | 53.4 | 10.5 | | | X |
| Brazil | 424 | 2.38 | S America | 52.1 | 26.2 | 13.0 | 7.1 | X | |
| Japan | 34 | 2.38 | Asia | 26.5 | 41.2 | 11.8 | 11.8 | | X |
| Italy | 235 | 2.39 | Europe | 43.0 | 33.6 | 13.2 | 8.9 | X | |
| Poland | 1425 | 2.42 | Europe | 52.8 | 18.2 | 20.6 | 6.9 | X | |
| Spain | 199 | 2.43 | Europe | 29.7 | 51.2 | 7.5 | 10.6 | | X |
| Denmark | 30 | 2.47 | Europe | 33.3 | 46.7 | 16.7 | 3.3 | | X |
| France | 445 | 2.49 | Europe | 36.4 | 33.5 | 19.1 | 10.3 | X | |
| Turkey | 88 | 2.52 | Asia | 35.2 | 34.1 | 14.8 | | X | |
| Group 2 * | >42% | >58% |
| Ireland | 40 | 2.66 | Europe | 42.5 | 35.0 | 15.0 | | X | |
| Taiwan | 113 | 2.68 | Asia | 57.5 | 27.4 | 7.1 | 2.7 | X | |
| The Netherlands | 1336 | 2.76 | Europe | 37.6 | 43.2 | 8.4 | 8.7 | | X |
| Greece | 42 | 2.77 | Europe | 42.9 | 21.4 | 16.7 | 16.7 | X | |
| Mexico | 77 | 2.77 | M America | 29.9 | 45.5 | 14.3 | 9.1 | | X |
| Czech Republic | 61 | 2.80 | Europe | 34.4 | 49.2 | 9.8 | 6.6 | | X |
| Portugal | 69 | 2.83 | Europe | 40.6 | 40.6 | 5.8 | | | |
| Saudi Arabia | 55 | 2.87 | Asia | 38.2 | 45.5 | 9.1 | | | X |
| Russia | 80 | 2.90 | Asia | 33.8 | 48.8 | 7.5 | 6.3 | | X |
| Malaysia | 31 | 2.90 | Asia | 41.9 | 29.0 | 16.1 | | X | |
| Belgium | 1407 | 2.92 | Europe | 39.2 | 41.1 | 11.3 | 7.0 | | X |
| Group 3 * | >45% | >64% |
| Argentina | 44 | 3.27 | S America | 22.8 | 63.6 | 2.3 | 6.8 | | X |
| Australia | 134 | 3.38 | Oceania | 42.5 | 42.5 | 6.7 | 7.5 | | |
| Morocco | 70 | 3.43 | Africa | 27.1 | 32.9 | 20.0 | 15.7 | | X |
| Norway | 50 | 3.54 | Europe | 28.0 | 52.0 | 12.0 | 6.0 | | X |
| India | 57 | 3.55 | Asia | 22.8 | 43.8 | 14.1 | | | X |
| Israel | 27 | 3.56 | Asia | 44.4 | 44.4 | 3.7 | | | |
| Bulgaria | 23 | 3.83 | Europe | 21.7 | 34.8 | 34.8 | 8.7 | | X |
| Jamaica | 28 | 4.23 | M America | 50.0 | 10.7 | 10.7 | | X | |
| Group 4 * | 13% | 63% |